A Nonlinear Fractional BEM Model for Magneto-Thermo-Visco-Elastic Ultrasound Waves in Temperature-Dependent FGA Rotating Granular Plates

Abstract

The primary goal of this study is to create a nonlinear fractional boundary element method (BEM) model for magneto-thermo-visco-elastic ultrasound wave problems in temperature-dependent functionally graded anisotropic (FGA) rotating granular plates in a constant primary magnetic field. Classical analytical methods are frequently insufficient to solve the governing equation system of such problems due to nonlinearity, fractional order heat conduction, and strong anisotropy of mechanical properties. To address this challenge, a BEM-based coupling scheme that is both reliable and efficient was proposed, with the Cartesian transformation method (CTM) used to compute domain integrals and the generalized modified shift-splitting (GMSS) method was used to solve the BEM-derived linear systems. The calculation results are graphed to show the effects of temperature dependence, anisotropy, graded parameter, and fractional parameter on nonlinear thermal stress in the investigated plates. The numerical results validate the consistency and effectiveness of the developed modeling methodology.

1. Introduction

Functionally graded materials (FGMs) are new composite materials with material properties that vary spatially continuously. This variation in material properties is achieved through gradient variation in the relative volume fraction of the material constituents within the solid. The fundamental benefit of FGMs over laminated composite materials is the seamless and smooth change in material properties over the length or depth of the structure, in contrast, the material properties of the laminated composite are discontinuous, resulting in a sharp shift in the mechanical properties between layers, which can cause delamination and cracks [1]. Functionally graded material (FGM) was first discussed in Japan in 1984, during a space aircraft project in which the materials used had to be able to withstand high-temperature gradients. FGMs have a wide range of engineering applications, including heat shields for spaceships, rocking-motor casings, critical engine parts, and the pharmaceutical industry [2]. Majak et al. [3] focused on the approximation of grading functions of FGM. The latter higher order function approximation technique is extended for modeling grading functions of FGM using the higher order Haar wavelet method (HOHWM). As a result, the generalized algorithm can be used to solve governing equations for various grading functions (exponential, power law, four-parameter functions, etc.). The second order derivatives of the grading functions are expanded into Haar wavelets, providing fourth order convergence with respect to mesh. Many researchers have recently developed different dual phase lag thermo-elastic models [4,5,6,7,8].

The theory [9] and applications [10,11,12] of calculus of any noninteger order are dealt with in fractional order calculus (FOC). Robotics, applied mathematics, food engineering, polymers, economics, finance, econophysics, mathematical biology, bioheat models, physics, chemistry, biomedicine, optimization, chaos theory, electro-hydraulic systems, quantum mechanics, continuum mechanics, fluid mechanics, signal and image processing, nanotechnology, and other applications have made FOC very popular.

For plate problems, the boundary element method (BEM) has emerged as a viable numerical solution. Wang and Huang [13] were the first to model orthotropic thick plates using the BEM. There has been a lot of interest in meshless approaches to continuum mechanics problems [14]. For such plates, meshless approaches with continuous stress approximation are more practical [15]. Krysl and Belytschko [16] used the element-free Galerkin approach to solve plate problems for the first time. Although their results demonstrated excellent convergence, their formulation is not applicable to shear deformable plate problems. Fahmy [17] investigated three-temperature distributions in carbon nanotube fiber-reinforced plates with inclusions using the BEM.

In general, finding an analytical solution to a problem is extremely difficult. As a result, several engineering papers devoted to numerical methods have investigated such problems in various thermo-elasticity topics, such as thermo-elastic metal and alloy discs [18], high-energy dissipation visco-elastic dampers [19], nonlocal thermo-elasticity [20], and micropolar magneto-thermo-visco-elasticity [21]. Several papers, however, have used the boundary element method in general to solve problems such as temperature-dependent composites [22], smart semiconductors [23], and circular cylindrical shells [24]. The meshless local Petrov–Galerkin (MLPG) method [25] has also been successfully applied to plate problems [26,27,28].

In the present paper, a new nonlinear fractional BEM-based coupling strategy is proposed employing the generalized modified shift-splitting (GMSS) method and the Cartesian transformation method (CTM) to solve magneto-thermo-visco-elastic ultrasound wave problems in temperature-dependent FGA rotating granular plates. The calculated results are graphed to demonstrate the effects of temperature dependence, anisotropy, graded parameter, and fractional parameter on nonlinear thermal stress in the investigated plates. The numerical results demonstrate the proposed modeling methodology’s dependability and efficiency.

2. Formulation of the Problem

The governing equations of magneto-thermo-visco-elastic ultrasonic wave propagation problems for temperature-dependent functionally graded anisotropic (FGA) rotating granular structures can be expressed as in Fahmy [29] as follows:

$${\sigma }_{pj,j}+{\tau }_{pj,j}+{\Gamma }_{pj}-\rho {\omega }^2{x}_p=\rho {\left(x+1\right)}^m{\ddot{u}}_p$$

(1)

$${\sigma }_{pj}={\left(x+1\right)}^m\left[C_{pjkl}\aleph u_{k,l}-{\beta }_{pj}T\left(x,y,\tau \right)\right]$$

(2)

$${\tau }_{pj}=\mu {\left(x+1\right)}^m\left({\tilde{h}}_p{H}_j+{\tilde{h}}_j{H}_p-{\delta }_{jp}\left({\tilde{h}}_k{H}_k\right)\right), h_p={\left(\nabla \times \left(u\times H\right)\right)}_p$$

(3)

$${\Gamma }_{pj}=-\rho {\left(x+1\right)}^{m}g\frac{\partial u_k}{\partial x_p}$$

(4)

The fractional temperature-dependent heat conduction equation can be written as

$$D_{\tau }^{a}T\left(x,\tau \right)=\xi \nabla \left[\lambda \left(T\right)\nabla \mathrm{T}\left(x, \tau \right)\right]+\xi Q\left(x, T, \tau \right), \xi =\frac{1}{\rho \left(T\right)c\left(T\right)}$$

(5)

where

$$Q\left(x, T, \tau \right)=\overline{Q}\left(x, T, \tau \right)+\frac{1-R}{x_0}{e}^{\left(-\frac{x_a}{x_0}\right)J\left(\tau \right)}, J\left(t\right)=\frac{J_0 \tau }{{\tau }_1^2}{e}^{-\frac{\tau }{{\tau }_1}}, a=1, 2, 3$$

(6)

For the present problem, it is assumed that the initial/boundary conditions are expressed as

$$u_k\left(x,0\right)={\dot{u}}_k\left(x,0\right)=0 \mathrm{for} x\in R{{\displaystyle \cup }}^{ }C$$

(7)

$$u_k\left(x,\tau \right)={\Psi }_{\mathrm{k}}\left(x,\mathsf{\tau }\right) \mathrm{for} x\in C_3$$

(8)

$$t_k\left(x,\tau \right)={\delta }_k\left(x,\tau \right) \mathrm{for} x\in C_4, \tau >0, C=C_3{{\displaystyle \cup }}^{ }{C}_4, C_3{{\displaystyle \cap }}^{ }{C}_4=\varnothing$$

(9)

$$T\left(x\right)=f\left(x\right) \mathrm{for} x\in R{{\displaystyle \cup }}^{ }C$$

(10)

$$T\left(x,\tau \right)=P\left(x,\tau \right) \mathrm{for} x\in C_1, \tau >0$$

(11)

$$q\left(x,\tau \right)=\overline{h}\left(x,\tau \right) \mathrm{for} x\in C_2, \tau >0, C=C_1{{\displaystyle \cup }}^{ }{C}_2, C_1{{\displaystyle \cap }}^{ }{C}_2=\varnothing$$

(12)

A comma followed by a subscript denotes partial differentiation with respect to the corresponding coordinates, while a superposed dot denotes differentiation with respect to time.

Based on Caputo’s scheme, the following formula can be written [30,31]:

$$D_{\tau }^a{T}^{f+1}+D_{\tau }^a{T}^f\approx {\displaystyle \sum }_{J=0}^k{W}_{a,J}\left(T^{f+1-J}\left(x\right)-T^{f-J}\left(x\right)\right)$$

(13)

where

$$W_{a,0}=\frac{{\left(\Delta \tau \right)}^{-a}}{\Gamma \left(2-a\right)} \mathrm{and} W_{a,J}=W_{a,0}\left({\left(J+1\right)}^{1-a}-{\left(J-1\right)}^{1-a}\right)$$

(14)

By applying Equations (5) and (13), the following formula can be made:

$$\begin{gathered} W_{a,0}{T}^{f+1}\left(x\right)-\lambda \left(x, T\right)T_{,ii}^{f+1}\left(x\right)-{\lambda }_{,i}\left(x, T\right)T_{,i}^{f+1}\left(x\right)=W_{a,0}{T}^f\left(x\right)-\lambda \left(x\right)T_{,ii}^f \left(x\right) \\ -{\lambda }_{,i}\left(x, T\right)T_{,j}^f \left(x\right)-{\displaystyle \sum }_{J=1}^f{W}_{a,J}\left(T^{f+1-J}\left(x\right)-T^{f-J}\left(x\right)\right)+h_m^{f+1}\left(x, T, \tau \right) \\ +h_m^f\left(x, T, \tau \right) \end{gathered}$$

(15)

3. BEM Solution of Temperature-Dependent Heat Conduction Equation

Based on the implementation of the following Kirchhoff conversion [32]:

$$\Theta ={{\displaystyle \int }}_{T_0}^T\frac{\lambda \left(\overline{T}\right)}{{\lambda }_0}d\overline{T}$$

(16)

Equation (5) can be written as

$${\nabla }^2\Theta \left(x,\mathsf{\tau }\right)+\frac{1}{{\lambda }_0}h\left(x,\Theta , \tau \right)=\frac{\rho (\Theta ) c(\Theta )}{\lambda (\Theta )}\frac{\partial \Theta \left(x,\tau \right)}{\partial \mathsf{\tau }}$$

(17)

The right-hand side of (17) can be deconstructed as follows:

$${\nabla }^2\Theta \left(x,\mathsf{\tau }\right)+\frac{1}{{\lambda }_0}h\left(x,\Theta ,\mathsf{\tau }\right)=\frac{{\rho }_0 c_0}{{\lambda }_0}\frac{\partial \Theta \left(x,\mathsf{\tau }\right)}{\partial \mathsf{\tau }}+Nl\left(x,\Theta , \dot{\Theta }\right)$$

(18)

where

$$Nl\left(x,\Theta , \dot{\Theta }\right)=\left[\frac{\rho (\Theta ) c(\Theta )}{\lambda (\Theta )}-\frac{{\rho }_0 c_0}{{\lambda }_0}\right] \dot{\Theta }$$

(19)

Equation (18) can be written as

$${\nabla }^2\Theta \left(x,\mathsf{\tau }\right)+\frac{1}{{\lambda }_0}{h}_{Nl}\left(x,\Theta , \dot{\Theta }, \mathsf{\tau }\right)=\frac{{\rho }_0 c_0}{{\lambda }_0}\frac{\partial \Theta \left(x,\mathsf{\tau }\right)}{\partial \mathsf{\tau }}$$

(20)

In which

$$h_{Nl}\left(x,\Theta , \dot{\Theta }, \mathsf{\tau }\right)=h\left(x,\Theta , \mathsf{\tau }\right)+\left[{\rho }_0 c_0-\frac{{\lambda }_0}{\lambda (\Theta )}\rho (\Theta ) c(\Theta )\right] \dot{\Theta }$$

(21)

The integral equation corresponding to (20) can be expressed using the fundamental solution of (15) as [33]

$$\begin{gathered} C\left(P\right)\Theta \left(P,{\overline{\tau }}_{n+1}\right)+a_0{{\displaystyle \int }}_{\Gamma }^{}{{\displaystyle \int }}_{{\overline{\tau }}_n}^{{\overline{\tau }}_{n+1}}\Theta \left(\mathrm{Q}, \mathsf{\tau }\right)q^{\ast }\left(P,{\overline{\tau }}_{n+1};Q,\mathsf{\tau }\right)d\mathsf{\tau } \mathrm{d}\Gamma \\ =a_0{{\displaystyle \int }}_{\Gamma }^{}{{\displaystyle \int }}_{{\overline{\tau }}_n}^{{\overline{\tau }}_{n+1}}q\left(\mathrm{Q}, \mathsf{\tau }\right){\Theta }^{\ast }\left(P,{\overline{\tau }}_{n+1};Q,\mathsf{\tau }\right)d\mathsf{\tau } \mathrm{d}\Gamma \\ +\frac{a_0}{{\lambda }_0}{{\displaystyle \int }}_{\Omega }^{}{{\displaystyle \int }}_{{\overline{\tau }}_n}^{{\overline{\tau }}_{n+1}}{h}_{Nl}\left(\mathrm{Q}, \Theta , \dot{\Theta }, \mathsf{\tau }\right){\Theta }^{\ast }\left(P,{\overline{\tau }}_{n+1};Q,\mathsf{\tau }\right)d\mathsf{\tau } \mathrm{d}\Omega \\ +{{\displaystyle \int }}_{\Omega }^{}\Theta \left(\mathrm{Q}, {\overline{\tau }}_n\right){\Theta }^{\ast }\left(P,{\overline{\tau }}_{n+1};Q,\mathsf{\tau }\right)\mathrm{d}\Omega , a_0=\frac{{\lambda }_0}{{\rho }_0{c}_0} \end{gathered}$$

(22)

The fundamental solution and its derivative can be expressed as

$${\Theta }^{\ast }\left(P,{\overline{\tau }}_{n+1};Q,\mathsf{\tau }\right)=\frac{1}{4\pi a_0\left(\overline{\tau }-\tau \right)}exp\left[\frac{-r^2}{4a_0\left(\overline{\tau }-\tau \right)}\right]H\left(\overline{\tau }-\tau \right)$$

(23)

$${\mathrm{q}}^{\ast }\left(P,\overline{\tau };Q,\mathsf{\tau }\right)=\frac{\partial }{\partial n}{\Theta }^{\ast }\left(P,\overline{\tau };Q,\mathsf{\tau }\right)=\frac{-r}{8\pi a_0{}^2{\left(\overline{\tau }-\tau \right)}^2}exp\left[\frac{-r^2}{4a_0\left(\overline{\tau }-\tau \right)}\right]H\left(\overline{\tau }-\tau \right)\frac{\partial r}{\partial n}$$

(24)

The time integrals for (23) and (24), respectively, can be expressed as

$${{\displaystyle \int }}_{t_n}^{t_{n+1}}{\Theta }^{\ast }\left(P,{\overline{\tau }}_{n+1};Q,\mathsf{\tau }\right)d\mathsf{\tau }=\frac{1}{4\pi a_0}\mathrm{Ei}\left(\frac{r^2}{4a_0\Delta \overline{\tau }}\right)$$

(25)

$${{\displaystyle \int }}_{t_n}^{t_{n+1}}{\mathrm{q}}^{\ast }\left(P,{\overline{\tau }}_{n+1};Q,\mathsf{\tau }\right)d\mathsf{\tau }=\frac{-1}{2\pi a_{0}r}\exp \left(\frac{-r^2}{4a_0\Delta \overline{\tau }}\right)\frac{\partial r}{\partial n}$$

(26)

In which

$$\mathrm{Ei}\left(\alpha \right)={{\displaystyle \int }}_{\alpha }^{\infty }\frac{\exp \left(-x\right)}{x}dx$$

(27)

Consider the following domain integral in Equation (22):

$$I_{Nl}=\frac{a_0}{{\lambda }_0}{{\displaystyle \int }}_{\Omega }^{}{{\displaystyle \int }}_{{\overline{\tau }}_n}^{{\overline{\tau }}_{n+1}}{h}_{Nl}\left(\mathrm{Q}, \Theta , \dot{\Theta }, \mathsf{\tau }\right){\Theta }^{\ast }\left(P,{\overline{\tau }}_{n+1};Q,\mathsf{\tau }\right)d\mathsf{\tau } \mathrm{d}\Omega$$

(28)

which can be stated as

$$I_{Nl}=\frac{a_0}{{\lambda }_0}{{\displaystyle \int }}_{\Omega }^{}{{\displaystyle \int }}_{{\overline{\tau }}_n}^{{\overline{\tau }}_{n+1}}\left\{h\left(\mathrm{Q}, \Theta , \mathsf{\tau }\right)+\left[{\rho }_0{c}_0-\frac{{\lambda }_0}{\lambda (\Theta )}\rho (\Theta ) c(\Theta )\right] \dot{\Theta }\right\}{\Theta }^{\ast }\left(P,{\overline{\tau }}_{n+1};Q,\mathsf{\tau }\right)d\mathsf{\tau } \mathrm{d}\Omega$$

(29)

Thus, the following equation can be written:

$$I_{Nl}=\frac{1}{4\pi {\lambda }_0}{{\displaystyle \int }}_{\Omega }^{}{h}_{Nl}\left(Q, {\Theta }_{n+\left(1/2\right)}, { \dot{\Theta }}_{n+\left(1/2\right)}, {\overline{\tau }}_{n+\left(1/2\right)}\right)\mathrm{Ei}\left(\frac{r^2}{4a_0\Delta \overline{\tau }}\right)\mathrm{d}\Omega$$

(30)

where

$$\begin{gathered} h_{Nl}\left(Q, {\Theta }_{n+\left(1/2\right)}, {\overline{\tau }}_{n+\left(1/2\right)}\right)=h\left(Q, {\Theta }_{n+\left(1/2\right)}, {\overline{\tau }}_{n+\left(1/2\right)}\right) \\ +\left[{\rho }_0{c}_0-\frac{{\lambda }_0}{\lambda \left({\Theta }_{n+\left(1/2\right)}\right)}\rho \left({\Theta }_{n+\left(1/2\right)}\right)c\left({\Theta }_{n+\left(1/2\right)}\right)\right]{ \dot{\Theta }}_{n+\left(1/2\right)} \end{gathered}$$

(31)

Then,

$${\Theta }_{n+\left(1/2\right)}=\frac{{\Theta }_n+{\Theta }_{n+1}}{2}, {\overline{\tau }}_{n+\left(1/2\right)}=\frac{{\overline{\tau }}_n+{\overline{\tau }}_{n+1}}{2}, { \dot{\Theta }}_{n+\left(1/2\right)}=\frac{{\Theta }_{n+1}-{\Theta }_n}{\Delta \overline{\tau }}$$

By replacing $\Theta \left(\mathrm{P},{\overline{\tau }}_{n+1}\right) \mathrm{with} 2\Theta \left(\mathrm{P},{\overline{\tau }}_{n+\left(1/2\right)}\right)-\Theta \left(\mathrm{P},{\overline{\tau }}_n\right)$ in Equation (31), we obtain

$$\begin{gathered} 2C\left(P\right)\Theta \left(\mathrm{P},{\overline{\tau }}_{n+\left(1/2\right)}\right)-\frac{1}{2\pi }{{\displaystyle \int }}_{\Gamma }^{}\frac{\Theta \left(Q, {\overline{\tau }}_{n+\left(1/2\right)}\right)}{r}exp\left[\frac{-r^2}{4a_0\Delta \overline{\tau }}\right]\frac{\partial r}{\partial n} \mathrm{d}\Gamma \\ =\frac{1}{4\pi }{{\displaystyle \int }}_{\Gamma }^{}\mathrm{q}\left(Q, {\overline{\tau }}_{n+\left(1/2\right)}\right) \mathrm{Ei}\left(\frac{r^2}{4a_0\Delta \overline{\tau }}\right)\mathrm{d}\Gamma \\ +\frac{1}{4\pi {\lambda }_0}{{\displaystyle \int }}_{\Omega }^{}{h}_{Nl}\left(Q, {\Theta }_{n+\left(1/2\right)}, { \dot{\Theta }}_{n+\left(1/2\right)}, {\overline{\tau }}_{n+\left(1/2\right)}\right)\mathrm{Ei}\left(\frac{r^2}{4a_0\Delta \overline{\tau }}\right)\mathrm{d}\Omega \\ +\frac{1}{4\pi a_0\Delta \overline{\tau }}{{\displaystyle \int }}_{\Omega }^{} \Theta \left(\mathrm{Q}, {\overline{\tau }}_n\right)\exp \left(\frac{-r^2}{4a_0\Delta \overline{\tau }}\right)\mathrm{d}\Omega +C\left(P\right)\Theta \left(\mathrm{P}, {\overline{\tau }}_n\right) \end{gathered}$$

(32)

Now, by using CTM [34,35,36,37], the domain integrals in Equation (32) can be calculated as in Appendix A and Appendix B.

The following equations can be used to compute the unknown boundary and internal values:

$$H{\Theta }^{\Gamma }=G{Q}^{\Gamma }+F+F_{Nl}$$

(33)

$${\Theta }^{\Omega }=\widehat{G}{Q}^{\Gamma }-\widehat{H}{\Theta }^{\Gamma }+\widehat{F}+{\widehat{F}}_{Nl}$$

(34)

As a result, we can express

$$𝕒{\rm X}=𝕓$$

(35)

In which $𝕒$ denotes an unknown matrix, and $𝕓$ and $\Delta$ denote well-known matrices.

4. BEM Solution of Displacement Field

Making use of (2), (3), and (4), we can write (1) as follows:

$$\begin{gathered} L_{pk}{u}_k=\rho {\ddot{u}}_p-\left(\left(D_{pk}+\Lambda D_{p1k}-\rho g\hslash \right)u_k+D_{p}T-\rho {\omega }^2{x}_p\right)= \\ \rho {\ddot{u}}_p-\rho b_p=\rho b_p^{\prime } \end{gathered}$$

(36)

where $L_{pk}=D_{pjk}\frac{\partial }{\partial x_j}$, $D_{pjk}=C_{pjkl}\aleph \frac{\partial }{\partial x_l}, D_{pk}=\mu H_0^2\left(\frac{\partial }{\partial x_p}+{\mathsf{\delta }}_{p1}\Lambda \right)\frac{\partial }{\partial x_k}$, $D_p=-{\beta }_{pj}\left(\frac{\partial }{\partial x_j}+{\mathsf{\delta }}_{\mathrm{j}1}\Lambda \right), \hslash =\frac{\partial }{\partial x_p}, \Lambda =\frac{m}{x+1}.$

The representation formula of (36) can be expressed as in Fahmy [29] as

$$u_m\left(\xi \right)={{\displaystyle \int }}_{\mathrm{C}}^{}\left(u_{mp}^{\ast }\left(x,\xi \right)t_p\left(x\right)-t_{mp}^{\ast }\left(x,\xi \right)u_p\left(x\right)\right)d\mathrm{C}-{{\displaystyle \int }}_{\mathrm{R}}^{}{u}_{mp}^{\ast }\left(x,\xi \right)\rho b_p^{\prime }\left(x\right)d\mathrm{R}$$

(37)

Let

$$\rho b_p^{\prime }=\rho {\ddot{u}}_p-\left(\left(D_{pk}+\Lambda D_{p1k}-\rho g\hslash \right)u_k+D_{p}T-\rho {\omega }^2{x}_p\right)\approx {\displaystyle \sum }_{\mathrm{q}=1}^{\mathrm{N}}{f}_{pn}^q{\mathsf{\alpha }}_n^q={\displaystyle \sum }_{\mathrm{q}=1}^{\mathrm{N}}\left(L_{pk}{u}_{kn}^q\right){\mathsf{\alpha }}_n^q$$

(38)

We proceed in the same way as Fahmy [30] to obtain the following representation formula:

$$u_m\left(\xi \right)={{\displaystyle \int }}_{\mathrm{C}}^{}\left(u_{mp}^{\ast }{t}_p-t_{mp}^{\ast }{u}_p\right)d\mathrm{C}+{\displaystyle \sum }_{q=1}^N\left(u_{mn}^q\left(\xi \right)-{{\displaystyle \int }}_{\mathrm{C}}^{}\left(u_{mp}^{\ast }{t}_{pn}^q-t_{mp}^{\ast }{u}_{pn}^q\right)d\mathrm{C}\right){\mathsf{\alpha }}_{\mathrm{n}}^{\mathrm{q}}$$

(39)

The approximate values of the unknowable field variables $\left\{u, t\right\}$ and solutions $\left\{u^q, t^q\right\}$ can be written as

$$\left\{u, t\right\}\approx {\displaystyle \sum }_{k=1}^N{\phi }_k\left\{{\check{u}}_k, {\check{t}}_k\right\}={\mathsf{\Phi }}^T\left\{\check{u}, \check{t}\right\}, \left\{u^q, t^q\right\}\approx {\displaystyle \sum }_{k=1}^N{\phi }_k\left\{{\check{u}}_k^q, {\check{t}}_k^q\right\}={\mathsf{\Phi }}^T\left\{{\check{u}}^q, {\check{t}}^q\right\}$$

(40)

where $\check{u}, \check{t}$, and $\mathsf{\Phi }$ are matrices.

Based on these approximations, the representation formula (39) can be expressed as

$$\zeta \check{u}-\eta \check{t}={\displaystyle \sum }_{q=1}^N\left(\zeta {\check{u}}^q-\eta {\check{t}}^q\right){\alpha }^q\left(\tau \right)$$

(41)

By letting

$$\check{U}=\left[{\check{u}}^1 {\check{u}}^2\dots {\check{u}}^N\right], \check{\Re }=\left[{\check{t}}^1 {\check{t}}^2\dots {\check{t}}^N\right], \alpha ={\left[{\alpha }^1 {\alpha }^2\dots {\alpha }^N\right]}^T$$

(42)

Equation (41) can be expressed as follows

$$\zeta \check{u}\left(\tau \right)-\eta \check{t}\left(\tau \right)=\left(\zeta \check{U}-\eta \check{\Re }\right)\alpha \left(\tau \right)$$

(43)

Using the point collocation approach, Equation (38), produces

$$\rho \check{\ddot{u}}\left(\tau \right)-\rho \check{b}\left(\tau \right)=F\alpha \left(\tau \right)$$

(44)

Now, Equation (44) can be expressed as

$$\alpha \left(\tau \right)=F^{-1}\left(\rho \check{\ddot{u}}\left(\tau \right)-\rho \check{b}\left(\tau \right)\right)$$

(45)

Substitution of (45) into (43) yields the system

$$ℳ\check{\ddot{u}}+\zeta \check{u}=\eta \check{t}\left(\tau \right)+\check{ℬ}\left(\tau \right)$$

(46)

where

$$\mho =\left(\eta \check{\Re }-\zeta \check{U}\right)F^{-1}, ℳ=\rho \mho , \check{ℬ}\left(\tau \right)=\rho \mho \check{b}\left(\tau \right).$$

(47)

Now, we suppose the following:

$$\left\{{\check{u}}^k, {\check{t}}^u\right\}\in {\mathrm{C}}_3, \left\{{\check{u}}^u, {\check{t}}^k\right\}\in {\mathrm{C}}_4$$

(48)

where $k$ and $u$ are known and unknown parts, respectively.

The system (46) can be written as

$$\left[\begin{array}{cc}{ℳ}^{11}& {ℳ}^{12}\\ {ℳ}^{21}& {ℳ}^{22}\end{array}\right]\left[\begin{array}{c}{\check{\ddot{u}}}^k\left(\tau \right)\\ {\check{\ddot{u}}}^u\left(\tau \right) \end{array}\right]+\left[\begin{array}{cc}{\zeta }^{11}& {\zeta }^{12}\\ {\zeta }^{21}& {\zeta }^{22}\end{array}\right]\left[\begin{array}{c}{\check{u}}^k\left(\tau \right)\\ {\check{u}}^u\left(\tau \right)\end{array}\right]=\left[\begin{array}{cc}{\eta }^{11}& {\eta }^{12}\\ {\eta }^{21}& {\eta }^{22}\end{array}\right]\left[\begin{array}{c}{\check{t}}^k\left(\tau \right)\\ {\check{t}}^u\left(\tau \right)\end{array}\right]+\left[\begin{array}{c}{\check{ℬ}}^1\left(\tau \right)\\ {\check{ℬ}}^2\left(\tau \right)\end{array}\right]$$

(49)

The unknown fluxes ${\check{t}}^u\left(\tau \right)$ can now be derived from (49) as

$${\check{t}}^u\left(\tau \right)={\left({\eta }^{12}\right)}^{-1}\left[{ℳ}^{11}{\check{\ddot{u}}}^k\left(\tau \right)+{ℳ}^{12}{\check{\ddot{u}}}^u\left(\tau \right)+{\zeta }^{11}{\check{u}}^k\left(\tau \right)+{\zeta }^{12}{\check{u}}^u\left(\tau \right)-{\eta }^{11}{\check{t}}^k\left(\tau \right)-{\check{ℬ}}^1\left(\tau \right)\right]$$

(50)

From Equations (49) and (50), we have

$${ℳ}^u{\check{\ddot{u}}}^u\left(\tau \right)+{\zeta }^u{\check{u}}^u\left(\tau \right)=Q^k\left(\tau \right)$$

(51)

In which

$$Q^k\left(\tau \right)={\check{ℬ}}^k\left(\tau \right)+{\eta }^k{\check{t}}^k\left(\tau \right)-{ℳ}^k{\check{\ddot{u}}}^k\left(\tau \right)-{\zeta }^k{\check{u}}^k\left(\tau \right), {\check{ℬ}}^k\left(\tau \right)={ℬ}^2\left(\tau \right)-{\eta }^{22}{\left({\eta }^{12}\right)}^{-1}{ℬ}^1\left(\tau \right),$$

$${ℳ}^u={ℳ}^{22}-{\eta }^{22}{\left({\eta }^{12}\right)}^{-1}{ℳ}^{12}, {\zeta }^u={\zeta }^{22}-{\eta }^{22}{\left({\eta }^{12}\right)}^{-1}{\zeta }^{12}$$

$${ℳ}^k={ℳ}^{21}-{\eta }^{22}{\left({\eta }^{12}\right)}^{-1}{ℳ}^{11}, {\zeta }^k={\zeta }^{21}-{\eta }^{22}{\left({\eta }^{12}\right)}^{-1}{\zeta }^{11}$$

At time step $n+1$, Equation (51) can be expressed as

$${ℳ}^u{\check{\ddot{u}}}_{n+1}^u\left(\tau \right)+{\zeta }^u{\check{u}}_{n+1}^u\left(\tau \right)=Q_{n+1}^k\left(\tau \right)$$

(52)

where

$$Q_{n+1}^k\left(\tau \right)={\check{ℬ}}_{n+1}^k\left(\tau \right)+{\eta }^k{\check{t}}_{n+1}^k\left(\tau \right)-{ℳ}^k{\check{\ddot{u}}}_{n+1}^k\left(\tau \right)-{\zeta }^k{\check{u}}_{n+1}^k\left(\tau \right)$$

Now, to reduce the ordinary differential equations system (52) to an algebraic system, Houbolt’s algorithm is implemented using the following implicit backward finite difference scheme:

$${\check{\dot{u}}}_{n+1}\approx \frac{1}{6\Delta \overline{\tau }}\left(11{\check{u}}_{n+1}-18{\check{u}}_n+9{\check{u}}_{n-1}-2{\check{u}}_{n-2}\right)$$

(53)

$${\check{\ddot{u}}}_{n+1}\approx \frac{1}{\Delta {\overline{\tau }}^2}\left(2{\check{u}}_{n+1}-5{\check{u}}_n+4{\check{u}}_{n-1}-{\check{u}}_{n-2}\right)$$

(54)

Substituting (53) and (54) into (52), we have

$${\varsigma }^u{\check{u}}_{n+1}^u\left(\tau \right)={\mathbb{Q}}_{n+1}^k\left(\tau \right)$$

(55)

where

$${\varsigma }^u=\frac{2{ℳ}^u}{\Delta {\overline{\tau }}^2}+{\zeta }^u, {\mathbb{Q}}_{n+1}^k=Q_{n+1}^k+\frac{{ℳ}^u}{\Delta {\overline{\tau }}^2}\left(5{\check{u}}_n-4{\check{u}}_{n-1}+{\check{u}}_{n-2}\right)$$

Our method is described by the following algorithm:

(I)

To resolve the system (55), we use successive over-relaxation (SOR), as outlined in Golub and Van Loan [38].

(II)

The values of ${\check{u}}_{n+1}^u$ are determined for each time step $n+1$.

(III)

The values ${\check{u}}_{n+1}^u$ can then be used to calculate the unknowns ${\check{\dot{u}}}_{n+1}^u$ and ${\check{\ddot{u}}}_{n+1}^u$ from (53) and (54), respectively.

(IV)

The method given in Bathe [39] is utilized along with the initial conditions for the scenario where $n=0$ to calculate $u_{-1}$ and $u_{-2}$.

(V)

The traction vector $t_{n+1}^u$ is then calculated using (50).

The semi-implicit predictor–corrector coupling algorithm of Breuer et al. [40] that was based on the generalized modified shift-splitting (GMSS) of Huang et al. [41] has been applied to solve the resulting linear Equations (35) and (55) arising from the BEM, where magneto-thermo-visco-elastic coupling is considered instead of fluid–structure interaction coupling of Breuer et al. [40].

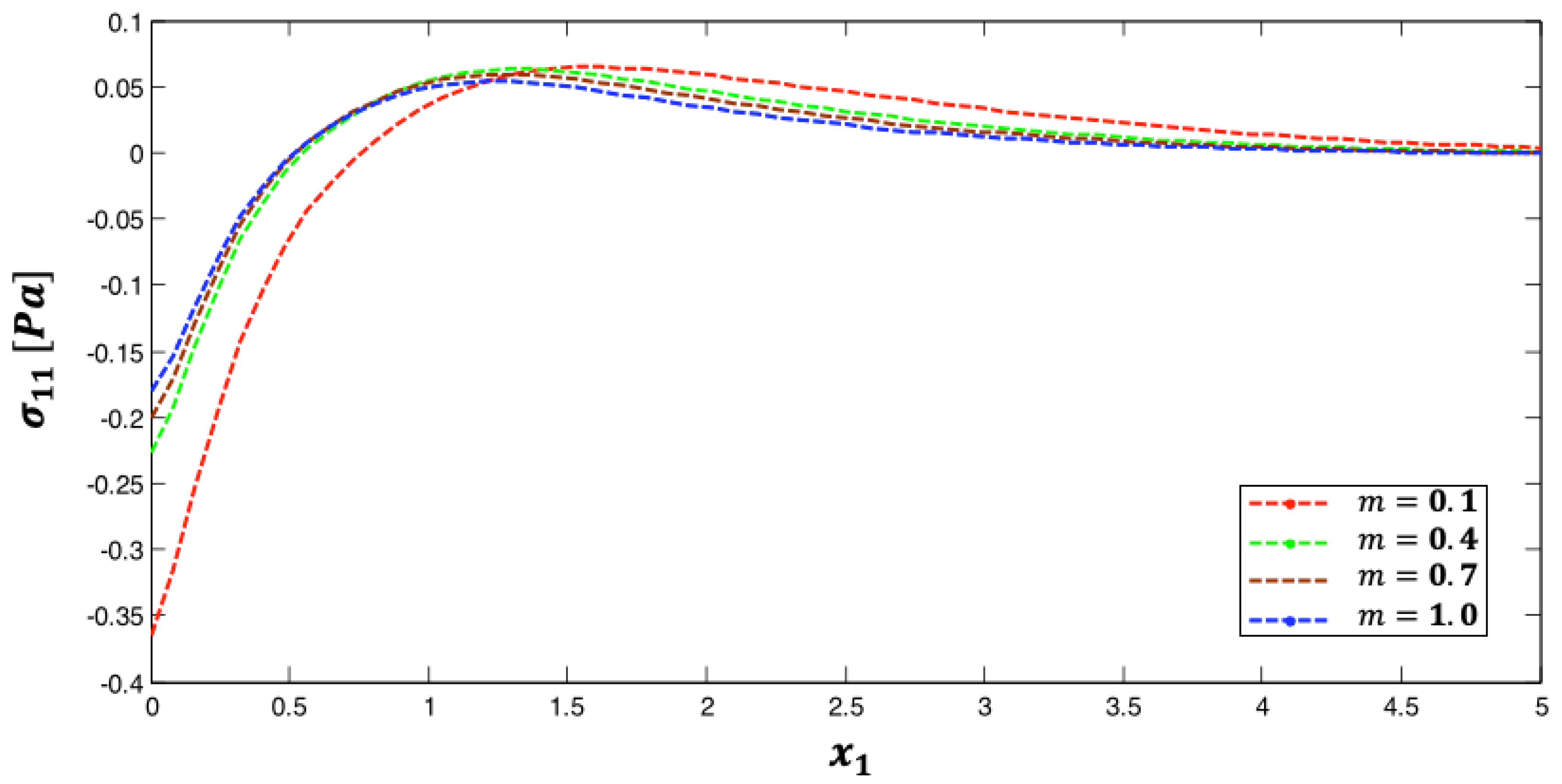
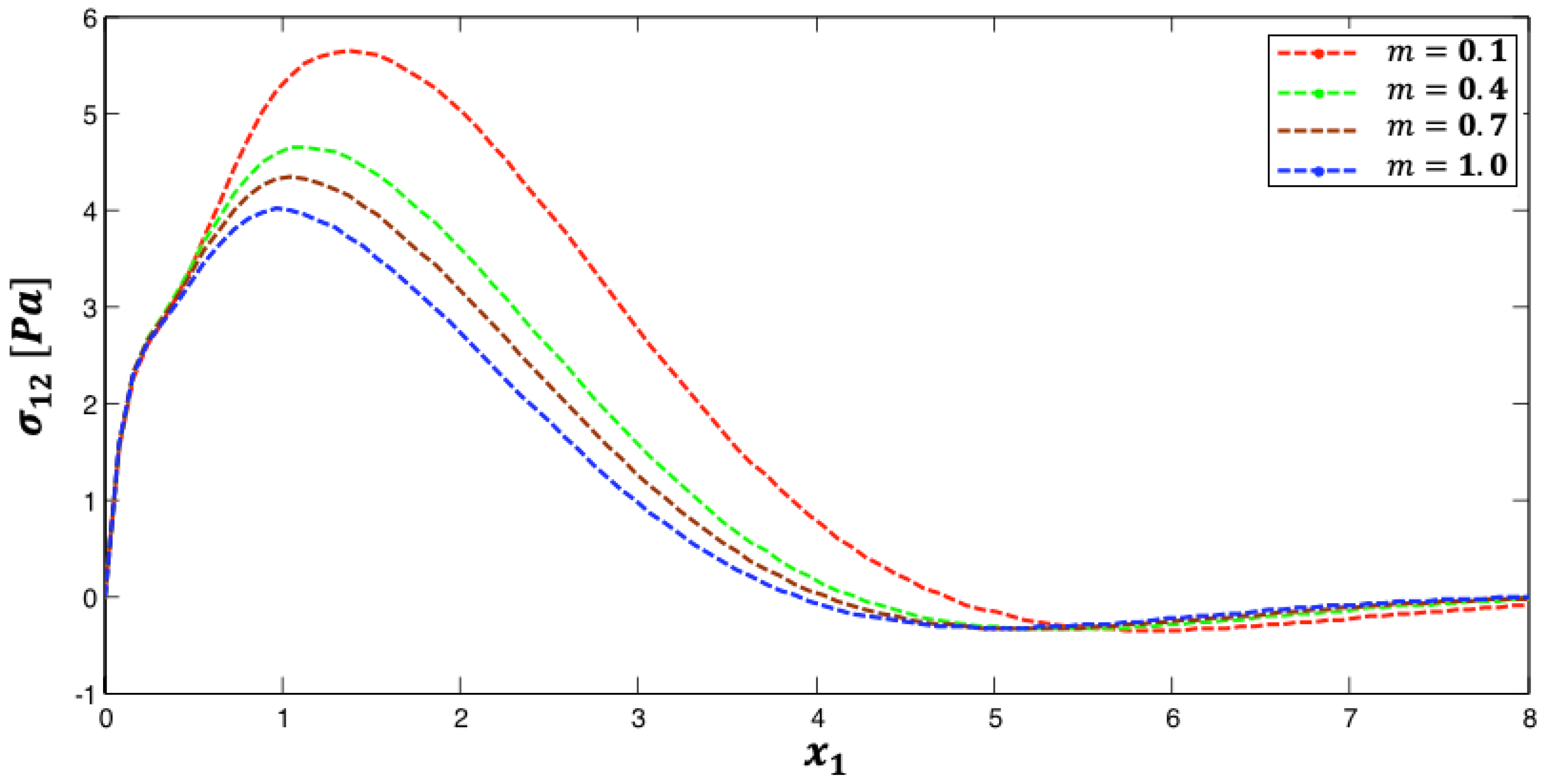
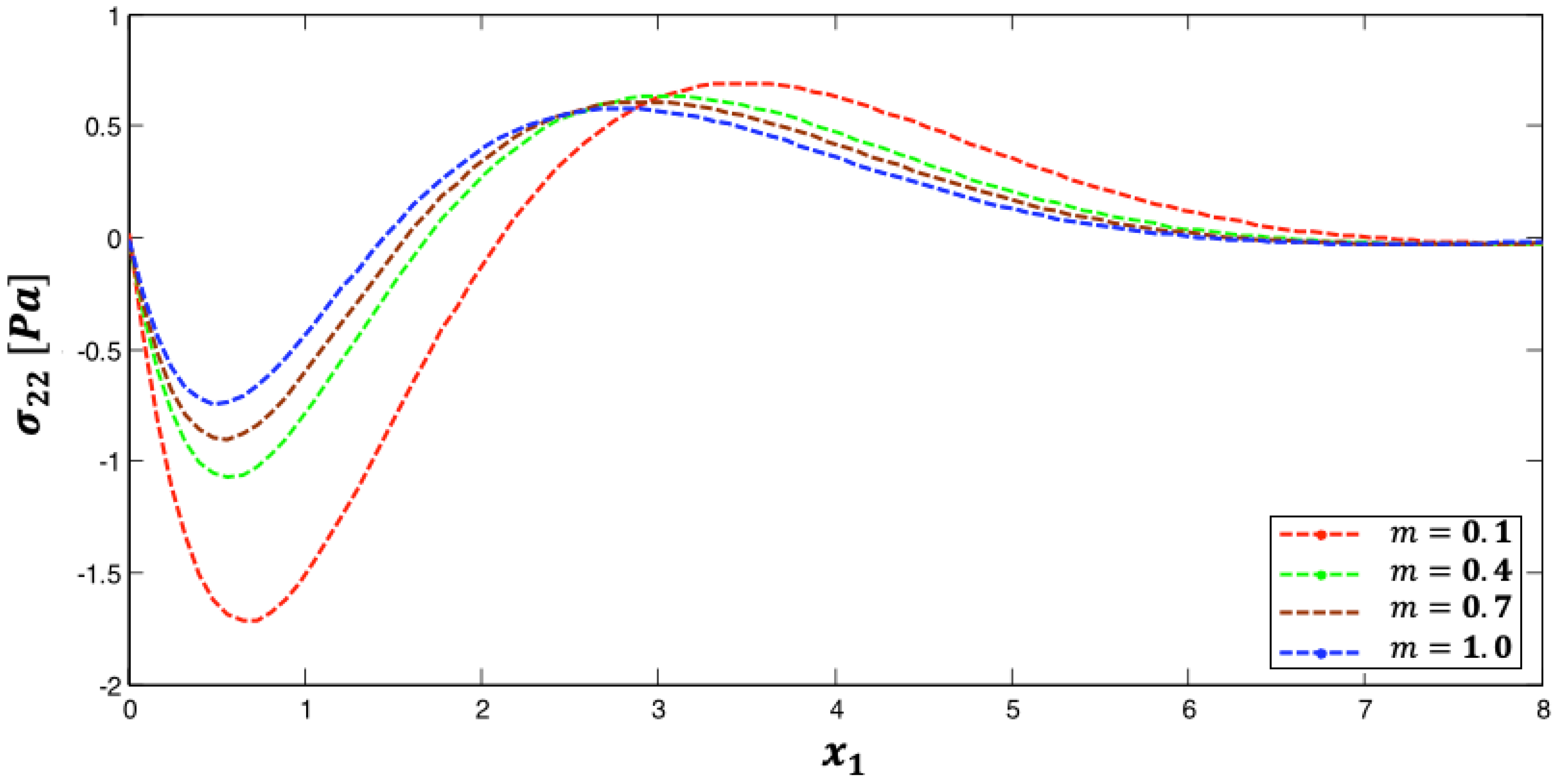
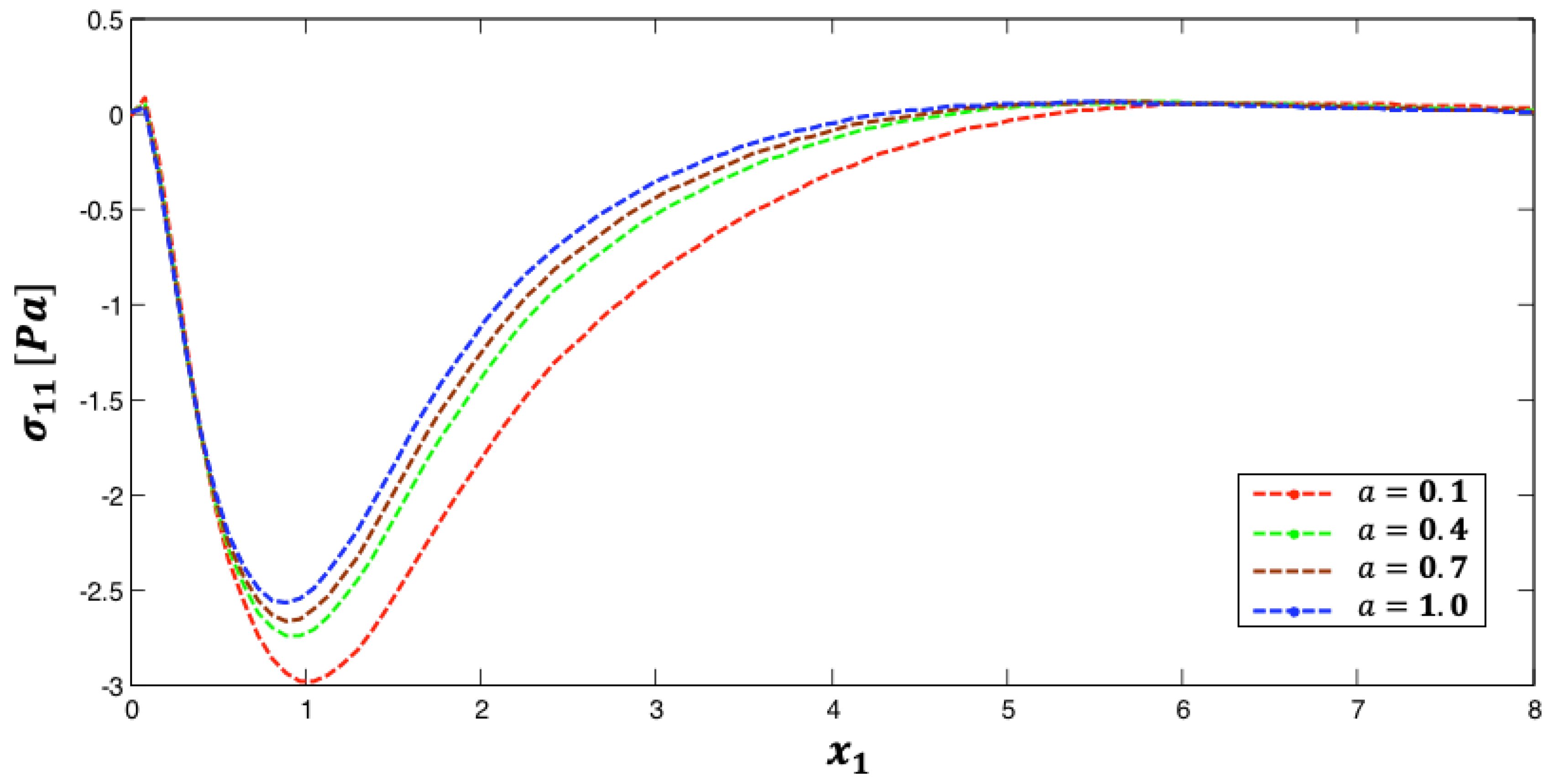
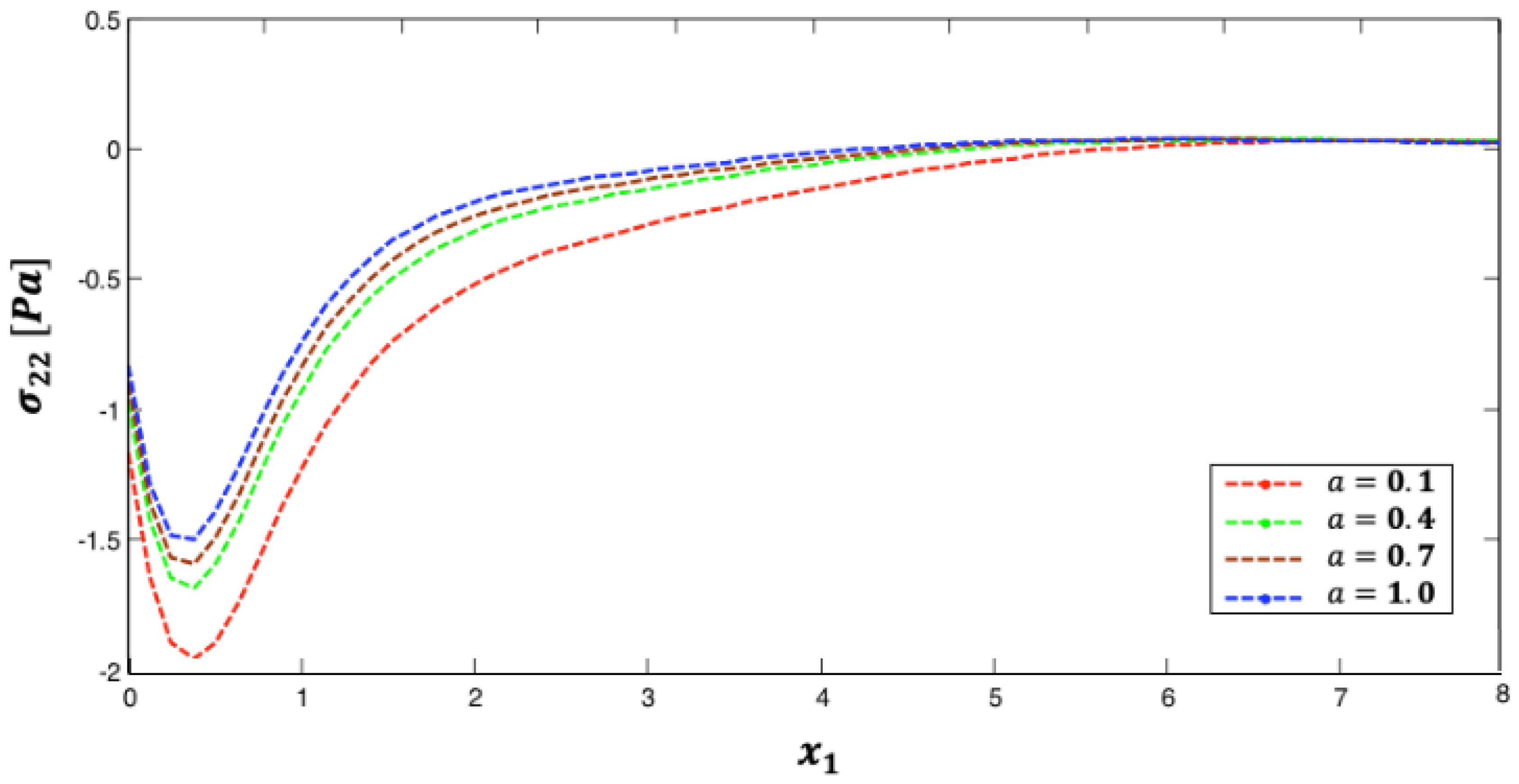
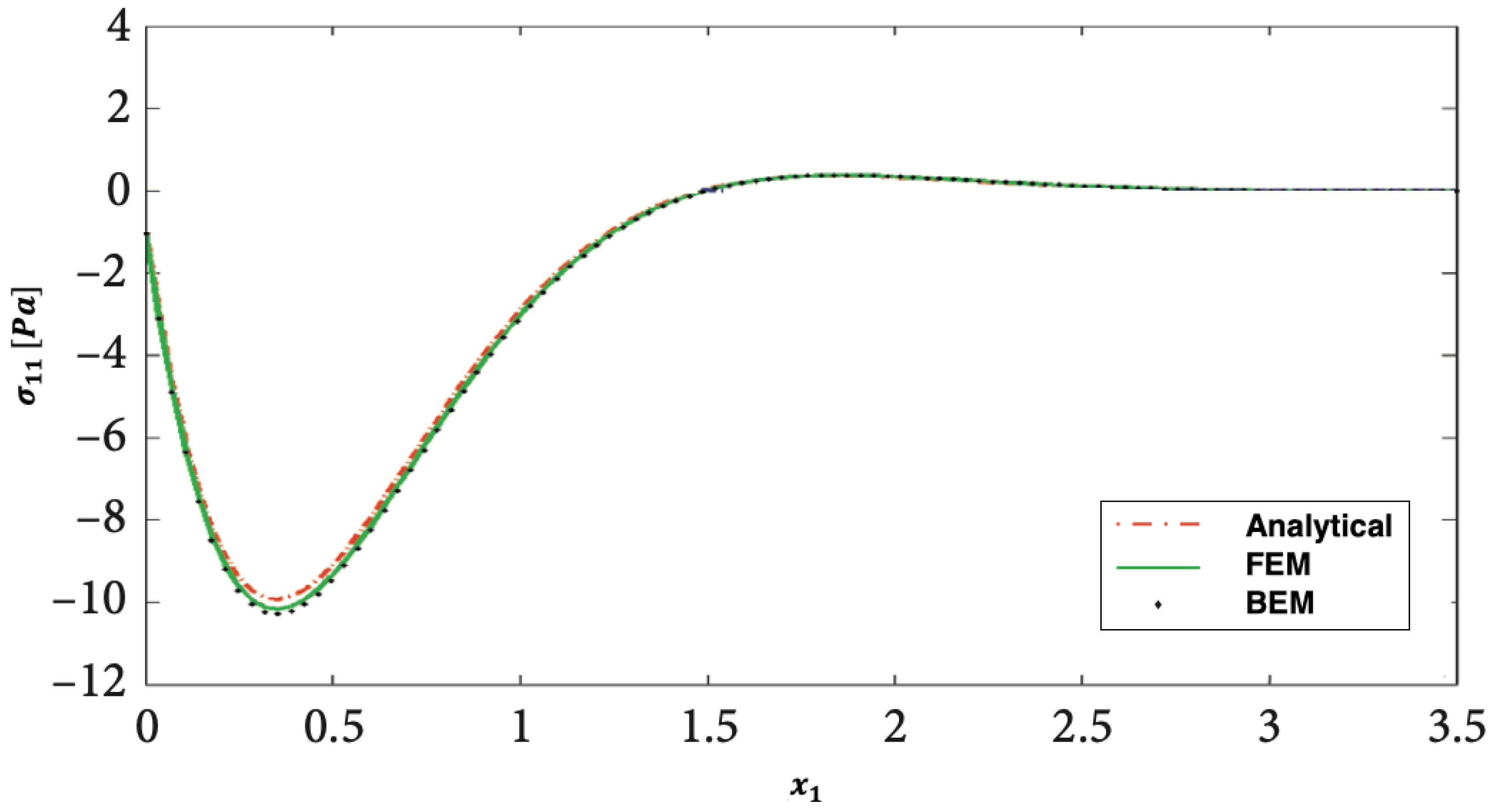
5. Numerical Results and Discussion

In the context of temperature-dependent FGA rotating granular plates, the proposed BEM technique can be applied to a wide range of nonlinear fractional BEM models for magneto-thermo-visco-elastic ultrasound wave problems. The BEM discretization was performed with 42 boundary elements and 68 internal points, as shown in Figure 1.

It is noticed from Figure 2 that the temperature-dependent (TD) curve of magneto-thermo-visco-elastic stress ${\sigma }_{11}$ along the $x_1$-axis is under a temperature-independent (TID) curve for isotropic (I) and anisotropic (A) cases. Additionally, it is noticed from this figure that the anisotropic (A) curve is under the isotropic (I) curve for temperature-dependent (TD) and temperature-independent (TID) cases.

It is noticed from Figure 3 and Figure 4 that the temperature-dependent (TD) curves of magneto-thermo-visco-elastic stress ${\sigma }_{12}$ and magneto-thermo-visco-elastic stress ${\sigma }_{22}$ along the $x_1$-axis are over temperature-independent (TID) curves for isotropic (I) and anisotropic (A) cases. In addition, it is noticed from these figures that the anisotropic (A) curve is over the isotropic (I) curve for temperature-dependent (TD) and temperature-independent (TID) cases.

Figure 5, Figure 6 and Figure 7 show the distributions of the magneto-thermo-visco-elastic stresses ${\sigma }_{11}$, ${\sigma }_{12}$, and ${\sigma }_{22}$ along the $x_1$-axis for different values of the functionally graded parameter ($m=0.1, 0.4, 0.7, \mathrm{and} 1.0$).

It is noticed from Figure 5 that the magneto-thermo-visco-elastic stress ${\sigma }_{11}$ along the $x_1$-axis increases with the increase in functionally graded parameter $m$. Then, it decreases with the increase in the functionally graded parameter $m$ after $x_1=1.4$.

It is noticed from Figure 6 that the magneto-thermo-visco-elastic stress ${\sigma }_{12}$ curves along the $x_1$-axis at different values of the functionally graded parameter ($m=0.1, 0.4, 0.7, \mathrm{and} 1.0$) coincide with each other in $0\le x_1\le 0.5$. Then, they decrease with the increase in functionally graded parameter $m$ until $x_1=5.7$, then they increase with the increase in functionally graded parameter $m$.

It is noted from Figure 7 that the magneto-thermo-visco-elastic stress ${\sigma }_{22}$ along the $x_1$-axis increases with the increase in functionally graded parameter $m$ until $x_1=3$. Then, it decreases with the increase in functionally graded parameter $m$.

Figure 8, Figure 9 and Figure 10 display the distributions of magneto-thermo-visco-elastic stresses ${\sigma }_{11}$, ${\sigma }_{12}$, and ${\sigma }_{22}$ along the $x_1$-axis for different values of fractional parameter $a=0.1, 0.4, 0.7, \mathrm{and} 1.0$.

It is noticed from Figure 8 that the magneto-thermo-visco-elastic stress ${\sigma }_{11}$ curves along the $x_1$-axis at different values of the fractional parameter ($a=0.1, 0.4, 0.7, \mathrm{and} 1.0$) coincide with each other in $0\le x_1\le 0.5$. Then, they increase with the increase in fractional parameter $a$ until $x_1=5.85$, then they coincide with each other again.

It is noticed from Figure 9 that the magneto-thermo-visco-elastic stress ${\sigma }_{12}$ curves along the $x_1$-axis at different values of the fractional parameter coincide with each other in $0\le x_1\le 0.5$. Then, they increase with the increase in fractional parameter $a$ until $x_1=5.5$. Then, they decrease with the increase in fractional parameter $a$.

It is noticed from Figure 10 that the magneto-thermo-visco-elastic stress ${\sigma }_{22}$ along the $x_1$-axis increases with the increase in fractional parameter $a$ until $x_1=6.82$, then the magneto-thermo-visco-elastic stress ${\sigma }_{12}$ curves along the $x_1$-axis at considered values of fractional parameter $a$ coincide with each other.

The findings of the proposed technique were not supported by any published findings. However, some literary works might be seen as a part of the research under consideration. Thus, we took a special case of our research into consideration and applied the analytical method of Al-Basyouni et al. [42], the finite element method (FEM) of Pettermann and DeSimone [43], and current BEM to this special case, as shown in Figure 11, Figure 12 and Figure 13 below.

Figure 11, Figure 12 and Figure 13 show the distributions of the magneto-thermo-visco-elastic stresses ${\sigma }_{11}, {\sigma }_{12}, \mathrm{and} {\sigma }_{22}$ along the $x_1$-axis for the analytical method [42], finite element method [43], and current BEM. It is clear from these figures that the BEM is in excellent agreement with the analytical and FEM, thus confirming the validity and accuracy of our proposed technique.

The computation results of the two considered examples were found using Matlab R2018a on a MacBook Pro with 2.9 GHz quad-core Intel Core i9 processor and 16 GB RAM.

The proposed fractional boundary element technique in this study is applicable to a wide range of temperature-dependent FGA rotating granular plate problems. The three effective and potent iterative methods employed to solve the linear systems generated by the proposed technique are communication-avoiding Arnoldi (CA-Arnoldi) [44], Dehdezi and Karimi (D-K) [45], and generalized modified shift-splitting (GMSS) [41] methods.

Table 1. CPU times and iteration number for CA-Arnoldi, D-K, and GMSS.

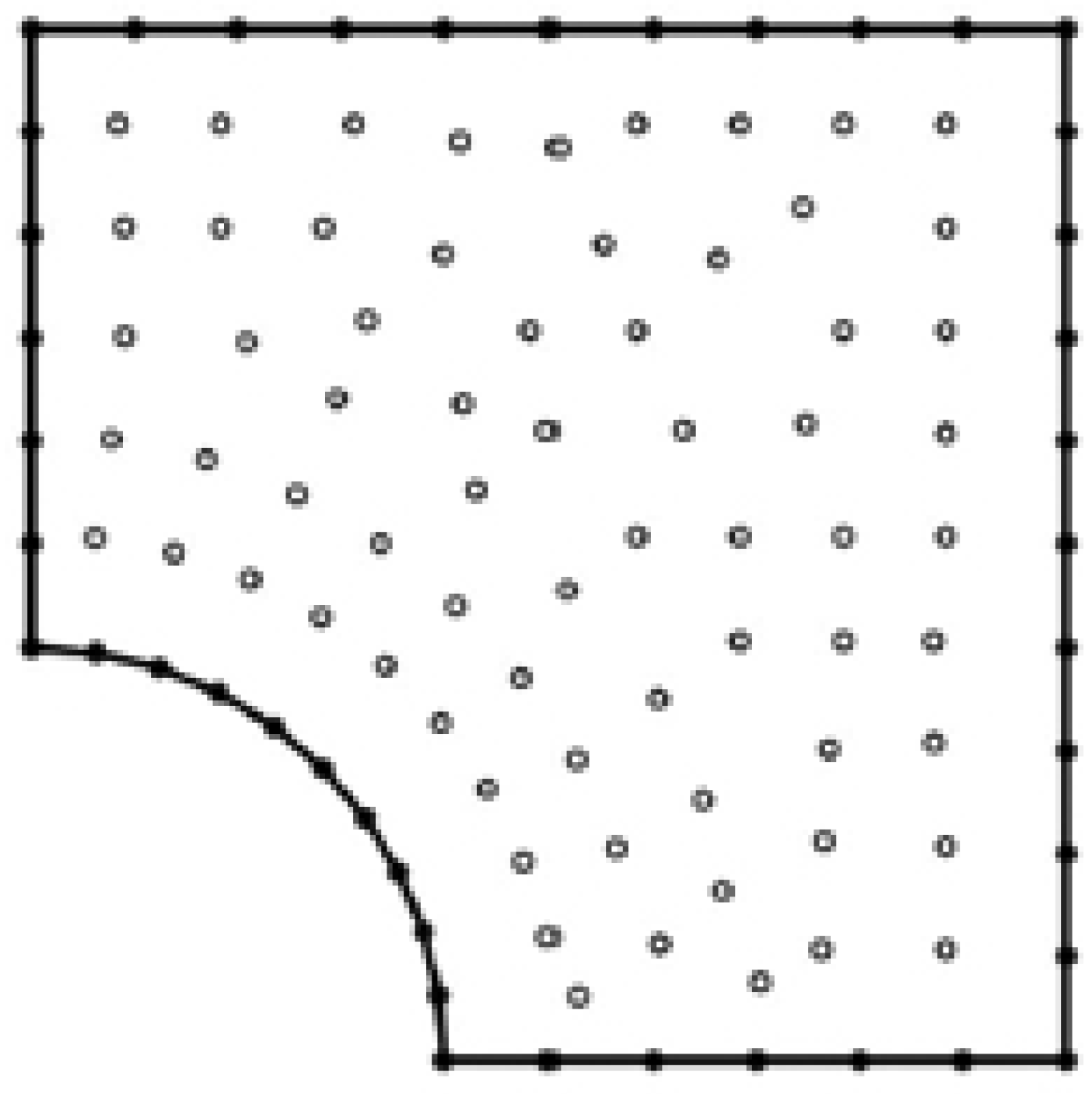
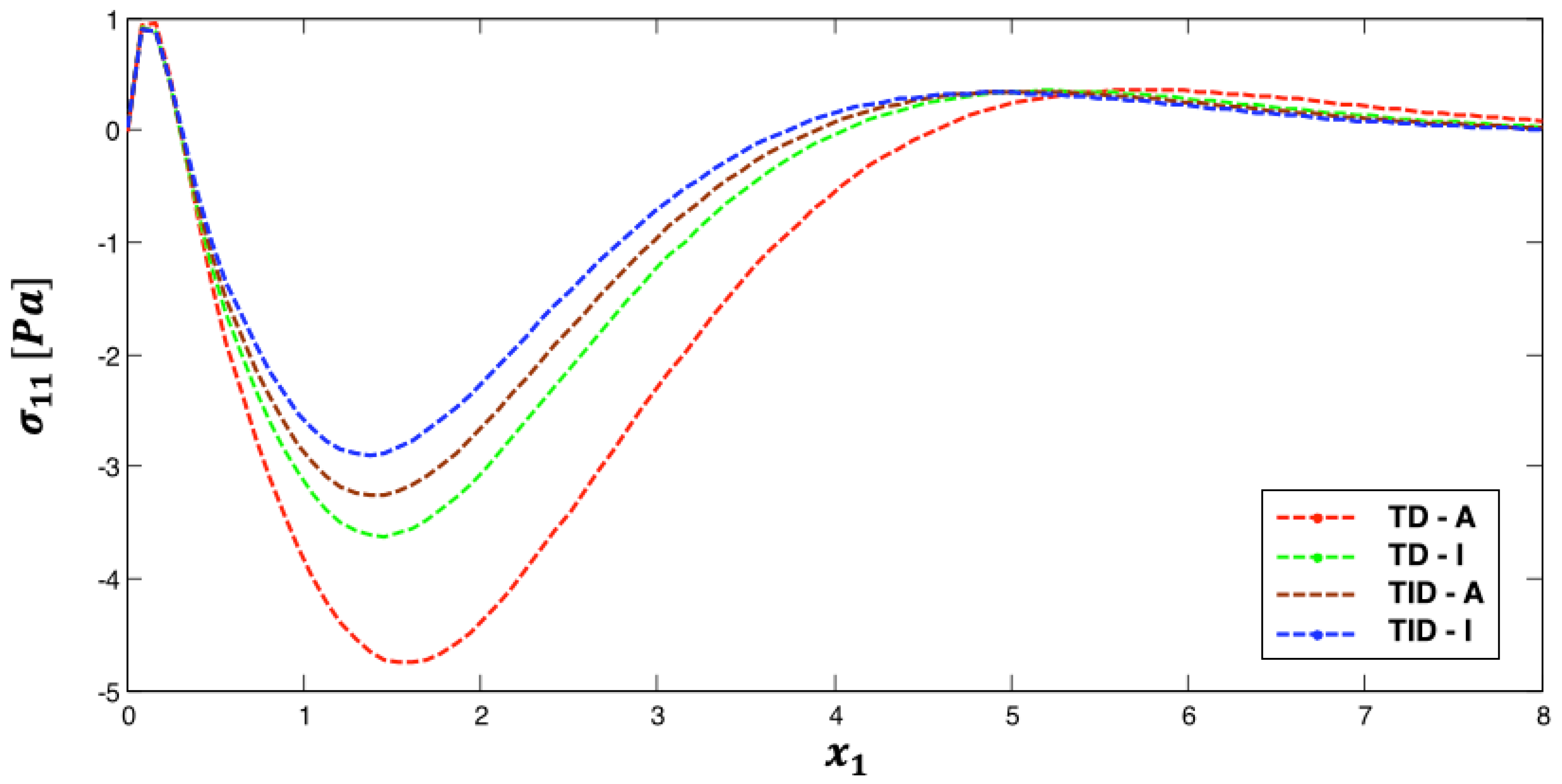
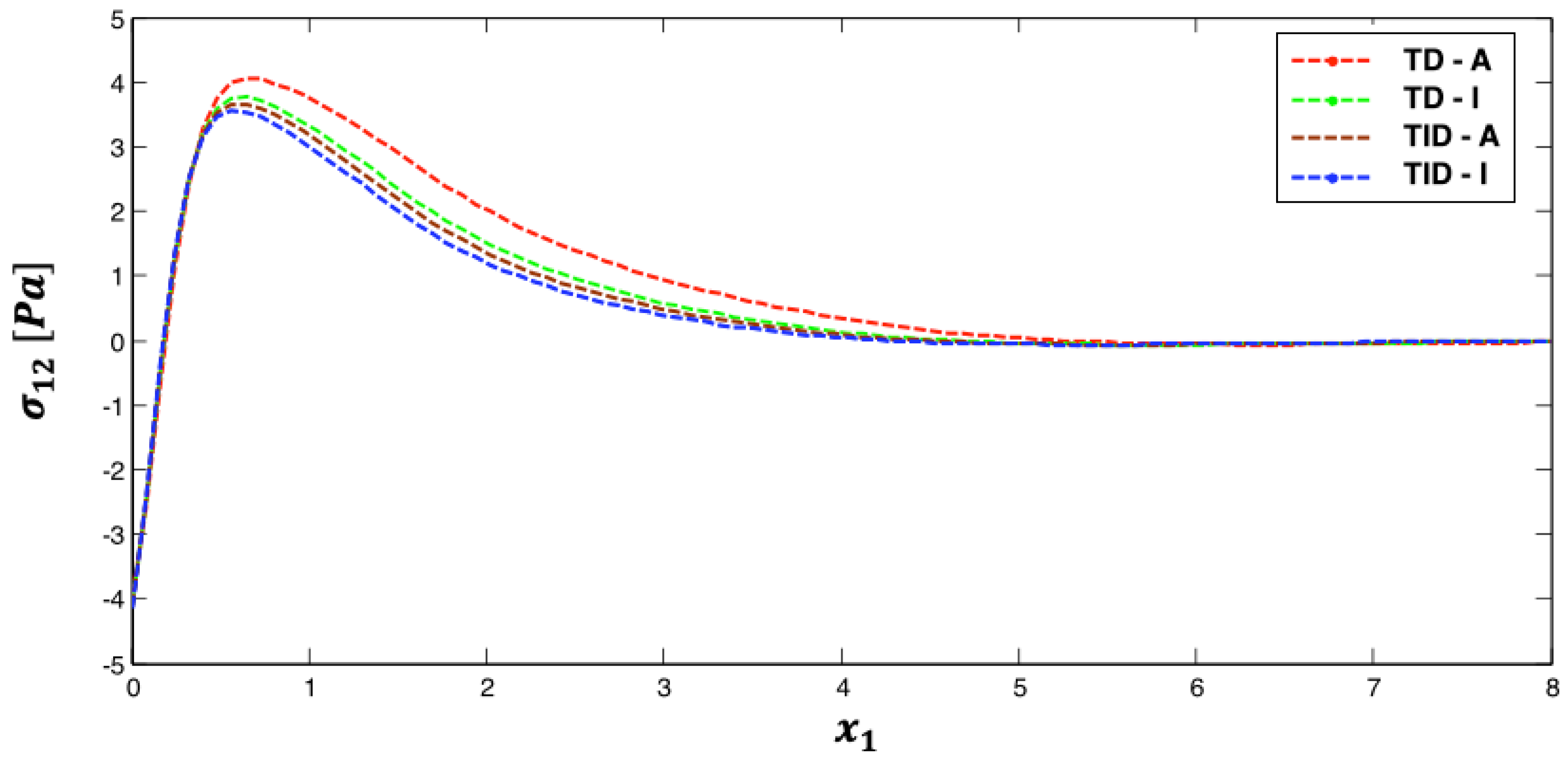
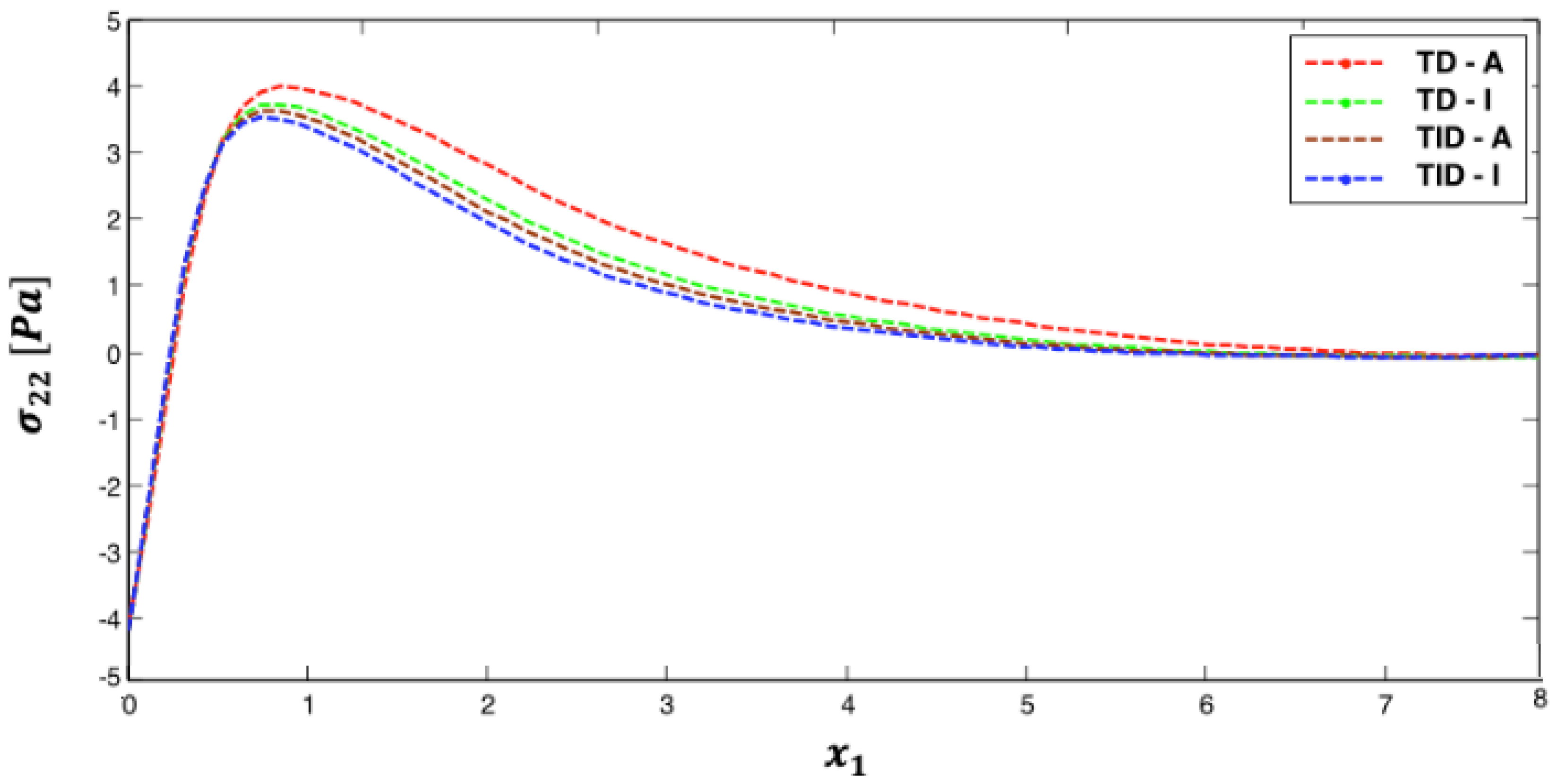
Discretization	Preconditioning	CA-Arnoldi [44]		D-K [45]		GMSS [41]
Level	Level	CPU Time	Iteration Number	CPU Time	Iteration Number	CPU Time	Iteration Number
1 (32)	0	0.06	6	0.07	6	0.04	6
2 (56)	0	0.18	8	0.22	8	0.14	7
	1	0.14	6	0.18	6	0.1	5
3 (104)	0	0.54	10	0.6	11	0.4	9
	1	0.48	8	0.54	9	0.32	5
	2	0.42	5	0.46	7	0.24	3
4 (200)	0	2.42	13	2.52	17	1.86	11
	1	1.88	11	2.1	15	1.56	7
	2	1.65	7	1.82	10	1.4	5
	3	1.4	6	1.52	7	1.36	3
5 (392)	0	10.01	15	12.02	19	7.88	13
	1	9.09	10	10.16	17	6.87	9
	2	8.19	9	9.29	15	6.09	7
	3	7.24	7	8.48	11	5.82	5
	4	6.6	5	7	7	5.18	3
6 (776)	0	42	19	48.3	21	35.9	15
	1	36.9	17	43.5	19	33.9	11
	2	34.5	15	41.6	17	30.1	9
	3	29.6	11	37.7	13	25.7	7
	4	27.4	9	33.4	11	21.7	5
	5	25.5	7	29.6	9	19.6	3

displays the CPU time and number of iterations for the CA-Arnoldi, D-K, and GMSS iterative methods at each discretization level, with the equation values in parentheses. According to Table 1, the GMSS method performs better than the CA-Arnoldi and D-K methods.

Table 2. Estimating the computational resources needed to model the temperature-dependent FGA rotating granular plate problems.

	LBM	FEM	BEM
Number of nodes	52,000	50,000	50
Number of elements	11,000	10,000	15
CPU time (min)	170	180	2
Memory (MB)	120	130	1
Disc space (MB)	250	270	0
Accuracy of results (%)	2.2	2.0	1.0

compares computational resources for modeling temperature-dependent FGA rotating granular plate problems using the lattice Boltzmann method (LBM) of Oshtorjani et al. [46], finite element method (FEM) of Pettermann and DeSimone [43], and the proposed boundary element method (BEM). Table 2 also shows the effectiveness of our proposed boundary element methodology.

6. Conclusions

A summary of this paper is as follows:

• A numerical BEM scheme is applied to a nonlinear fractional boundary element model for magneto-thermo-visco-elastic ultrasound wave problems in temperature-dependent FGA rotating granular plates.
• The BEM-based coupling scheme that is both reliable and efficient was proposed, with the Cartesian transformation method (CTM) used to compute domain integrals.
• The generalized modified shift-splitting (GMSS) method was used to solve the BEM-derived linear systems.
• Effects of temperature dependence, anisotropy, graded parameter, and fractional parameter on nonlinear thermal stress in the investigated plates are established.
• The numerical results validate the consistency and effectiveness of the developed modeling methodology.
• The results presented in this paper can be used in a variety of commercial applications, including the pharmaceutical industry, agriculture, and energy production.