Laplace-Residual Power Series Method for Solving Time-Fractional Reaction–Diffusion Model

Abstract

Despite the fact the Laplace transform has an appreciable efficiency in solving many equations, it cannot be employed to nonlinear equations of any type. This paper presents a modern technique for employing the Laplace transform LT in solving the nonlinear time-fractional reaction–diffusion model. The new approach is called the Laplace-residual power series method (L-RPSM), which imitates the residual power series method in determining the coefficients of the series solution. The proposed method is also adapted to find an approximate series solution that converges to the exact solution of the nonlinear time-fractional reaction–diffusion equations. In addition, the method has been applied to many examples, and the findings are found to be impressive. Further, the results indicate that the L-RPSM is effective, fast, and easy to reach the exact solution of the equations. Furthermore, several actual and approximate solutions are graphically represented to demonstrate the efficiency and accuracy of the proposed method.

1. Introduction

Fractional integral and derivatives are a branch of applied mathematical analysis and have been developed theoretically in recent years [1,2,3,4,5,6,7,8,9,10,11]; the application of this field has been used in many areas such as sciences, engineering, aerodynamic, thermodynamic, mechatronics, image processing, physics, and fluid flow phenomena [12,13]. The essential improvement of fractional differential equations (FDEs) is to provide a tool for the definition of different behaviors in different fields.

Most FDEs do not have exact analytic solutions, so approximation methods (numerical or analytical) must be used, such as the Jacobi Tau method [14], the Sinc–Legendre collocation method [15], the Petrov–Galerkin algorithm [16], the decomposition method [8,17], the Variational iteration method [18], and the homotopy transformation perturbation method [19]. The RPSM is an effective method used to solve wide classes of differential equations [20].

Eriqat et al. [21] proposed a new scheme to solve a class of fractional differential equations by combining the LT and the RPSM and called it the L-RPSM. This new method is guaranteed to have more simplicity than RPSM for creating the exact and approximate solutions (ASs) to the linear and nonlinear FDEs, such as the neutral FDEs [21], the nonlinear time-dispersive fractional partial differential equations (FPDEs) [22], the nonlinear fractional reaction–diffusion for bacteria growth model [23], the time-fractional nonlinear fisher PDE [24], the fuzzy fractional population dynamics model [25], the fuzzy quadratic Riccati differential equations [26], the fractional Lane-Emden equations [27], and the high-order FPDEs [28].

The reaction–diffusion equations describe the behavior of a large range of chemical systems where the diffusion of material competes with the production of that material by some form of chemical reaction. The simplest reaction–diffusion models are of the form [29]:

$$D_t\nu =M\left(x\right)D_x^2\nu +r\left(\nu \right),$$

(1)

where $\nu =\nu (x,t)$, $M\left(x\right)$ is a continous function, $x\in \mathbb{R}$, $t>0$, and $r\left(\nu \right)$ is a non-linear analytic function of $\nu$ that is chosen as reaction kinetics.

Recently, Equation (1) has been reformulated by replacing the time-first derivative with a time-fractional derivative, so it becomes as follows [19,30,31]:

$$D_t^{\alpha }\nu =M\left(x\right)D_x^2\nu +r\left(\nu \right),$$

(2)

where $\alpha$ ($0<\alpha \le 1$) is a parameter defining the time Caputo fractional derivative (C-FD) order.

Several researchers have used different methods to solve the non-linear time-fractional reaction diffusion equation (TFRDE) in Equation (2), such as Elzaki homotopy transformation perturbation method [19], the RPSM method [31], the homotopy analysis method [30], and other methods [32,33,34,35,36,37,38,39].

In this paper, the L-RPSM is modified and adapted to create a series solution for the TFRDE, and comparisons with previous methods are made to show the ease and efficiency of the technique. Solving TFRDE using the L-RPSM consists of three steps: (i) convert the given TFRDE into Laplace space, (ii) construct a series solution to the Laplace form of TFRDE, and (iii) convert the solution to the original space using the inverse LT. The L-RPSM introduces a new nice fractional expansion that is used to find the coefficients of a series solution without using fractional derivatives as in RPSM. Additionally, a few simple calculations give us the coefficients of a series compared to the RPSM, which requires several calculations to establish the fractional derivatives in the solution steps. Finally, the exact and accurate approximation solutions by L-RPSM can be obtained with a rapidly convergent series.

The paper is organized as follows: Section 2 reviews some important results related to C-FD and LT. In Section 3, we construct the ASs for TFRDE based on our proposed L-RPSM. In Section 4, applications are performed to validate the efficiency and accuracy of the proposed method. Finally, we provided a conclusion in Section 5.

2. C-FD Operator, LT, and Fractional Expansions

This section reviews some important concepts of C-FD and suggests fractional expansion in LT space to construct exact and ASs for the TFRDEs in the next section. For more information about C-FD and LT, the reader can refer to Refs. [1,2,3,4,5,6,21,22].

Definition 1

([1]). The C-FD of $v(x,t)$ for order α is given by:

$$D_t^{\alpha }v(x,t)=\frac{{\partial }^{\alpha }v(x,t)}{\partial t^{\alpha }}=\left\{\begin{array}{cc}{J}_t^{m-\alpha }\left(\frac{{\partial }^{m}v(x,t)}{\partial t^m}\right),\hfill & m-1<\alpha <m,\hfill \\ \frac{{\partial }^{m}v(x,t)}{\partial t^m},\hfill & \alpha =m\in \mathbb{N},\hfill \end{array}\right.$$

(3)

where $t\ge 0$, $x\in I$, I is an interval, $D_t^{\alpha }$ refers to the C-FD of order $\alpha ,m\in \mathbb{N}$, and $J_t^{\beta }$ denotes the Riemann–Liouville fractional integral operator of order β that given by:

$$J_t^{\beta }\nu (x,t)=\left\{\begin{array}{cc}\frac{1}{\Gamma \left(\beta \right)}{\int }_0^t{(t-\tau )}^{\beta -1}\nu (x,t)d\tau ,\hfill & \beta >0,t>\tau \ge 0,\hfill \\ \nu (x,t)\hfill & \beta =0,\hfill \end{array}\right.$$

(4)

provided the integral exists.

Lemma 1

([1]). For $m-1<\alpha \le m,\gamma >\alpha -1,t\ge 0$, and $\lambda \in \mathbb{R}$, we summarize some important properties for C-FD as follows:

1. 

$D_t^{\alpha }\lambda =0$.

2. 

$D_t^{\alpha }{t}^{\gamma }=\frac{\Gamma (\gamma +1)}{\Gamma (\gamma +1-\alpha )}{t}^{\gamma -\alpha }.$

3. 

$D_t^{\alpha }{J}_t^{\alpha }\nu (x,t)=\nu (x,t)$.

4. 

$J_t^{\alpha }{D}_t^{\alpha }\nu (x,t)=\nu (x,t)-{\sum }_{j=0}^{m-1}{\partial }_t^j\nu (x,0^{+})\frac{t^j}{j!}$.

Definition 2

([40]). Let $\nu (x,t)$ be a piecewise continuous function (PCF) on $I\times [0,\infty )$ and of exponential order (EO) δ. Then, the LT of the $\nu (x,t)$ is defined as:

$$V(x,s)=\mathcal{L}\left[\nu (x,t)\right]:={\int }_0^{\infty }{e}^{-st}\nu (x,t)dt,s>\delta ,$$

(5)

and the inverse LT of the $V(x,s)$ is defined as:

$$\nu (x,t)={\mathcal{L}}^{-1}\left[V(x,s)\right]:={\int }_{c-i\infty }^{c+i\infty }{e}^{st}V(x,s)ds,c=Re\left(s\right)>c_0,$$

(6)

where $c_0$ lies in the right half plane of the absolute convergence of the Laplace integral.

Lemma 2

([40]). Let $u(x,t)$ and $v(x,t)$ be PCFs on $I\times [0,\infty )$ and of EOs ${\delta }_1$ and ${\delta }_2$, respectively, where ${\delta }_1<{\delta }_2$. Suppose that $U(x,s)=\mathcal{L}\left[u\right(x,t\left)\right];V(x,s)=\mathcal{L}\left[v\right(x,t\left)\right]$; and $a,b$ are constants. Then,

1. 

$\mathcal{L}[au(x,t)+bv(x,t)]=aU(x,s)+bV(x,s),x\in I,s>{\delta }_1$.

2. 

$\mathcal{L}\left[e^{at}v(x,t)\right]=V(x,s-a),x\in I,s>a+{\delta }_1$.

3. 

$\underset{s\to \infty }{lim}sV(x,s)=v(x,0),x\in I$.

Lemma 3

([22]). Let $\nu (x,t)$ be a PCF on $I\times [0,\infty )$ and of EO δ, $V(x,s)=\mathcal{L}\left[\nu \right(x,t\left)\right]$. Then, the following properties of LT operator for C-FD are satisfied:

1. 

$\mathcal{L}\left[D_t^{\alpha }\nu (x,t)\right]=s^{\alpha }V(x,s)-{\sum }_{k=0}^{m-1}{s}^{\alpha -k-1}{\partial }_t^k\nu (x,0),m-1<\alpha <m$.

2. 

$\mathcal{L}\left[D_t^{n\alpha }\nu (x,t)\right]=s^{n\alpha }V(x,s)-{\sum }_{k=0}^{n-1}{s}^{(n-k)\alpha -1}{D}_t^{k\alpha }\nu (x,0),0<\alpha \le 1$,

where $D_t^{n\alpha }=D_t^{\alpha }.D_t^{\alpha }\dots D_t^{\alpha }$ (n-times).

Theorem 1

([22]). Let $\nu (x,t)$ be a PCF on $I\times [0,\infty )$ and of EO δ. If the function $V(x,s)=\mathcal{L}\left[\nu \right(x,t\left)\right]$ has a fractional expansion as follows:

$$V(x,s)=\sum _{n=0}^{\infty }\frac{f_n\left(x\right)}{s^{n\alpha +1}},0<\alpha \le 1,x\in I,s>\delta ,$$

(7)

then $f_n\left(x\right)=D_t^{n\alpha }u(x,0)$.

Remark 1

([22]). The inverse LT of the expansion in Theorem 1 has the following form:

$$\nu (x,t)=\sum _{n=0}^{\infty }\frac{D_t^{n\alpha }\nu (x,0)}{\Gamma (n\alpha +1)}{t}^{n\alpha },0<\alpha \le 1,t\ge 0.$$

(8)

3. The L-RPSM for Solving TFRDE

In this section, we apply L-RPSM to the nonlinear TFRDE to be discussed.

Step 1. 

Employ LT to both sides of Equation (2), i.e.,

$$\mathcal{L}\left[D_t^{\alpha }\nu (x,t)\right]=M\left(x\right)\mathcal{L}\left[D_x^2\nu (x,t)\right]+\mathcal{L}\left[r\left(\nu (x,t)\right)\right]$$

(9)

By the fact (1) in Lemma 3 at $\alpha \in (0,1]$, one can rewrite Equation (9) as

$$V(x,s)=\frac{\nu (x,0)}{s}+\frac{M\left(x\right)}{s^{\alpha }}{D}_x^{2}V(x,s)+\frac{R\left(x,s\right)}{s^{\alpha }},$$

(10)

where $V(x,s)=\mathcal{L}\left[\nu \right(x,t\left)\right]$ and $R\left(x,s\right)=\mathcal{L}\left[r\left(\nu (x,t)\right)\right]$.

Step 2. 

Construct a series solution to the Laplace form:

• Write the series solution, $V(x,s)$ of Equation (10) as follows:

  $$V(x,s)=\sum _{n=0}^{\infty }\frac{f_n\left(x\right)}{s^{n\alpha +1}},$$

  (11)

  and the kth-truncated solution as

  $$V_k(x,s)=\sum _{n=0}^k\frac{f_n\left(x\right)}{s^{n\alpha +1}}.$$

  (12)

  It is noteworthy that the convergence of the series (11) is discussed in detail in Ref. [22].
  We suppose that the initial guess of Equation (2) is $\nu (x,0)=f\left(x\right)$. Hence, according to fact (3) in Lemma 2 we have $f_0\left(x\right)=\underset{s\to \infty }{lim}sV(x,s)=\nu (x,0)=f\left(x\right)$. So, Equation (12) can be written as:

  $$V_k(x,s)=\frac{f\left(x\right)}{s}+\sum _{n=1}^k\frac{f_n\left(x\right)}{s^{n\alpha +1}}.$$

  (13)
• Construct the Laplace-Residual function (LRF), $LRes(x,s)$, to Equation (10) as:

  $$LRes(x,s)=V(x,s)-\frac{f\left(x\right)}{s}-\frac{M\left(x\right)}{s^{\alpha }}{D}_x^{2}V(x,s)-\frac{R\left(x,s\right)}{s^{\alpha }},$$

  (14)

  and the kth-LRF, $LRe{s}_k(x,s)$ is

  $$LRe{s}_k(x,s)=V_k(x,s)-\frac{f\left(x\right)}{s}-\frac{M\left(x\right)}{s^{\alpha }}{D}_x^2{V}_k(x,s)-\frac{R\left(x,s\right)}{s^{\alpha }}.$$

  (15)
• Substitute the kth-truncation, $V_k(x,s)$, as in Equation (13), into Equation (15) and multiply both sides of resulting equation by $s^{k\alpha +1},k=1,2,\dots$
• To obtain the requited coefficients, $f_n\left(x\right),n=1,2,\dots ,k$, in Equation (13), we solve the following algebraic equation recursively:

  $$\underset{s\to \infty }{lim}{s}^{k\alpha +1}LRe{s}_k(x,s)=0,k=1,2,\dots$$

  (16)
• Substitute the forms of the required coefficients, $f_n\left(x\right),n=1,2,\dots ,k$ into Equation (13) to obtain the kth-AS, $V_k(x,s)$, of Equation (10).

Step 3. 

Employ the inverse LT on the final form of $V_k(x,s)$ to ensure the existence of the kth-AS, ${\nu }_k(x,t)$ of Equation (2).

4. Applications

Five applications of TFRDEs are considered in this section to validate our proposed method. The MATHEMATICA 11 and MAPLE 2018 software packages are used in our computational process and graphical results.

Application 1.

Consider the TFRDE [30]:

$$D_t^{\alpha }\nu (x,t)=D_x^2\nu (x,t)+\nu (x,t)(1-\nu (x,t)),0<\alpha \le 1,x\in \mathbb{R},$$

(17)

subject to a constant initial condition

$$\nu (x,0)=c.$$

(18)

The exact solution for Equation (17) at $\alpha =1$ is $\nu (x,t)=c{e}^t/(1-c+c{e}^t)$.

Firstly, employ the LT to both sides of Equation (17) to obtain

$$\begin{array}{cc}\hfill V(x,s)& =\frac{c}{s}+\frac{D_x^{2}V(x,s)}{s^{\alpha }}+\frac{1}{s^{\alpha }}V(x,s)-\frac{1}{s^{\alpha }}\mathcal{L}\left[{\left({\mathcal{L}}^{-1}\left[V(x,s)\right]\right)}^2\right].\hfill \end{array}$$

(19)

The L-RPSM proposes the solution for the Laplace form as Equation (19) with a fractional power series. Suppose that the solution is given in the following form:

$$V(x,s)=\sum _{n=0}^{\infty }\frac{f_n\left(x\right)}{s^{n\alpha +1}}.$$

(20)

It is clear that by using the constant initial condition, we have $f_0\left(x\right)=\underset{s\to \infty }{lim}sV(x,s)={\nu }_0(x,t)=c$. Additionally, the kth-truncated series, $V_k(x,s)$, can be written as:

$$V_k(x,s)=\frac{c}{s}+\sum _{n=1}^k\frac{f_n\left(x\right)}{s^{n\alpha +1}}.$$

(21)

Before we go deep into the L-RPSM, let us define the LRF, $LRes(x,s)$, for Equation (19)

$$\begin{array}{cc}\hfill LRes(x,s)& =V(x,s)-\frac{c}{s}-\frac{D_x^{2}V(x,s)}{s^{\alpha }}-\frac{1}{s^{\alpha }}V(x,s)+\frac{1}{s^{\alpha }}\mathcal{L}\left[{\left({\mathcal{L}}^{-1}\left[V(x,s)\right]\right)}^2\right],\hfill \end{array}$$

(22)

and accordingly, the kth-LRF, $LRe{s}_k$, is

$$\begin{array}{cc}\hfill LRe{s}_k(x,s)& =V_k(x,s)-\frac{c}{s}-\frac{D_x^2{V}_k(x,s)}{s^{\alpha }}-\frac{1}{s^{\alpha }}{V}_k(x,s)+\frac{1}{s^{\alpha }}\mathcal{L}\left[{\left({\mathcal{L}}^{-1}\left[V_k(x,s)\right]\right)}^2\right].\hfill \end{array}$$

(23)

To determine the value of the first unknown coefficient, $f_1\left(x\right)$, we consider (k = 1) in Equation (23) to obtain

$$\begin{array}{cc}\hfill LRe{s}_1(x,s)& =V_1(x,s)-\frac{c}{s}-\frac{D_x^2{V}_1(x,s)}{s^{\alpha }}-\frac{1}{s^{\alpha }}{V}_1(x,s)+\frac{1}{s^{\alpha }}\mathcal{L}\left[{\left({\mathcal{L}}^{-1}\left[V_1(x,s)\right]\right)}^2\right],\hfill \end{array}$$

(24)

substitute $V_1(x,s)=c/s+f_1\left(x\right)/s^{\alpha +1}$ into Equation (24) as follows:

$$\begin{array}{cc}\hfill LRe{s}_1(x,s)=& \frac{f_1\left(x\right)}{s^{\alpha +1}}-\frac{D_x^2{f}_1\left(x\right)}{s^{2\alpha +1}}-\frac{c}{s^{\alpha +1}}-\frac{f_1\left(x\right)}{s^{2\alpha +1}}+\frac{c^2}{s^{\alpha +1}}+\frac{2c{f}_1\left(x\right)}{s^{2\alpha +1}}+\frac{\Gamma (2\alpha +1)f_1^2\left(x\right)}{\Gamma {(\alpha +1)}^2{s}^{3\alpha +1}}.\hfill \end{array}$$

(25)

According to the fact in Equation (16) for $k=1$, we have

$$\begin{array}{cc}\hfill \underset{s\to \infty }{lim}{s}^{\alpha +1}LRe{s}_1(x,s)& =f_1\left(x\right)-c+c^2=0.\hfill \end{array}$$

(26)

Solve the Equation (26) for $f_1\left(x\right)$, to obtain the following output:

$$\begin{array}{c}\hfill f_1\left(x\right)=c(1-c).\end{array}$$

(27)

In the same manner, to obtain the value of the second unknown coefficient, we consider (k = 2) in Equation (23):

$$\begin{array}{cc}\hfill LRe{s}_2(x,s)& =V_2(x,s)-\frac{c}{s}-\frac{D_x^2{V}_2(x,s)}{s^{\alpha }}-\frac{1}{s^{\alpha }}{V}_2(x,s)+\frac{1}{s^{\alpha }}\mathcal{L}\left[{\left({\mathcal{L}}^{-1}\left[V_2(x,s)\right]\right)}^2\right].\hfill \end{array}$$

(28)

Since $V_2(x,s)=c/s+c(1-c)/s^{\alpha +1}+f_2\left(x\right)/s^{2\alpha +1}$; therefore, we can rewrite Equation (28) as:

$$\begin{array}{cc}\hfill LRe{s}_2(x,s)=& -\frac{c^2}{s^{\alpha +1}}-\frac{c(1-c)-f_2\left(x\right)}{s^{2\alpha +1}}-\frac{f_2\left(x\right)+D_x^2{f}_2\left(x\right)}{s^{3\alpha +1}}\hfill \\ & +\frac{1}{s^{\alpha }}\mathcal{L}\left[{\left({\mathcal{L}}^{-1}\left[\frac{c}{s}+\frac{c(1-c)}{s^{\alpha +1}}+\frac{f_2\left(x\right)}{s^{2\alpha +1}}\right]\right)}^2\right].\hfill \end{array}$$

(29)

Multiplying both sides of Equation (29) by $s^{2\alpha +1}$ and solving the sequence equation $\underset{s\to \infty }{lim}{s}^{2\alpha +1}LRe{s}_2(x,s)=0$ for $f_2\left(x\right)$ yields

$$\begin{array}{c}\hfill f_2\left(x\right)=c(1-3c+2c^2).\end{array}$$

(30)

Proceeding, as stated in the previous steps, in determining the functions $f_k\left(x\right)$, one can easily obtain the following results:

$$\begin{array}{cc}\hfill f_3\left(x\right)=& (-1+c)c\left(-{(1-2c)}^2-\frac{(-1+c)c\Gamma (1+2\alpha )}{\Gamma {(1+\alpha )}^2}\right),\hfill \\ \hfill f_4\left(x\right)=& (-1+c)c(-1+2c)({(1-2c)}^2+\frac{1}{\Gamma (1+\alpha )}((-1+c)c(\frac{4^{\alpha }\Gamma (\frac{1}{2}+\alpha )}{\sqrt{\pi }}\hfill \\ & +\frac{2\Gamma (1+3\alpha )}{\Gamma (1+2\alpha )}\left)\right)).\hfill \end{array}$$

(31)

We can express the solution obtained by L-RPSM of Equation (19) in an infinite series as follows:

$$\begin{array}{cc}\hfill V(x,s)=& \frac{c}{s}-\frac{(-1+c)c}{s^{\alpha +1}}+\frac{(-1+c)c(-1+2c)}{s^{2\alpha +1}}\hfill \\ & +\frac{1}{s^{3\alpha +1}}\left((-1+c)c\left(-{(1-2c)}^2-\frac{(-1+c)c\Gamma (1+2\alpha )}{\Gamma {(1+\alpha )}^2}\right)\right)+\cdots \hfill \end{array}$$

(32)

Consequently, the solution of Equations (17) and (18) by taking the inverse LT of Equation (32) is

$$\begin{array}{cc}\hfill \nu (x,t)=& c-\frac{(-1+c)c{t}^{\alpha }}{\Gamma \left(\alpha +1\right)}+\frac{(-1+c)c(-1+2c)t^{2\alpha }}{\Gamma (2\alpha +1)}\hfill \\ & +\frac{t^{3\alpha }}{\Gamma \left(3\alpha +1\right)}\left((-1+c)c\left(-{(1-2c)}^2-\frac{(-1+c)c\Gamma (1+2\alpha )}{\Gamma {(1+\alpha )}^2}\right)\right)+\cdots \hfill \end{array}$$

(33)

Figure 1 shows the surface graphs of the 5th-AS at different values of $\alpha$ and the exact solutions at $\alpha =1$ of Equations (17) and (18) obtained by L-RPSM. It is clear from the figures that the 5th-AS of the Application 1 is in very good agreement with the exact solution at $\alpha =1$. In addition, the behavior of the solution did not change with the change in the values of $\alpha$.

Application 2.

Consider the non-homogeneous TFRDE

$$\begin{array}{cc}\hfill D_t^{\alpha }\nu (x,t)=& D_x^2\nu (x,t)+\nu (x,t)(1-\nu (x,t))+sinx+2sinx\frac{t^{\alpha }}{\Gamma (1+\alpha )}+{sin}^{2}x\frac{t^{2\alpha }}{\Gamma {(1+\alpha )}^2},\hfill \\ & t>0,0<\alpha \le 1,x\in \mathbb{R}.\hfill \end{array}$$

(34)

subject to the initial condition

$$\nu (x,0)=1.$$

(35)

Taking the LT to both sides of Equation (34) and using Equation (35), we obtain the following Laplace form:

$$\begin{array}{cc}\hfill V(x,s)=& \frac{1}{s}+\frac{D_x^{2}V(x,s)}{s^{\alpha }}+\frac{V(x,s)}{s^{\alpha }}-\frac{1}{s^{\alpha }}\mathcal{L}\left[{\left({\mathcal{L}}^{-1}\left[V(x,s)\right]\right)}^2\right]+\frac{sinx}{s^{\alpha +1}}+\frac{2sinx}{s^{1+2\alpha }}\hfill \\ & +\frac{{sin}^{2}x\Gamma (1+2\alpha )}{s^{1+3\alpha }\Gamma {(1+\alpha )}^2}.\hfill \end{array}$$

(36)

Suppose that the kth-AS of Equation (36) takes the following expansion form:

$$V_k(x,s)=\frac{1}{s}+\sum _{n=1}^k\frac{f_n\left(x\right)}{s^{n\alpha +1}}.$$

(37)

Define the kth-LRF, $LRe{s}_k(x,s)$, for Equation (36) as follows:

$$\begin{array}{cc}\hfill LRe{s}_k(x,s)=& V_k(x,s)-\frac{1}{s}-\frac{D_x^2{V}_k(x,s)}{s^{\alpha }}-\frac{V_k(x,s)}{s^{\alpha }}+\frac{1}{s^{\alpha }}\mathcal{L}\left[{\left({\mathcal{L}}^{-1}\left[V_k(x,s)\right]\right)}^2\right]-\frac{sinx}{s^{\alpha +1}}\hfill \\ & -\frac{2sinx}{s^{1+2\alpha }}-\frac{{sin}^{2}x\Gamma (1+2\alpha )}{s^{1+3\alpha }\Gamma {(1+\alpha )}^2}.\hfill \end{array}$$

(38)

To determine the form of first unknown coefficient, $f_1\left(x\right)$, we consider (k = 1) in Equation (38), to obtain:

$$\begin{array}{cc}\hfill LRe{s}_1(x,s)& =V_1(x,s)-\frac{1}{s}-\frac{D_x^2{V}_1(x,s)}{s^{\alpha }}-\frac{V_1(x,s)}{s^{\alpha }}+\frac{1}{s^{\alpha }}\mathcal{L}\left[{\left({\mathcal{L}}^{-1}\left[V_1(x,s)\right]\right)}^2\right]-\frac{sinx}{s^{\alpha +1}}\hfill \\ & -\frac{2sinx}{s^{2\alpha +1}}-\frac{{sin}^{2}x\Gamma (1+2\alpha )}{s^{3\alpha +1}\Gamma {(1+\alpha )}^2}.\hfill \end{array}$$

(39)

Substitute 1st-AS, $V_1(x,s)=1/s+f_1\left(x\right)/s^{\alpha +1}$, into Equation (39), to have:

$$\begin{array}{cc}\hfill LRe{s}_1(x,s)=& \frac{f_1\left(x\right)}{s^{\alpha +1}}-\frac{D_x^2{f}_1\left(x\right)}{s^{2\alpha +1}}+\frac{f_1\left(x\right)}{s^{2\alpha +1}}+\frac{f_1{\left(x\right)}^2\Gamma (1+2\alpha )}{s^{1+3\alpha }\Gamma {(1+\alpha )}^2}-\frac{sinx}{s^{\alpha +1}}\hfill \\ & -\frac{2sinx}{s^{1+2\alpha }}-\frac{{sin}^{2}x\Gamma (1+2\alpha )}{s^{1+3\alpha }\Gamma {(1+\alpha )}^2}.\hfill \end{array}$$

(40)

Multiply Equation (40) by $s^{\alpha +1}$, to obtain:

$$\begin{array}{cc}\hfill s^{\alpha +1}LRe{s}_1(x,s)=& f_1\left(x\right)-\frac{D_x^2{f}_1\left(x\right)}{s^{\alpha }}+\frac{f_1\left(x\right)}{s^{\alpha }}+\frac{f_1{\left(x\right)}^2\Gamma (1+2\alpha )}{s^{2\alpha }\Gamma {(1+\alpha )}^2}-sinx\hfill \\ & -\frac{2sinx}{s^{\alpha }}-\frac{{sin}^{2}x\Gamma (1+2\alpha )}{s^{2\alpha }\Gamma {(1+\alpha )}^2}.\hfill \end{array}$$

(41)

In reference to the fact in Equation (16) and to solve $\underset{s\to \infty }{lim}{s}^{k\alpha +1}LRe{s}_k(x,s)=0$ for $k=1$, we obtain the following output:

$$\begin{array}{c}\hfill f_1\left(x\right)=sinx.\end{array}$$

(42)

By repeating above-illustrated steps in determining the values of unknown coefficients, we obtain:

$$f_n\left(x\right)=0,n=2,3,4,\dots$$

(43)

Therefore, the 1st-AS, $V_1(x,s)$, of Equation (36) is the exact solution, which can be expressed as follows:

$$V(x,s)=\frac{1}{s}+\frac{sinx}{s^{\alpha +1}}.$$

(44)

Employ inverse LT to both sides of Equation (44) to obtain the exact solution (obtained in [31]), $\nu (x,t)$, of Equations (34) and (35) as follows:

$$\begin{array}{cc}\hfill \nu (x,t)& =1+sinx\frac{t^{\alpha }}{\Gamma (1+\alpha )}.\hfill \end{array}$$

(45)

Figure 2 shows the 2D graphs of the exact solution to Equations (34) and (35) at $\alpha =0.4,0.6,0.8,1$, and $t=0.1,0.7$. It is clear that with increasing time, the amplitude of the wave increases and the variation in amplitude decreases with different $\alpha$ values.

Application 3.

Consider time-fractional Fitzhugh–Nagumo equation

$$D_t^{\alpha }\nu (x,t)=D_x^2\nu (x,t)+\nu (x,t)(1-\nu (x,t))(\nu (x,t)-\theta ),t>0,0<\alpha \le 1,x\in R,0<\theta <1,$$

(46)

subject to the initial condition

$$\nu (x,0)=\frac{1}{1+e^{-\frac{x}{\sqrt{2}}}}.$$

(47)

In the special case when $\alpha =1$, the exact solution for Equations (46) and (47) is [19]:

$$\nu (x,t)=\frac{1}{\left(1+e^{-\frac{x}{\sqrt{2}}-\left(\frac{1}{2}-\theta \right)t}\right)}$$

(48)

Applying LT on both sides of Equations (46) and (47) gives:

$$\begin{array}{cc}\hfill V(x,s)=& \frac{1}{s(1+e^{-\frac{x}{\sqrt{2}}})}+\frac{D_x^{2}V(x,s)}{s^{\alpha }}+\frac{1}{s^{\alpha }}\mathcal{L}\left[{\left({\mathcal{L}}^{-1}\left[V(x,s)\right]\right)}^2\right]-\frac{1}{s^{\alpha }}\mathcal{L}\left[{\left({\mathcal{L}}^{-1}\left[V(x,s)\right]\right)}^3\right]\hfill \\ & -\frac{\theta }{s^{\alpha }}V(x,s)+\frac{\theta }{s^{\alpha }}\mathcal{L}\left[{\left({\mathcal{L}}^{-1}\left[V(x,s)\right]\right)}^2\right],\hfill \end{array}$$

(49)

thus, the kth-truncated series of Equation (49) is:

$$V_k(x,s)=\frac{1}{s(1+e^{-\frac{x}{\sqrt{2}}})}+\sum _{n=1}^k\frac{f_n\left(x\right)}{s^{n\alpha +1}},$$

(50)

and the kth-LRF, $LRe{s}_k(x,s)$, is:

$$\begin{array}{cc}\hfill LRe{s}_k(x,s)=& V_k(x,s)-\frac{1}{s(1+e^{-\frac{x}{\sqrt{2}}})}-\frac{D_x^2{V}_k(x,s)}{s^{\alpha }}-\frac{1}{s^{\alpha }}\mathcal{L}\left[{\left({\mathcal{L}}^{-1}\left[V_k(x,s)\right]\right)}^2\right]\hfill \\ & +\frac{1}{s^{\alpha }}\mathcal{L}\left[{\left({\mathcal{L}}^{-1}\left[V_k(x,s)\right]\right)}^3\right]+\frac{\theta }{s^{\alpha }}{V}_k(x,s)-\frac{\theta }{s^{\alpha }}\mathcal{L}\left[{\left({\mathcal{L}}^{-1}\left[V_k(x,s)\right]\right)}^2\right].\hfill \end{array}$$

(51)

To determine the forms of unknown coefficients $f_n\left(x\right),n=1,2,\dots$, we substitute the kth-truncated series of Equation (50) into the kth-LRF of Equation (51), multiply the new equation by $s^{k\alpha +1}$, and recursively solve the fact $\underset{s\to \infty }{lim}{s}^{k\alpha +1}LRe{s}_k(x,s)=0,k=1,2,\dots$ for $f_k\left(x\right)$. The following are the first few forms of the coefficients $f_k(x,s)$:

$$\begin{array}{cc}\hfill f_1\left(x\right)=& -\frac{e^{\frac{x}{\sqrt{2}}}(-1+2\theta )}{2{\left(1+e^{\frac{x}{\sqrt{2}}}\right)}^2},\hfill \\ \hfill f_2\left(x\right)=& -\frac{e^{\frac{x}{\sqrt{2}}}\left(-1+e^{\frac{x}{\sqrt{2}}}\right){(-1+2\theta )}^2}{4{\left(1+e^{\frac{x}{\sqrt{2}}}\right)}^3},\hfill \\ \hfill f_3\left(x\right)=& \frac{1}{8{(1+e^{\frac{x}{\sqrt{2}}})}^5\sqrt{\pi }\Gamma (1+\alpha )}\left(e^{\frac{x}{\sqrt{2}}}{(1-2\theta )}^2\right(2^{1+2\alpha }{e}^{\frac{x}{\sqrt{2}}}\left(1+e^{\frac{x}{\sqrt{2}}}(-2+\theta )+\theta \right)\Gamma \left(\frac{1}{2}+\alpha \right)\hfill \\ & -(-1+e^{\frac{x}{\sqrt{2}}})\sqrt{\pi }\left(1-6e^{\frac{x}{\sqrt{2}}}-2\theta +e^{\sqrt{2}x}(-1+2\theta )\right)\Gamma (1+\alpha )\left)\right).\hfill \end{array}$$

(52)

We can express the L-RPS solution of Equation (49) in an infinite series as:

$$\begin{array}{cc}\hfill V(x,s)& =\frac{1}{s(1+e^{-\frac{x}{\sqrt{2}}})}-\frac{e^{\frac{x}{\sqrt{2}}}(-1+2\theta )}{2s^{\alpha +1}{(1+e^{\frac{x}{\sqrt{2}}})}^2}-\frac{e^{\frac{x}{\sqrt{2}}}(-1+e^{\frac{x}{\sqrt{2}}}){(-1+2\theta )}^2}{4s^{2\alpha +1}{(1+e^{\frac{x}{\sqrt{2}}})}^3}+\cdots \hfill \end{array}$$

(53)

Consequently, the solution of time-fractional Fitzhugh–Nagumo Equations (46) and (47) by taking the inverse LT of Equation (53) is

$$\begin{array}{cc}\hfill \nu (x,t)& =\frac{1}{(1+e^{-\frac{x}{\sqrt{2}}})}-\frac{e^{\frac{x}{\sqrt{2}}}(-1+2\theta )t^{\alpha }}{2\Gamma \left(\alpha +1\right){(1+e^{\frac{x}{\sqrt{2}}})}^2}-\frac{e^{\frac{x}{\sqrt{2}}}(-1+e^{\frac{x}{\sqrt{2}}}){(-1+2\theta )}^2{t}^{2\alpha }}{4\Gamma \left(2\alpha +1\right){(1+e^{\frac{x}{\sqrt{2}}})}^3}+\cdots \hfill \end{array}$$

(54)

Figure 3 shows the surface graphs of the 4th approximate L-RPS and the exact solutions for Equations (46) and (47) when $\theta =0.8$ at different values of $\alpha$. From these sub-figures, it is clear that ${\nu }_4(x,t)$ close the exact solution as the value of $\alpha$ increases.

Application 4.

Consider the generalized Fisher’s equation such that [19]

$$D_t^{\alpha }\nu (x,t)=D_x^2\nu (x,t)+\nu (x,t)(1-{\nu (x,t)}^6),0<\alpha \le 1,x>0,$$

(55)

subject to the initial condition

$$\nu (x,0)=\frac{1}{\sqrt[3]{1+e^{\frac{3}{2}x}}}.$$

(56)

The exact solution for Equations (55) and (56) when $\alpha =1$ is $\nu (x,t)=\{\frac{1}{2}tanh[-\frac{3}{4}(x-\frac{5}{2}t)]+\frac{1}{2}{\}}^{\frac{1}{3}}$.

Taking the LT to both sides of Equation (55), we obtain:

$$\begin{array}{cc}\hfill V(x,s)& =\frac{1}{s\sqrt[3]{1+e^{\frac{3}{2}x}}}+\frac{D_x^{2}V(x,s)}{s^{\alpha }}+\frac{V(x,s)}{s^{\alpha }}-\frac{1}{s^{\alpha }}\mathcal{L}\left[{\left({\mathcal{L}}^{-1}\left[V(x,s)\right]\right)}^7\right].\hfill \end{array}$$

(57)

Suppose that the k-truncated series solution of Equation (57) takes the following expansion form:

$$V_k(x,s)=\frac{1}{s\sqrt[3]{1+e^{\frac{3}{2}x}}}+\sum _{n=1}^k\frac{f_n\left(x\right)}{s^{n\alpha +1}},$$

(58)

and the kth-LRF,$LRe{s}_k$ is:

$$\begin{array}{cc}\hfill LRe{s}_k(x,s)& =V_k(x,s)-\frac{1}{s\sqrt[3]{1+e^{\frac{3}{2}x}}}-\frac{D_x^2{V}_k(x,s)}{s^{\alpha }}-\frac{V_k(x,s)}{s^{\alpha }}+\frac{1}{s^{\alpha }}\mathcal{L}\left[{\left({\mathcal{L}}^{-1}\left[V_k(x,s)\right]\right)}^7\right].\hfill \end{array}$$

(59)

By applying L-RPSM, we obtain the first four unknown coefficients $f_n\left(x\right),n=1,2,3$ in Equation (58), which are as follows:

$$\begin{array}{cc}\hfill f_1\left(x\right)=& \frac{5e^{\frac{3}{2}x}}{4\sqrt[3]{{(1+e^{\frac{3}{2}x})}^4}},\hfill \\ \hfill f_2\left(x\right)=& \frac{25e^{\frac{3}{2}x}(-3+e^{\frac{3}{2}x})}{16\sqrt[3]{{(1+e^{\frac{3}{2}x})}^7}},\hfill \\ \hfill f_3\left(x\right)=& \frac{25\left(45e^{\frac{3}{2}x}+123e^{3x}-85e^{\frac{9}{2}x}+5e^{6x}-\frac{21{\left(4\right)}^{\alpha +1}{e}^{3x}\Gamma (\frac{1}{2}+\alpha )}{\sqrt{\pi }\Gamma (1+\alpha )}\right)}{64\sqrt[3]{{(1+e^{\frac{3}{2}x})}^{13}}}.\hfill \end{array}$$

(60)

We can express the solution of Equation (57) obtained by L-RPSM as follows:

$$\begin{array}{cc}\hfill V(x,s)=& \frac{5e^{\frac{3}{2}x}}{4s\sqrt[3]{{(1+e^{\frac{3}{2}x})}^4}}+\frac{25e^{\frac{3}{2}x}(-3+e^{\frac{3}{2}x})}{16s^{\alpha +1}\sqrt[3]{{(1+e^{\frac{3}{2}x})}^7}}+\cdots .\hfill \end{array}$$

(61)

Therefore, the solution to the generalized Fisher’s equation as in Equations (55) and (56) is:

$$\begin{array}{cc}\hfill \nu (x,t)& =\frac{5e^{\frac{3}{2}x}}{4\sqrt[3]{{(1+e^{\frac{3}{2}x})}^4}}+\frac{25t^{\alpha }{e}^{\frac{3}{2}x}(-3+e^{\frac{3}{2}x})}{16\Gamma \left(\alpha +1\right)\sqrt[3]{{(1+e^{\frac{3}{2}x})}^7}}+\cdots .\hfill \end{array}$$

(62)

Figure 4 shows the surface graphs of the 4th-AS at different values of $\alpha$ and the exact solutions at $\alpha =1$ for Equations (55) and (56). From this figure, it can be seen that the region of convergence of the series solution is small in direction of the t-axis and that the solution becomes smoother with increasing the value of $\alpha$.

Application 5.

Consider the fractional heat-like equation [14,15,17,18]

$$D_t^{\alpha }\nu (x,t)=\frac{1}{2}{x}^2{D}_x^2\nu (x,t),0<x\le 1,0<t\le 1,0<\alpha <1,$$

(63)

subject to the boundary conditions

$$\nu (0,t)=0,\nu (1,t)=E_{\alpha }\left(t^{\alpha }\right),$$

(64)

with the following initial condition:

$$\nu (x,0)=x^2.$$

(65)

By employing the LT to both sides of Equation (63), we obtain:

$$\begin{array}{cc}\hfill V(x,s)& =\frac{x^2}{s}+\frac{1}{2s^{\alpha }}{x}^2{D}_x^{2}V(x,s).\hfill \end{array}$$

(66)

Suppose that the kth-truncated series solution of Equation (66) takes the following expansion form:

$$V_k(x,s)=\frac{x^2}{s}+\sum _{n=1}^k\frac{f_n\left(x\right)}{s^{n\alpha +1}},$$

(67)

and the kth-LRF, $LRe{s}_k$ is:

$$\begin{array}{cc}\hfill LRe{s}_k(x,s)& =V_k(x,s)-\frac{x^2}{s}-\frac{1}{2s^{\alpha }}{x}^2{D}_x^{2}V(x,s).\hfill \end{array}$$

(68)

By applying L-RPSM, we obtain the unknown coefficients $f_n\left(x\right)$, in Equation (67), which are as follows:

$$\begin{array}{cc}\hfill f_1\left(x\right)=& x^2,\hfill \\ \hfill f_2\left(x\right)=& x^2,\hfill \\ \hfill f_3\left(x\right)=& x^2,\hfill \\ \hfill f_4\left(x\right)=& x^2\hfill \\ \hfill f_n\left(x\right)=& x^2,n=5,6,7,8,\dots .\hfill \end{array}$$

(69)

We can express the L-RPS solution of Equation (66) as follows:

$$\begin{array}{cc}\hfill V(x,s)=& \sum _{n=0}^{\infty }\frac{x^2}{s^{n\alpha +1}}.\hfill \end{array}$$

(70)

Upon using inverse LT for both sides of Equation (70), the solution of the fractional heat-like equation as in Equations (63)–(65) is

$$\begin{array}{cc}\hfill \nu (x,t)& =x^2\sum _{n=0}^{\infty }\frac{t^{n\alpha }}{\Gamma \left(n\alpha +1\right)}=x^2{E}_{\alpha }\left(t^{\alpha }\right),\hfill \end{array}$$

(71)

where $E_{\alpha }\left(z\right)$ is the Mittag–Leffler function and defined as $E_{\alpha }\left(z\right)={\sum }_{n=0}^{\infty }\frac{z^n}{\Gamma (1+n\alpha )}$. It is clear that when $\alpha =1$, we have $E_1\left(t\right)=e^t$. Hence, $x^2{e}^t$ is the exact solution of the classical heat-like equation [14,15,17,18].

Table 1. The numerical solutions and $Con.Err$ obtained by the L-RPSM for Application 5 at $\alpha$ = 0.75, 0.9, and 1.

		$\mathit{\alpha }=0.75$		$\mathit{\alpha }=0.90$		$\mathit{\alpha }=1.00$
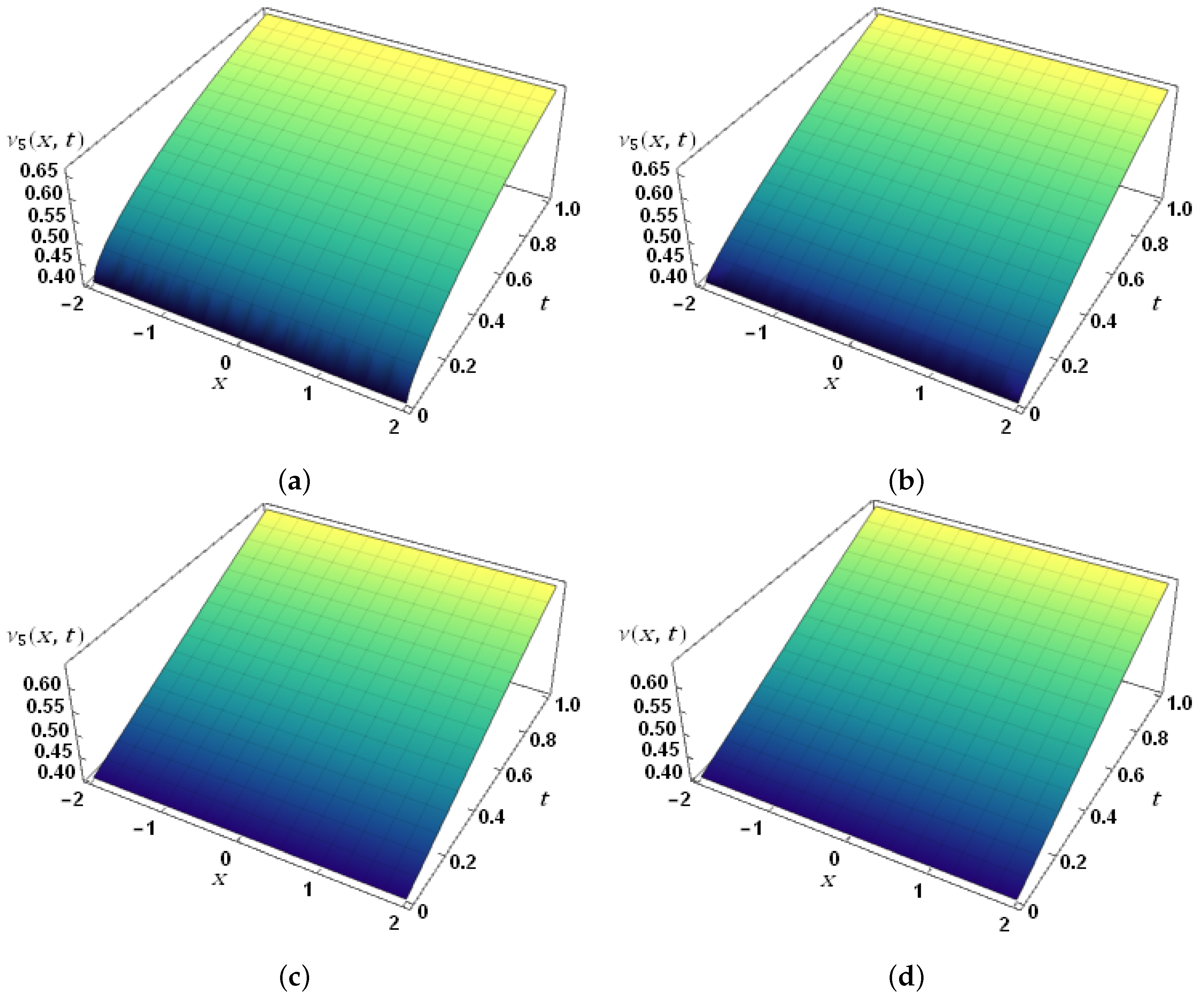
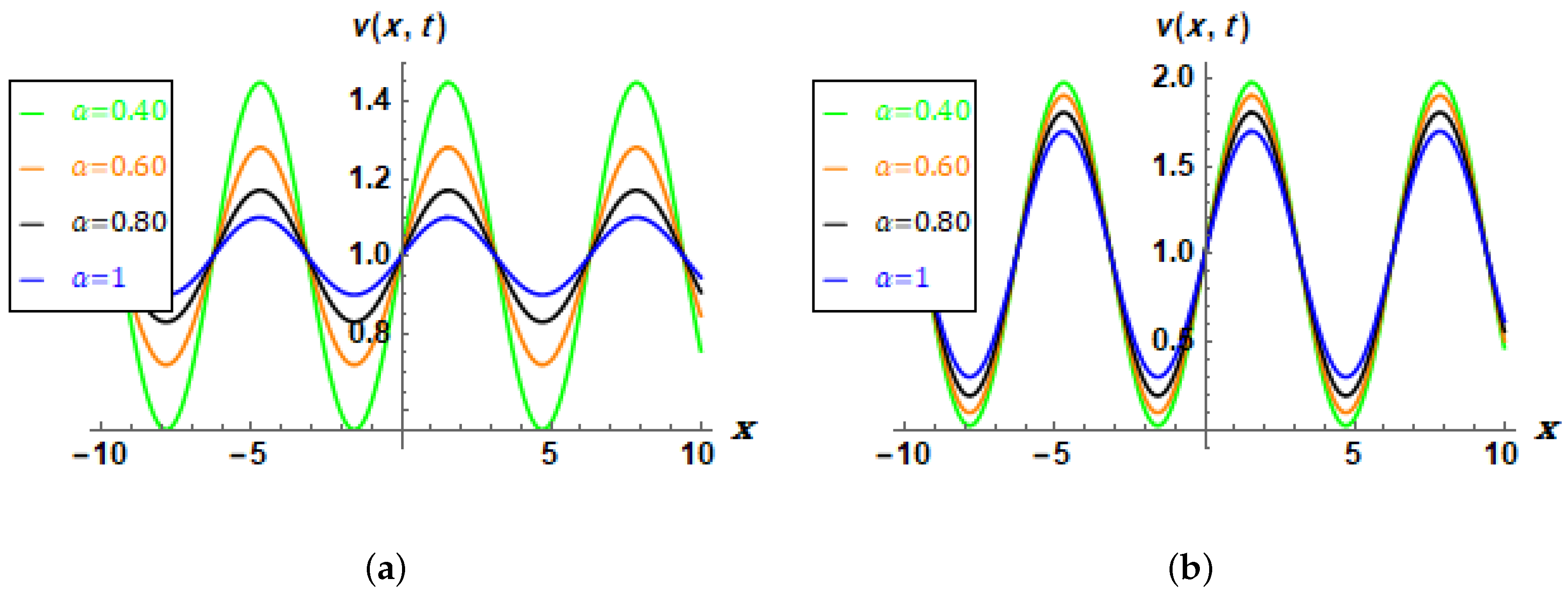
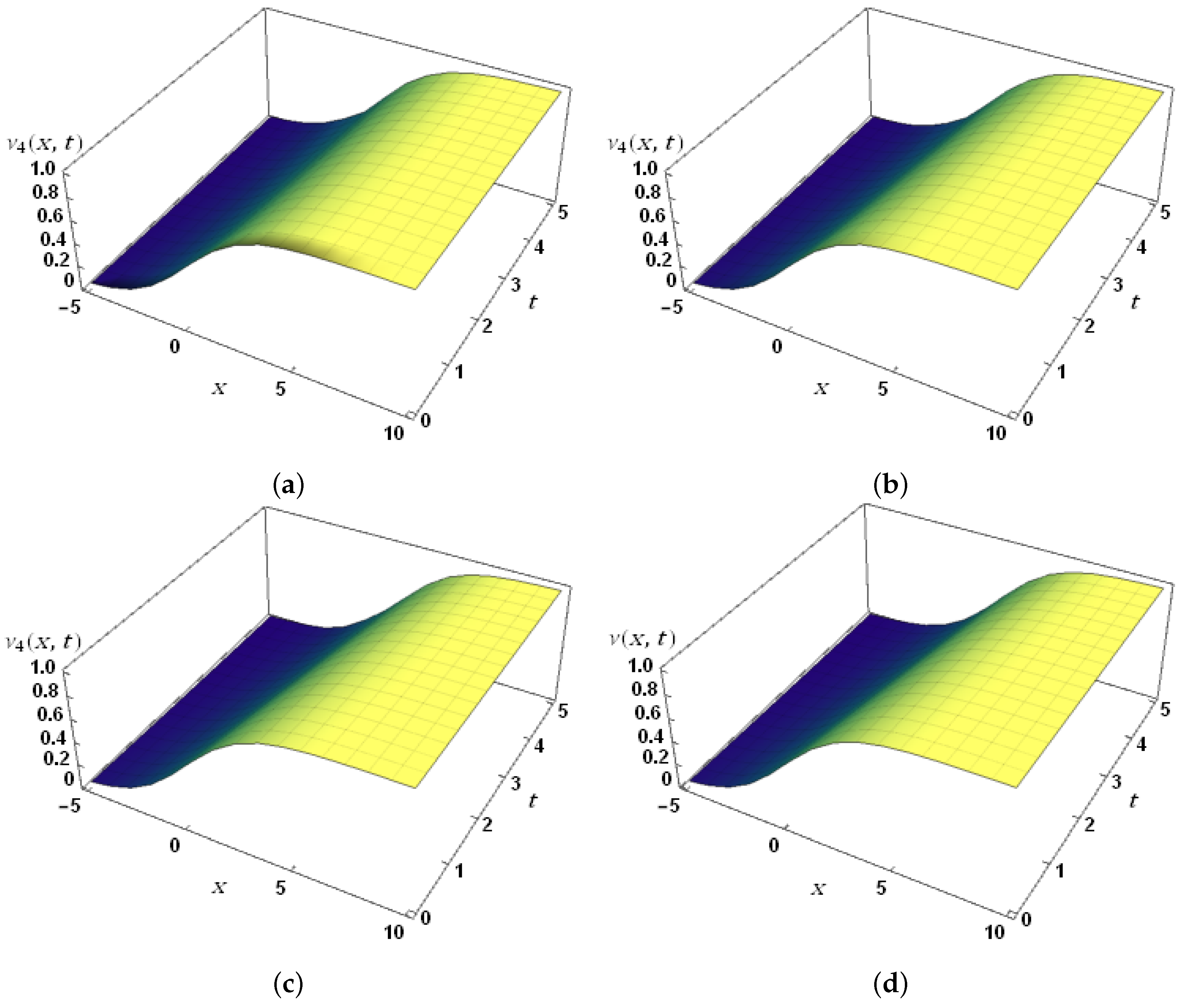
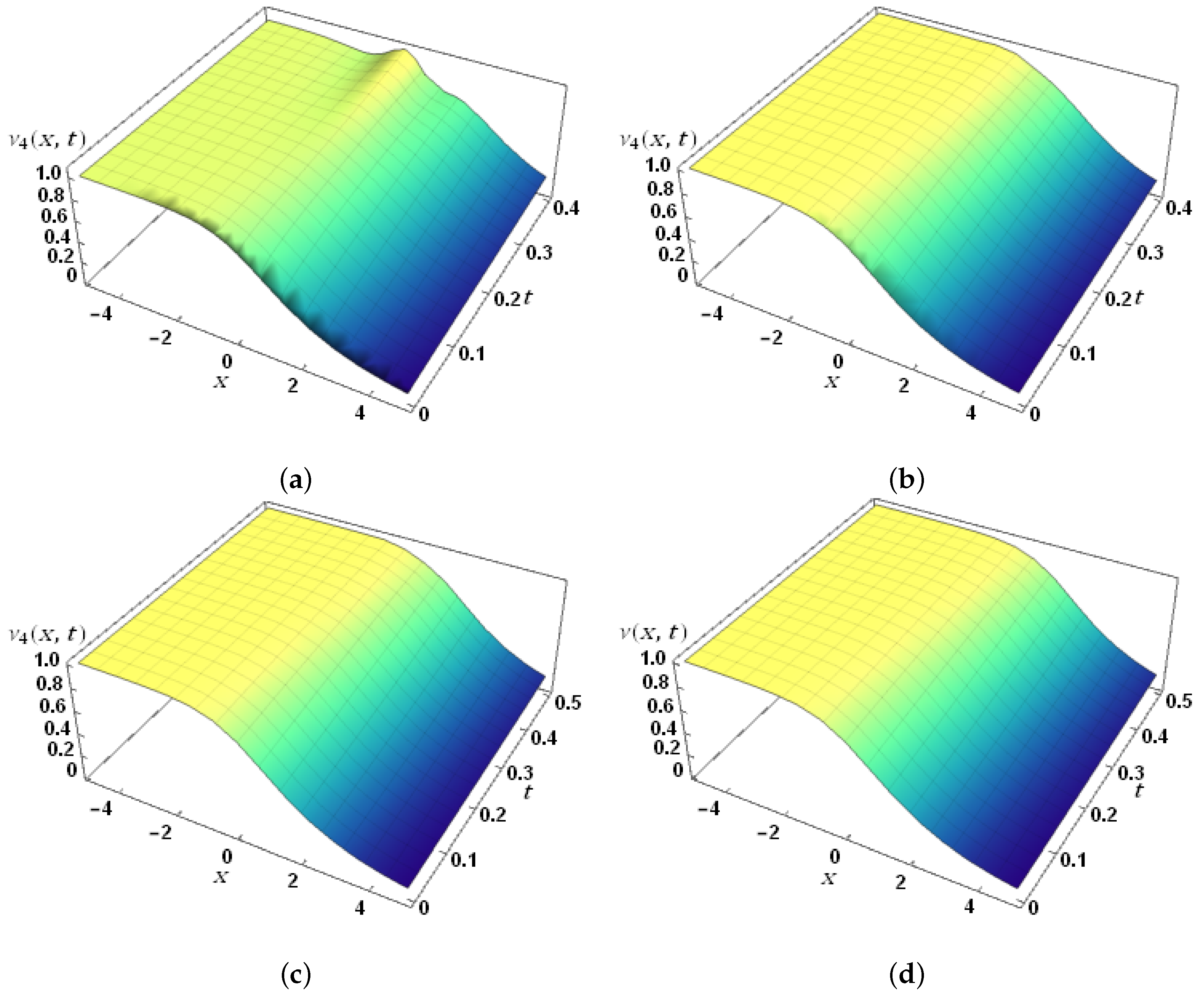
t	x	k = 17	Con.Err	k = 17	Con.Err	k = 17	Con.Err
0.25	0.3	$0.13491$	$1.1782\times {10}^{-17}$	$0.12186$	$7.7226\times {10}^{-22}$	0.11556	$1.0163\times {10}^{-24}$
	0.6	$0.53965$	$4.7127\times {10}^{-17}$	$0.48744$	$3.0890\times {10}^{-21}$	0.46225	$4.0650\times {10}^{-24}$
	0.9	$1.21422$	$1.0603\times {10}^{-16}$	$1.09675$	$6.9503\times {10}^{-21}$	1.04006	$9.1463\times {10}^{-24}$
0.50	0.3	$0.18196$	$4.9884\times {10}^{-14}$	$0.15953$	$1.7042\times {10}^{-17}$	0.14839	$6.7567\times {10}^{-20}$
	0.6	$0.72782$	$1.9954\times {10}^{-13}$	$0.63810$	$6.8169\times {10}^{-17}$	0.59354	$2.7027\times {10}^{-19}$
	0.9	$1.63759$	$4.4896\times {10}^{-13}$	$1.43573$	$1.5338\times {10}^{-16}$	1.33546	$6.0810\times {10}^{-19}$
0.75	0.3	$0.24016$	$6.6573\times {10}^{-12}$	$0.20709$	$5.9642\times {10}^{-15}$	0.19053	$4.5015\times {10}^{-17}$
	0.6	$0.96062$	$2.6629\times {10}^{-11}$	$0.82837$	$2.3857\times {10}^{-14}$	0.76212	$1.8006\times {10}^{-16}$
	0.9	$2.16140$	$5.9916\times {10}^{-11}$	$1.86383$	$5.3677\times {10}^{-14}$	1.71477	$4.0513\times {10}^{-16}$
1.00	0.3	$0.31373$	$2.1553\times {10}^{-10}$	$0.26775$	$3.8243\times {10}^{-13}$	0.24465	$4.5546\times {10}^{-15}$
	0.6	$1.25491$	$8.6213\times {10}^{-10}$	$1.07098$	$1.5297\times {10}^{-12}$	0.97858	$1.8218\times {10}^{-14}$
	0.9	$2.82355$	$1.9398\times {10}^{-09}$	$2.40970$	$3.4419\times {10}^{-12}$	2.20181	$4.0991\times {10}^{-14}$

shows the values of numerical solutions and consecutive errors ($Con.Err$) of 17th-AS obtained by L-RPSM for different values of $\alpha$, where the Con.Err of ${\nu }_{17}(x,t)$ is $Con.Err(x,t)=|{\nu }_{17}(x,t)-{\nu }_{15}(x,t)|$. From the results, we conclude that L-RPSM provides accurate AS and demonstrates rapid convergence in AS. Moreover, the time taken by the computer to calculate the symbolic and numerical quantities was very limited compared with other methods. That is why we can say that L-RPSM is a simplified and attractive method to find exact and ASs.

Table 2. The absolute error of the L-RPS solution obtained for Application 5 compared with various methods at $\alpha =1$.

		VIM [18] and	S-LCM [15]		JTM [14]		L-RPSM
t	x	ADM [17]	$\mathit{N}=15$	$\mathit{N}=25$	$\mathit{N}=10$	$\mathit{N}=15$	$\mathit{k}=15$	$\mathit{k}=17$
0.25	0.3	$1.54\times {10}^{-5}$	$1.09\times {10}^{-6}$	$9.92\times {10}^{-8}$	$2.26\times {10}^{-16}$	$1.05\times {10}^{-16}$	$1.12\times {10}^{-17}$	$1.12\times {10}^{-17}$
	0.6	$6.16\times {10}^{-5}$	$2.96\times {10}^{-5}$	$2.70\times {10}^{-6}$	$4.20\times {10}^{-16}$	$3.09\times {10}^{-17}$	$4.49\times {10}^{-17}$	$4.49\times {10}^{-17}$
	0.9	$1.38\times {10}^{-4}$	$9.94\times {10}^{-5}$	$1.02\times {10}^{-5}$	$1.51\times {10}^{-15}$	$3.54\times {10}^{-16}$	$1.37\times {10}^{-16}$	$1.37\times {10}^{-16}$
0.50	0.3	$2.60\times {10}^{-4}$	$6.45\times {10}^{-6}$	$5.56\times {10}^{-7}$	$4.08\times {10}^{-16}$	$1.02\times {10}^{-16}$	$1.64\times {10}^{-17}$	$1.64\times {10}^{-17}$
	0.6	$1.03\times {10}^{-3}$	$5.24\times {10}^{-5}$	$4.87\times {10}^{-6}$	$2.47\times {10}^{-16}$	$1.17\times {10}^{-16}$	$6.57\times {10}^{-17}$	$6.56\times {10}^{-17}$
	0.9	$2.34\times {10}^{-3}$	$1.47\times {10}^{-4}$	$1.30\times {10}^{-5}$	$2.66\times {10}^{-16}$	$2.45\times {10}^{-16}$	$6.65\times {10}^{-17}$	$6.59\times {10}^{-17}$
0.75	0.3	$1.39\times {10}^{-3}$	$1.40\times {10}^{-5}$	$1.14\times {10}^{-6}$	$6.24\times {10}^{-16}$	$4.70\times {10}^{-17}$	$3.60\times {10}^{-17}$	$9.16\times {10}^{-18}$
	0.6	$5.56\times {10}^{-3}$	$7.67\times {10}^{-5}$	$6.90\times {10}^{-6}$	$9.62\times {10}^{-16}$	$1.74\times {10}^{-16}$	$1.44\times {10}^{-16}$	$3.67\times {10}^{-17}$
	0.9	$1.25\times {10}^{-2}$	$2.01\times {10}^{-4}$	$1.59\times {10}^{-5}$	$1.61\times {10}^{-15}$	$1.43\times {10}^{-17}$	$4.82\times {10}^{-16}$	$7.67\times {10}^{-17}$
1.00	0.3	$4.64\times {10}^{-3}$	$1.83\times {10}^{-5}$	$9.83\times {10}^{-7}$	$1.77\times {10}^{-14}$	$3.11\times {10}^{-16}$	$4.56\times {10}^{-15}$	$7.71\times {10}^{-18}$
	0.6	$1.85\times {10}^{-2}$	$9.40\times {10}^{-5}$	$6.40\times {10}^{-6}$	$7.23\times {10}^{-14}$	$2.25\times {10}^{-16}$	$1.83\times {10}^{-14}$	$3.08\times {10}^{-17}$
	0.9	$4.18\times {10}^{-2}$	$4.26\times {10}^{-4}$	$2.58\times {10}^{-5}$	$1.62\times {10}^{-13}$	$1.80\times {10}^{-16}$	$4.08\times {10}^{-14}$	$1.86\times {10}^{-16}$

presents the comparison of absolute error obtained by L-RPSM with the variational iteration method (VIM) [18], the Adomian decomposition method (ADM) [17], the Sinc–Legendre spectral collocation method (S-LCM) [15], and the Jacopi Tau method (JTM) [14] at $\alpha =1$. From Table 2, it is clear that the absolute errors of the AS obtained by L-RPSM of the heat-like equation are small, and we can see that the number of absolute errors decreases as the number of iterations increases.

5. Conclusions

The main objective of this manuscript is to find exact and accurate ASs for the TFRDEs. We noticed during our research that the L-RPSM could be applied under the same conditions that must be met in the RPSM. It requires that the solution has a fractional expansion as in Equation (8). Without this condition, the L-RPSM cannot be used. However, the mechanism of the technique can be applied or adapted for applicability if a suitable expansion is available to the solution of the differential equation. The L-RPSM is generally simple in manual calculations and also fast in the case of using mathematical programs as it depends mainly on calculating the limit at infinity, unlike other methods that need to calculate the fractional derivative in all stages of the solution, resulting in a high cost in terms of effort and speed. So far, the presented technique has been used on limited classes of ordinary and partial differential equations of fractional order. Therefore, the field is open for researchers to adapt the method to apply it to other forms and types of equations, for example, integral equations, integrodifferential equations, and algebraic equations.