Parameters Identification and Numerical Simulation for a Fractional Model of Honeybee Population Dynamics †
Abstract
1. Introduction
2. Fractional Calculus Background
2.1. Caputo Derivative
2.2. Caputo–Fabrizio Derivative
3. Models’ Interpretations
3.1. Direct Problems
3.1.1. Model with Caputo Derivative
3.1.2. Model with Caputo–Fabrizio Derivative
3.2. Inverse Problems
4. Numerical Solution to the Direct and Inverse Problems
4.1. Model with Caputo Derivative
4.2. Model with Caputo–Fabrizio Derivative
5. Adjoint Optimization Method
5.1. Caputo Fractional Derivative Case
5.2. Caputo–Fabrizio Fractional Derivative Case
6. Numerical Algorithm
| Algorithm 1 Adjoint Equation Optimization Method |
Initialize and . repeat Compute by means of the formulae (14) Define the optimization parameter and compute the new parameter value by
until Set |
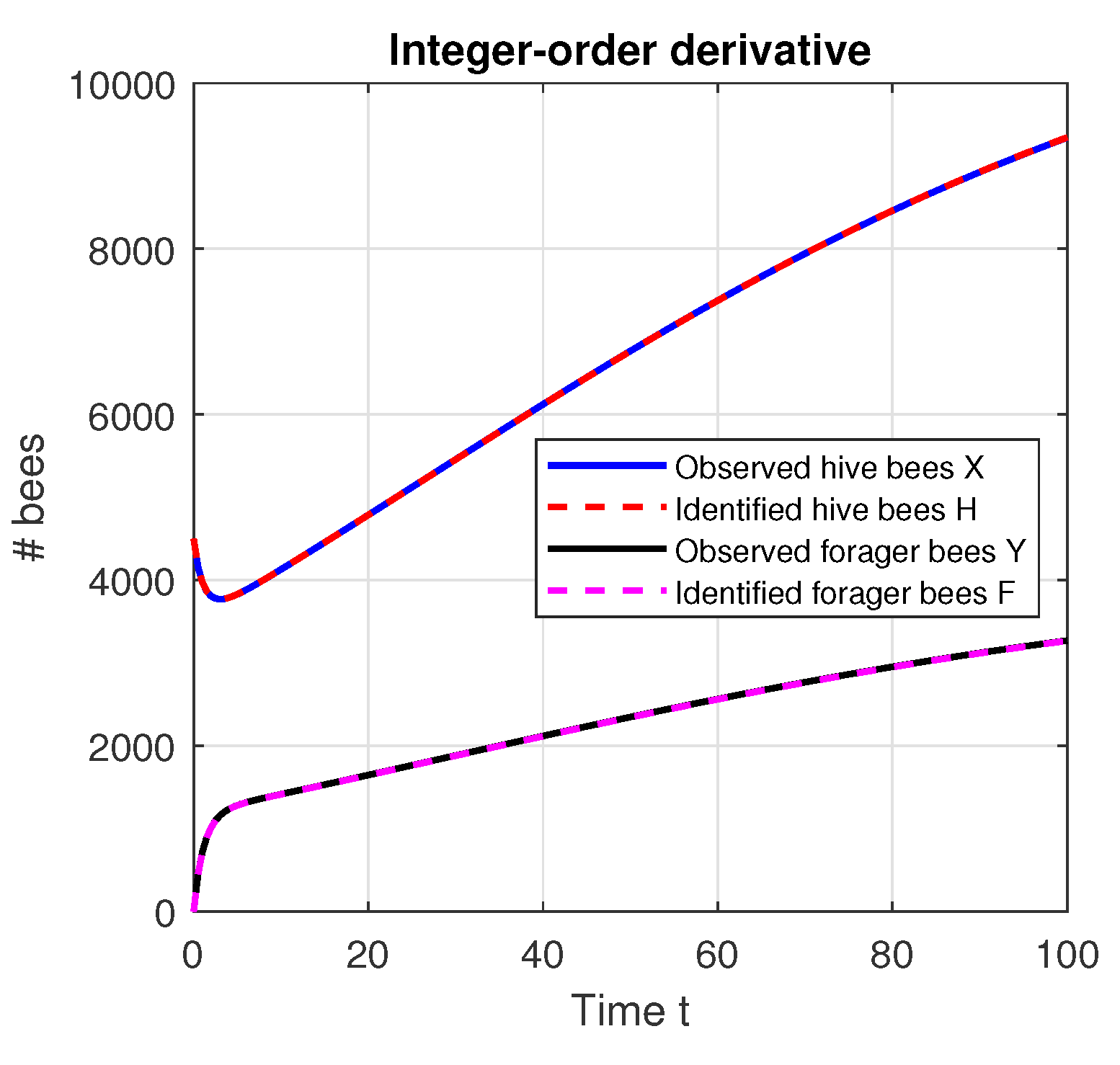
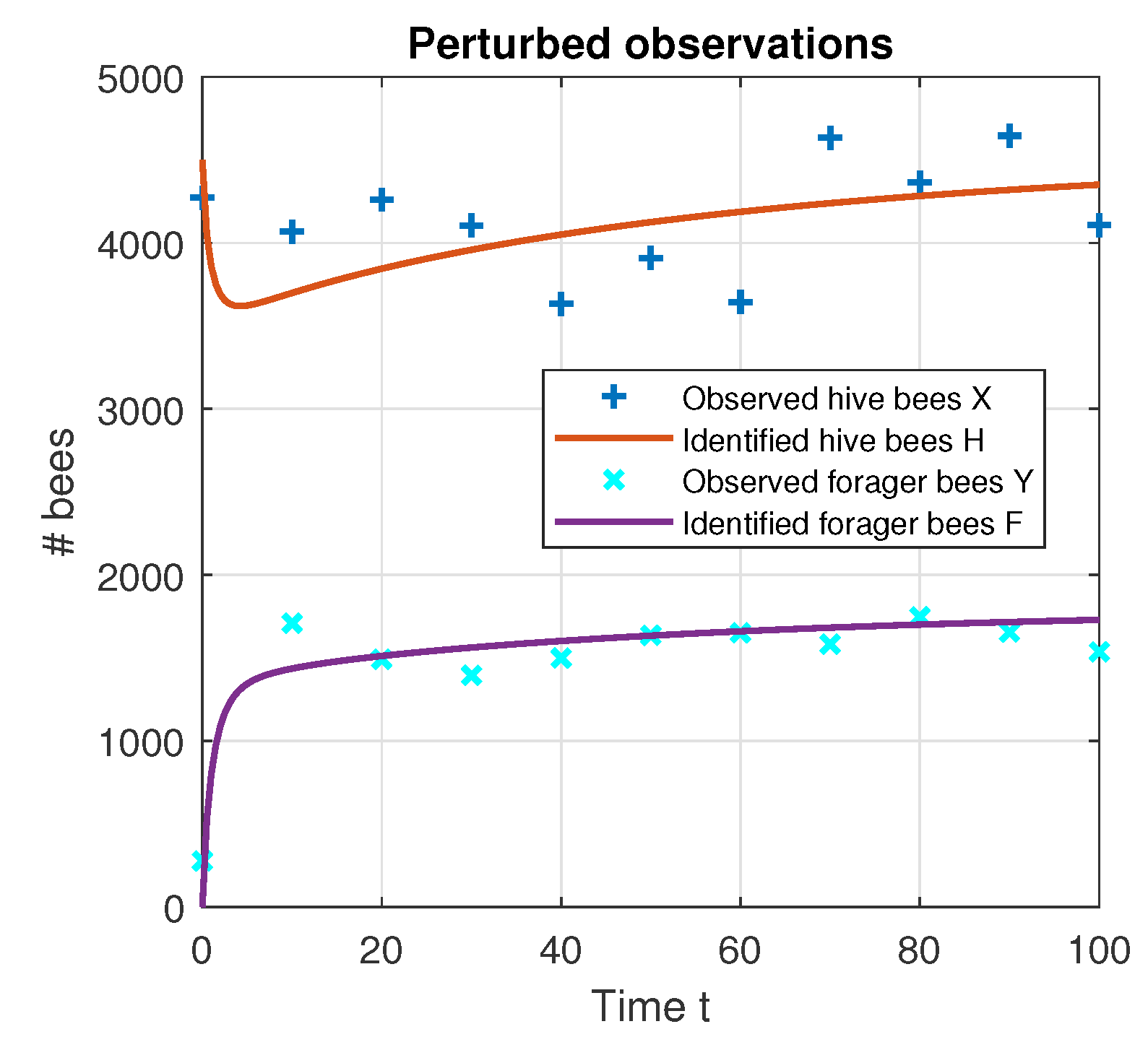
7. Model Simulations
7.1. Direct Problem
7.2. Inverse Problem
8. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Atanasov, A.Z.; Georgiev, I.R. A multicriteria model for optimal location of honey bee colonies in regions without overpopulation. AIP Conf. Proc. 2021, 2333, 090008. [Google Scholar]
- Booton, R.D.; Iwasa, Y.; Marshall, J.A.R.; Childs, D.Z. Stress-mediated Alle effects can cause the sudden collapse of honey bee colonies. J. Theor. Biol. 2017, 420, 213–219. [Google Scholar] [CrossRef] [PubMed]
- Russel, S.; Barron, A.B.; Harris, D. Dynamics modelling of honeybee (Apis mellifera) colony growth and failure. Ecol. Model. 2013, 265, 138–169. [Google Scholar]
- Harbo, J.R. Effect of brood rearing on honey consumption and the survival of worker honey bees. J. Apic. Res. 1993, 32, 11–17. [Google Scholar] [CrossRef]
- Khoury, D.S.; Myerscough, M.R.; Barron, A.B. A quantitative model of honey bee colony population dynamics. PLoS ONE 2011, 6, e18491. [Google Scholar] [CrossRef]
- Khoury, D.S.; Barron, A.B.; Meyerscough, M.R. Modelling food and population dynamics honey bee colonies. PLoS ONE 2013, 8, e0059084. [Google Scholar] [CrossRef]
- Switanek, M.; Crailsheim, K.; Truhetz, H.; Brodschneider, R. Modelling seasonal effects of temperature and precipitation on honey bee winter mortality in a temperate climate. Sci. Total Environ. 2017, 579, 1581–1587. [Google Scholar] [CrossRef]
- Le Conte, Y.; Ellis, M.; Ritter, W. Varroa mites and honey bee health: Can varroa explain part of the colony losses? Apidologie 2010, 41, 353–363. [Google Scholar] [CrossRef]
- Hayes, J., Jr.; Underwood, R.M.; Pettis, J.; van Engelsdorp, D. A survey of honey bee colony losses in the US, fall 2007 to spring 2008. PLoS ONE 2008, 3, e4071. [Google Scholar]
- Atanasov, A.Z.; Georgiev, S.G.; Vulkov, L.G. PParameters reconstruction in modeling of honeybee colonies infested with Varroa destructor. AIP Conf. Proc. 2022, 2522, 110005. [Google Scholar]
- Chen, J.; DeGrandi-Hoffman, G.; Ratti, V.; Kang, Y. Review on mathematical modeling of honeybee population dynamics. Math. Biosci. Eng. 2021, 18, 9606–9650. [Google Scholar] [CrossRef]
- Becher, M.A.; Osborne, J.L.; Thorbek, P.; Kennedy, P.J.; Grimm, V. Towards a systems approach for understanding honeybee decline: A stocktaking and synthesis of existing models. J. Appl. Ecol. 2013, 50, 868–880. [Google Scholar] [CrossRef] [PubMed]
- Li, C.-P.; Tao, C.-X. On the fractional Adams method. Comput. Math. Appl. 2009, 58, 1573–1588. [Google Scholar] [CrossRef]
- Akman, T.; Yıldız, B.; Baleanu, D. New discretization of Caputo–Fabrizio derivative. Comput. Appl. Math. 2018, 37, 3307–3333. [Google Scholar] [CrossRef]
- Baleanu, D.; Diethelm, K.; Scalas, E.; Trujillo, J.J. Fractional Calculus. In Models and Numerical Methods; World Scientific: Singapore, 2017. [Google Scholar]
- Li, C.-P.; Zeng, F.-H. The finite difference methods for fractional ordinary differential equations. Numer. Funct. Anal. Optim. 2013, 34, 149–179. [Google Scholar] [CrossRef]
- Mahatekar, Y.; Scindia, P.S.; Kumar, P. A new numerical method to solve fractional differential equations in terms of Caputo-Fabrizio derivatives. Phys. Scr. 2023, 98, 024001. [Google Scholar] [CrossRef]
- Ionescu, C.; Lopes, A.M.; Copot, D.; Machado, J.A.T.; Bates, J.H.T. The role of fractional calculus in modelling biological phenomena: A review. Commun. Nonlinear Sci. Numer. Simul. 2017, 51, 141–159. [Google Scholar] [CrossRef]
- Magin, R.L. Fractional calculus in bioengineering, part 3. Crit. Rev. Biomed. Eng. 2004, 32, 195–377. [Google Scholar] [CrossRef]
- Yıldız, T.A. A fractional dynamical model for honeybee colony population. Int. J. Biomath. 2018, 11, 1850063. [Google Scholar]
- Georgiev, S.G.; Vulkov, L.G. Parameter identification approach for a fractional dynamics model of honeybee population. In Lecture Notes in Computer Science; Springer: Cham, Switzerland, 2022; Volume 13127, pp. 40–48. [Google Scholar]
- Caputo, M.; Fabrizio, M. A new definition of fractional derivative without singular kernel. Progr. Fract. Differ. Appl. 2015, 1, 73–85. [Google Scholar]
- Baleanu, D.; Jajarmi, A.; Mohammadi, H.; Rezapour, S. A new study on the mathematical modelling of human liver with Caputo–Fabrizio fractional derivative. Chaos Solitons Fractals 2020, 134, 109705. [Google Scholar] [CrossRef]
- Kilbas, A.-A.; Srivastava, H.M.; Trujillo, J.J. Theory and Applications of Fractional Differential Equations; Elsevier B. V.: Amsterdam, The Netherlands, 2006. [Google Scholar]
- Losada, J.; Nieto, J.J. Properties of a new fractional derivative without singular kernel. Progr. Fract. Differ. Appl. 2015, 1, 87–92. [Google Scholar]
- Zine, H.; Lotfi, E.M.; Torres, D.F.M.; Yousfi, N. Taylor’s formula for generalized weighted fractional derivatives with nonsingular kernels. Axioms 2022, 11, 231. [Google Scholar] [CrossRef]
- Lin, W. Global existence theory and chaos control of fractional differential equations. J. Math. Anal. Appl. 2007, 332, 709–726. [Google Scholar] [CrossRef]
- Marchuk, G.I.; Agoshkov, V.I.; Shutyaev, V.P. Adjoint Equations and Perturbation Algorithms in Nonlinear Problems; CRC Press: Boca Raton, FL, USA, 1996. [Google Scholar]
- Diethelm, K.; Ford, N.J.; Freed, A.D. Detailed error analysis for a fractional Adams method. Numer. Algor. 2004, 36, 31–52. [Google Scholar] [CrossRef]
- Kabanikhin, S.I. Inverse and Ill-Posed Problems; De Gruyter: Leipzig, Germany, 2012. [Google Scholar]
- Atanasov, A.Z.; Georgiev, S.G. A numerical parameter estimation approach of the honeybee population. In Modelling and Development of Intelligent Systems; Springer: Cham, Switzerland, 2021; Volume 1341, pp. 349–362. [Google Scholar]
- Atanasov, A.Z.; Georgiev, S.G.; Vulkov, L.G. Parameter identification of colony collapse disorder in honeybees as a contagion. In Communications in Computer and Information Science; Springer: Cham, Switzerland, 2021; Volume 1341, pp. 363–377. [Google Scholar]
- Atanasov, A.Z.; Georgiev, S.G.; Vulkov, L.G. Reconstruction analysis of honeybee colony collapse disorder modeling. Optim. Eng. 2021, 22, 2481–2503. [Google Scholar] [CrossRef]
- Georgiev, S.; Vulkov, L. Numerical coefficient reconstruction of time-depending integer- and fractional-order SIR models for economic analysis of COVID-19. Mathematics 2022, 10, 4247. [Google Scholar] [CrossRef]
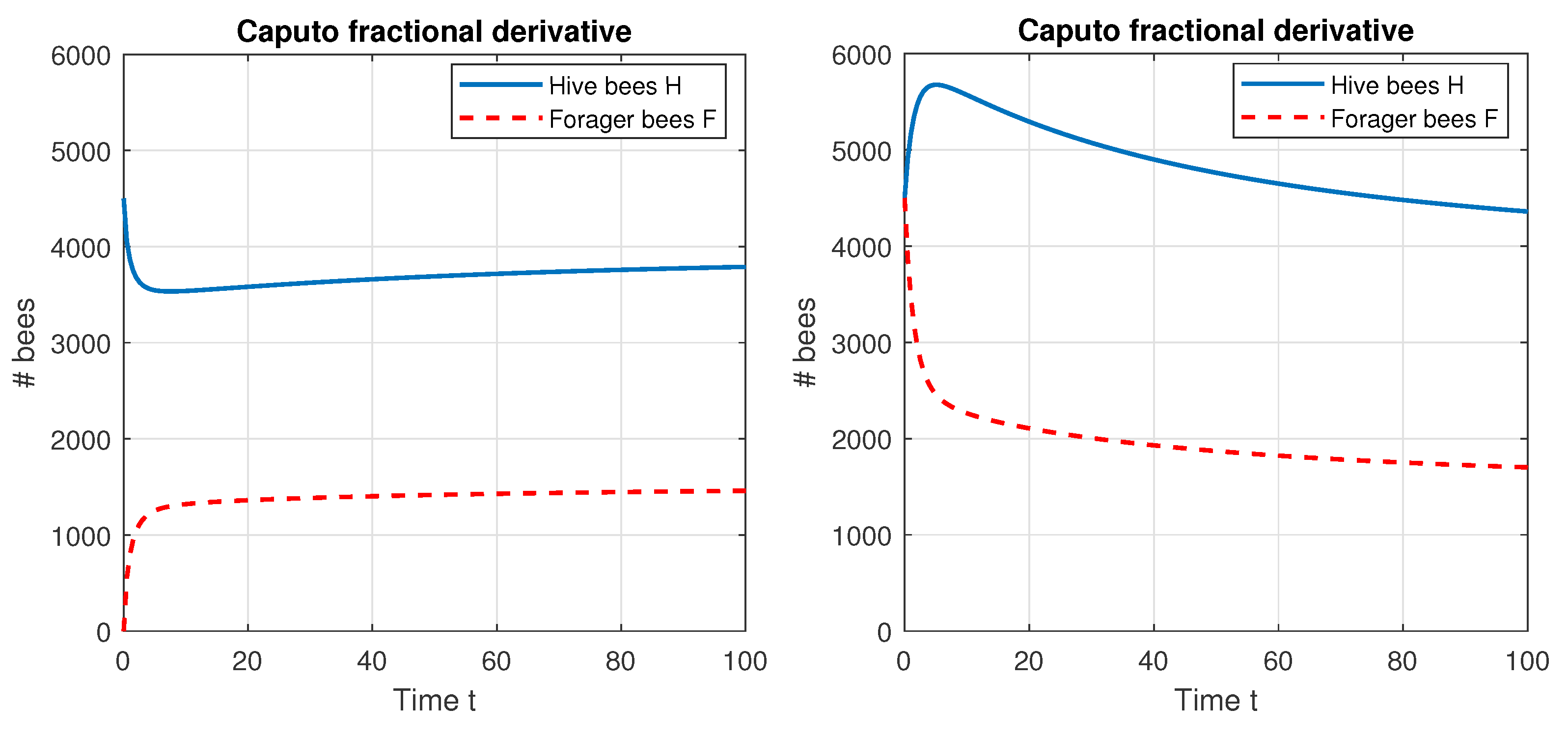
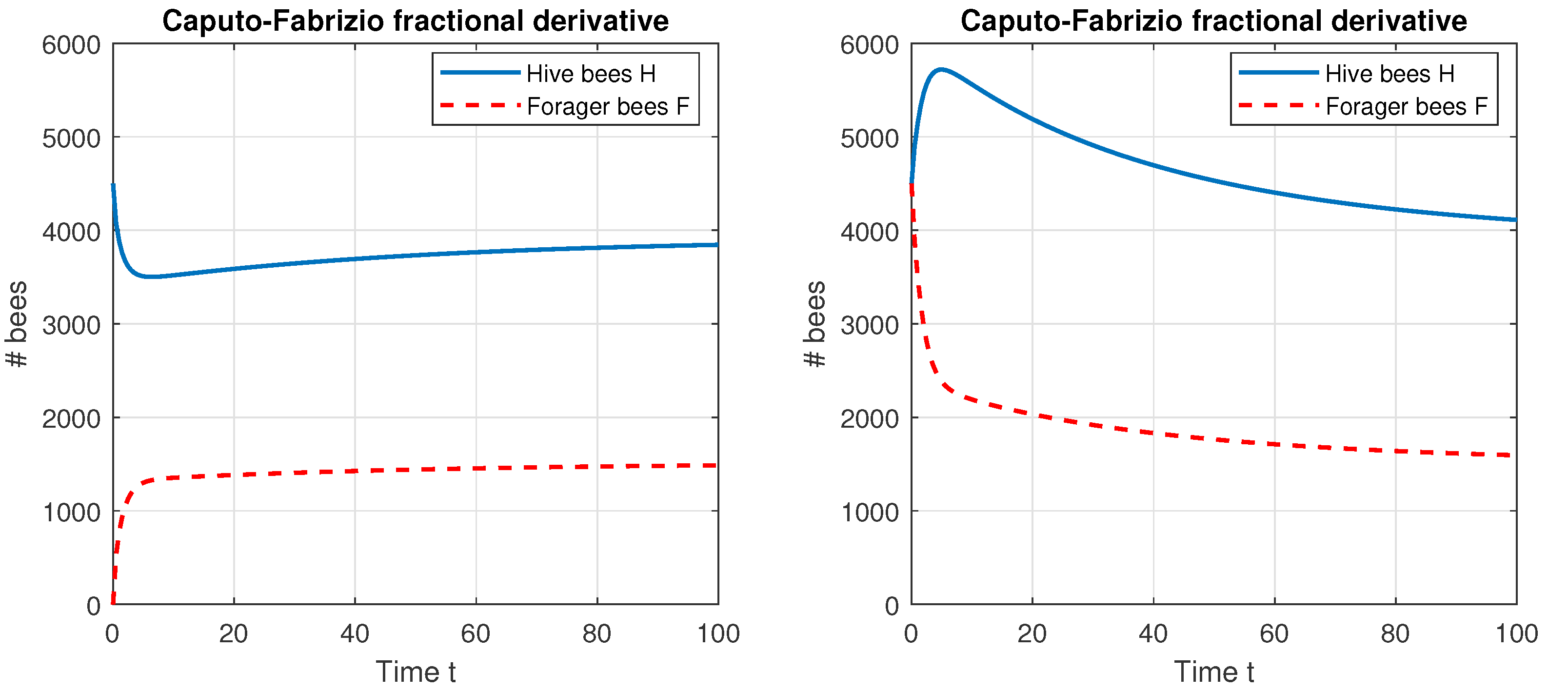
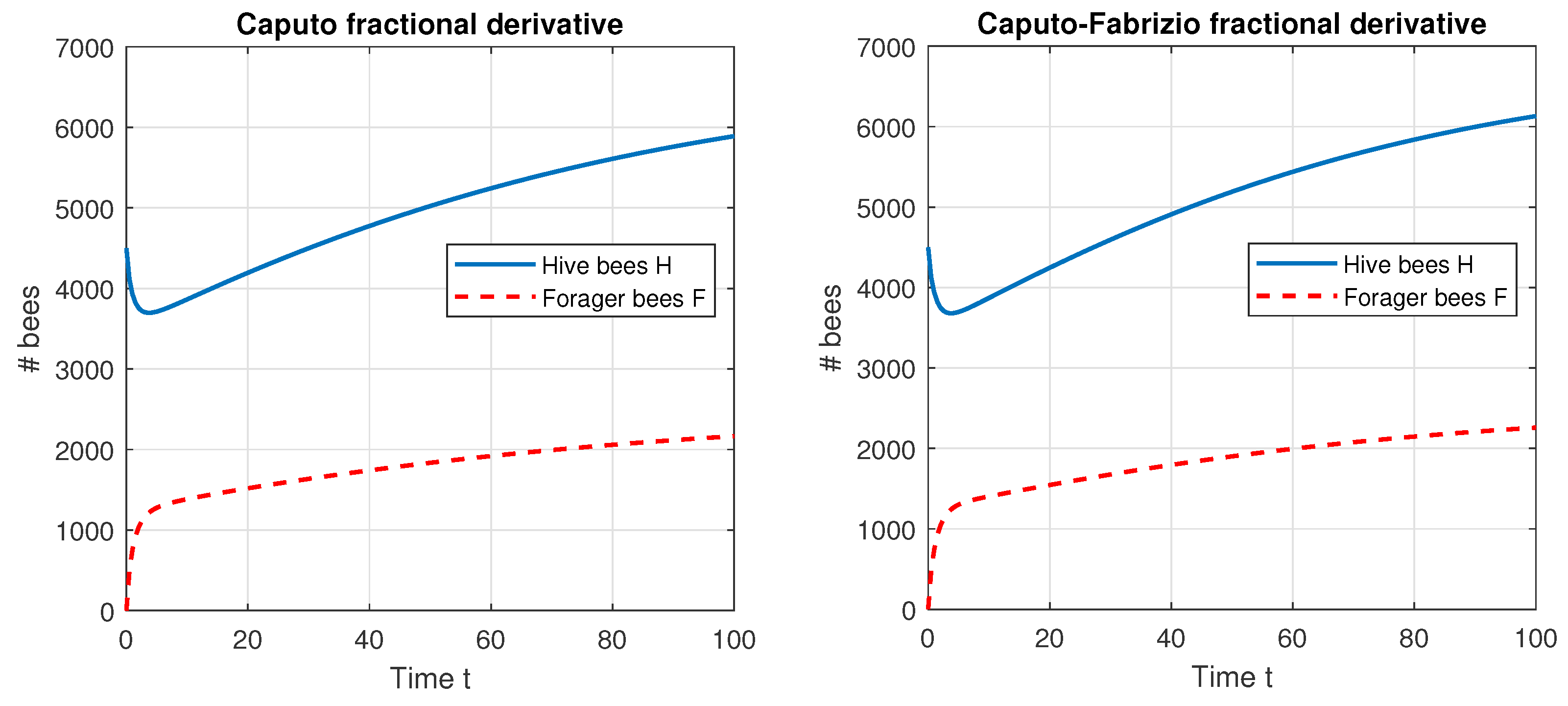

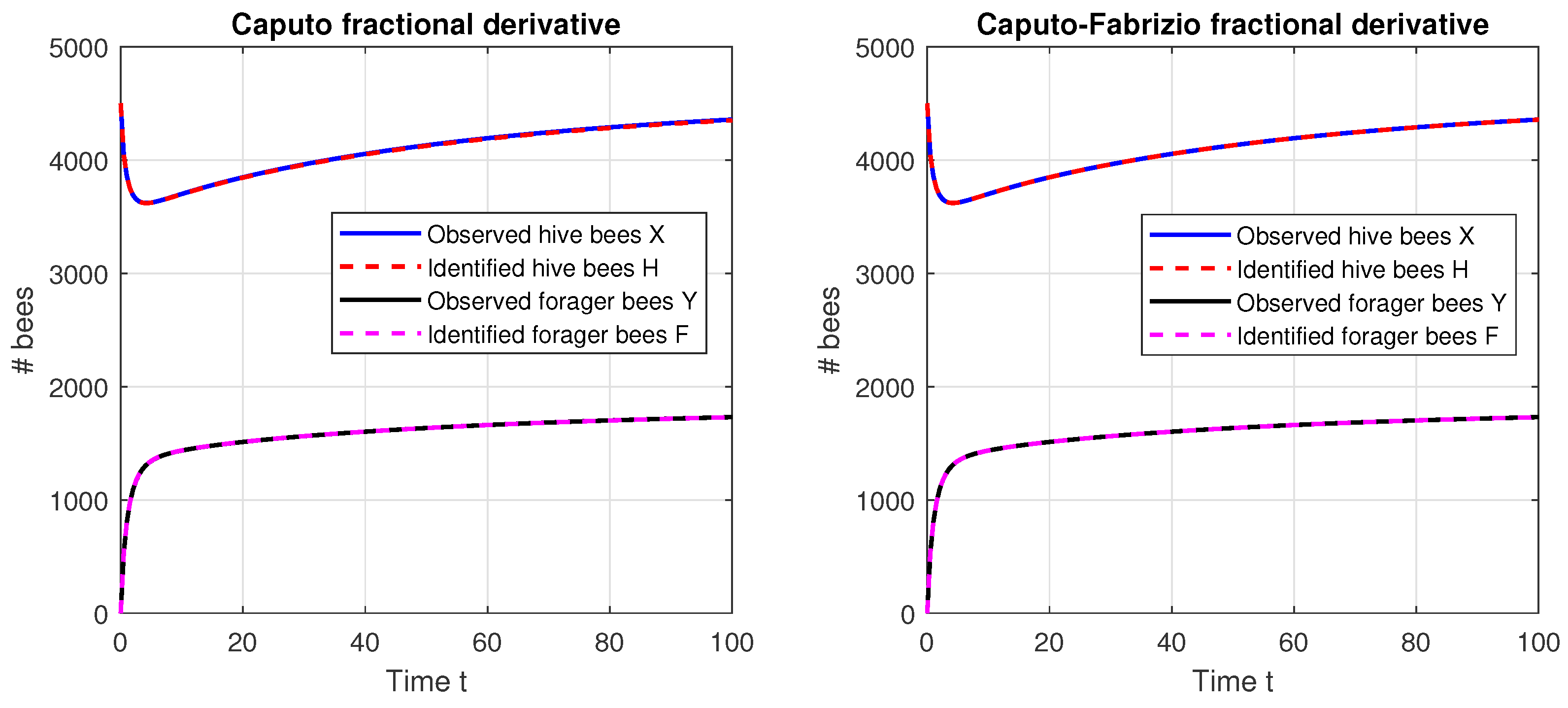

| Parameter | ||||||
|---|---|---|---|---|---|---|
| m | 0.20 | 0.1540 | 0.1538 | 2.2148 × 10−4 | 0.0014 | 3.40 × 10−13 |
| n | 0.01 | 0.0086 | 0.0086 | 1.0541 × 10−5 | 0.0012 | 3.25 × 10−15 |
| 0.30 | 0.2500 | 0.2501 | 1.1786 × 10−4 | 4.7145 × 10−4 | 4.50 × 10−13 | |
| 0.70 | 0.7500 | 0.7499 | 5.5183 × 10−5 | 7.3578 × 10−5 | 1.55 × 10−12 | |
| 30,000 | 27,000 | 26,995 | 5.1638 | 1.9125 × 10−4 | 2.55 × 10−3 |
| Parameter | ||||||
|---|---|---|---|---|---|---|
| m | 0.20 | 0.1540 | 0.1536 | 3.5212 × 10−4 | 0.0023 | 3.40 × 10−13 |
| n | 0.01 | 0.0086 | 0.0086 | 1.4920 × 10−5 | 0.0017 | 3.25 × 10−15 |
| 0.30 | 0.2500 | 0.2502 | 2.4980 × 10−4 | 9.9920 × 10−4 | 4.60 × 10−13 | |
| 0.70 | 0.7500 | 0.7503 | 3.0453 × 10−4 | 4.0604 × 10−4 | 1.60 × 10−12 | |
| 30,000 | 27,000 | 27,023 | 22.9362 | 8.4949 × 10−4 | 2.54 × 10−3 |
| Parameter | ||||||
|---|---|---|---|---|---|---|
| m | 0.20 | 0.1540 | 0.1539 | 7.3542 × 10−5 | 4.7754 × 10−4 | 3.36 × 10−13 |
| n | 0.01 | 0.0086 | 0.0086 | 6.0311 × 10−6 | 7.0493 × 10−4 | 3.34 × 10−15 |
| 0.30 | 0.2500 | 0.2501 | 1.1972 × 10−4 | 4.7887 × 10−4 | 4.57 × 10−13 | |
| 0.70 | 0.7500 | 0.7499 | 9.9080 × 10−5 | 1.3211 × 10−4 | 1.53 × 10−12 | |
| 30,000 | 27,000 | 27,016 | 16.0889 | 5.9589 × 10−4 | 2.63 × 10−3 |
| Parameter | ||||||
|---|---|---|---|---|---|---|
| m | 0.20 | 0.1540 | 0.1541 | 7.8712 × 10−5 | 5.1112 × 10−4 | 3.30 × 10−13 |
| n | 0.01 | 0.0086 | 0.0085 | 6.7634 × 10−6 | 7.9053 × 10−4 | 3.34 × 10−15 |
| 0.30 | 0.2500 | 0.2501 | 1.0681 × 10−4 | 4.2724 × 10−4 | 4.61 × 10−13 | |
| 0.70 | 0.7500 | 0.7504 | 4.1135 × 10−4 | 5.4847 × 10−4 | 1.56 × 10−12 | |
| 30,000 | 27,000 | 26,690 | 10.0159 | 3.7096 × 10−4 | 2.63 × 10−3 |
| Parameter | ||||||
|---|---|---|---|---|---|---|
| m | 0.20 | 0.1540 | 0.1539 | 1.4229 × 10−4 | 9.2398 × 10−4 | 3.40 × 10−13 |
| n | 0.01 | 0.0086 | 0.0086 | 1.4492 × 10−7 | 1.6939 × 10−5 | 3.15 × 10−15 |
| 0.30 | 0.2500 | 0.2496 | 3.7857 × 10−4 | 1.5143 × 10−3 | 4.54 × 10−13 | |
| 0.70 | 0.7500 | 0.7500 | 3.9556 × 10−6 | 5.2741 × 10−6 | 1.60 × 10−12 | |
| 30,000 | 27,000 | 27,055 | 54.8891 | 2.0329 × 10−3 | 2.66 × 10−3 |
| Parameter | ||||||
|---|---|---|---|---|---|---|
| m | 0.20 | 0.1540 | 0.1543 | 2.5642 × 10−4 | 0.0017 | 3.40 × 10−13 |
| n | 0.01 | 0.0086 | 0.0086 | 1.5084 × 10−5 | 0.0018 | 3.25 × 10−15 |
| 0.30 | 0.2500 | 0.2497 | 3.0945 × 10−4 | 0.0012 | 4.50 × 10−13 | |
| 0.70 | 0.7500 | 0.7504 | 3.6251 × 10−4 | 4.8335 × 10−4 | 1.55 × 10−12 | |
| 30,000 | 27,000 | 27,007 | 7.2513 | 2.6857 × 10−4 | 2.55 × 10−3 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Georgiev, S.; Vulkov, L. Parameters Identification and Numerical Simulation for a Fractional Model of Honeybee Population Dynamics. Fractal Fract. 2023, 7, 311. https://doi.org/10.3390/fractalfract7040311
Georgiev S, Vulkov L. Parameters Identification and Numerical Simulation for a Fractional Model of Honeybee Population Dynamics. Fractal and Fractional. 2023; 7(4):311. https://doi.org/10.3390/fractalfract7040311
Chicago/Turabian StyleGeorgiev, Slavi, and Lubin Vulkov. 2023. "Parameters Identification and Numerical Simulation for a Fractional Model of Honeybee Population Dynamics" Fractal and Fractional 7, no. 4: 311. https://doi.org/10.3390/fractalfract7040311
APA StyleGeorgiev, S., & Vulkov, L. (2023). Parameters Identification and Numerical Simulation for a Fractional Model of Honeybee Population Dynamics. Fractal and Fractional, 7(4), 311. https://doi.org/10.3390/fractalfract7040311








