Investigation of Fractional Order Dynamics of Tuberculosis under Caputo Operator
Abstract
1. Introduction
2. Preliminaries
3. Existence and Uniqueness
- only if
- The operator is compact and continuous;
- is a contraction mapping.
4. Approximate Solution by LADM
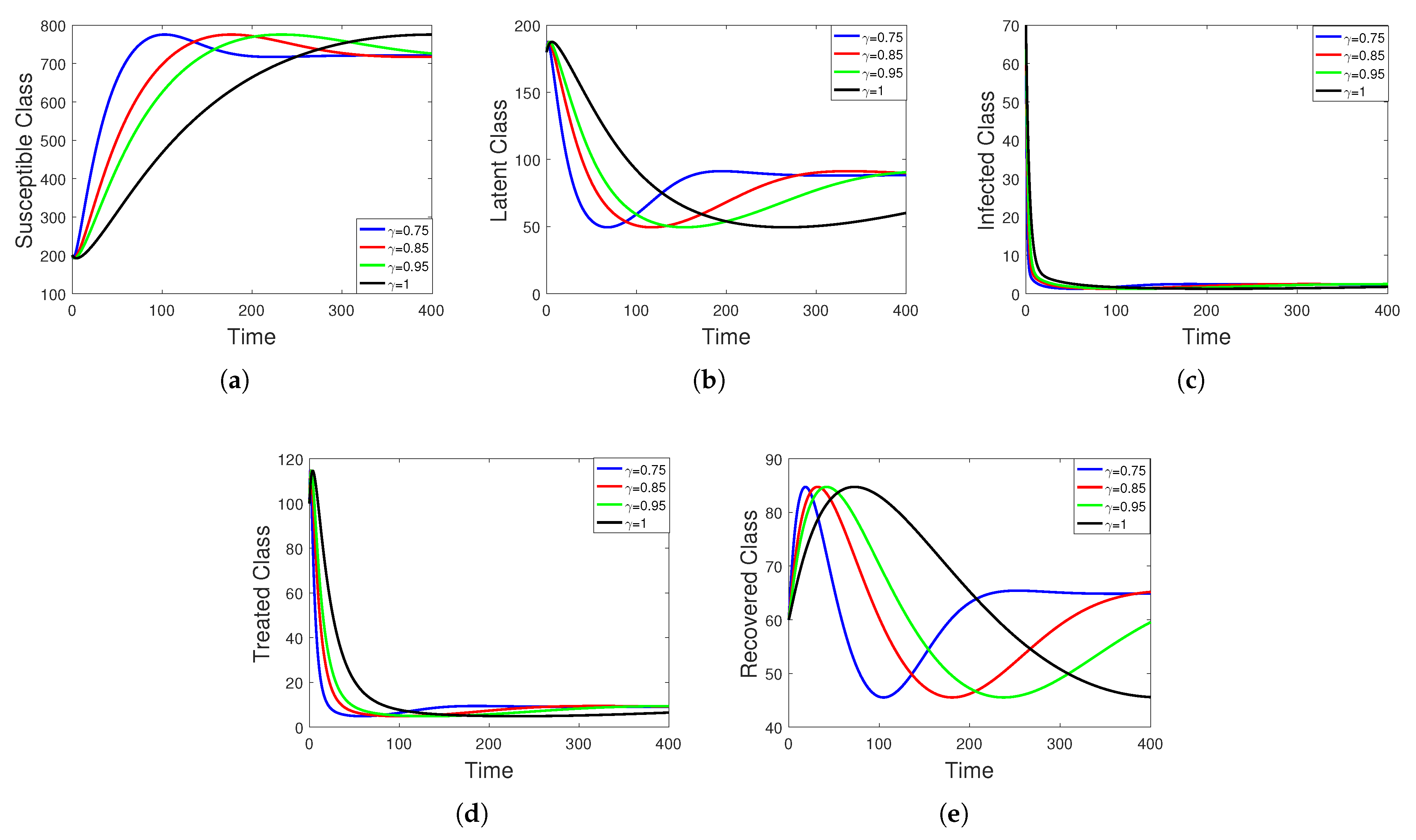
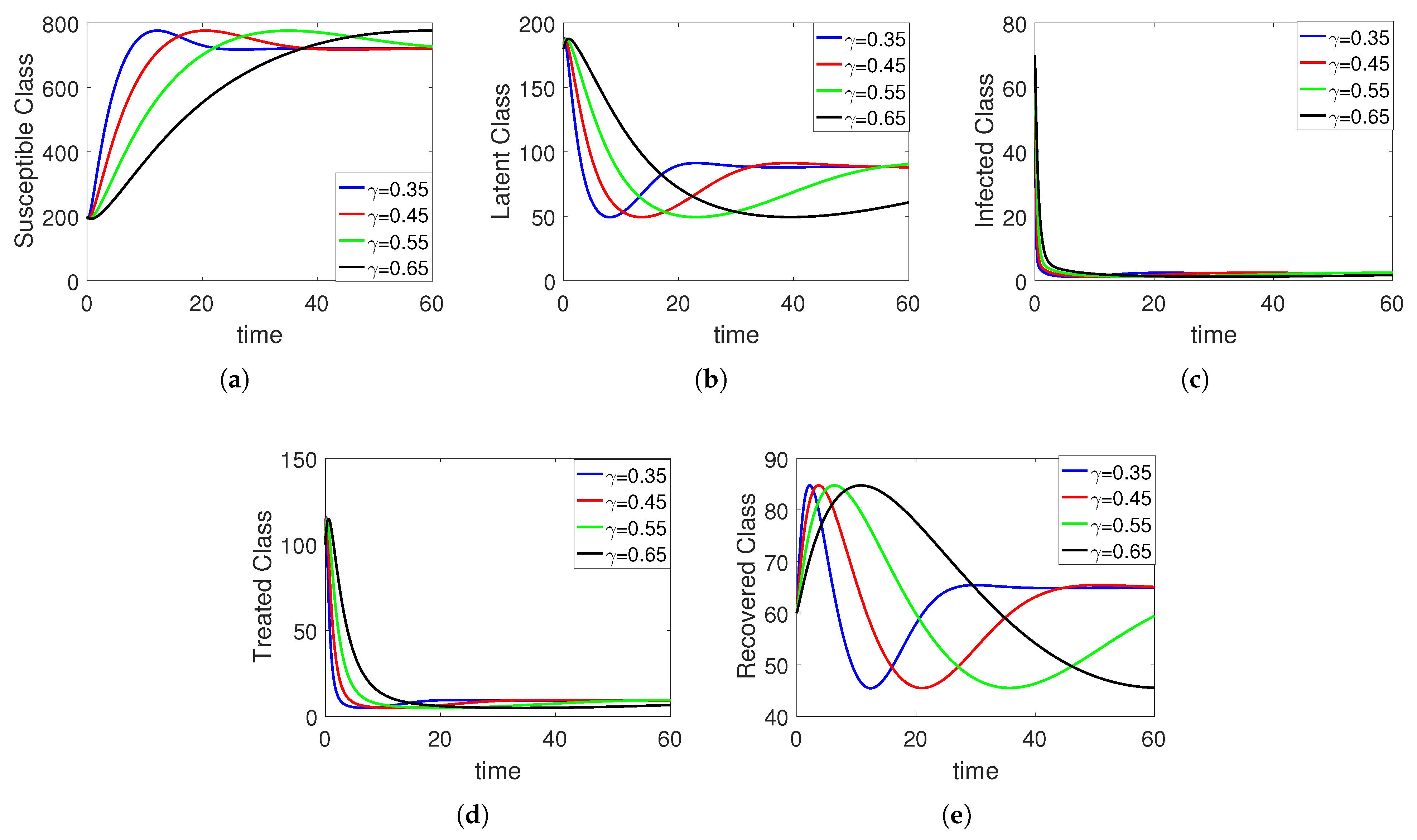
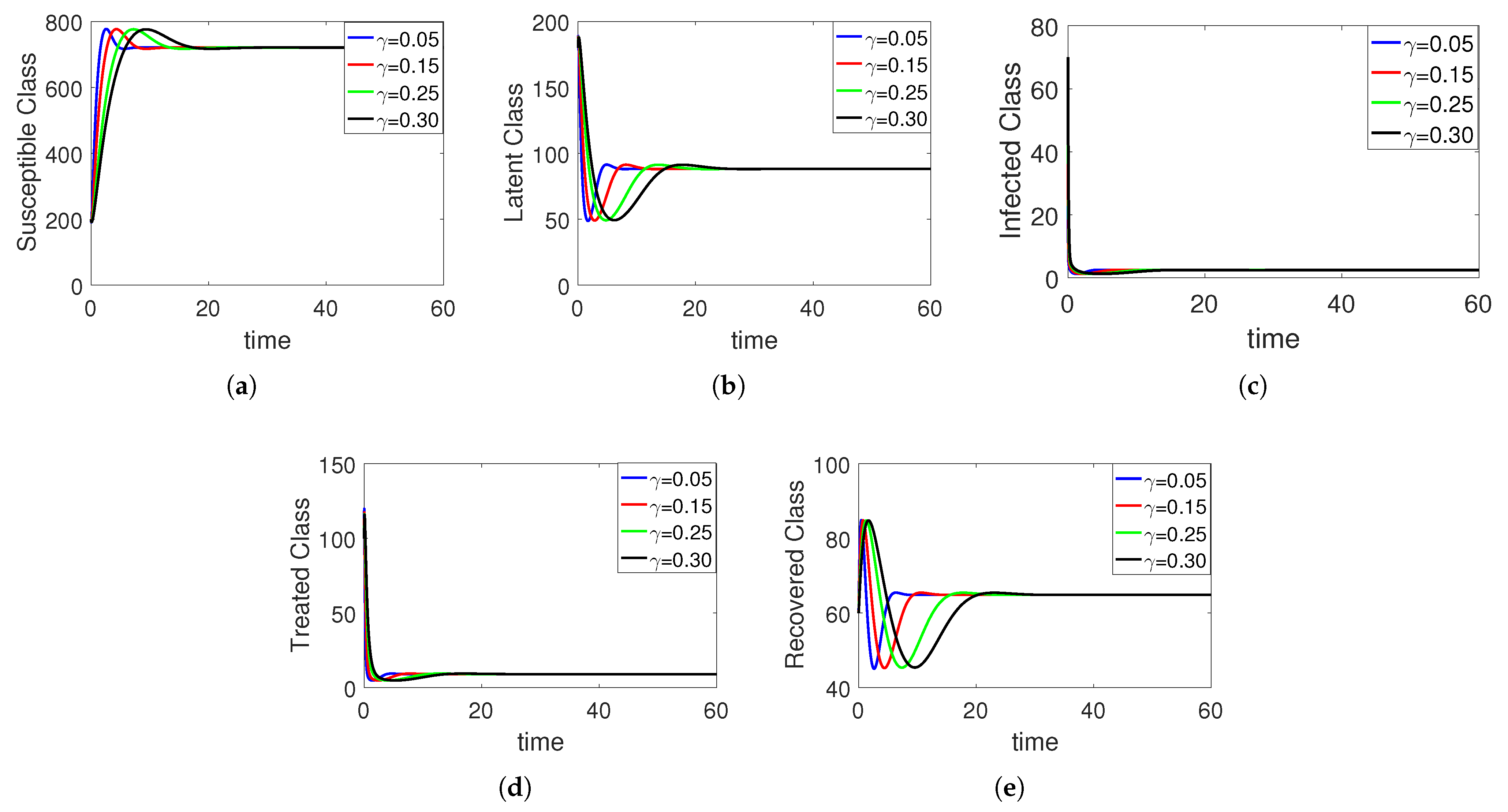
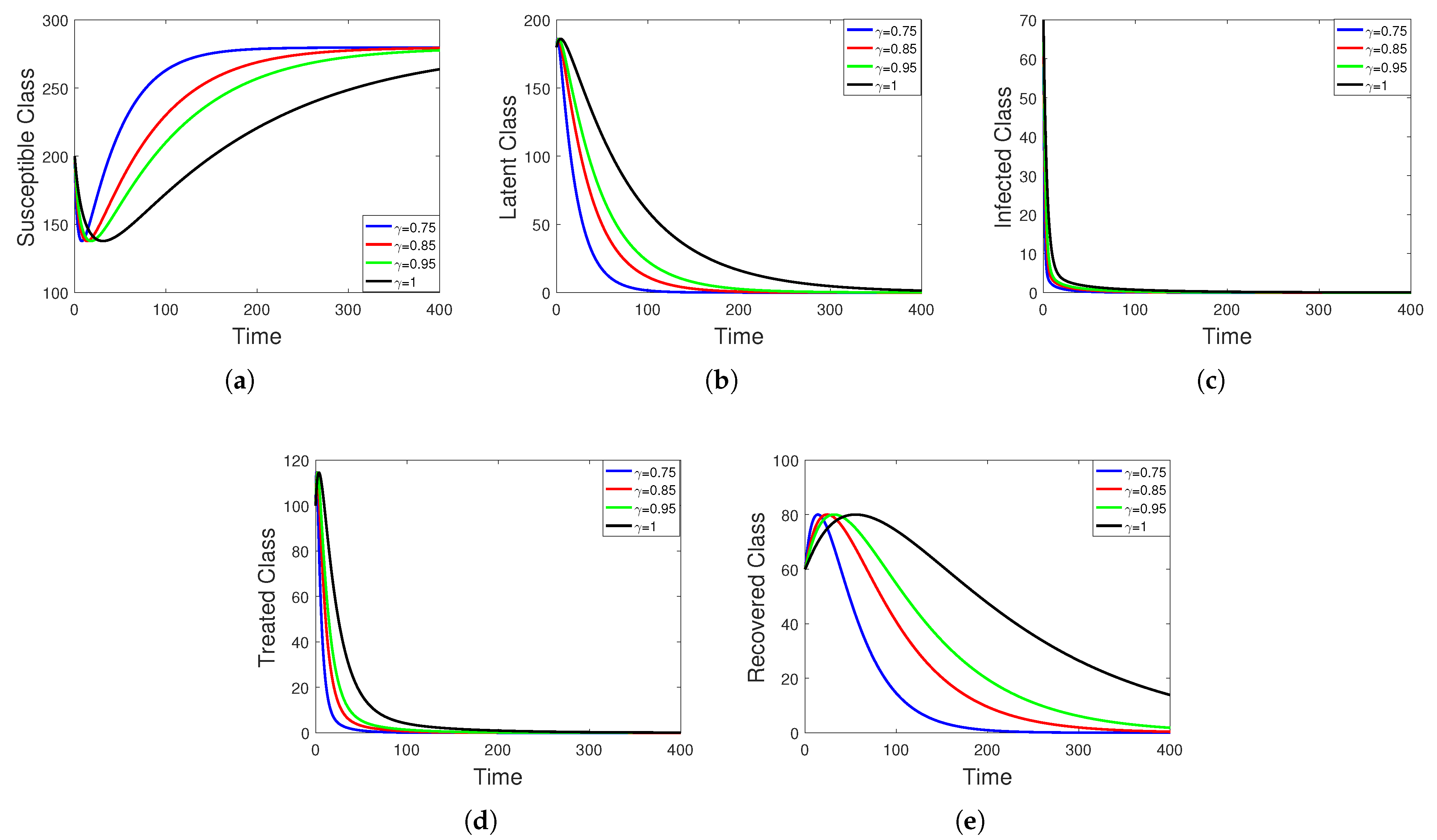
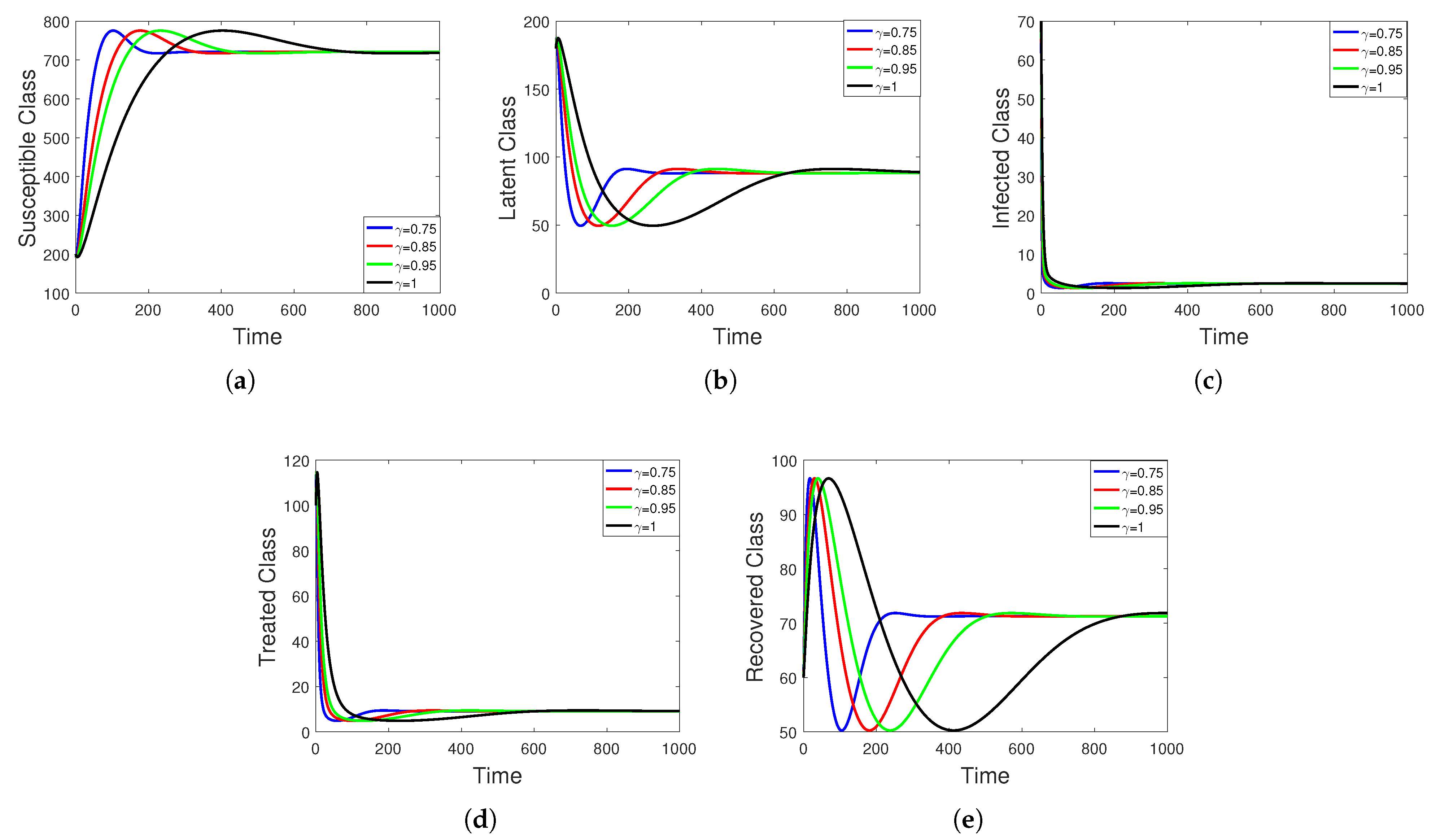
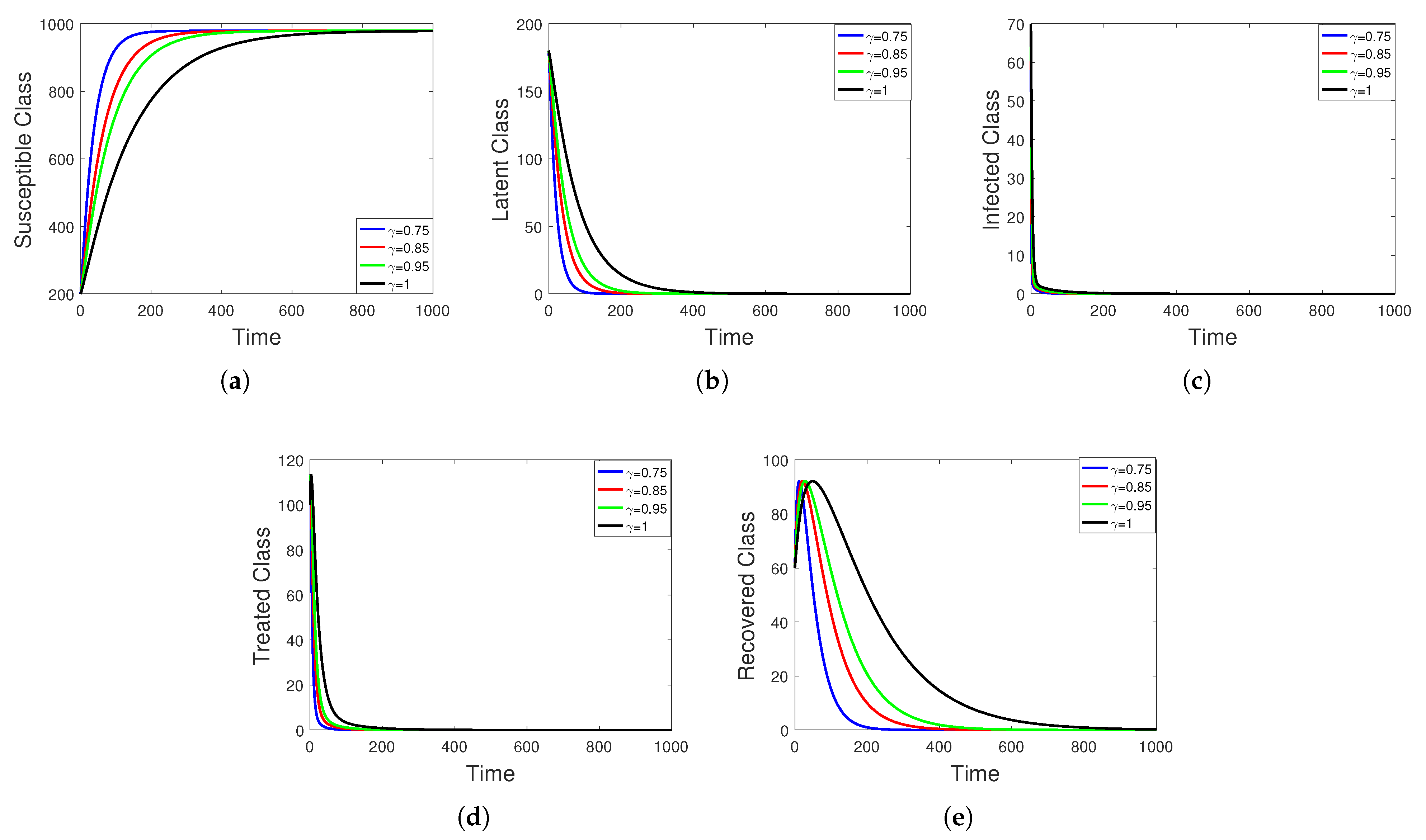
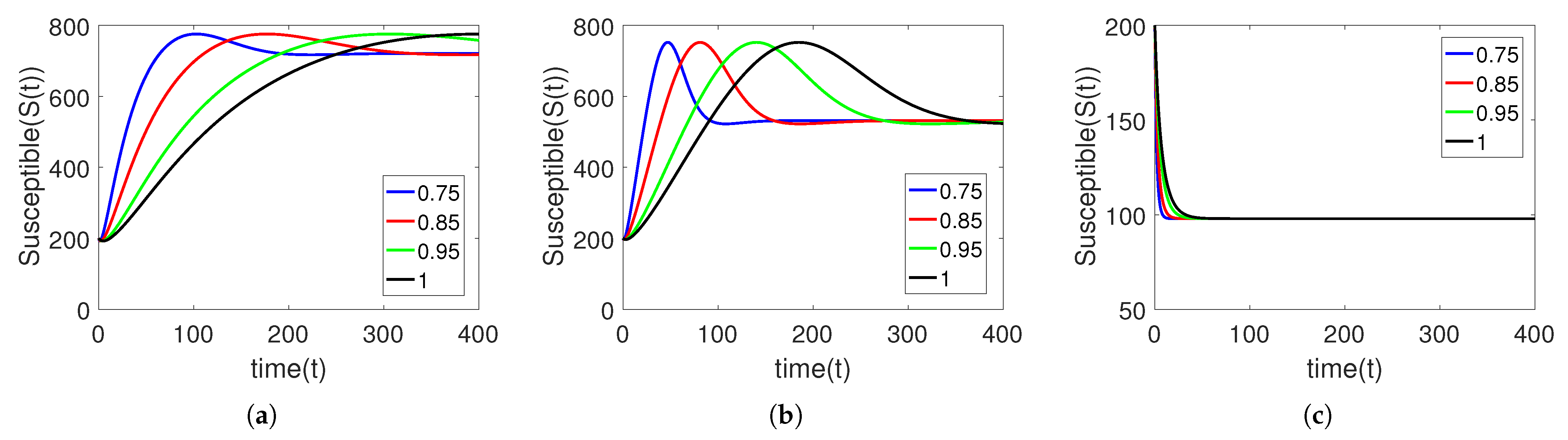
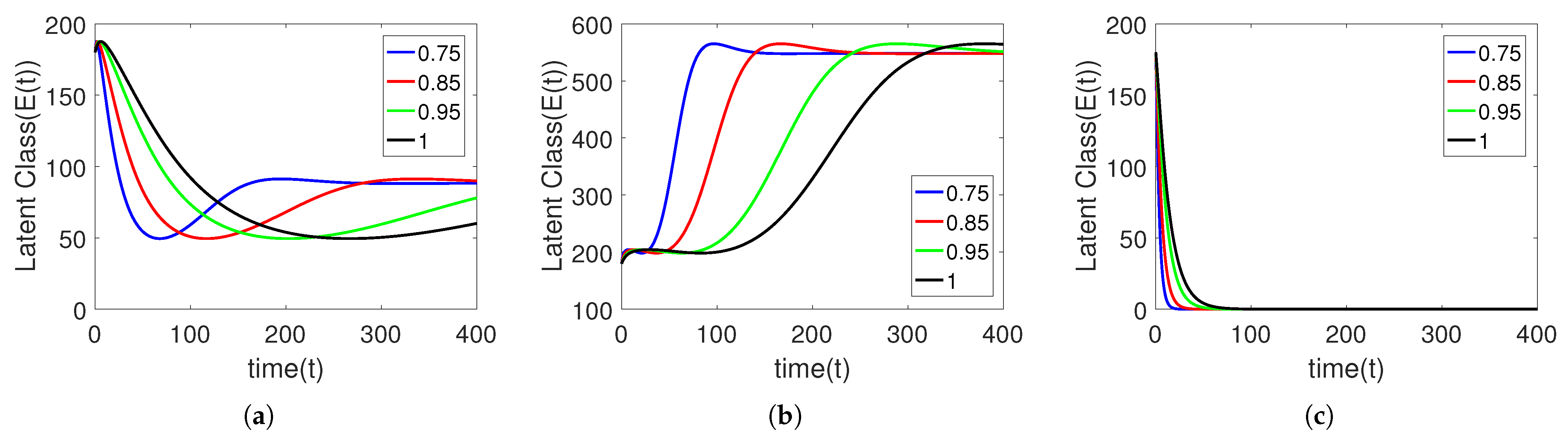
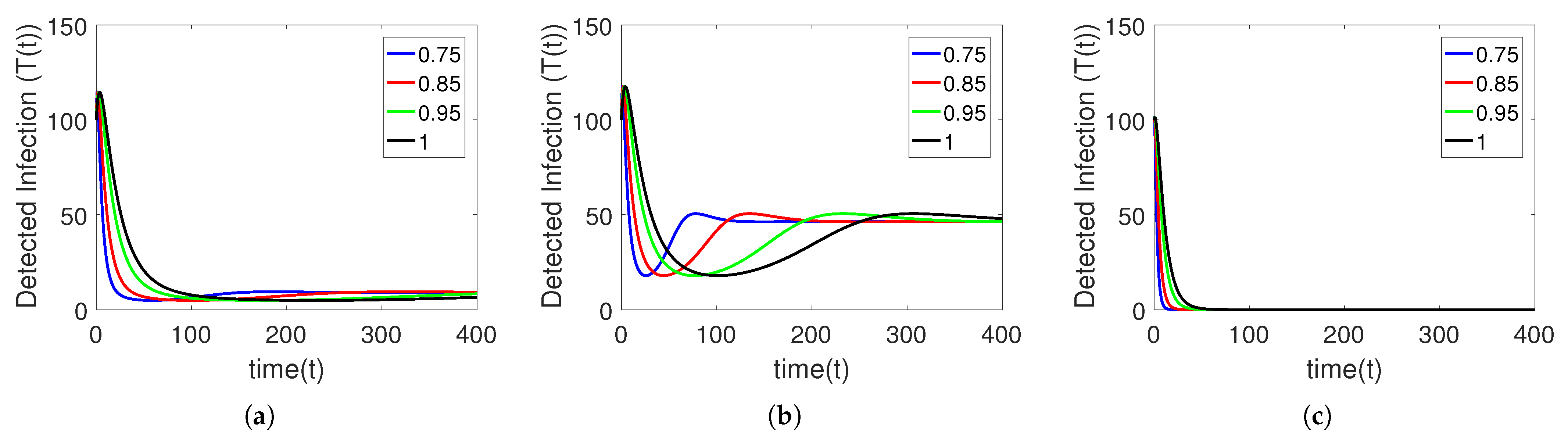
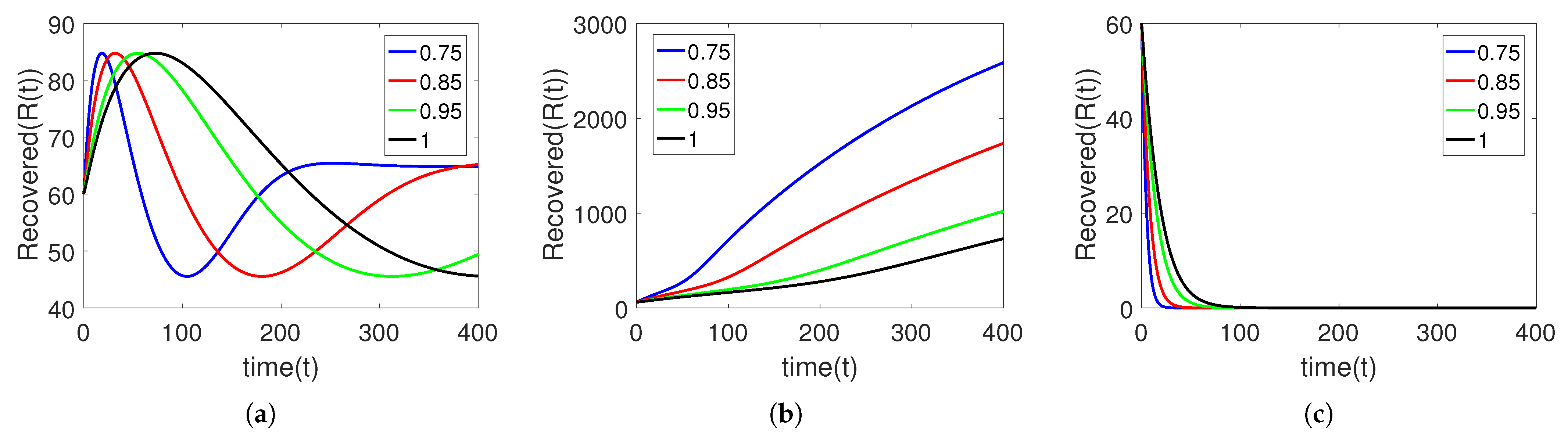
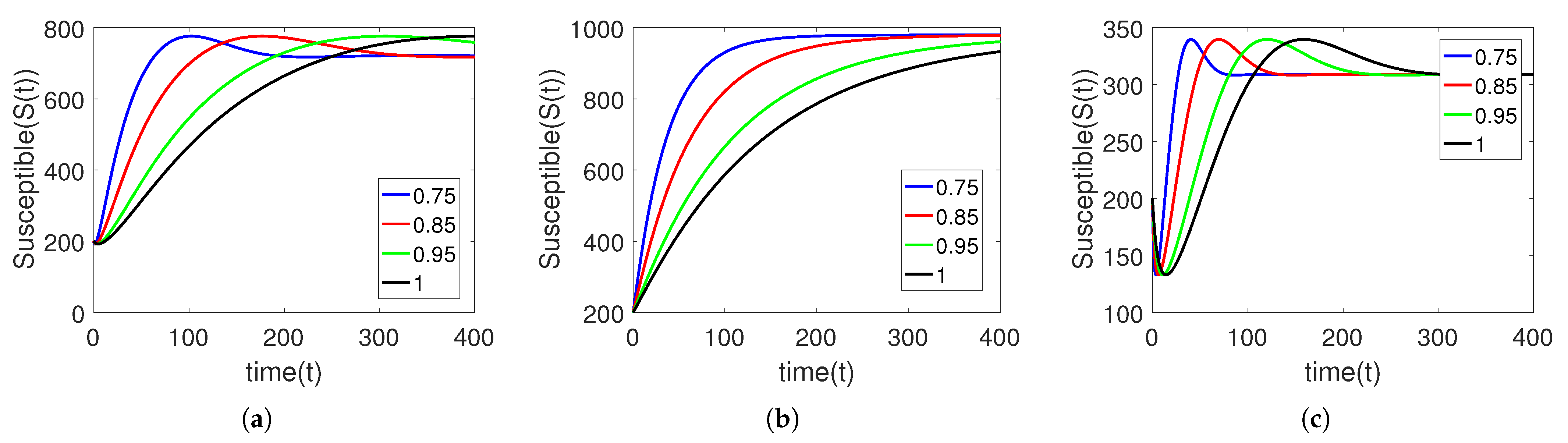
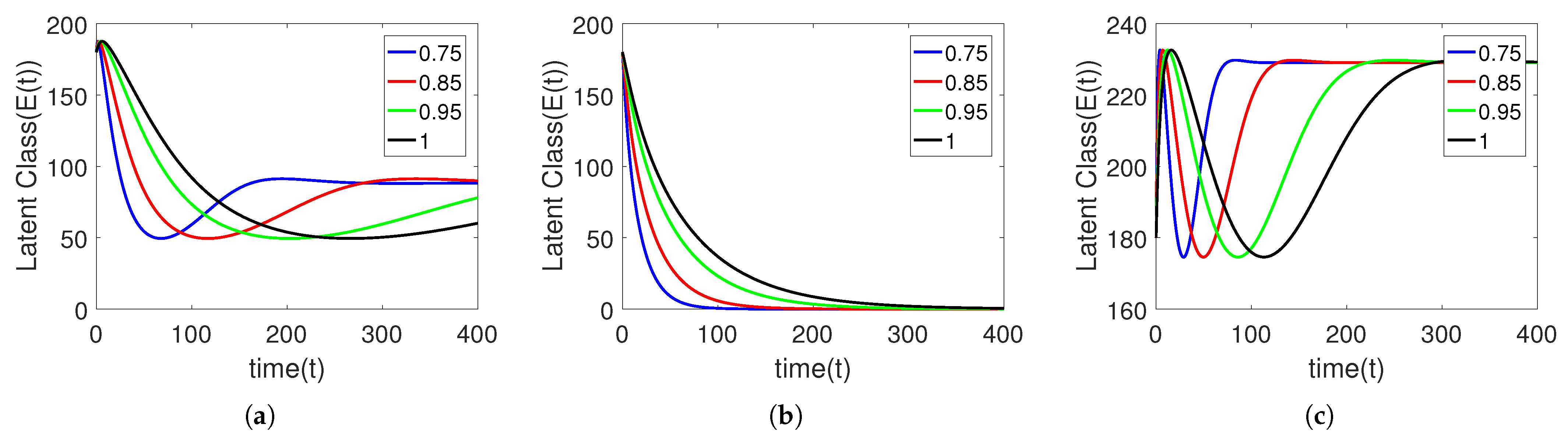
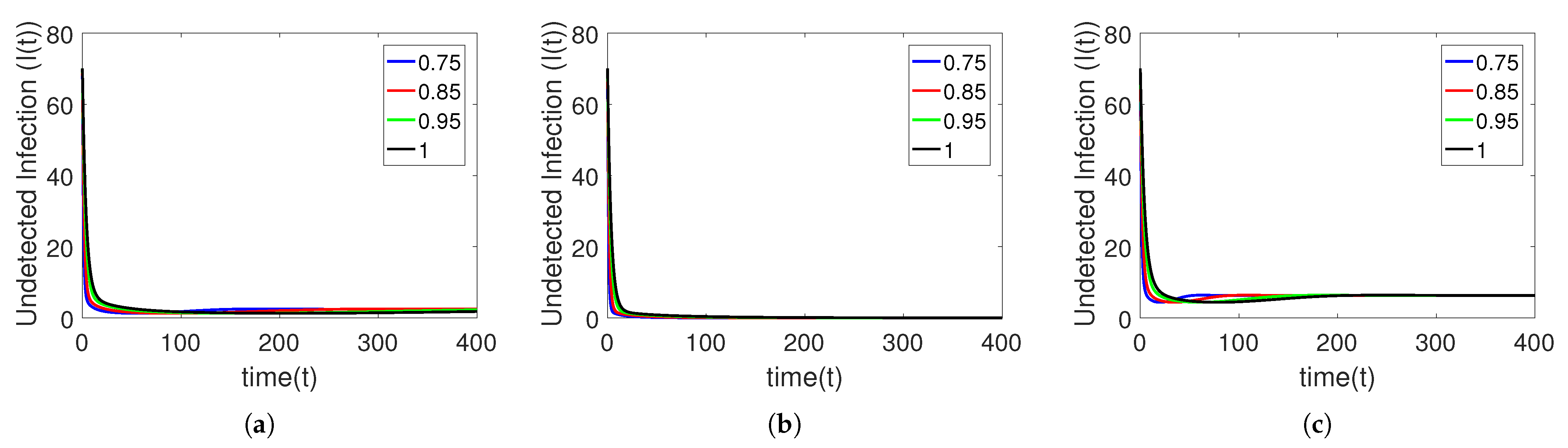
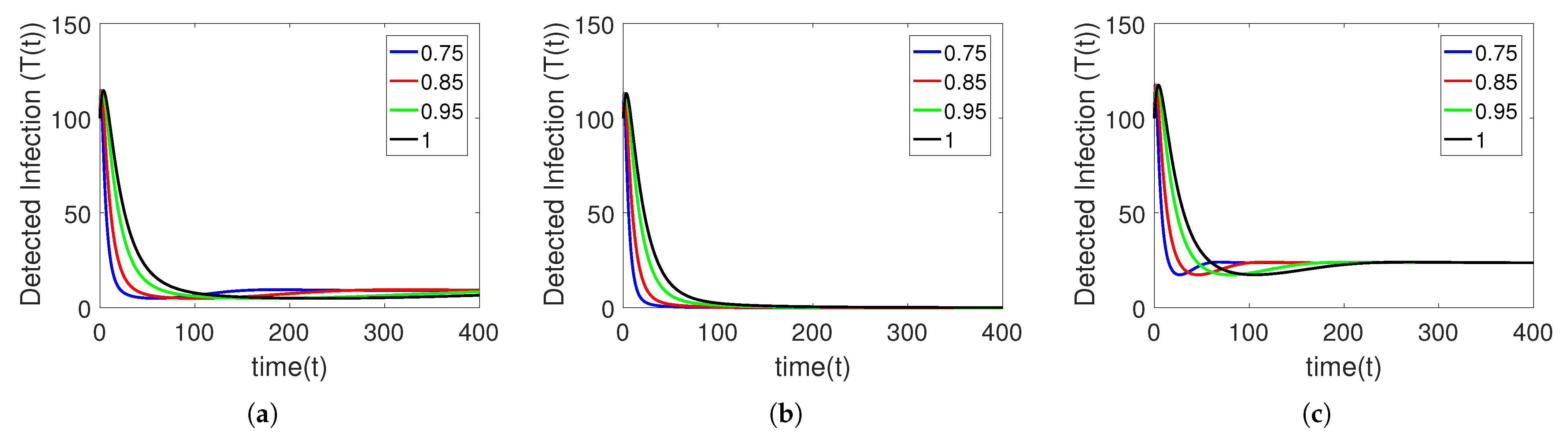
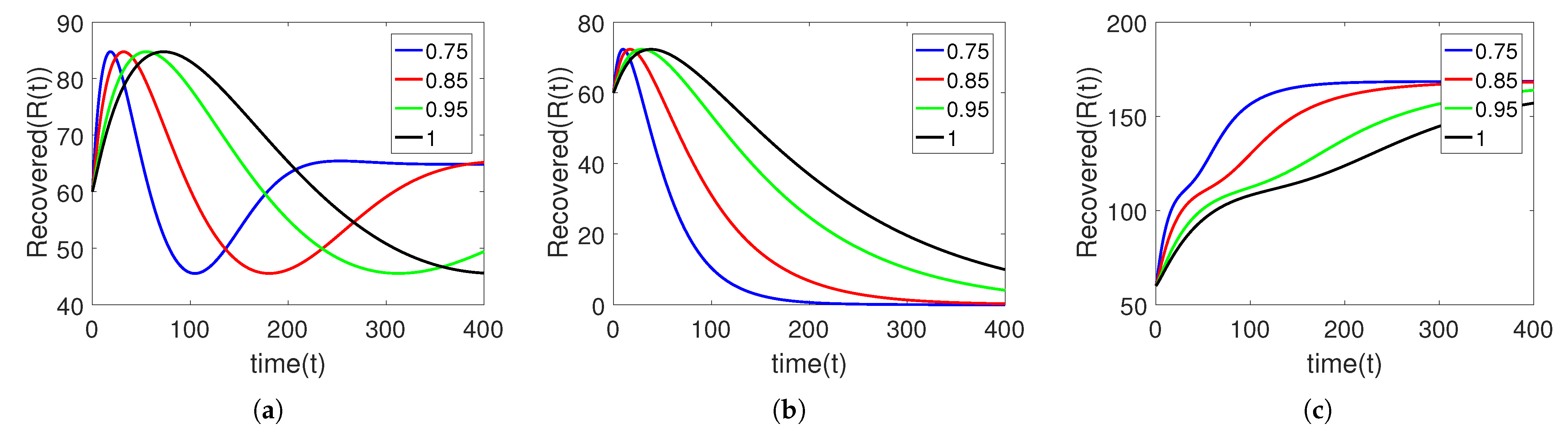
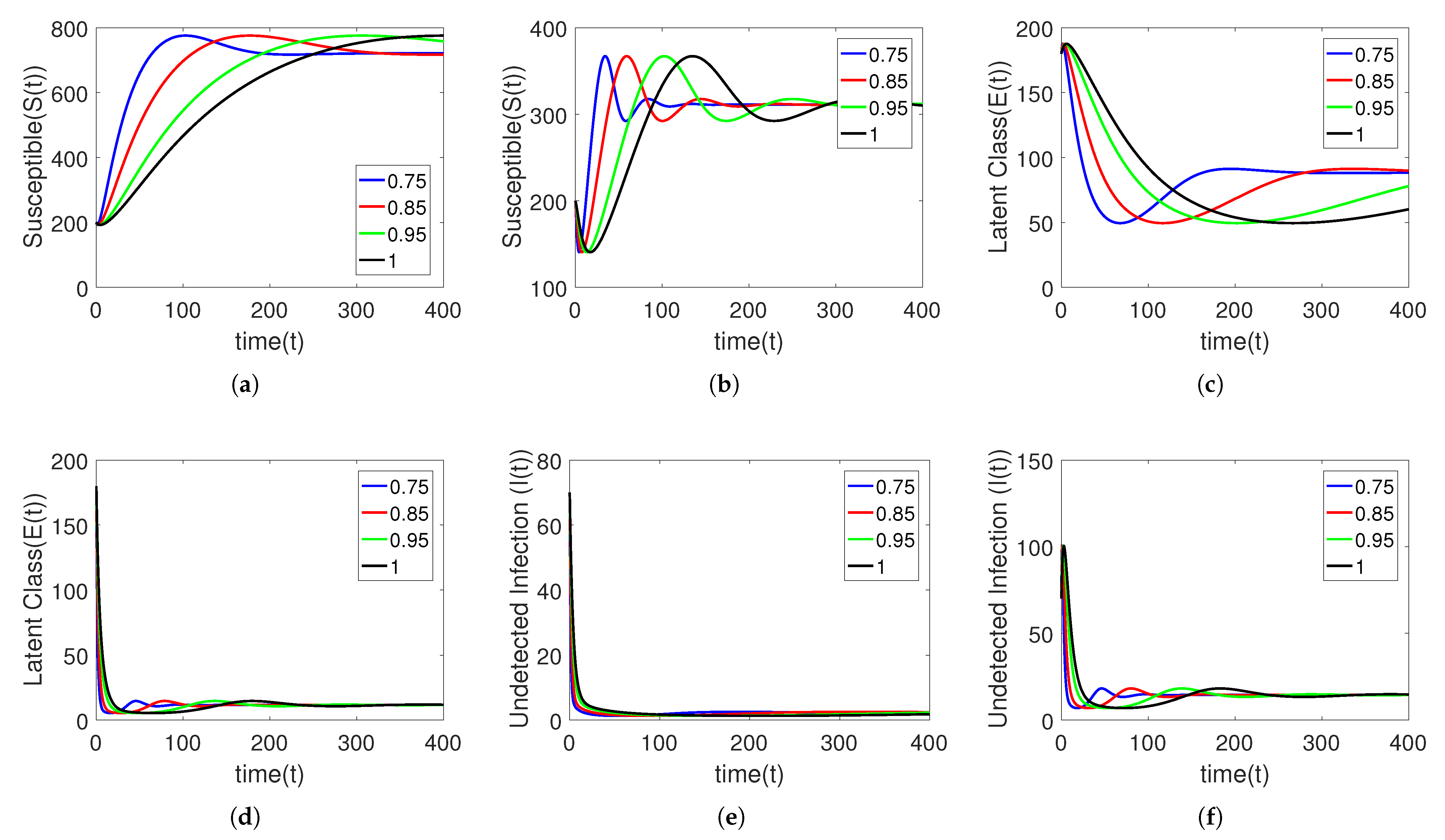
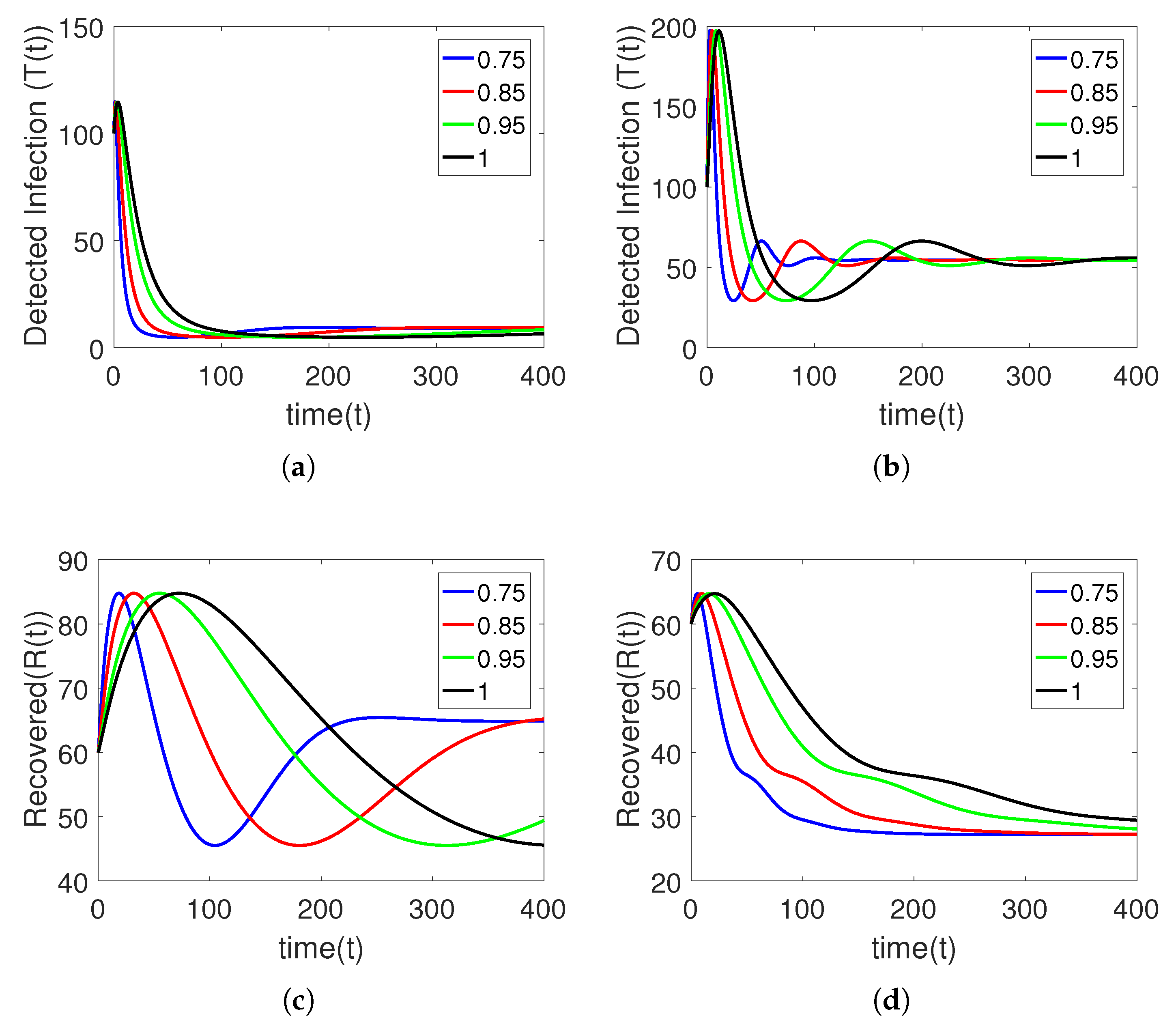
5. Numerical Simulation
Sensitivity Analysis
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Morse, D.; Brothwell, D.R.; Ucko, P.J. Tuberculosis in ancient Egypt. Am. Rev. Respir. Dis. 1964, 90, 524–541. [Google Scholar] [PubMed]
- Chakaya, J.; Khan, M.; Ntoumi, F.; Aklillu, E.; Fatima, R.; Mwaba, P.; Zumla, A. Global Tuberculosis Report 2020–Reflections on the Global TB burden, treatment and prevention efforts. Int. J. Infect. Dis. 2021, 113, S7–S12. [Google Scholar] [CrossRef] [PubMed]
- World Health Organization (WHO). Global Tuberculosis Report 2018; World Health Organization (WHO): Geneva, Switzerland, 2018; Available online: https://apps.who.int/iris/handle/10665/274453 (accessed on 10 July 2020).
- Centers for Disease Control and Prevention. How TB Spreads. Available online: https://www.cdc.gov/tb/topic/basics/howtbspreads.htm (accessed on 11 March 2016).
- Li, B.; Liang, H.; He, Q. Multiple and generic bifurcation analysis of a discrete Hindmarsh-Rose model. Chaos Solitons Fractals 2021, 146, 110856. [Google Scholar] [CrossRef]
- Li, B.; Liang, H.; Shi, L.; He, Q. Complex dynamics of Kopel model with nonsymmetric response between oligopolists. Chaos Solitons Fractals 2022, 156, 111860. [Google Scholar] [CrossRef]
- Eskandari, Z.; Avazzadeh, Z.; Khoshsiar Ghaziani, R.; Li, B. Dynamics and bifurcations of a discrete-time Lotka–Volterra model using nonstandard finite difference discretization method. Math. Methods Appl. Sci. 2022; early view. [Google Scholar] [CrossRef]
- Li, B.; Zhang, Y.; Li, X.; Eskandari, Z.; He, Q. Bifurcation analysis and complex dynamics of a Kopel triopoly model. J. Comput. Appl. Math. 2023, 426, 115089. [Google Scholar] [CrossRef]
- Zhang, J.; Feng, G. Global stability for a tuberculosis model with isolation and incomplete treatment. Comput. Appl. Math. 2015, 34, 1237–1249. [Google Scholar] [CrossRef]
- Trauera, J.M.; Denholm, J.T.; McBryde, E.S. Construction of a mathematical model for tuberculosis transmission in highly endemic regions of the Asia-pacific. J. Theor. Biol. 2014, 358, 74–84. [Google Scholar] [CrossRef]
- Al-arydah, M.; Hayes, B.; Mushayabasa, S.; Bhunu, C.; Dimitro, D.; Smith, R. Modelling the impact of treatment on tuberculosis transmission dynamic. Int. J. Biomath. Syst. Biol. 2015, 1, 1–19. [Google Scholar]
- Bhunu, C.P.; Mushayabasa, S.; Smith, R.J. Assessing the effects of poverty in tuberculosis transmission dynamics. Appl. Math. Model. 2012, 36, 4173–4185. [Google Scholar] [CrossRef]
- Ullah, I.; Ahmad, S.; ur Rahman, M.; Arfan, M. Investigation of fractional order tuberculosis (TB) model via Caputo derivative. Chaos Solitons Fractals 2021, 142, 110479. [Google Scholar] [CrossRef]
- Ullah, I.; Ahmad, S.; Zahri, M. Investigation of the effect of awareness and treatment on Tuberculosis infection via a novel epidemic model. Alex. Eng. J. 2023, 68, 127–139. [Google Scholar] [CrossRef]
- Saifullah, S.; Ali, A.; Irfan, M.; Shah, K. Time-fractional Klein–Gordon equation with solitary/shock waves solutions. Math. Probl. Eng. 2021, 2021, 6858592. [Google Scholar] [CrossRef]
- Goufo, E.F.D.; Khumalo, M.; Toudjeu, I.T.; Yildirim, A. Mathematical application of a non-local operator in language evolutionary theory. Chaos Solitons Fractals 2020, 131, 109541. [Google Scholar] [CrossRef]
- Opoku, M.O.; Wiah, E.N.; Okyere, E.; Sackitey, A.L.; Essel, E.K.; Moore, S.E. Stability Analysis of Caputo Fractional Order Viral Dynamics of Hepatitis B Cellular Infection. Math. Comput. Appl. 2023, 28, 24. [Google Scholar] [CrossRef]
- Huo, H.F.; Dang, S.J.; Li, Y.N. Stability of a two-strain tuberculosis model with general contact rate. In Abstract and Applied Analysis; Hindawi: London, UK, 2010; Volume 2010. [Google Scholar]
- Ain, Q.T.; Anjum, N.; Din, A.; Zeb, A.; Djilali, S.; Khan, Z.A. On the analysis of Caputo fractional order dynamics of Middle East Lungs Coronavirus (MERS-CoV) model. Alex. Eng. J. 2022, 61, 5123–5131. [Google Scholar] [CrossRef]
- Kumar, S.; Chauhan, R.P.; Momani, S.; Hadid, S. A study of fractional TB model due to mycobacterium tuberculosis bacteria. Chaos Solitons Fractals 2021, 153, 111452. [Google Scholar] [CrossRef]
- Adnan Ali, A.; Shah, Z.; Kumam, P. Investigation of a time-fractional covid-19 mathematical model with singular kernel. Adv. Contin. Discret. Model. 2022, 2022, 34. [Google Scholar] [CrossRef]
- Ahmad, S.; Ullah, A.; Akgül, A.; De la Sen, M. A study of fractional order Ambartsumian equation involving exponential decay kernel. AIMS Math. 2021, 6, 9981–9997. [Google Scholar] [CrossRef]
- Jin, F.; Qian, Z.S.; Chu, Y.M.; ur Rahman, M. On nonlinear evolution model for drinking behavior under Caputo-Fabrizio derivative. J. Appl. Anal. Comput. 2022, 12, 790–806. [Google Scholar] [CrossRef]
- Doungmo Goufo, E.F. Chaotic processes using the two-parameter derivative with non-singular and non-local kernel: Basic theory and applications. Chaos Interdiscip. J. Nonlinear Sci. 2016, 26, 084305. [Google Scholar] [CrossRef] [PubMed]
- Kanno, R. Representation of random walk in fractal space-time. Phys. A Stat. Mech. Its Appl. 1998, 248, 165–175. [Google Scholar] [CrossRef]
- Chen, W.; Sun, H.; Zhang, X.; Korošak, D. Anomalous diffusion modeling by fractal and fractional derivatives. Comput. Math. Appl. 2010, 59, 1754–1758. [Google Scholar] [CrossRef]
- Sun, H.; Meerschaert, M.M.; Zhang, Y.; Zhu, J.; Chen, W. A fractal Richards’ equation to capture the non-Boltzmann scaling of water transport in unsaturated media. Adv. Water Resour. 2013, 52, 292–295. [Google Scholar] [CrossRef]
- Atangana, A. Fractal-fractional differentiation and integration: Connecting fractal calculus and fractional calculus to predict complex system. Chaos Solitons Fractals 2017, 102, 396–406. [Google Scholar] [CrossRef]
- Shojaeizadeh, T.; Mahmoudi, M.; Darehmiraki, M. Optimal control problem of advection-diffusion-reaction equation of kind fractal-fractional applying shifted Jacobi polynomials. Chaos Solitons Fractals 2021, 143, 110568. [Google Scholar] [CrossRef]
- Xu, C.; Saifullah, S.; Ali, A. Theoretical and numerical aspects of Rubella disease model involving fractal fractional exponential decay kernel. Results Phys. 2022, 34, 105287. [Google Scholar] [CrossRef]
- Miller, K.S.; Ross, B. An Introduction to the Fractional Calculus and Fractional Differential Equations; Wiley: Hoboken, NJ, USA, 1993. [Google Scholar]
- Biazar, J. Solution of the epidemic model by Adomian decomposition method. Appl. Math. Comput. 2006, 173, 1101–1106. [Google Scholar] [CrossRef]
- Khan, A.M.; Ahmad, M.; Ullah, S.; Farooq, M.; Gul, T. Modelling the transmission dynamics of tuberculosis in Khyber Pakhtunkhwa Pakistan. Adv. Mech. Eng. 2019, 11, 1–13. [Google Scholar] [CrossRef]
- Egonmwan, A.O.; Okuonghae, D. Analysis of a mathematical model for tuberculosis with diagnosis. J. Appl. Math. Comput. 2019, 59, 129–162. [Google Scholar] [CrossRef]
- Yang, Y.; Li, J.; Ma, Z.; Liu, L. Global stability of two models with incomplete treatment for tuberculosis. Chaos Solitons Fractals 2010, 43, 79–85. [Google Scholar] [CrossRef]

| Variables | The Physical Representation |
|---|---|
| The number of susceptible individuals | |
| The number of Latent class | |
| The number of Undetected Infectious class | |
| The number of Detected infectious class | |
| The number of Recovered class | |
| New recruitment rate | |
| Mutual contact rate | |
| v | Decrease rate in infectiousness relative to treatment stages |
| p | Awareness ratio of human population |
| q | Treatment adherence level |
| Natural death rate | |
| Death rate for class | |
| Death rate for class | |
| Reactivation rate | |
| Detection rate for active TB cases | |
| Recovery rate from | |
| r | Rate of Transferring from to or |
| c | Fraction of new infection progress to latent class |
| Parameter | Description | Baseline Value | Source |
|---|---|---|---|
| Rate of recruitment | 14 | Assumed | |
| Natural death rate | 0.0143 | [33] | |
| Rate of effective contact | Variable | Assumed | |
| Rate of reactivation | 0.005 | [33] | |
| Detection rate | 0.25 | [34] | |
| Rates of Recovery | 0.01, 0.35 | Assumed | |
| c | Portion of freshly infected people with latent TB | 0.75 | [33] |
| Death rates due to disease | 0.08, 0.1 | [35] | |
| v | Modification parameter | 0.39 | Assumed |
| q | Treatment adherence level | Assumed | |
| p | Level of Awareness | Assumed |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ullah, I.; Ahmad, S.; Arfan, M.; De la Sen, M. Investigation of Fractional Order Dynamics of Tuberculosis under Caputo Operator. Fractal Fract. 2023, 7, 300. https://doi.org/10.3390/fractalfract7040300
Ullah I, Ahmad S, Arfan M, De la Sen M. Investigation of Fractional Order Dynamics of Tuberculosis under Caputo Operator. Fractal and Fractional. 2023; 7(4):300. https://doi.org/10.3390/fractalfract7040300
Chicago/Turabian StyleUllah, Ihsan, Saeed Ahmad, Muhammad Arfan, and Manuel De la Sen. 2023. "Investigation of Fractional Order Dynamics of Tuberculosis under Caputo Operator" Fractal and Fractional 7, no. 4: 300. https://doi.org/10.3390/fractalfract7040300
APA StyleUllah, I., Ahmad, S., Arfan, M., & De la Sen, M. (2023). Investigation of Fractional Order Dynamics of Tuberculosis under Caputo Operator. Fractal and Fractional, 7(4), 300. https://doi.org/10.3390/fractalfract7040300








