Finite-Time Synchronization for Fractional Order Fuzzy Inertial Cellular Neural Networks with Piecewise Activations and Mixed Delays

Abstract

This paper investigates a class of finite-time synchronization problems of fractional order fuzzy inertial cellular neural networks (FFICNNs) with piecewise activations and mixed delays. First, the Caputo FFICNNs are established. A suitable transformation variable is constructed to rewrite FFICNNs with mixed delays into a first-order differential system. Secondly, some new effective criteria are constructed on the basis of the finite-time stability theory and Lyapunov functionals to realize the synchronization of the drive-response system. Finally, two numerical simulation examples show that the proposed method is effective.

1. Introduction

Yang et al. [1,2] put forward cellular neural networks (CNNs) in 1988, which have since been extensively investigated and applied in such fields as secondary optimization, pattern classification, pattern recognition, associative memory, and image processing. Yang et al. [3] put forward the fuzzy cellular neural networks (FCNNs) in 1996. Compared with the CNNs, the FCNNs contains fuzzy logics, and there is a local connection between cells [4,5,6,7,8,9,10]. FCNNs have superior performance applications in image encryption, psychophysics, perception, robots, secure communication, and medical diagnosis, etc.

Babcock et al. [11] supplemented an inertial term to neural networks to make up inertial neural networks (INNs) in 1986, which caused more complex bifurcation and chaotic dynamic behaviors of neuron coupling as instability and concussion behaviors. Adding an inertia term to electronic neural networks may bring about complex behaviors such as spontaneous concussion, instability, and chaotic behavior. Moreover, there exist significant biological backgrounds for bringing the inertial term into neural systems. Many researchers have paid extensive attention to inertial neural networks, and have made important progress (see [12,13,14,15,16]).

Fractional order calculus is an extension of integer calculus to arbitrary order, has become a mathematical tool to solve practical problems in pattern recognition, information processing, robot control, physics, statistics, and other fields for its superiority, which is characterized by infinite memory considering the current states and all its previous ones. Scholars [17,18,19,20,21,22] used fractional operators to build fractional order neural network models.

In practical application, the signals of processing and transmission between neurons are limited by the switching speed of the amplifier, the delay time is inevitable, and this will influence the stability of the neural networks and give rise to divergence, instability, and oscillation in network systems. In fact, mixed delays include constant ones, time-varying ones, and distributed ones, which are considered to be more effective than single ones at modeling network systems in that these simple delays are often impractical, while network systems become more complex.

Synchronization is the dynamic behavior of the drive system and reponse system to attain the same state after a certain time. Nowadays, much attention has been paid to synchronization, owing to its potential applications in medicine, information science, optimized calculation, automatic control, and other fields. At present, there are many achievements in synchronous research. According to the convergence time, it is mainly divided into three categories: global asymptotical synchronization, exponential synchronization, and finite-time synchronization. In comparison with the global asymptotical synchronization of neural networks, finite-time synchronization has better convergence performance. However, the final convergence time is closely related to the initial state of the drive-response system. To achieve synchronization quickly, we can rely on control methods—for example, feedback control, adaptive control, intermittent control, etc. Of course, we sincerely hope that systems can achieve synchronization with practical engineering applications in a finite time. Therefore, the research for finite-time synchronization of neural networks is of great significance. At present, the research result of the inertial neural networks’ synchronization mainly includes the following aspects. Yang et al. [23] designed three different types of controllers by using the maximum analysis method to ensure the global asymptotic synchronization between the drive-response system. Feng et al. [24] investigated the exponential synchronization control of inertial neural networks with time-varying delays. By designing Lyapunov–Krasovskii functionals and utilizing new weighted integral inequalities, the delay-related criteria of linear matrix inequality (LMI) are obtained. Zhang et al. [25] obtained two new strategies to solve the synchronization for fractional neural networks with two inertia terms and a time delay by constructing Lyapunov function and using the LMI method. Tang et al. [26] researched the exponential synchronization of INNs with finite and discrete distributed mixed delays by using intermittent control. Liang et al. [27] introduced the exponential synchronization control of inertial Cohen–Grossberg neural networks with time-varying delays. Shi et al. [28] studied the lag synchronization and global exponential stabilization of INNs via adaptive control by constructing nonnegative function and employing inequality techniques, and obtained several new results. Zhang et al. [29] introduced the finite-time synchronization control of FINNs with the maximum method of functions. Hua et al. [30] introduced a new control method to solve the finite-time synchronization problem of IMNNs with time-varying delay. It can effectively dispose of the problems caused by mixed delay and memristor connection weight. Chen et al. [31] design four different kinds of feedback controllers, under which the considered inertial memristive neural networks can realize fixed-time synchronization perfectly. Alimi et al. [32] introduced the finite/fixed time synchronization of the INNs with multiple proportional delays. Yang et al. [33] studies the synchronization control of a new FICNNs with piecewise activation and mixed delay. However, few reports are found in the existing works for finite-time synchronization of FFICNNs with piecewise activation and mixed delay.

Motivated by these, this paper will investigate the problems of finite-time synchronization analysis for a class of FFICNNs with piecewise activation and mixed delay. There are the following primary innovations in this paper.

• The Caputo fractional order fuzzy inertial cellular neural networks model is established. It can be used to describe many systems of internal coherence in the real environment. In addition, it is easy to implement in engineering applications and has important application prospects.
• A novel nonlinear controller is designed to realize the finite-time synchronization of FFICNNs with piecewise activation and mixed delay. It is of high reliability and great accuracy, and can better synchronize the position and motion of the system.
• The Lyapunov direct method is applied in the analysis of the inertial system to avoid the loss of the inertia. The numerical simulation results show that the designed method is effective. Therefore, it is of more important practical significance.

The other parts of this paper are structured as follows. Section 2 introduces the network system model of FICNNs with piecewise activations and mixed delays, assumptions, lemmas, and definitions of finite-time synchronization. In Section 3, the synchronization of the neural network system is analyzed. In Section 4, two examples are given to demonstrate the effectiveness of the obtained results. The conclusion is revealed in Section 5.

2. Preliminaries and Problem Formulation

2.1. Preliminaries

In this article, the system model is defined by Caputo fractional order. First, some basic definitions, lemmas, and assumptions about fractional calculus are introduced.

Definition 1

([34]). By using Equation (1) to define the fractional integral of the function $z\left(t\right)$, we have

$${}_{t_0}^C{D}_t^{-\alpha }z\left(t\right)=\frac{1}{\Gamma \left(\alpha \right)}{\int }_{t_0}^t{(t-x)}^{\alpha -1}z\left(x\right)dx,$$

(1)

where $\alpha >0$, $t>t_0$, $\Gamma (·)$ is gamma function.

Definition 2

([34]). By using Equation (2) to define the the fractional derivative of the function $z\left(t\right)$, we have

$${}_{t_0}^C{D}_t^{\alpha }z\left(t\right)=\frac{1}{\Gamma (n-\alpha )}{\int }_{t_0}^t{(t-x)}^{n-\alpha -1}{z}^{\left(n\right)}\left(x\right)dx,$$

(2)

where $t>t_0$, $\alpha \in (m-1,m]$, $m\in {\mathrm{Z}}^{+}$. If $\alpha \in (0,1]$, then

$${}_{t_0}^C{D}_t^{\alpha }z\left(t\right)=\frac{1}{\Gamma (1-\alpha )}{\int }_{t_0}^t\frac{z^{{}^{\prime }}\left(x\right)}{{(t-x)}^{\alpha }}dx.$$

(3)

For simplicity, we use $D_t^{\alpha }z\left(t\right)$ to represent ${}_0^C{D}_t^{\alpha }z\left(t\right)$ in this article. Some useful lemmas are given as follows.

Lemma 1

([35]). Suppose that $z\left(t\right)\in C^1[0,T]$, $T>0$ and $\beta \in (0,1]$, and then Equation (4) holds,

$$D_t^{-\beta }{D}_t^{\beta }z\left(t\right)=z\left(t\right)-z\left(0\right)$$

(4)

and

$$D_t^{\beta }{D}_t^{-\beta }z\left(t\right)=z\left(t\right).$$

(5)

Lemma 2

([35]). Suppose that $z\left(t\right)\in C^n[0,T]$, $T>0$, and then Equation (6) holds,

$$D_t^{\beta }z\left(t\right)=D_t^{{\beta }_m}···D_t^{{\beta }_2}{D}_t^{{\beta }_1}z\left(t\right),$$

(6)

where $t\in [0,T]$, $\beta ={\sum }_{i=1}^m{\beta }_i$, ${\beta }_i\in (0,1]$, $n-1<\beta \le n\in {\mathrm{Z}}^{+}$, and there exist $i_l<m$ s.t. ${\sum }_{j=1}^{i_l}{\beta }_j=l$ ($l=1,2,···,n-1$).

Lemma 3

([36]). Suppose that $a,b\in R$, $\forall \beta >0$, and then Equation (7) holds:

$$D_t^{\beta }(a{z}_1\left(t\right)+b{z}_2\left(t\right))=a{D}_t^{\beta }{z}_1\left(t\right)+b{D}_t^{\beta }{z}_2\left(t\right).$$

(7)

Lemma 4

([37]). Suppose that $z\left(t\right)\in C^1[t_0,\infty ],\beta \in (0,1]$, and then Equation (8) holds:

$$D_t^{\beta }\left|z\left(t\right)\right|\le sign\left(z\left(t\right)\right)D_t^{\beta }z\left(t\right).$$

(8)

Lemma 5

([38]). Suppose that function $z\left(t\right):[0,+\infty ]\to R^m$ is differentiable and bounded, and $\beta \in (0,1]$, and then Equation (9) holds:

$$D_t^{\beta }{z}^T\left(t\right)z\left(t\right)\le 2z^T\left(t\right)D_t^{\beta }z\left(t\right).$$

(9)

Lemma 6

([3]). Suppose that $a_{kr},b_{kr},x_r,y_r\in R,h_r:R\to R$ are continuous functions for $k,r=1,2,\cdots ,m$, and then Equation (10) holds:

$$\begin{array}{cc}\hfill |\underset{r=1}{\overset{m}{\bigwedge }}{a}_{kr}{h}_r\left(x_r\right)-\underset{r=1}{\overset{m}{\bigwedge }}{a}_{kr}{h}_r\left(y_r\right)|& \le \sum _{r=1}^m|a_{kr}\left|\right|h_r\left(x_r\right)-h_l\left(y_r\right)|\hfill \\ \hfill |\underset{r=1}{\overset{m}{\bigvee }}{b}_{kr}{h}_r\left(x_r\right)-\underset{r=1}{\overset{m}{\bigvee }}{b}_{kr}{h}_r\left(y_r\right)|& \le \sum _{r=1}^m|b_{kr}\left|\right|h_r\left(x_r\right)-h_r\left(y_r\right)|\hfill \end{array}.$$

(10)

Lemma 7

([39]). If $a_1,a_2,\cdots ,a_m\ge 0,0<\nu \le 1,\mu >1$, then Equation (11) holds:

$$\sum _{k=1}^m{a}_k^{\mu }\ge n^{1-\mu }{\left(\sum _{k=1}^m{a}_k\right)}^{\mu },\sum _{k=1}^m{a}_k^{\nu }\ge {\left(\sum _{k=1}^m{a}_k\right)}^{\nu }.$$

(11)

Lemma 8

([40]). Suppose that $V\left(t\right)$ is a nonnegative and continuous definite function, if it satisfies the inequality Equation (12), and then Equation (13) holds,

$$D_t^{q}V\left(t\right)\le -c{V}^{\eta }\left(t\right)$$

(12)

$$V^{q-\eta }\left(t\right)\le V^{q-\eta }\left(t_0\right)-\frac{c\Gamma (1+q-\eta ){(t-t_0)}^q}{\Gamma (1+q)\Gamma (1-\eta )},t\in [t_0,T],$$

(13)

where $c>0,\eta \in (0,q)$, and $q>0$. T may be given by the following:

$$T=t_0+{\left(\frac{\Gamma (1+q)\Gamma (1-\eta )V^{q-\eta }\left(t_0\right)}{c\Gamma (1+q-\eta )}\right)}^{\frac{1}{q}}.$$

2.2. Problem Formulation

In this paper, the system of the m-dimensional FFCNNs with piecewise activation and mixed delays is defined as

$$\left\{\begin{array}{cc}\hfill D_t^{2\alpha }{z}_k\left(t\right)& =-a_k{D}_t^{\alpha }{z}_k\left(t\right)-b_k{x}_k\left(t\right)+\sum _{r=1}^m{c}_{kr}{h}_k\left(z_r\left(t\right)\right)+\sum _{r=1}^m{d}_{kr}{\int }_{t-{\sigma }_0\left(t\right)}^t{h}_r\left(z_r\left(s\right)\right)ds\hfill \\ \hfill & +\sum _{r=1}^m{g}_{kr}{v}_k+\underset{r=1}{\overset{m}{\bigwedge }}{P}_k{\nu }_r+\underset{r=1}{\overset{m}{\bigwedge }}{\alpha }_{kr}{h}_r\left(z_r(t-{\sigma }_r\left(t\right))\right)+\underset{r=1}{\overset{m}{\bigvee }}{Q}_k{\nu }_r\hfill \\ \hfill & +\underset{r=1}{\overset{m}{\bigvee }}{\beta }_{kr}{h}_r\left(z_r(t-{\sigma }_r\left(t\right))\right)+I_k\hfill \\ \hfill z_k\left(\iota \right)& ={\psi }_k\left(\iota \right),D_t^{\alpha }{x}_k\left(\iota \right)={\phi }_k\left(\iota \right),\iota \in [-\sigma ,t_0],k=1,\cdots ,m\hfill \end{array},\right.$$

(14)

where $0<\alpha \le 1$. $z_k\left(t\right)$ represent the state of the kth neuron. $a_k,b_k$ represent the passive decay rate to the state of kth neuron. $c_{kr},d_{kr}$ represent elements of feedback template and $g_{kr}$ denotes the feedforward template. $v_k$ and $I_k$ are input and bias of the kth neuron, respectively. ${\alpha }_{kr},{\beta }_{kr}$ are fuzzy feedback MIN and MAX template, $P_{kr},Q_{kr}$ are fuzzy feedforward MIN and MAX template. $h_k(·)$ denotes activation functions, ${\sigma }_0\left(t\right)$ and ${\sigma }_k\left(t\right)$ represent the delay of the kth neuron.

Remark 1.

The mixed delay σ meets the following conditions: $\sigma =\begin{array}{c}\max \\ 0\le r\le m\end{array}\left\{\begin{array}{c}\sup \\ t\in R^{+}\end{array}{\sigma }_r\left(t\right)\right\}$, ${\psi }_k\left(s\right),{\phi }_k\left(s\right)\in C([-\sigma ,t_0],R^m)$ with $C([-\sigma ,t_0],R^m)$ represents the Banach space of continuous functions $[-\sigma ,t_0]$ into $R^n$. If the activation functions $h_k(·)$ is piecewise, it has a Filippov solution.

We assume that the following assumptions about activation functions are satisfied.

Assumption 1.

There exist nonnegative constants $L_k$ and $S_k$ such that

$$\begin{array}{c}\hfill |{\lambda }_k-{\zeta }_k|\le L_k|p_k-q_k|+S_k,\forall p_k,q_k\in R,k=1,2,\cdots ,m,\end{array}$$

(15)

where ${\lambda }_k\in \overline{co}\left[h_k\left(p_k\right)\right]$ and ${\zeta }_k\in \overline{co}\left[h_k\left(q_k\right)\right]$; $\overline{co}$ represents the convex closure of the set.

Assumption 2.

$x_i:R\to R$ is continuous except on a countable set of isolation points $\left\{{\varrho }_k^i\right\}$ for each $i=1,2,\cdots ,n$, where there exists a finite left limit $x_i\left({\varrho }_k^{i-}\right)$ and right limit $x_i\left({\varrho }_k^{i+}\right)$. Moreover, $g_i$ has at most a finite number of jump discontinuities in every compact interval of R.

Remark 2.

Assumptions 1 and 2 are not restrictive. Generally, the neural network model can satisfy Assumptions 1 and 2 in [41,42,43]. In addition, to obtain the main results, the concept of Filippov solution, which comes from Filippov for system (14), is given.

Definition 3.

If (i) and (ii) are satisfied, then the function $z={(z_1,z_2,\cdots ,z_m)}^T$ is said to be a solution of system (14) on $[-\sigma ,T)$. Here, $\sigma =\begin{array}{c}\max \\ 0\le r\le m\end{array}\left\{\begin{array}{c}\sup \\ t\in R^{+}\end{array}{\sigma }_r\left(t\right)\right\}$, $T\in (0,+\infty )$.

(i) The function $z={(z_1,z_2,\cdots ,z_m)}^T$ is continuous in the interval $[-\sigma ,T)$, and it is absolutely continuous in the interval $[0,T)$.

(ii) The $\lambda ={({\lambda }_1,{\lambda }_2,\cdots ,{\lambda }_m)}^T:[-\sigma ,T)\to R^m$ is a measurable function, such that ${\lambda }_l\left(t\right)\in \overline{co}\left[h_k\left(z_l\left(t\right)\right)\right]$ for $t\in [-\sigma ,T]$ and

$$\begin{array}{cc}\hfill D_t^{2\alpha }{z}_k\left(t\right)& =-a_k{D}_t^{\alpha }{z}_k\left(t\right)-b_k{z}_k\left(t\right)+\sum _{r=1}^m{c}_{kr}{\lambda }_r\left(t\right)+\sum _{r=1}^m{d}_{kr}{\int }_{t-{\sigma }_0\left(t\right)}^t{\lambda }_r\left(s\right)ds\hfill \\ \hfill & +\sum _{r=1}^m{g}_{kr}{v}_k+\underset{r=1}{\overset{m}{\bigwedge }}{P}_k{\nu }_r+\underset{r=1}{\overset{m}{\bigwedge }}{\alpha }_{kr}{\lambda }_r(t-{\sigma }_r\left(t\right))+\underset{r=1}{\overset{m}{\bigvee }}{Q}_k{\nu }_r\hfill \\ \hfill & +\underset{r=1}{\overset{m}{\bigvee }}{\beta }_{kr}{\lambda }_r(t-{\sigma }_r\left(t\right))+I_k,k=1,\cdots ,m\hfill \end{array}.$$

(16)

Let $g_k\left(t\right)=D_t^{\alpha }{z}_k\left(t\right)+{\xi }_k{z}_k\left(t\right)$, where ${\xi }_k$ is constant. According to Lemmas 2 and 3, the system (16) can be transformed into the Equation (17), and it is chosen as the drive system. We have

$$\left\{\begin{array}{cc}\hfill D_t^{\alpha }{z}_k\left(t\right)& =-{\xi }_k{z}_k\left(t\right)+g_k\left(t\right)\hfill \\ \hfill D_t^{\alpha }{g}_k\left(t\right)& =-{\varphi }_k{g}_k\left(t\right)+{\delta }_k{z}_k\left(t\right)+\sum _{r=1}^m{c}_{kr}{\lambda }_r\left(t\right)+\sum _{r=1}^m{d}_{kr}{\int }_{t-{\sigma }_0\left(t\right)}^t{\lambda }_r\left(s\right)ds\hfill \\ \hfill & +\sum _{r=1}^m{g}_{kr}{v}_r+\underset{r=1}{\overset{m}{\bigwedge }}{P}_k{\nu }_r+\underset{r=1}{\overset{m}{\bigwedge }}{\alpha }_{kr}{\lambda }_r(t-{\sigma }_r\left(t\right))+\underset{r=1}{\overset{m}{\bigvee }}{Q}_k{\nu }_r\hfill \\ \hfill & +\underset{r=1}{\overset{m}{\bigvee }}{\beta }_{kr}{\lambda }_r(t-{\sigma }_r\left(t\right))+I_k,k=1,2,\cdots ,m\hfill \end{array},\right.$$

(17)

where ${\varphi }_k=a_k-{\xi }_k,{\delta }_k=-{\xi }_k^2+{\xi }_k{a}_k-b_k$, and Equation (18) is the initial value of system. We have

$$\left\{\begin{array}{cc}\hfill z_k\left(\iota \right)& ={\psi }_k\left(\iota \right)\hfill \\ \hfill g_k\left(\iota \right)& ={\xi }_k{\psi }_k\left(\iota \right)+{\phi }_k\left(\iota \right),\iota \in [-\sigma ,t_0].\hfill \end{array}\right.$$

(18)

Now, we choose the system (19) as the response system. We have

$$\left\{\begin{array}{cc}\hfill D_t^{\alpha }{p}_k\left(t\right)& =-{\xi }_k{p}_k\left(t\right)+q_k\left(t\right)+u_k\left(t\right)\hfill \\ \hfill D_t^{\alpha }{q}_k\left(t\right)& =-{\varphi }_k{q}_k\left(t\right)+{\delta }_k{p}_k\left(t\right)+\sum _{r=1}^m{c}_{kr}{\zeta }_r\left(t\right)+\sum _{r=1}^m{d}_{kr}{\int }_{t-{\sigma }_0\left(t\right)}^t{\zeta }_r\left(s\right)ds\hfill \\ \hfill & +\sum _{r=1}^m{g}_{kr}{v}_r+\underset{r=1}{\overset{m}{\bigwedge }}{P}_k{\nu }_r+\underset{r=1}{\overset{m}{\bigwedge }}{\alpha }_{kr}{\zeta }_r(t-{\sigma }_r\left(t\right))+\underset{r=1}{\overset{m}{\bigvee }}{Q}_k{\nu }_r\hfill \\ \hfill & +\underset{r=1}{\overset{m}{\bigvee }}{\beta }_{kr}{\zeta }_r(t-{\sigma }_r\left(t\right))+I_k+{\tilde{u}}_k\left(t\right),k=1,2,\cdots ,m\hfill \end{array},\right.$$

(19)

where ${\tilde{u}}_k\left(t\right),u_k\left(t\right)$ represent the designed controller. Equation (20) is the error system:

$$\left\{\begin{array}{cc}\hfill {\theta }_k\left(t\right)& =p_k\left(t\right)-z_k\left(t\right)\hfill \\ \hfill {\tilde{\theta }}_k\left(t\right)& =q_k\left(t\right)-g_k\left(t\right).\hfill \end{array}\right.$$

(20)

According to Equation (17) and Equation (19), we obtain

$$\left\{\begin{array}{cc}\hfill D_t^{\alpha }{\theta }_k\left(t\right)& =-{\xi }_k{\theta }_k\left(t\right)+{\tilde{\theta }}_k\left(t\right)+u_k\left(t\right)\hfill \\ \hfill D_t^{\alpha }{\tilde{\theta }}_k\left(t\right)& =-{\varphi }_k{\tilde{\theta }}_k\left(t\right)+{\delta }_k{\theta }_k\left(t\right)+\sum _{r=1}^m{c}_{kr}{\zeta }_r\left(t\right)-\sum _{r=1}^m{c}_{kr}{\lambda }_r\left(t\right)\hfill \\ \hfill & +\sum _{r=1}^m{d}_{kr}{\int }_{t-{\sigma }_0\left(t\right)}^t{\zeta }_r\left(s\right)ds-\sum _{r=1}^m{d}_{kr}{\int }_{t-{\sigma }_0\left(t\right)}^t{\lambda }_r\left(s\right)ds\hfill \\ \hfill & +\underset{r=1}{\overset{m}{\bigwedge }}{\alpha }_{kr}{\zeta }_r(t-{\sigma }_r\left(t\right))-\underset{r=1}{\overset{m}{\bigwedge }}{\alpha }_{kr}{\lambda }_r(t-{\sigma }_r\left(t\right))\hfill \\ \hfill & +\underset{r=1}{\overset{m}{\bigvee }}{\beta }_{kr}{\zeta }_r(t-{\sigma }_r\left(t\right))-\underset{r=1}{\overset{m}{\bigvee }}{\beta }_{kr}{\lambda }_r(t-{\sigma }_r\left(t\right))\hfill \\ \hfill & +{\tilde{u}}_k\left(t\right),k=1,2,\cdots ,m\hfill \end{array}.\right.$$

(21)

The structure of this FICNN is shown in Figure 1.

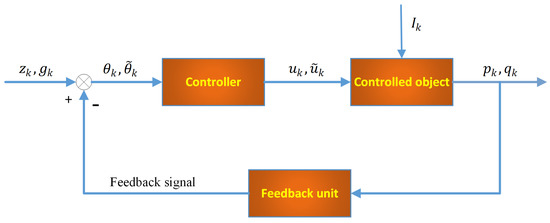
Figure 1. Framework of feedback control.

Definition 4

([32]). The drive system(17) and response systems (19) are synchronized within a finite time, if $T>t_0$ exists under properly designed controllers ${\tilde{u}}_k\left(t\right),u_k\left(t\right)$, such that

$$\underset{t\to T}{\lim }\parallel p_k\left(t\right)-z_k\left(t\right)\parallel =\underset{t\to T}{\lim }\parallel q_k\left(t\right)-g_k\left(t\right)\parallel =0$$

and $\parallel p_k\left(t\right)-z_k\left(t\right)\parallel =\parallel q_k\left(t\right)-g_k\left(t\right)\parallel =0$ for all $t>T,k=1,2,\cdots ,m$.

3. Finite-Time Synchronization

In this section, we will design controller $u_k\left(t\right),{\tilde{u}}_k\left(t\right)$ to get the finite-time synchronization between the drive-response systems. The controller is designed,

$$\left\{\begin{array}{cc}\hfill u_k\left(t\right)& =-\rho sign\left({\theta }_k\left(t\right)\right)\left(|{\theta }_k\left(t\right){|}^{\mu }+{\omega }_k|{\theta }_k(t-{\sigma }_k\left(t\right))|\right)-k_k{\theta }_k\left(t\right)\hfill \\ \hfill {\tilde{u}}_k\left(t\right)& =-sign\left({\tilde{\theta }}_k\left(t\right)\right)\left({\eta }_{k2}+\rho |{\tilde{\theta }}_k\left(t\right){|}^{\mu }\right)-{\eta }_{k1}{\tilde{\theta }}_k\left(t\right)\hfill \\ \hfill & -\sum _{r=1}^m{d}_{kr}\left({\int }_{t-{\sigma }_0\left(t\right)}^t{\zeta }_r\left(s\right)ds-{\int }_{t-{\sigma }_0\left(t\right)}^t{\lambda }_r\left(s\right)ds\right)\hfill \\ \hfill ,\end{array},\right.$$

(22)

where $0<\mu <1,\rho >0,k_k,{\omega }_k,{\eta }_{k1},and{\eta }_{k2}$ are the control parameters.

Theorem 1.

Assumptions 1 and 2 are true if the following conditions (23) hold; then, the system (17) and (19) can achieve finite-time synchronization under controller (22). We have

$$\left\{\begin{array}{cc}\hfill {\eta }_{k1}& \ge 1-{\varphi }_k\hfill \\ \hfill {\eta }_{k2}& \ge \sum _{r=1}^m\left(|{\alpha }_{kr}|+|{\beta }_{kr}|+|c_{kr}|\right)S_r\hfill \\ \hfill k_k& \ge \sum _{r=1}^m\left|c_{rk}\right|L_k+{\delta }_k-{\xi }_k\hfill \\ \hfill {\omega }_k& \ge \sum _{r=1}^m\left(|{\alpha }_{kr}|+|{\beta }_{kr}|\right)L_k\hfill \end{array}\right.$$

(23)

for $k=1,2,\cdots ,m$. Furthermore, the T can be calculated by Equation (24),

$$T=t_0+{\left(\frac{\Gamma (1+\alpha )\Gamma (1-\mu )V^{\alpha -\mu }\left(t_0\right)}{c\Gamma (1+\alpha -\mu )}\right)}^{\frac{1}{\alpha }},$$

(24)

where

$$V\left(t_0\right)=\sum _{k=1}^m\left|{\theta }_k\left(t_0\right)\right|+\sum _{k=1}^m\left|{\tilde{\theta }}_k\left(t_0\right)\right|.$$

Proof. 

Select the following Lyapunov function:

$$V\left(t\right)=\sum _{k=1}^m\left|{\theta }_k\left(t\right)\right|+\sum _{k=1}^m\left|{\tilde{\theta }}_k\left(t\right)\right|.$$

(25)

According to Lemmas 3 and 4, the derivative of $V\left(t\right)$ is calculated, and we obtain

$$\begin{array}{cc}\hfill D_t^{\alpha }V\left(t\right)& \le \sum _{k=1}^{m}sign\left({\theta }_k\left(t\right)\right)D_t^{\alpha }{\theta }_k\left(t\right)+\sum _{k=1}^{m}sign\left({\tilde{\theta }}_k\left(t\right)\right)D^{\alpha }{\tilde{\theta }}_k\left(t\right)\hfill \\ \hfill & =\sum _{k=1}^{m}sign\left({\theta }_k\left(t\right)\right)\left(-{\xi }_k{\theta }_k\left(t\right)+{\tilde{\theta }}_k\left(t\right)+u_k\left(t\right)\right)+\sum _{k=1}^{m}sign\left({\tilde{\theta }}_k\left(t\right)\right)(-{\varphi }_k{\tilde{\theta }}_k\left(t\right)+{\delta }_k{\theta }_k\left(t\right)\hfill \\ \hfill & +\sum _{r=1}^m{c}_{kr}{\zeta }_r\left(t\right)-\sum _{r=1}^m{c}_{kr}{\lambda }_r\left(t\right)+\sum _{r=1}^m{d}_{kr}{\int }_{t-{\sigma }_0\left(t\right)}^t{\zeta }_r\left(s\right)ds-\sum _{r=1}^m{d}_{kr}{\int }_{t-{\sigma }_0\left(t\right)}^t{\lambda }_r\left(s\right)ds\hfill \\ \hfill & +\underset{r=1}{\overset{m}{\bigwedge }}{\alpha }_{kr}{\zeta }_r(t-{\sigma }_r\left(t\right))-\underset{r=1}{\overset{m}{\bigwedge }}{\alpha }_{kr}{\lambda }_r(t-{\sigma }_r\left(t\right))\hfill \\ \hfill & +\underset{r=1}{\overset{m}{\bigvee }}{\beta }_{kr}{\zeta }_r(t-{\sigma }_r\left(t\right))-\underset{r=1}{\overset{m}{\bigvee }}{\beta }_{kr}{\lambda }_r(t-{\sigma }_r\left(t\right))+{\tilde{u}}_k\left(t\right))\hfill \end{array}.$$

(26)

Substituting the controller (22) into Equation (26), and we have

$$\begin{array}{cc}\hfill D_t^{\alpha }V\left(t\right)& \le \sum _{k=1}^{m}sign\left({\theta }_k\left(t\right)\right)(-{\xi }_k{\theta }_k\left(t\right)+{\tilde{\theta }}_k\left(t\right)-k_k{\theta }_k\left(t\right)-sign\left({\theta }_k\left(t\right)\right)(\rho |{\theta }_k\left(t\right){|}^{\mu }\hfill \\ \hfill & +{\omega }_k\left|{\theta }_k(t-{\sigma }_k\left(t\right))\right|\left)\right)+\sum _{k=1}^{m}sign\left({\tilde{\theta }}_k\left(t\right)\right)(-{\varphi }_k{\tilde{\theta }}_k\left(t\right)+{\delta }_k{\theta }_k\left(t\right)+\sum _{r=1}^m{c}_{kr}{\zeta }_r\left(t\right)\hfill \\ \hfill & -\sum _{r=1}^m{c}_{kr}{\lambda }_r\left(t\right)+\sum _{r=1}^m{d}_{kr}{\int }_{t-{\sigma }_0\left(t\right)}^t{\zeta }_r\left(s\right)ds-\sum _{r=1}^n{d}_{kr}{\int }_{t-{\sigma }_0\left(t\right)}^t{\lambda }_r\left(s\right)ds\hfill \\ \hfill & +\underset{r=1}{\overset{m}{\bigwedge }}{\alpha }_{kr}{\zeta }_r(t-{\sigma }_r\left(t\right))-\underset{r=1}{\overset{m}{\bigwedge }}{\alpha }_{kr}{\lambda }_r(t-{\sigma }_r\left(t\right))\hfill \\ \hfill & +\underset{r=1}{\overset{m}{\bigvee }}{\beta }_{kr}{\zeta }_k(t-{\sigma }_r\left(t\right))-\underset{r=1}{\overset{m}{\bigvee }}{\beta }_{kr}{\lambda }_r(t-{\sigma }_r\left(t\right))-{\eta }_{k1}{\tilde{\theta }}_k\left(t\right)\hfill \\ \hfill & -sign\left({\tilde{\theta }}_k\left(t\right)\right)\left({\eta }_{k2}+\rho |{\tilde{\theta }}_k\left(t\right){|}^{\mu }\right)-\sum _{r=1}^m{d}_{kr}{\int }_{t-{\sigma }_0\left(t\right)}^t{\zeta }_r\left(s\right)ds\hfill \\ \hfill & +\sum _{r=1}^m{d}_{kr}{\int }_{t-{\sigma }_0\left(t\right)}^t{\lambda }_r\left(s\right)ds)\hfill \end{array},$$

which yields

$$\begin{array}{cc}\hfill D_t^{\alpha }V\left(t\right)& \le \sum _{k=1}^m\left[-{\xi }_k-k_k+{\delta }_k\right]\left|{\theta }_k\left(t\right)\right|+\sum _{k=1}^m\left[1+{\varphi }_k-{\eta }_{k1}\right]\left|{\tilde{\theta }}_k\left(t\right)\right|\hfill \\ \hfill & -\sum _{k=1}^m{\omega }_k\left|{\theta }_k(t-{\sigma }_k\left(t\right))\right|-\sum _{k=1}^m\rho |{\theta }_k\left(t\right){|}^{\mu }-\sum _{k=1}^m\left({\eta }_{k1}+\rho |{\tilde{\theta }}_k\left(t\right){|}^{\mu }\right)\hfill \\ \hfill & +\sum _{k=1}^m|\underset{r=1}{\overset{m}{\bigwedge }}{\alpha }_{kr}{\zeta }_r(t-{\sigma }_r\left(t\right))-\underset{r=1}{\overset{m}{\bigwedge }}{\alpha }_{kr}{\lambda }_r(t-{\sigma }_r\left(t\right))|\hfill \\ \hfill & +\sum _{k=1}^m|\underset{r=1}{\overset{m}{\bigvee }}{\beta }_{kr}{\zeta }_r(t-{\sigma }_r\left(t\right))-\underset{r=1}{\overset{m}{\bigvee }}{\beta }_{kr}{\lambda }_r(t-{\sigma }_r\left(t\right))|\hfill \\ \hfill & +\sum _{k=1}^m\sum _{r=1}^m\left|c_{kr}\right||{\zeta }_r\left(t\right)-{\lambda }_l\left(t\right)|\hfill \end{array}.$$

According to Assumption 1, we have

$$\begin{array}{cc}\hfill \sum _{k=1}^m\sum _{r=1}^m\left|c_{kr}\right||{\zeta }_r\left(t\right)-{\lambda }_r\left(t\right)|& \le \sum _{k=1}^m\sum _{r=1}^m\left|c_{kr}\right|\left(L_r\left|{\theta }_r\left(t\right)\right|+S_r\right)\hfill \\ \hfill & =\sum _{k=1}^m\sum _{r=1}^m\left|c_{rk}\right|\left(L_k\left|{\theta }_k\left(t\right)\right|+S_k\right)\hfill \end{array}.$$

By using Assumption 1 and Lemma 6, we have

$$\begin{array}{cc}\hfill |\underset{r=1}{\overset{m}{\bigwedge }}{\alpha }_{kr}{\zeta }_r(t-{\sigma }_r\left(t\right))-\underset{r=1}{\overset{m}{\bigwedge }}{\alpha }_{kr}{\lambda }_r(t-{\sigma }_r\left(t\right))|& \le \sum _{k=1}^m\left|{\alpha }_{kr}\right||{\zeta }_r(t-{\sigma }_r\left(t\right))-{\lambda }_r(t-{\sigma }_r\left(t\right))|\hfill \\ \hfill & \le \sum _{r=1}^m\left|{\alpha }_{rk}\right|\left(L_r\left|{\theta }_r(t-{\sigma }_r\left(t\right))\right|+S_r\right)\hfill \end{array}.$$

Similarly,

$$\begin{array}{cc}\hfill |\underset{r=1}{\overset{m}{\bigvee }}{\beta }_{kr}{\zeta }_r(t-{\sigma }_r\left(t\right))-\underset{r=1}{\overset{m}{\bigvee }}{\beta }_{kr}{\lambda }_r(t-{\sigma }_r\left(t\right))|& \le \sum _{k=1}^m\left|{\beta }_{kr}\right||{\zeta }_r(t-{\sigma }_r\left(t\right))-{\lambda }_r(t-{\sigma }_r\left(t\right))|\hfill \\ \hfill & \le \sum _{r=1}^m\left|{\beta }_{rk}\right|\left(L_r\left|{\theta }_r(t-{\sigma }_r\left(t\right))\right|+S_r\right)\hfill \end{array}.$$

By using the above inequality, we have

$$\begin{array}{cc}\hfill D_t^{\alpha }V\left(t\right)& \le \sum _{k=1}^m\left[-{\xi }_k-k_k+{\delta }_k+\sum _{r=1}^m\left|c_{rk}{L}_k\right|\right]\left|{\theta }_k\left(t\right)\right|+\sum _{k=1}^m\left[1+{\varphi }_k-{\eta }_{k1}\right]\left|{\tilde{\theta }}_k\left(t\right)\right|\hfill \\ \hfill & +\sum _{k=1}^m\left(\sum _{r=1}^m\left(\left|{\alpha }_{rk}\right|+\left|{\beta }_{rk}\right|\right)L_k-{\omega }_k\right)\left|{\theta }_k(t-{\sigma }_k\left(t\right))\right|\hfill \\ \hfill & +\sum _{k=1}^m\left(\sum _{r=1}^m\left(\left|{\alpha }_{kr}\right|+\left|{\beta }_{kr}\right|+\left|c_{kr}\right|\right)S_r-{\eta }_{k2}\right)\hfill \\ \hfill & -\sum _{k=1}^{m}c|{\theta }_k\left(t\right){|}^{\mu }-\sum _{k=1}^{m}c|{\tilde{\theta }}_k\left(t\right){|}^{\mu }\hfill \end{array}.$$

(27)

By using Lemma 7, it follows that

$$\begin{array}{cc}\hfill D_t^{\alpha }V\left(t\right)& \le -\sum _{k=1}^{m}c|{\theta }_k\left(t\right){|}^{\mu }-\sum _{k=1}^{m}c|{\tilde{\theta }}_k\left(t\right){|}^{\mu }\hfill \\ \hfill & \le -c{\left(\sum _{k=1}^m\left|{\theta }_k\left(t\right)\right|+\sum _{k=1}^m\left|{\tilde{\theta }}_k\left(t\right)\right|\right)}^{\mu }\hfill \\ \hfill & =-c{V}^{\mu }\left(t\right)\hfill \end{array}.$$

Therefore, the drive (17) and the response (19) system can achieve to synchronization in the finite-time by Lemma 8. ☐

Remark 3.

The finite-time synchronization of FFICNNs with piecewise activations and mixed delays is achieved by constructing a suitable controller in Theorem 1. However, the control laws $u_k\left(t\right)$ and ${\tilde{u}}_k\left(t\right)$ are not easily adaptive, and they must meet some special conditions. Therefore, we will optimize the applicable laws $u_k\left(t\right)$ and ${\tilde{u}}_k\left(t\right)$ to improve the feasibility.

The controller is redesigned as follows,

$$\left\{\begin{array}{cc}\hfill u_k\left(t\right)=& -k_{k1}{\theta }_k\left(t\right)-k_{k2}sign\left({\theta }_k\left(t\right)\right)|{\theta }_k\left(t\right){|}^{\mu }\hfill \\ \hfill {\tilde{u}}_k\left(t\right)=& -{\eta }_{k1}{\tilde{\theta }}_k\left(t\right)-sign\left({\tilde{\theta }}_k\left(t\right)\right)\left({\eta }_{k2}\right|{\tilde{\theta }}_k\left(t\right){|}^{\mu }+{\omega }_k\left|{\theta }_k(t-{\sigma }_k\left(t\right))\right|\hfill \\ \hfill & +\sum _{r=1}^m{L}_r\left|d_{kr}\right|{\int }_{t-{\sigma }_0\left(t\right)}^t\left|{\theta }_r\left(s\right)\right|ds+{\rho }_k),\hfill \end{array}\right.$$

(28)

where $0<\mu <1,k_{k1},k_{k2},{\eta }_{k1},{\eta }_{k2},{\rho }_k,{\omega }_k$ are the control parameters. Then we have the following theorem.

Theorem 2.

Assumptions 1 and 2 are true if the following conditions (29) hold, and then the system (17) and (19) can achieve finite-time synchronization under controller (28). We have

$$\left\{\begin{array}{cc}\hfill k_{k1}& \ge \frac{1}{2}+\frac{1}{2}{\delta }_k+\frac{1}{2}\sum _{r=1}^m{L}_k\left|c_{rk}\right|-{\xi }_k\hfill \\ \hfill {\eta }_{k1}& \ge \frac{1}{2}+\frac{1}{2}{\delta }_k+\frac{1}{2}\sum _{r=1}^m{L}_r\left|c_{kr}\right|-{\varphi }_k\hfill \\ \hfill {\rho }_k& \ge \sum _{r=1}^m\left(|{\alpha }_{kr}|+|{\beta }_{kr}|+|c_{kr}|+\sigma |d_{kr}|\right)S_r\hfill \\ \hfill {\omega }_k& \ge \sum _{r=1}^m\left(|{\alpha }_{kr}|+|{\beta }_{kr}|\right)L_r\hfill \\ \hfill k_{k2}& >0,{\eta }_{k2}>0\hfill \end{array}\right.$$

(29)

for $k=1,2,\cdots ,m$. Furthermore, the T can be calculated by Equation (30),

$$\begin{array}{c}\hfill T=t_0+{\left(\frac{\Gamma \left(1+\alpha \right)\Gamma \left(\frac{1-\mu }{2}\right)V^{\frac{2\alpha -\mu -1}{2}}\left(t_0\right)}{c\Gamma \left(\frac{2\alpha -\mu +1}{2}\right)}\right)}^{\frac{1}{\alpha }}\end{array},$$

(30)

where

$$V\left(t_0\right)=\frac{1}{2}\sum _{k=1}^m{\theta }_k^2\left(t_0\right)+\frac{1}{2}\sum _{k=1}^m{\tilde{\theta }}_k^2\left(t_0\right).$$

Proof. 

Select the following Lyapunov function:

$$V\left(t\right)=\frac{1}{2}\sum _{k=1}^m{\theta }_k^2\left(t\right)+\frac{1}{2}\sum _{k=1}^m{\tilde{\theta }}_k^2\left(t\right).$$

(31)

Calculating the derivative of $V\left(t\right)$, according to Lemma 3, 5, we have

$$\begin{array}{cc}\hfill D_t^{\alpha }V\left(t\right)& \le \sum _{k=1}^m{\theta }_k\left(t\right)D_t^{\alpha }{\theta }_k\left(t\right)+\sum _{k=1}^m{\tilde{\theta }}_k\left(t\right)D^{\alpha }{\tilde{\theta }}_k\left(t\right)\hfill \\ \hfill & =\sum _{k=1}^m{\theta }_k\left(t\right)\left(-{\xi }_k{\theta }_k\left(t\right)+{\tilde{\theta }}_k\left(t\right)+u_k\left(t\right)\right)+\sum _{k=1}^m{\tilde{\theta }}_k\left(t\right)(-{\varphi }_k{\tilde{\theta }}_k\left(t\right)+{\delta }_k{\theta }_k\left(t\right)\hfill \\ \hfill & +\sum _{r=1}^m{c}_{kr}{\zeta }_r\left(t\right)-\sum _{r=1}^m{c}_{kr}{\lambda }_r\left(t\right)+\sum _{r=1}^m{d}_{kr}{\int }_{t-{\sigma }_0\left(t\right)}^t{\zeta }_r\left(s\right)ds-\sum _{r=1}^m{d}_{kr}{\int }_{t-{\sigma }_0\left(t\right)}^t{\lambda }_r\left(s\right)ds\hfill \\ \hfill & +\underset{r=1}{\overset{m}{\bigwedge }}{\alpha }_{kr}{\zeta }_r(t-{\sigma }_r\left(t\right))-\underset{r=1}{\overset{m}{\bigwedge }}{\alpha }_{kr}{\lambda }_r(t-{\sigma }_r\left(t\right))\hfill \\ \hfill & +\underset{r=1}{\overset{m}{\bigvee }}{\beta }_{kr}{\zeta }_r(t-{\sigma }_r\left(t\right))-\underset{r=1}{\overset{m}{\bigvee }}{\beta }_{kr}{\lambda }_r(t-{\sigma }_r\left(t\right))+{\tilde{u}}_k\left(t\right))\hfill \end{array}.$$

(32)

Substituting the controller (28) into Equation (32), we have

$$\begin{array}{cc}\hfill D_t^{\alpha }V\left(t\right)& \le \sum _{k=1}^m{\theta }_k\left(t\right)\left(-{\xi }_k{\theta }_k\left(t\right)+{\tilde{\theta }}_k\left(t\right)-k_{k1}{\theta }_k\left(t\right)-k_{k2}sign\left({\theta }_k\left(t\right)\right)|{\theta }_k\left(t\right){|}^{\mu }\right)\hfill \\ \hfill & +\sum _{k=1}^m{\tilde{\theta }}_k\left(t\right)(-{\varphi }_k{\tilde{\theta }}_k\left(t\right)+{\delta }_k{\theta }_k\left(t\right)+\sum _{r=1}^m{c}_{kr}{\zeta }_r\left(t\right)-\sum _{r=1}^m{c}_{kr}{\lambda }_r\left(t\right)+\sum _{r=1}^m{d}_{kr}{\int }_{t-{\sigma }_0\left(t\right)}^t{\zeta }_r\left(s\right)ds\hfill \\ \hfill & -\sum _{r=1}^m{d}_{kr}{\int }_{t-{\sigma }_0\left(t\right)}^t{\lambda }_r\left(s\right)ds+\underset{r=1}{\overset{m}{\bigwedge }}{\alpha }_{kr}{\zeta }_r(t-{\sigma }_r\left(t\right))-\underset{r=1}{\overset{m}{\bigwedge }}{\alpha }_{kr}{\lambda }_r(t-{\sigma }_r\left(t\right))\hfill \\ \hfill & +\underset{r=1}{\overset{m}{\bigvee }}{\beta }_{kr}{\zeta }_r(t-{\sigma }_r\left(t\right))-\underset{r=1}{\overset{m}{\bigvee }}{\beta }_{kr}{\lambda }_r(t-{\sigma }_r\left(t\right))-{\eta }_{k1}{\tilde{\theta }}_k\left(t\right)\hfill \\ \hfill & -sign\left({\tilde{\theta }}_k\left(t\right)\right)\left({\eta }_{k2}|{\tilde{\theta }}_k\left(t\right){|}^{\mu }+{\rho }_k\right)-sign\left({\tilde{\theta }}_k\left(t\right)\right){\omega }_k\left|{\theta }_k(t-{\sigma }_k\left(t\right))\right|)\hfill \\ \hfill & -sign\left({\tilde{\theta }}_k\left(t\right)\right)\sum _{r=1}^m{L}_r\left|d_{kr}\right|{\int }_{t-{\sigma }_0\left(t\right)}^t\left|{\theta }_r\left(s\right)\right|ds)\hfill \end{array},$$

which yields

$$\begin{array}{cc}\hfill D_t^{\alpha }V\left(t\right)& \le -\sum _{k=1}^m{\xi }_k{\theta }_k^2\left(t\right)+\sum _{k=1}^m\left|{\theta }_k\left(t\right)\right|\left|{\tilde{\theta }}_k\left(t\right)\right|-\sum _{k=1}^m{k}_{k1}{\theta }_k^2\left(t\right)-\sum _{k=1}^m{k}_{k2}|{\theta }_k\left(t\right){|}^{\mu +1}\hfill \\ \hfill & -\sum _{k=1}^m{\varphi }_k{\tilde{\theta }}_k^2\left(t\right)+\sum _{k=1}^m{\delta }_k\left|{\theta }_k\left(t\right)\right|\left|{\tilde{\theta }}_k\left(t\right)\right|+\sum _{k=1}^m\sum _{r=1}^m\left|c_{kr}\right||{\zeta }_r\left(t\right)-{\lambda }_r\left(t\right)|\left|{\tilde{\theta }}_r\left(t\right)\right|\hfill \\ \hfill & +\sum _{k=1}^m\sum _{r=1}^m\left|d_{kr}\right|\left|{\tilde{\theta }}_k\left(t\right)\right||{\int }_{t-{\sigma }_0\left(t\right)}^t{\zeta }_r\left(s\right)ds-{\int }_{t-{\sigma }_0\left(t\right)}^t{\lambda }_r\left(s\right)ds|\hfill \\ \hfill & +\sum _{k=1}^m\left|{\tilde{\theta }}_k\left(t\right)\right||\underset{r=1}{\overset{m}{\bigwedge }}{\alpha }_{kr}{\zeta }_r(t-{\sigma }_r\left(t\right))-\underset{r=1}{\overset{m}{\bigwedge }}{\alpha }_{kr}{\lambda }_r(t-{\sigma }_r\left(t\right))|\hfill \\ \hfill & +\sum _{k=1}^m\left|{\tilde{\theta }}_k\left(t\right)\right||\underset{r=1}{\overset{m}{\bigvee }}{\beta }_{kr}{\zeta }_r(t-{\sigma }_r\left(t\right))-\underset{r=1}{\overset{m}{\bigvee }}{\beta }_{kr}{\lambda }_r(t-{\sigma }_r\left(t\right))|\hfill \\ \hfill & -\sum _{k=1}^m{\eta }_{k1}{\tilde{\theta }}_k^2\left(t\right)-\sum _{k=1}^m\left({\eta }_{k2}|{\tilde{\theta }}_k\left(t\right){|}^{\mu +1}+{\rho }_k|{\tilde{\theta }}_k\left(t\right)|\right)-\sum _{k=1}^m{\omega }_k\left|{\theta }_k(t-{\sigma }_k\left(t\right))\right|\left|{\tilde{\theta }}_k\left(t\right)\right|\hfill \\ \hfill & -\sum _{k=1}^m\sum _{r=1}^m{L}_r\left|d_{kr}\right|\left|{\tilde{\theta }}_k\left(t\right)\right|{\int }_{t-{\sigma }_0\left(t\right)}^t\left|{\theta }_r\left(s\right)\right|ds\hfill \end{array}.$$

According to Assumption 1 and Lemma 6, we have

$$\begin{array}{cc}\hfill \sum _{k=1}^m\sum _{r=1}^m\left|c_{kr}\right|\left|{\tilde{\theta }}_k\left(t\right)\right||{\zeta }_r\left(t\right)-{\lambda }_r\left(t\right)|& \le \sum _{k=1}^m\sum _{r=1}^m\left|c_{kr}\right|\left|{\tilde{\theta }}_k\left(t\right)\right|\left(L_r\left|{\theta }_r\left(t\right)\right|+S_r\right)\hfill \\ \hfill & \le \sum _{k=1}^m\sum _{r=1}^m{L}_k\left|c_{kr}\right|\left(\frac{1}{2}{\theta }_r^2\left(t\right)+\frac{1}{2}{\tilde{\theta }}_r^2\left(t\right)\right)+\sum _{k=1}^m\sum _{r=1}^m{S}_r\left|c_{kr}\right|\left|{\tilde{\theta }}_k\left(t\right)\right|\hfill \end{array}$$

and

$$\begin{array}{cc}\hfill \sum _{k=1}^m\sum _{r=1}^m\left|d_{kr}\right|\left|{\tilde{\theta }}_k\left(t\right)\right||& {\int }_{t-{\sigma }_0\left(t\right)}^t{\zeta }_k\left(s\right)ds-{\int }_{t-{\sigma }_0\left(t\right)}^t{\lambda }_r\left(s\right)ds|\hfill \\ \hfill & \le \sum _{k=1}^m\sum _{r=1}^m\left|d_{kr}\right|\left|{\tilde{\theta }}_k\left(t\right)\right|{\int }_{t-{\sigma }_0\left(t\right)}^t|{\zeta }_r\left(s\right)-{\lambda }_r\left(s\right)|ds\hfill \\ \hfill & \le \sum _{k=1}^m\sum _{r=1}^m\left|d_{kr}\right|\left|{\tilde{\theta }}_k\left(t\right)\right|{\int }_{t-{\sigma }_0\left(t\right)}^t\left(L_r\left|{\theta }_r\left(s\right)\right|+S_r\right)ds\hfill \\ \hfill & \le \sum _{k=1}^m\sum _{r=1}^m{L}_r\left|d_{kr}\right|\left|{\tilde{\theta }}_k\left(t\right)\right|{\int }_{t-{\sigma }_0\left(t\right)}^t\left|{\theta }_r\left(s\right)\right|ds\hfill \\ \hfill & +\sum _{k=1}^m\sum _{r=1}^m\sigma S_r\left|d_{kr}\right|\left|{\tilde{\theta }}_k\left(t\right)\right|\hfill \end{array},$$

so we can easily get

$$\begin{array}{cc}\hfill \sum _{k=1}^m\left|{\tilde{\theta }}_k\left(t\right)\right||\underset{r=1}{\overset{m}{\bigwedge }}{\alpha }_{kr}{\zeta }_r(t-{\sigma }_r\left(t\right))& -\underset{r=1}{\overset{m}{\bigwedge }}{\alpha }_{kr}{\lambda }_r(t-{\sigma }_r\left(t\right))|\hfill \\ \hfill & \le \sum _{k=1}^m\sum _{r=1}^m\left|{\alpha }_{kr}\right|\left|{\tilde{\theta }}_k\left(t\right)\right||{\zeta }_r(t-{\sigma }_r\left(t\right))-{\lambda }_r(t-{\sigma }_r\left(t\right))|\hfill \\ \hfill & \le \sum _{k=1}^m\sum _{r=1}^m\left|{\alpha }_{rk}\right|\left|{\tilde{\theta }}_k\left(t\right)\right|\left(L_r\left|{\theta }_r(t-{\sigma }_r\left(t\right))\right|+S_r\right)\hfill \end{array}.$$

Similarly,

$$\begin{array}{cc}\hfill \sum _{k=1}^m\left|{\tilde{\theta }}_k\left(t\right)\right||\underset{r=1}{\overset{m}{\bigvee }}{\beta }_{kr}{\zeta }_r(t-{\sigma }_r\left(t\right))& -\underset{r=1}{\overset{m}{\bigvee }}{\beta }_{kr}{\lambda }_r(t-{\sigma }_r\left(t\right))|\hfill \\ \hfill & \le \sum _{k=1}^m\left|{\beta }_{kr}\right|\left|{\tilde{\theta }}_k\left(t\right)\right||{\zeta }_r(t-{\sigma }_r\left(t\right))-{\lambda }_r(t-{\sigma }_r\left(t\right))|\hfill \\ \hfill & \le \sum _{r=1}^m\left|{\beta }_{kr}\right|\left|{\tilde{\theta }}_k\left(t\right)\right|\left(L_k\left|{\theta }_k(t-{\sigma }_k\left(t\right))\right|+S_r\right)\hfill \end{array}.$$

We further obtain the following inequality:

$$\begin{array}{cc}\hfill D_t^{\alpha }V\left(t\right)& \le \sum _{k=1}^m\left[\frac{1}{2}+\frac{1}{2}{\delta }_k+\frac{1}{2}\sum _{l=1}^m{L}_k\left|c_{lk}\right|-{\xi }_k-k_{k1}\right]{\theta }_k^2\left(t\right)\hfill \\ \hfill & +\sum _{k=1}^m\left[\frac{1}{2}+\frac{1}{2}{\delta }_k+\frac{1}{2}\sum _{r=1}^m{L}_r\left|c_{kl}\right|-{\varphi }_k-{\eta }_{k1}\right]{\tilde{\theta }}_k^2\left(t\right)\hfill \\ \hfill & +\sum _{k=1}^m\left[\sum _{r=1}^m\left(|{\alpha }_{kr}|+|{\beta }_{kr}|+|c_{kr}|+\sigma |d_{kr}|\right)S_r-{\rho }_k\right]\left|{\tilde{\theta }}_k\left(t\right)\right|\hfill \\ \hfill & +\sum _{k=1}^m\left[\sum _{r=1}^m\left(|{\alpha }_{kr}|+|{\beta }_{kr}|\right)L_r-{\omega }_k\right]\left|{\tilde{e}}_k\left(t\right)\right|\left|{\theta }_k(t-{\sigma }_k\left(t\right))\right|\hfill \\ \hfill & -\sum _{k=1}^m{k}_{k2}|{\theta }_k\left(t\right){|}^{\mu +1}-\sum _{k=1}^m{\eta }_{k2}|{\tilde{\theta }}_k\left(t\right){|}^{\mu +1}\hfill \end{array}.$$

By using Lemma 7, we obtain

$$\begin{array}{cc}\hfill D_t^{\alpha }V\left(t\right)& \le -\sum _{k=1}^m{k}_{k2}|{\theta }_k\left(t\right){|}^{\mu +1}-\sum _{k=1}^m{\eta }_{k2}|{\tilde{\theta }}_k\left(t\right){|}^{\mu +1}\hfill \\ \hfill & \le -\min \{\min \left\{k_{k2}\right\},\min \left\{{\eta }_{k2}\right\}\}\sum _{k=1}^m\left[|{\theta }_k\left(t\right){|}^{\mu +1}+|{\tilde{\theta }}_k\left(t\right){|}^{\mu +1}\right]\hfill \\ \hfill & \le -\min \{\min \left\{k_{k2}\right\},\min \left\{{\eta }_{k2}\right\}\}\sum _{k=1}^m{\left[|{\theta }_k\left(t\right){|}^2+|{\tilde{\theta }}_k\left(t\right){|}^2\right]}^{\frac{\mu +1}{2}}\hfill \\ \hfill & \le -\min \{\min \left\{k_{k2}\right\},\min \left\{{\eta }_{k2}\right\}\}{2}^{\frac{\mu +1}{2}}{V}^{\frac{\mu +1}{2}}\left(t\right)\hfill \\ \hfill & =-\gamma V^{\frac{\mu +1}{2}}\left(t\right)\hfill \end{array},$$

where $\gamma =\min \{\min \left\{k_{i2}\right\},\min \left\{{\eta }_{i2}\right\}\}{2}^{\frac{\mu +1}{2}}$. Therefore, the drive (17) and the response (19) system can achieve synchronization in the finite time by Lemma 8. ☐

4. Numerical Simulations

In this section, we use two numerical examples to verify the validity of the results of Theorems 1 and 2.

Example 1.

Consider a two-dimensional FFINNs with piecewise activations and mixed delay.

The drive system is given by

$$\left\{\begin{array}{cc}\hfill D_t^{\alpha }{z}_k\left(t\right)& =-{\xi }_k{z}_i\left(t\right)+g_k\left(t\right)\hfill \\ \hfill D_t^{\alpha }{g}_k\left(t\right)& =-{\varphi }_k{g}_k\left(t\right)+{\delta }_k{z}_k\left(t\right)+\sum _{r=1}^2{c}_{kr}{\lambda }_r\left(t\right)+\sum _{r=1}^2{d}_{kr}{\int }_{t-{\sigma }_0\left(t\right)}^t{\lambda }_r\left(s\right)ds\hfill \\ \hfill & +\sum _{r=1}^2{g}_{kr}{v}_r+\underset{r=1}{\overset{2}{\bigwedge }}{P}_k{\nu }_r+\underset{r=1}{\overset{2}{\bigwedge }}{\alpha }_{kr}{\lambda }_r(t-{\sigma }_r\left(t\right))+\underset{r=1}{\overset{2}{\bigvee }}{Q}_k{\nu }_r\hfill \\ \hfill & +\underset{r=1}{\overset{2}{\bigvee }}{\beta }_{kr}{\lambda }_r(t-{\sigma }_r\left(t\right))+I_k,k=1,2\hfill \end{array}\right.$$

(33)

and the response system

$$\left\{\begin{array}{cc}\hfill D_t^{\alpha }{p}_k\left(t\right)& =-{\xi }_k{p}_k\left(t\right)+q_k\left(t\right)+u_k\left(t\right)\hfill \\ \hfill D_t^{\alpha }{q}_k\left(t\right)& =-{\varphi }_k{q}_k\left(t\right)+{\delta }_k{p}_k\left(t\right)+\sum _{r=1}^2{c}_{kr}{\zeta }_r\left(t\right)+\sum _{r=1}^2{d}_{kr}{\int }_{t-{\sigma }_0\left(t\right)}^t{\zeta }_r\left(s\right)ds\hfill \\ \hfill & +\sum _{r=1}^2{g}_{kr}{v}_r+\underset{r=1}{\overset{2}{\bigwedge }}{P}_k{\nu }_r+\underset{r=1}{\overset{2}{\bigwedge }}{\alpha }_{kr}{\zeta }_r(t-{\sigma }_r\left(t\right))+\underset{r=1}{\overset{2}{\bigvee }}{Q}_k{\nu }_r\hfill \\ \hfill & +\underset{r=1}{\overset{2}{\bigvee }}{\beta }_{kr}{\zeta }_r(t-{\sigma }_r\left(t\right))+I_k+{\tilde{u}}_k\left(t\right),k=1,2.\hfill \end{array},\right.$$

(34)

where

$$h_k\left(x\right)=\left\{\begin{array}{c}\tanh \left(x\right)+0.8,x\ge 0\hfill \\ \tanh \left(x\right)-0.8,x<0\hfill \end{array}.\right.$$

Obviously, $h_k\left(x\right)$ satisfies Assumptions 1 and 2 with $L_k=1,S_k=1,k=1,2$. The parameters of drive (33) and response (34) system are chosen as follows:

$$\left\{\begin{array}{c}\alpha =0.95;\hfill \\ a_1=3,a_2=2,b_1=b_2=1,{\xi }_1=0.2,{\xi }_2=0.1;\hfill \\ c_{11}=c_{21}=-0.1,c_{12}=0.3,c_{22}=0.2\hfill \\ {\alpha }_{11}={\alpha }_{12}={\alpha }_{21}={\alpha }_{22}=-0.01;\hfill \\ {\beta }_{11}={\beta }_{12}={\beta }_{21}={\beta }_{22}=0.1;\hfill \\ d_{11}=d_{12}=d_{21}=d_{22}=-0.1;\hfill \\ I_1=0.2,I_2=0.5,{\sigma }_k\left(t\right)=0.3\cos \left(2t\right)+0.7,k=1,2\hfill \end{array}.\right.$$

The controller is designed as follows:

$$\left\{\begin{array}{cc}\hfill u_k\left(t\right)& =-k_k{e}_k\left(t\right)-\rho sign\left(e_k\left(t\right)\right)\left(|e_k\left(t\right){|}^{\mu }+{\omega }_k|e_k(t-{\sigma }_k\left(t\right))|\right)\hfill \\ \hfill {\tilde{u}}_k\left(t\right)& =-{\eta }_{k1}{\tilde{e}}_k\left(t\right)-sign\left({\tilde{e}}_k\left(t\right)\right)\left({\eta }_{k2}+\rho |{\tilde{e}}_k\left(t\right){|}^{\mu }\right)\hfill \\ \hfill & -\sum _{r=1}^2{d}_{kr}{\int }_{t-{\sigma }_0\left(t\right)}^t{\zeta }_r\left(s\right)ds+\sum _{r=1}^2{d}_{kr}{\int }_{t-{\sigma }_0\left(t\right)}^t{\lambda }_r\left(s\right)ds.\hfill \end{array}.\right.$$

(35)

The controller parameters are as follows:

$$\left\{\begin{array}{c}{k}_1=2,k_2=2,{\omega }_1=1,{\omega }_2=1,\rho =4;\hfill \\ {\eta }_{11}={\eta }_{12}={\eta }_{21}={\eta }_{22}=2,\mu =0.8\hfill \end{array}.\right.$$

The initial conditions are given as

$$\left\{\begin{array}{c}{z}_1\left(t\right)=2,z_2\left(t\right)=3,g_1\left(t\right)=4,g_2\left(t\right)=1;\hfill \\ p_1\left(t\right)=4,p_2\left(t\right)=1,q_1\left(t\right)=2,q_2\left(t\right)=4\hfill \end{array}.\right.$$

The time T is calculated by Theorem 1, which means that (34) and (35) can achieve synchronization in a finite time T. Furthermore, here $T=1.7220$.

Figure 2, Figure 3 and Figure 4 show the simulation results of the drive(33) and response(34) system. Figure 2 and Figure 3 show the trajectories of states $p\left(t\right)$ and $z\left(t\right)$, and $q\left(t\right)$ and $g\left(t\right)$, respectively. Equation (34) indeed converges to (33) with the controller (35) in T, and the convergence error continues to remain zero. The time evolution of synchronization errors $\theta \left(t\right)$ and $\tilde{\theta }\left(t\right)$ between systems (33) and (34) are presented in Figure 4. Simulation results show that the main results of the finite-time synchronization entrenched are correct in this article.

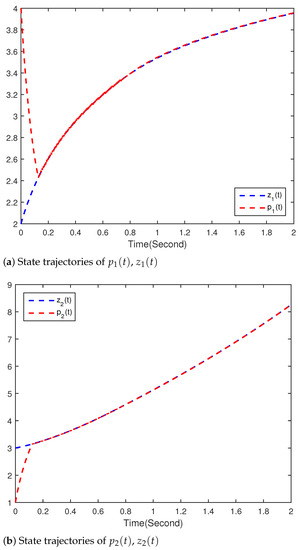
Figure 2. Time responses of $p\left(t\right)$ and $z\left(t\right)$.

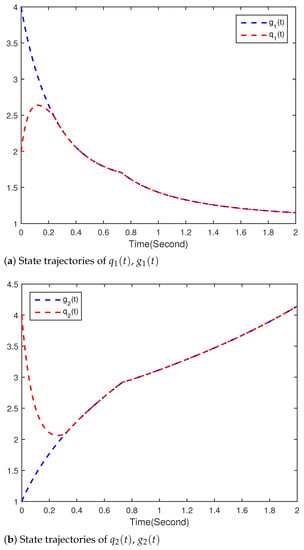
Figure 3. Time responses of $q\left(t\right)$ and $g\left(t\right)$.

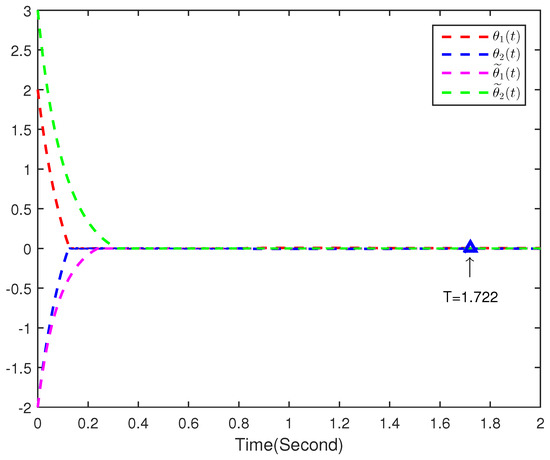
Figure 4. Synchronization error $\theta \left(t\right)$ and $\tilde{\theta }\left(t\right)$ between the drive-response system

Example 2.

Consider a two-dimensional FFINNs with piecewise activations and mixed delay.

The drive system is given by

$$\left\{\begin{array}{cc}\hfill D_t^{\alpha }{z}_k\left(t\right)& =-{\xi }_k{z}_k\left(t\right)+g_k\left(t\right)\hfill \\ \hfill D_t^{\alpha }{g}_k\left(t\right)& =-{\varphi }_k{g}_k\left(t\right)+{\delta }_k{z}_k\left(t\right)+\sum _{r=1}^2{c}_{kr}{\lambda }_r\left(t\right)+\sum _{r=1}^2{d}_{kr}{\int }_{t-{\sigma }_0\left(t\right)}^t{\lambda }_r\left(s\right)ds\hfill \\ \hfill & +\sum _{r=1}^2{g}_{kr}{v}_r+\underset{r=1}{\overset{2}{\bigwedge }}{P}_k{\nu }_r+\underset{l=1}{\overset{2}{\bigwedge }}{\alpha }_{kr}{\lambda }_r(t-{\sigma }_r\left(t\right))+\underset{r=1}{\overset{2}{\bigvee }}{Q}_k{\nu }_r\hfill \\ \hfill & +\underset{r=1}{\overset{2}{\bigvee }}{\beta }_{kr}{\lambda }_r(t-{\sigma }_r\left(t\right))+I_k,k=1,2\hfill \end{array}.\right.$$

(36)

and the response system is given by

$$\left\{\begin{array}{cc}\hfill D_t^{\alpha }{p}_k\left(t\right)& =-{\xi }_k{p}_k\left(t\right)+q_k\left(t\right)+u_k\left(t\right)\hfill \\ \hfill D_t^{\alpha }{q}_k\left(t\right)& =-{\varphi }_k{q}_k\left(t\right)+{\delta }_k{p}_k\left(t\right)+\sum _{r=1}^2{c}_{kr}{\zeta }_l\left(t\right)+\sum _{r=1}^2{d}_{kr}{\int }_{t-{\sigma }_0\left(t\right)}^t{\zeta }_r\left(s\right)ds\hfill \\ \hfill & +\sum _{r=1}^2{g}_{kr}{v}_r+\underset{r=1}{\overset{2}{\bigwedge }}{P}_k{\nu }_r+\underset{r=1}{\overset{2}{\bigwedge }}{\alpha }_{kr}{\zeta }_r(t-{\sigma }_r\left(t\right))+\underset{r=1}{\overset{2}{\bigvee }}{Q}_k{\nu }_r\hfill \\ \hfill & +\underset{r=1}{\overset{2}{\bigvee }}{\beta }_{kr}{\zeta }_r(t-{\sigma }_r\left(t\right))+I_k+{\tilde{u}}_k\left(t\right),k=1,2\hfill \end{array},\right.$$

(37)

where

$$h_k\left(x\right)=\left\{\begin{array}{c}\tanh \left(x\right)+0.5,x\ge 0\hfill \\ \tanh \left(x\right)-0.5,x<0\hfill \end{array}.\right.$$

Obviously, $h_k\left(x\right)$ satisfies Assumptions 1 and 2 with $L_k=1,S_k=1,k=1,2$. The parameters of drive (33) and response (34) system are chosen as follows:

$$\left\{\begin{array}{c}\alpha =0.95;\hfill \\ a_1=b_2=1,a_2=b_1=2,{\xi }_1=0.2,{\xi }_2=0.1;\hfill \\ c_{11}=c_{21}=-0.2,c_{12}=c_{22}=0.1\hfill \\ {\alpha }_{11}={\alpha }_{12}={\alpha }_{21}={\alpha }_{22}=-1;\hfill \\ {\beta }_{11}={\beta }_{12}={\beta }_{21}={\beta }_{22}=0.5;\hfill \\ d_{11}=d_{21}=-0.1,d_{12}=d_{22}=0.2;\hfill \\ I_1=0.2,I_2=0.5,{\sigma }_k\left(t\right)=0.3\cos \left(2t\right)+0.7,k=1,2\hfill \end{array}.\right.$$

The controller is designed as follows:

$$\left\{\begin{array}{cc}\hfill u_k\left(t\right)=& -k_{k1}{\theta }_k\left(t\right)-k_{k2}sign\left({\theta }_k\left(t\right)\right)|{\theta }_k\left(t\right){|}^{\mu }\hfill \\ \hfill {\tilde{u}}_k\left(t\right)=& -{\eta }_{k1}{\tilde{\theta }}_k\left(t\right)-sign\left({\tilde{\theta }}_k\left(t\right)\right)\left({\eta }_{k2}\right|{\tilde{\theta }}_k\left(t\right){|}^{\mu }+{\omega }_k\left|{\theta }_k(t-{\sigma }_k\left(t\right))\right|\hfill \\ \hfill & +\sum _{r=1}^2{L}_r\left|d_{kr}\right|{\int }_{t-{\sigma }_0\left(t\right)}^t\left|{\theta }_r\left(s\right)\right|ds+{\rho }_k)\hfill \end{array}.\right.$$

(38)

The controller parameter is given by

$$\left\{\begin{array}{c}{k}_{11}=k_{21}=6,k_{12}=k_{22}=4,{\omega }_1=1.2,{\omega }_2=0.8;\hfill \\ {\eta }_{11}={\eta }_{21}=6,{\eta }_{12}={\eta }_{21}=2,{\rho }_1={\rho }_2=9,\mu =0.7\hfill \end{array}.\right.$$

The initial conditions are given as

$$\left\{\begin{array}{c}{z}_1\left(t\right)=5,z_2\left(t\right)=3,g_1\left(t\right)=-4,g_2\left(t\right)=3;\hfill \\ p_1\left(t\right)=-5,p_2\left(t\right)=-2,q_1\left(t\right)=2,q_2\left(t\right)=6\hfill \end{array}.\right.$$

The time T is calculated by Theorem 2, which means that (37) and (38) can achieve synchronization in a finite time T. Furthermore, here $T=1.9082$.

Figure 5, Figure 6 and Figure 7 show the simulation results of the drive(36)-response(37) system. Figure 5 and Figure 6 show the trajectories of states $p\left(t\right)$ and $z\left(t\right)$, $q\left(t\right)$ and $g\left(t\right)$, respectively. Equation (37) indeed converges to (36) with the controller (38) in T, and the convergence error continues to remain zero. The time evolution of synchronization errors $\theta \left(t\right)$ and $\tilde{\theta }\left(t\right)$ between systems (36) and (37) are presented in Figure 7. Simulation results show that the main results of the finite-time synchronization entrenched are correct in this article.

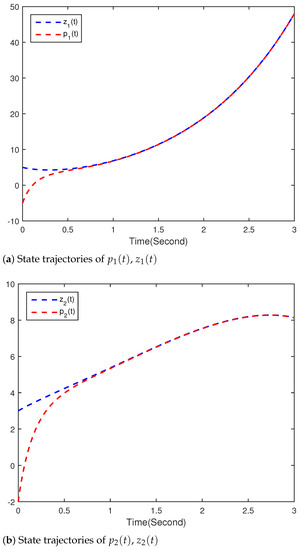
Figure 5. Time responses of $p\left(t\right)$ and $z\left(t\right)$.

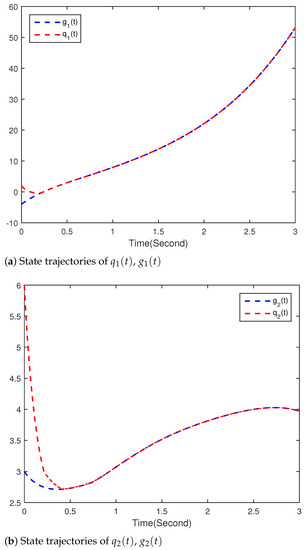
Figure 6. Time responses of $q\left(t\right)$ and $g\left(t\right)$.

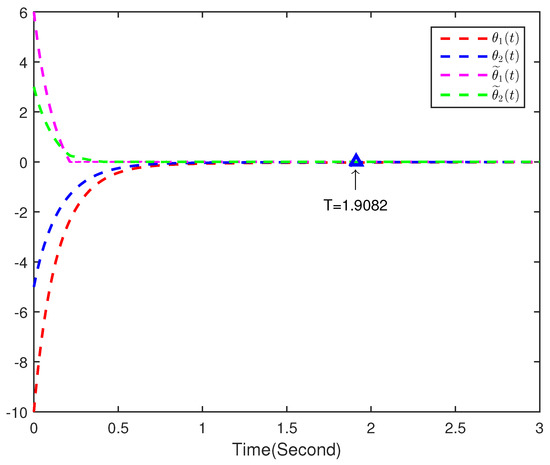
Figure 7. Synchronization error $\theta \left(t\right)$ and $\tilde{\theta }\left(t\right)$ between the drive-response system.

5. Conclusions

In this paper, a class of fractional order fuzzy inertial cellular neural network system with piecewise activation and mixed delay is proposed, and the finite-time synchronization of the system is discussed. By using the finite-time stability theory, Lyapunov functionals, and analytical techniques, some novel methods for finite-time synchronization of drive-response systems are obtained. Finally, two numerical simulation examples show that the proposed method is effective. In the future, we propose to expand our results to better apply FFINNs and implement it by designing hardware. The more efficient control laws will be considered, which is a challenging topic.