Compound Adaptive Fuzzy Synchronization Controller Design for Uncertain Fractional-Order Chaotic Systems
Abstract
1. Introduction
2. Preliminaries
2.1. Definitions and Lemmas
2.2. The Fuzzy Logic System
3. Main Results
3.1. System Description
3.2. Design of the Disturbance Observer
3.3. Controller Design
- All signals remain bounded in a closed-loop system.
- The synchronization error eventually converges to a small neighborhood of zero.
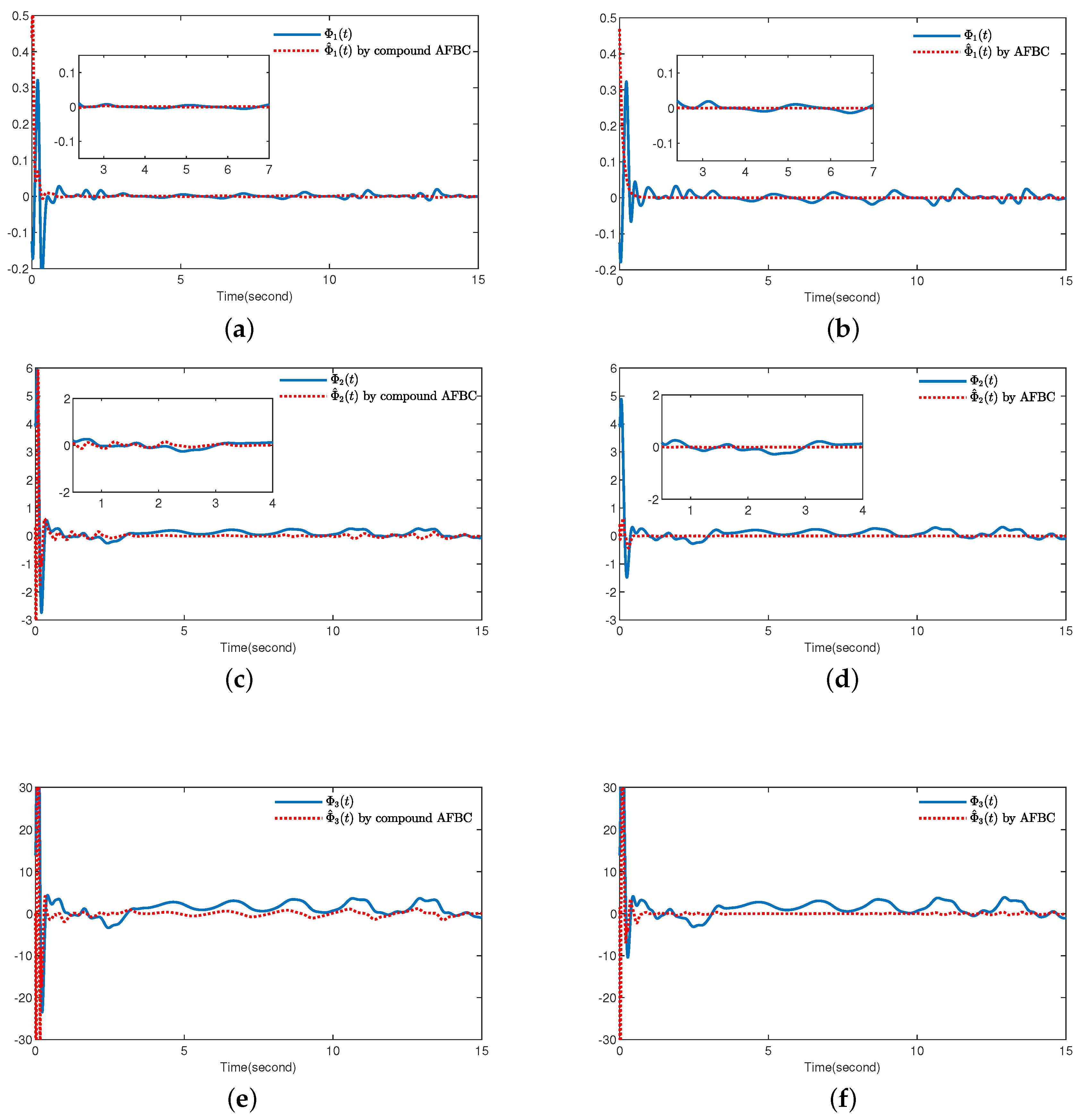
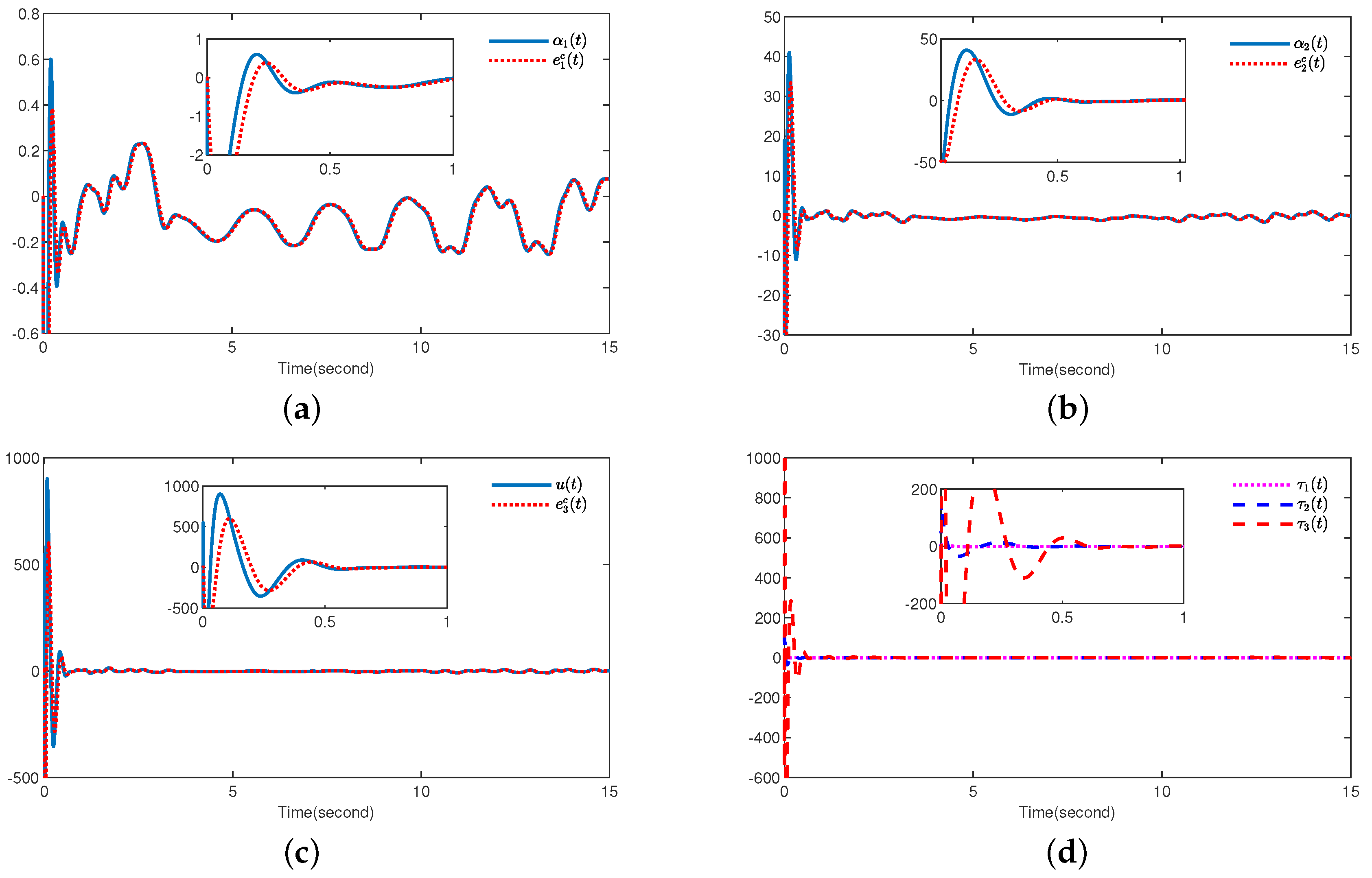
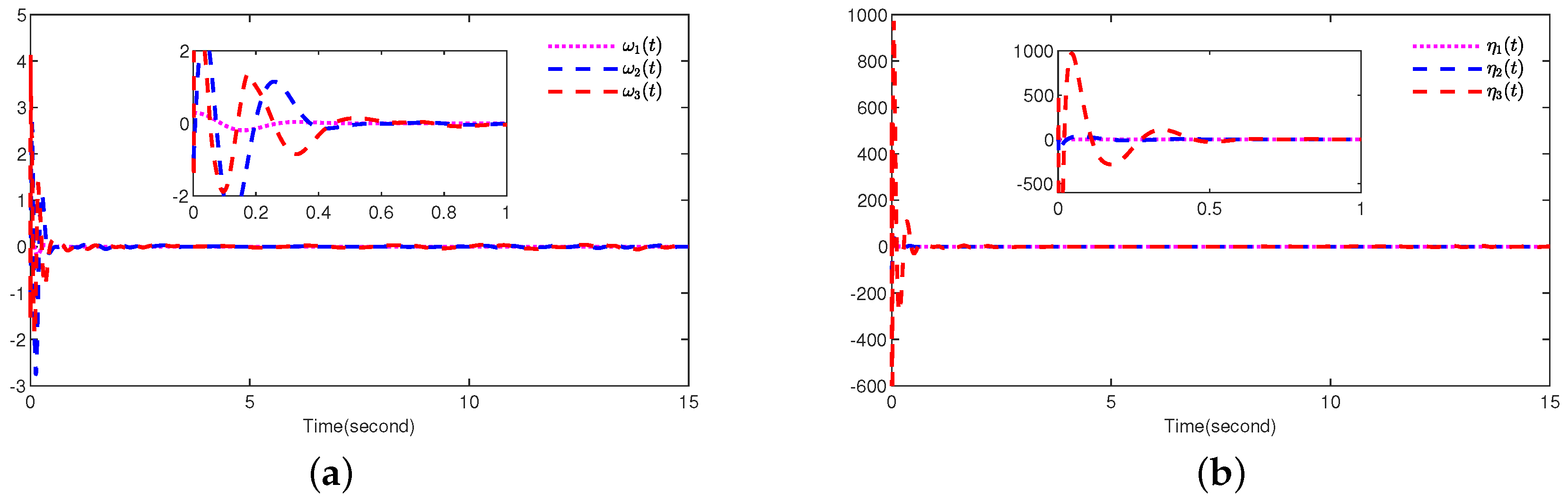
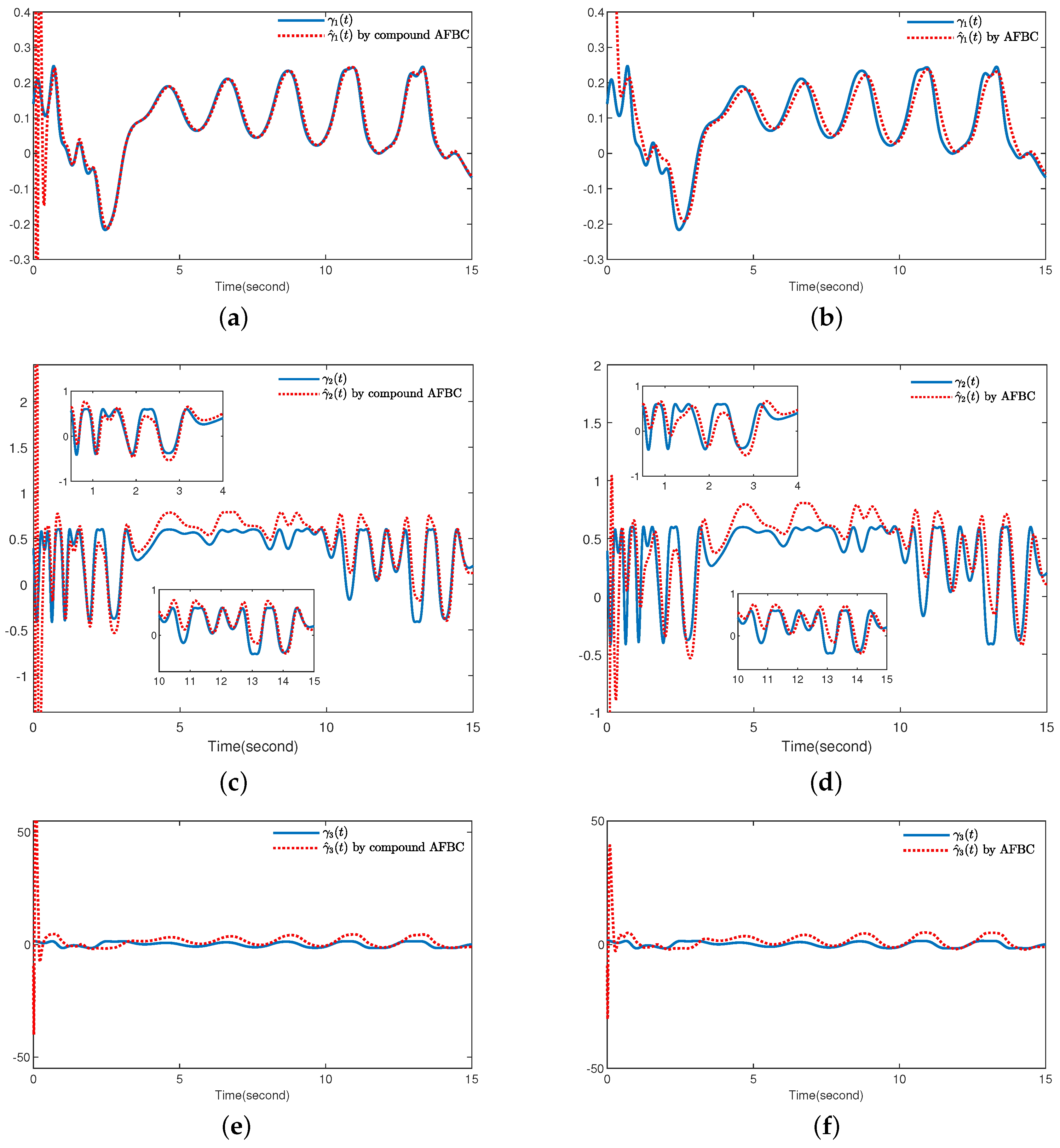
4. Simulation Results
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Wang, S.; He, S.; Yousefpour, A.; Jahanshahi, H.; Repnik, R.; Perc, M. Chaos and complexity in a fractional-order financial system with time delays. Chaos Solitons Fractals 2020, 131, 109521. [Google Scholar] [CrossRef]
- Homaeinezhad, M.; Yaqubi, S.; Gholyan, H. Control of MIMO mechanical systems interacting with actuators through viscoelastic linkages. Mech. Mach. Theory 2020, 147, 103763. [Google Scholar] [CrossRef]
- Cunha-Filho, A.; Briend, Y.; de Lima, A.; Donadon, M. A new and efficient constitutive model based on fractional time derivatives for transient analyses of viscoelastic systems. Mech. Syst. Signal Process. 2021, 146, 107042. [Google Scholar] [CrossRef]
- He, Y.; Zhang, Y.; Sari, H.M.K.; Wang, Z.; Lü, Z.; Huang, X.; Liu, Z.; Zhang, J.; Li, X. New insight into Li metal protection: Regulating the Li-ion flux via dielectric polarization. Nano Energy 2021, 89, 106334. [Google Scholar] [CrossRef]
- Bouzeriba, A.; Boulkroune, A.; Bouden, T. Projective synchronization of two different fractional-order chaotic systems via adaptive fuzzy control. Neural Comput. Appl. 2016, 27, 1349–1360. [Google Scholar] [CrossRef]
- Khan, A.; Jahanzaib, L.S. Synchronization on the adaptive sliding mode controller for fractional order complex chaotic systems with uncertainty and disturbances. Int. J. Dyn. Control 2019, 7, 1419–1433. [Google Scholar] [CrossRef]
- Wei, Z. Dynamical behaviors of a chaotic system with no equilibria. Phys. Lett. A 2011, 376, 102–108. [Google Scholar] [CrossRef]
- Qi, G.; Chen, G.; Du, S.; Chen, Z.; Yuan, Z. Analysis of a new chaotic system. Phys. A Stat. Mech. Its Appl. 2005, 352, 295–308. [Google Scholar] [CrossRef]
- Fradkov, A.L.; Evans, R.J. Control of chaos: Methods and applications in engineering. Annu. Rev. Control 2005, 29, 33–56. [Google Scholar] [CrossRef]
- Yin, X.; Pan, L.; Cai, S. Robust adaptive fuzzy sliding mode trajectory tracking control for serial robotic manipulators. Robot. Comput. Integr. Manuf. 2021, 72, 101884. [Google Scholar] [CrossRef]
- Boulkroune, A.; Bouzeriba, A.; Bouden, T.; Azar, A.T. Fuzzy adaptive synchronization of uncertain fractional-order chaotic systems. In Advances in Chaos Theory and Intelligent Control; Springer: Berlin/Heidelberg, Germany, 2016; pp. 681–697. [Google Scholar]
- Huang, S.; Wang, J.; Xiong, L.; Liu, J.; Li, P.; Wang, Z.; Yao, G. Fixed-Time Backstepping Fractional-Order Sliding Mode Excitation Control for Performance Improvement of Power System. IEEE Trans. Circuits Syst. I Regul. Pap. 2021, 69, 956–969. [Google Scholar] [CrossRef]
- Ha, S.; Liu, H.; Li, S.; Liu, A. Backstepping-based adaptive fuzzy synchronization control for a class of fractional-order chaotic systems with input saturation. Int. J. Fuzzy Syst. 2019, 21, 1571–1584. [Google Scholar] [CrossRef]
- Shi, X.; Cheng, Y.; Yin, C.; Dadras, S.; Huang, X. Design of fractional-order backstepping sliding mode control for quadrotor UAV. Asian J. Control 2019, 21, 156–171. [Google Scholar] [CrossRef]
- Moezi, S.A.; Zakeri, E.; Eghtesad, M. Optimal adaptive interval type-2 fuzzy fractional-order backstepping sliding mode control method for some classes of nonlinear systems. ISA Trans. 2019, 93, 23–39. [Google Scholar] [CrossRef]
- Ha, S.; Chen, L.; Liu, H.; Zhang, S. Command filtered adaptive fuzzy control of fractional-order nonlinear systems. Eur. J. Control 2022, 63, 48–60. [Google Scholar] [CrossRef]
- Han, S. Fractional-order command filtered backstepping sliding mode control with fractional-order nonlinear disturbance observer for nonlinear systems. J. Frankl. Inst. 2020, 357, 6760–6776. [Google Scholar] [CrossRef]
- Xue, G.; Lin, F.; Li, S.; Liu, H. Adaptive fuzzy finite-time backstepping control of fractional-order nonlinear systems with actuator faults via command-filtering and sliding mode technique. Inf. Sci. 2022, 600, 189–208. [Google Scholar] [CrossRef]
- Liu, H.; Wang, H.; Cao, J.; Alsaedi, A.; Hayat, T. Composite learning adaptive sliding mode control of fractional-order nonlinear systems with actuator faults. J. Frankl. Inst. 2019, 356, 9580–9599. [Google Scholar] [CrossRef]
- Zhou, Y.; Liu, H.; Cao, J.; Li, S. Composite learning fuzzy synchronization for incommensurate fractional-order chaotic systems with time-varying delays. Int. J. Adapt. Control Signal Process. 2019, 33, 1739–1758. [Google Scholar] [CrossRef]
- Han, Z.; Li, S.; Liu, H. Composite learning sliding mode synchronization of chaotic fractional-order neural networks. J. Adv. Res. 2020, 25, 87–96. [Google Scholar] [CrossRef]
- Mofid, O.; Mobayen, S.; Khooban, M.H. Sliding mode disturbance observer control based on adaptive synchronization in a class of fractional-order chaotic systems. Int. J. Adapt. Control Signal Process. 2019, 33, 462–474. [Google Scholar] [CrossRef]
- Li, Z.; Ma, X.; Li, Y. Nonlinear partially saturated control of a double pendulum offshore crane based on fractional-order disturbance observer. Autom. Constr. 2022, 137, 104212. [Google Scholar] [CrossRef]
- Guha, D.; Roy, P.K.; Banerjee, S. Adaptive fractional-order sliding-mode disturbance observer-based robust theoretical frequency controller applied to hybrid wind–diesel power system. ISA Trans. 2022; in press. [Google Scholar] [CrossRef]
- Liu, H.; Pan, Y.; Li, S.; Chen, Y. Adaptive fuzzy backstepping control of fractional-order nonlinear systems. IEEE Trans. Syst. Man Cybern. Syst. 2017, 47, 2209–2217. [Google Scholar] [CrossRef]
- Abbas, S.; Benchohra, M. Fractional order partial hyperbolic differential equations involving Caputo’s derivative. Stud. Univ. Babes-Bolyai Math 2012, 57, 469–479. [Google Scholar]
- Shen, J.; Lam, J. Non-existence of finite-time stable equilibria in fractional-order nonlinear systems. Automatica 2014, 50, 547–551. [Google Scholar] [CrossRef]
- Aguila-Camacho, N.; Duarte-Mermoud, M.A.; Gallegos, J.A. Lyapunov functions for fractional order systems. Commun. Nonlinear Sci. Numer. Simul. 2014, 19, 2951–2957. [Google Scholar] [CrossRef]
- Li, J.; Cao, J.; Liu, H. State observer-based fuzzy echo state network sliding mode control for uncertain strict-feedback chaotic systems without backstepping. Chaos Solitons Fractals 2022, 162, 112442. [Google Scholar] [CrossRef]
- Zirkohi, M.M. Robust adaptive backstepping control of uncertain fractional-order nonlinear systems with input time delay. Math. Comput. Simul. 2022, 196, 251–272. [Google Scholar] [CrossRef]
- Ha, S.; Chen, L.; Liu, H. Command filtered adaptive neural network synchronization control of fractional-order chaotic systems subject to unknown dead zones. J. Frankl. Inst. 2021, 358, 3376–3402. [Google Scholar] [CrossRef]
- Petráš, I. Fractional-Order Nonlinear Systems: Modeling, Analysis and Simulation; Springer Science & Business Media: Berlin/Heidelberg, Germany, 2011. [Google Scholar]

Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liu, F.; Zhang, X. Compound Adaptive Fuzzy Synchronization Controller Design for Uncertain Fractional-Order Chaotic Systems. Fractal Fract. 2022, 6, 652. https://doi.org/10.3390/fractalfract6110652
Liu F, Zhang X. Compound Adaptive Fuzzy Synchronization Controller Design for Uncertain Fractional-Order Chaotic Systems. Fractal and Fractional. 2022; 6(11):652. https://doi.org/10.3390/fractalfract6110652
Chicago/Turabian StyleLiu, Fengyan, and Xiulan Zhang. 2022. "Compound Adaptive Fuzzy Synchronization Controller Design for Uncertain Fractional-Order Chaotic Systems" Fractal and Fractional 6, no. 11: 652. https://doi.org/10.3390/fractalfract6110652
APA StyleLiu, F., & Zhang, X. (2022). Compound Adaptive Fuzzy Synchronization Controller Design for Uncertain Fractional-Order Chaotic Systems. Fractal and Fractional, 6(11), 652. https://doi.org/10.3390/fractalfract6110652




