Sequential Predictors for Uncertain Euler–Lagrange Systems with Large Transmission Delays
Abstract
1. Introduction
2. Preliminaries and Problem Statement
3. Sequential Predictor Design Using Both Delayed Position and Velocity Measurements
3.1. Construction of Sequential Predictor
3.2. Convergence Analysis of Prediction Errors
4. Sequential Predictor Design without Velocity Measurements
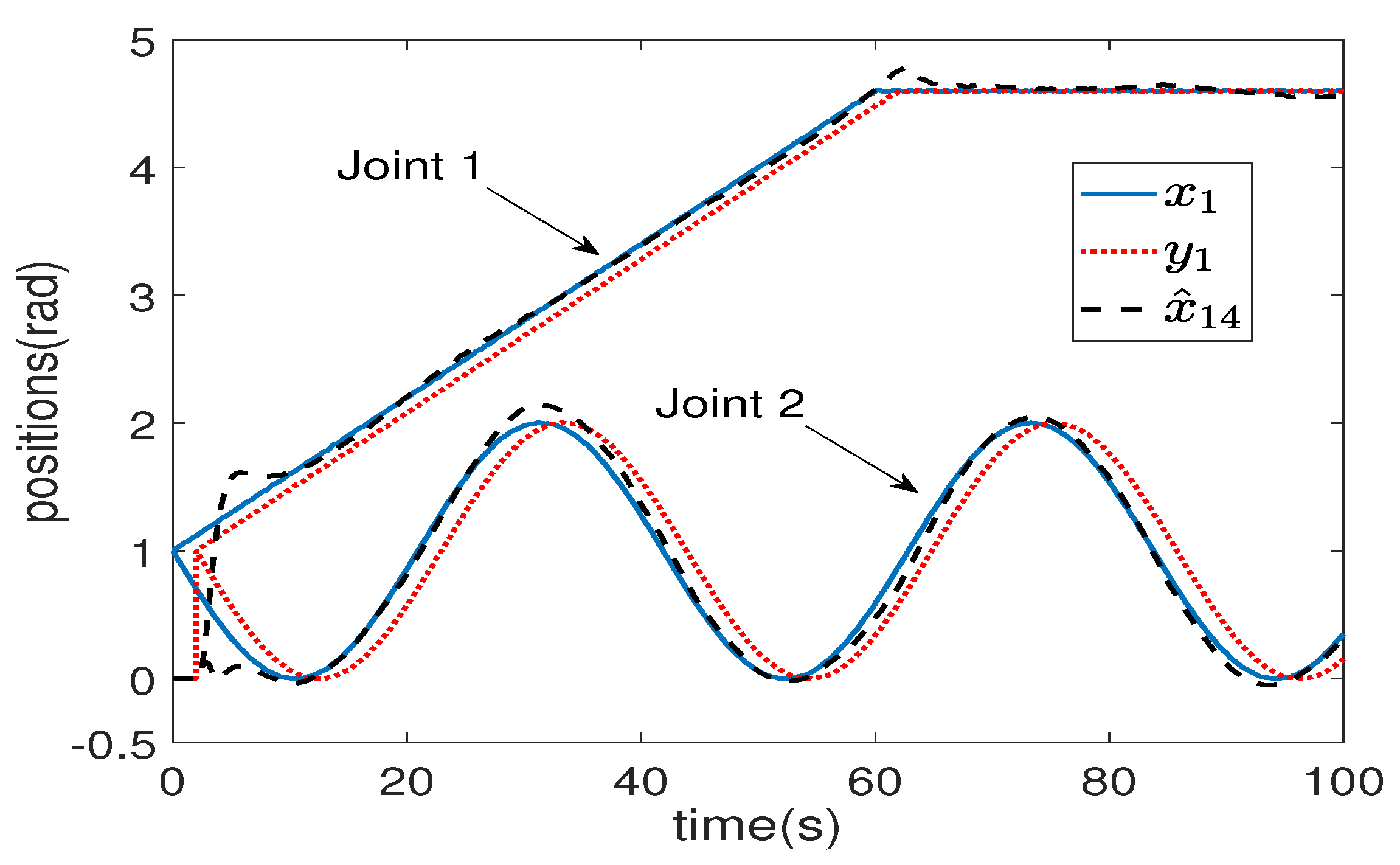
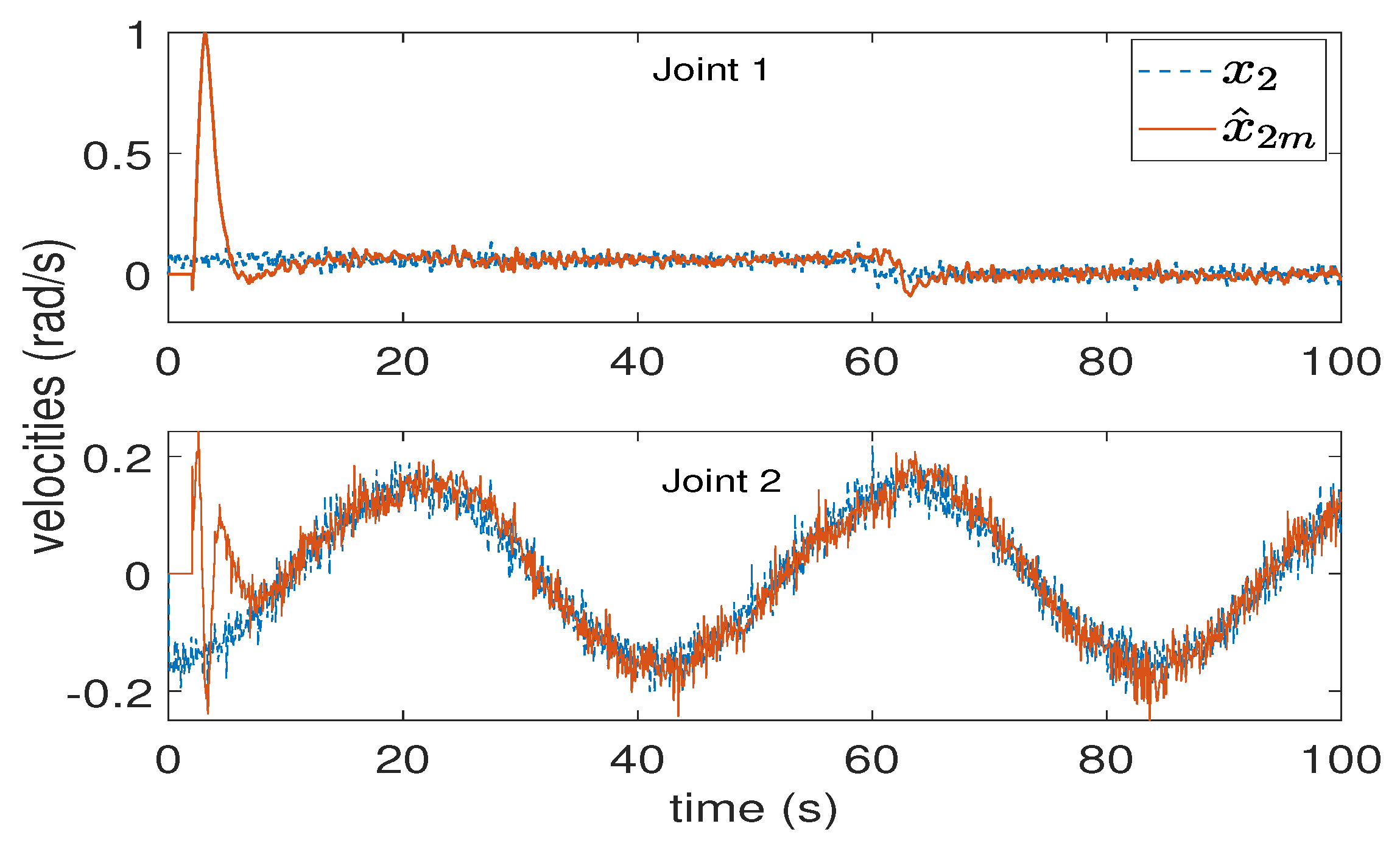
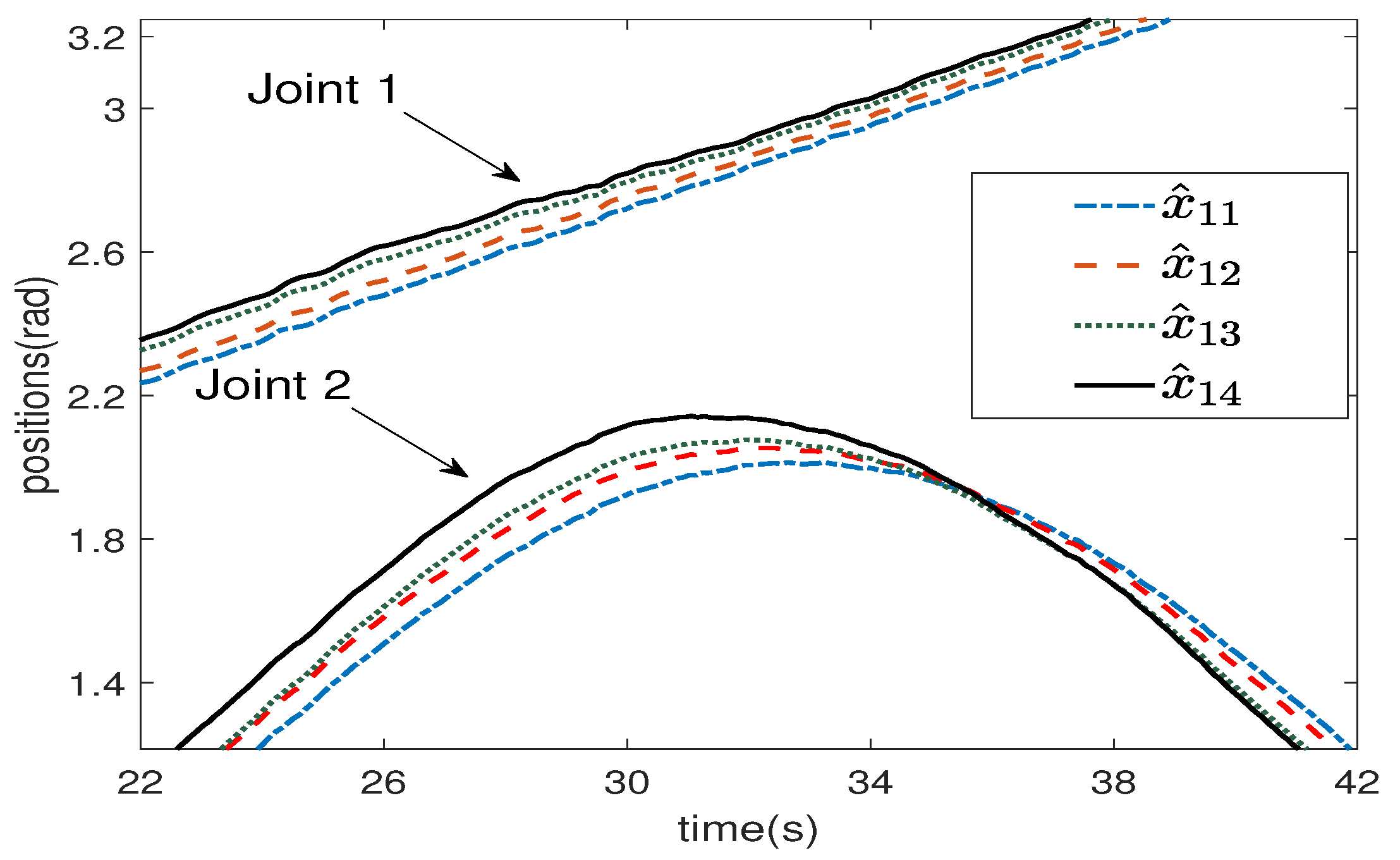
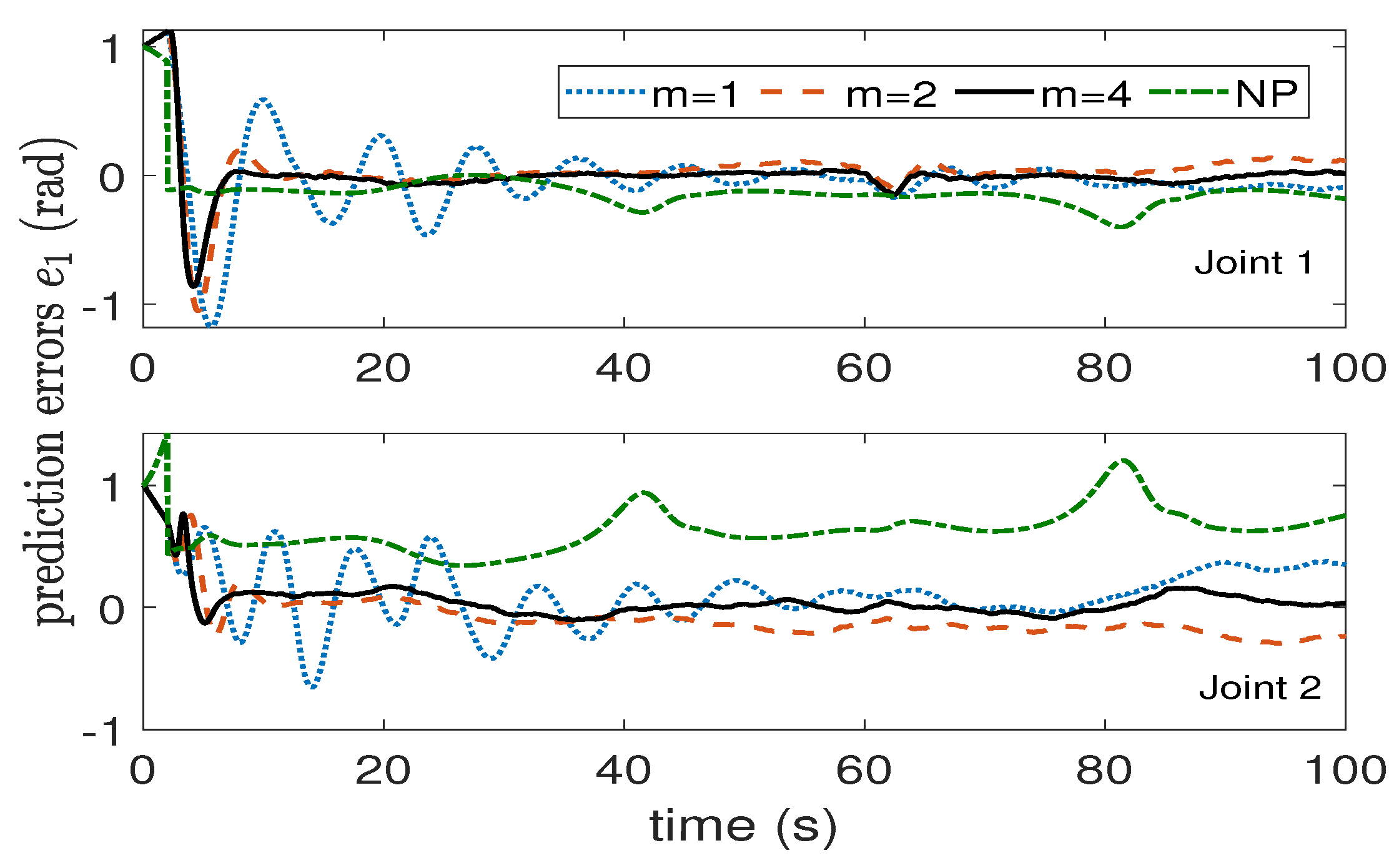
5. Simulation Results
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Makhbouche, A.; Boudjehem, B.; Birs, I.; Muresan, C. Fractional-order PID controller based on immune feedback mechanism for time-delay systems. Fractal Fract. 2023, 7, 53. [Google Scholar] [CrossRef]
- Li, X.; Li, P. Stability of time-delay systems with impulsive control involving stabilizing delays. Automatica 2021, 124, 109336. [Google Scholar] [CrossRef]
- Chen, Y.; Cao, Y.; Wang, R. Acoustic Source Tracking Based on Probabilistic Data Association and Distributed Cubature Kalman Filtering in Acoustic Sensor Networks. Sensors 2022, 22, 7160. [Google Scholar] [CrossRef] [PubMed]
- Zhao, K. Stability of a nonlinear Langevin system of ML-type fractional derivative affected by time-varying delays and differential feedback control. Fractal Fract. 2022, 6, 725. [Google Scholar] [CrossRef]
- Boonsatit, N.; Rajendran, S.; Lim, C.; Jirawattanapanit, A.; Mohandas, P. New adaptive finite-time cluster synchronization of neutral-type complex-valued coupled neural networks with mixed time delays. Fractal Fract. 2022, 6, 515. [Google Scholar] [CrossRef]
- Yang, X.; Liu, Y.; Cao, J.; Rutkowski, L. Synchronization of coupled time-delay neural networks with mode-dependent average dwell time switching. IEEE Trans. Neural Netw. Learn. Syst. 2020, 31, 5483–5496. [Google Scholar] [CrossRef]
- Chen, Y.; Zhang, G.; Wang, R.; Rong, H.; Yang, B. Acoustic vector sensor multi-source detection based on multimodal fusion. Sensors 2023, 23, 1301. [Google Scholar] [CrossRef]
- Yang, B.; Yan, G.; Wang, P.; Chan, C.; Song, X.; Chen, Y. A novel graph-based trajectory predictor with pseudo-oracle. IEEE Trans. Neural Netw. Learn. Syst. 2022, 33, 7064–7078. [Google Scholar] [CrossRef]
- Wang, Y.; Zhang, J.; Wu, H. Distributed adaptive mittag–leffler formation control for second-order fractional multi-agent systems via event-triggered control strategy. Fractal Fract. 2022, 6, 380. [Google Scholar] [CrossRef]
- Yan, B.; Lev-Ari, H.; Stanković, A.M. Networked state estimation with delayed and irregularly spaced time-stamped observations. IEEE Trans. Control Netw. Syst. 2017, 5, 888–900. [Google Scholar] [CrossRef]
- Hou, M.; Zítek, P.; Patton, R.J. An observer design for linear time-delay systems. IEEE Trans. Autom. Control 2002, 47, 121–125. [Google Scholar] [CrossRef]
- Sanz, R.; Garcia, P.; Fridman, E.; Albertos, P. Rejection of mismatched disturbances for systems with input delay via a predictive extended state observer. Int. J. Robust Nonlinear Control 2018, 28, 2457–2467. [Google Scholar] [CrossRef]
- Li, W.; Xie, Z.; Zhao, J.; Wong, P.K.; Wang, H.; Wang, X. Static-output-feedback based robust fuzzy wheelbase preview control for uncertain active suspensions with time delay and finite frequency constraint. IEEE/CAA J. Autom. Sin. 2020, 8, 664–678. [Google Scholar] [CrossRef]
- Wang, C.; Zuo, Z.; Lin, Z.; Ding, Z. A truncated prediction approach to consensus control of lipschitz nonlinear multiagent systems with input delay. IEEE Trans. Control Netw. Syst. 2016, 4, 716–724. [Google Scholar] [CrossRef]
- Astrom, K.J.; Hang, C.C.; Lim, B. A new smith predictor for controlling a process with an integrator and long dead-time. IEEE Trans. Autom. Control 1994, 39, 343–345. [Google Scholar] [CrossRef]
- Artstein, Z. Linear systems with delayed controls: A reduction. IEEE Trans. Autom. Control 1982, 27, 869–879. [Google Scholar] [CrossRef]
- Krstic, M. Input delay compensation for forward complete and strict-feedforward nonlinear systems. IEEE Trans. Autom. Control 2009, 55, 287–303. [Google Scholar] [CrossRef]
- Bekiaris-Liberis, N.; Krstic, M. Predictor-feedback stabilization of multi-input nonlinear systems. IEEE Trans. Autom. Control 2016, 62, 516–531. [Google Scholar] [CrossRef]
- Osuna-Ibarra, L.P.; Caballero-Barragan, H.; Loukianov, A. Predictor-based control for nonlinear mechanical systems with measurement delay. IFAC-PapersOnLine 2020, 53, 5783–5788. [Google Scholar] [CrossRef]
- Liberis, N.B.; Krstic, M. Stability of predictor-based feedback for nonlinear systems with distributed input delay. Automatica 2016, 70, 195–203. [Google Scholar] [CrossRef]
- Xu, X.; Liu, L.; Krstic, M.; Feng, G. Stability analysis and predictor feedback control for systems with unbounded delays. Automatica 2022, 135, 109958. [Google Scholar] [CrossRef]
- Mazenc, F.; Malisoff, M. Local stabilization of nonlinear systems through the reduction model approach. IEEE Trans. Autom. Control 2014, 59, 3033–3039. [Google Scholar] [CrossRef]
- Lei, J.; Khalil, H.K. High-gain-predictor-based output feedback control for time-delay nonlinear systems. Automatica 2016, 71, 324–333. [Google Scholar] [CrossRef]
- Cacace, F.; Germani, A.; Manes, C. An observer for a class of nonlinear systems with time varying observation delay. Syst. Control Lett. 2010, 59, 305–312. [Google Scholar] [CrossRef]
- Assche, V.V.; Ahmed-Ali, T.; Hann, C.; Lamnabhi-Lagarrigue, F. High gain observer design for nonlinear systems with time varying delayed measurements. IFAC Proc. Vol. 2011, 44, 692–696. [Google Scholar] [CrossRef]
- Sun, J.; Yang, J.; Zeng, Z. Predictor-based periodic event-triggered control for nonlinear uncertain systems with input delay. Automatica 2022, 136, 110055. [Google Scholar] [CrossRef]
- Sun, J.; Yang, J.; Li, S.; Zeng, Z. Predictor-based global sampled-data output feedback stabilization for nonlinear uncertain systems subject to delayed output. IEEE Trans. Autom. Control 2022, 68, 1839–1846. [Google Scholar] [CrossRef]
- Bhogaraju, I.; Farasat, M.; Malisoff, M.; Krstic, M. Sequential predictors for delay-compensating feedback stabilization of bilinear systems with uncertainties. Syst. Control Lett. 2021, 152, 104933. [Google Scholar] [CrossRef]
- Ahmed-Ali, T.; Cherrier, E.; Lamnabhi-Lagarrigue, F. Cascade high gain predictors for a class of nonlinear systems. IEEE Trans. Autom. Control 2011, 57, 221–226. [Google Scholar] [CrossRef]
- Germani, A.; Manes, C.; Pepe, P. A new approach to state observation of nonlinear systems with delayed output. IEEE Trans. Autom. Control 2002, 47, 96–101. [Google Scholar] [CrossRef]
- Farza, M.; Hernández-González, O.; Ménard, T.; Targui, B.; M’saad, M.; Astorga-Zaragoza, A.C.-M. Cascade observer design for a class of uncertain nonlinear systems with delayed outputs. Automatica 2018, 89, 125–134. [Google Scholar] [CrossRef]
- Farza, M.; M’Saad, M.; Menard, T.; Fall, M.L.; Gehan, O.; Pigeon, E. Simple cascade observer for a class of nonlinear systems with long output delays. IEEE Trans. Autom. Control 2015, 60, 3338–3343. [Google Scholar] [CrossRef]
- Battilotti, S. Continuous-time and sampled-data stabilizers for nonlinear systems with input and measurement delays. IEEE Trans. Autom. Control 2019, 65, 1568–1583. [Google Scholar] [CrossRef]
- Ramírez-Rasgado, F.; Farza, M.; M’Saad, M.; Hernández-González, O.; Astorga-Zaragoza, A.C. Observer design for a class of disturbed nonlinear systems with multirate sampled outputs involving multiple long time-varying delays. In Proceedings of the 2021 9th International Conference on Systems and Control (ICSC), Caen, France, 24–26 November 2021; pp. 493–498. [Google Scholar]
- Mazenc, F.; Malisoff, M.; Bhogaraju, I.N.S. Sequential predictors for delay compensation for discrete time systems with time-varying delays. Automatica 2020, 122, 109188. [Google Scholar] [CrossRef]
- Obuz, S.; Parikh, A.; Chakraborty, I.; Dixon, W. Lyapunov-based control of an uncertain euler-lagrange system with uncertain time-varying input delays without delay rate constraints. IFAC-PapersOnLine 2016, 49, 141–146. [Google Scholar] [CrossRef]
- Obuz, S.; Klotz, J.R.; Kamalapurkar, R.; Dixon, W. Unknown time-varying input delay compensation for uncertain nonlinear systems. Automatica 2017, 76, 222–229. [Google Scholar] [CrossRef]
- Kamalapurkar, R.; Fischer, N.; Obuz, S.; Dixon, W.E. Time-varying input and state delay compensation for uncertain nonlinear systems. IEEE Trans. Autom. Control 2015, 61, 834–839. [Google Scholar] [CrossRef]
- Yang, B.; Fan, F.; Ni, R.; Li, J.; Kiong, L.; Liu, X. Continual learning-based trajectory prediction with memory augmented networks. Knowl.-Based Syst. 2022, 258, 110022. [Google Scholar] [CrossRef]
- Shen, S.; Song, A.; Li, H.; Li, T. Cascade predictor for a class of mechanical systems under large uncertain measurement delays. Mech. Syst. Signal Process. 2022, 167, 108536. [Google Scholar] [CrossRef]
- Sajadi, M.; Ataei, M.; Ekramian, M. Cascade high-gain observers for a class of nonlinear systems with large delayed measurements. Int. J. Syst. Sci. 2018, 49, 2558–2570. [Google Scholar] [CrossRef]
- Tréangle, C.; Farza, M.; M’Saad, M. Observer design for a class of disturbed nonlinear systems with time-varying delayed outputs using mixed time-continuous and sampled measurements. Automatica 2019, 107, 231–240. [Google Scholar] [CrossRef]
- Sun, T.; Cheng, L.; Wang, W.; Pan, Y. Semiglobal exponential control of euler–lagrange systems using a sliding-mode disturbance observer. Automatica 2020, 112, 108677. [Google Scholar] [CrossRef]
- Sharma, N.; Bhasin, S.; Wang, Q.; Dixon, W.E. Predictor-based control for an uncertain euler–lagrange system with input delay. Automatica 2011, 47, 2332–2342. [Google Scholar] [CrossRef]
- Hua, C.; Liu, X. Delay-dependent stability criteria of teleoperation systems with asymmetric time-varying delays. IEEE Trans. Robot. 2010, 26, 925–932. [Google Scholar] [CrossRef]
- Yuan, J.; Chen, T. Switched fractional order multiagent systems containment control with event-triggered mechanism and input quantization. Fractal Fract. 2022, 6, 77. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Shen, S.; Fu, L.; Song, A.; Li, T. Sequential Predictors for Uncertain Euler–Lagrange Systems with Large Transmission Delays. Fractal Fract. 2023, 7, 244. https://doi.org/10.3390/fractalfract7030244
Shen S, Fu L, Song A, Li T. Sequential Predictors for Uncertain Euler–Lagrange Systems with Large Transmission Delays. Fractal and Fractional. 2023; 7(3):244. https://doi.org/10.3390/fractalfract7030244
Chicago/Turabian StyleShen, Shaobo, Liyue Fu, Aiguo Song, and Tao Li. 2023. "Sequential Predictors for Uncertain Euler–Lagrange Systems with Large Transmission Delays" Fractal and Fractional 7, no. 3: 244. https://doi.org/10.3390/fractalfract7030244
APA StyleShen, S., Fu, L., Song, A., & Li, T. (2023). Sequential Predictors for Uncertain Euler–Lagrange Systems with Large Transmission Delays. Fractal and Fractional, 7(3), 244. https://doi.org/10.3390/fractalfract7030244









