Fractional Gradient Methods via ψ-Hilfer Derivative
Abstract
1. Introduction
2. General Fractional Derivatives and Special Functions
- Riemann–Liouville: , , and ;
- Caputo: , , and ;
- Katugampola: , with , , and ;
- Caputo-Katugampola: , with , , and ;
- Hadamard: , , and ;
- Caputo-Hadamard: , , and .
3. Auxiliary Results
4. Continuous Gradient Method via the -Hilfer Derivative
4.1. The Convex Case
4.2. The Strongly Convex Case
4.3. Convergence at an Exponential Rate
5. -Hilfer Fractional Gradient Method
5.1. The One-Dimensional Case
5.1.1. Design of the Numerical Method
| Algorithm 1:-FGM with higher order truncation. |
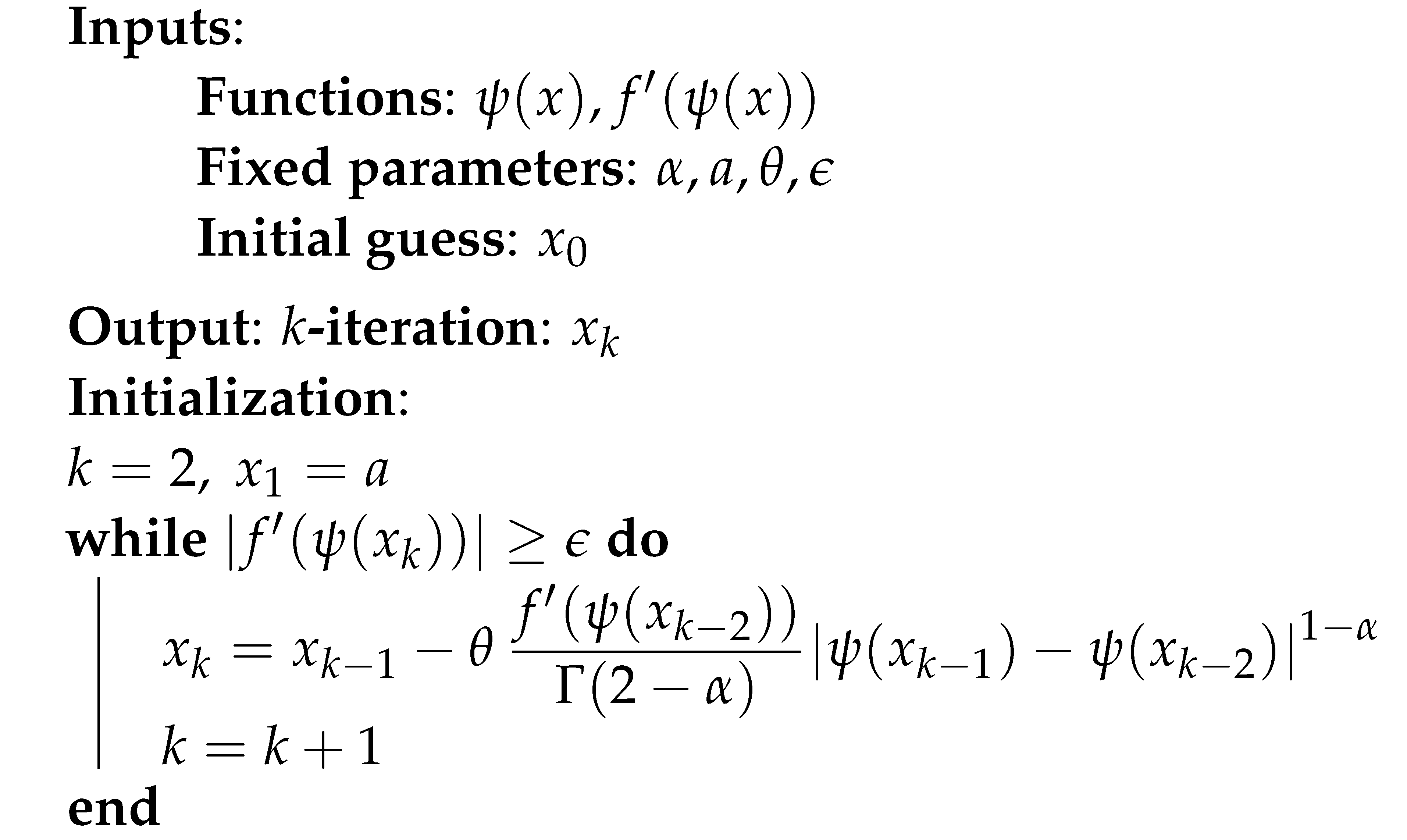 |
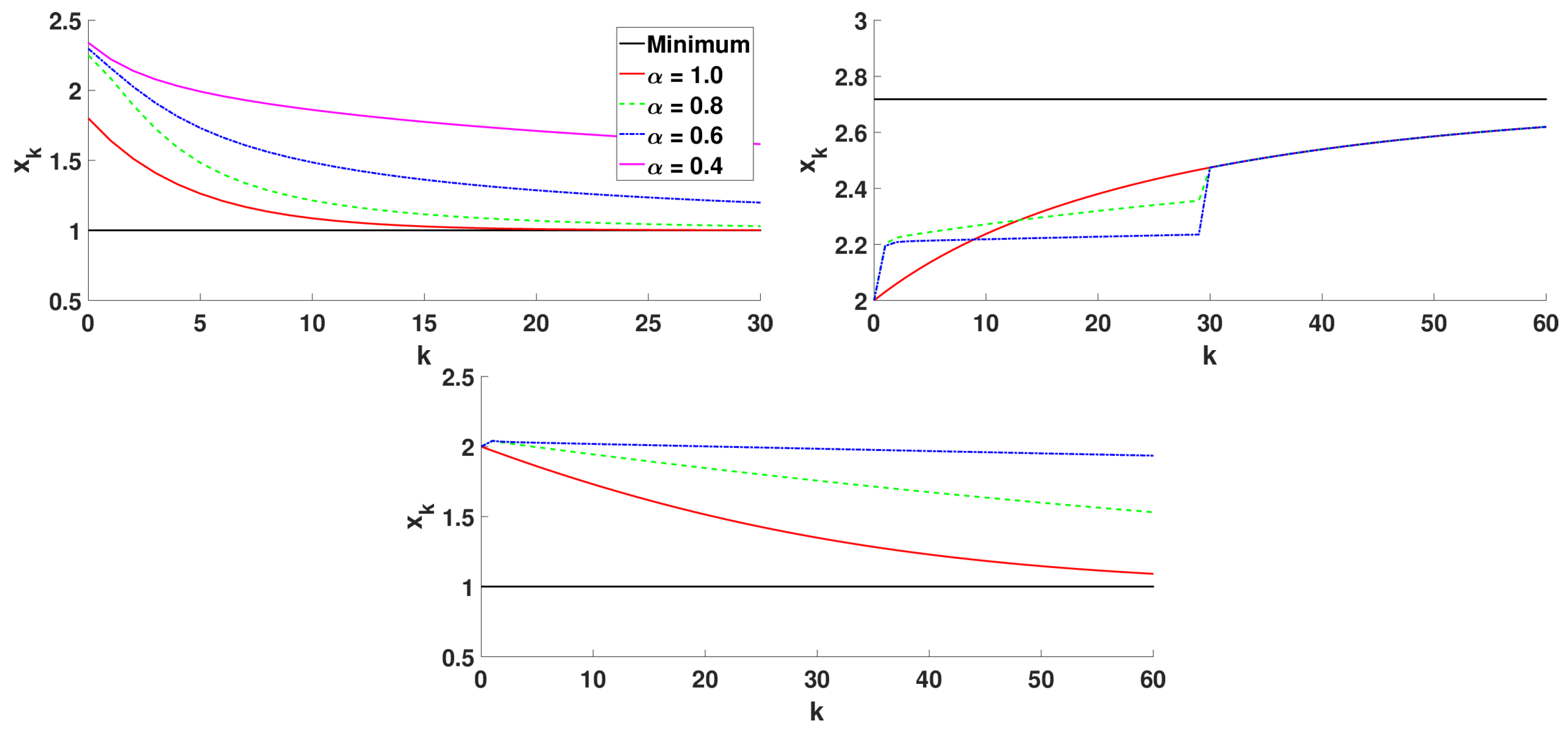
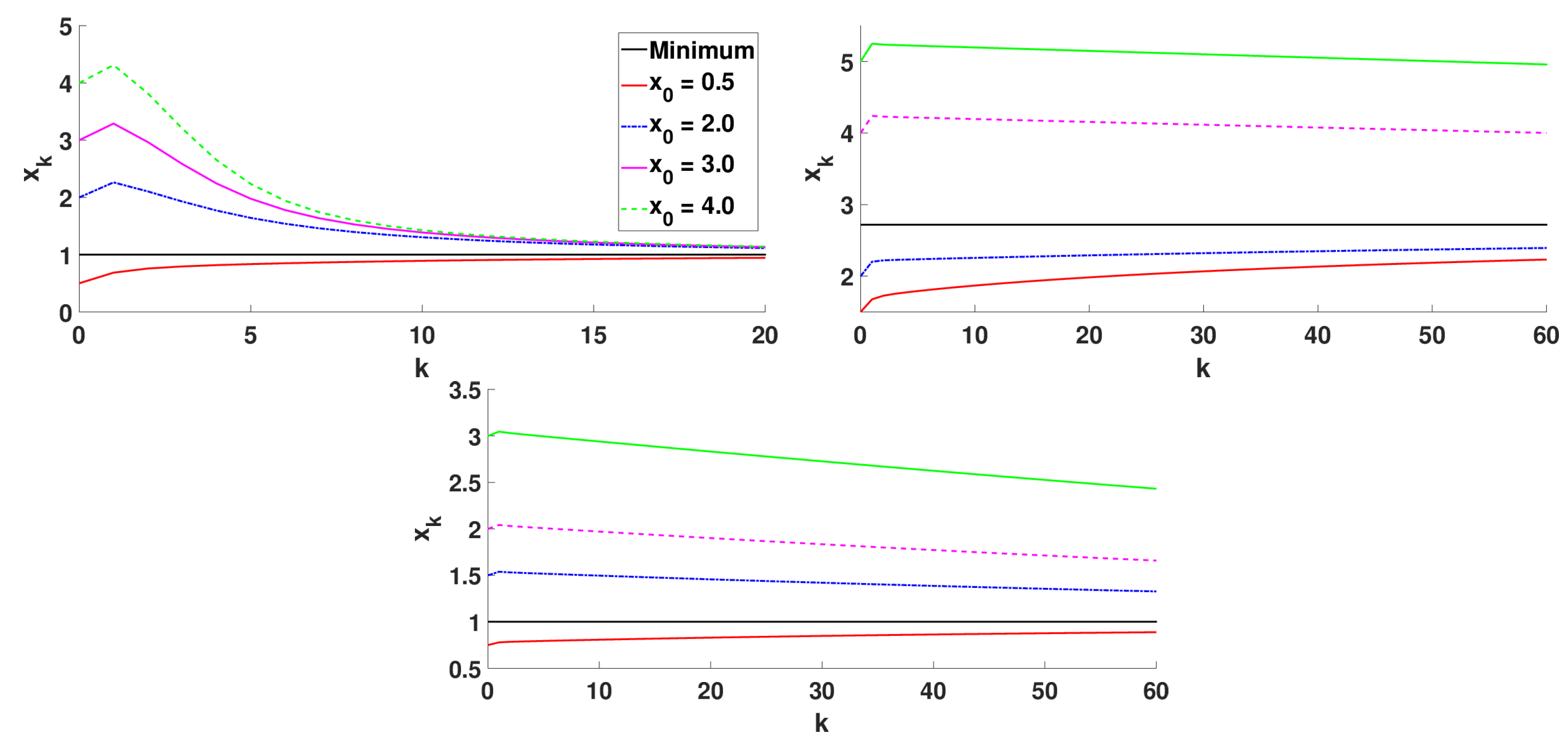
5.1.2. Numerical Simulations
- Caputo and Riemann–Liouville fractional derivatives: , , and ;
- Hadamard fractional derivative: , , and ;
- Katugampola fractional derivative: , , and . In this case, a cannot coincide with the lower limit of the interval I because is not defined at .
5.2. The Two-Dimensional Case
5.2.1. Untrained Approach
| Algorithm 2: 2D -FGM with higher order truncation. |
 |
5.2.2. The Trained Approach
| Algorithm 3: 2D -FGM with variable fractional order and optimized step size. |
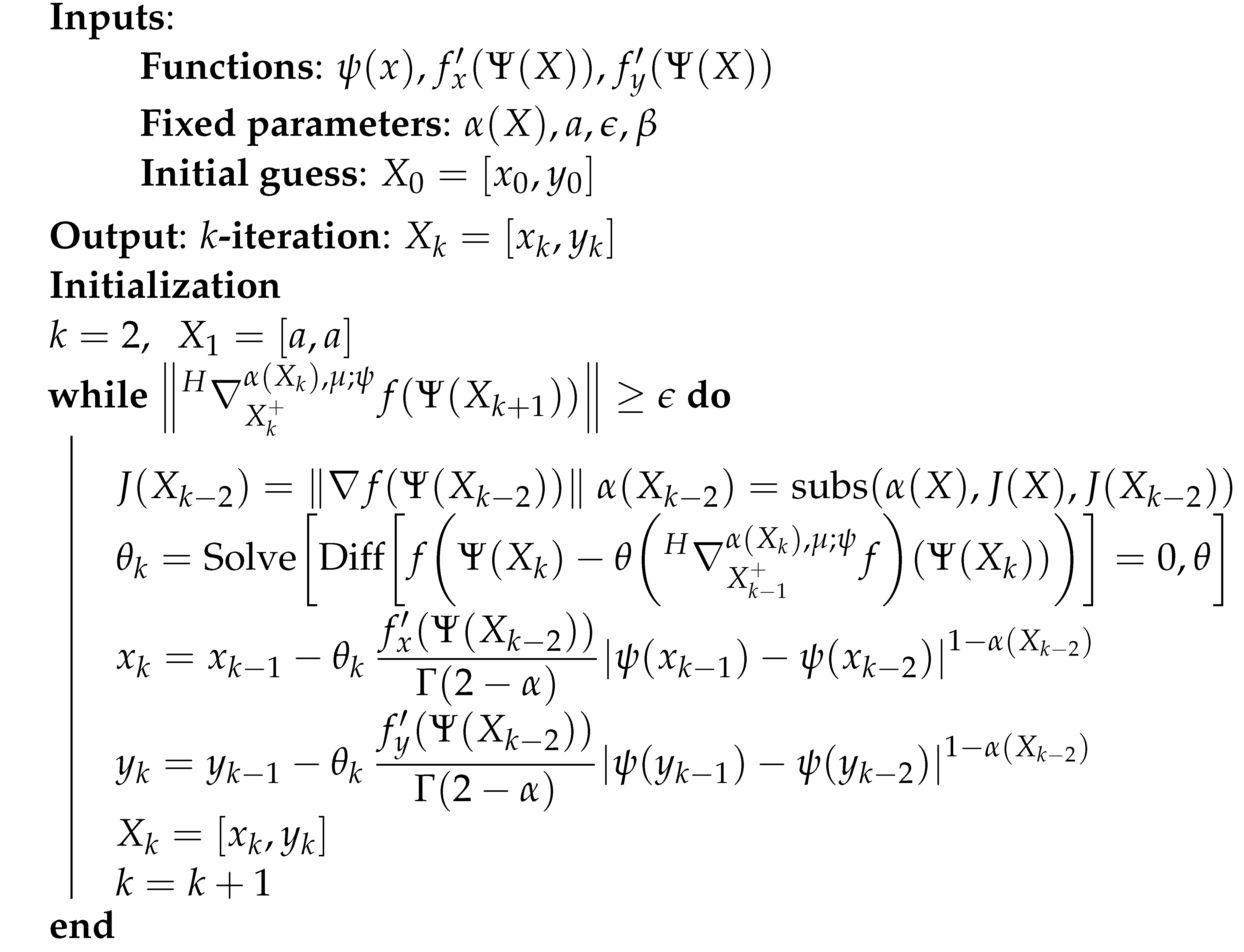 |
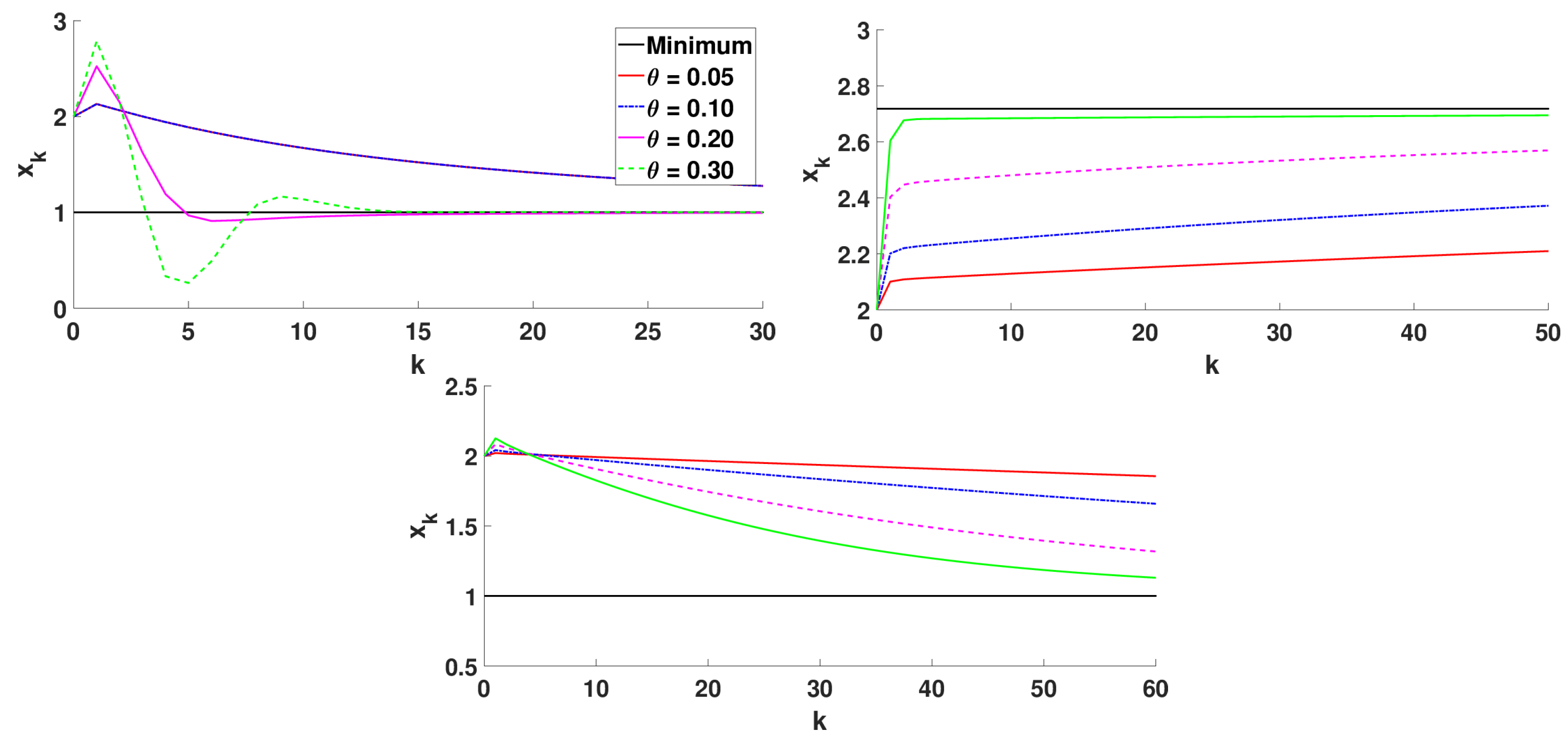
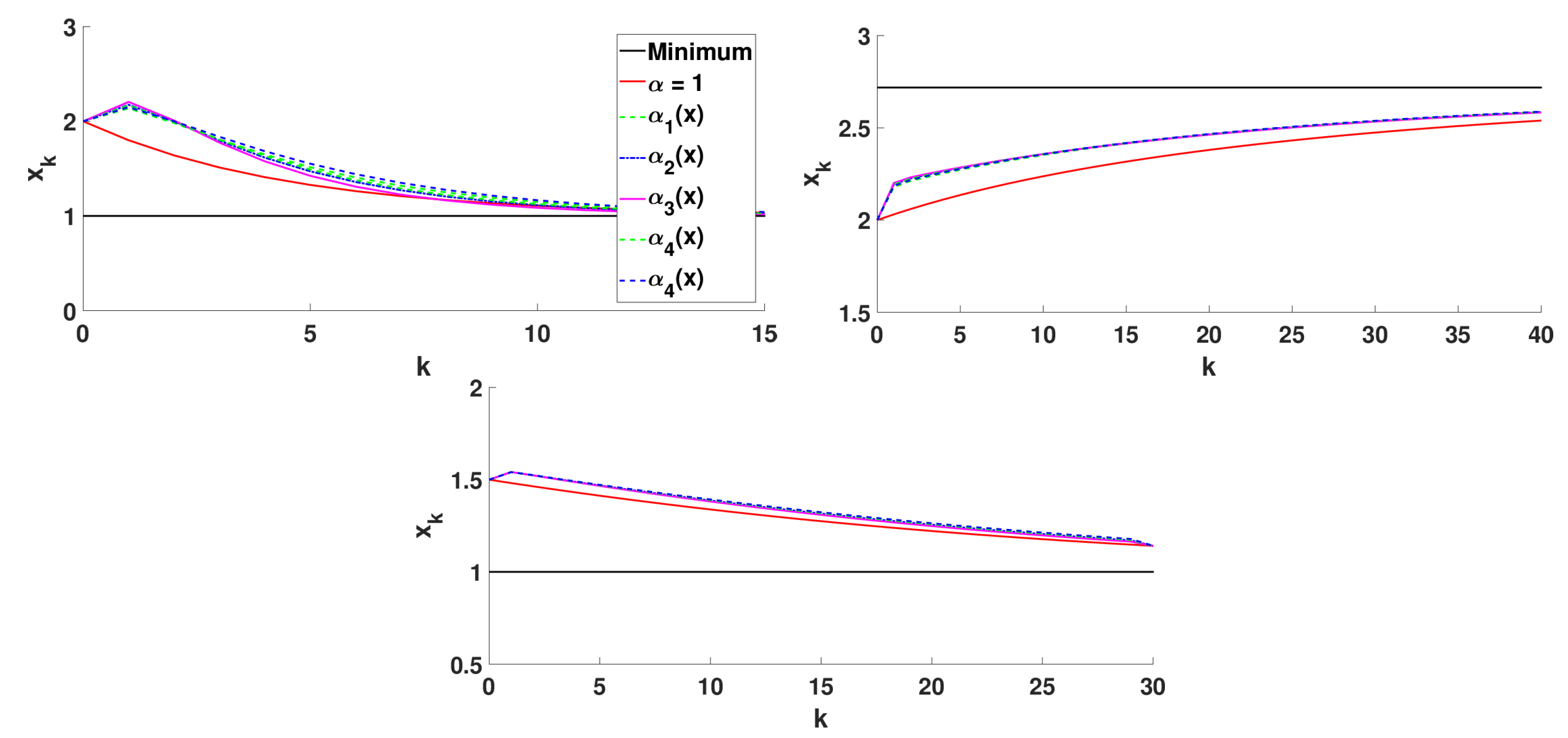
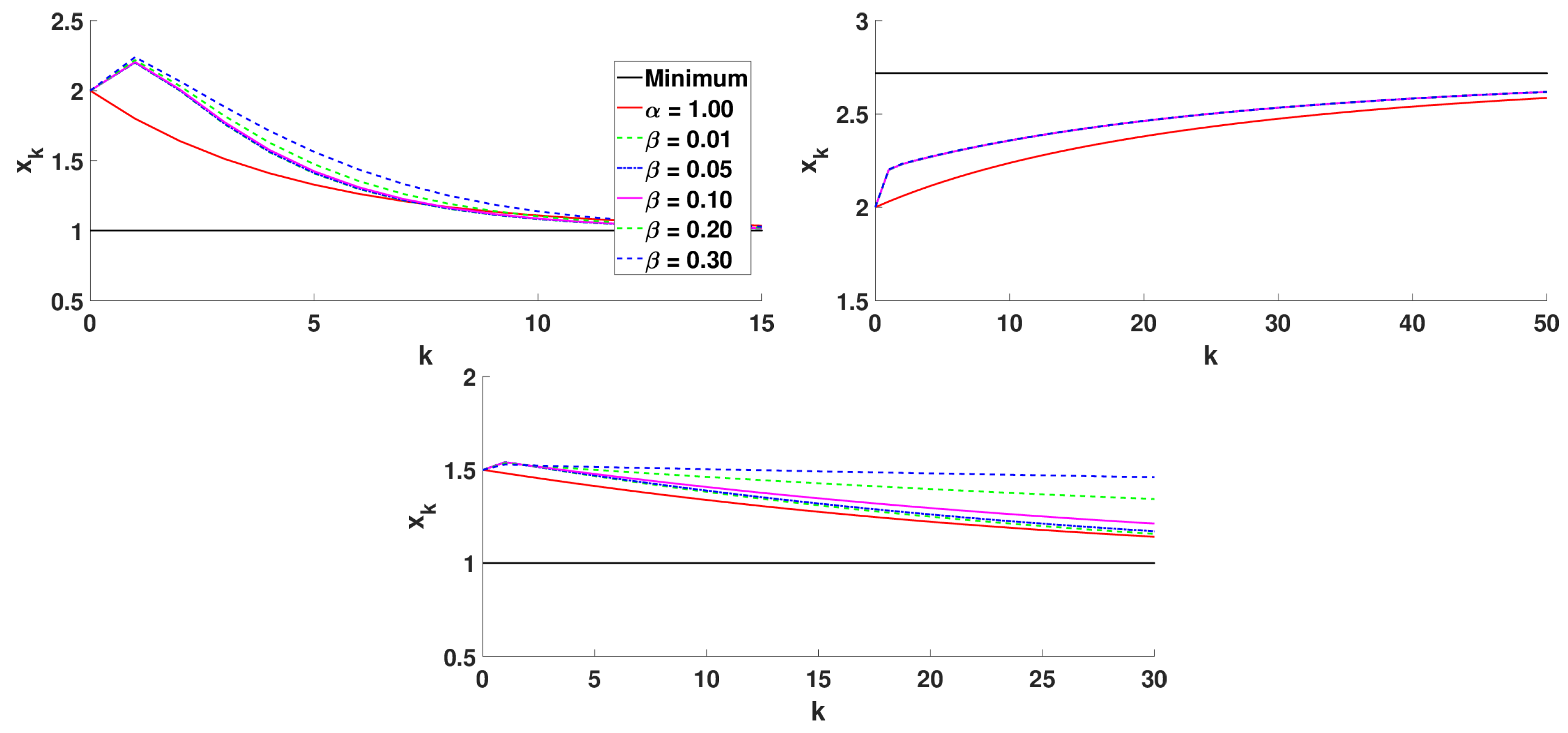
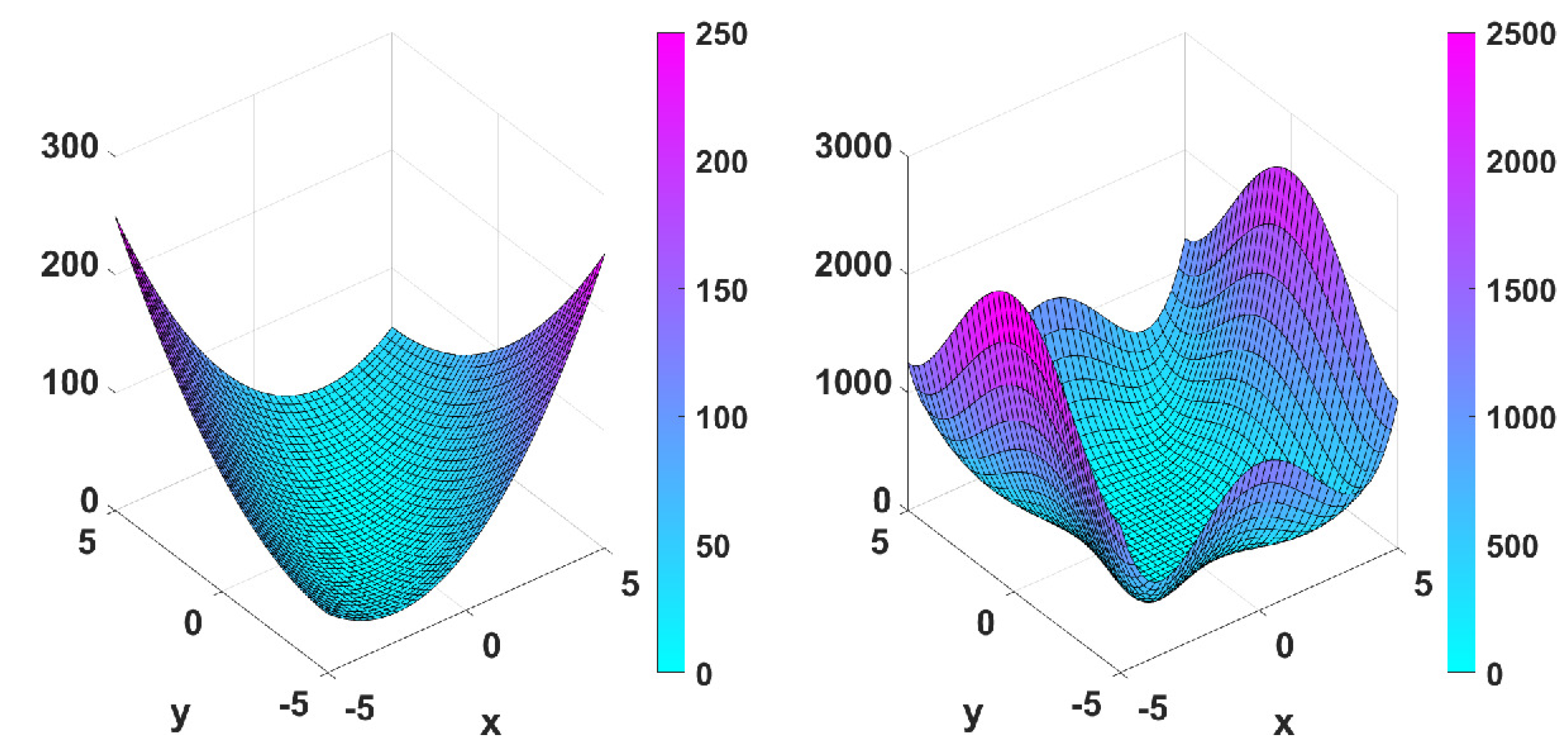
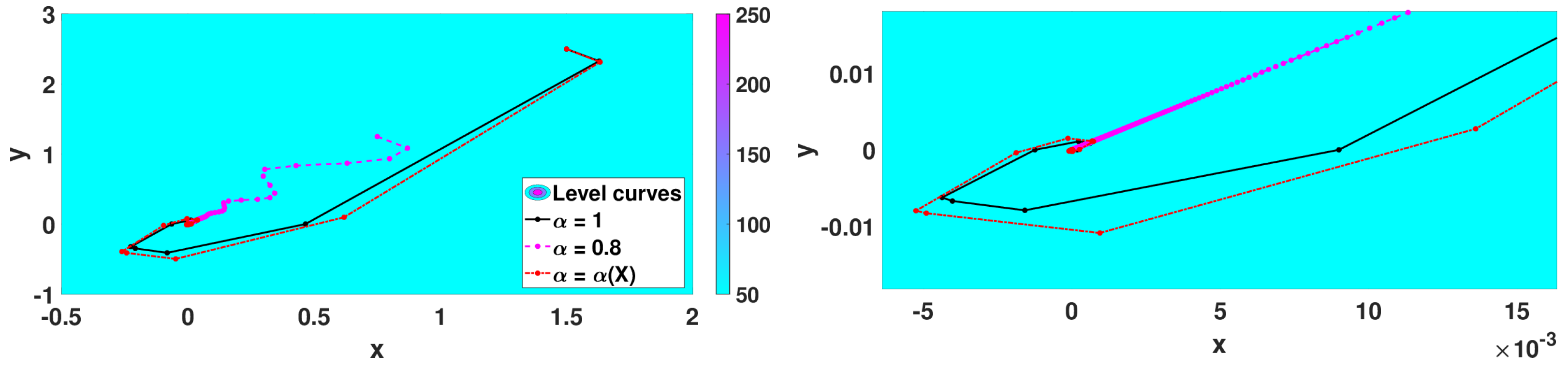
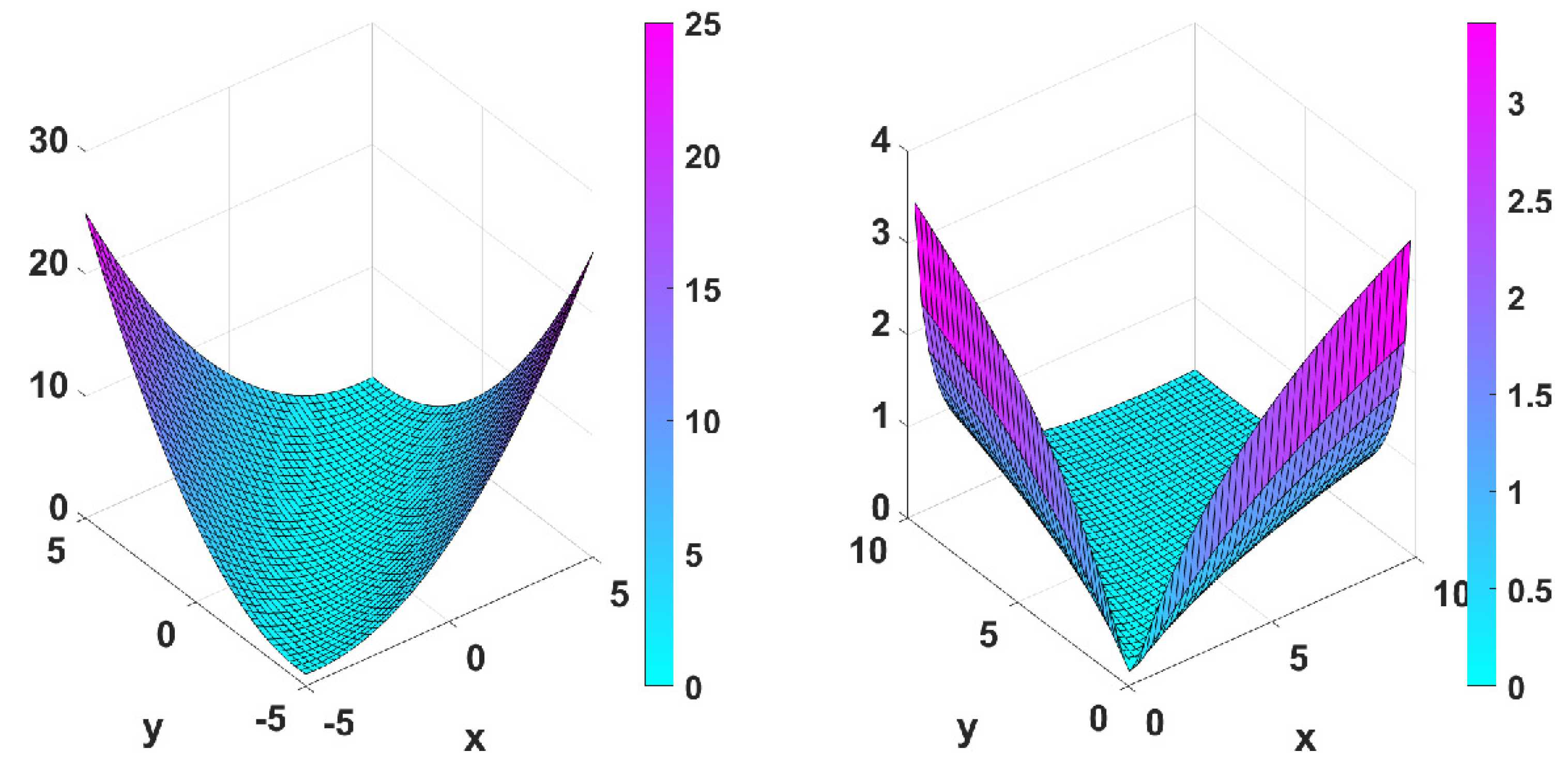
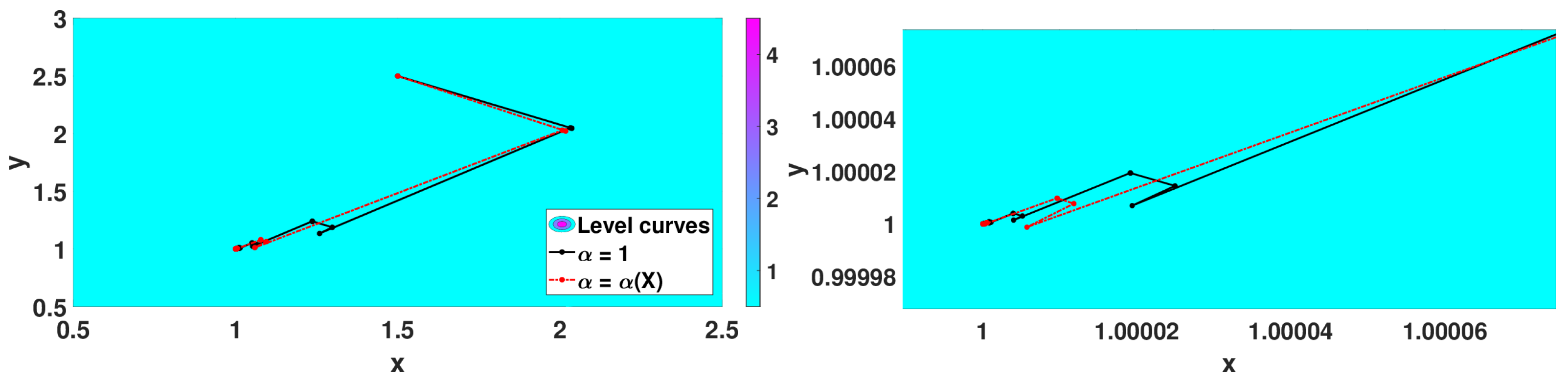
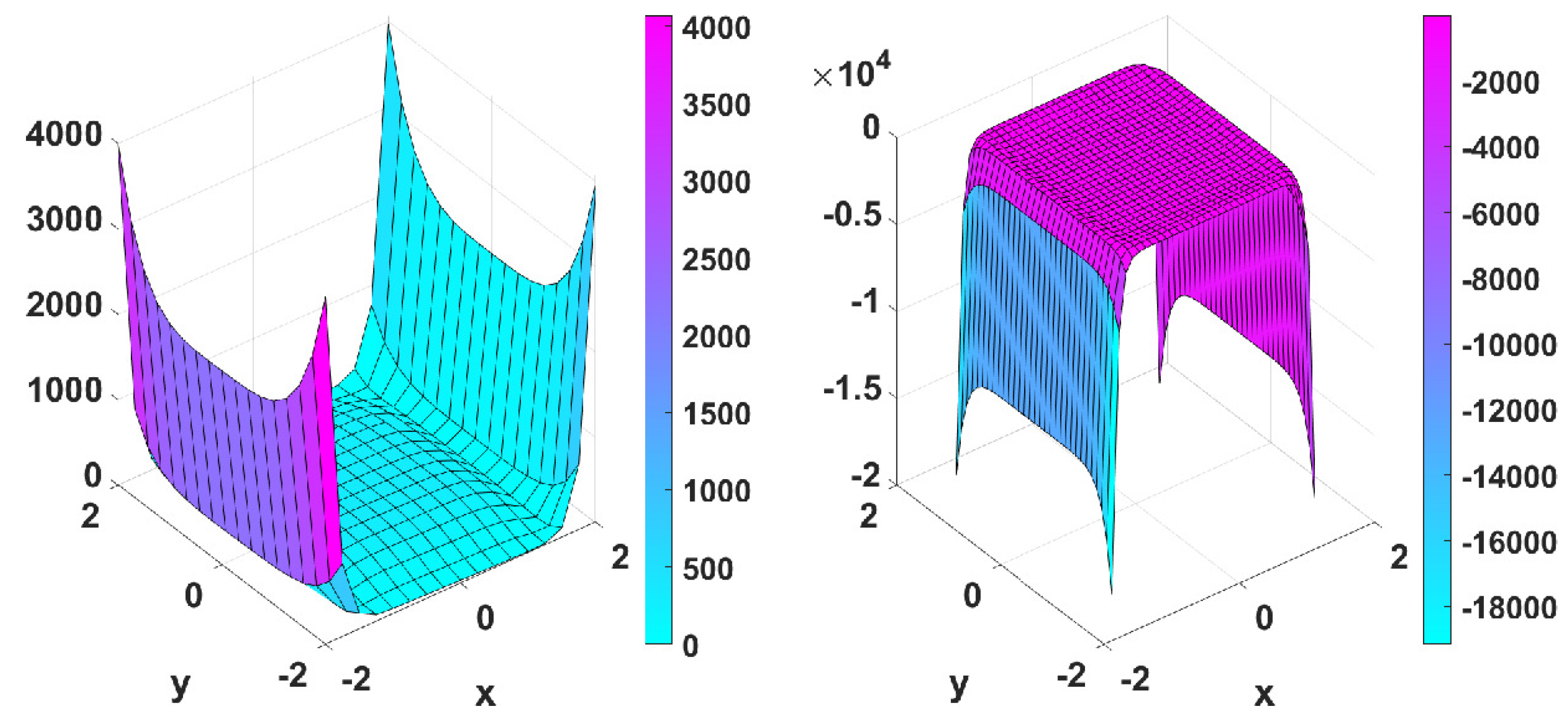
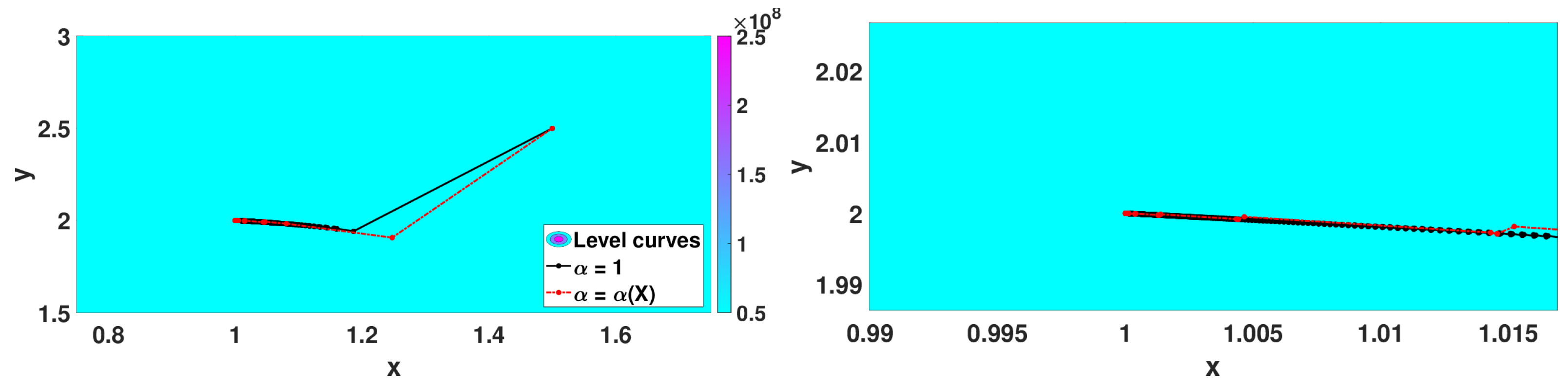
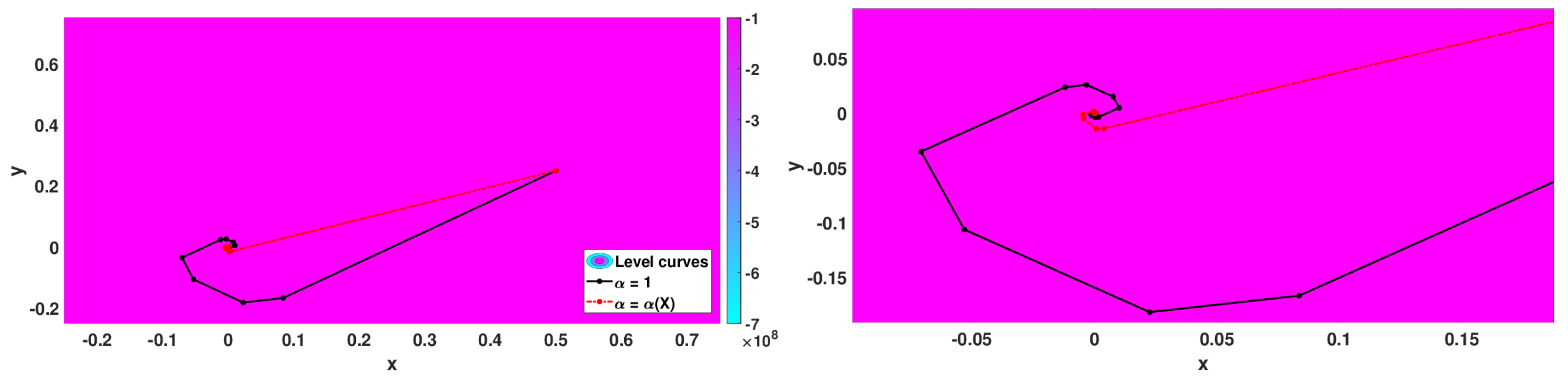
5.2.3. Numerical Simulations
- with minimum point at ,
- Matyas function: with minimum point at ,
- Wayburn and Seader No. 1 function: with minimum point at .
- , with ,
- , with ,
- with .
- Algorithm 3 with that corresponds to the classical 2D gradient descent method,
- Algorithm 2 with and step size ,
- Algorithm 3 with with .
| k | ||||||
|---|---|---|---|---|---|---|
| Classical Gradient | 1.0 | optimized | 43 | |||
| Algorithm 2 | 0.8 | 1.0 | 94777 | |||
| Algorithm 3 | variable | optimized | 27 | |||
| Classical Gradient | 1.0 | optimized | 51 | |||
| Algorithm 2 | 0.8 | 0.1 | divergence | — | — | |
| Algorithm 3 | variable | optimized | 29 | |||
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Lin, J.Y.; Liao, C.W. New IIR filter-based adaptive algorithm in active noise control applications: Commutation error-introduced LMS algorithm and associated convergence assessment by a deterministic approach. Automatica 2008, 44, 2916–2922. [Google Scholar] [CrossRef]
- Pu, Y.F.; Zhou, J.L.; Zhang, Y.; Zhang, N.; Huang, G.; Siarry, P. Fractional extreme value adaptive training method: Fractional steepest descent approach. IEEE Trans. Neural Netw. Learn. Syst. 2015, 26, 653–662. [Google Scholar] [CrossRef] [PubMed]
- Ge, Z.W.; Ding, F.; Xu, L.; Alsaedi, A.; Hayat, T. Gradient-based iterative identification method for multivariate equation-error autoregressive moving average systems using the decomposition technique. J. Frankl. Inst. 2019, 356, 1658–1676. [Google Scholar] [CrossRef]
- LeCun, Y.; Bengio, Y.; Hinton, G. Deep learning. Nature 2015, 521, 436–444. [Google Scholar] [CrossRef] [PubMed]
- Wong, C.C.; Chen, C.C. A hybrid clustering and gradient descent approach for fuzzy modeling. IEEE Trans. Syst. Man Cybern. Part B Cybern. 1999, 29, 686–693. [Google Scholar] [CrossRef] [PubMed]
- Ren, Z.G.; Xu, C.; Zhou, Z.C.; Wu, Z.Z.; Chen, T.H. Boundary stabilization of a class of reaction-advection-difffusion systems via a gradient-based optimization approach. J. Frankl. Inst. 2019, 356, 173–195. [Google Scholar] [CrossRef]
- Tan, Y.; He, Z.; Tian, B. A novel generalization of modified LMS algorithm to fractional order. IEEE Signal Process. Lett. 2015, 22, 1244–1248. [Google Scholar] [CrossRef]
- Cheng, S.S.; Wei, Y.H.; Chen, Y.Q.; Li, Y.; Wang, Y. An innovative fractional order LMS based on variable initial value and gradient order. Signal Process. 2017, 133, 260–269. [Google Scholar] [CrossRef]
- Raja, M.A.Z.; Chaudhary, N.I. Two-stage fractional least mean square identification algorithm for parameter estimation of CARMA systems. Signal Process. 2015, 107, 327–339. [Google Scholar] [CrossRef]
- Shah, S.M.; Samar, R.; Khan, N.M.; Raja, M.A.Z. Design of fractional-order variants of complex LMS and NLMS algorithms for adaptive channel equalization. Nonlinear Dyn. 2017, 88, 839–858. [Google Scholar] [CrossRef]
- Viera-Martin, E.; Gómez-Aguilar, J.F.; Solís-Pérez, J.E.; Hernández-Pérez, J.A.; Escobar-Jiménez, R.F. Artificial neural networks: A practical review of applications involving fractional calculus. Eur. Phys. J. Spec. Top. 2022, 231, 2059–2095. [Google Scholar] [CrossRef] [PubMed]
- Sheng, D.; Wei, Y.; Chen, Y.; Wang, Y. Convolutional neural networks with fractional order gradient method. Neurocomputing 2020, 408, 42–50. [Google Scholar] [CrossRef]
- Wang, Y.L.; Jahanshahi, H.; Bekiros, S.; Bezzina, F.; Chu, Y.M.; Aly, A.A. Deep recurrent neural networks with finite-time terminal sliding mode control for a chaotic fractional-order financial system with market confidence. Chaos Solitons Fractals 2021, 146, 110881. [Google Scholar] [CrossRef]
- Chen, Y.Q.; Gao, Q.; Wei, Y.H.; Wang, Y. Study on fractional order gradient methods. Appl. Math. Comput. 2017, 314, 310–321. [Google Scholar] [CrossRef]
- Wei, Y.; Kang, Y.; Yin, W.; Wang, Y. Generalization of the gradient method with fractional order gradient direction. J. Frankl. Inst. 2020, 357, 2514–2532. [Google Scholar] [CrossRef]
- Samko, S.G.; Kilbas, A.A.; Marichev, O.I. Fractional Integrals and Derivatives: Theory and Applications; Gordon and Breach: New York, NY, USA, 1993. [Google Scholar]
- Kilbas, A.A.; Srivastava, H.M.; Trujillo, J.J. Theory and Applications of Fractional Differential Equations; North-Holland Mathematics Studies; Elsevier: Amsterdam, The Netherlands, 2006; Volume 204. [Google Scholar]
- Almeida, R. A Caputo fractional derivative of a function with respect to another function. Commun. Nonlinear Sci. Numer. Simul. 2017, 44, 460–481. [Google Scholar] [CrossRef]
- Sousa, J.V.C.; Oliveira, E.C. On the ψ-Hilfer derivative. Commun. Nonlinear Sci. Numer. Simulat. 2018, 60, 72–91. [Google Scholar] [CrossRef]
- Gorenflo, R.; Kilbas, A.A.; Mainardi, F.; Rogosin, S.V. Mittag-Leffler Functions, Related Topics and Applications; Springer: Berlin/Heidelberg, Germany, 2020. [Google Scholar]
- Hai, P.V.; Rosenfeld, J.A. The gradient descent method from the perspective of fractional calculus. Math. Meth. Appl. Sci. 2021, 44, 5520–5547. [Google Scholar] [CrossRef]
- Kucche, K.D.; Mali, A.D.; Sousa, J.V.C. On the nonlinear ψ-Hilfer fractional differential equations. Comput. Appl. Math. 2019, 38, 73. [Google Scholar] [CrossRef]


| k | ||||||
|---|---|---|---|---|---|---|
| Classical Gradient | 1.0 | optimized | 49 | |||
| Algorithm 2 | 0.8 | 0.1 | 2480 | |||
| Algorithm 3 | variable | optimized | 50 | |||
| Classical Gradient | 1.0 | optimized | 77 | |||
| Algorithm 2 | 0.8 | 0.1 | divergence | — | — | |
| Algorithm 3 | variable | optimized | 73 | |||
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Vieira, N.; Rodrigues, M.M.; Ferreira, M. Fractional Gradient Methods via ψ-Hilfer Derivative. Fractal Fract. 2023, 7, 275. https://doi.org/10.3390/fractalfract7030275
Vieira N, Rodrigues MM, Ferreira M. Fractional Gradient Methods via ψ-Hilfer Derivative. Fractal and Fractional. 2023; 7(3):275. https://doi.org/10.3390/fractalfract7030275
Chicago/Turabian StyleVieira, Nelson, M. Manuela Rodrigues, and Milton Ferreira. 2023. "Fractional Gradient Methods via ψ-Hilfer Derivative" Fractal and Fractional 7, no. 3: 275. https://doi.org/10.3390/fractalfract7030275
APA StyleVieira, N., Rodrigues, M. M., & Ferreira, M. (2023). Fractional Gradient Methods via ψ-Hilfer Derivative. Fractal and Fractional, 7(3), 275. https://doi.org/10.3390/fractalfract7030275







