A Computational Technique for Solving Three-Dimensional Mixed Volterra–Fredholm Integral Equations

Abstract

In this article, a novel and efficient approach based on Lucas polynomials is introduced for solving three-dimensional mixed Volterra–Fredholm integral equations for the two types (3D-MVFIEK2). This method transforms the 3D-MVFIEK2 into a system of linear algebraic equations. The error evaluation for the suggested scheme is discussed. This technique is implemented in four examples to illustrate the efficiency and fulfillment of the approach. Examples of numerical solutions to both linear and nonlinear integral equations were used. The Lucas polynomial method and other approaches were contrasted. A collection of tables and figures is used to present the numerical results. We observe that the exact solution differs from the numerical solution if the exact solution is an exponential or trigonometric function, while the numerical solution is the same when the exact solution is a polynomial. The Maple 18 program produced all of the results.

1. Introduction

The multi-dimensional integral equations (MDIE) provide considerable flexibility in order to implement a wide range of problems and relationships as well as resolve boundary issues for differential equations (DE). In three-dimensional electromagnetic modeling, Hursan and Zhdanov [1] pioneered the Contraction integral equation method. Pachpatte presented numerous MDIE applications in [2]. Cheng investigated quantum mechanics with thermal radiation effect in [3]. Chew et al used integral equation methods for electromagnetic and Elastic Waves in [4]. Integral equations with two or more variables are challenging to resolve analytically. Thus, in such instances, it is essential to utilize numerical procedures to approach the solution.

The numerical solution of MDIE has been the subject of research. To illustrate, Guoqiang et al in [5], calculated the numeric solution of two-dimensional nonlinear Volterra integral equations (VIE) via employment and repeated employment techniques. Bazm, in [6], used Bernoulli polynomials to obtain the solution of a class of nonlinear two-dimensional integral equations. The numeric solution of two-dimensional nonlinear Fredholm integral equations (FIE), in the most general type of kernels, is based on Bernstien polynomials introduced by Maleknejad et al. in [7]. In [8], a three-dimensional differential converts technique is implemented for overcoming nonlinear three-dimensional VIE. Basseem, in [9], implemented the degenerate kernel technique for solving three-dimensional nonlinear integral equations of the two types. Kazemi et al., in [10], applied the Haar wavelet procedure for solving the three-dimensional nonlinear FIE. Using the 3D-block-pulse functions developed by Manafian and Bolghar in [11], the numerical solution of nonlinear three-dimensional Volterra integro-differential equations is presented.

Many works have been concentrated on the expansion of a better, higher, and more powerful technique for solving Volterra–Fredholm integral equations (VFIE), such as Maleknejad et al. in [12], applying the Bernstein’s approximation for solving the three-dimensional VFIE of the initial and two types. Mirzaee and Hadadiyan, in [13], applied a computing technique for overcoming the nonlinear composite VFIE. Mirzaee et al., in [14], presented triangular functions for solving the nonlinear mixed VFIE. Moreover, Mirzaee et al., in [15], implemented the amendment block-pulse functions to clarify the three-dimensional VFIE.

In this work, the approximate solution of 3D-MVFIEK2 have been obtained using three-dimensional Lucas polynomials. These polynomials are non-orthogonal. This polynomial was used by several scientists to solve fractional differential equations [16,17]. Cetin et al., in [18], utilized the Lucas polynomial procedure to research a system of higher-order DE. Baykus and Sezer, in [19], implemented a hybrid Taylor–Lucas employment procedure for the delay DE. Nadir, in [20], procured a solution of the differential-integro equation utilization of the Lucas series. Haq and Ali, in [21], analyze the approach to solving two-dimensional Sobolev equality utilization mixed Lucas and Fibonacci polynomials. Nisar et al., in [22], applied Lucas polynomials for solving 1D and 2D advection–diffusion–reaction equations. The properties of Lucas polynomials are presented in [23]. In [24], Chelyshkov polynomials approach the first class of two-dimensional nonlinear VIE. In [25], Lucas polynomials are used to approximate the solution of Cauchy integral equations. Modified Lucas polynomials were used by Youssri et al. [26] to numerically solve boundary value issues. The primary benefit of the current approach is that the issue at hand is converted into a set of algebraic equations that can be quickly resolved using computer programming.

The paper is set up as shows: Section 2 presents various Lucas polynomial properties. Lucas polynomials are used to solve 3D-MVFIEK2 in Section 3. Error analysis is discussed in Section 4. Numerical outcomes and comparisons with other techniques are presented in Section 5. The conclusion of the paper is presented in Section 6.

In this article, we shall contemplate the numerical solution of a size of 3D-MVFIEK2 in the next section, to create:

$$w(x,y,z)=g(x,y,z)+\lambda {\int }_0^1{\int }_0^1{\int }_0^{1}K(x,y,z,s,t,r)w(s,t,r)dsdtdr+$$

$$+\lambda {\int }_0^1{\int }_0^1{\int }_0^1{k}_2(x,y,z,s,t,r)w(s,t,r)dsdtdr,$$

(1a)

where

$$K(x,y,z,s,t,r)=\left\{\begin{array}{c}{k}_1(x,y,z,s,t,r)(s,t,r)\le (x,y,z),\\ \\ 0,(s,t,r)>(x,y,z),\end{array}\right.$$

(1b)

$x,y,z\in [0,1),\lambda \in R,$ and w is the unknown function, $g,k_1$ and $k_2$ have analytic functions on D and $D\times D$ severally, where $D=[0,1)\times [0,1)\times [0,1).$

Equation (1a) could be expressed as follows:

$$w(x,y,z)=g(x,y,z)+\lambda {\int }_0^1{\int }_0^1{\int }_0^{1}H(x,y,z,s,t,r)w(s,t,r)dsdtdr,$$

(1c)

where

$$H(x,y,z,s,t,r)=K(x,y,z,s,t,r)+k_2(x,y,z,s,t,r).$$

2. Properties of Lucas Polynomials

Definition 1.

([23]) The Lucas polynomials have specified via the recurrence relationship

$$L_{m+2}\left(\zeta \right)=\zeta L_{m+1}\left(\zeta \right)+L_m\left(\zeta \right),m\ge 0,$$

(2a)

with $L_0\left(\zeta \right)=2$ and $L_1\left(\zeta \right)=\zeta .$

These polynomials possess the following expression, to establish:

$$L_m\left(\zeta \right)=\frac{{(\zeta +\sqrt{{\zeta }^2+4})}^m+{(\zeta -\sqrt{{\zeta }^2+4})}^m}{2^m},$$

(2b)

furthermore, they possess the subsequent explicit power form ofrepresentation

$$L_m\left(\zeta \right)=\sum _{k=0}^{\lceil \frac{m}{2}\rceil }\frac{n}{n-k}\left(\genfrac{}{}{0pt}{}{m-k}{k}\right){\zeta }^{m-2k},m\ge 1,$$

(2c)

where

$$\lceil \frac{m}{2}\rceil =\left\{\begin{array}{c}\frac{m}{2},meven,\\ \\ \frac{m-1}{2},modd.\end{array}\right.$$

The initially smaller Lucas polynomials have expressed lower, and the collection of these factors is in Table 1.

Table 1. The initially smaller Lucas polynomials are the array of these factors.

Polynomials’ Lucas	Coefficients’ Array
$L_1\left(\zeta \right)=\zeta$	1
$L_2\left(\zeta \right)={\zeta }^2+2$	1	2
$L_3\left(\zeta \right)={\zeta }^3+3\zeta$	1	3
$L_4\left(\zeta \right)={\zeta }^4+4{\zeta }^2+2$	1	4	2
$L_5\left(\zeta \right)={\zeta }^5+5{\zeta }^3+5\zeta$	1	5	5
$L_6\left(\zeta \right)={\zeta }^6+6{\zeta }^4+9{\zeta }^2+2$	1	6	9	2
$L_7\left(\zeta \right)={\zeta }^7+7{\zeta }^5+14{\zeta }^3+7\zeta$	1	7	14	7
$L_8\left(\zeta \right)={\zeta }^8+8{\zeta }^6+20{\zeta }^4+16{\zeta }^2+2$	1	8	20	16	2
$L_9\left(\zeta \right)={\zeta }^9+9{\zeta }^7+27{\zeta }^5+30{\zeta }^3+9\zeta$	1	9	27	30	9
$L_{10}\left(\zeta \right)={\zeta }^{10}+10{\zeta }^8+35{\zeta }^6+50{\zeta }^4+25{\zeta }^2+2$	1	10	35	50	25	2

Definition 2.

(Rodrigues’s formula).The Lucas polynomials $L_m\left(\zeta \right)$ shall be obtained over the Rodrigue polynomials, andthe formula is specified via

$$L_m\left(\zeta \right)=2\frac{m!}{\left(2m\right)!}{({\zeta }^2+4)}^{1/2}\frac{d^m}{d{\zeta }^m}\left\{{({\zeta }^2+4)}^{m-\frac{1}{2}}\right\}.$$

(2d)

Proposition 1.

The producing function for Lucas polynomials is determined as [23]

$$G(\zeta ,t)=\sum _{m=0}^{\infty }{L}_m\left(\zeta \right)t^m=\frac{1+t^2}{1-t^2-\zeta t}=1+\zeta t+({\zeta }^2+2)t^2+({\zeta }^3+3\zeta )t^3+\dots .$$

Approximation function

Let $w\left(x\right)$ be square integrable function on $(0,1)$, and we assume it shall be displayed in terms of the Lucas polynomials, as shows:

$$w\left(x\right)\simeq w_N\left(x\right)=\sum _{i=0}^M{c}_i{L}_i\left(x\right),$$

(2e)

where $L_i\left(x\right)$ is the Lucas polynomials and $c_i,i=0,1,\dots ,M$ are the unknown coefficients. The Lucas series (2e) can be expressed as a matrix, as shows:

$$w\left(x\right)\cong w_M\left(x\right)=\mathbf{L}\left(x\right)\mathbf{C},$$

(2f)

where $\mathbf{L}\left(\mathbf{x}\right)=[L_0\left(x\right)L_1\left(x\right)\dots L_M\left(x\right)]$ is the $(M+1)\times (M+1)$ matrix of Lucas polynomials, $\mathbf{C}={[c_0{c}_1\dots c_M]}^T$ is the $(M+1)\times 1$ unknown coefficients in a vector.

Then, by utilization of the Lucas polynomials $L_n\left(x\right)$, specified via (2c), we write the matrix form $\mathbf{L}\left(x\right)$, as follows:

$$\mathbf{L}\left(x\right)=\chi \left(x\right)Q^T,$$

(2g)

where $\chi \left(x\right)=[1x{x}^2\dots x^M],$

If M is odd

$$Q=\left(\begin{array}{ccccc}2& 0& 0& \dots & 0\\ \\ \\ 0& \frac{1}{1}\left(\genfrac{}{}{0pt}{}{1}{0}\right)& 0& \dots & 0\\ \\ \\ \frac{2}{1}\left(\genfrac{}{}{0pt}{}{1}{1}\right)& 0& \frac{2}{2}\left(\genfrac{}{}{0pt}{}{2}{0}\right)& \dots & 0\\ \\ \\ 0& \frac{3}{2}\left(\genfrac{}{}{0pt}{}{2}{1}\right)& 0& \dots & 0\\ \\ \\ ⋮& ⋮& ⋮& \ddots & ⋮\\ \\ \frac{(m-1)}{(m-1)/2}\left(\genfrac{}{}{0pt}{}{(m-1)/2}{(m-1)/2}\right)& 0& \frac{(m-1)}{(m+1)/2}\left(\genfrac{}{}{0pt}{}{(m+1)/2}{(m-3)/2}\right)& \dots & 0\\ \\ \\ 0& \frac{\left(m\right)}{(m+1)/2}\left(\genfrac{}{}{0pt}{}{(m+1)/2}{(m-1)/2}\right)& 0& \dots & \frac{m}{m}\left(\genfrac{}{}{0pt}{}{m}{0}\right)\end{array}\right),$$

if M even

$$Q=\left(\begin{array}{ccccc}2& 0& 0& \dots & 0\\ \\ \\ 0& \frac{1}{1}\left(\genfrac{}{}{0pt}{}{1}{0}\right)& 0& \dots & 0\\ \\ \\ \frac{2}{1}\left(\genfrac{}{}{0pt}{}{1}{1}\right)& 0& \frac{2}{2}\left(\genfrac{}{}{0pt}{}{2}{0}\right)& \dots & 0\\ \\ \\ 0& \frac{3}{2}\left(\genfrac{}{}{0pt}{}{2}{1}\right)& 0& \dots & 0\\ \\ \\ ⋮& ⋮& ⋮& \ddots & ⋮\\ \\ 0& \frac{(m-1)}{m/2}\left(\genfrac{}{}{0pt}{}{m/2}{(m-2)/2}\right)& 0& \dots & 0\\ \\ \\ \frac{m}{m/2}\left(\genfrac{}{}{0pt}{}{m/2}{m/2}\right)& 0& \frac{m}{(m+2)/2}\left(\genfrac{}{}{0pt}{}{(m+2)/2}{(m-2)/2}\right)& \dots & \frac{m}{m}\left(\genfrac{}{}{0pt}{}{m}{0}\right)\end{array}\right).$$

By the matrix (2f) and (2g), it follows that

$$w_M\left(x\right)=\chi \left(x\right)Q^T\mathbf{C}.$$

(2h)

The function of two-dimensional continuous $w(x,y)$ shall be expressed using Lucas polynomials in the following manner:

$$w(x,y)\simeq w_M(x,y)=\sum _{k=0}^M\sum _{m=0}^M{c}_{km}{L}_k\left(x\right)L_m\left(y\right)=\sum _{k=0}^M\sum _{m=0}^M{c}_{km}{L}_{km}(x,y)=\mathbf{C}\mathbf{L}(x,y),$$

(2i)

where $\mathbf{C}={[c_{00}{c}_{01}{c}_{0M}{c}_{M0}\dots c_{MM}]}^T$ is the order vector with an unknown coefficient for Lucas ${(M+1)}^2\times 1$ and $\mathbf{L}(x,y)=[L_{00}(x,y)L_{0M}(x,y)L_{M0}(x,y)\dots L_{MM}(x,y)]$ is the square matrix of order ${(M+1)}^2.$

Assume that the following Lucas polynomials are to be used to define a three-dimensional continuous function $w(x,y,z)$:

$$w(x,y,z)\simeq w_M(x,y,z)=\sum _{k=0}^M\sum _{m=0}^M\sum _{n=0}^M{c}_{kmn}{L}_k\left(x\right)L_m\left(y\right)L_m\left(z\right)$$

$$=\sum _{k=0}^M\sum _{m=0}^M\sum _{m=0}^M{c}_{kmn}{L}_{kmn}(x,y,z)=\overline{\mathbf{C}}\mathbf{L}(x,y,z),$$

(2j)

where $\overline{\mathbf{C}}={[c_{000}{c}_{00M}{c}_{0MM}\dots c_{MMM}]}^T$ is the order vector with an unknown coefficient for Lucas ${(M+1)}^3\times 1$ and $\mathbf{L}(x,y,z)=[L_{000}(x,y,z)L_{00M}(x,y,z)L_{0MM}(x,y,z)\dots$$L_{MMM}(x,y,z)]$ is the square matrix of the order ${(M+1)}^3.$

Let $g(x,y,z)\in L^2\left(D\right)$ be any function; we must calculate it using a truncated Lucas series:

$$g(x,y,z)\simeq \sum _{k=0}^M\sum _{m=0}^M\sum _{m=0}^M{g}_{kmn}{L}_k\left(x\right)L_m\left(y\right)L_m\left(z\right)=\sum _{k=0}^M\sum _{m=0}^M\sum _{m=0}^M{g}_{kmn}{L}_{kmn}(x,y,z)={\mathbf{L}}^T(x,y,z)\mathbf{G},$$

(2k)

where $\mathbf{G}$ is an ${(M+1)}^3\times 1$ vector given by $\mathbf{G}={[g_{000}{g}_{00M}{g}_{0MM}\dots g_{MMM}]}^T.$

Assume $k(x,y,z,s,t,r)\in L^2(D\times D).$ It shall correspondingly expanded with respect to Lucas polynomials from:

$$k(x,y,z,s,t,r)\simeq {\mathbf{L}}^T(x,y,z)\mathbf{K}\mathbf{L}(s,t,r),$$

(2l)

where $\mathbf{K}$ is the ${(M+1)}^3\times {(M+1)}^3$ Lucas coefficients.

3. Technique of Solution

In this part, we use the Lucas polynomials technique to solve Equation (1c), which corresponds to Equation (1a).

Approximating the functions $w,g,$ and H with respect to three-dimensional Lucas polynomials, as specified in part 2, we find

$$w(x,y,z)\simeq {\mathbf{L}}^T(x,y,z)\overline{\mathbf{C}},$$

$$g(x,y,z)\simeq {\mathbf{L}}^T(x,y,z)\mathbf{G},$$

$$H(x,y,z,s,t,r)\simeq {\mathbf{L}}^T(x,y,z)\mathbf{H}\mathbf{L}(s,t,r).$$

(3a)

Substituting from (3a) into (1c), we procure

$${\mathbf{L}}^T(x,y,z)\overline{\mathbf{C}}\simeq {\mathbf{L}}^T(x,y,z)\mathbf{G}+\lambda {\int }_0^1{\int }_0^1{\int }_0^1{\mathbf{L}}^T(x,y,z)\mathbf{H}\mathbf{L}(s,t,r){\mathbf{L}}^T(s,t,r)\overline{\mathbf{C}}dsdtdr.$$

Thus,

$${\mathbf{L}}^T(x,y,z)\overline{\mathbf{C}}={\mathbf{L}}^T(x,y,z)\mathbf{G}+\lambda {\mathbf{L}}^T(x,y,z)\mathbf{H}{\int }_0^1{\int }_0^1{\int }_0^1\mathbf{L}(s,t,r){\mathbf{L}}^T(s,t,r)\overline{\mathbf{C}}dsdtdr.$$

(3b)

By using

$$\mathbf{L}(x,y,z){\mathbf{L}}^T(x,y,z)\overline{\mathbf{C}}=\overline{\overline{\mathbf{C}}}\mathbf{L}(x,y,z),$$

(3c)

where $\overline{\overline{\mathbf{C}}}=diag\left(\overline{\mathbf{C}}\right)$ is a ${(M+1)}^3\times {(M+1)}^3$ matrix in a diagonal.

It is clear that

$${\int }_0^1{\int }_0^1{\int }_0^1\mathbf{L}(s,t,r)dsdtdr={\mathbf{B}}_1.$$

(3d)

Substituting from (3c) and (3d) into (3b), we procure

$${\mathbf{L}}^T(x,y,z)\overline{\mathbf{C}}={\mathbf{L}}^T(x,y,z)\mathbf{G}+\lambda {\mathbf{L}}^T(x,y,z)\mathbf{H}\overline{\overline{\mathbf{C}}}{\mathbf{B}}_1,$$

(3e)

therefore

$${\mathbf{L}}^T(x,y,z)\overline{\mathbf{C}}={\mathbf{L}}^T(x,y,z)\mathbf{G}+\lambda {\mathbf{L}}^T(x,y,z)Y,$$

where $Y=\mathbf{H}\overline{\overline{\mathbf{C}}}{\mathbf{B}}_1.$

By inserting the collocation point

$$(x_i,y_j,z_k)=(\frac{i}{M},\frac{j}{M},\frac{k}{M}),i,j,k=0,1,\dots ,M,$$

(3f)

we obtain

$${\mathbf{L}}^T(x_i,y_j,z_k)\overline{\mathbf{C}}={\mathbf{L}}^T(x_i,y_j,z_k)\mathbf{G}+\lambda {\mathbf{L}}^T(x_i,y_j,z_k)Y.$$

(3g)

By simplifying (3g), we obtain

$$\overline{\mathbf{C}}=\mathbf{G}+\lambda Y.$$

(3h)

Next, when resolving the top linear system, we may discover the factor and we procure the estimated solution.

4. Error Analysis

To generalize Lucas polynomials of the fractional DE, Abd-Elhameed and Youssri researched the convergence and error analysis in their paper from [16]. This section covers the equation’s error analysis (1c).

Assume that $\left(C\right(D),\parallel .\parallel )$ has the Banach space of every continuous function on D with a norm of

$$\parallel w(x,y,z)\parallel =\underset{(x,y,z)\in D}{max}\mid w(x,y,z)\mid .$$

(4a)

Furthermore, we denote the error by

$$e_M(x,y,z)=\mid w_M(x,y,z)-w(x,y,z)\mid ,$$

(4b)

where w and $w_M$ are the analytical and approximate solutions of the three-dimensional integral Equation (1c) severally.

Theorem 1.

Suppose that $g(x,y,z)$ in Equation (1c) is bounded $\forall (x,y,z)\in D$ and $\Vert H(x,y,z,s,t,r)$$\Vert \le M_1$$\forall (x,y,z,s,t,r)\in D\times D$. Subsequently, Equation (1c) has a unique solution whenever $0<\alpha <1,\mid \lambda \mid M_1=\alpha .$

Proof. 

Let

$$\Vert e_M(x,y,z)\Vert =\Vert w_M(x,y,z)-w(x,y,z)\Vert =\underset{(x,y,z)\in D}{max}\mid w_M(x,y,z)-w(x,y,z)\mid$$

$$=\underset{(x,y,z)\in D}{max}\mid \lambda {\int }_0^1{\int }_0^1{\int }_0^{1}H(x,y,z,s,t,r)w_M(s,t,r)dsdtdr-\lambda {\int }_0^1{\int }_0^1{\int }_0^{1}H(x,y,z,s,t,r)w(s,t,r)dsdtdr\mid$$

$$=\underset{(x,y,z)\in D}{max}\mid \lambda {\int }_0^1{\int }_0^1{\int }_0^{1}H(x,y,z,s,t,r)(w_M(s,t,r)-w(s,t,r)dsdtdr\mid$$

$$\le \Vert w_M(x,y,z)-w(x,y,z)\Vert \underset{(x,y,z)\in D}{max}\mid \lambda {\int }_0^1{\int }_0^1{\int }_0^{1}H(x,y,z,s,t,r)dsdtdr\mid .$$

Subsequently,

$$\Vert e_M(x,y,z)\Vert \le \Vert e_M(x,y,z)\Vert (\mid \lambda \mid M_1)\le \alpha \Vert e_M(x,y,z)\Vert ,$$

therefore

$$(1-\alpha )\Vert e_M(x,y,z)\Vert \le 0.$$

Thus, if $0<\alpha <1$, we have $\Vert e_M(x,y,z)\Vert ⟶0$ as $M⟶\infty$, and this completes the proof of the theorem.

For an error estimation of the approximate solution of Equation (1c), we consider

$$r_M(x,y,z)+g(x,y,z)=w_M(x,y,z)-\lambda {\int }_0^1{\int }_0^1{\int }_0^{1}H(x,y,z,s,t,r)w_M(x,y,z)dsdtdr,$$

(4c)

where $r_M$ is the perturbation function.

By deducting Equation (4c) from Equation (1c) we get

$$\parallel r_M(x,y,z)\parallel \le \Vert e_M(x,y,z)\Vert +\mid \lambda \mid M_1\Vert e_M(x,y,z)\Vert .$$

Therefore,

$$\parallel r_M(x,y,z)\parallel \le (1+\mid \lambda \mid M_1)\Vert e_M(x,y,z)\Vert ,$$

then $r_M(x,y,z)$ is bounded. □

5. Numerical Examples

In this part, four numerical illustrations are introduced to explain the suggested technique. All computations have been formed by using Maple 18.

Example 1.

Let the next three-dimensional FIE of the second type be:

$$w(x,y,z)=g(x,y,z)+0.01{\int }_0^1{\int }_0^1{\int }_0^1\left(e^{-\left(xyz\right)}{s}^{2}t{r}^2\right)w^p(s,t,r)dsdtdr,(x,y,z)\in D,p=1,2,$$

(5a)

with the analytical solution $w(x,y,z)=x^2{y}^2{z}^2.$

Case (I) if $p=1$, we obtain the following linear integral equation (LIE):

$$w(x,y,z)=x^2{y}^2{z}^2-\frac{1}{10000}{e}^{-\left(xyz\right)}+0.01{\int }_0^1{\int }_0^1{\int }_0^1\left(e^{-\left(xyz\right)}{s}^{2}t{r}^2\right)w(s,t,r)dsdtdr,(x,y,z)\in D.$$

(5b)

Case (II) if $p=2$, we obtain the following nonlinear integral equation (NIE):

$$w(x,y,z)=x^2{y}^2{z}^2-\frac{1}{29400}{e}^{-\left(xyz\right)}+0.01{\int }_0^1{\int }_0^1{\int }_0^1\left(e^{-\left(xyz\right)}{s}^{2}t{r}^2\right)w^2(s,t,r)dsdtdr,(x,y,z)\in D.$$

(5c)

Implementation Lucas polynomial technique for Equation (5b) with M = 2 and via utilization of the employment points (3f). We receive a set of 27 linear algebraic equations with an equivalent number of unknowns. We reverse this scheme and obtain the sum calculated, as follows:

$$c_{0,0,0}=-1,c_{0,0,1}=0,c_{0,0,2}=1,c_{0,1,0}=0,c_{0,1,1}=0,c_{0,1,2}=0,c_{0,2,0}=1,$$

$$c_{0,2,1}=0,c_{0,2,2}=-1,c_{1,0,0}=0,c_{1,0,1}=0,c_{1,0,2}=0,c_{1,1,0}=0,c_{1,1,1}=0,$$

$$c_{1,1,2}=0,c_{1,2,0}=0,c_{1,2,1}=0,c_{1,2,2}=0,c_{2,0,0}=1,c_{2,0,1}=0,c_{2,0,2}=-1,$$

$$c_{2,1,0}=0,c_{2,1,1}=0,c_{2,1,2}=0,c_{2,2,0}=-1,a_{2,2,1}=0,c_{2,2,2}=1$$

and, we receive the approximate resolution that is the same as the accurate resolution.

Similarly, applying the Lucas polynomial method for Equation (5c), we obtain the approximate solution in the form of

$$w_2(x,y,x)=x^2{y}^2{z}^2-1.011599486\times {10}^{-10}xyz-3.102400059\times {10}^{-10}{x}^{2}y{z}^2-3.102400059\times {10}^{-10}{x}^2{y}^{2}z$$

$$+1.917200016\times {10}^{-10}xy{z}^2+1.917200016\times {10}^{-10}x{y}^{2}z-3.102400059\times {10}^{-10}x{y}^2{z}^2+1.917200016\times {10}^{-10}{x}^{2}yz.$$

This is a comparison between the exact solution, approximate solution and absolute error presented in Table 2. Figure 1 represented absolute error of example 1 when $z=0.5$.

Table 2. Numerical outcomes of example 1, case II.

$(\mathit{x},\mathit{y},\mathit{z})$	Exact Solution	Approximate Solution	Absolute Error
$(0,0,0)$	0	0	0
$(0.1,0.1,0.1)$	$0.000001$	$9.999999471\times {10}^{-7}$	$5.295114830\times {10}^{-14}$
$(0.2,0.2,0.2)$	$0.000064$	$0.00006399999982$	$1.868539870\times {10}^{-13}$
$(0.3,0.3,0.3)$	$0.000729$	$0.0007289999997$	$3.341722165\times {10}^{-13}$
$(0.4,0.4,0.4)$	$0.004096$	$0.004095999998$	$1.280713568\times {10}^{-12}$
$(0.5,0.5,0.5)$	$0.015625$	$0.01562499999$	$5.782493832\times {10}^{-12}$
$(0.6,0.6,0.6)$	$0.046656$	$0.04665599996$	$1.968260082\times {10}^{-11}$
$(0.7,0.7,0.7)$	$0.117649$	$0.1176490000$	$5.302805863\times {10}^{-11}$
$(0.8,0.8,0.8)$	$0.262144$	$0.2621439999$	$1.211866911\times {10}^{-10}$
$(0.9,0.9,0.9)$	$0.531441$	$0.5314409998$	$2.459639868\times {10}^{-10}$
$(1,1,1)$	1	$0.9999999996$	$4.567199615\times {10}^{-10}$

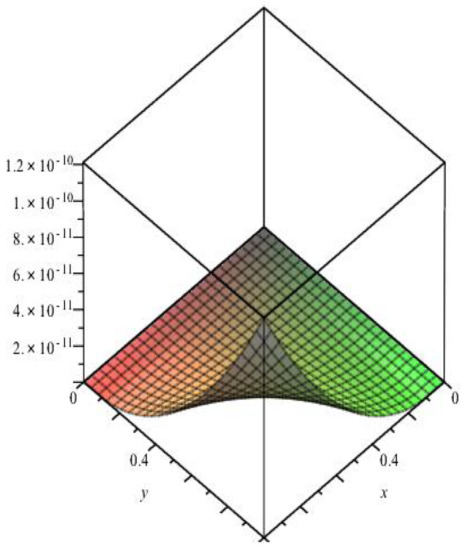
Figure 1. Absolute error of example 1, M = 2 and z = 0.5.

Example 2.

Let the next three-dimensional IE of the second type be [9,10]:

$$w(x,y,z)=g(x,y,z)+0.01{\int }_0^1{\int }_0^1{\int }_0^1(x^{2}srz{t}^2+x^{2}syrz)w^p(s,t,r)dsdtdr,(x,y,z)\in D,p=1,2,$$

(5d)

with the exact solution $w(x,y,z)=x^2{y}^{2}z.$

Comparing Equation (5d) with Equation (1c), we note that

$$H(x,y,z,s,t,r)=k_1(x,y,z,s,t,r)+k_2(x,y,z,s,t,r)=x^{2}srz{t}^2+x^{2}syrz,$$

$$k_1(x,y,z,s,t,r)=\left\{\begin{array}{c}{x}^{2}srz{t}^2(s,t,r)\le (x,y,z),\\ \\ 0,(s,t,r)>(x,y,z),\end{array}\right.$$

$k_2(x,y,z,s,t,r)=x^{2}syrz.$

Case (I) if $p=1$, we obtain the following LIE

$$w(x,y,z)=x^2{y}^{2}z-\frac{1}{6000}{x}^{2}z-\frac{1}{3600}{x}^{2}yz+0.01{\int }_0^1{\int }_0^1{\int }_0^1(x^{2}srz{t}^2+x^{2}syrz)w(s,t,r)dsdtdr.$$

(5e)

Case (II) if $p=2$, we obtain the following NIE

$$w(x,y,z)=x^2{y}^{2}z-\frac{1}{16800}{x}^{2}z-\frac{1}{12000}{x}^{2}yz+0.01{\int }_0^1{\int }_0^1{\int }_0^1(x^{2}srz{t}^2+x^{2}syrz)w^2(s,t,r)dsdtdr.$$

(5f)

Similarly, as in example 1, and applying the Lucas polynomial method for Equation (5e) with M = 2 via utilization, the employment points are (3f). We receive a set of 27 linear algebraic equations with an equivalent number of unknowns. We reverse this scheme and obtain the sum calculated, as follows:

$$c_{0,0,0}=0,c_{0,0,1}=1,c_{0,0,2}=0,c_{0,1,0}=0,c_{0,1,1}=0,c_{0,1,2}=0,c_{0,2,0}=0,$$

$$c_{0,2,1}=-1,c_{0,2,2}=0,c_{1,0,0}=0,c_{1,0,1}=0,c_{1,0,2}=0,c_{1,1,0}=0,c_{1,1,1}=0,$$

$$c_{1,1,2}=0,c_{1,2,0}=0,c_{1,2,1}=0,c_{1,2,2}=0,c_{2,0,0}=0,c_{2,0,1}=-1,c_{2,0,2}=0,$$

$$c_{2,1,0}=0,c_{2,1,1}=0,c_{2,1,2}=0,c_{2,2,0}=0,a_{2,2,1}=1,c_{2,2,2}=0,$$

and we receive the approximate resolution, which is the same as the accurate resolution.

Similarly, when applying the Lucas polynomial method for Equation (5f), we obtain the approximate solution in the form

$$w_2(x,y,x)=-1.62042\times {10}^{-9}xyz+1.80048\times {10}^{-9}xy{z}^2+2.52052\times {10}^{-9}x{y}^{2}z-2.80064\times {10}^{-9}x{y}^2{z}^2$$

$$+2.482404895\times {10}^{-9}{x}^{2}yz-2.80056\times {10}^{-9}{x}^{2}y{z}^2+4.0008\times {10}^{-9}{x}^2{y}^2{z}^2+0.9999999965x^2{y}^{2}z.$$

Comparisons between the absolute errors of the presented technique and the Haar wavelet technique [10] are shown in Table 3. Figure 2 represented the absolute error of example 2 when $z=0.5$.

Table 3. Numerical outcomes of example 2, case II.

$(\mathit{x},\mathit{y},\mathit{z})$	Abs Error of Our Technique, M = 2	Abs Error of [10], M = 4	Abs Error of [10], M = 8
$(0,0,0)$	0	0	0
$(0.1,0.1,0.1)$	$1.027090710\times {10}^{-12}$	$3.513425711\times {10}^{-9}$	$8.93185232\times {10}^{-10}$
$(0.2,0.2,0.2)$	$4.734244968\times {10}^{-12}$	$3.075653759\times {10}^{-8}$	$7.81583453\times {10}^{-9}$
$(0.3,0.3,0.3)$	$7.843093150\times {10}^{-12}$	$1.127441345\times {10}^{-7}$	$2.86408818\times {10}^{-8}$
$(0.4,0.4,0.4)$	$6.348725880\times {10}^{-12}$	$2.884384112\times {10}^{-7}$	$7.32523191\times {10}^{-8}$
$(0.5,0.5,0.5)$	$7.60305950\times {10}^{-13}$	$6.047489575\times {10}^{-7}$	$1.53545196\times {10}^{-7}$
$(0.6,0.6,0.6)$	$1.066256719\times {10}^{-11}$	$1.116532759\times {10}^{-6}$	$2.83425621\times {10}^{-7}$
$(0.7,0.7,0.7)$	$1.874489071\times {10}^{-11}$	$1.886594200\times {10}^{-6}$	$4.78810760\times {10}^{-7}$
$(0.8,0.8,0.8)$	$2.352410432\times {10}^{-11}$	$2.985685054\times {10}^{-6}$	$7.57628837\times {10}^{-7}$
$(0.9,0.9,0.9)$	$3.444933645\times {10}^{-11}$	$4.492504497\times {10}^{-6}$	$1.13981913\times {10}^{-6}$
$(1,1,1)$	$8.2584895\times {10}^{-11}$	$6.493699097\times {10}^{-6}$	$1.64733199\times {10}^{-6}$

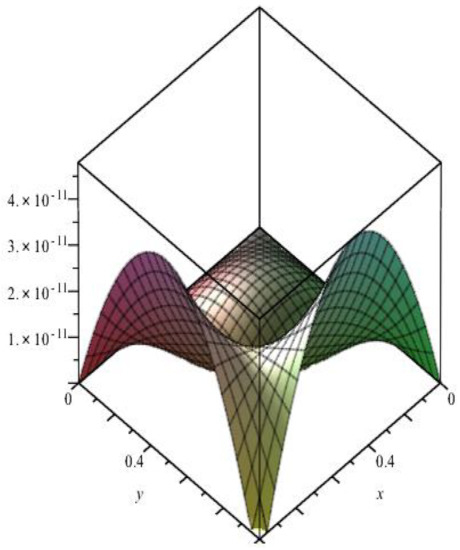
Figure 2. Absolute error of example 2, M = 2, z = 0.5.

Example 3.

Let the next three-dimensional FIE of the second type be:

$$w(x,y,z)=g(x,y,z)+0.01{\int }_0^1{\int }_0^1{\int }_0^1\left(e^{-r}{x}^2{y}^{2}st\right)w^p(s,t,r)dsdtdr,(x,y,z)\in D,p=1,2,$$

(5g)

with analytical solution $w(x,y,z)=xy{e}^{-z}.$

Case (I) if $p=1$ we obtain the following LIE:

$$w(x,y,z)=xy{e}^{-z}-(\frac{1}{1800}{y}^2{x}^2-\frac{1}{1800}{e}^{-2}{x}^2{y}^2)+0.01{\int }_0^1{\int }_0^1{\int }_0^1\left(e^{-r}{x}^2{y}^{2}st\right)w(s,t,r)dsdtdr.$$

(5h)

Case (II) if $p=2$, we obtain the following NIE:

$$w(x,y,z)=xy{e}^{-z}-(\frac{1}{4800}{x}^2{y}^2-\frac{1}{4800}{x}^2{y}^2{e}^{-3})+0.01{\int }_0^1{\int }_0^1{\int }_0^1\left(e^{-r}{x}^2{y}^{2}st\right)w^2(s,t,r)dsdtdr.$$

(5i)

Similarly as examples 1 and 2, we obtain the approximate solutions of Equations (5h) and (5i), respectively, in the forms

$$w_2(x,y,z)=-1.3\times {10}^{-16}x+1.2\times {10}^{-16}y-0.9417567917xyz+0.3096362366xy{z}^2-9.1\times {10}^{-9}x{y}^{2}z$$

$$+5.290847763\times {10}^{-9}x{y}^2{z}^2-1.08\times {10}^{-8}{x}^{2}yz+6.616953330\times {10}^{-9}{x}^{2}y{z}^2+8\times {10}^{-9}{x}^2{y}^{2}z-3.7500021\times {10}^{-9}{x}^2{y}^2{z}^2$$

$$+0.9999999962xy+4.281458270\times {10}^{-9}x{y}^2+4.571508262\times {10}^{-9}{x}^{2}y+7.348829758\times {10}^{-7}{x}^2{y}^2+4.0\times {10}^{-16}{y}^2,$$

and

$$w_2(x,y,z)=-1.28\times {10}^{-9}x{y}^2{z}^2+1.04\times {10}^{-9}{x}^{2}yz-1.28\times {10}^{-9}{x}^{2}y{z}^2+9.6\times {10}^{-10}{x}^2{y}^{2}z-3.2\times {10}^{-10}{x}^2{y}^2{z}^2$$

$$-0.9417568054xyz+0.3096362465xy{z}^2+1.040000000\times {10}^{-9}x{y}^{2}z+1.000000001xy-3.96292120\times {10}^{-10}x{y}^2$$

$$-3.96292120\times {10}^{-10}{x}^{2}y+9.724822738\times {10}^{-7}{x}^2{y}^2.$$

Absolute errors of example 3 is shown in Table 4 and Figure 3 and Figure 4.

Table 4. Numeric outcomes of example 3.

$(\mathit{x},\mathit{y},\mathit{z})=(2^{-\mathit{\ell }},2^{-\mathit{\ell }},2^{-\mathit{\ell }})$	Abs. Error for Case I, M = 2	Error for Case II, M = 2
$\ell =1$	$4.641\times {10}^{-8}$	$6.08\times {10}^{-8}$
$\ell =2$	$1.9520440\times {10}^{-4}$	$3.1952140\times {10}^{-4}$
$\ell =3$	$7.221208467\times {10}^{-5}$	$7.221218\times {10}^{-5}$
$\ell =4$	$1.147130303\times {10}^{-5}$	$1.1471321\times {10}^{-5}$
$\ell =5$	$1.600822047\times {10}^{-6}$	$1.6008264\times {10}^{-6}$
$\ell =6$	$2.109874999\times {10}^{-7}$	$2.109887\times {10}^{-7}$

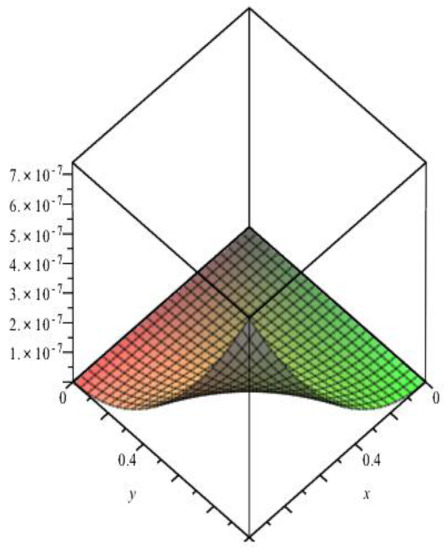
Figure 3. Absolute error of example 3, case I, M = 2 and z = 0.5.

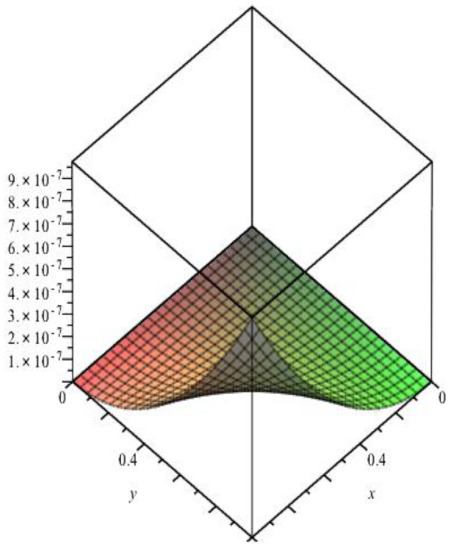
Figure 4. Absolute error of example 3 case II, M = 2 and z = 0.5.

Example 4.

Let the next three-dimensional Fredholm integral equation of the second type be:

$$w(x,y,z)=xyz{e}^{-x^2-y^2-z^2}+\frac{1}{16}{(1-e^{-1})}^{3}xyz+\frac{1}{2}{\int }_0^1{\int }_0^1{\int }_0^{1}xyzw(s,t,r)dsdtdr,$$

(5j)

with exact solution $w(x,y,z)=xyz{e}^{-x^2-y^2-z^2}.$

The numeric outcomes of example 4 are displayed in Table 5 according to the suggested procedure, and Figure 5 represented the Absolute error when $z=0.5$.

Table 5. Numeric outcomes of example 4.

$(\mathit{x},\mathit{y},\mathit{z})=(2^{-\mathit{\ell }},2^{-\mathit{\ell }},2^{-\mathit{\ell }})$	Abs. Error for  M = 2
$\ell =1$	$9.8458149\times {10}^{-5}$
$\ell =2$	$1.957533070\times {10}^{-3}$
$\ell =3$	$6.463230447\times {10}^{-4}$
$\ell =4$	$1.190393926\times {10}^{-4}$
$\ell =5$	$1.772988091\times {10}^{-5}$
$\ell =6$	$2.409198170\times {10}^{-6}$

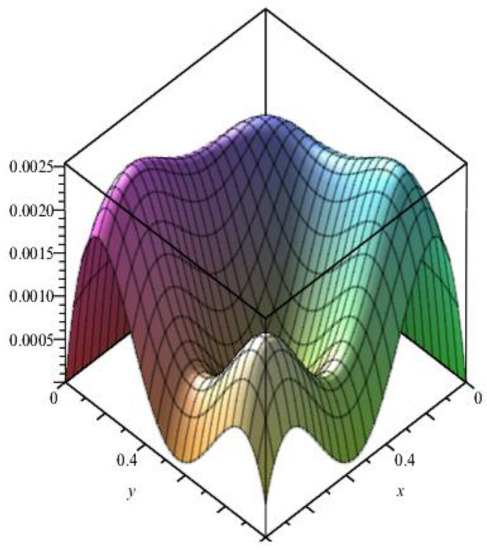
Figure 5. Absolute error of example 4, M = 2 and z = 0.5.

6. Conclusions

A numeric technique depending on the Lucas polynomial is proposed in this document for the approximate solution of 3D-MVFIEK2. As the numeric outcome has demonstrated, by comparing the present method with other numerical techniques, it is clear that the results of the Lucas polynomial method are better than the results of the Haar wavelet technique [10], and the CPT time used for solving the examples is very small when using the Maple program.

Future Work

We can develop this method for solving the singular 3D-VFIEK2 with some modifications. Moreover, we can use the finite difference method for solving different kinds of integral equations.