Nanoscale 3D Spatial Analysis of Zirconia Disc Surfaces Subjected to Different Laser Treatments
Abstract
1. Introduction
2. Materials and Methods
2.1. Preparation of Zirconia Ceramic Discs
2.2. AFM Imaging
2.3. Morphology Analysis
2.4. Fractal and Multifractal Analysis
2.5. Statistical Analysis
3. Results and Discussion
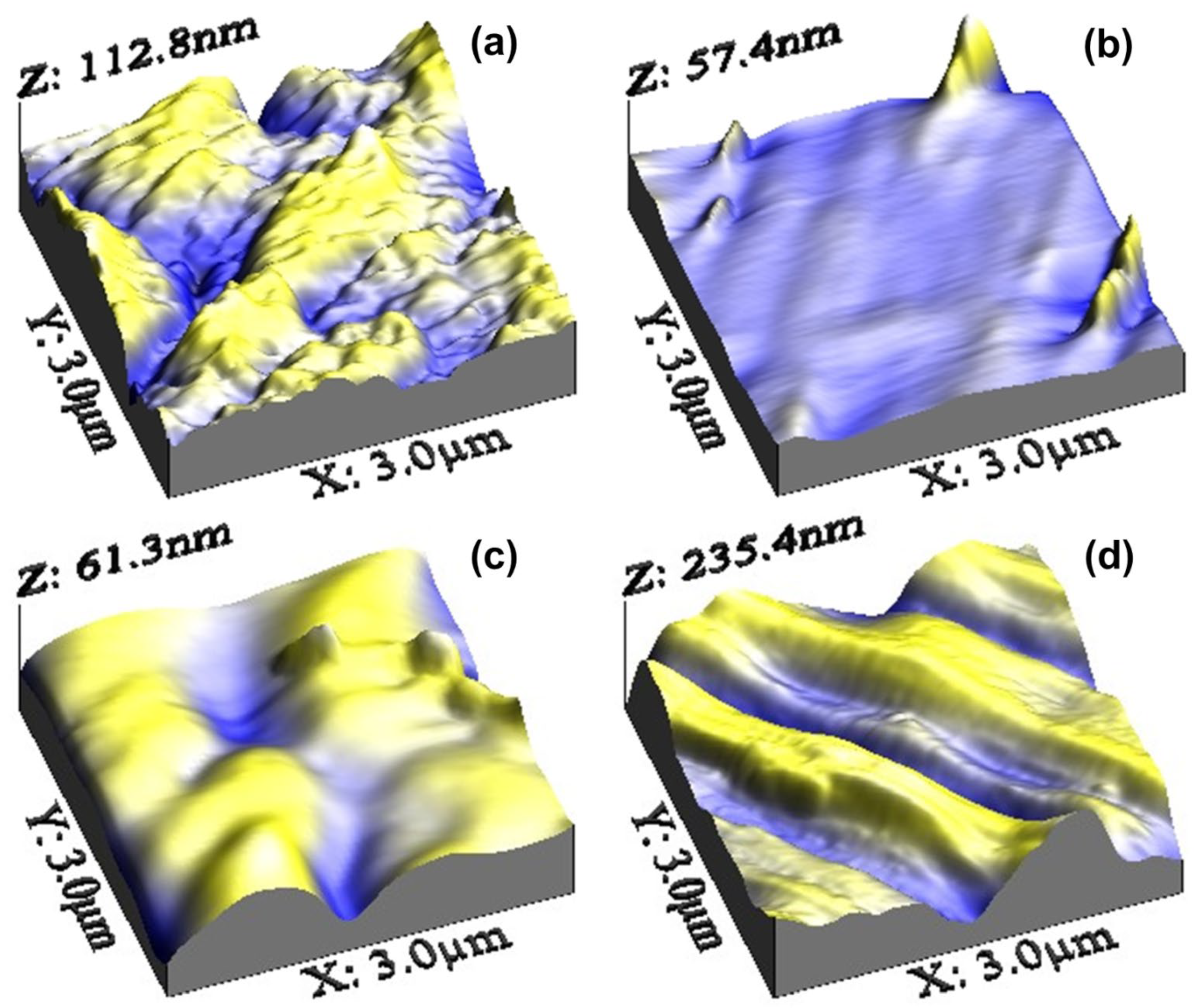
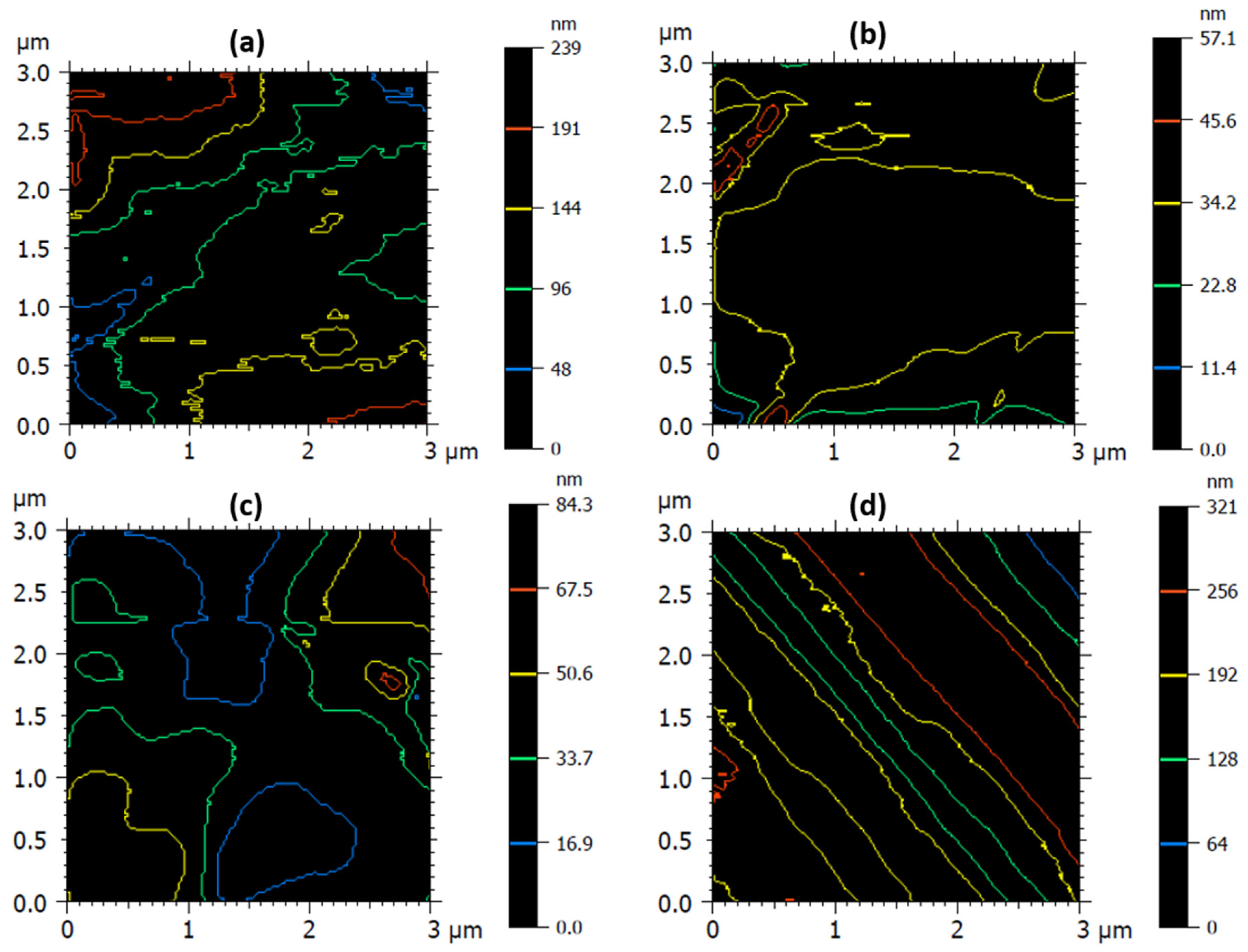
3.1. Standard Morphology Analysis
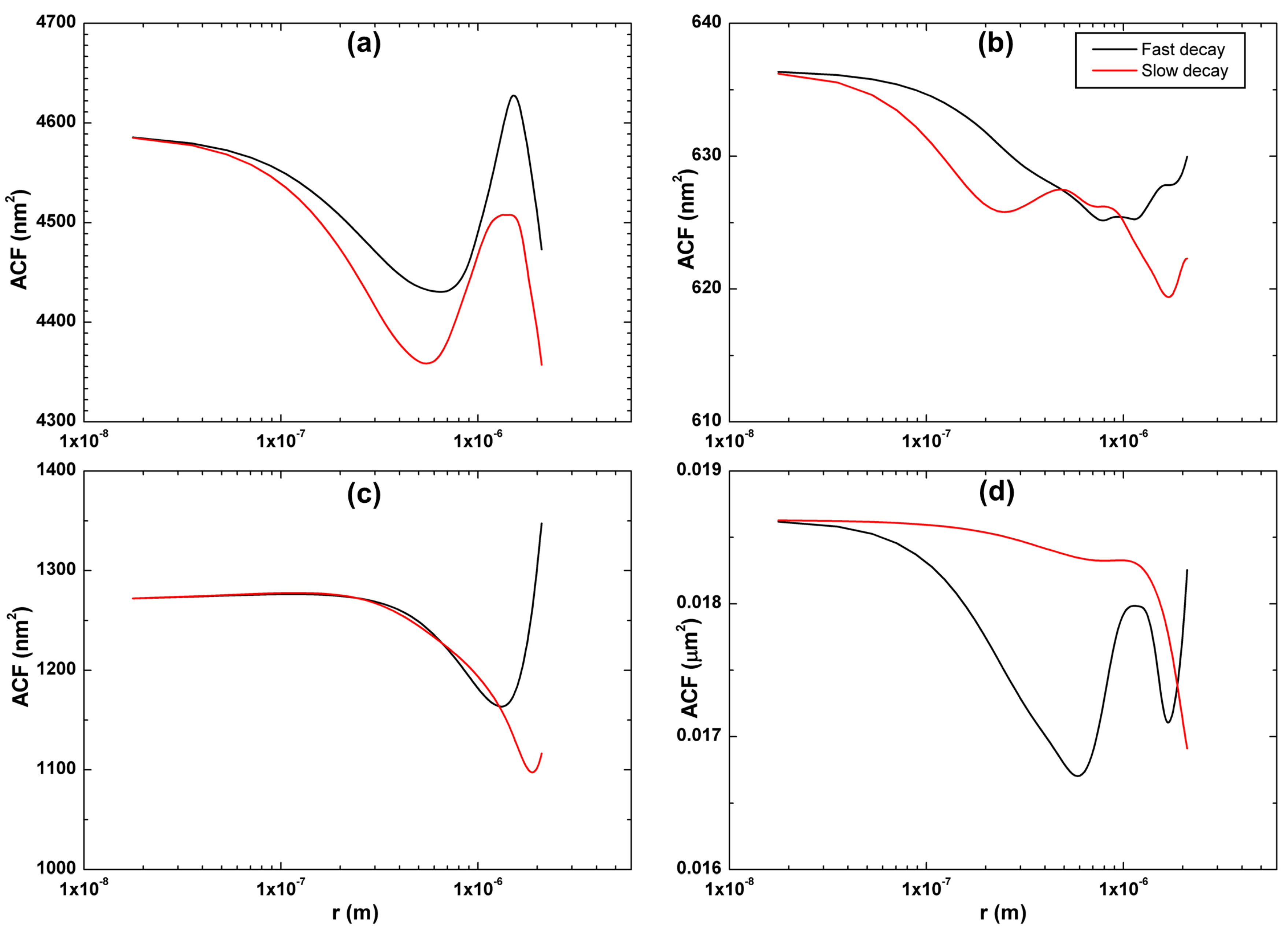
3.2. Spatial Autocorrelation (ACF) and Moran’s Correlogram
3.3. Minkowski Functionals
3.4. Fractal Analysis
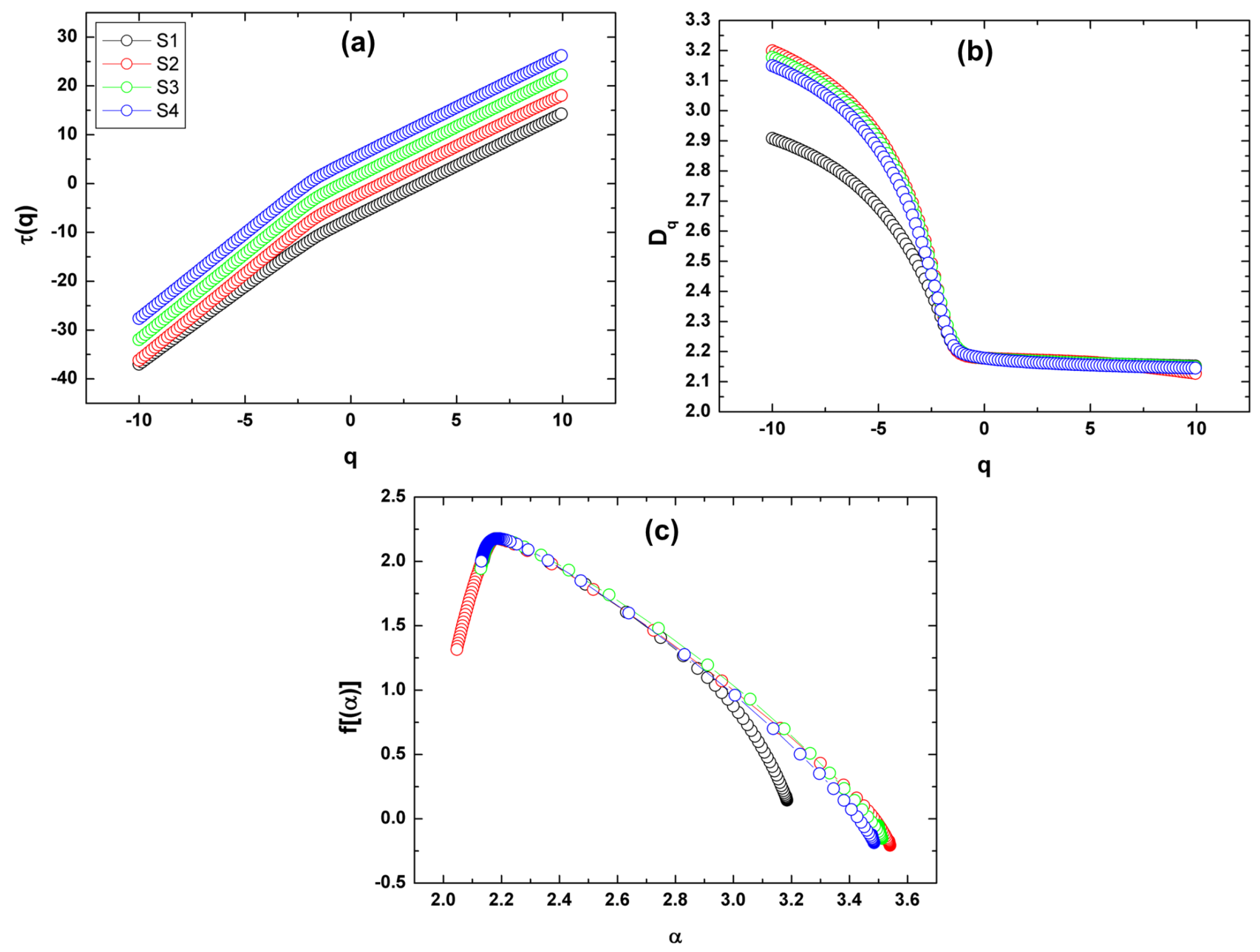
3.5. Multifractal Analysis
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Han, J.; Zhang, F.; Van Meerbeek, B.; Vleugels, J.; Braem, A.; Castagne, S. Laser Surface Texturing of Zirconia-Based Ceramics for Dental Applications: A Review. Mater. Sci. Eng. C 2021, 123, 112034. [Google Scholar] [CrossRef] [PubMed]
- Osman, R.; Swain, M. A Critical Review of Dental Implant Materials with an Emphasis on Titanium versus Zirconia. Materials 2015, 8, 932–958. [Google Scholar] [CrossRef] [PubMed]
- Yoshinari, M. Future Prospects of Zirconia for Oral Implants—A Review. Dent. Mater. J. 2020, 39, 37–45. [Google Scholar] [CrossRef] [PubMed]
- Elnayef, B.; Lázaro, A.; Suárez-López del Amo, F.; Galindo-Moreno, P.; Wang, H.-L.; Gargallo-Albiol, J.; Hernández-Alfaro, F. Zirconia Implants as an Alternative to Titanium: A Systematic Review and Meta-Analysis. Int. J. Oral Maxillofac. Implants 2017, 32, e125–e134. [Google Scholar] [CrossRef]
- Faria, D.; Madeira, S.; Buciumeanu, M.; Silva, F.S.; Carvalho, O. Novel Laser Textured Surface Designs for Improved Zirconia Implants Performance. Mater. Sci. Eng. C 2020, 108, 110390. [Google Scholar] [CrossRef]
- Fattahi, M.; Nezafat, N.B.; Ţălu, Ş.; Solaymani, S.; Ghoranneviss, M.; Elahi, S.M.; Shafiekhani, A.; Rezaee, S. Topographic Characterization of Zirconia-Based Ceramics by Atomic Force Microscopy: A Case Study on Different Laser Irradiations. J. Alloys Compd. 2020, 831, 154763. [Google Scholar] [CrossRef]
- Sennerby, L.; Dasmah, A.; Larsson, B.; Iverhed, M. Bone Tissue Responses to Surface-Modified Zirconia Implants: A Histomorphometric and Removal Torque Study in the Rabbit. Clin. Implant Dent. Relat. Res. 2005, 7, s13–s20. [Google Scholar] [CrossRef]
- Gahlert, M.; Gudehus, T.; Eichhorn, S.; Steinhauser, E.; Kniha, H.; Erhardt, W. Biomechanical and Histomorphometric Comparison between Zirconia Implants with Varying Surface Textures and a Titanium Implant in the Maxilla of Miniature Pigs. Clin. Oral Implants Res. 2007, 18, 662–668. [Google Scholar] [CrossRef]
- Park, Y.-S.; Chung, S.-H.; Shon, W.-J. Peri-Implant Bone Formation and Surface Characteristics of Rough Surface Zirconia Implants Manufactured by Powder Injection Molding Technique in Rabbit Tibiae. Clin. Oral Implants Res. 2013, 24, 586–591. [Google Scholar] [CrossRef]
- Delgado-Ruíz, R.; Markovic, A.; Calvo-Guirado, L.; Lazic, Z.; Piattelli, A.; Boticelli, D.; Maté-Sánchez, J.; Negri, B.; Ramírez-Fernández, M.; Misic, T. Implant Stability and Marginal Bone Level of Microgrooved Zirconia Dental Implants: A 3-Month Experimental Study on Dogs. Vojnosanit. Pregl. 2014, 71, 451–461. [Google Scholar] [CrossRef]
- Tzanakakis, E.-G.C.; Tzoutzas, I.G.; Koidis, P.T. Is There a Potential for Durable Adhesion to Zirconia Restorations? A Systematic Review. J. Prosthet. Dent. 2016, 115, 9–19. [Google Scholar] [CrossRef]
- Kim, H.-K.; Woo, K.M.; Shon, W.-J.; Ahn, J.-S.; Cha, S.; Park, Y.-S. Comparison of Peri-Implant Bone Formation around Injection-Molded and Machined Surface Zirconia Implants in Rabbit Tibiae. Dent. Mater. J. 2015, 34, 508–515. [Google Scholar] [CrossRef]
- Hempel, U.; Hefti, T.; Kalbacova, M.; Wolf-Brandstetter, C.; Dieter, P.; Schlottig, F. Response of Osteoblast-like SAOS-2 Cells to Zirconia Ceramics with Different Surface Topographies. Clin. Oral Implants Res. 2010, 21, 174–181. [Google Scholar] [CrossRef]
- Calvo-Guirado, J.L.; Aguilar Salvatierra, A.; Gargallo-Albiol, J.; Delgado-Ruiz, R.A.; Maté Sanchez, J.E.; Satorres-Nieto, M. Zirconia with Laser-Modified Microgrooved Surface vs. Titanium Implants Covered with Melatonin Stimulates Bone Formation. Experimental Study in Tibia Rabbits. Clin. Oral Implants Res. 2015, 26, 1421–1429. [Google Scholar] [CrossRef]
- Wang, G.; Meng, F.; Ding, C.; Chu, P.K.; Liu, X. Microstructure, Bioactivity and Osteoblast Behavior of Monoclinic Zirconia Coating with Nanostructured Surface. Acta Biomater. 2010, 6, 990–1000. [Google Scholar] [CrossRef]
- Hao, L.; Ma, D.R.; Lawrence, J.; Zhu, X. Enhancing Osteoblast Functions on a Magnesia Partially Stabilised Zirconia Bioceramic by Means of Laser Irradiation. Mater. Sci. Eng. C 2005, 25, 496–502. [Google Scholar] [CrossRef]
- Cheng, J.; Liu, C.; Shang, S.; Liu, D.; Perrie, W.; Dearden, G.; Watkins, K. A Review of Ultrafast Laser Materials Micromachining. Opt. Laser Technol. 2013, 46, 88–102. [Google Scholar] [CrossRef]
- Mirhashemi, A.; Emadian Razavi, E.s.; Behboodi, S.; Chiniforush, N. Effect of Laser-Assisted Bleaching with Nd:YAG and Diode Lasers on Shear Bond Strength of Orthodontic Brackets. Lasers Med. Sci. 2015, 30, 2245–2249. [Google Scholar] [CrossRef]
- Mohammad Asnaashari, M.M. Effectiveness of Lasers in the Treatment of Dentin Hypersensitivity. J. Lasers Med. Sci. 2013, 4, 1–7. [Google Scholar]
- Marcondes, M.; Gandolfi Paranhos, M.P.; Spohr, A.M.; Mota, E.G.; Lima da Silva, I.N.; Souto, A.A.; Burnett, L.H. The Influence of the Nd:YAG Laser Bleaching on Physical and Mechanical Properties of the Dental Enamel. J. Biomed. Mater. Res. Part B Appl. Biomater. 2008, 90, 388–395. [Google Scholar] [CrossRef]
- Michiels, R.; Vergauwen, T.E.M.; Mavridou, A.; Meire, M.; De Bruyne, M.; De Moor, R.J.G. Investigation of Coronal Leakage of Root Fillings after Smear-Layer Removal with EDTA or Nd:YAG Lasing through Capillary-Flow Porometry. Photomed. Laser Surg. 2010, 28, S-43–S-50. [Google Scholar] [CrossRef] [PubMed]
- Singhvi, R.; Stephanopoulos, G.; Wang, D.I.C. Effects of Substratum Morphology on Cell Physiology. Biotechnol. Bioeng. 1994, 43, 764–771. [Google Scholar] [CrossRef] [PubMed]
- Curtis, A.; Wilkinson, C. Topographical Control of Cells. Biomaterials 1997, 18, 1573–1583. [Google Scholar] [CrossRef] [PubMed]
- Zhou, W.; Cao, Y.; Zhao, H.; Li, Z.; Feng, P.; Feng, F. Fractal Analysis on Surface Topography of Thin Films: A Review. Fractal Fract. 2022, 6, 135. [Google Scholar] [CrossRef]
- Mwema, F.M.; Jen, T.-C.; Kaspar, P. Fractal Theory in Thin Films: Literature Review and Bibliometric Evidence on Applications and Trends. Fractal Fract. 2022, 6, 489. [Google Scholar] [CrossRef]
- Gavriil, V.; Chatzichristidi, M.; Kollia, Z.; Cefalas, A.-C.; Spyropoulos-Antonakakis, N.; Semashko, V.; Sarantopoulou, E. Photons Probe Entropic Potential Variation during Molecular Confinement in Nanocavities. Entropy 2018, 20, 545. [Google Scholar] [CrossRef]
- Spyropoulos-Antonakakis, N.; Sarantopoulou, E.; Trohopoulos, P.N.; Stefi, A.L.; Kollia, Z.; Gavriil, V.E.; Bourkoula, A.; Petrou, P.S.; Kakabakos, S.; Semashko, V.V.; et al. Selective Aggregation of PAMAM Dendrimer Nanocarriers and PAMAM/ZnPc Nanodrugs on Human Atheromatous Carotid Tissues: A Photodynamic Therapy for Atherosclerosis. Nanoscale Res. Lett. 2015, 10, 210. [Google Scholar] [CrossRef]
- Starodubtseva, M.N.; Starodubtsev, I.E.; Starodubtsev, E.G. Novel Fractal Characteristic of Atomic Force Microscopy Images. Micron 2017, 96, 96–102. [Google Scholar] [CrossRef]
- Yamada, M.K.; Uo, M.; Ohkawa, S.; Akasaka, T.; Watari, F. Three-Dimensional Topographic Scanning Electron Microscope and Raman Spectroscopic Analyses of the Irradiation Effect on Teeth by Nd:YAG, Er: YAG, and CO2 Lasers. J. Biomed. Mater. Res. 2004, 71, 7–15. [Google Scholar] [CrossRef]
- Ghaderi, A.; Shafiekhani, A.; Solaymani, S.; Ţălu, Ş.; da Fonseca Filho, H.D.; Ferreira, N.S.; Matos, R.S.; Zahrabi, H.; Dejam, L. Advanced Microstructure, Morphology and CO Gas Sensor Properties of Cu/Ni Bilayers at Nanoscale. Sci. Rep. 2022, 12, 12002. [Google Scholar] [CrossRef]
- Dong, W.P.; Sullivan, P.J.; Stout, K.J. Comprehensive Study of Parameters for Characterising Three-Dimensional Surface Topography. Wear 1994, 178, 45–60. [Google Scholar] [CrossRef]
- Pinto, E.P.; Pires, M.A.; Matos, R.S.; Zamora, R.R.M.; Menezes, R.P.; Araújo, R.S.; de Souza, T.M. Lacunarity Exponent and Moran Index: A Complementary Methodology to Analyze AFM Images and Its Application to Chitosan Films. Phys. A Stat. Mech. Appl. 2021, 581, 126192. [Google Scholar] [CrossRef]
- Nečas, D.; Klapetek, P. One-Dimensional Autocorrelation and Power Spectrum Density Functions of Irregular Regions. Ultramicroscopy 2013, 124, 13–19. [Google Scholar] [CrossRef]
- Matos, R.S.; Pinto, E.P.; Ramos, G.Q.; Fonseca de Albuquerque, M.D.; Fonseca Filho, H.D. Stereometric Characterization of Kefir Microbial Films Associated with Maytenus Rigida Extract. Microsc. Res. Tech. 2020, 83, 1401–1410. [Google Scholar] [CrossRef]
- Cocu, N.; Harrington, R.; Hullé, M.; Rounsevell, M.D.A. Spatial Autocorrelation as a Tool for Identifying the Geographical Patterns of Aphid Annual Abundance. Agric. For. Entomol. 2005, 7, 31–43. [Google Scholar] [CrossRef]
- Ţălu, Ş.; Stach, S.; Mahajan, A.; Pathak, D.; Wagner, T.; Kumar, A.; Bedi, R.K. Multifractal Analysis of Drop-Casted Copper (II) Tetrasulfophthalocyanine Film Surfaces on the Indium Tin Oxide Substrates. Surf. Interface Anal. 2014, 46, 393–398. [Google Scholar] [CrossRef]
- Zelati, A.; Mardani, M.; Rezaee, S.; Matos, R.S.; Pires, M.A.; da Fonseca Filho, H.D.; Das, A.; Hafezi, F.; Rad, G.A.; Kumar, S.; et al. Morphological and Multifractal Properties of Cr Thin Films Deposited onto Different Substrates. Microsc. Res. Tech. 2022, 86, 157–168. [Google Scholar] [CrossRef]
- Chen, Y. New Approaches for Calculating Moran’s Index of Spatial Autocorrelation. PLoS ONE 2013, 8, e68336. [Google Scholar] [CrossRef]
- Boelens, A.M.P.; Tchelepi, H.A. QuantImPy: Minkowski Functionals and Functions with Python. SoftwareX 2021, 16, 100823. [Google Scholar] [CrossRef]
- Vogel, H.-J.; Weller, U.; Schlüter, S. Quantification of Soil Structure Based on Minkowski Functions. Comput. Geosci. 2010, 36, 1236–1245. [Google Scholar] [CrossRef]
- Ţălu, Ş.; Boudour, S.; Bouchama, I.; Astinchap, B.; Ghanbaripour, H.; Akhtar, M.S.; Zahra, S. Multifractal Analysis of Mg-doped ZnO Thin Films Deposited by Sol–Gel Spin Coating Method. Microsc. Res. Tech. 2022, 85, 1213–1223. [Google Scholar] [CrossRef] [PubMed]
- Salat, H.; Murcio, R.; Arcaute, E. Multifractal Methodology. Phys. A Stat. Mech. Appl. 2017, 473, 467–487. [Google Scholar] [CrossRef]
- Ihlen, E.A.F. Introduction to Multifractal Detrended Fluctuation Analysis in Matlab. Front. Physiol. 2012, 3, 141. [Google Scholar] [CrossRef] [PubMed]
- Ţălu, Ş. Micro and Nanoscale Characterization of Three Dimensional Surfaces. Basics and Applications; Napoca Star Publishing House: Cluj-Napoca, Romania, 2015; ISBN 978-606-690-349-3. [Google Scholar]
- Shakoury, R.; Rezaee, S.; Mwema, F.; Luna, C.; Ghosh, K.; Jurečka, S.; Ţălu, Ş.; Arman, A.; Grayeli Korpi, A. Multifractal and optical bandgap characterization of Ta2O5 thin films deposited by electron gun method. Opt. Quant. Electron. 2020, 52, 95. [Google Scholar] [CrossRef]





| Parameter | Unit | S1 | S2 | S3 | S4 |
|---|---|---|---|---|---|
| Sq | [nm] | 14.13 ± 2.6 | 3.247 ± 0.3 | 7.097 ± 0.5 | 35.07 ± 2.7 |
| Sp | [µm] | 46.50 ± 3.1 | 32.38 ± 2.7 | 26.33 ± 2.6 | 103.5 ± 4.2 |
| Sv | [µm] | 66.30 ± 3.9 | 25.01 ± 2.6 | 34.92 ± 2.7 | 131.9 ± 4.4 |
| Sz | [µm] | 112.8 ± 4.3 | 57.39 ± 2.9 | 61.25 ± 2.9 | 235.4 ± 6.8 |
| Parameter | Unit | S1 | S2 | S3 | S4 |
|---|---|---|---|---|---|
| Maximum depth of furrows | nm | 39.2 ± 2.9 | 14.8 ± 1.8 | 14 ± 1.8 | 85.4 ± 5.7 |
| Mean depth of furrows | nm | 15.2 ± 1.8 | 3.92 ± 0.3 | 5.71 ± 0.5 | 20.1 ± 1.9 |
| Mean density of furrows | cm/cm2 | 36,208 ± 215 | 45,410 ± 284 | 27,721 ± 187 | 43,765 ± 275 |
| Parameter | Unit | S1 | S2 | S3 | S4 |
|---|---|---|---|---|---|
| θmin | [°] | −10.01 | −41.42 | −14.86 | 31.50 |
| θmax | [°] | 47.26 | 51.93 | −89.65 | −45.00 |
| rmin | [nm] | 303.3 | 132.8 | 297.0 | 213.0 |
| rmax | [nm] | 630.3 | 617.7 | 966.8 | 2113 |
| Str | [-] | 0.4815 ± 0.091 | 0.2151 ± 0.052 | 0.3072 ± 0.074 | 0.1008 ± 0.021 |
| Parameter | Unit | S1 | S2 | S3 | S4 |
|---|---|---|---|---|---|
| V | [-] | 0.767 | 0.043 | 0.745 | 0.660 |
| S [10−3] | [-] | 0.043 | 0.011 | 0.021 | 0.036 |
| χ [10−6] | [-] | −0.0003 | 9.16 × 10−5 | −6.10 × 10−5 | −7.63 × 10−5 |
| Parameter | Unit | S1 | S2 | S3 | S4 |
|---|---|---|---|---|---|
| FD | [-] | 2.183 | 2.067 | 2.089 | 2.15 |
| FS | [-] | 0.601 | 0.976 | 0.533 | 0.448 |
| β | [-] | 0.032 | 0.007 | 0.035 | 0.083 |
| Parameter | S1 | S2 | S3 | S4 |
|---|---|---|---|---|
| f(αmax) | 2.007 | 1.316 | 1.944 | 2.002 |
| f(αmin) | 0.143 | −0.207 | −0.153 | −0.185 |
| Δf = f(αmax) − f(αmin) | 1.864 | 1.523 | 2.097 | 2.187 |
| αmax | 3.184 | 3.540 | 3.513 | 3.485 |
| αmin | 2.137 | 2.046 | 2.128 | 2.131 |
| Δα = αmax − αmin | 1.047 | 1.494 | 1.385 | 1.354 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Pinto, E.P.; Matos, R.S.; Pires, M.A.; Lima, L.d.S.; Ţălu, Ş.; da Fonseca Filho, H.D.; Ramazanov, S.; Solaymani, S.; Larosa, C. Nanoscale 3D Spatial Analysis of Zirconia Disc Surfaces Subjected to Different Laser Treatments. Fractal Fract. 2023, 7, 160. https://doi.org/10.3390/fractalfract7020160
Pinto EP, Matos RS, Pires MA, Lima LdS, Ţălu Ş, da Fonseca Filho HD, Ramazanov S, Solaymani S, Larosa C. Nanoscale 3D Spatial Analysis of Zirconia Disc Surfaces Subjected to Different Laser Treatments. Fractal and Fractional. 2023; 7(2):160. https://doi.org/10.3390/fractalfract7020160
Chicago/Turabian StylePinto, Erveton Pinheiro, Robert S. Matos, Marcelo A. Pires, Lucas dos Santos Lima, Ştefan Ţălu, Henrique Duarte da Fonseca Filho, Shikhgasan Ramazanov, Shahram Solaymani, and Claudio Larosa. 2023. "Nanoscale 3D Spatial Analysis of Zirconia Disc Surfaces Subjected to Different Laser Treatments" Fractal and Fractional 7, no. 2: 160. https://doi.org/10.3390/fractalfract7020160
APA StylePinto, E. P., Matos, R. S., Pires, M. A., Lima, L. d. S., Ţălu, Ş., da Fonseca Filho, H. D., Ramazanov, S., Solaymani, S., & Larosa, C. (2023). Nanoscale 3D Spatial Analysis of Zirconia Disc Surfaces Subjected to Different Laser Treatments. Fractal and Fractional, 7(2), 160. https://doi.org/10.3390/fractalfract7020160













