Bifurcation and Analytical Solutions of the Space-Fractional Stochastic Schrödinger Equation with White Noise

Abstract

The qualitative theory for planar dynamical systems is used to study the bifurcation of the wave solutions for the space-fractional nonlinear Schrödinger equation with multiplicative white noise. Employing the first integral, we introduce some new wave solutions, assorted into periodic, solitary, and kink wave solutions. The dependence of the solutions on the initial conditions is investigated. Some solutions are clarified by the display of their 2D and 3D representations with varying levels of noise to show the influence of multiplicative white noise on the solutions.

1. Introduction

Stochastic partial differential equations have been used to describe nonlinear phenomena in engineering and the applied sciences, see, e.g., [1,2,3,4,5,6,7]. The presence of noise may lead to several statistical characteristics that cannot be ignored. Various fields, such as fluid mechanics, meteorology, chemistry, geophysics, physics, biology, engineering, have emphasized the importance of considering random noise when predicting, simulating, analyzing, and modeling complicated processes [8,9,10,11,12]. Fractional derivatives have been successfully used to model nonlinear phenomena, making fractional calculus an important tool in sciences such as physics, mechanics, chemistry, and biology [13,14,15,16,17,18]. The nonlinear phenomena are well-described by fractional stochastic partial differential equations. Compared to deterministic PDEs, fractional PDEs containing stochastic terms are typically harder to solve. The importance of discovering traveling wave solutions to fractional stochastic partial differential equations lies in the fact that these solutions are crucial to understanding and interpreting the studied phenomena.

In general, traveling wave solutions to nonlinear partial differential equations can be constructed through a variety of methods, for instance, the Hirota bilinear method [19,20], Darboux transformation [21], complete discriminant system method [22,23,24], Weierstrass elliptic function method [25], uniform algebraic method [26], and Lie symmetries method [27,28,29]. The majority of techniques that can be used to create wave solutions rely on the assumption of a particular form for the solution of the reduced ordinary differential equation. However, the bifurcation study of the traveling wave system allows for us to create the traveling wave solution for a range of bifurcation parameter values, without the need to for such assumptions. Several works have used this techniques successfully [30,31,32,33,34].

The current paper studies the stochastic Schrödinger equation forced by multiplicative noise in the Stratonovich sense

$$\mathrm{i}{U}_t+{\beta }_1{\mathbb{T}}_{xx}^{\alpha }U+{\beta }_2{\mathbb{T}}_{yy}^{\alpha }U+{\beta }_3\left({\left|U\right|}^{2}U\right)+{\beta }_4{\mathbb{T}}_{xy}^{\alpha }U=-\mathrm{i}\sigma U\circ {\mathbb{G}}_t,$$

(1)

In the above equation, ${\mathbb{T}}^{\alpha }$ denotes the conformable fractional derivative of order $\alpha \in ]0,1[$, $\sigma$ is the intensity of the noise, ${\mathbb{G}}_t=\frac{d\mathbb{G}}{dt}$ is the time derivative of Brownian motion $\mathbb{G}\left(t\right)$, and U is the complex envelope function associated with the optical-pulse electric field in a combining frame. The variables $t,x$ and y are the retarded time, normalized distance along the longitudinal axis of the fiber, and normalized distance along the transverse axis of the fiber, respectively. The constant ${\beta }_1,{\beta }_2,{\beta }_4$ characterize the influences of the second-order dispersion, and ${\beta }_3$ introduces the Kerr non-linearity effect.

The motivation for the current study is the difficulty of considering all aspects that affect the problem under consideration. Therefore, we considered the stochastic perturbations to the $(2+1)$ equation, which takes the form [35]

$$\mathrm{i}{U}_t+{\beta }_1{U}_{xx}+{\beta }_2{U}_{yy}+{\beta }_3{\left(\right|U|}^{2}U)+{\beta }_4{U}_{xy}=0,$$

(2)

with space-fractional derivatives. With this addition, Equation (1) becomes a good model for describing the optical-pulse electric field in a combined frame. Equation (1) can also be considered a generalization of Equation (2) by inserting the stochastic and fractional derivatives. Thus, the solutions of classical versions, i.e., (when $\sigma =0$ or $\alpha \to 1$ or both) can be obtained as a special case of the solutions of Equation (1).

Equation (2) was first introduced in [35] and has been subsequently studied in several works, such as [36]. For ${\beta }_2={\beta }_4=0$, and ${\beta }_3=1$, Equation (2) reduces to

$$\mathrm{i}{U}_t+{\beta }_1{U}_{xx}+{\left|U\right|}^{2}U=0,$$

(3)

which is a nonlinear shrödinger equation in anomalous and normal dispersion regimes with ${\beta }_1=\pm \frac{1}{2}$. Equation (2) was considered in [35], in which the author utilized the variational iteration method (VIM) to obtain bright and dark optical solitons.

As far as the author knows, fractional stochastic partial differential equations have not been previously studied. Their study could help to investigate the influence of the space-fractional order derivatives and noise on the solutions. To keep the paper self-contained, some properties of the conformable fractional derivatives and the definition of the Brownian motion are given in Appendix A.

The current work is organised as follows: Section 2 is the mathematical analysis of the problem with the aim of converting the fractional stochastic partial differential equation into an ordinary differential equation. Section 3 includes a study of the bifurcation and phase portrait description of the dynamical system, corresponding to the reduced ordinary differential equation. Section 4 contains some bounded-wave solutions and examines their degeneracy through transition between the phase orbits. In Section 5, the influence of noise on the obtained solutions is examined by producing two- and three-dimensional graphical representations of the solutions for different values of the noise parameter.

2. Mathematical Analysis

We will assume the solution for the Equation (1) has the form

$$U(x,y,t)=\psi \left(\eta \right)\exp [\mathrm{i}\mathcal{N}(x,y,t)-\sigma \mathbb{G}-{\sigma }^{2}t],$$

(4)

where

$$\eta =\frac{1}{\alpha }\left(a_1{x}^{\alpha }+a_2{y}^{\alpha }\right)+a_{3}t,\mathcal{N}=\frac{1}{\alpha }\left(b_1{x}^{\alpha }+b_2{y}^{\alpha }\right)+b_{3}t,$$

(5)

where $a_i,b_i$, $i=1,2,3$ are non-zero constants, and $\psi \left(\eta \right)$ is a real valued function that characterizes the amplitude of the traveling wave solution. By substituting Equations (4) and (5) into Equation (1) and using the following identities

$$\begin{array}{}& \mathrm{d}U=\exp [\mathrm{i}\mathcal{N}(x,y,t)-\sigma \mathbb{G}-{\sigma }^{2}t]\left[(a_3{\psi }^{\prime }+\mathrm{i}{b}_3\psi )\mathrm{d}t-\sigma \psi {\mathbb{G}}_t-\frac{1}{2}{\sigma }^2\psi \right],\mathrm{(6a)}& =\exp [\mathrm{i}\mathcal{N}(x,y,t)-\sigma \mathbb{G}-{\sigma }^{2}t]\left[(a_3{\psi }^{\prime }+\mathrm{i}{b}_3\psi )\mathrm{d}t-\sigma \psi \circ {\mathbb{G}}_t\right],\mathrm{(6b)}\hfill & {\mathbb{T}}_{xx}^{\alpha }U=\exp [\mathrm{i}\mathcal{N}(x,y,t)-\sigma \mathbb{G}-{\sigma }^{2}t]\left[(a_1^2{\psi }^{″}-b_1^2\psi )+2\mathrm{i}{a}_1{b}_1{\psi }^{\prime }\right],\hfill \mathrm{(6c)}\hfill & {\mathbb{T}}_{yy}^{\alpha }U=\exp [\mathrm{i}\mathcal{N}(x,y,t)-\sigma \mathbb{G}-{\sigma }^{2}t]\left[(a_2^2{\psi }^{″}-b_2^2\psi )+2\mathrm{i}{a}_2{b}_2{\psi }^{\prime }\right],\hfill \mathrm{(6d)}\hfill & {\mathbb{T}}_{xy}^{\alpha }U=\exp [\mathrm{i}\mathcal{N}(x,y,t)-\sigma \mathbb{G}-{\sigma }^{2}t]\left[(a_1{a}_2{\psi }^{″}-b_1{b}_2\psi )+\mathrm{i}(b_1{a}_2+a_1{b}_2){\psi }^{\prime }\right],\hfill \end{array}$$

and then separating the imaginary and real parts, we obtain

$$\begin{array}{}\mathrm{(7a)}\hfill & {\psi }^{\prime }\left[a_3+2{\beta }_1{a}_1{b}_1+2{\beta }_2{a}_2{b}_2+(b_1{a}_2+a_1{b}_2)\right]=0,\hfill \mathrm{(7b)}\hfill & [{\beta }_1{a}_1^2+{\beta }_2{a}_2^2+{\beta }_4{a}_1{a}_2]{\psi }^{″}+[{\beta }_1{b}_1^2-{\beta }_2{b}_2^2-b_3-{\beta }_4{b}_1{b}_2]\psi +{\beta }_3{\psi }^3\exp [-2{\sigma }^{2}t]\exp (-2\sigma \mathbb{G})=0.\hfill \end{array}$$

In the above equations, the notation ${}^{\prime }$ denotes the derivative with respect to $\eta$. As can be seen in Equation (7a), this holds identically if

$$a_3=-2[{\beta }_1{a}_1{b}_1+{\beta }_2{a}_2{b}_2]-(b_1{a}_2+a_1{b}_2).$$

(8)

Taking the expectation for both sides of Equation (7b), we can obtain

$$[{\beta }_1{a}_1^2+{\beta }_2{a}_2^2+{\beta }_4{a}_1{a}_2]{\psi }^{″}+[{\beta }_1{b}_1^2-{\beta }_2{b}_2^2-b_3-{\beta }_4{b}_1{b}_2]\psi +{\beta }_3{\psi }^3\exp [-2{\sigma }^{2}t]\mathbb{E}[\exp (-2\sigma \mathbb{G})]=0.$$

(9)

Since $\mathbb{G}\left(t\right)$ has a normal distribution, we can see that $\mathbb{E}(\exp [-2\sigma \mathbb{G}])=\exp \left[2{\sigma }^{2}t\right]$. Thus, Equation (9) reduces to

$${\psi }^{″}\left(\eta \right)+2{\rho }_1\psi \left(\eta \right)+4{\rho }_2\psi {\left(\eta \right)}^3=0,$$

(10)

where

$${\rho }_1=\frac{{\beta }_1{b}_1^2-{\beta }_2{b}_2^2-b_3-{\beta }_4{b}_1{b}_2}{2[{\beta }_1{a}_1^2+{\beta }_2{a}_2^2+{\beta }_4{a}_1{a}_2]},{\rho }_2=\frac{{\beta }_3}{4[{\beta }_1{a}_1^2+{\beta }_2{a}_2^2+{\beta }_4{a}_1{a}_2]}.$$

(11)

Thus, the problem of solving the stochastic partial differential Equation (1) reduces to finding the solution of Equation (10). If we integrate both sides of Equation (10) with respect to $\psi$ and separate the variables, we obtain a first-order differential form

$$\frac{\mathrm{d}\psi }{\sqrt{{\mathcal{F}}_4\left(\psi \right)}}=\pm \sqrt{2}\mathrm{d}\eta ,$$

(12)

where $\gamma$ is an integration constant, and

$${\mathcal{F}}_4\left(\psi \right)=\gamma -{\rho }_1{\psi }^2-{\rho }_2{\psi }^4.$$

(13)

To integrate both sides of Equation (12), the range of the parameters ${\rho }_1,{\rho }_2$, and E must be determined. There are two methods for accomplishing this. These are the complete discriminate of the quartic polynomial ${\mathcal{F}}_4\left(\psi \right)$ and bifurcation theory. Bifurcation theory is the more useful method. In addition to determining the range of the parameters, it yields useful information about the solution. For example, bifurcation theory yields information about the existence of periodic, homoclinic, and hetroclinic orbits, which translates to the existence of periodic, solitary, and kink (or anti-kink) wave solutions. We will, additionally, study the degeneracy of the obtained solutions by examining the transition between the phase orbits.

3. Bifurcation of the Phase Portraits

Using ${\psi }^{\prime }=z$ transforms Equation (10) into the following dynamical system

$$\begin{array}{}\mathrm{(14a)}\hfill & {\psi }^{\prime }=z,\hfill \mathrm{(14b)}\hfill & z^{\prime }=-2{\rho }_1\psi -4{\rho }_2{\psi }^3.\hfill \end{array}$$

System (14) is conservative, since $\mathrm{div}({\psi }^{\prime },z^{\prime })=0$, and has the Hamiltonian function

$$H(\psi ,z)=\frac{1}{2}{z}^2+{\rho }_1{\psi }^2+{\rho }_2{\psi }^4,$$

(15)

With this function, the system in (14) is the Hamilton canonical equations ${\psi }^{\prime }=\frac{\partial H}{\partial z},z^{\prime }=-\frac{\partial H}{\partial \psi }$. That is, system (14) is a Hamiltonian system with one degree of freedom describing the motion of a particle under the influence of the two-parameters potential function

$$V\left(\psi \right)={\rho }_1{\psi }^2+{\rho }_2{\psi }^4.$$

(16)

Note that the Hamiltonian (15) does not explicitly depend on $\eta$, which plays the role of time in our system. Thus, it is a conserved quantity and we have the first integral

$$\frac{1}{2}{z}^2+{\rho }_1{\psi }^2+{\rho }_2{\psi }^4=\gamma .$$

(17)

The equilibrium points for the Hamiltonian system (14) are the critical points for the potential function (16), i.e., are the points $E=({\psi }^{*},0)$ where ${\psi }^{*}$ is a solution of $\frac{\partial V}{\partial \psi }=2{\psi }^{*}[{\rho }_1+2{\rho }_2{\psi }^{{*}^2}]=0$. Thus, if ${\rho }_1{\rho }_2>0$, the system (14) has one equilibrium point $E_0=(0,0)$. However, if ${\rho }_1{\rho }_2<0$, it has three equilibrium points, $E_0=(0,0),E_{1,2}=(\pm \sqrt{\frac{-{\rho }_1}{2{\rho }_2}},0)$. These equilibrium points can be classified as local maximum or local minimum points for the potential function (16). To do this, we calculate the second derivative

$$\frac{{\partial }^{2}V}{\partial {\psi }^2}{{|}_{E_0}=2{\rho }_1,\frac{{\partial }^{2}V}{\partial {\psi }^2}|}_{E_{1,2}}=-4{\rho }_1,$$

(18)

To carry out this classification, we will take

$$\begin{array}{cc}\hfill & {\mathcal{R}}_1=\{({\rho }_1,{\rho }_2)\in {\mathbb{R}}^2:{\rho }_1>0,{\rho }_2>0\},\hfill \\ \hfill & {\mathcal{R}}_2=\{({\rho }_1,{\rho }_2)\in {\mathbb{R}}^2:{\rho }_1<0,{\rho }_2<0\},\hfill \\ \hfill & {\mathcal{R}}_3=\{({\rho }_1,{\rho }_2)\in {\mathbb{R}}^2:{\rho }_1>0,{\rho }_2<0\},\hfill \\ \hfill & {\mathcal{R}}_4=\{({\rho }_1,{\rho }_2)\in {\mathbb{R}}^2:{\rho }_1<0,{\rho }_2>0\}.\hfill \end{array}$$

(19)

Then, we can classify the equilibrium points as follows:

1.

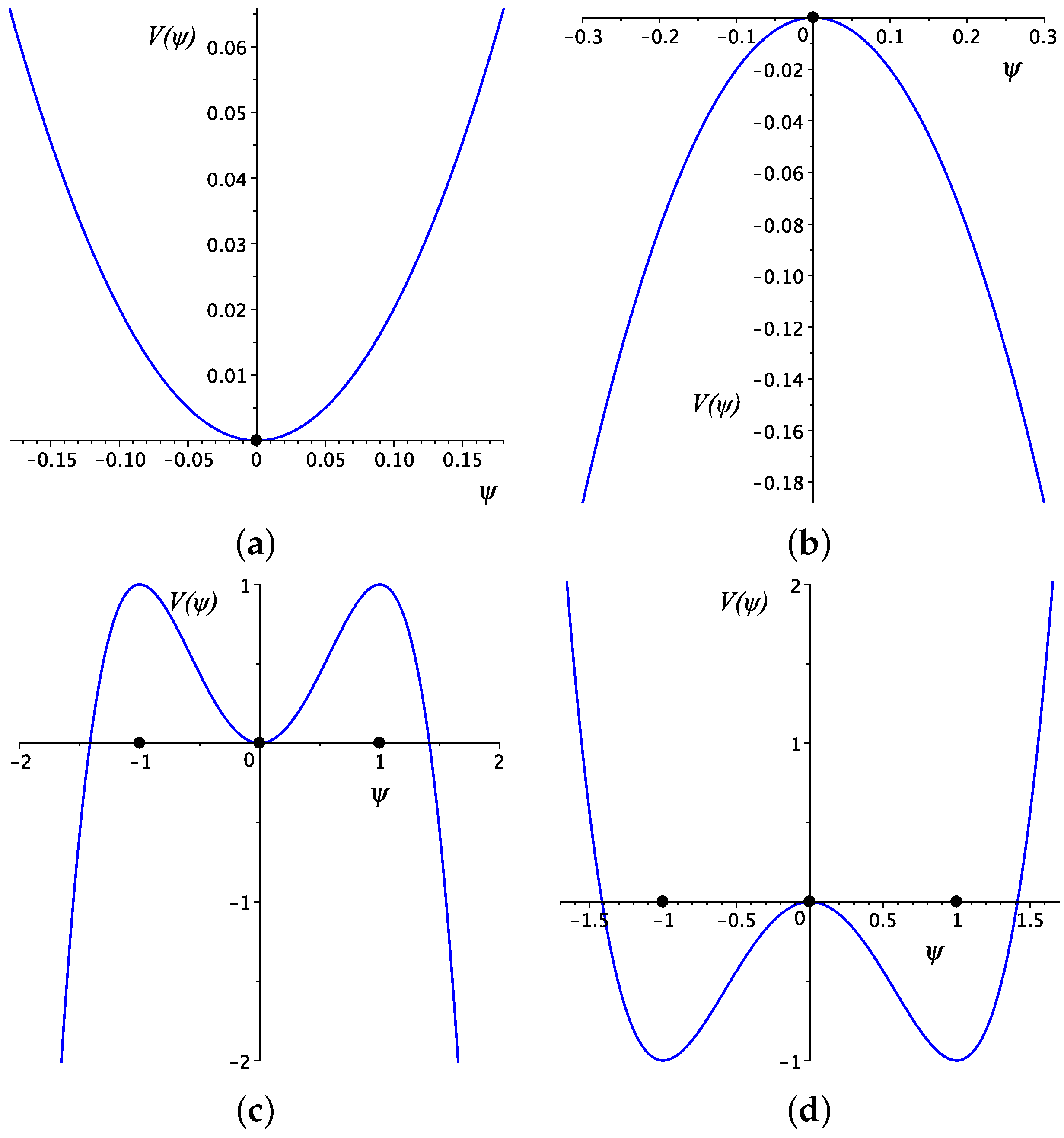
If $({\rho }_1,{\rho }_2)\in {\mathcal{R}}_1$, then $E_0$ is the unique equilibrium point for system (14), and a local minimum for the potential function (16) as illustrated in Figure 1a. Hence, it is a center for the Hamiltonian system (14).

2.

If $({\rho }_1,{\rho }_2)\in {\mathcal{R}}_2$, then system (14) has $E_0$ as the unique equilibrium, and a local maximum for the potential function (16), as illustrated in Figure 1b. Hence, it is a saddle point for the Hamiltonian system (14).

3.

If $({\rho }_1,{\rho }_2)\in {\mathcal{R}}_3$, then system (14) has three equilibrium points $E_{0,1,2}$. As illustrated in Figure 1, $E_0$ is local minimum for the potential (16) while $E_{1,2}$ are local maxima points for the potential (1). Hence, $E_0$ is a center and $E_{1,2}$ are saddle points for the Hamiltonian system (14).

4.

If $({\rho }_1,{\rho }_2)\in {\mathcal{R}}_4$, then there are three equilibrium points $E_{0,1,2}$ for the system (14) with $E_0$ a saddle and $E_{1,2}$ centers.

The phase orbits are the energy levels parameterized by the parameter $\gamma$ and are given by

$${\mathcal{C}}_{\gamma }=\{(\psi ,z)\in {\mathbb{R}}^2:z^2=2{\mathcal{F}}_4\left(\psi \right)\}.$$

(20)

The values of the parameter E at the equilibrium points, which are used to describe the phase portrait for the system (14), are

$${\gamma }_0=V\left(0\right)=0,{\gamma }_1=V(\pm \sqrt{\frac{-{\rho }_1}{2{\rho }_2}})=-\frac{{\rho }_1^2}{4{\rho }_2}.$$

(21)

We provide a short description for the phase portrait of the Hamilton system (14).

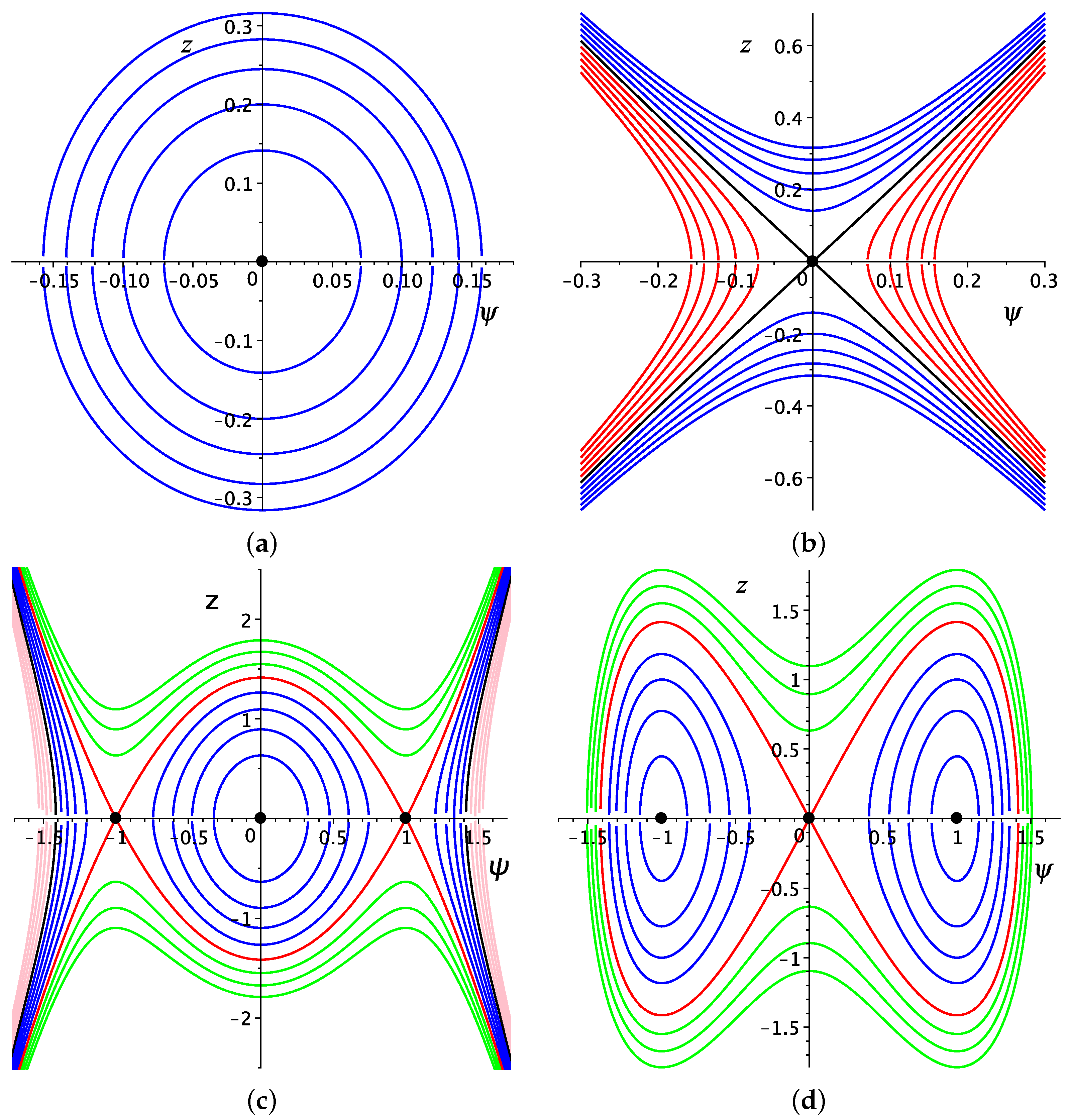
• For $({\rho }_1,{\rho }_2)\in {\mathcal{R}}_1$, the phase portrait consists of a family of bounded periodic orbits ${\mathcal{C}}_{\gamma >0}$ about the center equilibrium point $E_0$, as shown in Figure 2a. These orbits indicate the existence of periodic wave solutions for the system (14).
• For $({\rho }_1,{\rho }_2)\in {\mathcal{R}}_2$, the phase orbits for the system (14) are unbounded, as shown in Figure 2b, where these orbits are color-coded with ${\mathcal{C}}_{\gamma =0}$ shown in black, ${\mathcal{C}}_{\gamma >0}$ in blue, and ${\mathcal{C}}_{\gamma <0}$ in red. These orbits indicate the existence of unbounded wave solutions.
• For $({\rho }_1,{\rho }_2)\in {\mathcal{R}}_3$, the phase portrait for the system (14) is shown in Figure 2c. There is a family of unbound orbits ${\mathcal{C}}_{\gamma >{\gamma }_1}$, shown in green. For $\gamma ={\gamma }_1$, we obtain a heteroclinic orbit, shown in red, connecting the two saddle points $E_{1,2}$ with two unbounded extensions. The heteroclinic orbit indicate the existence of kink (or anti-kink) wave solution and unbounded wave solutions. For $0<\gamma <{\gamma }_1$, there are three families of orbits shown in blue. One is periodic and lies inside the heteroclinic orbit while the others are unbounded. Finally, for $\gamma <0$, we have two unbounded family of orbits in pink while, when $\gamma =0$, there are two unbounded orbits in black, in addition to the equilibrium point $E_0$.
• For $({\rho }_1,{\rho }_2)\in {\mathcal{R}}_4$, all the orbits of the Hamilton system (14) are bounded, as shown in Figure 2d. There are two periodic families of bounded orbits, shown in blue ${\mathcal{C}}_{{\gamma }_1<\gamma <0}$. These families are contained in the homoclinic orbit ${\mathcal{C}}_{\gamma =0}$, shown in red, which provides a solitary solution. For $\gamma >0$, there is a family of super periodic orbits, shown in green. These indicate the existence of the super periodic wave solution.

4. Traveling Wave Solutions

We will use the study of the bifurcation and phase portrait to classify the solutions of the wave solutions Equation (1). We are only concerned with the construction of bounded wave solutions, since unbounded wave solutions are neither desired nor useful in physical applications. Additionally, the way of building these solutions is similar to that of constructing the bounded solutions. The bounded solutions arise from the bounded orbits in the phase plane. With that in mind, we collected the conditions for the existence bounded solutions and their classifications with the following lemma.

Lemma 1.

System (14) has bounded orbits in the following cases

1.

periodic solutions if $({\rho }_1,{\rho }_2,\gamma )\in ({\mathbb{R}}^{+}\times {\mathbb{R}}^{+}\times {\mathbb{R}}^{+})\cup ({\mathbb{R}}^{+}\times {\mathbb{R}}^{-}\times ]0,{\gamma }_1\left[\right)\cup ({\mathbb{R}}^{-}\times {\mathbb{R}}^{+}\times \left(\right]{\gamma }_1,0[\cup ]0,\infty \left[\right))$,

2.

kink (anti-kink) solution if $({\rho }_1,{\rho }_2)\in {\mathbb{R}}^{+}\times {\mathbb{R}}^{-}\times \left\{{\gamma }_1\right\}$,

3.

solitary solution if ${\mathbb{R}}^{-}\times {\mathbb{R}}^{+}\times \left\{0\right\}$.

All other orbits are unbounded.

4.1. Periodic Solutions

There are four types of periodic orbits, as shown in Figure 2a,c,d. We integrated both sides of Equation (12) along the possible interval of real wave propagation.

1.

For $({\rho }_1,{\rho }_2)\in {\mathcal{R}}_1$ and $\gamma >0$, system (14) has a bounded family of periodic orbits, shown in Figure 2a. Each orbit of this family intersects $\psi$ axis at two points, indicating that ${\mathcal{F}}_4\left(\psi \right)$ has two real roots, which denote $\pm u_1$. Thus, we can write ${\mathcal{F}}_4\left(\psi \right)={\rho }_2({\psi }^2-u_1^2)({\psi }^2+u_2^2)$. The interval of the real solution is $\psi \in ]-u_1,u_1[$. Integrating both sides of Equation (12) along this interval, we obtain

$${\int }_0^{\psi }\frac{\mathrm{d}\psi }{\sqrt{(u_1^2-{\psi }^2)({\psi }^2+u_2^2)}}=\pm \sqrt{2{\rho }_2}{\int }_0^{\eta }\mathrm{d}\eta .$$

(22)

Thus, we can obtain a bi-periodic wave solution, given by

$${\psi }_{1,2}\left(\eta \right)=\pm \frac{u_1{u}_2}{\sqrt{u_1^2+u_2^2)}}\mathrm{sd}(\sqrt{2{\rho }_2(u_1^2+u_2^2)}\eta ,\frac{u_1}{\sqrt{u_1^2+u_2^2}}).$$

(23)

This gives us a solution of Equation (1), with the the form

$$\begin{array}{cc}\hfill U_{1,2}(x,y,t)& =\pm \frac{u_1{u}_2}{\sqrt{u_1^2+u_2^2)}}\mathrm{sd}(\sqrt{2{\rho }_2(u_1^2+u_2^2)}[\frac{1}{\alpha }(b_1{x}^{\alpha }+b_2{y}^{\alpha })+b_{3}t],\frac{u_1}{\sqrt{u_1^2+u_2^2}})\hfill \\ \hfill & \times \exp [\mathrm{i}\mathcal{N}(x,y,t)-\sigma \mathbb{G}-{\sigma }^{2}t].\hfill \end{array}$$

(24)

We note that solution (24) is a new solution for Equation (1).

2.

For $({\rho }_1,{\rho }_2)\in {\mathcal{R}}_3$ and $0<\gamma <{\gamma }_1$, system (14) has two types of orbits, shown in blue in Figure 2c one periodic and the other unbounded. An orbit of this family crosses the $\psi -$ axis in four points; hence, ${\mathcal{F}}_4\left(\psi \right)$ has four real roots, $\pm u_3,\pm u_4$, where $0<u_3<u_4$, i.e., ${\mathcal{F}}_4\left(\psi \right)=\sqrt{-{\rho }_2}({\psi }^2-u_3^2)(\psi -u_4^2)$. The interval of real solutions is $\psi \in ]-\infty ,-u_4[\cup ]-u_3,u_3[\cup ]u_4,\infty [$. We will only consider $\psi \in ]-u_3,u_3[$, avoiding the investigation of the unbounded solutions at present. Integrating both sides of Equation (12) gives

$${\int }_{-u_3}^{\psi }\frac{\mathrm{d}\psi }{\sqrt{(u_3^2-{\psi }^2)(u_4^2-{\psi }^2)}}=\pm \sqrt{-2{\rho }_2}{\int }_0^{\eta }\mathrm{d}\eta .$$

(25)

This equation gives

$${\psi }_{3,4}\left(\eta \right)=\pm u_3\mathrm{sn}(u_4\sqrt{-2{\rho }_2}\eta ,\frac{u_3}{u_4}).$$

(26)

Thus, Equation (1) has a novel solution in the form

$$U_{3,4}(x,y,t)=\pm u_3\mathrm{sn}(u_4\sqrt{-2{\rho }_2}[\frac{1}{\alpha }(b_1{x}^{\alpha }+b_2{y}^{\alpha })+b_{3}t],\frac{u_3}{u_4})\exp [\mathrm{i}\mathcal{N}(x,y,t)-\sigma \mathbb{G}-{\sigma }^{2}t].$$

(27)

3.

If $({\rho }_1,{\rho }_2)\in {\mathcal{R}}_4$, system (14) has two families of periodic orbits, as shown in blue and green in Figure 2d. These families are:

• For ${\gamma }_1<\gamma <0$, the system (14) has a family of periodic orbits, shown in blue, each of which cuts the $\psi -$ axis at four points, showing that ${\mathcal{F}}_4\left(\psi \right)$ has four real roots, denoted as $\pm u_5,\pm u_6$, where $0<u_5<u_6$. Thus, we can write ${\mathcal{F}}_4\left(\psi \right)={\rho }_2(u_5^2-{\psi }^2)({\psi }^2-u_6^2)$. The interval of the real solution is $\psi \in ]-u_6,-u_5[\cup ]u_5,u_6[$, with $\psi \in ]-u_6,-u_5[$ corresponding to a periodic family on the left of the oval homoclinic orbit, shown in red, and $\psi \in ]u_5,u_6[$ to a periodic family lying to the right of the oval homoclinic orbit. We will only consider the one on the left, as the calculation for the other is similar. The integration of both sides of Equation (12) along the interval $\psi \in ]-u_6,-u_5[$ shows

  $${\int }_{-u_6}^{\psi }\frac{\mathrm{d}\psi }{\sqrt{(u_5^2-{\psi }^2)({\psi }^2-u_6^2)}}=\pm \sqrt{2{\rho }_2}{\int }_0^{\eta }\mathrm{d}\eta .$$

  (28)
  From which it follows that

  $${\psi }_{5,6}\left(\eta \right)=\pm u_6\mathrm{dn}(u_6\sqrt{2{\rho }_2}\eta ,\sqrt{1-\frac{u_5^2}{u_6^2}}).$$

  (29)
  Therefore, Equation (1) has the solution

  $$\begin{array}{cc}\hfill U_{5,6}& =\pm u_6\mathrm{dn}(u_6\sqrt{2{\rho }_2}[\frac{1}{\alpha }(b_1{x}^{\alpha }+b_2{y}^{\alpha })+b_{3}t],\sqrt{1-\frac{u_5^2}{u_6^2}})\exp [\mathrm{i}\mathcal{N}(x,y,t)-\sigma \mathbb{G}-{\sigma }^{2}t].\hfill \end{array}$$

  (30)
  Solution (33) is a new solution for Equation (1).
• For $\gamma >0$, there is a family of super-periodic orbits, shown in green. A member of this family intersects $\psi -$ axis at two points, and so ${\mathcal{F}}_4\left(\psi \right)$ has two real zeros, namely, $\pm u_7$, and two purely imaginary roots $\pm i{u}_8$. Thus, ${\mathcal{F}}_4\left(\psi \right)={\rho }_2(u_7^2-{\psi }^2)(u_8^2+{\psi }^2)$. The interval of the real solution is $\psi \in ]-u_7,u_7[$. By integrating both sides of Equation (12), we obtain

  $${\int }_{u_7}^{\psi }\frac{\mathrm{d}\psi }{\sqrt{(u_7^2-{\psi }^2)({\psi }^2+u_8^2)}}=\pm \sqrt{2{\rho }_2}{\int }_0^{\eta }\mathrm{d}\eta .$$

  (31)
  From the above equation, we can obtain

  $${\psi }_7=u_7\mathrm{cn}(\sqrt{2{\rho }_2(u_7^2+u_8^2)}\eta ,\frac{u_7}{\sqrt{u_7^2+u_8^2}}).$$

  (32)
  Therefore, Equation (12) has the solution

  $$\begin{array}{cc}\hfill U_7(x,y,t)& =u_7\mathrm{cn}\left(\sqrt{2{\rho }_2(u_7^2+u_8^2)}\right[\frac{1}{\alpha }(b_1{x}^{\alpha }+b_2{y}^{\alpha })\hfill \\ \hfill & +b_{3}t],\frac{u_7}{\sqrt{u_7^2+u_8^2}})\exp [\mathrm{i}\mathcal{N}(x,y,t)-\sigma \mathbb{G}-{\sigma }^{2}t].\hfill \end{array}$$

  (33)

The last solution is a novel solution for Equation (1).

4.2. Kink(Anti-Kink) Solutions

System (14) has a kink or anti-kink solution if $({\rho }_1,{\rho }_2)\in {\mathcal{R}}_3$ and $\gamma ={\gamma }_1$, since it has a heteroclinic phase orbit connecting the two saddle points $E_{1,2}$, as shown in Figure 2c. The interval of real solutions for the Hamilton system (14) is $\psi \in ]-\sqrt{\frac{-{\rho }_1}{2{\rho }_2}},\sqrt{\frac{-{\rho }_1}{2{\rho }_2}}[$. Integrating both sides of Equation (12) gives

$${\int }_0^{\psi }\frac{\mathrm{d}\psi }{{\psi }^2+\frac{{\rho }_1}{2{\rho }_2}}=\pm \sqrt{-2{\rho }_2}{\int }_0^{\eta }\mathrm{d}\eta .$$

(34)

This shows that

$$\psi \left(\eta \right)=\pm \sqrt{\frac{-{\rho }_1}{2{\rho }_2}}\tanh \sqrt{-2{\rho }_2}\eta .$$

(35)

Thus, Equation (1) has a solution in the form

$$U_8(x,y,t)=\pm \sqrt{\frac{-{\rho }_1}{2{\rho }_2}}\tanh \sqrt{-2{\rho }_2}[\frac{1}{\alpha }(b_1{x}^{\alpha }+b_2{y}^{\alpha })+b_{3}t]\exp [\mathrm{i}\mathcal{N}(x,y,t)-\sigma \mathbb{G}-{\sigma }^{2}t].$$

(36)

Solution (36) is a novel solution for Equation (1).

4.3. Solitary Solution

System (14) has two homoclinic orbits that connect the saddle point $O=(0,0)$ to itself if $({\rho }_1,{\rho }_2)\in {\mathcal{R}}_4$ and $\gamma =0$, as shown in Figure 2d in red. The two orbits are the right and the left ovals in the figure. We calculate the solution corresponding to the left oval. The interval of real solution is $\psi \in ]-\sqrt{\frac{-{\rho }_1}{{\rho }_2},0}[$. Integrating both sides of Equation (12), we obtain

$$\psi \left(\eta \right)=\pm \sqrt{\frac{-{\rho }_1}{{\rho }_2}}\mathrm{sech}\sqrt{-2{\rho }_1}\eta .$$

(37)

Hence, Equation (1) has the solution

$$U_9(x,y,t)=\pm \sqrt{\frac{-{\rho }_1}{{\rho }_2}}\mathrm{sech}[\sqrt{-2{\rho }_1}[\frac{1}{\alpha }(b_1{x}^{\alpha }+b_2{y}^{\alpha })+b_{3}t]\exp [\mathrm{i}\mathcal{N}(x,y,t)-\sigma \mathbb{G}-{\sigma }^{2}t].$$

(38)

The solution (38) is new.

Some remarks on Equation (1) and the obtained solutions are provided below.

Remark 1.

From the solutions to Equation (1) we have the following:

1.

In the absence of the noise $\sigma =0$, the stochastic fractional-space partial differential Equation (1) becomes a fractional-space partial differential equation. Thus, setting $\sigma =0$ in the solutions (24), (27), (33), (32), (36), and (38), we obtain new solutions for the latter equation.

2.

Equation (1) approaches the stochastic partial differential equation when the fractional-order derivative α approaches one. Thus, when $\alpha \to 1$, the solutions (24), (27), (33), (32), (36), and (38) converge to new solutions for the stochastic equation.

3.

When $\alpha \to 1$ and $\sigma =0$, Equation (1) becomes a classical partial differential equation. Thus, the solutions (24), (27), (33), and (32) yield new solutions to the classical equations.

In the following remark, we look at the degeneracy of the Jacobi elliptic solutions through the transmission between the phase orbits. This remark confirms the correctness and consistency of the obtained solutions.

Remark 2.

Depending on the value of the parameter γ, we have the following:

1.

The periodic family of orbits around the center point O shown in Figure 2a degenerates to the center point $O=(0,0)$ when $\gamma \to 0$, which means that $u_1,u_2\to 0$ when $\gamma \to 0$. Thus, the solution (24) approaches $U_{1,2}=0$, which are the $\psi -$ coordinates of the equilibrium point O.

2.

The periodic family of orbits around the center point O shown in blue in Figure 2c degenerates into:

• The center point O when $\gamma \to 0$, which means that $u_3,u_4\to 0$. Thus, the solution (27) approaches $U_{3,4}=0$, the $\psi -$ coordinates of the equilibrium point O.
• The hetroclinic orbit shown in red in Figure 2c when $\gamma \to {\gamma }_1$ and then $u_3\to \sqrt{\frac{-{\rho }_1}{2{\rho }_2}}$ and $u_4\to -\sqrt{\frac{-{\rho }_1}{2{\rho }_2}}$. Hence, the solution (27) approaches the solution (36).

3.

The periodic family of orbits shown in blue in Figure 2d will approach the homoclinic orbit, shown in red, when $\gamma \to 0$ and therefore, $u_5\to 0,u_6\to \sqrt{\frac{-{\rho }_1}{{\rho }_2}}$. Thus, the solution (33) approaches the solution (38).

4.

The family of super-periodic orbits in green in Figure 2d will approach the two homoclinic orbits in red when $\gamma \to 0$; therefore, $u_7\to \sqrt{\frac{-{\rho }_1}{{\rho }_2}},u_8\to 0$. Hence, the solution (32) will approach the solution (38).

5. Graphic Representation

In this section, we explore the influence of noise $\sigma$ on some of the solutions obtained above. We will use various graphical representations to illustrate the impact of the stochastic Wiener process on the solutions. Initially, we assume that parameters $b_1=0.2,b_2=0.4,b_3=0.5$, with the values of ${\rho }_1,{\rho }_2$, fall in the regions of (19) corresponding to the solutions given in Section 4, and for different noise values $\sigma$.

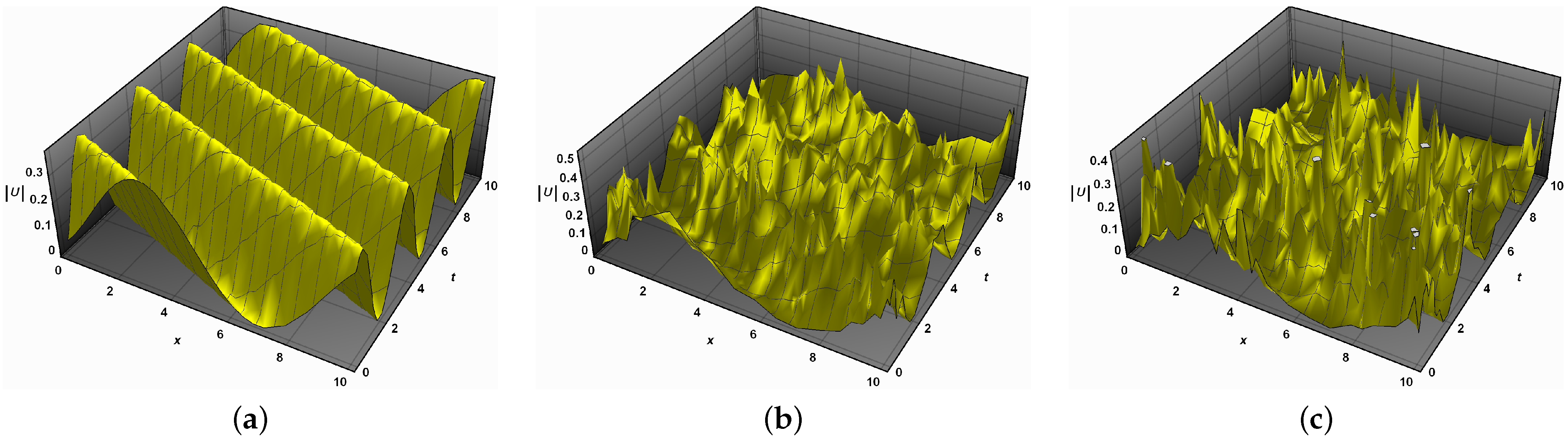
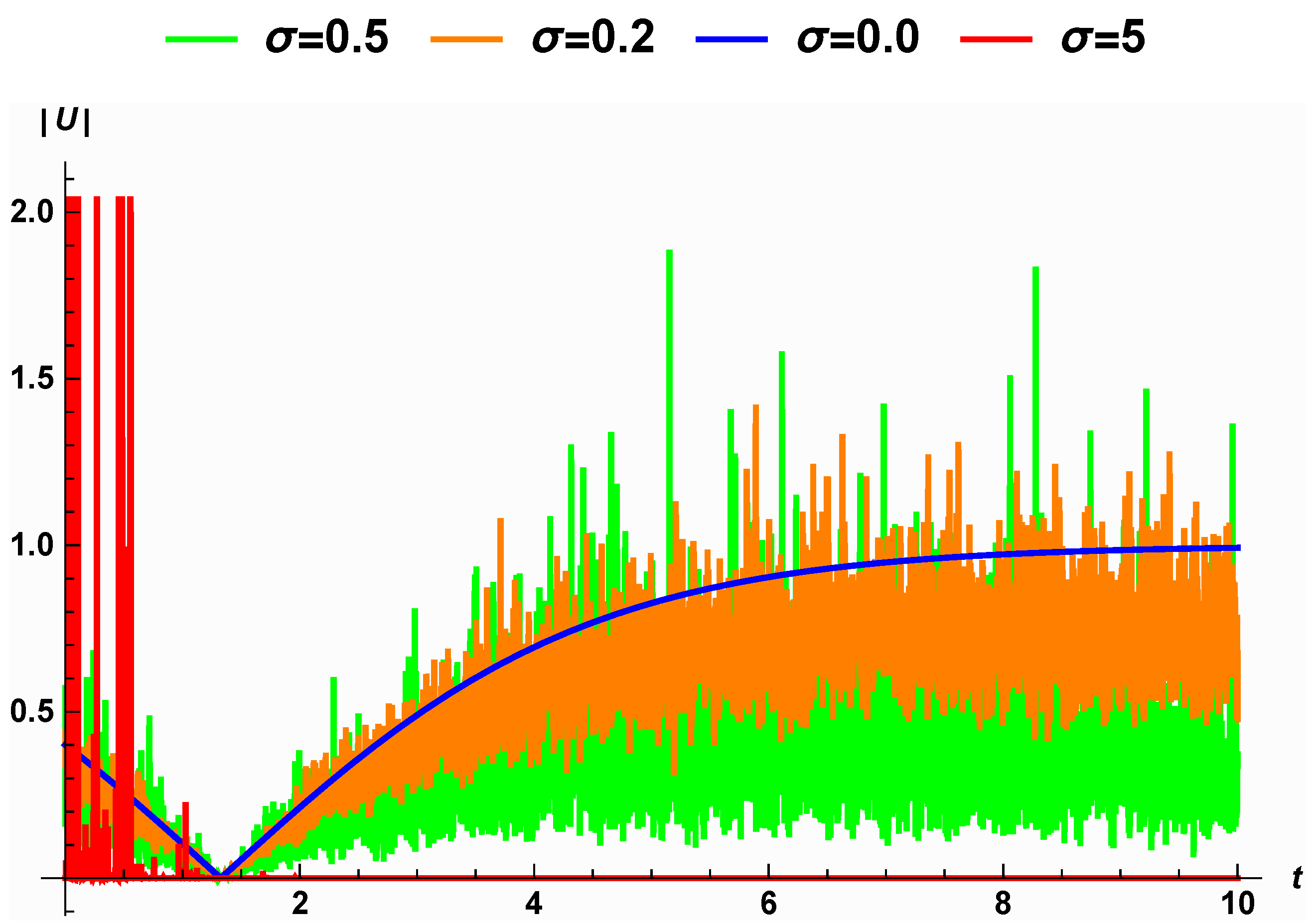
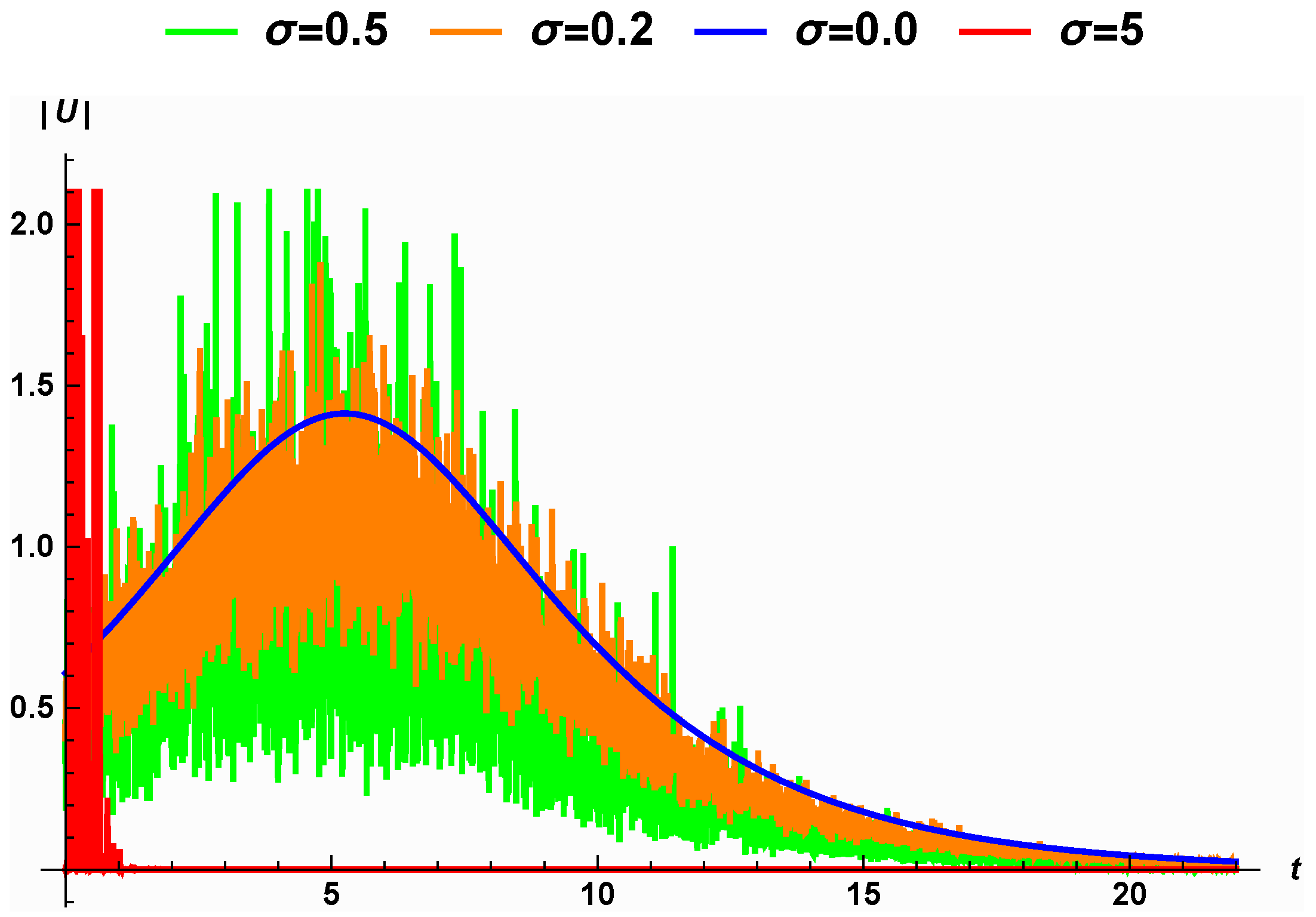
• The effect of the noise on the solution (24) for the noise values $\sigma =0.0,\sigma =0.2$, and $\sigma =0.5$ is shown in Figure 3. Figure 3a shows the solution of (24), which is periodic in the absence of the noise ($\sigma =0$). The introduction of noise generates disturbances in the solution, as shown in Figure 3b,c. In Figure 4, we present a 2D representation of the solution of (24). When $\sigma =0$, the solution, shown in blue, is periodic. Increasing the noise causes increasing disturbances to the periodic solution. Additionally, the 2D representation of the surface, shown in red in Figure 4, shows that when the noise $\sigma$ increases, the surface becomes significantly flatter after minor transit patterns.
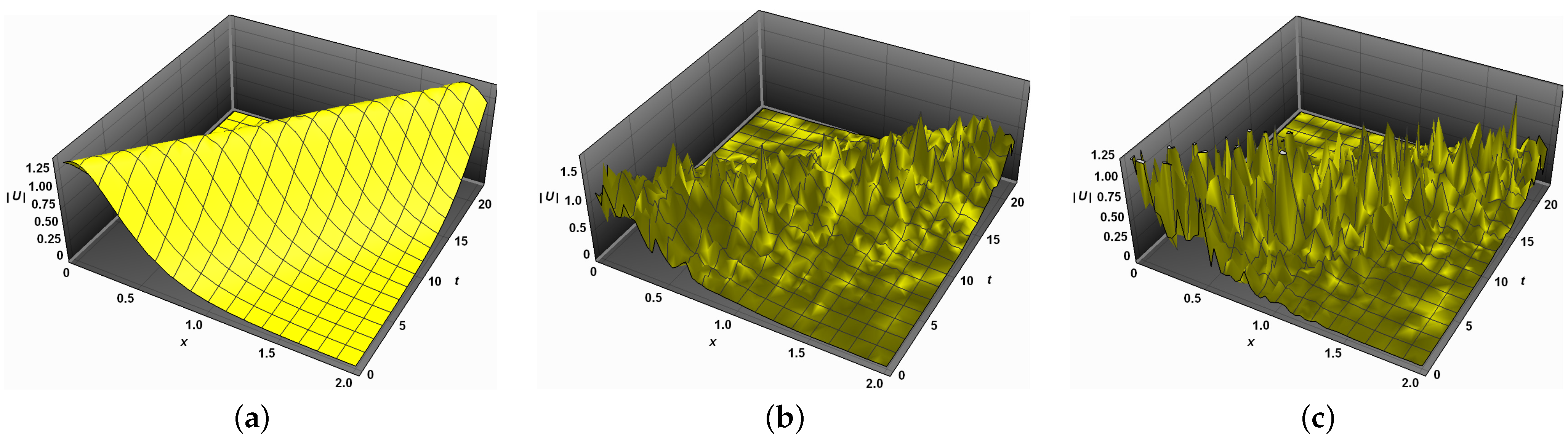
• The classical version of Equation (1) with zero noise and integer fractional order has a kink solution (36), as shown in Figure 5a, and its 2D representation is shown in blue in Figure 6. Figure 5b,c show the changes in the shape of the solution (36) due to small noise values $\sigma =0.2,\sigma =0.4$, and their 2D representations clarify these changes. For larger noise values, the surface that characterizes the wave solution (36) become significantly flat, as shown in red by Figure 6.
• In the absence of noise $\sigma =0$ and fractional order, $\alpha \to 1$, Equation (1) has one soliton solution, as shown in Figure 7a, with its 2D representation appearing in blue in Figure 8. For low noise values $\sigma =0.2$ and $\sigma =0.5$, the surface representing the solution (38) has some disturbances, which increasing with increases in noise $\sigma$, as shown in Figure 7b,c. This is also shown in Figure 8, presenting a 2D representation of the solution. For large noise values $\sigma$, the surface representing the solution (38) becomes flat, as shown in Figure 8 in red. Thus, it is clear that the stochastic Wiener process influences the solution (38) of Equation (1) and also stabilizes the solutions at around zero.

Thus, the graphical representation of the surfaces representing the wave solutions (24), (36), and (38) have some disturbances due to the presence of noise $\sigma$, and these surfaces become significantly flatter as the value of the noise increases. Thus, we can conclude that adding a stochastic Wiener process stabilizes the solutions at around zero.

6. Discussion

We analyzed the space-fractional nonlinear Schrödinger equation with multiplicative white noise. This equation was transformed to a one-degree-of-freedom Hamiltonian system. The qualitative theory of the resulting planar dynamical system was applied to study the bifurcation and the phase portrait of the reduced system. A brief description of the phase plane was given. In Lemma 1, we listed the conditions leading to bounded wave solutions. We constructed some new solutions leading to periodic, solitary, and kink(anti-kink) wave solutions. From these solutions, we obtained new solutions for the space-fractional version of this equation in the absence of noise, and for its stochastic version when the fractional order derivative tends to one. We studied the degeneracy of the solutions due to the transition between the phase orbits. This study shows the consistency and correctness of the solutions. The 2D and 3D graphical representations of some solutions are included for different noise values. The multiplicative white noise’s effect on the solutions was addressed. As the noise increases, the surface represented by the wave solution becomes significantly flatter, leading us to the conclusion that introducing a stochastic Wiener process stabilizes the solutions at around zero.