Spectral Collocation Approach via Normalized Shifted Jacobi Polynomials for the Nonlinear Lane-Emden Equation with Fractal-Fractional Derivative

Abstract

Herein, we adduce, analyze, and come up with spectral collocation procedures to iron out a specific class of nonlinear singular Lane–Emden (LE) equations with generalized Caputo derivatives that appear in the study of astronomical objects. The offered solution is approximated as a truncated series of the normalized shifted Jacobi polynomials under the assumption that the exact solution is an element in $L_2$. The spectral collocation method is used as a solver to obtain the unknown expansion coefficients. The Jacobi roots are used as collocation nodes. Our solutions can easily be a generalization of the solutions of the classical LE equation, by obtaining a numerical solution based on new parameters, by fixing these parameters to the classical case, we obtain the solution of the classical equation. We provide a meticulous convergence analysis and demonstrate rapid convergence of the truncation error concerning the number of retained modes. Numerical examples show the effectiveness and applicability of the method. The primary benefits of the suggested approach are that we significantly reduce the complexity of the underlying differential equation by solving a nonlinear system of algebraic equations that can be done quickly and accurately using Newton’s method and vanishing initial guesses.

1. Introduction

The Lane–Emden equation appears in astrophysics and is a dimensionless form of Poisson’s equation for the gravitational potential of a Newtonian self-gravitating, spherically symmetric, polytropic fluid. This equation was first named in 1870 after astrophysicists Jonathan Homer Lane and Robert Emden [1]. The classical form of the LE equations is

$${\theta }^{″}\left(\xi \right)+2{\xi }^{-1}{\theta }^{\prime }\left(\xi \right)+{\theta }^n\left(\xi \right)=0,$$

subject to the standard boundary conditions

$$\theta \left(0\right)=1,{\theta }^{\prime }\left(0\right)=0,$$

where $\xi$ is an independent variable representing the dimensionless radius, $\theta \left(\xi \right)$ is the density function, and thus the pressure $\rho ={\rho }_c{\theta }^n$ is the central density, and the number n denotes the polytropic index. This equation has no closed-form solution in general; for the three cases $n=0,1,$ and 5, we have the following closed-form solutions

$$\theta \left(\xi \right)={\theta }_0\left(\xi \right)=1-\frac{{\xi }^2}{6},\theta \left(\xi \right)={\theta }_1\left(\xi \right)=\frac{sin\xi }{\xi },\theta \left(\xi \right)={\theta }_5\left(\xi \right)=\frac{1}{\sqrt{1+\frac{1}{3}{\xi }^2}}.$$

The LE equation describes the dimensionless density distribution in an isothermal gas sphere and plays an important role in galactic dynamics and in the theory of stellar structure and evolution [2]. The LE equation was further investigated with more general nonlinear terms of the form $f(\xi ,\theta )$ in both classical and fractional cases, and recently, many numerical and analytical methods have been applied to handle this LE equation, for instance, the high-order wavelets method [3], the Bernoulli wavelets method [4], the Monte Carlo method [5], the Taylor series method [6], the Morlet wavelets neural network method [7], the Bessel polynomials method [8], the neuro-evolution approach [9], the power series method [10], the implicit method [11], the composite Chebyshev finite difference method [12], the computational approximate method [13], the collocation method [14], and the tau and Galerkin methods [15,16]. Within our study, we use the typical shifted Jacobi collocation method; the collocation method is very important in solving many types of differential problems [17,18,19,20].

The study of the calculus of nonintegral order generalizes the concept of differentiation and integration in the classical sense; it takes into consideration the memory effect of the phenomena, which extensively helps to manipulate real-life phenomena that cannot be precisely characterized by the classical differentiation definition. For the purpose of establishing a formula for the fractional order, Riemann used a generalization of a Taylor series and invented an arbitrary complementary function. This idea motivated Caputo, in 1967, to precisely define the most significant definition of the fractional derivatives, which was named Caputo fractional derivative [21]. Later, some seminal textbooks discussed in-depth these definitions in the theory of fractional differential equations, for instance, [22,23].

Recently, a more general helpful generalization of fractional integral operators was introduced and used to describe the derivatives with more nonlocality properties by introducing a fractional-order integral of a given function related to another function [24,25,26]. This definition and its promising properties allowed researchers to study the availability of spectral methods to handle the LE equation in a more general form by replacing the term ${\theta }^{\prime }$ with the fractional derivative in the fractal–fractional sense and replacing the term ${\theta }^n$ with a nonlinear quadratic function in $\theta$.

Orthogonal Jacobi polynomials [27,28,29] have many lucrative fixtures that make them very important in the numerical solution of different kinds of differential problems, primarily via spectral methods. The most important features of Jacobi polynomials are orthogonality, exponential accuracy, and the existence of two parameters that may affect the variety of the approximate solutions, which make these polynomials appropriate for solving diverse problems. In our work, we use the orthonormal Jacobi polynomials, which help us construct a spectral collocation algorithm to handle the nonlinear fractal–fractional LE equation.

It is worth reporting that, within this study, we handled a more general form of the LE equation with a generalized fractional derivative, which helps the interpretation of the solutions with a wide temporal capture of the phenomena of astronomical objects. As far as we know, this is the first time in the literature that the orthonormal shifted Jacobi polynomials are used as basis functions to solve spectrally the LE equation with generalized a fractal–fractional derivative with a detailed study of the truncation error. The main advantages of the proposed methods are that we drastically convert the underlying problem to that of solving a nonlinear system of algebraic equations that can be easily solved via Newton’s method with vanishing initial guesses, with stunted computational time; for recent advances in the field of numerical treatment of related models, the interested readers are referred to [30,31,32].

In bullet points, the main contributions of this study are as follows:

• We suggest orthonormal Jacobi polynomials as the basis of the solution.
• We build and prove all derivatives needed within the algorithm.
• We construct and implement a collocation scheme to handle the nonlinear LE equation with a generalized fractional derivative.
• We study in detail the truncation error of the method.
• We perform some numerical examples with comparisons, when possible, with other existing methods.

This manuscript is organized as follows: in Section 2, we report all needed definitions, and state and prove very essential lemmas and theorems. Section 3 is devoted to the structure of the spectral collocation algorithm for handling the generalized fractal–fractional LE equation. In Section 4, we give an upper estimate of the truncation error. In Section 5, we perform some numerical experiments with comparisons to test and validate the method; some concluding remarks are reported in Section 6.

2. Preliminaries

In this section, the essential definitions of the generalized Caputo fractional operators and some relevant properties of the orthonormal normalized Jacobi polynomials are reported, which are subsequently of important use.

2.1. Generalized Caputo Type Fractional Derivative

Definition 1

([24]). Let ρ be a positive constant, the generalized fractional integral of a continuous function $\phi \left(z\right)$ of order $\alpha >0$ is defined by

$${\displaystyle I^{\alpha ,\rho }\phi \left(z\right)=\frac{{\rho }^{1-\alpha }}{\mathsf{\Gamma }\left(\alpha \right)}{\int }_0^z{n}^{\rho -1}{(z^{\rho }-n^{\rho })}^{\alpha -1}\phi \left(n\right)dn.}$$

Definition 2

([24]). Let $\rho >0,s-1<\alpha <s$, and $s=⌈\alpha ⌉$; the generalized Caputo fractional derivative of order α of a function $\phi \left(z\right)\in C^s[0,1]$ is defined as

$${\displaystyle D^{\alpha ,\rho }\phi \left(z\right)=\frac{{\rho }^{\alpha -s+1}}{\mathsf{\Gamma }(s-\alpha )}{\int }_0^z{n}^{\rho -1}{(z^{\rho }-n^{\rho })}^{s-\alpha -1}{\left(n^{1-\rho }\frac{d}{dn}\right)}^s\phi \left(n\right)dn.}$$

The generalized Caputo fractional derivative satisfies:

$$D^{\alpha ,\rho }\mathrm{const}.=0,$$

if $\alpha \in (s-1,s),\ell >s-1$, then

$$D^{\alpha ,\rho }{z}^{\rho \ell }=\left\{\begin{array}{c}\begin{array}{cc}{\rho }^{\alpha }\frac{\mathsf{\Gamma }(\ell +1)}{\mathsf{\Gamma }(\ell +1-\alpha )}{z}^{\rho (\ell -\alpha )},& \ell \in {\mathbb{N}}_0,\ell \ge ⌈\alpha ⌉,\\ 0,& \ell \in {\mathbb{N}}_0,\ell <⌈\alpha ⌉.\end{array}\hfill \end{array}\right.$$

It should be noted here that, in Definition 2, if we set $\rho =1$, we directly obtain the usual Caputo derivative.

2.2. An Account of Shifted Orthonormal Normalized Jacobi Polynomials

The shifted normalized Jacobi polynomials on the interval $[0,1]$ associated with the real parameters $(a,b>-1,)$ are a sequence of polynomials $\{{\varphi }_m^{(a,b)}(2t-1):m=0,1,2,\dots \}$ that can be defined as

$${\varphi }_m^{(a,b)}(2t-1)=\frac{m!\mathsf{\Gamma }(a+1)}{\mathsf{\Gamma }(a+m+1)}{P}_m^{(a,b)}(2t-1),$$

(1)

where $P_m^{(a,b)}(2t-1)$ are the shifted classical Jacobi polynomials.

Suppose that

$${\psi }_m^{(a,b)}\left(t\right)=\sqrt{h_m}{\varphi }_m^{(a,b)}(2t-1),$$

(2)

where

$$h_m=\frac{(a+b+2m+1)\mathsf{\Gamma }(a+m+1)\mathsf{\Gamma }(a+b+m+1)}{m!\mathsf{\Gamma }{(a+1)}^2\mathsf{\Gamma }(b+m+1)}.$$

(3)

The orthonormality relation of ${\psi }_m^{(a,b)}\left(t\right)$ is given by

$${\int }_0^1{\psi }_n^{(a,b)}\left(t\right){\psi }_m^{(a,b)}\left(t\right)\omega \left(t\right)dt={\delta }_{n,m},$$

(4)

where $\omega \left(t\right)={(1-t)}^a{t}^b$ and

$${\delta }_{n,m}=\left\{\begin{array}{cc}1,\hfill & \mathrm{if}n=m,\hfill \\ 0,\hfill & \mathrm{if}n\ne m.\hfill \end{array}\right.$$

(5)

The power-form representation of ${\psi }_m^{(a,b)}\left(t\right)$ can be represented as

$${\psi }_j^{(a,b)}\left(t\right)=\sum _{r=0}^j\frac{{(-1)}^{j+r}(a+b+2j+1)\mathsf{\Gamma }(a+b+j+r+1)}{\sqrt{h_j}r!\mathsf{\Gamma }(a+1)(j-r)!\mathsf{\Gamma }(b+r+1)}{t}^r.$$

(6)

Moreover, the inversion formula of ${\psi }_m^{(a,b)}\left(t\right)$ is

$$t^p=\sum _{r=0}^p{B}_{r,p}{\psi }_r^{(a,b)}\left(t\right),$$

(7)

where

$$B_{r,p}=\frac{(a+b+2r+1){(a+1)}_r\mathsf{\Gamma }(b+p+1){(p-r+1)}_r\mathsf{\Gamma }(a+b+r+1)}{\sqrt{h_r}r!\mathsf{\Gamma }(b+r+1)\mathsf{\Gamma }(a+b+p+r+2)}.$$

(8)

Lemma 1.

For all nonnegative integers i and j, the following linearization formula is valid [33]

$${\psi }_i^{(a,a+1)}\left(t\right){\psi }_j^{(a,a+1)}\left(t\right)=\sum _{p=\left|i-j\right|}^{i+j}\sqrt{\frac{h_i{h}_j}{h_p}}{\chi }_{p,a,i,j}{\psi }_p^{(a,a+1)}\left(t\right),$$

(9)

where

$$\begin{array}{cc}\hfill {\chi }_{p,a,i,j}=& \frac{2^{2a+1}i!j!\mathsf{\Gamma }(a+1)}{\sqrt{\pi }\mathsf{\Gamma }\left(a+\frac{3}{2}\right)\mathsf{\Gamma }(i+2a+2)\mathsf{\Gamma }(j+2a+2)}\hfill \\ & \times \left\{\begin{array}{cc}\frac{\mathsf{\Gamma }\left(\frac{1}{2}(i+j-p+3)+a\right)\mathsf{\Gamma }\left(\frac{1}{2}(i-j+p+3)+a\right)\mathsf{\Gamma }\left(\frac{1}{2}(-i+j+p+3)+a\right)\mathsf{\Gamma }\left(\frac{1}{2}(i+j+p+4a+4)\right)}{\mathsf{\Gamma }\left(\frac{1}{2}(i+j-p+2)\right)\mathsf{\Gamma }\left(\frac{1}{2}(i-j+p+2)\right)\mathsf{\Gamma }\left(\frac{1}{2}(-i+j+p+2)\right)\mathsf{\Gamma }\left(\frac{1}{2}(i+j+p+3)+a\right)},\hfill & if(i+j-p)even\hfill \\ \\ -\frac{\mathsf{\Gamma }\left(\frac{1}{2}(i+j-p)+a+1\right)\mathsf{\Gamma }\left(\frac{1}{2}(i-j+p+2)+a\right)\mathsf{\Gamma }\left(\frac{1}{2}(-i+j+p+2)+a\right)\mathsf{\Gamma }\left(\frac{1}{2}(i+j+p+4a+5)\right)}{\mathsf{\Gamma }\left(\frac{1}{2}(i+j-p+1)\right)\mathsf{\Gamma }\left(\frac{1}{2}(i-j+p+1)\right)\mathsf{\Gamma }\left(\frac{1}{2}(-i+j+p+1)\right)\mathsf{\Gamma }\left(\frac{1}{2}(i+j+p+4)+a\right)},\hfill & otherwise.\hfill \end{array}\right.\hfill \end{array}$$

(10)

The generalized hypergeometric function is defined by

$${}_r{F}_s\left.\left(\begin{array}{c}{p}_1,p_2,\cdots ,p_r\\ q_1,q_2,\cdots ,q_s\end{array}\right|t\right)=\sum _{n=0}^{\infty }\frac{{\left(p_1\right)}_n{\left(p_2\right)}_n\cdots {\left(p_r\right)}_n}{{\left(q_1\right)}_n{\left(q_2\right)}_n\cdots {\left(qs\right)}_n}\frac{t^n}{n!}.$$

(11)

Theorem 1

([34]). The qth derivative of ${\varphi }_n^{(a,b)}\left(t\right)$ is given explicitly by

$$D^q{\varphi }_n^{(a,b)}\left(t\right)=\sum _{i=0}^{n-q}{\lambda }_{i,n,q}^{(a,b)}{\varphi }_i^{(a,b)}\left(t\right),$$

(12)

where

$$\begin{array}{cc}\hfill {\lambda }_{i,n,q}^{(a,b)}& =\frac{2^{-q}n!\mathsf{\Gamma }(a+b+i+1){(a+b+n+1)}_q{(a+i+q+1)}_{-i+n-q}{(a+b+n+q+1)}_i}{i!(-i+n-q)!\mathsf{\Gamma }(a+b+2i+1){(a+i+1)}_{n-i}}\hfill \\ & \times {}_3{F}_2\left.\left(\begin{array}{c}i-n+q,a+b+i+n+q+1,a+i+1\\ a+i+q+1,a+b+2i+2\end{array}\right|1\right).\hfill \end{array}$$

(13)

Corollary 1.

The first derivative of ${\psi }_i^{(a,b)}\left(t\right)$ is given explicitly by

$$\frac{d{\psi }_i^{(a,b)}\left(t\right)}{dt}=\sum _{s=0}^{i-1}{\theta }_{s,i}^{(a,b)}{\psi }_s^{(a,b)}\left(t\right),$$

(14)

where

$$\begin{array}{cc}\hfill {\theta }_{s,i}^{(a,b)}& =\frac{i!\sqrt{h_i}\mathsf{\Gamma }(1+a+b+s)(a+b+i+1){(a+s+2)}_{-s+i-1}{(a+b+i+2)}_s}{s!\sqrt{h_s}(-s+i-1)!\mathsf{\Gamma }(1+a+b+2s){(a+s+1)}_{i-s}}\hfill \\ & \times {}_3{F}_2\left.\left(\begin{array}{c}a+s+1,s-i+1,a+b+s+i+2\\ a+s+2,a+b+2s+2\end{array}\right|1\right).\hfill \end{array}$$

(15)

Corollary 2.

The second derivative of ${\psi }_i^{(a,b)}\left(t\right)$ is given explicitly by

$$\frac{d^2{\psi }_i^{(a,b)}\left(t\right)}{d{t}^2}=\sum _{s=0}^{i-2}{\mu }_{s,i}^{(a,b)}{\psi }_s^{(a,b)}\left(t\right),$$

(16)

where

$$\begin{array}{cc}\hfill {\mu }_{s,i}^{(a,b)}& =\frac{i!\sqrt{h_i}\mathsf{\Gamma }(a+b+s+1){(a+b+i+1)}_2{(a+s+3)}_{-s+i-2}{(a+b+i+3)}_s}{s!\sqrt{h_s}(-s+i-2)!\mathsf{\Gamma }(a+b+2s+1){(a+s+1)}_{i-s}}\hfill \\ & \times {}_3{F}_2\left.\left(\begin{array}{c}a+s+1,s-i+2,a+b+s+i+3\\ a+s+3,a+b+2s+2\end{array}\right|1\right).\hfill \end{array}$$

(17)

Proof.

The proof of Corollaries 1 and 2 are a direct result from using the definition of ${\psi }_i^{(a,b)}\left(t\right)$ along with Theorem 1.    □

Corollary 3.

The following relation is valid for $\rho >0$ and $0<\beta <1$

$$D^{\beta ,\rho }{t}^m={\rho }^{\beta }\frac{\mathsf{\Gamma }\left(\frac{m}{\rho }+1\right)}{\mathsf{\Gamma }\left(\frac{m}{\rho }-\beta +1\right)}{t}^{m-\beta \rho },\forall m\ge 1.$$

(18)

Proof.

Putting $\phi \left(t\right)=t^m$ and $s=1$ in Definition 2, one has

$${\displaystyle D^{\beta ,\rho }{t}^m=\frac{m{\rho }^{\beta }}{\mathsf{\Gamma }(1-\beta )}{\int }_0^t{(t^{\rho }-n^{\rho })}^{-\beta }{n}^{m-1}dn.}$$

Integrating the right-hand side of the previous equation, we get

$${\displaystyle D^{\beta ,\rho }{t}^m=\frac{m{\rho }^{\beta -1}}{\mathsf{\Gamma }(1-\beta )}\beta \left(1-\beta ,\frac{m}{\rho }\right)t^{m-\beta \rho },}$$

where $\beta (.,.)$ is the well-known beta function. Hence, the last equation can be simplified and written alternatively in the following form

$$D^{\beta ,\rho }{t}^m={\rho }^{\beta }\frac{\mathsf{\Gamma }\left(\frac{m}{\rho }+1\right)}{\mathsf{\Gamma }\left(\frac{m}{\rho }-\beta +1\right)}{t}^{m-\beta \rho }.$$

This completes the proof of this corollary.    □

Theorem 2.

The following formula holds for $0<\beta <1,$

$$D^{\beta ,\rho }{\psi }_i^{(a,b)}\left(t\right)=t^{-\rho \beta }\left(\sum _{p=0}^i\sum _{r=p}^i{A}_{r,i}{B}_{p,r}{\psi }_p^{(a,b)}\left(t\right)-\left(B_{0,0}{A}_{0,i}\right){\psi }_0^{(a,b)}\left(t\right)\right).$$

(19)

Proof.

Using Corollary 3 along with the power form of ${\psi }_i^{(a,b)}\left(t\right),$ one has

$$D^{\beta ,\rho }{\psi }_i^{(a,b)}\left(t\right)=\sum _{p=\lceil \beta \rceil }^i{A}_{p,i}{t}^{p-\rho \beta },$$

(20)

where

$$A_{p,i}=\frac{{\rho }^{\beta }{(-1)}^{i+p}(a+b+2i+1)\mathsf{\Gamma }\left(\frac{p}{\rho }+1\right)\mathsf{\Gamma }(a+b+i+p+1)}{p!\mathsf{\Gamma }(a+1)\sqrt{h_i}(i-p)!\mathsf{\Gamma }(b+p+1)\mathsf{\Gamma }\left(\frac{p}{\rho }-\beta +1\right)}.$$

(21)

Now, $t^{p-\rho \beta }$ can be written with the aid of the inversion formula (7) as

$$t^{p-\rho \beta }=t^{-\rho \beta }\sum _{r=0}^p{B}_{r,p}{\psi }_r^{(a,b)}\left(t\right).$$

(22)

Inserting Equation (22) into Equation (20) yields

$$D^{\beta ,\rho }{\psi }_i^{(a,b)}\left(t\right)=t^{-\rho \beta }\sum _{p=\lceil \beta \rceil }^i\sum _{r=0}^p{A}_{p,i}{B}_{r,p}{\psi }_r^{(a,b)}\left(t\right).$$

(23)

After expanding and rearranging the right-hand side of the last equation, we get the desired result. This completes the proof of the theorem.    □

3. Collocation Approach for the Nonlinear Generalized Fractional LE Equation

Consider the following nonlinear generalized fractional LE equation:

$$u_{tt}\left(t\right)+\frac{2}{t}{D}^{\beta ,\rho }u\left(t\right)+a_0{u}^2\left(t\right)+a_{1}u\left(t\right)=f\left(t\right),t\in (0,1),$$

(24)

subject to the initial conditions

$$u\left(0\right)=y_0,u^{\prime }\left(0\right)=y_1,$$

(25)

where $0<\beta \le 1$, $a_0,a_1,y_0,y_1$ are known constants, and $f\left(t\right)$ is a known continuous source term.

As we know, the set $\{{\psi }_i^{(a,b)}\left(t\right),i:0,\dots ,\infty \}$ forms an orthonormal basis function in the space function $L_{\omega \left(t\right)}^2(0,1)$. Consequently, any function $u\left(t\right)\in L_{\omega \left(t\right)}^2(0,1)$ can be written as

$$u\left(t\right)=\sum _{i=0}^{\infty }{c}_i{\psi }_i^{(a,b)}\left(t\right),$$

(26)

and approximated as

$$u\left(t\right)\approx u_N\left(t\right)=\sum _{i=0}^N{c}_i{\psi }_i^{(a,b)}\left(t\right).$$

(27)

Now, we present our technique when $b=a+1$ for the following two cases:

• The case in which $0<\beta <1$ and $\rho >0.$
• The case in which $\beta =1$ and $\rho =1.$

3.1. The Case in Which $0<\beta <1$ and $\rho >0$

The application of Lemma 1 and Corollary 2 along with Theorem 2 enables us to write the residual $\mathbf{R}\left(t\right)$ of Equation (24) as

$$\begin{array}{cc}\hfill \mathbf{R}\left(t\right)& =\frac{d^2{u}_N\left(t\right)}{d{t}^2}+\frac{2}{t}{D}^{\beta ,\rho }{u}_N\left(t\right)+a_0{u_N}^2\left(t\right)+a_1{u}_N\left(t\right)-f\left(t\right)\hfill \\ & =\sum _{i=0}^N\sum _{s=0}^{i-2}{c}_i{\mu }_{s,i}^{(a,a+1)}{\psi }_s^{(a,a+1)}\left(t\right)+2t^{-\rho \beta -1}\sum _{i=0}^N\left(\sum _{p=0}^i\sum _{r=p}^i{c}_i{A}_{r,i}{B}_{p,r}{\psi }_p^{(a,a+1)}\left(t\right)-\left(B_{0,0}{A}_{0,i}\right){\psi }_0^{(a,a+1)}\left(t\right)\right)\hfill \\ & +a_0\sum _{i,j=0}^N\sum _{p=\left|i-j\right|}^{i+j}{c}_i\sqrt{\frac{h_i{h}_j}{h_p}}{\chi }_{p,a,i,j}{\psi }_p^{(a,a+1)}\left(t\right)+a_1\sum _{i=0}^N{c}_i{\psi }_i^{(a,a+1)}\left(t\right)-f\left(t\right).\hfill \end{array}$$

(28)

Multiplying the last equation by $t^{1+\rho \beta }$, we get

$$\begin{array}{cc}\hfill \overline{\mathbf{R}}\left(t\right)& =t^{1+\rho \beta }\sum _{i=0}^N\sum _{s=0}^{i-2}{c}_i{\mu }_{s,i}^{(a,a+1)}{\psi }_s^{(a,a+1)}\left(t\right)+2\sum _{i=0}^N\left(\sum _{p=0}^i\sum _{r=p}^i{c}_i{A}_{r,i}{B}_{p,r}{\psi }_p^{(a,a+1)}\left(t\right)-\left(B_{0,0}{A}_{0,i}\right){\psi }_0^{(a,a+1)}\left(t\right)\right)\hfill \\ & +a_0{t}^{1+\rho \beta }\sum _{i,j=0}^N\sum _{p=\left|i-j\right|}^{i+j}{c}_i\sqrt{\frac{h_i{h}_j}{h_p}}{\chi }_{p,a,i,j}{\psi }_p^{(a,a+1)}\left(t\right)+a_1{t}^{1+\rho \beta }\sum _{i=0}^N{c}_i{\psi }_i^{(a,a+1)}\left(t\right)-t^{1+\rho \beta }f\left(t\right),\hfill \end{array}$$

(29)

Now, equations $t,$$t^{1+\rho \beta }$, and $t^{1+\rho \beta }f\left(t\right)$ may be approximated as

$$\begin{array}{cc}\hfill & t=\sum _{m=0}^1{a}_m{\psi }_m^{(a,a+1)}\left(t\right),\hfill \\ & t^{1+\rho \beta }=\sum _{n=0}^M{b}_n{\psi }_n^{(a,a+1)}\left(t\right),\hfill \\ & t^{1+\rho \beta }f\left(t\right)=\sum _{l=0}^M{g}_l{\psi }_l^{(a,a+1)}\left(t\right),\hfill \end{array}$$

(30)

where M is an arbitrary positive number and

$$\begin{array}{cc}\hfill & a_m={\int }_0^{1}t{\psi }_m^{(a,a+1)}\left(t\right)\omega \left(t\right)dt,\forall m=0,1,\hfill \\ & b_n={\int }_0^1{t}^{1+\rho \beta }{\psi }_n^{(a,a+1)}\left(t\right)\omega \left(t\right)dt,\hfill \\ & g_l={\int }_0^1{t}^{1+\rho \beta }f\left(t\right){\psi }_l^{(a,a+1)}\left(t\right)\omega \left(t\right)dt.\hfill \end{array}$$

(31)

Inserting Equation (30) into Equation (29), $\overline{\mathbf{R}}\left(t\right)$ can be obtained. Hence, the application of the collocation method [35,36,37] enables us to get the following $(N+1)$ nonlinear algebraic system of equations in the unknown expansion coefficients $c_i$

$$\begin{array}{cc}\hfill & \overline{\mathbf{R}}\left(t_i\right)=0,i=1,2,\dots ,N-1,\hfill \\ & u_N\left(0\right)=y_0,u_N^{\prime }\left(0\right)=y_1,\hfill \end{array}$$

(32)

where $\{t_i:i=1,2,\dots ,N-1\}$ are the first $(N-1)$ distinct roots of ${\psi }_{N+1}^{(a,a+1)}\left(t\right).$ Hence, the system (32) can be solved with the aid of the well-known Newton iterative method.

3.2. The Case in Which $\beta =1$ and $\rho =1$

Using similar steps as those given in the previous case along with Lemma 1, Corollary 1, and Corollary 2, we get the $(N+1)$ nonlinear algebraic system of equations in the unknown expansion coefficients $c_i$ that can be solved using Newton’s iterative method.

Remark 1.

Algorithm 1 shows all the steps required to obtain the numerical solution of Equation (24) governed by the conditions (25).

Algorithm 1: Coding algorithm for the proposed scheme.

Input $\beta ,a,\rho ,a_0,a_1,y_0,y_1,N,M$ and $f\left(t\right)$.

Step 1. Assume an approximate solution $u_N\left(t\right)$ as in (27).

Step 2. Compute $\overline{\mathbf{R}}\left(t\right)$ as in (29).

Step 3. Apply the collocation method to obtain the system in (32).

Step 4. Use FindRoot command with initial guess $\{c_i={10}^{-i},i:0,1,...,N\},$

to solve the system in (32) to get $c_i$.

Output $u_N\left(t\right)$

4. Error Bound

We first define the following error norms:

$$L_2[0,1]={\{u:\parallel u\parallel }_2={\left({\displaystyle {\int }_0^1{u}^2{t}^b{(1-t)}^{a}dt}\right)}^{\frac{1}{2}}<\infty \},$$

$${\displaystyle L_{\infty }[0,1]={\{u:\parallel u\parallel }_{\infty }=\underset{t\in [0,1]}{max}\left|u\right|<\infty \}.}$$

Consider the following space functions

$$V_N^{(a,b)}=\mathrm{span}\{{\psi }_i^{(a,b)}\left(t\right):i=0,1,\dots ,N\}$$

(33)

and assume that $u_N\left(t\right)\in V_N^{(a,b)}$ is the best approximation of $u\left(t\right)$; then, by the definition of the best approximation, we have

$$\left|\right|u\left(t\right)-u_N{\left(t\right)\left|\right|}_{\infty }\le \left|\right|u\left(t\right)-v_N\left(t\right){\left|\right|}_{\infty },\forall v_N\left(t\right)\in V_N^{(a,b)}.$$

(34)

It turns out that the previous inequality is also true if $v_N\left(t\right)$ denotes the interpolating polynomial for $u\left(t\right)$ at points $t_i$, where $t_i$ are the roots of ${\psi }_i^{(a,b)}\left(t\right)$. Then, by similar procedures as in [38]

$$u\left(t\right)-v_N\left(t\right)=\frac{d^{N+1}{u}_N\left(\eta \right)}{d{t}^{N+1}(N+1)!}\prod _{i=0}^N(t-t_i),$$

(35)

where $\eta \in [0,1]$ and hence, one has

$$\left|\right|u\left(t\right)-v_N\left(t\right){\left|\right|}_{\infty }\le \underset{t\in [0,1]}{max}\left|\frac{d^{N+1}{u}_N\left(\eta \right)}{d{t}^{N+1}}\right|\frac{\left|\right|{\prod }_{i=0}^N(t-t_i){\left|\right|}_{\infty }}{(N+1)!}.$$

(36)

Since $u\left(t\right)$ is a smooth function on $[0,1]$, then there exist a constant k, such that

$$\underset{t\in [0,1]}{max}\left|\frac{d^{N+1}{u}_N\left(t\right)}{d{t}^{N+1}}\right|\le k$$

(37)

To minimize the factor $\left|\right|{\prod }_{i=0}^N(t-t_i){\left|\right|}_{\infty }$, let us use the one-to-one mapping $t=\frac{1}{2}(z+1)$ between the intervals $[-1,1]$ and $[0,1]$ to deduce that

$$\begin{array}{cc}\hfill \underset{t_i\in [0,1]}{min}\underset{t\in [0,1]}{max}\left|\prod _{i=0}^N(t-t_i)\right|& =\underset{z_i\in [-1,1]}{min}\underset{z\in [-1,1]}{max}\left|\prod _{i=0}^N\frac{1}{2}(z-z_i)\right|\hfill \\ & ={\left(\frac{1}{2}\right)}^{N+1}\underset{z_i\in [-1,1]}{min}\underset{z\in [-1,1]}{max}\left|\prod _{i=0}^N(z-z_i)\right|\hfill \\ & ={\left(\frac{1}{2}\right)}^{N+1}\underset{z_i\in [-1,1]}{min}\underset{z\in [-1,1]}{max}\left|\frac{{\psi }_{N+1}^{(a,a+1)}\left(z\right)}{y_N^{(a,a+1)}}\right|,\hfill \end{array}$$

(38)

where $y_N^{(a,a+1)}=\frac{2^{-N}(N+1)\sqrt{h_{N+1}}\mathsf{\Gamma }(a+1)\mathsf{\Gamma }(2a+2N+2)}{\mathsf{\Gamma }(a+N+2)\mathsf{\Gamma }(2a+N+2)}$ is the leading coefficient of ${\psi }_{N+1}^{(a,a+1)}\left(z\right)$ and $z_i$ are the roots of ${\psi }_{N+1}^{(a,a+1)}\left(z\right).$

It is known that

$$\underset{z\in [-1,1]}{max}\left|{\psi }_{N+1}^{(a,a+1)}\left(z\right)\right|={\psi }_{N+1}^{(a,a+1)}\left(1\right)=\sqrt{h_{N+1}}$$

(39)

Therefore, inequality (37) along with Equations (38) and (39) enable us to get the following desired result

$$\begin{array}{cc}\hfill \left|\right|u\left(t\right)-u_N\left(t\right){\left|\right|}_{\infty }& \le k\frac{\sqrt{h_{N+1}}}{2^{N+1}{y}_N^{(a,a+1)}(N+1)!}\hfill \\ & =k\frac{\mathsf{\Gamma }(a+N+2)\mathsf{\Gamma }(2a+N+2)}{2(N+1)(N+1)!\mathsf{\Gamma }(a+1)\mathsf{\Gamma }(2a+2N+2)}.\hfill \end{array}$$

(40)

Hence, an upper bound of the absolute error is obtained for the approximate and exact solutions.

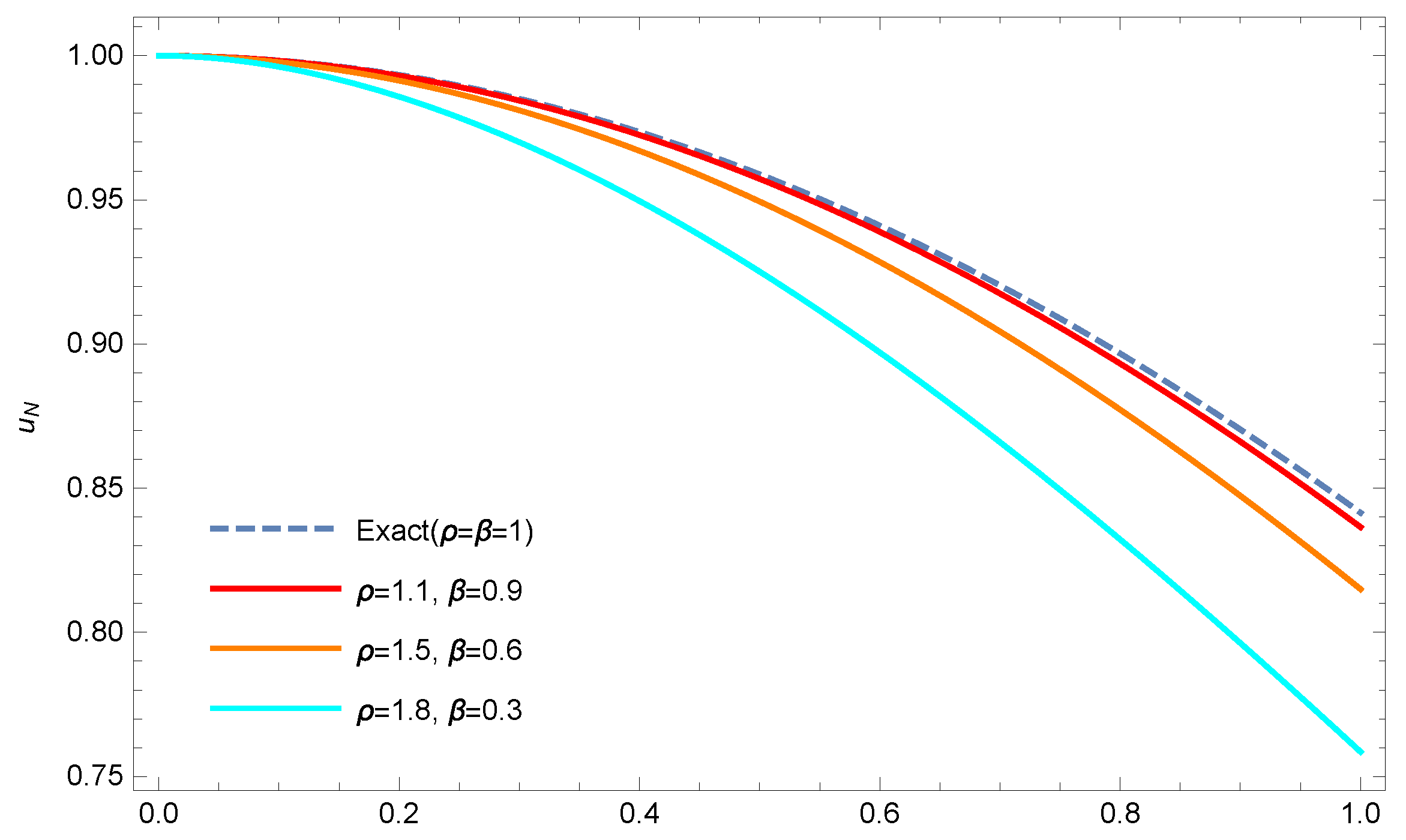
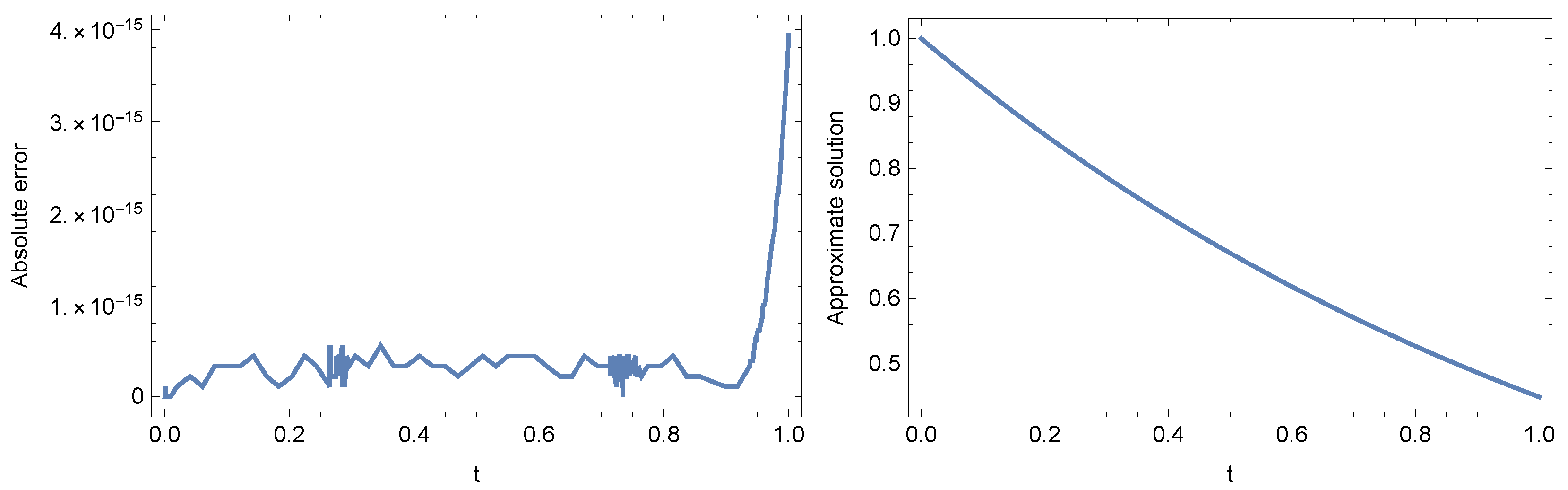
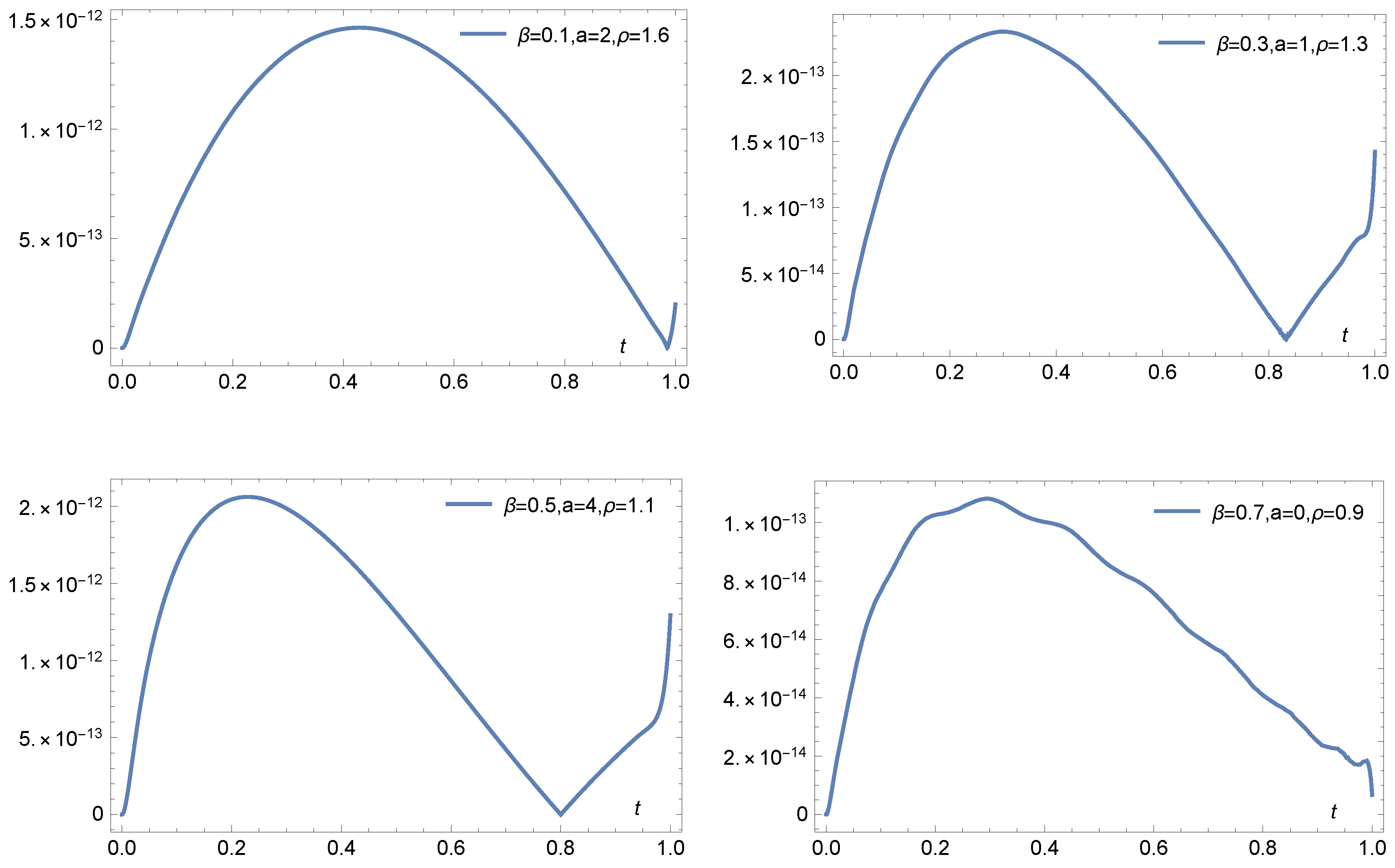
5. Illustrative Examples and Comparisons

Before providing the following examples, we would like to mention that all codes were written and debugged using Mathematica 11 on an HP Z420 workstation, with an Intel (R) Xeon(R) CPU E5-1620 3.6 GHz processor, 16 GB RAM DDR3, and 512 GB storage.

Example 1

([39]). Consider the following nonlinear generalized fractional LE equation

$$u_{tt}\left(t\right)+\frac{2}{t}{D}^{\beta ,\rho }u\left(t\right)+u\left(t\right)=0,t\in (0,1),$$

(41)

subject to the initial conditions

$$u\left(0\right)=1,u^{\prime }\left(0\right)=0,$$

(42)

where $u\left(t\right)=\frac{sin\left(t\right)}{t}$ is the exact solution when $\beta =1$. Figure 1 shows that the approximate solutions have smaller variations for values of ρ and β near the value $\rho =\beta =1$ when $N=12$, $M=20$, and $a=2.$ Table 1 presents a comparison of the $L_{\infty }$ error between our method at $\rho =\beta =a=1,$ $M=20$ and the methods in [39,40,41,42,43].

Figure 1. Different solutions of Example 1.

Table 1. Comparison of $L_{\infty }$ error of Example 1.

N = 64
$E_{ADM}$ [40]	$E_{HWCM}$ [41]	$E_{HWAGM}$ [42]	$E_{HWCAM}$ [43]	$E_{CWCQM}$ [39]	Our method at $N=12$
$8.0733\times {10}^{-3}$	$3.2854\times {10}^{-7}$	$9.1857\times {10}^{-8}$	$9.7345\times {10}^{-6}$	$7.2153\times {10}^{-12}$	$3.33067\times {10}^{-16}$

Example 2.

Consider the following nonlinear generalized fractional LE equation

$$u_{tt}\left(t\right)+\frac{2}{t}{D}^{\beta ,\rho }u\left(t\right)+u^2\left(t\right)+u\left(t\right)=f\left(t\right),t\in (0,1),$$

(43)

subject to the initial conditions

$$u\left(0\right)=1,u^{\prime }\left(0\right)=-\beta ,$$

(44)

where $f\left(t\right)$ is chosen such that the exact solution is $u\left(t\right)=e^{-\beta t}$. Table 2 shows the $L_2$ and $L_{\infty }$ errors at different values of ρ, β, a, and N when $M=20.$ Figure 2 illustrates the absolute error (left) and approximate solution (right) at $\rho =1$, $\beta =0.8$, $a=1,$ $N=12$, and $M=20.$

Table 2. $L_2$ and $L_{\infty }$ errors of Example 2.

a	$\mathit{N}$	$\mathit{\rho }=1.2$, $\mathit{\beta }=0.1$		$\mathit{\rho }=0.9$, $\mathit{\beta }=0.5$		$\mathit{\rho }=0.7$, $\mathit{\beta }=0.9$
		${\mathit{L}}_2$ Error	${\mathit{L}}_{\mathit{\infty }}$ Error	${\mathit{L}}_2$ Error	${\mathit{L}}_{\mathit{\infty }}$ Error	${\mathit{L}}_2$ Error	${\mathit{L}}_{\mathit{\infty }}$ Error
	4	2.63416$\times {10}^{-10}$	1.53419 $\times {10}^{-9}$	3.56771$\times {10}^{-7}$	4.94507$\times {10}^{-6}$	5.18941$\times {10}^{-6}$	7.99767$\times {10}^{-5}$
1	8	1.61411$\times {10}^{-15}$	6.39142$\times {10}^{-14}$	7.61436$\times {10}^{-14}$	3.64833$\times {10}^{-13}$	9.68827$\times {10}^{-12}$	1.42884$\times {10}^{-10}$
	12	1.76776$\times {10}^{-15}$	1.01641 $\times {10}^{-13}$	5.56363$\times {10}^{-16}$	3.31957$\times {10}^{-14}$	2.09734$\times {10}^{-16}$	8.46545$\times {10}^{-15}$
	4	1.69006$\times {10}^{-10}$	1.42379$\times {10}^{-9}$	2.37063$\times {10}^{-7}$	5.65026 $\times {10}^{-6}$	3.3588$\times {10}^{-6}$	9.01696$\times {10}^{-5}$
2	8	1.20331$\times {10}^{-17}$	1.94289 $\times {10}^{-16}$	7.22686$\times {10}^{-14}$	6.96721$\times {10}^{-13}$	9.06465$\times {10}^{-12}$	2.20747$\times {10}^{-10}$
	12	1.19946$\times {10}^{-17}$	1.76942$\times {10}^{-16}$	1.57298$\times {10}^{-17}$	1.94289$\times {10}^{-16}$	2.76152$\times {10}^{-17}$	5.82867$\times {10}^{-16}$
	4	9.71126$\times {10}^{-11}$	1.75633$\times {10}^{-11}$	1.41421$\times {10}^{-7}$	5.98682$\times {10}^{-6}$	1.99222$\times {10}^{-6}$	9.46116$\times {10}^{-5}$
3	8	5.09106$\times {10}^{-18}$	1.11022$\times {10}^{-16}$	5.46102$\times {10}^{-14}$	1.07617 $\times {10}^{-12}$	6.80349$\times {10}^{-12}$	3.10428$\times {10}^{-10}$
	12	1.77111$\times {10}^{-17}$	2.89699$\times {10}^{-16}$	2.21721$\times {10}^{-17}$	3.88578$\times {10}^{-16}$	4.23896$\times {10}^{-18}$	6.38378$\times {10}^{-16}$

Figure 2. The absolute error (left) and approximate solution (right) of Example 2.

Example 3.

Consider the following nonlinear generalized fractional LE equation

$$u_{tt}\left(t\right)+\frac{2}{t}{D}^{\beta ,\rho }u\left(t\right)+u^2\left(t\right)+u\left(t\right)=t^2\left(2{\rho }^{\beta }\frac{\mathsf{\Gamma }\left(1+\frac{4}{\rho }\right)}{\mathsf{\Gamma }\left(-\beta +\frac{4}{\rho }+1\right)}{t}^{1-\rho \beta }+t^6+t^2+12\right),t\in (0,1),$$

(45)

subject to the initial conditions

$$u\left(0\right)=0,u^{\prime }\left(0\right)=0,$$

(46)

where $u\left(t\right)=t^4$ is the exact solution. Figure 3 illustrates the absolute errors at different values of β when $\rho =1.01$, $a=2$, $N=4$, and $M=20.$ Table 3 shows the $L_2$ and $L_{\infty }$ errors at different values of ρ, β, and N at $a=1$ and $M=20.$ Moreover, we have reported the CPU running times in Table 3.

Figure 3. The absolute errors of Example 3.

Table 3. $L_2$ and $L_{\infty }$ errors of Example 3.

$\mathit{N}$	$\mathit{\rho }=0.8$, $\mathit{\beta }=0.85$				$\mathit{\rho }=0.5$, $\mathit{\beta }=0.95$
	${\mathit{L}}_2$ Error	CPU Time	${\mathit{L}}_{\mathit{\infty }}$ Error	CPU Time	${\mathit{L}}_2$ Error	CPU Time	${\mathit{L}}_{\mathit{\infty }}$ Error	CPU Time
4	0	8.97	2.78666$\times {10}^{-14}$	8.923	0	7.847	4.32987$\times {10}^{-15}$	7.831
6	3.86623 $\times {10}^{-18}$	8.441	3.19189$\times {10}^{-15}$	8.051	3.50141 $\times {10}^{-18}$	9.983	8.88178 $\times {10}^{-16}$	9.437

Example 4.

Consider the following nonlinear generalized fractional LE equation

$$u_{tt}\left(t\right)+\frac{2}{t}{D}^{\beta ,\rho }u\left(t\right)+2u^2\left(t\right)+3u\left(t\right)=f\left(t\right),t\in (0,1),$$

(47)

subject to the initial conditions

$$u\left(0\right)=0,u^{\prime }\left(0\right)=0,$$

(48)

where $f\left(t\right)$ is chosen such that the exact solution is $u\left(t\right)=ln\left(1+t^2\right)$. Figure 4 shows the maximum absolute errors when $\beta =0.95$ at different values of ρ, a, and N when $M=20$, while Figure 5 illustrates the absolute errors at different values of β, ρ, and a when $N=20$ and $M=20.$ It can be seen that the approximate solution is quite near to the precise one.

Figure 4. The maximum absolute errors of Example 4.

Figure 5. The absolute errors of Example 4.

Example 5.

Consider the following nonlinear generalized fractional LE equation

$$u_{tt}\left(t\right)+\frac{2}{t}{D}^{\beta ,\rho }u\left(t\right)+u^2\left(t\right)+3u\left(t\right)=0,t\in (0,1),$$

(49)

subject to the initial conditions

$$u\left(0\right)=0,u^{\prime }\left(0\right)=0.$$

(50)

Since the exact solution is not available, we define the following error norm

$$E=\underset{t\in [0,1]}{max}\left|t{u_N}_{tt}\left(t\right)+2D^{\beta ,\rho }{u}_N\left(t\right)+t{u_N}^2\left(t\right)+3t{u}_N\left(t\right)\right|.$$

(51)

We applied our technique with when $N=8$ and $M=20.$ The values of E at various values of ρ, β, and a are listed in Table 4. Moreover, we report the CPU running times in that table.

Table 4. Residual error of Example 5.

$\mathit{a}$	$\mathit{\rho }=0.5$, $\mathit{\beta }=0.5$		$\mathit{\rho }=0.7$, $\mathit{\beta }=0.7$		$\mathit{\rho }=0.9$, $\mathit{\beta }=0.9$
	E	CPU Time	E	CPU Time	E	CPU Time
1	4.14113 $\times {10}^{-24}$	15.132	5.24048 $\times {10}^{-25}$	10.872	3.75029 $\times {10}^{-11}$	16.706
3	2.99225 $\times {10}^{-17}$	15.881	2.20543 $\times {10}^{-20}$	16.693	7.55597 $\times {10}^{-25}$	16.069

6. Closing Remarks

Within this research work, we presented and analyzed an accurate collocation solver for a specific nonlinear LE equation with a generalized fractal–fractional Caputo derivative. We also discussed the truncation error of the suggested approximate orthonormal Jacobi solution. Some numerical results and comparisons were exhibited to check and verify the validity and the accuracy of the proposed algorithm. We believe that the offered scheme can be extended to more general models in different disciplines in engineering, mathematics, and physics. As an expected future work, we aim to employ the developed theoretical results in this paper along with suitable spectral methods to treat numerically some other types of generalized fractional differential equations; see, e.g., [44,45].