Abstract
Due to the complexity of the microstructure of porous media, it is of great significance to explore the heat transport mechanism in porous media in many engineering applications. In this study, an expression for effective thermal conductivity (ETC) of porous media embedded with randomly distributed damaged tree-like bifurcation networks is derived based on the theory of thermodynamics and fractal features of tree-like bifurcation networks. We investigate the effect of heat conduction and heat convection in porous media embedded with randomly distributed damaged tree-like bifurcation networks on the ETC of the porous media. It is found that our fractal model has good consistency with the existing available experimental data. In addition, the influence of the microstructural parameters of the model on heat transfer in the porous media is analyzed in detail. The research results can provide significant theoretical guidance for the development and design of heat transfer systems.
1. Introduction
The metric known as ETC plays a crucial role in quantifying the heat transfer properties inside porous material. The estimation of ETC in porous media has extensive use in several domains such as thermoelectric materials, porous construction materials, the chemical industry, petroleum extraction, and related sectors [1,2,3,4,5,6]. It is well known that porous media are usually composed of pore space and solid matrix, and the microstructure exhibits a high degree of complexity and chaos. Therefore, describing it using normal means poses challenges. The application of fractal geometry theory enables the characterization of pore properties in porous media when the microstructure of porous media has self-similar characteristics [7] and offers a novel approach for investigating the challenges associated with transportation in intricate and disorganized porous materials [8,9,10]. At present, many scholars use fractal theory to explore gas flow [11,12,13], gas diffusion [14,15,16], and seepage characteristics [17,18] in porous media. In addition, the investigation of heat transfer in porous media can be conducted through the utilization of fractal geometry theory [19,20,21]. For example, Xiao [22] introduced a novel ETC model that incorporates a microscale effect, leveraging the fractal properties exhibited by porous media. Shen et al. [23] developed a three-phase unsaturated porous media model based on fractal theory, employing thermoelectric simulation and a capillary bundle model. The study investigated the impact of liquid saturation and porosity on the ETC of porous media, elucidating the underlying influence mechanism.
The tree-like bifurcation network structure exhibits distinct transport characteristics; therefore, it has attracted the interest and attention of a large number of scholars, and it has been widely used in related practical applications, such as microelectronic chip cooling systems and production engineering, etc. [24,25]. Chen and Cheng [26] discussed a comparative analysis to examine the distinctions between traditional parallel pipes and rectangular tree-like bifurcation networks in the context of heat convection. They discovered that the heat dissipation performance of pipes can be significantly enhanced by employing rectangular tree-like bifurcation networks, in contrast to the conventional parallel pipe configurations. Yu and Li [27] conducted a study on the ETC of composites that contain tree-like bifurcation networks, focusing on the self-similarity properties of these networks. The results show that the ETC of each component embedded in the networks exerts a substantial impact on the ETC of the composite [28]. However, the above research only focuses on the symmetric tree-like bifurcation networks and does not involve the damage of branches in the networks. Miao et al. [29] conducted a study on the heat transport and fluid flow, focusing on the fractal self-similarity exhibited by tree-like bifurcation networks. Xiao et al. [30] published a study to investigate the impact of pore surface roughness on the ETC of damaged tree-like bifurcation networks, building upon the research conducted by Miao et al. [29]. The model considered the effects of roughness and damaged structure of the pipeline on ETC; however, the impact of heat convection resulting from the movement of liquid was not taken into account. Based on these premises, Shao et al. [31] introduced an ETC model for porous media that incorporates a damaged tree-like branching network, taking into account the impact of roughness. The development of this model takes into account the distinctive features of tree-like bifurcation networks that have been damaged and conducts separate analyses on the impacts of heat convection and heat conduction on the ETC of porous media. The underlying assumption of the model posits the presence of a solitary tree-like bifurcation network within the porous media. However, in reality, a porous medium is usually composed of tree-like bifurcation networks that conform to fractal scale distribution. Xia et al. [32] studied the influence of heat convection caused by liquid flow on ETC by establishing the joint expression of heat conduction and heat convection in a tree branch network with rough surfaces. Nevertheless, the impact of branch damage within the tree-like bifurcation networks was not considered in the scope of this research [33].
The study conducted by Valvano et al. [34] introduces an improved methodology for the in vivo assessment of thermal conductivity, thermal diffusivity, and perfusion. This is achieved through the utilization of a self-heated spherical thermistor probe. The methodology encompasses the resolution of a time-dependent thermal model that is coupled with the probe–tissue system. This model is utilized to quantify the “effective” thermal conductivity and “effective” thermal diffusivity, which serve as representative measures of the thermal properties of perfused tissue. This study introduces a highly reproducible thermal conductivity probe with precise temperature control, emphasizing its application to measure and understand the influence of moisture content on ETC in a diverse biological cell. Afterwards, Liang et al. [35] introduced the highly repeatable thermal conductivity probe with precise temperature control to measure and understand the impact of water content on thermal conductivity in different biological tissues. Bhattacharya et al. [36] employed a new transient technique, using specialized thermal resistance wire probes to experimentally establish thermal conductivity of cells, revealing reversible changes within a specific temperature range, and emphasizing the significant impact of blood perfusion on enhancing heat transfer in living tissues. Valvano et al. [34] employed various methodologies to assess the thermal conductivity and thermal conductivity resulting from thermal convection in organisms. However, the intricate microstructure of porous media poses challenges in experimentally elucidating the influence of this complexity on thermal transport properties.
In the above brief literature research, the current research considering the effect of heat convection on the ETC did not meditate on The damaged structure of randomly distributed tree-like bifurcation networks. In our previous study [31], we exclusively examined the phenomena of heat convection and heat conduction within a solitary tree-like branching network that was integrated within a porous medium. The pore structure of the main pipe with random distribution was not considered. As a result, we will talk about heat conduction and heat convection in our model, which has bifurcation networks that resemble damaged trees and are scattered at random. A fractal model of ETC will be built, and the influence of microstructural parameters of the composite on thermal transport will be studied. The outcome of this study can contribute to the comprehension of the heat transfer mechanism occurring within a porous medium that contains tree-like bifurcation networks that have been damaged.
2. Fractal Characteristics of Porous Media
Creating a mathematical model that faithfully captures the ETC of porous media embedded with randomly distributed damaged tree-like bifurcation networks is the main goal of this work. It is postulated that a significant quantity of impaired tree-like bifurcation networks is uniformly dispersed inside porous media, with the primary diameters of said networks following the principles of fractal scaling. Refer to Figure 1a.
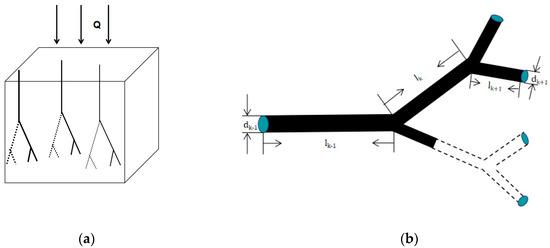
Figure 1.
(a) Diagrammatic schematic of the porous media with randomly distributed damaged tree-like bifurcation networks; (b) diagrammatic schematic of a single damaged tree-like bifurcation network.
Therefore, the total number N of tree-like bifurcation networks with a diameter scale L larger than or equal to the diameter of the main channel can be expressed as [8]:
where is the maximum diameter of the main channels, and is the fractal dimension of the main channels. The can be obtained by [8]:
where is areal porosity, is the minimum diameter of the main channels, and is the Euclidean dimension. in two-dimensional space, and in three-dimensional space. Since there are many tree-like bifurcation networks in the porous media, Equation (1) can be regarded as a continuous and differentiable function. The number of main channels with sizes ranging from to can be calculated by differentiating with based on Equation (1) [7,8,9]:
where ; the negative sign of the Equation (3) indicates that the number of main channels decreases with the increase in the diameter of the main channels. Therefore, when is equal to the minimum diameter of the main channels, the total number of main channels in porous media can be expressed as [8]:
Dividing Equation (3) by Equation (4), we have [7,8,9]:
where is the probability function for pore size distribution and can be given by [7]:
According to the basic theory of probability theory, Equation (6) should meet the normalization condition; please see Ref. [18].
Equations (1)–(6) describe the randomly fractal distribution of tree-like bifurcation networks with mother channel diameter , as shown in Figure 1a. In the following, we will introduce the geometric structure of the single damaged tree-like bifurcation network (see Figure 1b), which is made up of “point to line” Y-shaped networks. In our model, we suppose that each branch in the bifurcation networks is a cylindrical tube, and the roughness and the thickness of the tube wall are ignored [25]. Figure 1b illustrates the utilization of and to denote the length and diameter, respectively, of the kth branching level (where k ranges from 0 to m). The network bifurcation numbers, denoted as m, represent the maximum number of branches that occur in a network. At each level of the network, every tube undergoes a bifurcation, resulting in the formation of n new tubes. In order to elucidate the geometric configuration of a bifurcation network resembling that of a tree, next, we proceed to present two scale variables, namely the length ratio and the diameter ratio [33].
So we obtain:
where and are the length and diameter of the 0th branching level, respectively.
In order to consider an asymmetric tree-like bifurcation network, we assume that p channels of the kth branching level have been damaged, but the other parts of the network are intact. For example, if a branch of the tree-like bifurcation network in Figure 1b is damaged, the damaged part will not generate new branches, and the undamaged part will not be affected.
These equations above provide a theoretical basis for the analysis of heat transfer in the porous media embedded with randomly distributed damaged tree-like bifurcation networks.
3. Fractal Model of Effective Thermal Conductivity of Porous Media
3.1. The Effective Thermal Conductivity of Heat Conduction
In general, the heat transport process in the damaged tree-like bifurcation networks is different from that in the symmetric tree-like bifurcation networks.
According to Fourier’s law and the thermal–electrical analogy technique, for a single damaged tree-like bifurcation network, the thermal resistance of the damaged tree-like bifurcation network can be written as [31]:
where , is the thermal conductivity of the fluid, is the branching number of the tree-like branching network, is total numbers of branching levels, and is the numbers of damaged channels. With the help of Equations (4) and (11), the reciprocal of the total thermal resistance of the entire randomly distributed damaged tree-like bifurcation networks can be calculated by the following relation:
Here, we add up the length of each branch of a single tree-like branching network as a straight pipe and consider the length of this straight pipe as the equivalent length. Then, the equivalent length of a single damaged tree-like bifurcation network, , can be written as [31]:
The total volume of the single damaged tree-like bifurcation network, , can be expressed as [31]:
where , and is the volume of the single pipe in the ith branching level. In the present study, we consider the singularly impaired tree-like bifurcation network as an exemplary model characterized by a solitary conduit exhibiting a consistent volume. The ETC of the single channel that is equivalent to the entire network is equivalent to the ETC of the entire network. Hence, utilizing Equations (13) and (14), the effective cross-sectional area of the individual tree-like bifurcation network, denoted as , can be determined [31]:
Due to the distribution of the diameter of main pipes conforming to the fractal scaling law, the effective cross-sectional area of the total porous media can be calculated from Equations (2), (4), and (15):
when m = 0, n = 0, and p = 0, the effective cross-sectional area is equal to the total cross-sectional area of main channels, . At this point, a single tree-like branching network can be seen as an undamaged channel, while the porous medium at this time can be seen as a porous medium with a fractal distribution of the diameter of the main pipe, which is similar to in Yu’s study [10]:
The area of the complete cross-section of the media, A, according to the notion of porosity, , is determined by:
Likely, the thermal resistance of the media matrix of porous media, , is given by Fourier’s law and can be calculated as follows:
where is the thermal conductivity of the media matrix.
According to Fourier’s law, the ETC of the randomly distributed damaged tree-like bifurcation network part, , and the ETC of the media matrix part, , can be respectively described as [31]:
According to Fourier’s law and the series-parallel model, the ETC of the whole porous media, , can be divided into two components: the randomly distributed damaged tree-like bifurcation network component and the media matrix component, which can be described as [31]:
Inserting Equations (12), (13), (18), and (19) into Equation (22), the ETC of the whole porous media, , can be calculated as:
3.2. The Effective Thermal Conductivity of Heat Convection
The derivation of the ETC of the whole porous media is presented in Section 3.1. Nevertheless, the convective heat transfer occurring between the fluid and the wall plays a crucial role in facilitating the transportation of heat within porous media. This section primarily focuses on the determination of the ETC associated with heat convection .
According to Chen and Cheng [26], the fluid dynamics within the tree-like bifurcation networks exhibit laminar flow, and it is seen that the Nusselt number remains constant across each layer. Consequently, the coefficient of heat convection, , can be made explicit as [26]:
The pipe’s characteristic length, denoted as , is equivalent to the diameter of the pipe. The Nusselt number, denoted as , represents the dimensionless ratio of convective heat transfer to conductive heat transfer. Hence, the heat convection coefficient of the th branching level of the tree-like bifurcation network, denoted as , can be determined [26]:
where is the heat convection coefficient of the single main pipe of the tree-like bifurcation network, which can be written as [26]:
where is the diameter of the 0th branching level. In line with Newton’s cooling formula, the convective heat transfer rate in a solitary primary pipe, , can be written as:
where is temperature difference. is the heat convection area of a single main pipe of the tree-like bifurcation network, which can be determined by:
where is the length of the 0th branching level. According to Chen and Cheng [26], the temperature difference between tree-like bifurcation networks at different levels is invariable. Then, by means of Equations (25)–(28), the flow of the heat convection of the undamaged part of the single damaged tree-like bifurcation network before the kth branching level, , can be modified as [31]:
where is the heat convection area of the th branching level in the tree-like bifurcation network.
It is likely that the flow of the heat convection of the damaged part of a single damaged tree-like bifurcation network, , can be modified as [31]:
The heat convection flow of a singular damaged tree-like bifurcation network with smooth surfaces, denoted as , can be computed using Equations (29) and (30) [31]:
The heat convection area of the intact portion of a singular damaged tree-like bifurcation network prior to the kth level of branching, denoted as , can be expressed in a similar manner:
The heat convection area of the damaged part of a single damaged tree-like bifurcation network, , is:
The calculation of the heat convection area of a single damaged tree-like bifurcation network, denoted as , may be performed using Equations (32) and (33).
The diameter distribution of the main pipes exhibits fractal scaling, according to the underlying principle, the heat flow, , and the heat convection area, , can be obtained by respectively integrating the individual heat flow, , and the individual heat convection area, .
In accordance with Fourier’s law, the thermal conductivity of heat convection resulting from fluid flow in porous media, denoted as , is [31]:
The thickness of the thermal boundary layer in thermal convection, denoted as , is primarily influenced by the fluid’s characteristics.
Inserting Equations (35) and (36) into Equation (37), the thermal conductivity of heat convection caused by fluid flow in the porous media, , is:
According to the research of Yu et al. [10], only when does the diameter of the main channels of damaged tree-like bifurcation networks, conform to fractal scaling law. Therefore, the thermal conductivity of heat convection caused by fluid flow in the porous media can be simplified as:
The average diameter, of the main channels of randomly distributed tree-like bifurcation networks can be obtained from Equation (6) [32]:
Inserting Equation (40) into Equation (39), the thermal conductivity of heat convection caused by fluid flow in the porous media can be simplified again as:
3.3. The Total Effective Thermal Conductivity of Porous Media
The development of the thermal conductivity model for heat conduction and the thermal conductivity model for heat convection in porous media was conducted in Section 3.1 and Section 3.2, respectively. The current investigation proposes that the heat transfer mechanism in bifurcation networks resembling trees is facilitated by the combined effects of heat conduction and heat convection. In alternative terms, the equation representing the effective thermal conductivity (ETC) of porous media, which encompasses randomly distributed damaged tree-like bifurcation networks written as , can be formulated as [31]:
With respect to Equations (23), (41), and (42), the ETC of whole porous media can be derived as:
The dimensionless ETC of porous media with randomly distributed damaged tree-like bifurcation networks is defined by , and it can be expressed as:
Equation (44) is the dimensionless coefficient of heat conductivity for the whole porous media. It is also a theoretical model, which can be used for analyzing the effect of structural parameters of tree-like bifurcation networks (), the porosity, , the thermal conductivity of porous media matrix, and the thermal conductivity of fluid, , on the dimensionless thermal conductivity coefficient. In Equation (44), all parameters have a clear physical meaning, and there are not any empirical constants.
4. Results and Discussion
Figure 2 presents a comparative analysis of the experimental data obtained from the study conducted by Liang et al. [34,35,36] and ETC, versus for varying quantities of impaired channels, as determined by Equation (43). The values of relevant parameters are all from experimental information from Liang et al. [34,35,36]. In Figure 2, the permeable media’s thermal conductivity fluid is , which is given by the experimental information from Liang et al. [35]. The porosity used in the experimental information of Valvano et al. is 0.0041–0.1645. The porosity used in the experimental data of Liang et al. is 0.1, and the porosity used in the experimental data of Bhattacharya et al. is 0.013–0.1645 [34,35,36]. Therefore, the porosity we select in the Figure 2 is 0.1, and the experiment data from Liang et al. gives the length ratio and diameter ratio of the arterial vascular tree, which are 1.30 and 1.25 [34,35,36]. So, we select = 1/1.30 = 0.77, = 1/1.25 = 0.8. The structural parameters of pores in reality, such as , and , are difficult to obtain in experiments. In Tien’s research [37], the Nusselt number, denoted as Nu, characterizes the convective heat transfer in a porous medium confined between two parallel plates in the fully developed regime. This analysis is based on the Darcy flow model, specifically considering slug flow. For the case of constant wall temperature, the Nusselt number is represented by Nu = 4.93. Conversely, for constant wall heat flux, the Nusselt number is given by Nu = 6.0. In this study, we assume that heat transfer in porous media occurs under constant temperature conditions. Due to the complex microporous structure of the tree-like branching network, which is difficult to measure, we arbitrarily select , . So, we take , , . Consistent with the experimental data, we choose the thickness of the thermal boundary layer as and the average diameter of the randomly distributed tree-like network as m [34,35,36]. The picture reveals that the ETC of porous media containing randomly distributed damaged tree-like bifurcation networks, as predicted using the ETC model described by Equation (43), exhibits a notable level of concordance with the experimental findings. It has also been observed that the ETC exhibits a positive correlation with the thermal conductivity of the media matrix while displaying a negative correlation with the number of damaged channels. The observed outcome can be rationalized by considering that an augmentation in the number of impaired channels results in a reduction in both the effective cross-sectional area and thermal convection area. Consequently, the dimensionless ETC experiences a decline as the number of damaged channels increases.
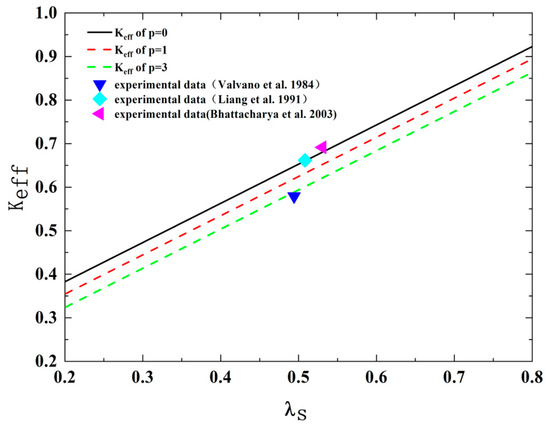
Figure 2.
The comparison between experimental data and ETC versus at , , , m, , m [34,35,36].
Figure 3 illustrates the relationship between the dimensionless ETC and the length ratio for varying numbers of damaged channels. The data presented in the figure demonstrate a positive correlation between the dimensionless ETC and the length ratio, indicating that as the length ratio increases, the ETC also increases. Conversely, there is a negative correlation between the dimensionless ETC and the number of damaged channels, suggesting that as the number of damaged channels increases, the ETC decreases. The reason for this phenomenon is that as the length ratio increases, the heat convection area of the bifurcation network pipeline also increases, thereby leading to an increase in the overall ETC. It is worth noting that when p = 4, the dimensionless ETC hardly changes with the change of the length ratio. The reason for this result is that when all branches of the networks are damaged, only the heat conduction of matrix part exists in porous media. At this time, the porous medium can be regarded as a solid medium with all the pipes damaged. The length ratio hardly influences the dimensionless ETC of porous media.
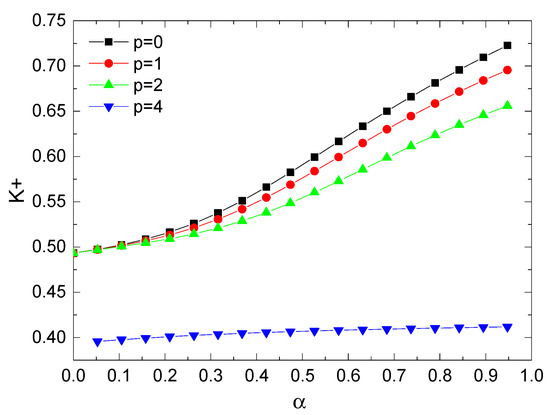
Figure 3.
The dimensionless ETC versus and at , , , , , m, , m.
Figure 4 illustrates the impact of the diameter ratio, denoted as , on the dimensionless ETC for varying numbers of damaged channels and compares it with the data in Ref. [31]. The rationale behind this phenomenon is that an increase in the diameter ratio results in a decrease in the overall thermal resistance. Consequently, the ETC decreases while the length ratio remains constant. It can be observed from the figure that the dimensionless ETC exhibits a decreasing trend as the diameter ratio increases. Additionally, it is observed that the dimensionless ETC exhibits a minor variation with the change in the diameter ratio when p = 4. The aforementioned statement aligns with the result presented in Figure 4. Interestingly, by comparing the data with Ref. [31] (m = 5, ), it can be seen that when p = 2, our model has a higher ETC, but the trends of the two are basically consistent.
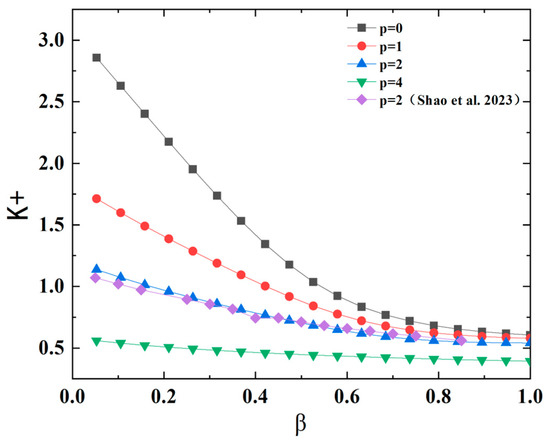
Figure 4.
The dimensionless conductivity versus and at , , , , , m, , m [31].
Figure 5 illustrates the relationship between the ETC, , the ETC of the network part, , the ETC of the matrix part, , and the heat convection ETC, , with respect to the fractal dimension of the porous media. This relationship is examined for various numbers of damaged channels. The research indicates that there is a positive correlation between the fractal dimension of porous media and the ETC. Specifically, as the fractal dimension increases, the ETC also increases. On the other hand, the ETC of the randomly distributed damaged tree-like bifurcation network component falls when the fractal dimension of porous media increases. The influence of the fractal dimension of porous media on ETC resulting from heat convection is negligible. The ETC of the matrix exhibits a decrease as the fractal dimension of the porous media increases. The observed phenomenon can be attributed to the positive correlation between the fractal dimension of pores and the porosity of porous media. As the fractal dimension of holes increases, the porosity of the media also increases, thereby resulting in a decrease in the matrix composition of the porous media. The determination of the total ETC of the porous media may be observed from Equation (41), which indicates that it is influenced by the ETC of the three constituent parts. The dominance of heat transmission in porous media by the heat conduction of the randomly distributed damaged tree-like bifurcation network component as the fractal dimension grows can be observed in Figure 4.
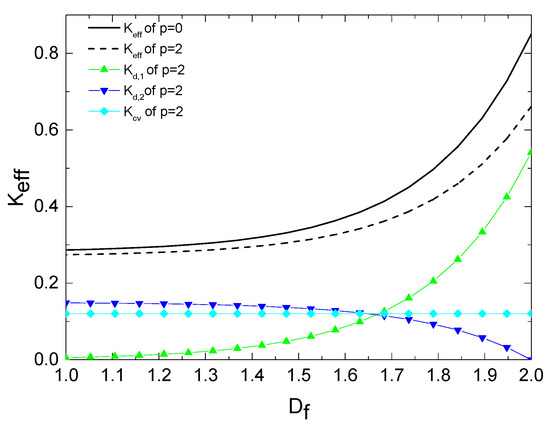
Figure 5.
The ETC of each component , , , versus , and at ,, , , m, , m.
Figure 6 illustrates the impact of the ratio between the ETC of the wall and the ETC of the fluid on the dimensionless ETC of the porous media considering various fractal dimensions. Based on the analysis of Figure 6, it can be inferred that an increase in the ratio of the ETC of the wall to that of the fluid results in a corresponding increase in the dimensionless ETC. It is noteworthy to mention that the dimensionless ETC remains consistent across various fractal dimensions, provided that the ratio between the ETC of the wall and that of the fluid is approximately 1.1. When the ratio is below 1.1, there is an observed rise in the dimensionless ETC as the fractal dimension increases. However, when the ratio exceeds 1.1, a decrease in the fractal dimension is associated with an increase in the dimensionless ETC. The relationship between porosity and fractal dimension can be elucidated by observing that an increase in fractal dimension corresponds to an increase in porosity. In cases when the ETC of the fluid surpasses that of the matrix component, an increase in porosity leads to a more significant involvement of tree-like bifurcation networks in the heat conduction process inside porous media. In contrast, if the ETC of the fluid is lower than that of the matrix, an increase in porosity will result in a reduction in the heat transfer area of the matrix. Consequently, the overall ETC will fall.
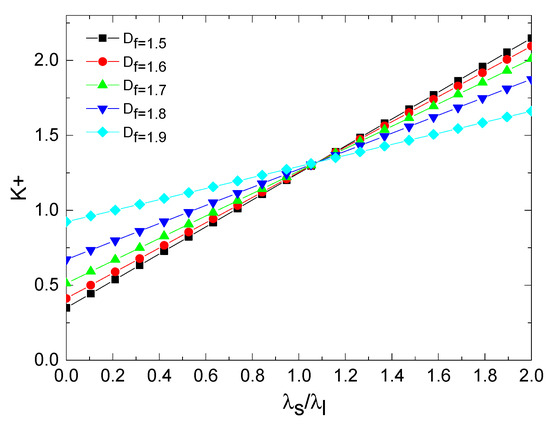
Figure 6.
The dimensionless ETC versus and at ,, , m, , m.
5. Conclusions
This research presents the derivation of a dimensionless equation for the ETC of porous media including randomly distributed damaged tree-like bifurcation networks. Furthermore, the impact of the structural features of the porous media on the ETC is investigated. In this study, we took into account not only the heat conduction of the bifurcation network and matrix components, but also the heat convection resulting from liquid flow. Our findings indicate that when the ratio of ETC of the wall to that of the fluid is less than 1.1, there is an observed increase in the dimensionless ETC as the fractal dimension increases. Conversely, when the ratio exceeds 1.1, a decrease in the fractal dimension corresponds to an increase in the dimensionless ETC. Additionally, it was observed that an increase in the fractal dimension results in the dominance of heat conduction in the heat transfer process of porous medium, namely, inside the randomly distributed damaged tree-like bifurcation network segment. Furthermore, by a comparative analysis of the available experimental data and the fractal model suggested in our study, it was shown that the ETC model for porous media presented in this research has favorable concurrence with the experimental data. The proposed model aims to enhance the understanding of heat transport mechanisms in porous media and offer valuable insights for a wide range of engineering applications. The omission of considering the impact of capillary surface roughness on the effective heat conductivity of porous media is acknowledged in this study. Hence, our forthcoming research will focus on investigating the impact of surface roughness on the effective heat conductivity.
Author Contributions
Conceptualization, Y.S. and Q.Z.; Methodology, Q.Z.; Validation, Q.Z.; Formal analysis, Y.S., X.G., H.W., L.Z. and Q.Z.; Investigation, H.W., L.Z. and Q.Z.; Resources, Q.Z.; Data curation, Y.S. and Q.Z.; Writing—original draft, Y.S. and Q.Z.; Writing—review & editing, Q.Z.; Visualization, Q.Z.; Supervision, Q.Z.; Project administration, Q.Z.; Funding acquisition, Q.Z. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by the National Natural Science Foundation of China under grant no. 11972266, the Knowledge Innovation Program of Wuhan—Basic Research under grant no. 2022010801010248, Applied Program of Wuhan—Basic Research under grant no. 2022013988065194 and no. 2022013988065210, and the Research Project of Hubei Provincial Department of Education under grant no. T2022016.
Data Availability Statement
No new data were created or analyzed in this study. Data sharing is not applicable to this article.
Conflicts of Interest
The authors declare no conflict of interest.
Nomenclature
| Symbols | Description | the coefficient of heat convection | |
| branching number | the thermal resistance of the media matrix | ||
| L | diameter scale | the thermal resistance of the network | |
| the length of the kth branching level | the porosity of the cross-section of the media | ||
| the diameter of the kth branching level | temperature difference | ||
| dimension of the main channels’ fractal | the porosity of the cross-section of the media | ||
| areal porosity | the total thermal resistance of the network | ||
| Euclidean dimension | temperature difference | ||
| n | the branching number | the heat convection flow of a single main pipe | |
| fractal dimension | the tree-like bifurcation network’s single main pipe’s heat convection area | ||
| Euclidean dimension | the heat convection flow in the undamaged part | ||
| the primary channels’ largest diameter | the heat convection flow in the damaged part | ||
| the primary channels’ minimum diameter | the heat convection area of the undamaged part | ||
| the length ratio | the heat convection area of the damaged part | ||
| the diameter ratio | the effective thermal conductivity of the media matrix part | ||
| the kth level channel’s single channel’s thermal resistance | the effective thermal conductivity of the network part | ||
| total number of levels in a branch | the average diameter of the main channels | ||
| the number of damaged channels | the thermal conductivity of heat convection | ||
| the equivalent length | the total heat flow | ||
| the total volume | the total heat convection area | ||
| the single pipe’s volume at the branching level | the individual heat flow | ||
| the thermal conductivity of the fluid part | the individual heat convection area | ||
| the thermal conductivity of the media matrix | the thickness of the thermal boundary layer of thermal convection caused by fluid flow is mainly related to the characteristics of the fluid | ||
| the overall main channel cross-sectional area | the coefficient of heat convection | ||
| the area encompassing the whole spectrum of media | the effective thermal conductivity | ||
| the ETC of network part | the dimensionless thermal conductivity | ||
| the ETC of the media matrix part | |||
| the ETC of the whole porous media | |||
| the Nusselt number | |||
| the thermal conductivity of heat convection |
References
- He, Y.L.; Xie, T. Advances of thermal conductivity model of nanoscale silica aerogel insulation material. Appl. Therm. Eng. 2015, 81, 28–50. [Google Scholar] [CrossRef]
- Mao, N.; Ye, J.; Quan, Z.Z.; Zhang, H.N.; Wu, D.Q.; Qin, X.H.; Wang, R.W.; Yu, J.Y. Tree-like structure driven water transfer in 1D fiber assemblies for Functional Moisture-Wicking Fabrics. Mater. Des. 2020, 186, 108305. [Google Scholar] [CrossRef]
- Liang, M.; Fu, C.; Xiao, B.; Luo, L.; Wang, Z. A fractal study for the effective electrolyte diffusion through charged porous media. Int. J. Heat Mass Transf. 2019, 137, 365–371. [Google Scholar] [CrossRef]
- Zhang, N.; Wang, Z.Y. Review of soil thermal conductivity and predictive models. Int. J. Therm. Sci. 2017, 117, 172–183. [Google Scholar] [CrossRef]
- Liu, H.; Zhao, X. Thermal conductivity analysis of high porosity structures with open and closed pores. Int. J. Heat Mass Transfer 2022, 183, 122089. [Google Scholar] [CrossRef]
- Pan, Y.; Zhao, R.; Nian, Y. Study on the flow and heat transfer characteristics of pin-fin manifold microchannel heat sink. Int. J. Heat Mass Transfer 2022, 183, 122052. [Google Scholar] [CrossRef]
- Mandelbrot, B.B. The Fractal Geometry of Nature; W H Freeman: San Francisco, CA, USA, 1982. [Google Scholar]
- Yu, B.M.; Li, J. Some fractal characters of porous media. Fractals 2001, 9, 365–372. [Google Scholar] [CrossRef]
- Yu, B.M.; Lee, L.J.; Cao, H. A fractal in-plane permeability model for fabrics. Polym. Compos. 2002, 23, 201–221. [Google Scholar] [CrossRef]
- Yu, B.M.; Cheng, P. A fractal model for permeability of bi-dispersed porous media. Int. J. Heat Mass Transfer 2002, 45, 2983–2993. [Google Scholar] [CrossRef]
- Zheng, Q.; Wang, H.L.; Guo, X.Y. Research on the effect of surface roughness on gas diffusion coefficient of porous media embedded with a fractal-like tree network. Fractals 2021, 29, 2150195. [Google Scholar] [CrossRef]
- Miao, T.J.; Chen, A.M.; Zhang, L.W. A novel fractal model for permeability of damaged tree-like branching networks. Int. J. Heat Mass Transfer 2018, 127, 278–285. [Google Scholar] [CrossRef]
- Kou, J.L.; Chen, Y.Y.; Zhou, X.Y.; Lu, H.J.; Wu, F.M.; Fan, J.T. Optimal structure of tree-like branching networks for fluid flow. Phys. A 2014, 393, 527–534. [Google Scholar] [CrossRef]
- Zheng, Q.; Wang, H.L.; Jiang, J.; Xu, C. Fractal analysis of surface roughness effects on gas diffusion in porous nanofibers. Fractals 2020, 28, 2050125. [Google Scholar] [CrossRef]
- Zheng, Q.; Yu, B.M.; Wang, S.F.; Luo, L. A diffusivity model for gas diffusion through fractal porous media. Chem. Eng. Sci. 2020, 68, 650–655. [Google Scholar] [CrossRef]
- Zheng, Q.; Xu, J.; Yang, B.; Yu, B.M. Research on the effective gas diffusion coefficient in dry porous media embedded with a fractal-like tree network. Phys. A 2013, 392, 1557–1566. [Google Scholar] [CrossRef]
- Wang, F.Y.; Cheng, H. A fractal permeability model for 2D complex tortuous fractured porous media. J. Pet. Sci. Eng. 2020, 188, 106938. [Google Scholar] [CrossRef]
- Zheng, Q.; Yu, B.M. A fractal permeability model for gas flow through dual-porosity media. J. Appl. Phys. 2012, 111, 024316. [Google Scholar] [CrossRef]
- Zhang, J.; Raza, A.; Khan, U.; Ali, Q.; Zaib, A.; Weera, W.; Galal, A. Thermophysical Study of Oldroyd-B Hybrid Nanofluid with Sinusoidal Conditions and Permeability: A Prabhakar Fractional Approach. Fractal Fract. 2022, 6, 357. [Google Scholar] [CrossRef]
- Xie, B.; Hu, Y.H.; Liu, L.T. Thermal conduction model of asymmetric structural aramid nanofiber aerogel membranes based on fractal theory. Int. J. Heat Mass Transfer 2023, 208, 124086. [Google Scholar] [CrossRef]
- Shi, Q.T.; Feng, C.; Li, B.; Ming, P.W.; Zhang, C.M. Fractal model for the effective thermal conductivity of microporous layer. Int. J. Heat Mass Transfer 2023, 205, 123884. [Google Scholar] [CrossRef]
- Xiao, B.Q. A fractal model for predicting the effective thermal conductivity of roughened porous media with microscale conductivity. Fractals 2021, 29, 2150114. [Google Scholar] [CrossRef]
- Shen, Y.Q.; Xu, P. A generalized thermal conductivity model for unsaturated porous media with fractal geometry. Int. J. Heat Mass Transfer 2020, 152, 119540. [Google Scholar] [CrossRef]
- Jing, D.L.; He, L.; Wang, X.M. Optimization analysis of fractal tree-like microchannel network for electroviscous flow to realize minimum hydraulic resistance. Int. J. Heat Mass Transfer 2018, 125, 749–752. [Google Scholar] [CrossRef]
- Xu, L.; Xu, Y.; Gu, H. Thermal-hydraulic performance of flat-plate microchannel with fractal tree-like structure and self-affine rough wall. Eng. Appl. Comput. Fluid Mech. 2023, 17, e2153174. [Google Scholar] [CrossRef]
- Chen, Y.P.; Cheng, P. Heat transfer and pressure drop in fractal tree-like microchannel nets. Int. J. Heat Mass Transfer 2002, 45, 2643–2648. [Google Scholar] [CrossRef]
- Li, Y.; Yu, B.M. Study of the starting pressure gradient in branching network. Sci. China Technol. Sci. 2010, 53, 2397–2403. [Google Scholar] [CrossRef]
- Zhang, J.; Wang, Y.Z.; Lou, G.; Kou, J.L. A fractal model for effective thermal conductivity of dual-porosity media with randomly distributed tree-like networks. Fractals 2021, 29, 2150146. [Google Scholar] [CrossRef]
- Miao, T.J.; Chen, A.M.; Xu, Y.; Yang, S.S.; Yu, B.M. Optimal structure of damaged tree-like branching networks for the equivalent thermal conductivity. Therm. Sci. 2016, 102, 89–99. [Google Scholar] [CrossRef]
- Xiao, B.Q.; Fang, J.; Long, G.B.; Tao, Y.Z.; Huang, Z.J. Analysis Of Thermal Conductivity Of Damaged Tree-Like Bifurcation Network With Fractal Roughened Surfaces. Fractals 2022, 30, 1–13. [Google Scholar] [CrossRef]
- Shao, Y.H.; Yang, H.; Guo, X.Y.; Wang, H.L.; Zhu, L.M.; Ma, X.; Chen, R.J.; Ruan, S.F.; Ren, L.L.; Zheng, Q. Thermal conductivity model of porous media embedded with a damaged tree-like branching network considering the influence of roughness. Fractal Fract. 2023, 7, 5. [Google Scholar] [CrossRef]
- Xia, Y.L.; Zheng, S.; Yang, S.S.; Yi, S. Analysis on effective thermal conductivity model of porous media with rough fractal-like tree network. J. Cent. China Norm. Univ. 2022, 2, 255–261. [Google Scholar]
- Xu, P.; Yu, B.M.; Yun, M.J.; Zou, M.Q. Heat conduction in fractal tree-like branched networks. Int. J. Heat Mass Transfer 2006, 49, 3746–3751. [Google Scholar] [CrossRef]
- Valvano, J.W.; Allen, J.T.; Bowman, H.F. The simultaneous measurement of thermal conductivity, thermal diffusivity, and perfusion in small volumes of tissue. J. Biomech. Eng. 1984, 106, 192–197. [Google Scholar] [CrossRef] [PubMed]
- Liang, X.G.; Ge, X.S.; Zhang, Y.P. A convenient method of measuring the thermal conductivity of biological tissue. Phys. Med. Biol. 1991, 36, 1599. [Google Scholar] [CrossRef] [PubMed]
- Bhattacharya, A.; Mahajan, R.L. Temperature dependence of thermal conductivity of biological tissues. Physiol. Meas. 2003, 24, 769–783. [Google Scholar] [CrossRef] [PubMed]
- Tien, C.L.; Vafai, K. Convective and radiative heat transfer in porous media. Adv. Appl. Mech. 1989, 27, 225–281. [Google Scholar]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).