Fractional-Order Phase Lead Compensation Multirate Repetitive Control for Grid-Tied Inverters
Abstract
:1. Introduction
- (1)
- A PIMR-MRC controller is introduced to enhance control performance, offering reduced computational load and lower memory consumption for grid-tied inverters. It not only provides a wider stability region but also maintains excellent harmonic suppression performance.
- (2)
- Using an IIR-FL filter to approximate the fractional part of the phase lead step, precise compensation for the phase lag problem in the PIMR-MRC system is achieved.
- (3)
- The proposed FPL-PIMR-MRC scheme not only improves the system stability and the quality of the grid-injected current but also has a fast error convergence rate, because it can accommodate a larger RC gain. A comprehensive analysis of FPL-PIMR-MRC based on an IIR-FL filter, and an FIR-FL filter, respectively, is also provided.
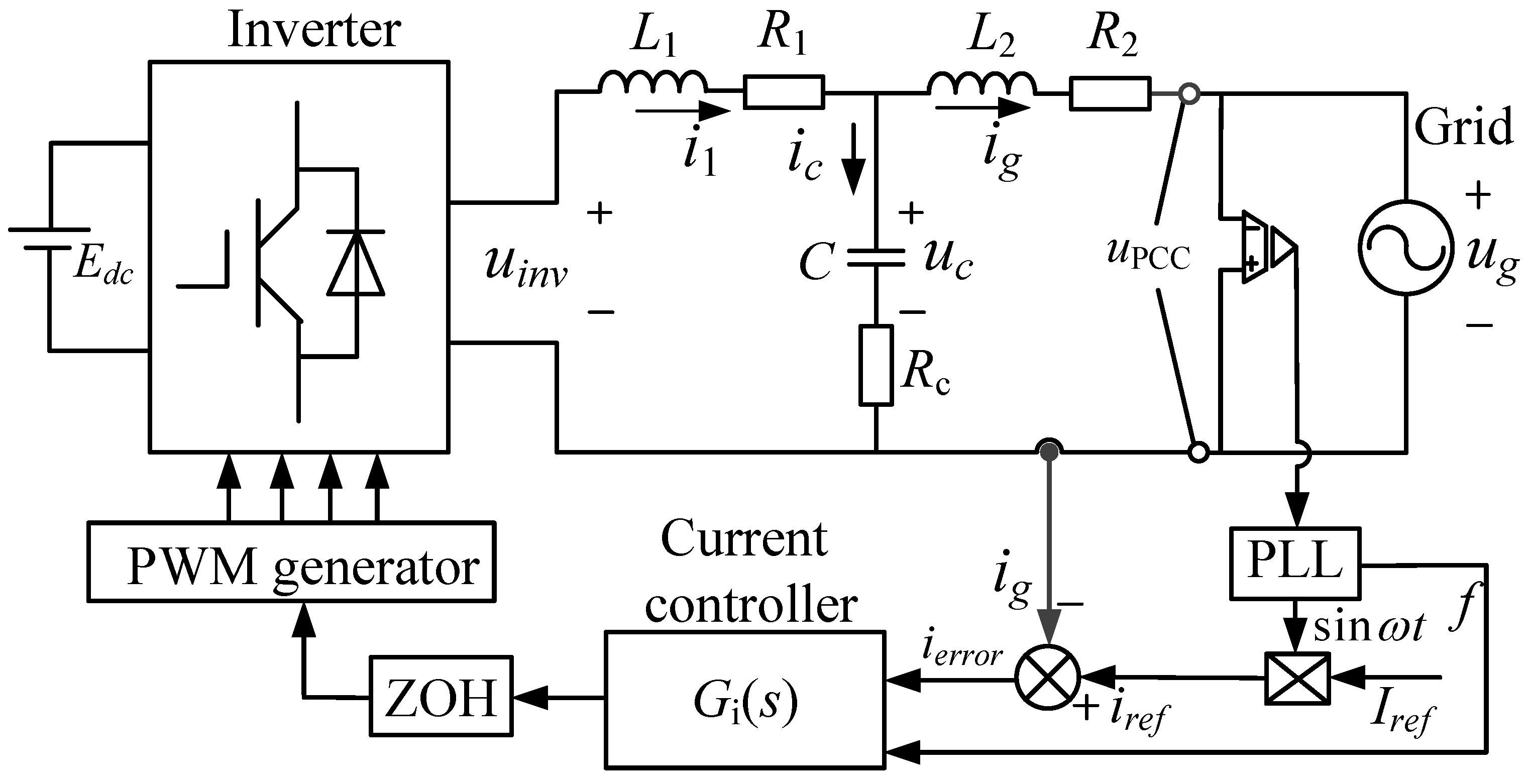
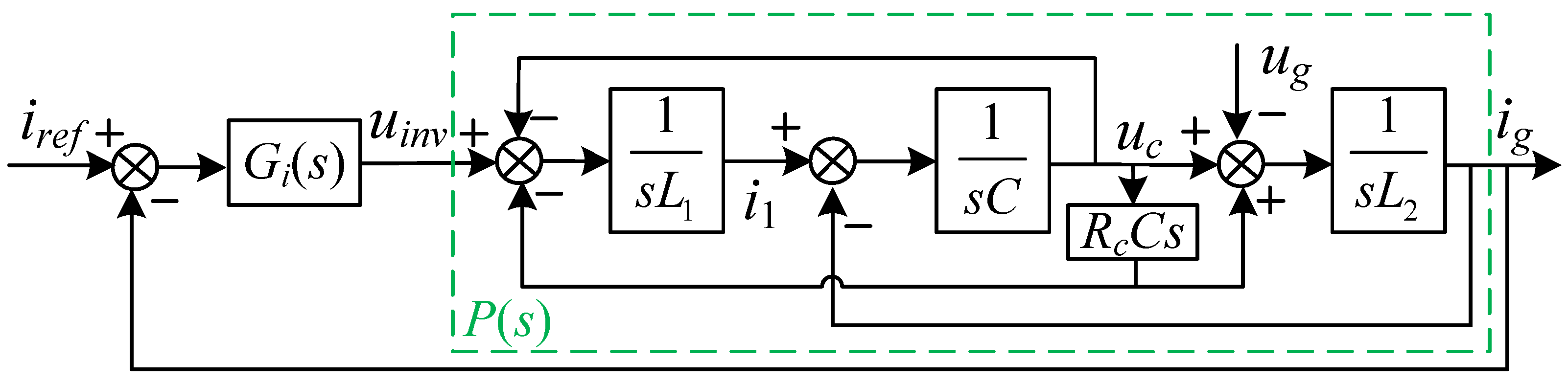
2. Modeling the Single-Phase PWM Inverter
3. Multirate Repetitive Control
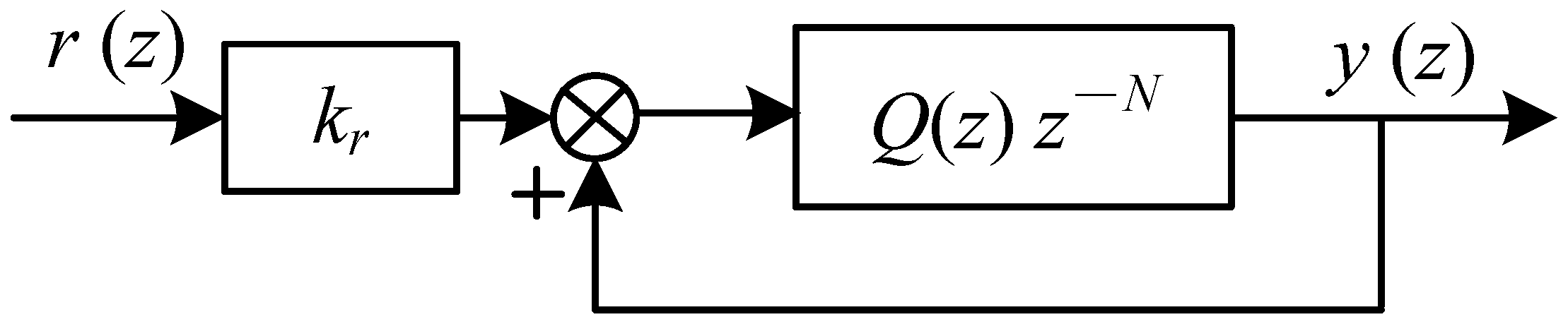
3.1. Conventional Repetitive Control
3.2. Proportional-Integral Multi-Resonant Repetitive Control
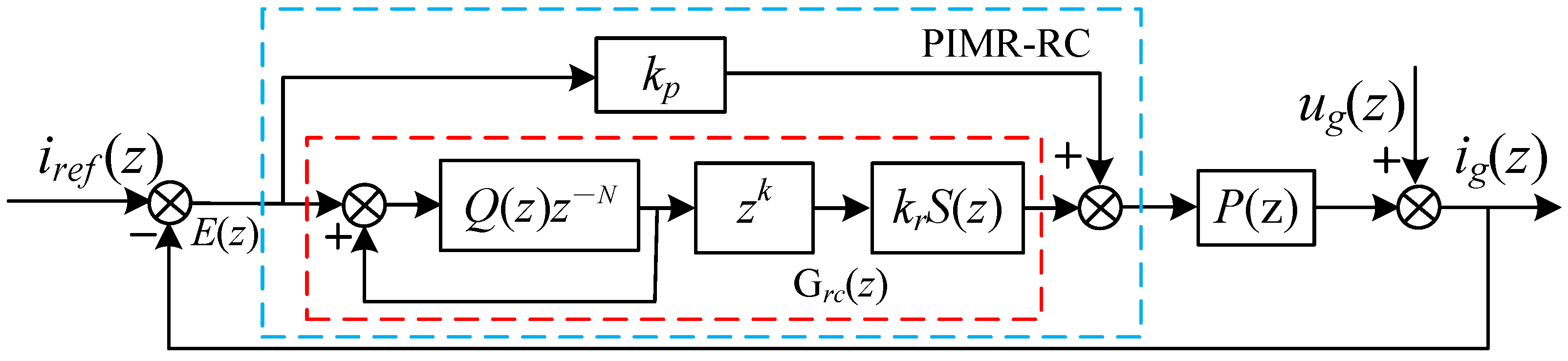
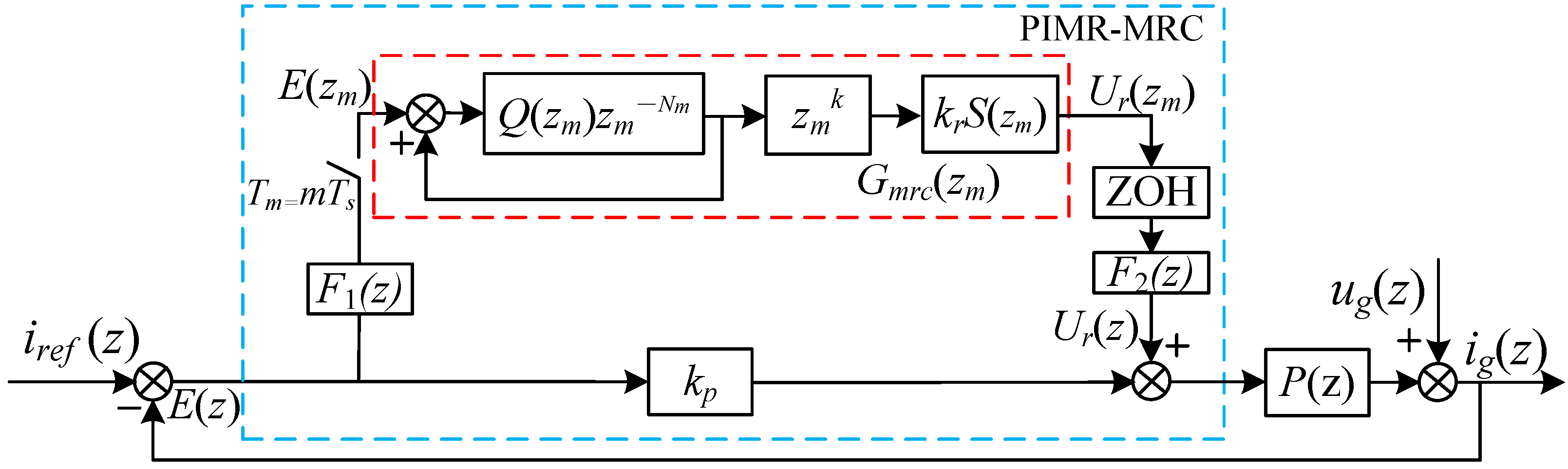
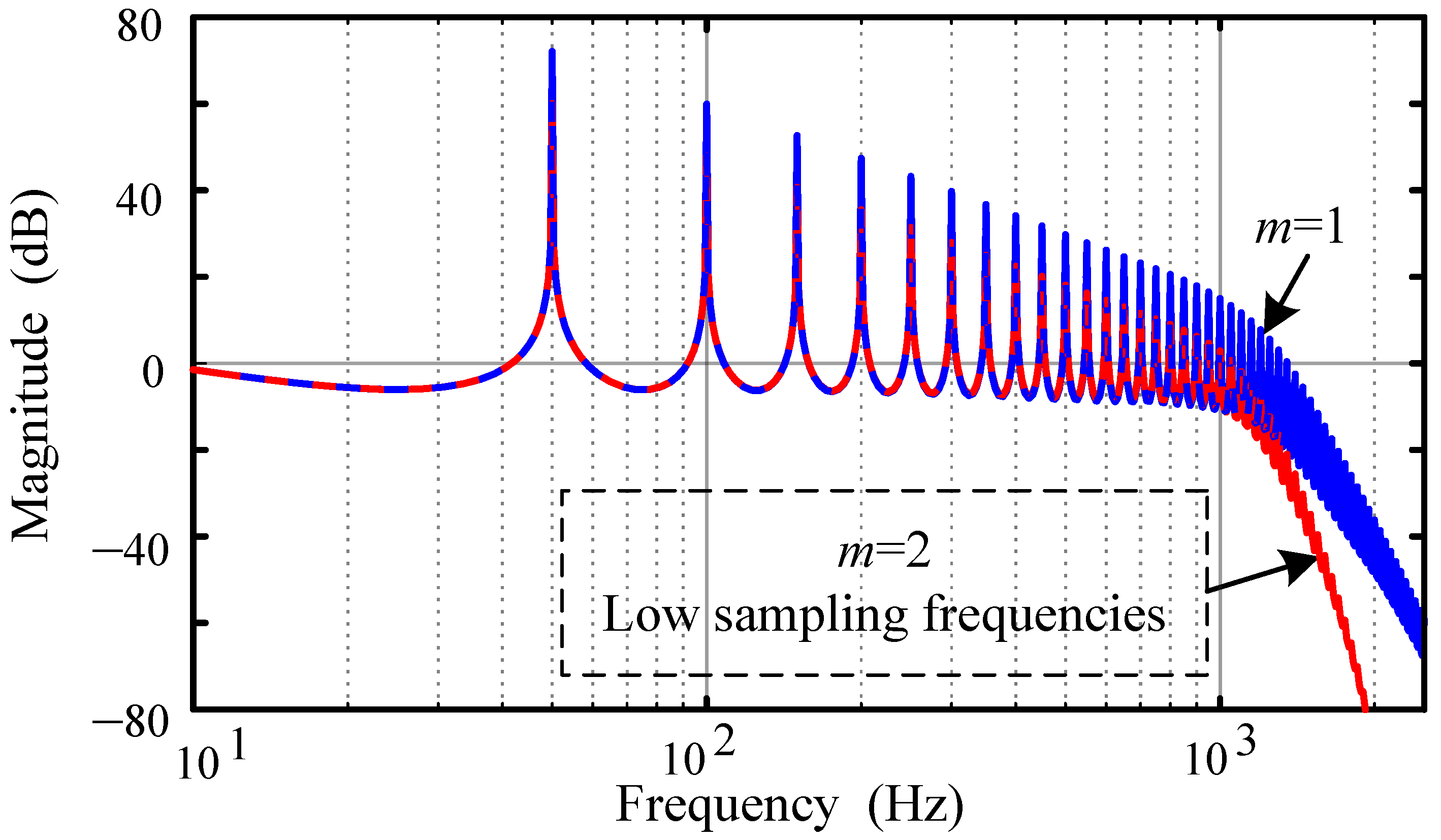
3.3. Proportional-Integral Multi-Resonant Multirate Repetitive Control
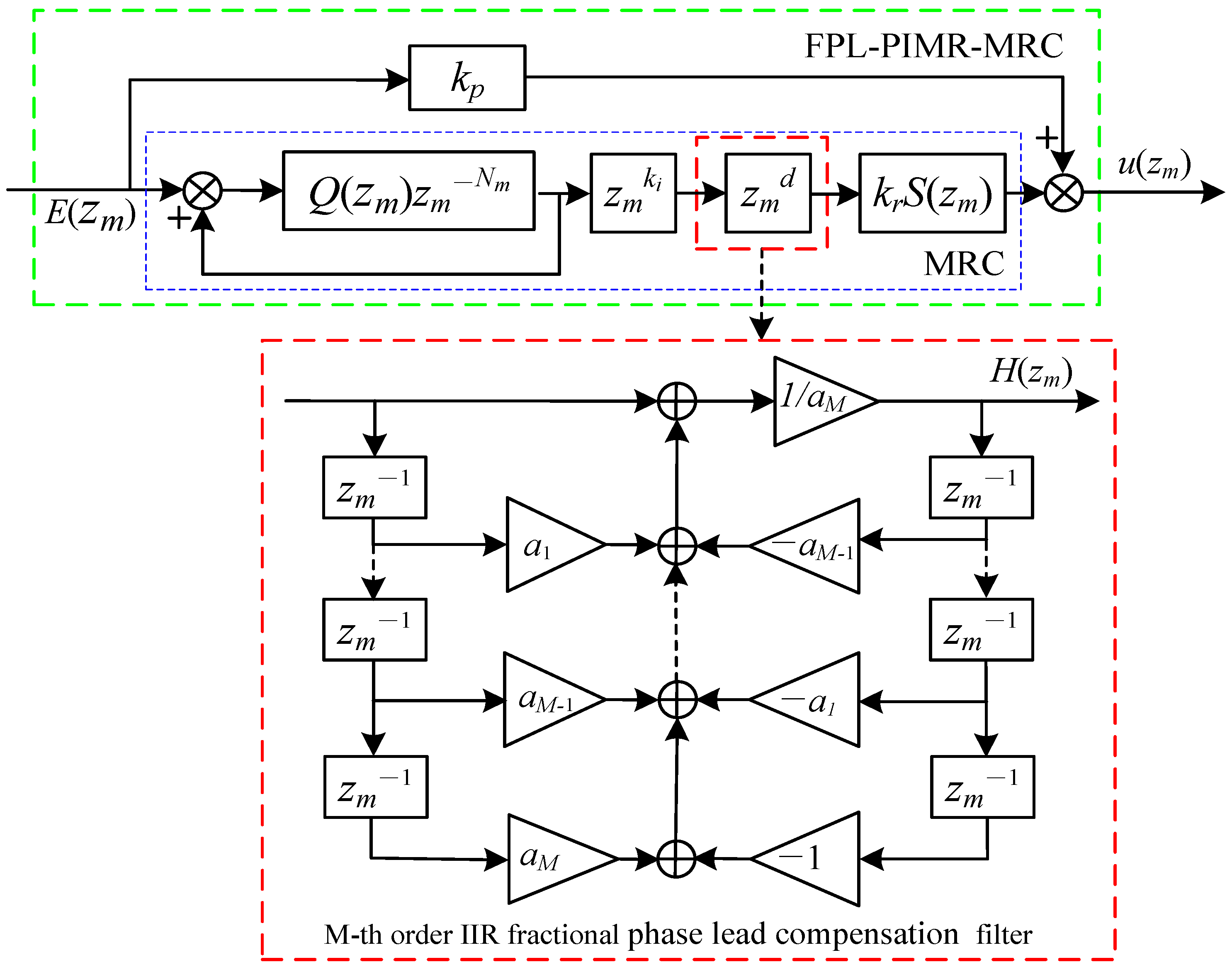
4. Fractional-Order Phase Lead Compensation Multirate Repetitive Control
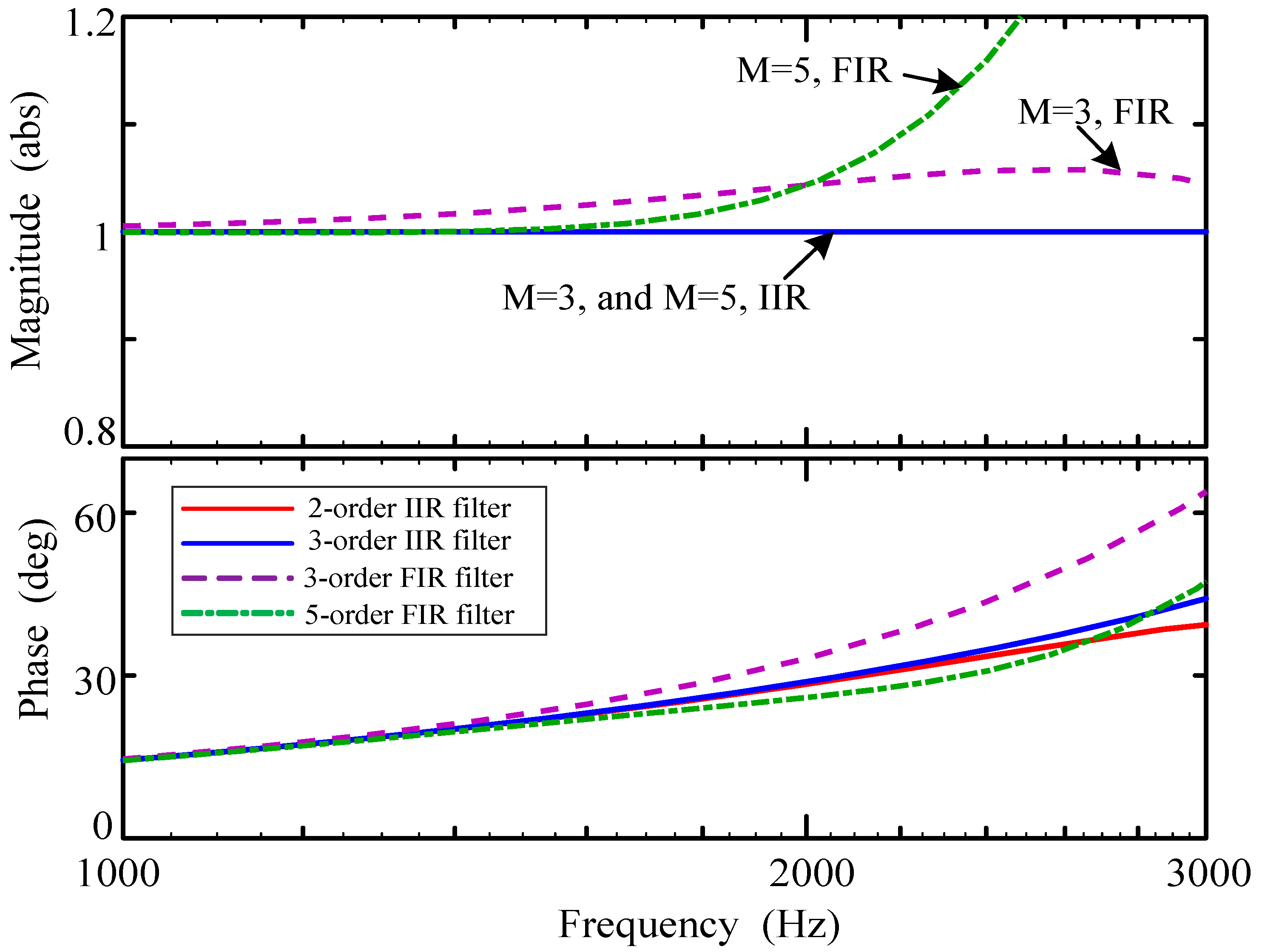
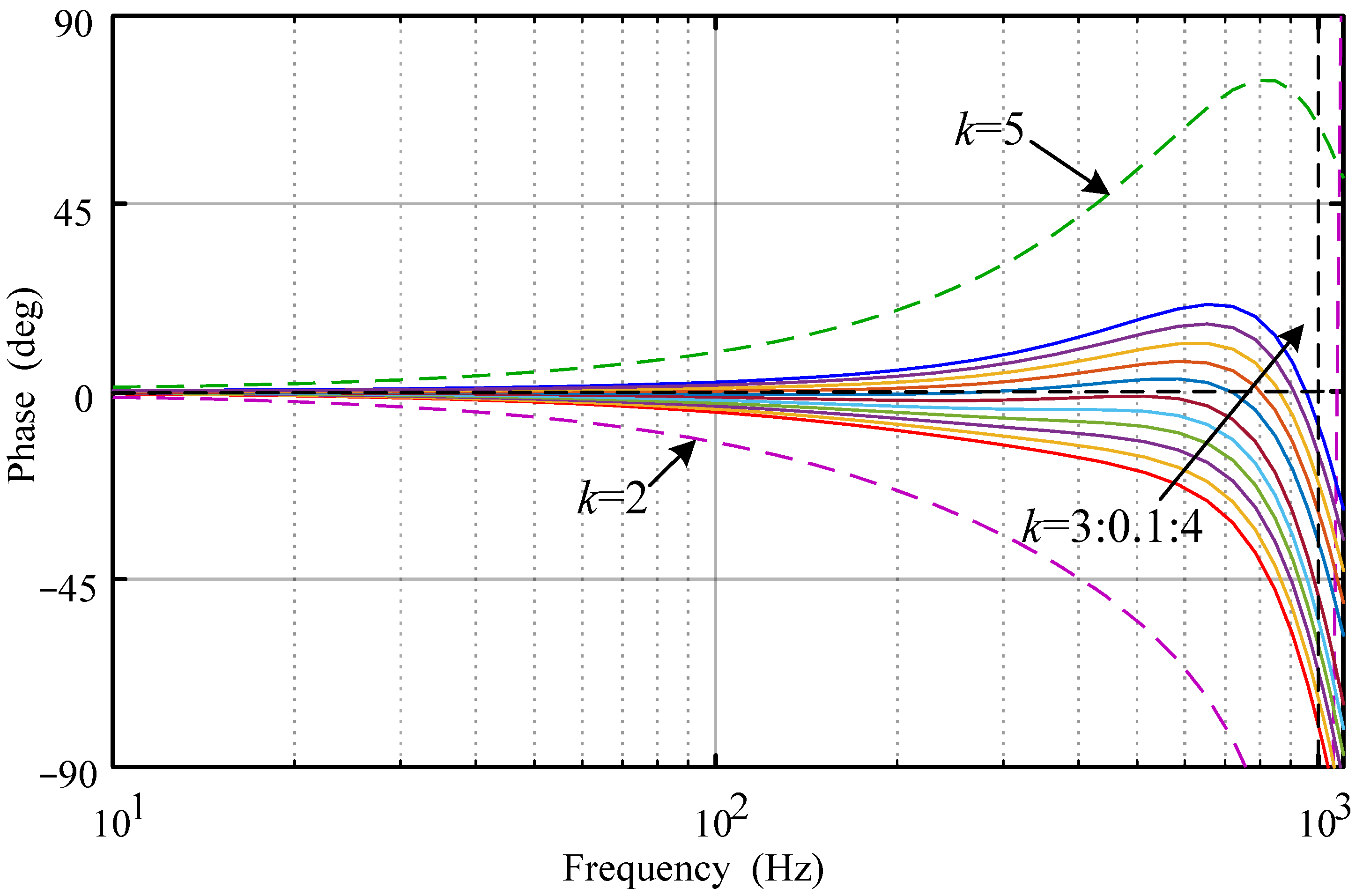
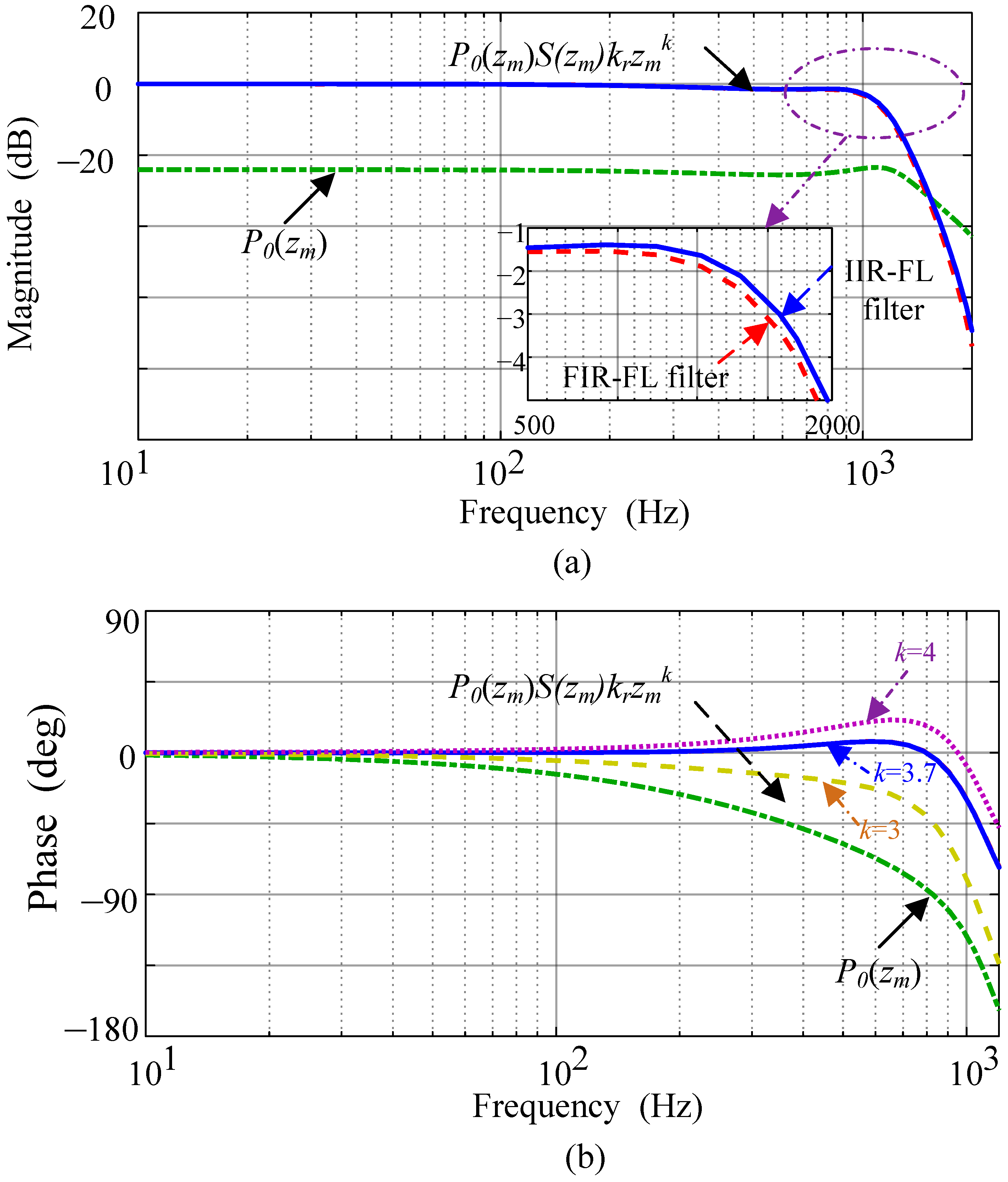
4.1. Design of Fractional-Order Phase Lead Compensation Filter
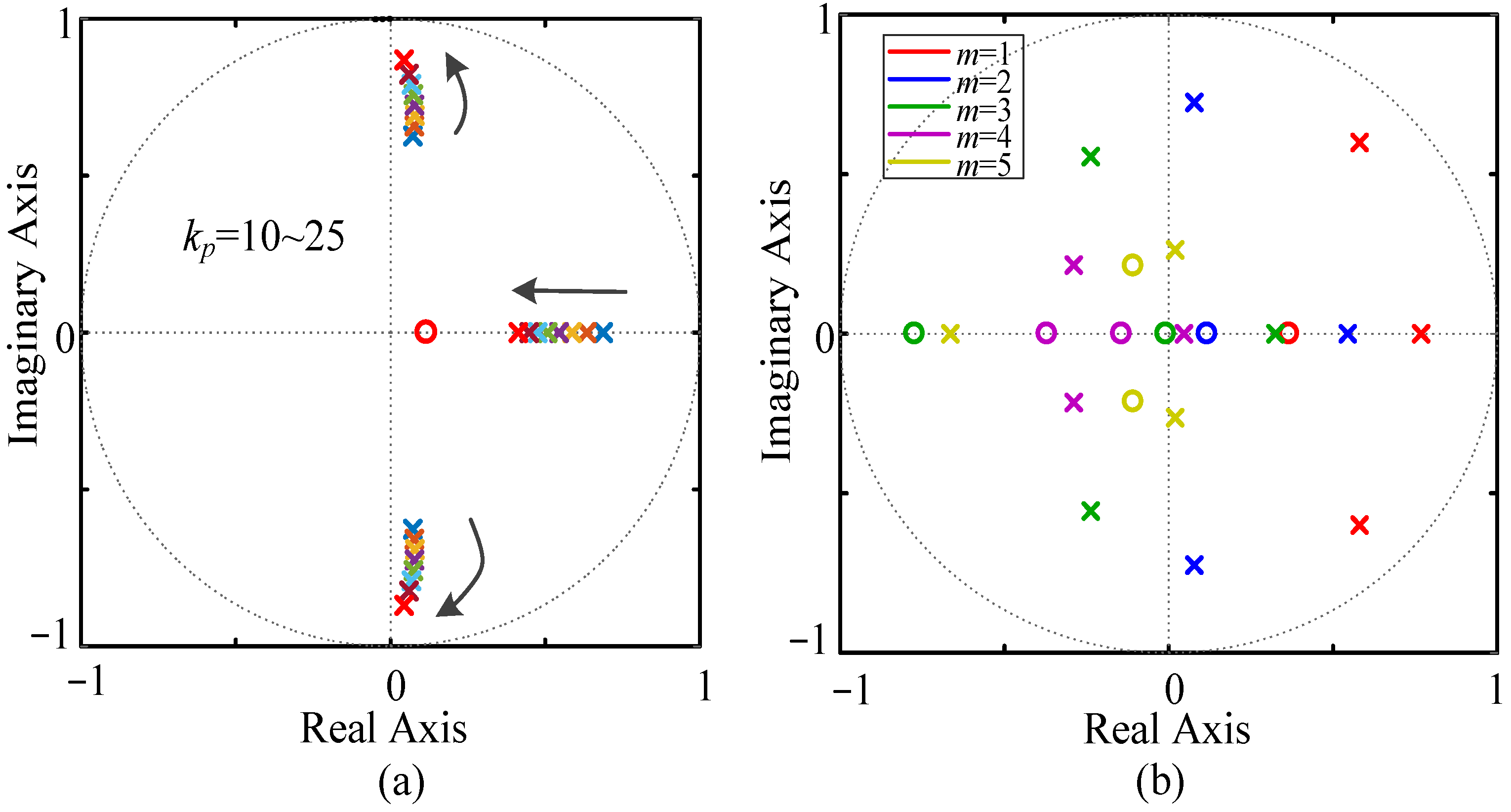
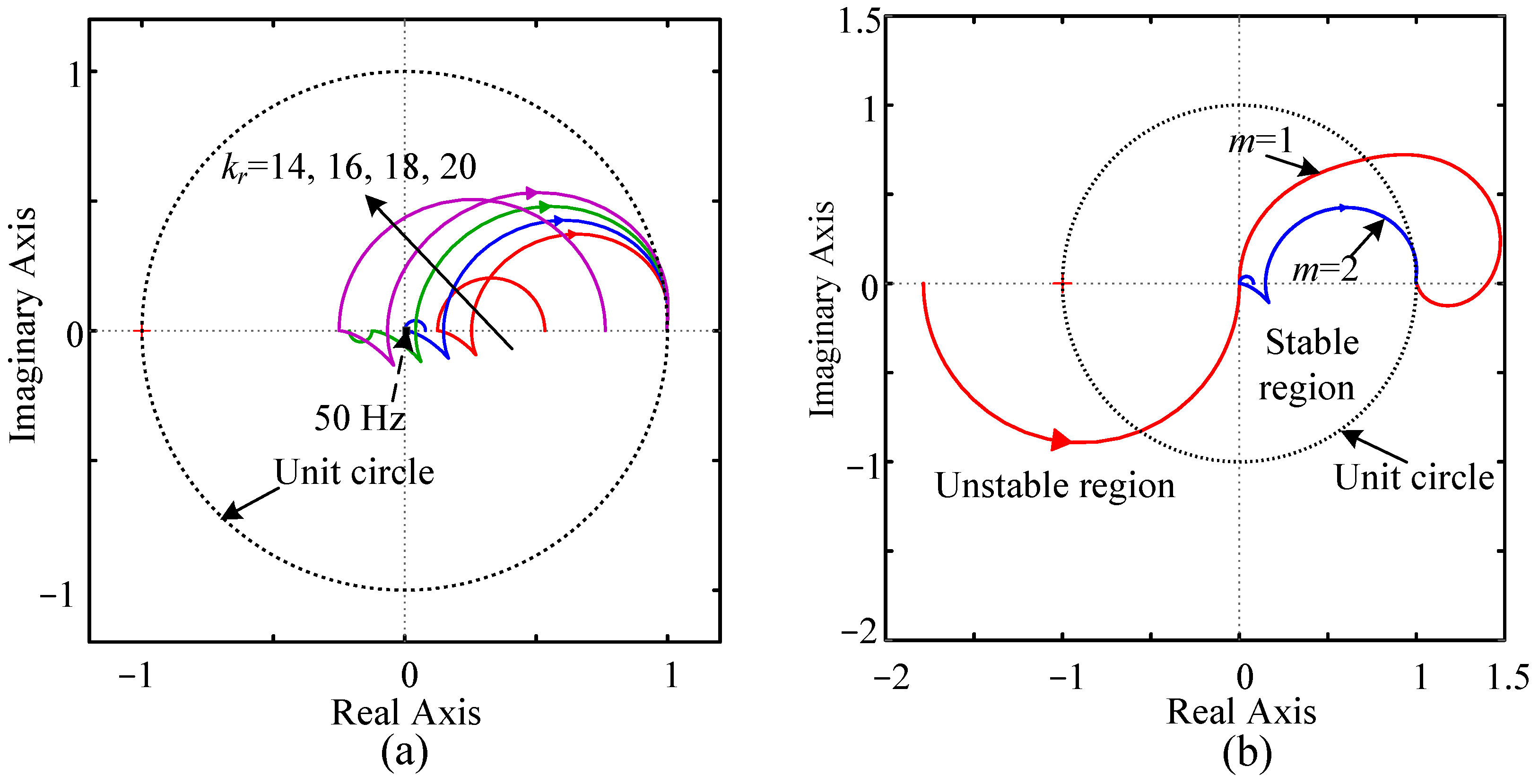
4.2. Stability Analysis of Fractional-Order Phase Lead Proportional-Integral Multi-Resonant Multirate Repetitive Control
5. Parameters Design of Fractional-Order Phase Lead Proportional-Integral Multi-Resonant Multirate Repetitive Control
5.1. Proportional Gain
5.2. Internal Mode Filter
5.3. Low-Pass Filter
5.4. RC Gain and Phase Lead Compensator
6. Simulation
6.1. Steady-State Response
6.2. Transient Response
7. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Abbreviations
| MRC | Multirate repetitive control |
| PIMR-RC | Proportional–integral multi-resonant repetitive control |
| PIMR-MRC | Proportional–integral multi-resonant multirate repetitive control |
| IIR | Infinite impulse response |
| FPL-PIMR-MRC | Fractional-order phase lead proportional–integral multi-resonant multirate repetitive control |
| PWM | Pulse-width modulated |
| THD | Total harmonic distortion |
| FOC | Fractional-order control |
| RC | Repetitive control |
| PI | Proportional integral |
| PR | Proportional resonant |
| SRC | Single-rate repetitive control |
| CRC | Conventional repetitive control |
| APF | Active power filters |
| FIR-FL | Finite impulse response fractional-order lead |
| IIR-FL | Infinite impulse response fractional-order lead |
| PLL | Phase-locked loop |
| PCC | Point of common coupling |
References
- Chen, D.; Zhang, J.; Qian, Z. An Improved Repetitive Control Scheme for Grid-Connected Inverter with Frequency-Adaptive Capability. IEEE Trans. Power Electron. 2013, 60, 814–823. [Google Scholar] [CrossRef]
- Prasad, B.S.; Jain, S.; Agarwal, V. Universal Single-Stage Grid-Connected Inverter. IEEE Trans. Energy Convers. 2008, 23, 128–137. [Google Scholar] [CrossRef]
- Wu, Y.; Ye, Y. Internal Model-Based Disturbance Observer with Application to CVCF PWM Inverter. IEEE Trans. Ind. Electron. 2018, 65, 5743–5753. [Google Scholar] [CrossRef]
- di Benedetto, M.; Faro, A.; Bigarelli, L.; Lidozzi, A.; Solero, L. Constant Delay-Line Frequency Adaptive Repetitive-Resonant Control for Grid-Tied and Intentional Islanding Operations. IEEE Trans. Ind. Appl. 2023, 59, 1944–1955. [Google Scholar] [CrossRef]
- Zhou, K.; Wang, D. Digital Repetitive Learning Controller for Three-Phase CVCF PWM Inverter. IEEE Trans. Ind. Electron. 2001, 48, 820–830. [Google Scholar] [CrossRef]
- Ye, J.; Liu, L.; Xu, J.; Shen, A. Frequency Adaptive Proportional-Repetitive Control for Grid-Connected Inverters. IEEE Trans. Ind. Electron. 2021, 68, 7965–7974. [Google Scholar] [CrossRef]
- Zou, Z.; Zhou, K.; Wang, Z.; Cheng, M. Frequency-Adaptive Fractional-Order Repetitive Control of Shunt Active Power Filters. IEEE Trans. Ind. Electron. 2015, 62, 1659–1668. [Google Scholar] [CrossRef]
- Xu, F.; Zhu, M.; Ye, Y. The Stability of LCL-Type Grid-Tied Inverter Based on Repetitive Control and Grid Voltage Feed-Forward. IEEE J. Emerg. Sel. Top. Power Electron. 2023, 11, 1496–1506. [Google Scholar] [CrossRef]
- Zhang, K.; Kang, Y.; Xiong, J.; Chen, J. Direct Repetitive Control of SPWM Inverter for UPS Purpose. IEEE Trans. Power Electron. 2003, 18, 784–792. [Google Scholar] [CrossRef]
- Yang, Y.; Zhou, K.; Blaabjerg, F. Enhancing the Frequency Adaptability of Periodic Current Controllers with a Fixed Sampling Rate for Grid-Connected Power Converters. IEEE Trans. Power Electron. 2016, 31, 7273–7285. [Google Scholar] [CrossRef]
- Zhao, Q.; Ye, Y. A PIMR-Type Repetitive Control for a Grid-Tied Inverter: Structure, Analysis, and Design. IEEE Trans. Power Electron. 2018, 33, 2730–2739. [Google Scholar] [CrossRef]
- Wu, W.; He, Y.; Blaabjerg, F. An LLCL Power Filter for Single-Phase Grid-Tied Inverter. IEEE Trans. Power Electron. 2012, 27, 782–789. [Google Scholar] [CrossRef]
- Zundert, J.; Oomen, T.; Verhaegh, J.; Aangenent, W.; Antunes, D.J.; Heemels, W.P.M.H. Beyond Performance/Cost Tradeoffs in Motion Control: A Multirate Feedforward Design with Application to a Dual-Stage Wafer System. IEEE Trans. Control Syst. Technol. 2020, 28, 448–461. [Google Scholar] [CrossRef]
- Fujimoto, H.; Kawakami, F.; Kondo, S. Multirate Repetitive Control and Applications. In Proceedings of the American Control Conference, Denver, CO, USA, 4–6 June 2003; pp. 2875–2880. [Google Scholar]
- Xie, C.; Zhao, X.; Savaghebi, M.; Meng, L.; Guerrero, J.M.; Vasquez, J.C. Multirate Fractional-Order Repetitive Control of Shunt Active Power Filter Suitable for Microgrid Applications. IEEE J. Emerg. Sel. Top. Power Electron. 2017, 5, 809–819. [Google Scholar] [CrossRef]
- Zhang, B.; Zhou, K.; Wang, D. Multirate Repetitive Control for PWM DC/AC Converters. IEEE Trans. Ind. Electron. 2014, 61, 2883–2890. [Google Scholar] [CrossRef]
- Zeng, C.; Li, S.; Wang, H.; Miao, H. A Fractional Phase Compensation Scheme of PRMRC for LCL Inverter Connected to Weak Grid. IEEE Access 2021, 9, 167027–167038. [Google Scholar] [CrossRef]
- Ohnishi, W.; Strijbosch, N.; Oomen, T. Multirate State Tracking for Improving Inters ample Behavior in Iterative Learning Control. In Proceedings of the IEEE International Conference on Mechatronics (ICM), Kashiwa, Japan, 7–9 March 2021; pp. 1–6. [Google Scholar]
- Sadegh, N.; Hu, A.; James, C. Synthesis, Stability Analysis, and Experimental Implementation of a Multirate Repetitive Learning Controller. J. Dyn. Syst. Meas. Control 2002, 124, 668–674. [Google Scholar] [CrossRef]
- Chen, S.; Zhao, Q.; Ye, Y.; Qu, B. Using IIR Filter in Fractional Order Phase Lead Compensation PIMR-RC for Grid-Tied Inverters. IEEE Trans. Ind. Electron. 2023, 70, 9399–9409. [Google Scholar] [CrossRef]
- Zhao, Q.; Ye, Y. Fractional Phase Lead Compensation RC for an Inverter: Analysis, Design, and Verification. IEEE Trans. Ind. Electron. 2017, 64, 3127–3136. [Google Scholar] [CrossRef]
- Han, B.; Lai, J.; Kim, M. Down-Sampled Repetitive Controller for Grid-Connected Ćuk CCM Inverter. IEEE Trans. Emerg. Sel. Top. Power Electron. 2022, 10, 1125–1137. [Google Scholar] [CrossRef]
- Kurniawan, E.; Cao, Z.; Man, Z. Design of Robust Repetitive Control with Time-varying Sampling Periods. IEEE Trans. Ind. Electron. 2014, 61, 2834–2841. [Google Scholar] [CrossRef]
- Liu, Z.; Zhang, B.; Zhou, K. Universal Fractional-Order Design of Linear Phase Lead Compensation Multirate Repetitive Control for PWM Inverters. IEEE Trans. Ind. Electron. 2017, 64, 7132–7140. [Google Scholar] [CrossRef]
- Zou, Z.; Wang, Z.; Cheng, M. Modeling, Analysis, and Design of Multifunction Grid-Interfaced Inverters with Output LCL Filter. IEEE Trans. Power Electron. 2014, 29, 3830–3839. [Google Scholar] [CrossRef]
- Albalawi, H.; Bakeer, A.; Zaid, S.A.; Aggoune, E.-H.; Ayaz, M.; Bensenouci, A.; Eisa, A. Fractional-Order Model-Free Predictive Control for Voltage Source Inverters. Fractal Fract. 2023, 7, 433. [Google Scholar] [CrossRef]
- Azghandi, M.A.; Barakati, S.M.; Yazdani, A. Passivity-Based Design of a Fractional-Order Virtual Capacitor for Active Damping of Multiparalleled Grid-Connected Current-Source Inverters. IEEE Trans. Power Electron. 2022, 37, 7809–7818. [Google Scholar] [CrossRef]
- Roohi, M.; Zhang, C.; Taheri, M.; Basse-O’Connor, A. Synchronization of Fractional-Order Delayed Neural Networks Using Dynamic-Free Adaptive Sliding Mode Control. Fractal Fract. 2023, 7, 682. [Google Scholar] [CrossRef]
- Fečkan, M.; Wang, J.; Pospíšil, M. Fractional-Order Equations and Inclusions; Walter de Gruyter GmbH & Co KG: Berlin, Germany; Boston, MA, USA, 2017; pp. 37–90. [Google Scholar]
- Micula, S. An iterative numerical method for fractional integral equations of the second kind. J. Comput. Appl. Math. 2018, 339, 124–133. [Google Scholar] [CrossRef]
- Jafari, H.; Tuan, N.A.; Ganji, R.M. A new numerical scheme for solving pantograph type nonlinear fractional integro-differential equations. J. King Saud Univ. Sci. 2021, 33, 101185. [Google Scholar] [CrossRef]
- Moumen, A.; Mennouni, A.; Bouye, M. A Novel Vieta–Fibonacci Projection Method for Solving a System of Fractional Integrodifferential Equations. Mathematics 2023, 11, 3985. [Google Scholar] [CrossRef]
- Xiong, Y.; Ye, Y.; Zhu, M. UDE-Based Current Controller with Enhanced Grid Frequency Fluctuation Adaptability for LCL-Type Grid-Tied Inverters. IEEE Trans. Power Electron. 2023, 38, 1683–1691. [Google Scholar] [CrossRef]
- Solatialkaran, D.; Khajeh, K.G.; Zare, F. A Novel Filter Design Method for Grid-Tied Inverters. IEEE Trans. Power Electron. 2021, 36, 5473–5485. [Google Scholar] [CrossRef]
- Zhang, Z.; Chu, B.; Liu, Y.; Ren, H.; Li, Z.; Owens, D.H. Multiperiodic Repetitive Control for Functional Electrical Stimulation-Based Wrist Tremor Suppression. IEEE Trans. Control Syst. Technol. 2022, 30, 1494–1509. [Google Scholar] [CrossRef]
- Guo, Q.; Wang, J.; Ma, H. Frequency Adaptive Repetitive Controller for Grid-Connected Inverter with an All-pass Infinite Impulse Response (IIR) filter. In Proceedings of the IEEE 23rd International Symposium on Industrial Electronics (ISIE), Istanbul, Turkey, 1–4 June 2014; pp. 491–496. [Google Scholar]
- Shukl, P.; Singh, B. Combined IIR and FIR Filter for Improved Power Quality of PV Interfaced Utility Grid. IEEE Trans. Ind. Appl. 2021, 57, 774–783. [Google Scholar] [CrossRef]
- Huang, L.; Yang, J.; Wei, K.; Chen, Z.; Zhang, X. Peak Cancellation Method with IIR Filters and Its FPGA Implementation. IEEE Trans. Circuits Syst. II Express Briefs 2023, 70, 3704–3708. [Google Scholar] [CrossRef]
- Valimaki, V.; Laakso, T.I. Principles of Fractional Delay Filters. In Proceedings of the IEEE International Conference on Acoustics, Speech, and Signal Processing, Istanbul, Turkey, 5–9 June 2000; Volume 6, pp. 3870–3873. [Google Scholar]
- Zhao, Q.; Zhang, H.; Gao, Y.; Chen, S.; Wang, Y. Novel Fractional-Order Repetitive Controller Based on Thiran IIR Filter for Grid-Connected Inverters. IEEE Access 2022, 10, 82015–82024. [Google Scholar] [CrossRef]
- Zhao, Q.; Liu, K.; Li, H. A Fractional-Order Multi-Rate Repetitive Controller for Single-Phase Grid-Connected Inverters. Electronics 2023, 12, 1021. [Google Scholar] [CrossRef]





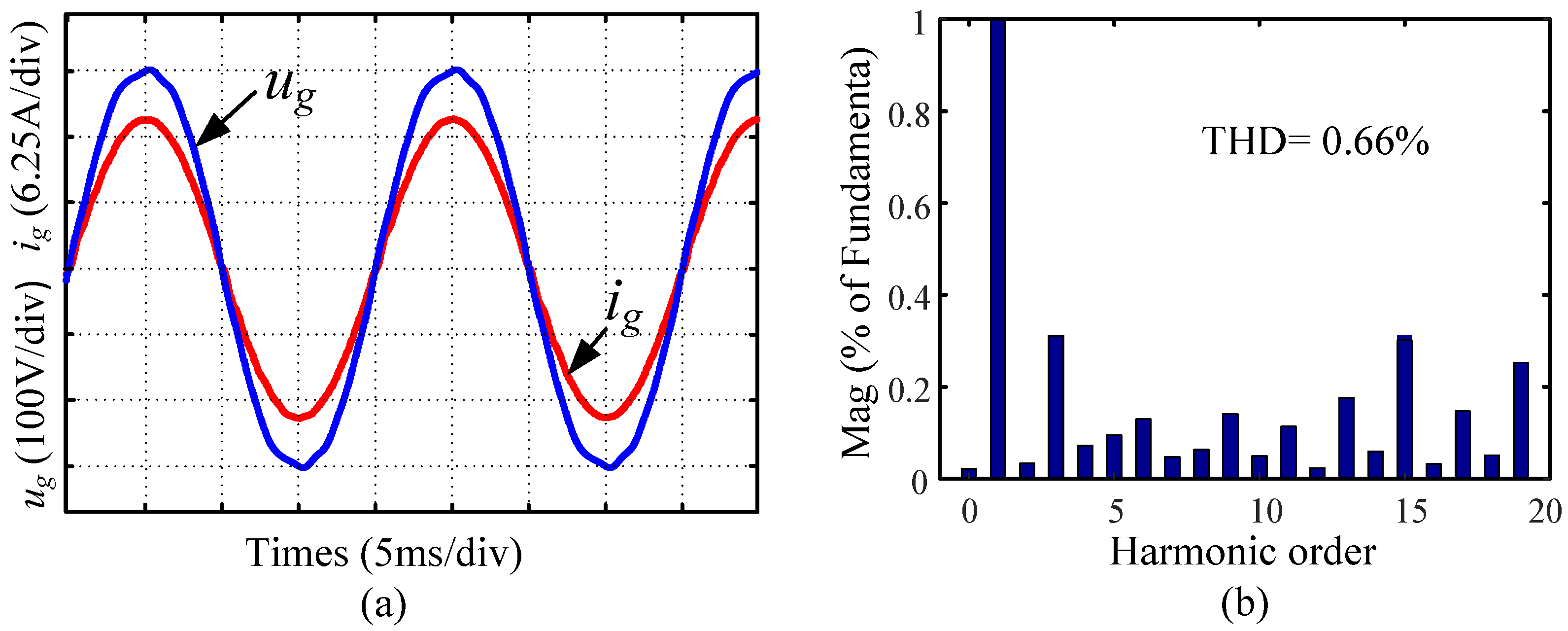

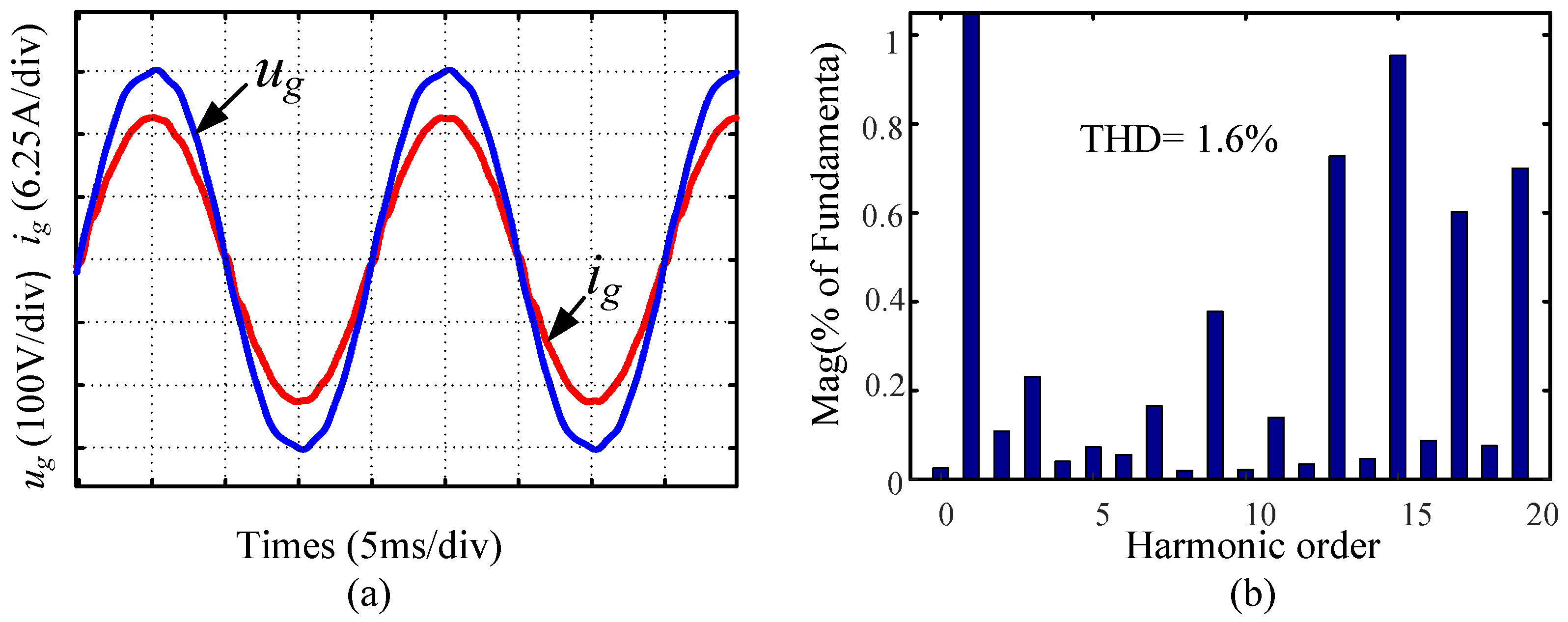


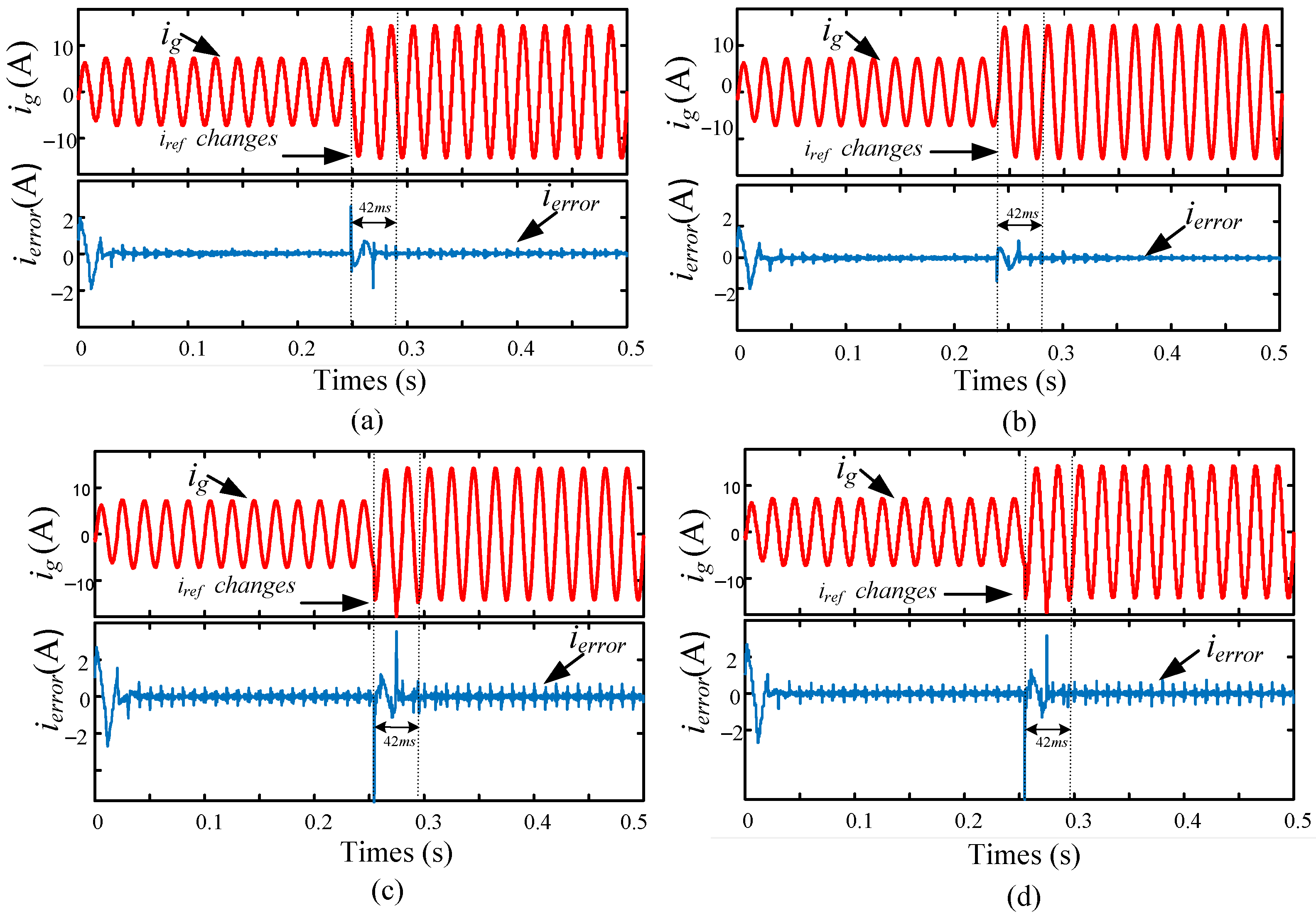
| Parameters | Symbols | Values |
|---|---|---|
| DC-link voltage | 380 V | |
| RMS value of grid voltage | 220 V | |
| Inverter side inductor | 3.8 mH | |
| Grid side inductor | 2.3 mH | |
| Capacitor | C | 10 F |
| equivalent resistance | 0.48 | |
| equivalent resistance | 0.32 | |
| Passive damping resistance | 10 | |
| Grid frequency | 50 Hz | |
| Switching frequency | 10 kHz | |
| Sampling frequency | 10 kHz | |
| Switching dead time | − | 3 s |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liang, F.; Lee, H.-J.; Zhang, H. Fractional-Order Phase Lead Compensation Multirate Repetitive Control for Grid-Tied Inverters. Fractal Fract. 2023, 7, 848. https://doi.org/10.3390/fractalfract7120848
Liang F, Lee H-J, Zhang H. Fractional-Order Phase Lead Compensation Multirate Repetitive Control for Grid-Tied Inverters. Fractal and Fractional. 2023; 7(12):848. https://doi.org/10.3390/fractalfract7120848
Chicago/Turabian StyleLiang, Fen, Ho-Joon Lee, and Hongwei Zhang. 2023. "Fractional-Order Phase Lead Compensation Multirate Repetitive Control for Grid-Tied Inverters" Fractal and Fractional 7, no. 12: 848. https://doi.org/10.3390/fractalfract7120848
APA StyleLiang, F., Lee, H.-J., & Zhang, H. (2023). Fractional-Order Phase Lead Compensation Multirate Repetitive Control for Grid-Tied Inverters. Fractal and Fractional, 7(12), 848. https://doi.org/10.3390/fractalfract7120848








