An Analysis of the Effects of Lifestyle Changes by Using a Fractional-Order Population Model of the Overweight/Obese Diabetic Population
Abstract
:1. Introduction
- When —cells that synthesize and release insulin and amylin in pancreatic islets become extinct, it results in type 1 diabetes, which is also known as insulin-dependent diabetes (IDD), which is characterized by insufficient insulin production and hyperglycemia.
- Type 2 diabetes, also known as non-insulin-dependent diabetes (NIDD), has a variety of causes, with heredity and lifestyle being two of the most crucial causes.
- —Population of overweight/obese adults;
- —Adult population of diabetics without complications;
- —Adult population of diabetics with complications;
- —The prevalence of the population of adults;
- —The frequency of healthy people suffering from difficulties;
- —The rate at which healthy people develop diabetes;
- —The frequency of complications emerging in persons with diabetes;
- —The ratio of healthy people who become overweight or obese;
- —The ratio of overweight or obese people who become healthy;
- —The ratio of overweight or obese people who become diabetic;
- —The ratio of overweight or obese people who develop complications;
- —The rate of natural mortality;
- —The mortality rate due to complications.
- —Number of people not following a healthy lifestyle ( overweight/obese) on a regular basis;
- —Number of people with diabetes without any complication;
- —Number of people with diabetes with complications;
- —The prevalence of the population;
- —The rate at which individuals following a healthy lifestyle are unable to maintain it regularly and become obese;
- —The ratio of obese people who do not follow a healthy lifestyle regularly and become diabetic;
- —The rate at which individuals following a healthy lifestyle are able to control obesity;
- —The ratio of obese/overweight people who do not follow a healthy lifestyle and develop diabetes with complications;
- — The rate at which people following a healthy lifestyle on a daily basis develop diabetes without complications;
- — The frequency of complications emerging in persons with diabetes; —The rate of natural mortality;
- —The rate at which diabetics with complications die or are removed due to permanent disability;
- —The probability rate at which people following a healthy lifestyle go into the remission category can be seen as the rate at which pre-diabetic individuals do not become diabetic by adopting a healthy lifestyle;
- —The probability rate at which diabetic patients without complications fall into the remission category by regularly applying a healthy lifestyle.
2. Preliminaries and Notations
- For , the integral is called the identity operator as
- Unless specified, we will use
- The integral for the power function is defined as
- The Riemann–Liouville fractional derivative of the constant is
- The Riemann–Liouville σ order fractional derivative for the power function is defined as
3. Model Validation and Stability Analysis
3.1. Existence and Uniqueness
3.2. Non-Negativity and Boundedness
3.3. Equilibrium Points and Stability Analysis
4. Solution and Simulation
4.1. Approximate Solution
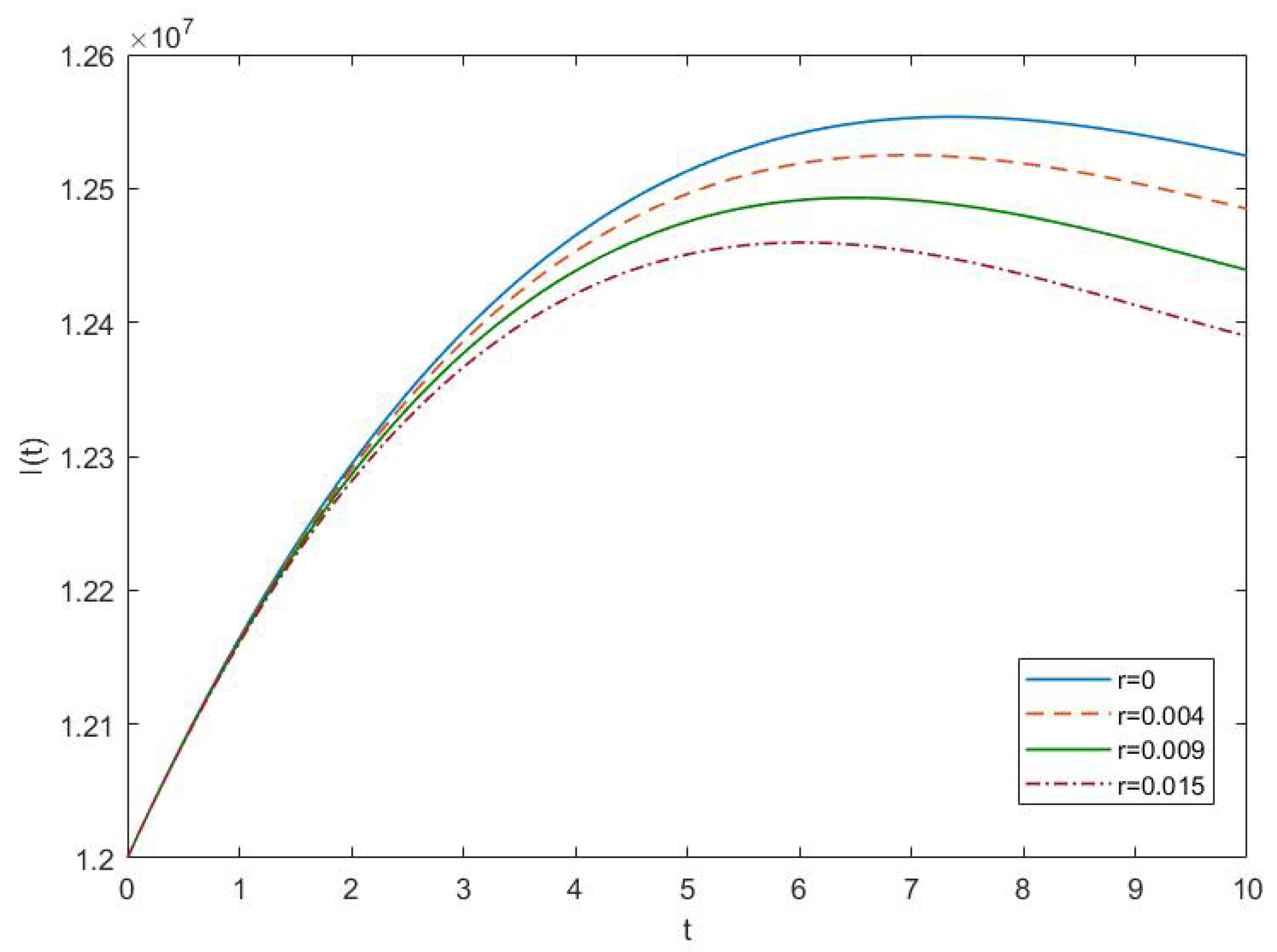
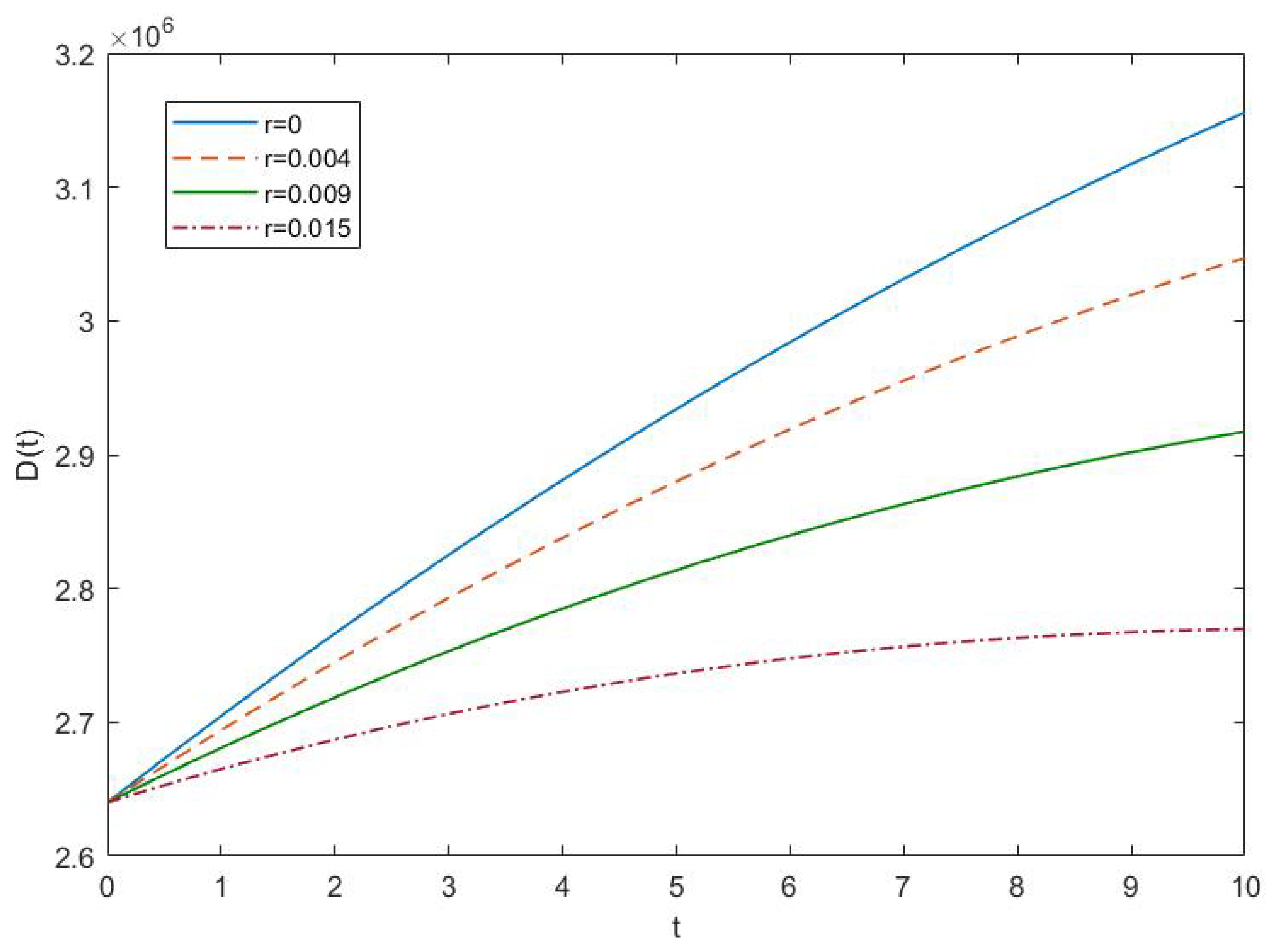
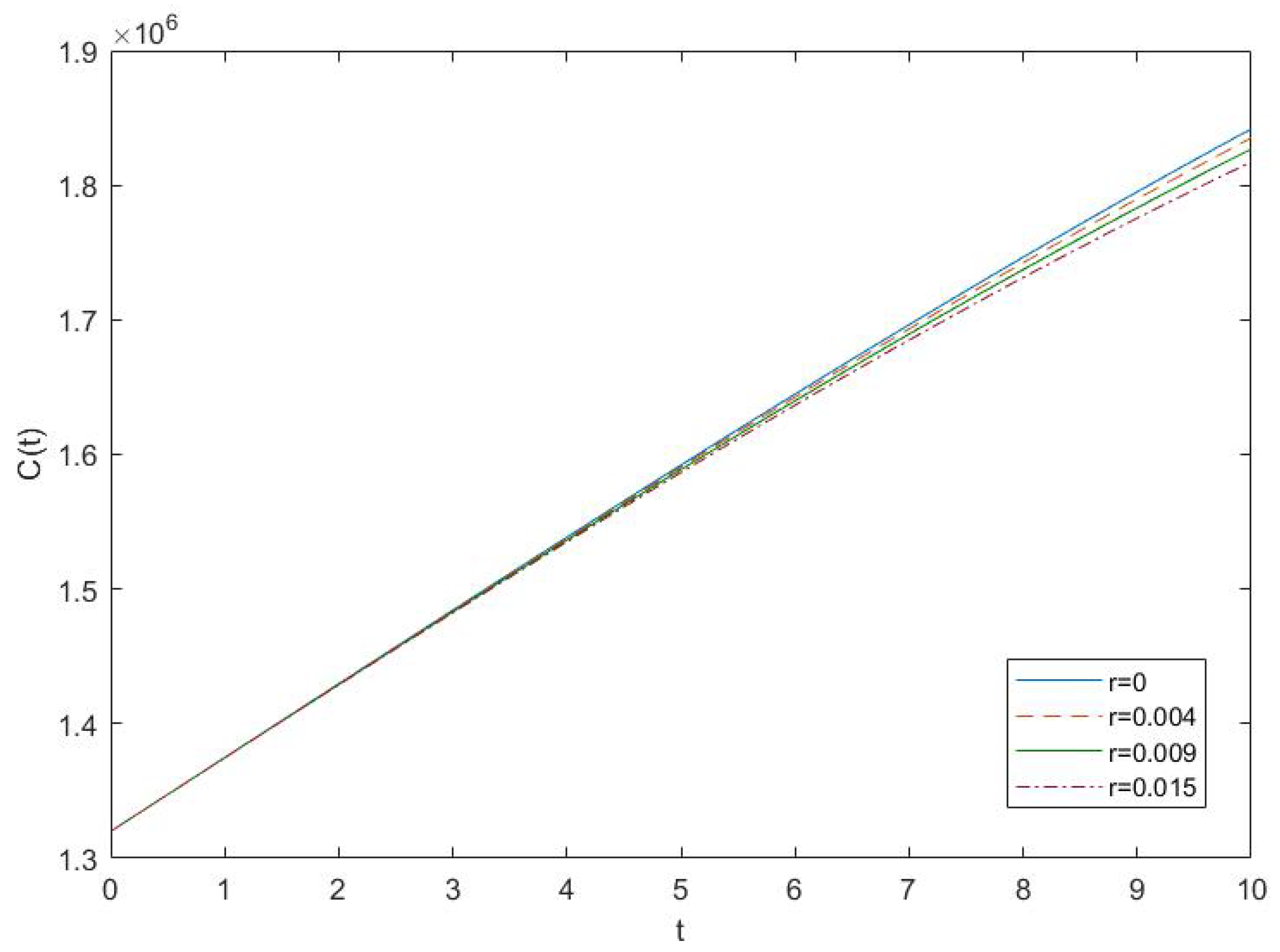
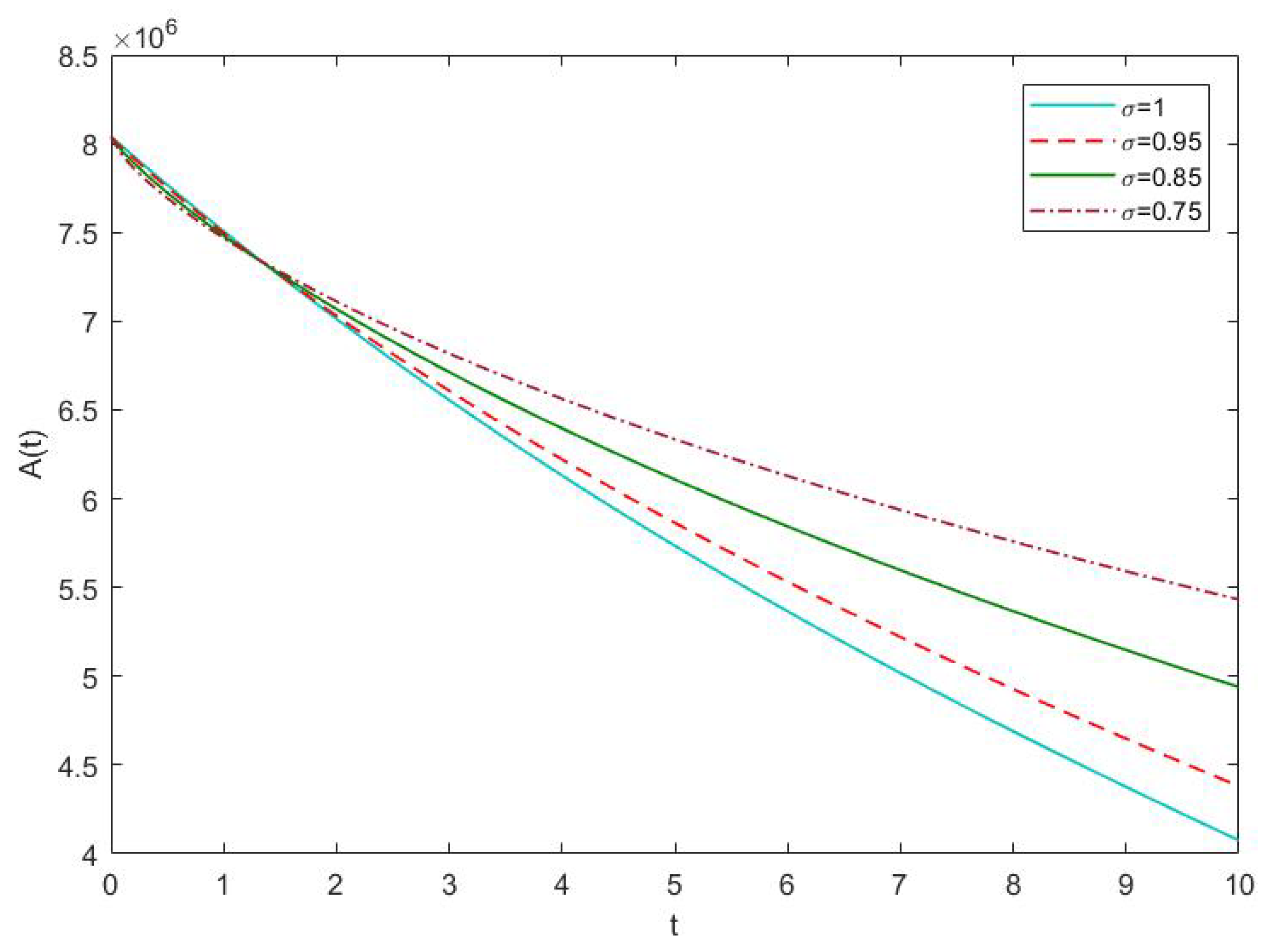
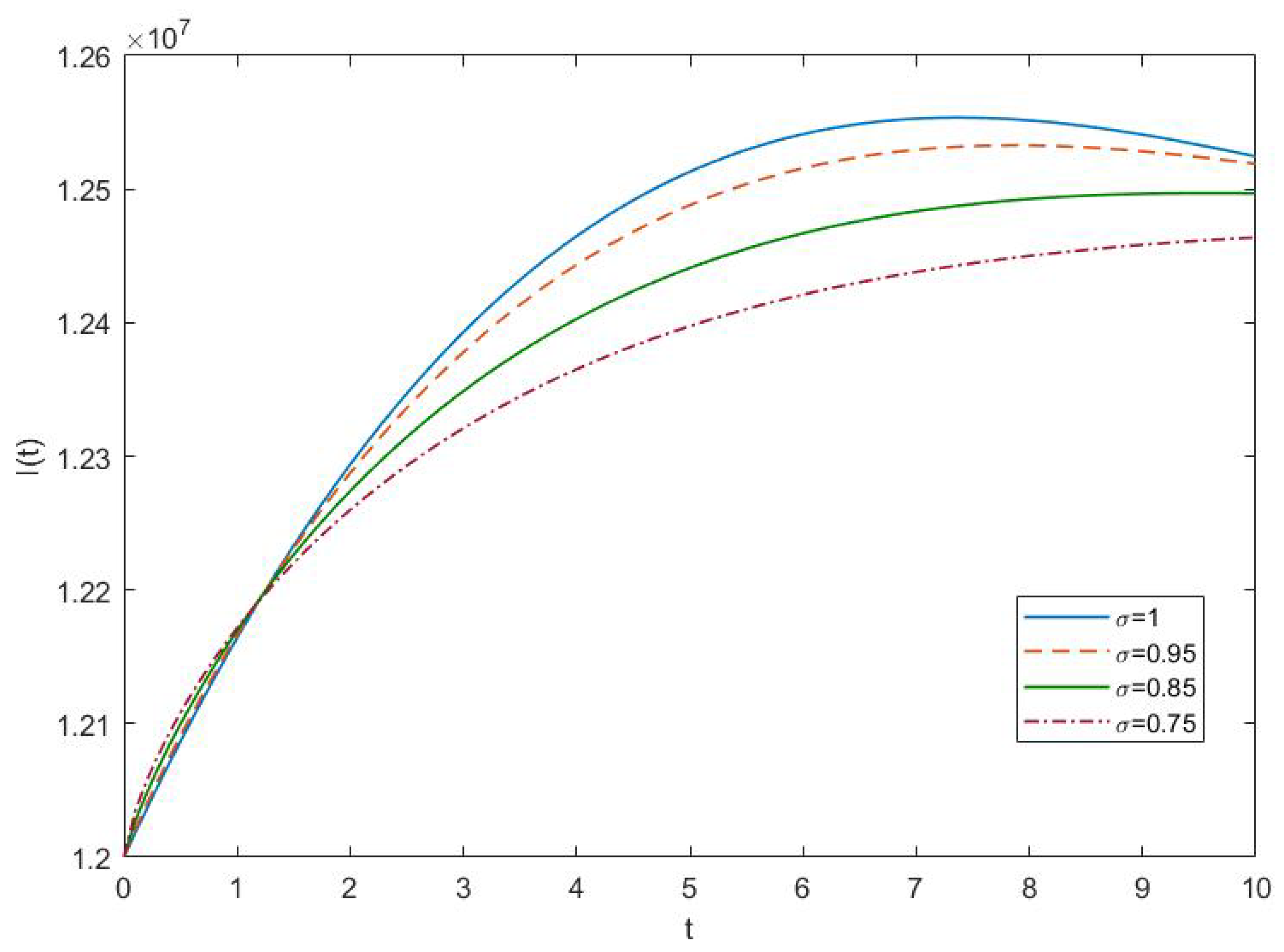
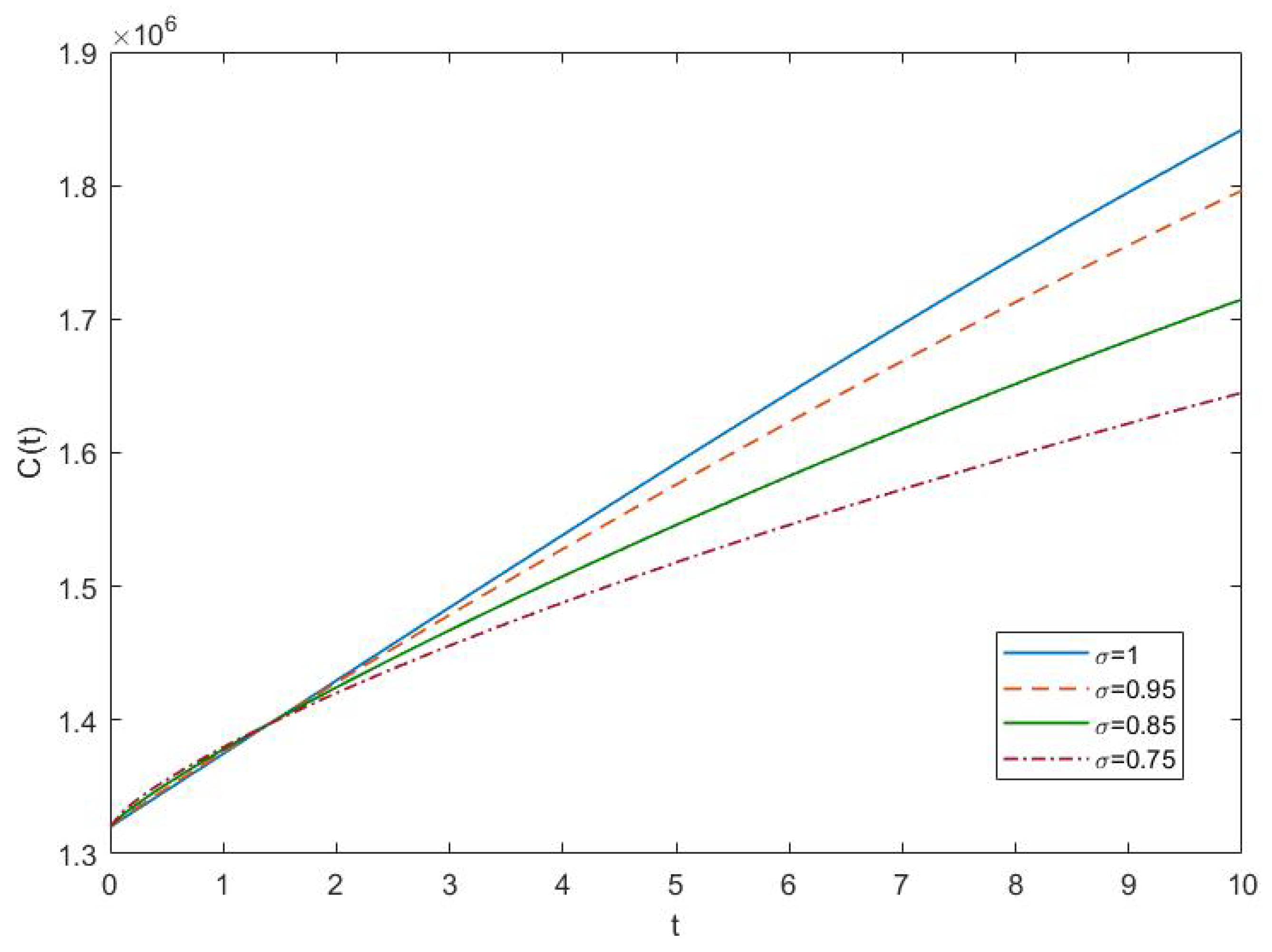
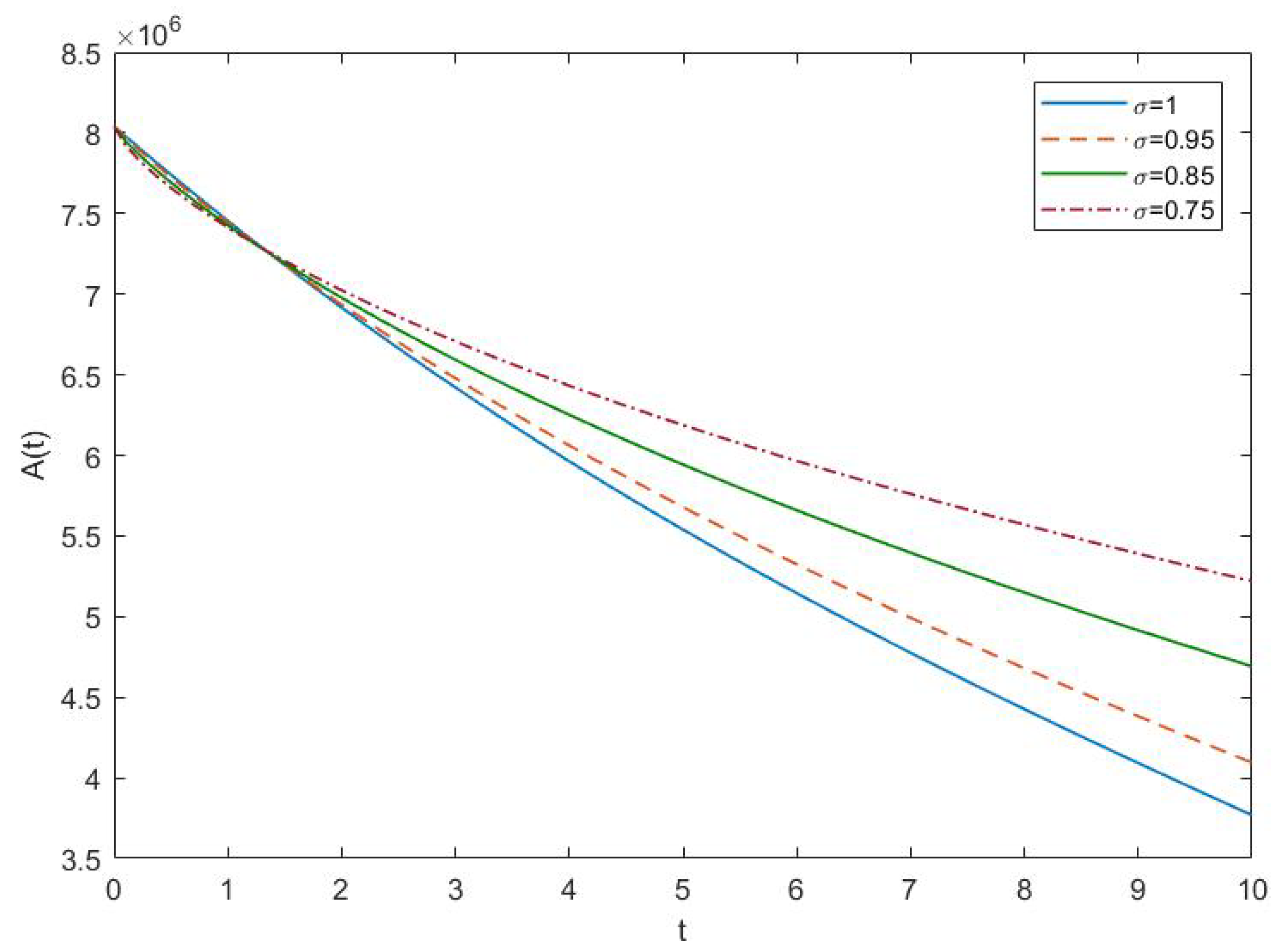
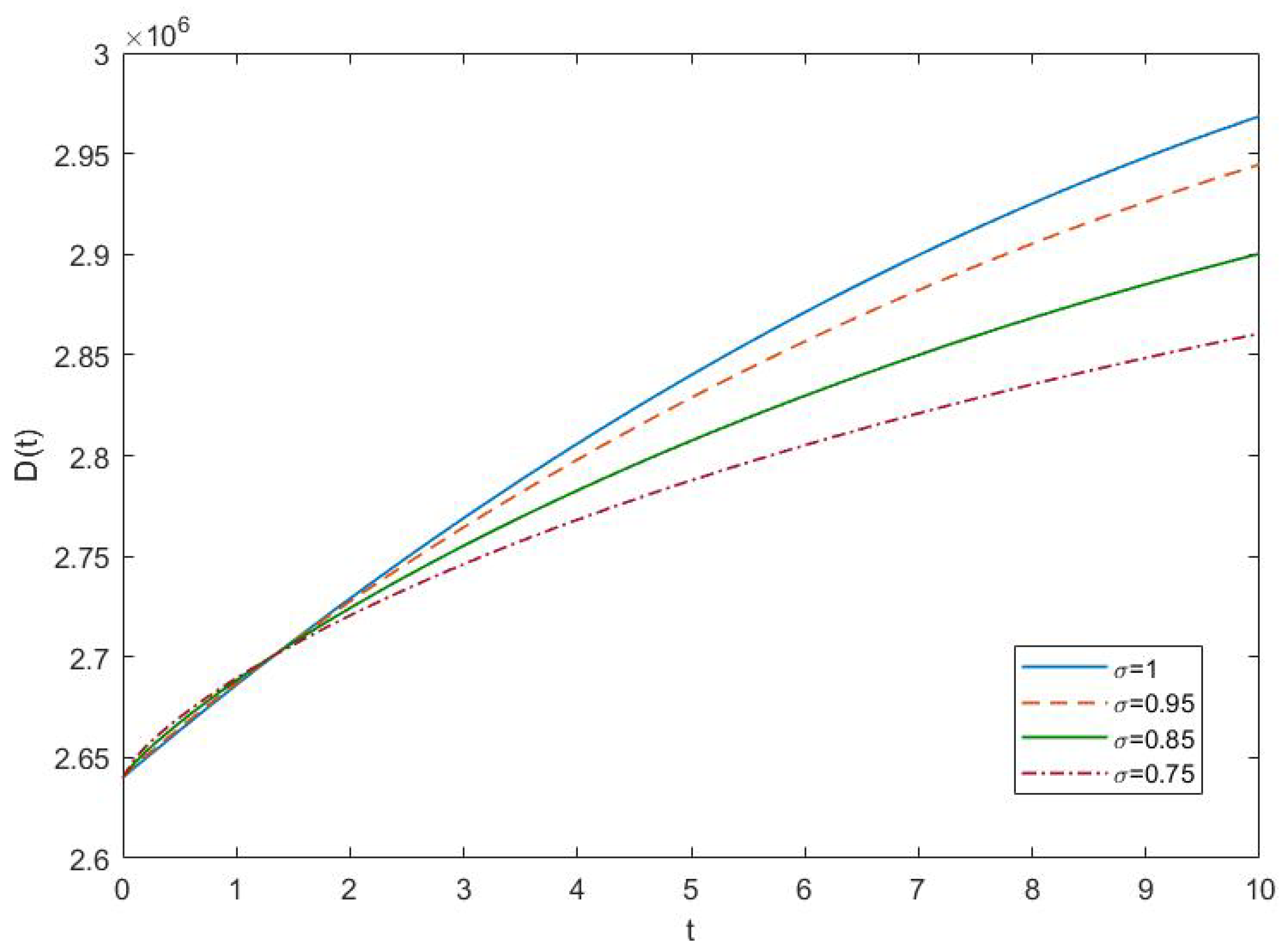
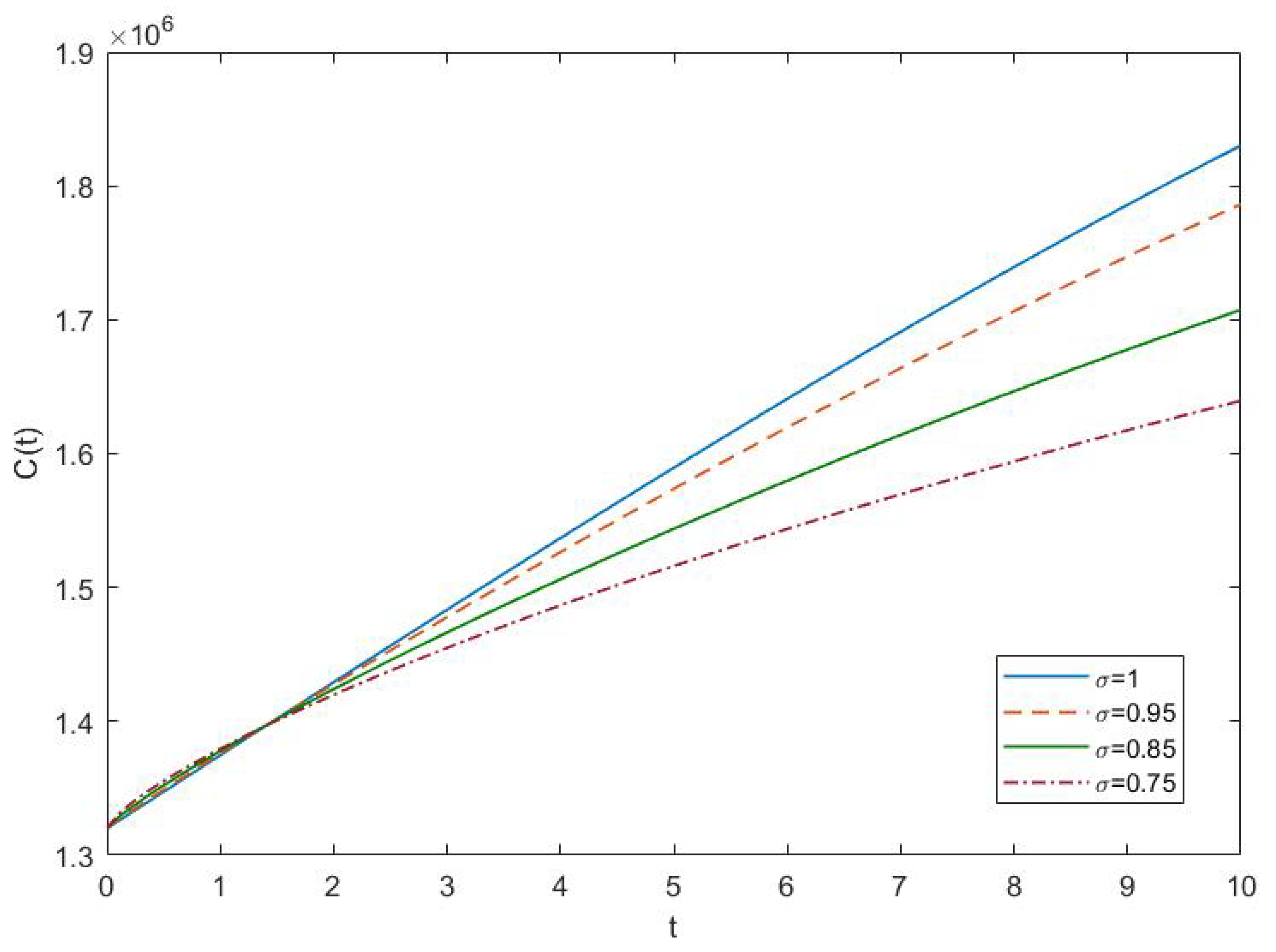
4.2. Results and Discussion
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- World Health Organization. Global Diffusion of eHealth: Making Universal Health Coverage Achievable: Report of the Third Global Survey on eHealth; World Health Organization: Geneva, Switzerland, 2017. [Google Scholar]
- Ogurtsova, K.; Guariguata, L.; Barengo, N.C.; Ruiz, P.L.D.; Sacre, J.W.; Karuranga, S.; Sun, H.; Boyko, E.J.; Magliano, D.J. IDF diabetes Atlas: Global estimates of undiagnosed diabetes in adults for 2021. Diabetes Res. Clin. Pr. 2022, 183, 109118. [Google Scholar] [CrossRef] [PubMed]
- Sun, H.; Saeedi, P.; Karuranga, S.; Pinkepank, M.; Ogurtsova, K.; Duncan, B.B.; Stein, C.; Basit, A.; Chan, J.C.; Mbanya, J.C.; et al. IDF Diabetes Atlas: Global, regional and country-level diabetes prevalence estimates for 2021 and projections for 2045. Diabetes Res. Clin. Pract. 2022, 183, 109119. [Google Scholar] [CrossRef] [PubMed]
- Roth, G. Global Burden of Disease Collaborative Network. Global Burden of Disease Study 2017 (GBD 2017) Results. Seattle, United States: Institute for Health Metrics and Evaluation (IHME), 2018. Lancet 2018, 392, 1736–1788. [Google Scholar] [CrossRef] [PubMed]
- Korsmo-Haugen, H.K.; Brurberg, K.G.; Mann, J.; Aas, A.M. Carbohydrate quantity in the dietary management of type 2 diabetes: A systematic review and meta-analysis. Diabetes Obes. Metab. 2019, 21, 15–27. [Google Scholar] [CrossRef]
- Boutayeb, A.; Twizell, E.; Achouayb, K.; Chetouani, A. A mathematical model for the burden of diabetes and its complications. Biomed. Eng. Online 2004, 3, 1–8. [Google Scholar] [CrossRef]
- Sweatman, C.Z.H. Mathematical model of diabetes and lipid metabolism linked to diet, leptin sensitivity, insulin sensitivity and VLDLTG clearance predicts paths to health and type II diabetes. J. Theor. Biol. 2020, 486, 110037. [Google Scholar]
- Al-Hussein, A.B.A.; Rahma, F.; Jafari, S. Hopf bifurcation and chaos in time-delay model of glucose-insulin regulatory system. Chaos Solitons Fractals 2020, 137, 109845. [Google Scholar] [CrossRef]
- Kouidere, A.; Labzai, A.; Ferjouchia, H.; Balatif, O.; Rachik, M. A new mathematical modeling with optimal control strategy for the dynamics of population of diabetics and its complications with effect of behavioral factors. J. Appl. Math. 2020, 2020. [Google Scholar] [CrossRef]
- Mollah, S.; Biswas, S. Effect of awareness program on diabetes mellitus: Deterministic and stochastic approach. J. Appl. Math. Comput. 2021, 66, 61–86. [Google Scholar] [CrossRef]
- Mollah, S.; Biswas, S.; Khajanchi, S. Impact of awareness program on diabetes mellitus described by fractional-order model solving by homotopy analysis method. In Ricerche di Matematica; Springer: Berlin/Heidelberg, Germany, 2022; pp. 1–26. [Google Scholar]
- Xue, D.; Zhao, C.; Chen, Y. Fractional order PID control of a DC-motor with elastic shaft: A case study. In Proceedings of the 2006 American Control Conference, Minneapolis, MN, USA, 14–16 June 2006; p. 6. [Google Scholar]
- Gutierrez, R.E.; Rosário, J.M.; Tenreiro Machado, J. Fractional order calculus: Basic concepts and engineering applications. Math. Probl. Eng. 2010, 2010, 375858. [Google Scholar] [CrossRef]
- Ahmed, E.; Hashish, A.; Rihan, F. On fractional order cancer model. J. Fract. Calc. Appl. Anal. 2012, 3, 1–6. [Google Scholar]
- Srivastava, H.M.; Shanker Dubey, R.; Jain, M. A study of the fractional-order mathematical model of diabetes and its resulting complications. Math. Methods Appl. Sci. 2019, 42, 4570–4583. [Google Scholar] [CrossRef]
- Mohamed Lamlili, E.; Boutayeb, W.; Boutayeb, A. The Dynamics of a Population of Healthy Adults, Overweight/Obese and Diabetics With and Without Complications in Morocco. In Proceedings of the International Conference on Electronic Engineering and Renewable Energy Systems, Saidia, Morocco, 20–22 May 2022; pp. 29–36. [Google Scholar]
- Li, Y.; Chen, Y.; Podlubny, I. Stability of fractional-order nonlinear dynamic systems: Lyapunov direct method and generalized Mittag–Leffler stability. Comput. Math. Appl. 2010, 59, 1810–1821. [Google Scholar] [CrossRef]
- Odibat, Z.M.; Shawagfeh, N.T. Generalized Taylor’s formula. Appl. Math. Comput. 2007, 186, 286–293. [Google Scholar] [CrossRef]
- Li, H.L.; Zhang, L.; Hu, C.; Jiang, Y.L.; Teng, Z. Dynamical analysis of a fractional-order predator-prey model incorporating a prey refuge. J. Appl. Math. Comput. 2017, 54, 435–449. [Google Scholar] [CrossRef]
- De Boor, C.; Golub, G.H. The numerically stable reconstruction of a Jacobi matrix from spectral data. Linear Algebra Appl. 1978, 21, 245–260. [Google Scholar] [CrossRef]
- DeJesus, E.X.; Kaufman, C. Routh-Hurwitz criterion in the examination of eigenvalues of a system of nonlinear ordinary differential equations. Phys. Rev. A 1987, 35, 5288. [Google Scholar] [CrossRef]
- Kumar, M.; Jhinga, A.; Daftardar-Gejji, V. New algorithm for solving non-linear functional equations. Int. J. Appl. Comput. Math. 2020, 6, 26. [Google Scholar] [CrossRef]
- Daftardar-Gejji, V.; Jafari, H. An iterative method for solving nonlinear functional equations. J. Math. Anal. Appl. 2006, 316, 753–763. [Google Scholar] [CrossRef]
- Banaś, J.; O’Regan, D. On existence and local attractivity of solutions of a quadratic Volterra integral equation of fractional order. J. Math. Anal. Appl. 2008, 345, 573–582. [Google Scholar] [CrossRef]
- Dave, R.; Davis, R.; Davies, J. The impact of multiple lifestyle interventions on remission of type 2 diabetes mellitus within a clinical setting. Obes. Med. 2019, 13, 59–64. [Google Scholar] [CrossRef]



Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Albalawi, K.S.; Malik, K.; Alkahtani, B.S.T.; Goswami, P. An Analysis of the Effects of Lifestyle Changes by Using a Fractional-Order Population Model of the Overweight/Obese Diabetic Population. Fractal Fract. 2023, 7, 839. https://doi.org/10.3390/fractalfract7120839
Albalawi KS, Malik K, Alkahtani BST, Goswami P. An Analysis of the Effects of Lifestyle Changes by Using a Fractional-Order Population Model of the Overweight/Obese Diabetic Population. Fractal and Fractional. 2023; 7(12):839. https://doi.org/10.3390/fractalfract7120839
Chicago/Turabian StyleAlbalawi, Kholoud Saad, Kuldeep Malik, Badr Saad T. Alkahtani, and Pranay Goswami. 2023. "An Analysis of the Effects of Lifestyle Changes by Using a Fractional-Order Population Model of the Overweight/Obese Diabetic Population" Fractal and Fractional 7, no. 12: 839. https://doi.org/10.3390/fractalfract7120839
APA StyleAlbalawi, K. S., Malik, K., Alkahtani, B. S. T., & Goswami, P. (2023). An Analysis of the Effects of Lifestyle Changes by Using a Fractional-Order Population Model of the Overweight/Obese Diabetic Population. Fractal and Fractional, 7(12), 839. https://doi.org/10.3390/fractalfract7120839





