Application of Riemann–Liouville Derivatives on Second-Order Fractional Differential Equations: The Exact Solution
Abstract
:1. Introduction
2. Preliminaries
3. Analysis
4. Solution of the First Class:
4.1. Solution in Terms of the Mittag–Leffler Function as
Special Case as
4.2. Solution in Terms of Trigonometric Functions as
Special Case as
5. Solution of the Second Class:
5.1. Solution in Terms of the Mittag–Leffler Function as
5.2. Solution in Terms of Trigonometric and Hyperbolic Functions as
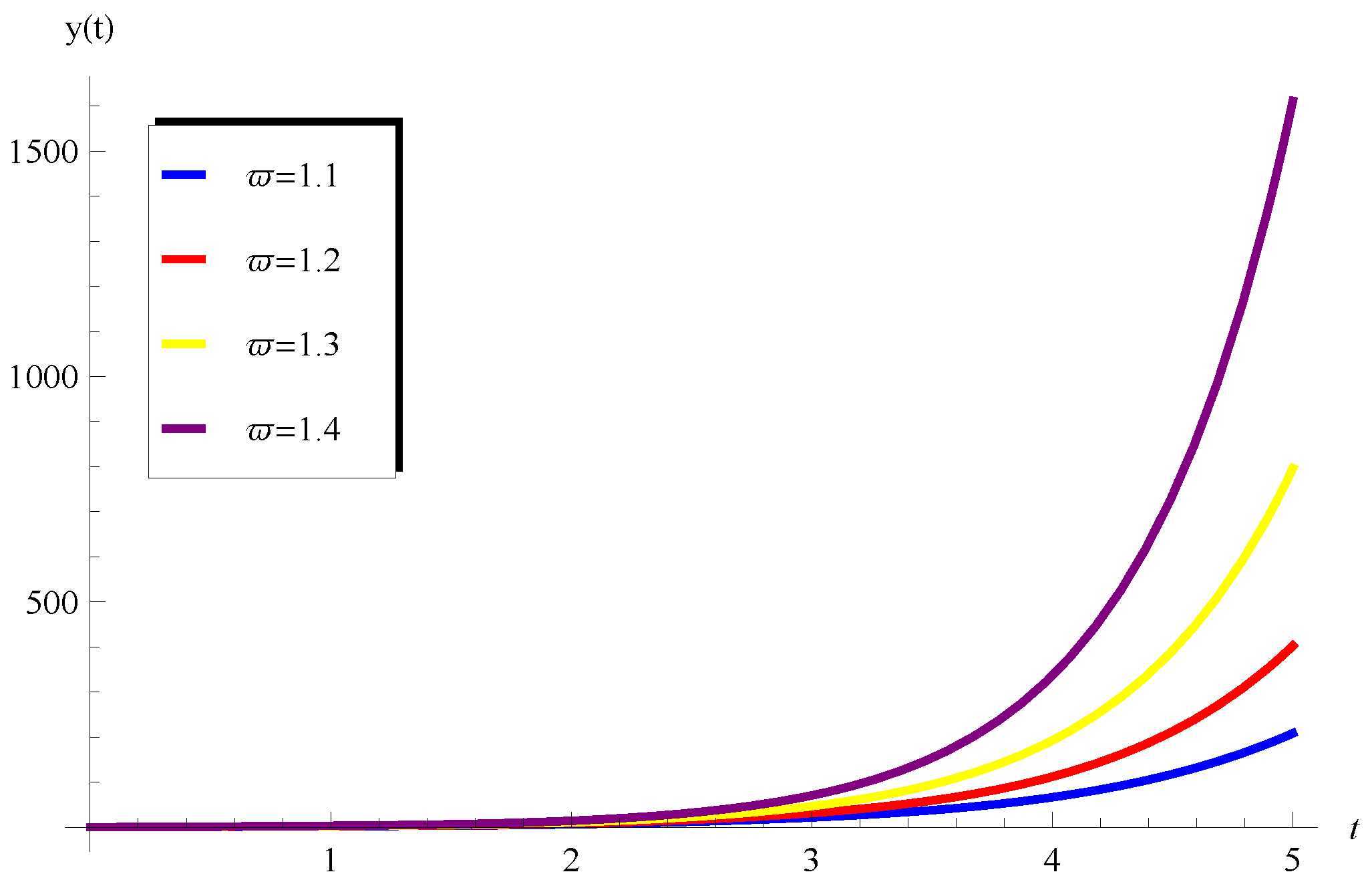
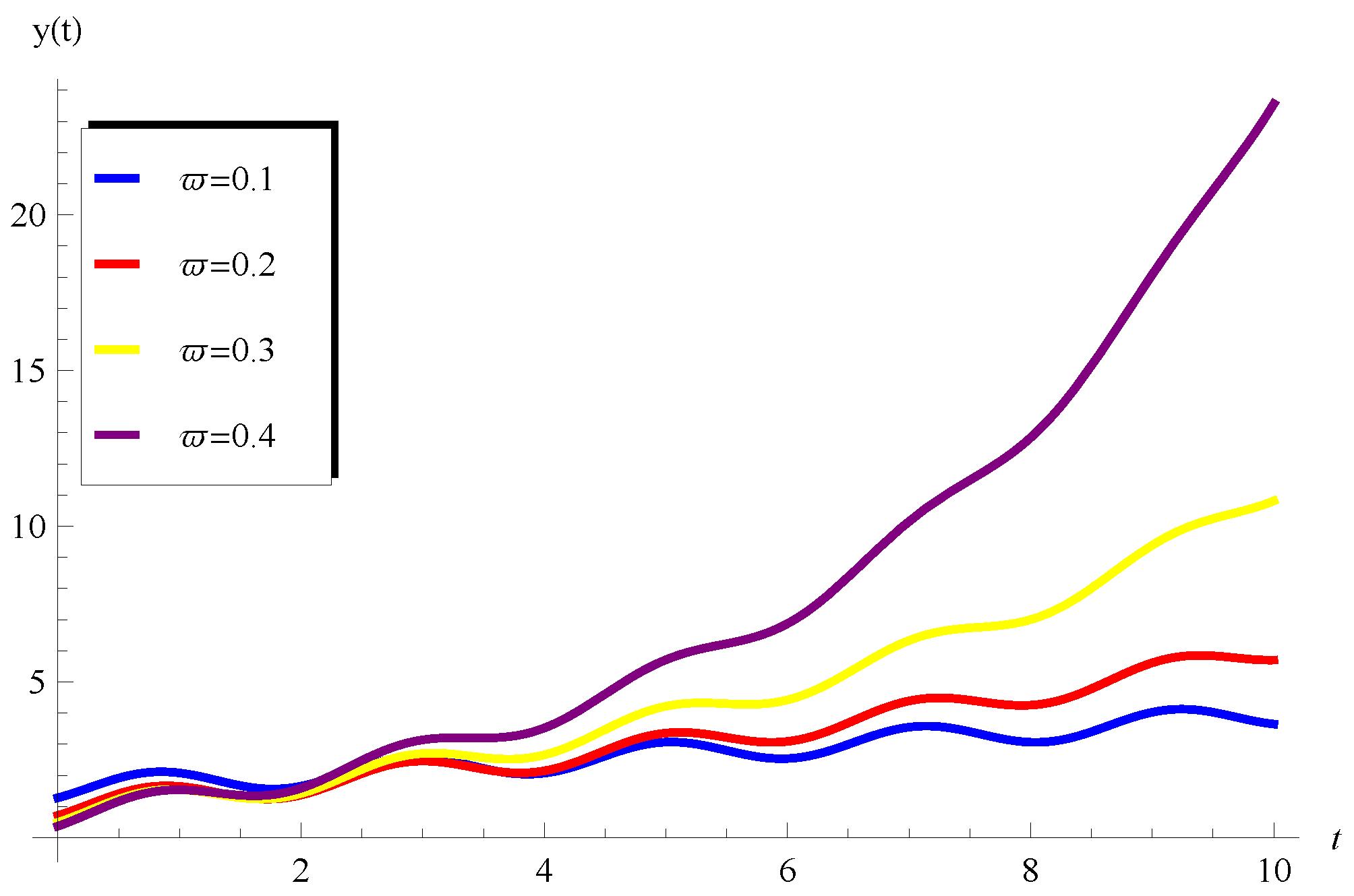
5.3. Behavior of the Solution
6. Conclusions
Funding
Data Availability Statement
Conflicts of Interest
References
- Miller, K.S.; Ross, B. An Introduction to the Fractional Calculus and Fractional Differential Equations; John Wiley & Sons: New York, NY, USA, 1993. [Google Scholar]
- Podlubny, I. Fractional Differential Equations; Academic Press: San Diego, CA, USA, 1999. [Google Scholar]
- Hilfer, R. Applications of Fractional Calculus in Physics; World Scientific Publishing Company: Singapore, 2000. [Google Scholar]
- Narahari Achar, B.N.; Hanneken, J.W.; Enck, T.; Clarke, T. Dynamics of the fractional oscillator. Phys. A 2001, 297, 361–367. [Google Scholar] [CrossRef]
- Sebaa, N.; Fellah, Z.E.A.; Lauriks, W.; Depollier, C. Application of fractional calculus to ultrasonic wave propagation in human cancellous bone. Signal Process. 2006, 86, 2668–2677. [Google Scholar] [CrossRef]
- Tarasov, V.E. Fractional Heisenberg equation. Phys. Lett. A 2008, 372, 2984–2988. [Google Scholar] [CrossRef]
- Ding, Y.; Yea, H. A fractional-order differential equation model of HIV infection of CD4+T-cells. Math. Comput. Model. 2009, 50, 386–392. [Google Scholar] [CrossRef]
- Wang, S.; Xu, M.; Li, X. Green’s function of time fractional diffusion equation and its applications in fractional quantum mechanics. Nonlinear Anal. Real World Appl. 2009, 10, 1081–1086. [Google Scholar] [CrossRef]
- Song, L.; Xu, S.; Yang, J. Dynamical models of happiness with fractional order. Commun. Nonlinear Sci. Numer. Simul. 2010, 15, 616–628. [Google Scholar] [CrossRef]
- Gómez-Aguilara, J.F.; Rosales-García, J.J.; Bernal-Alvarado, J.J. Fractional mechanical oscillators. Rev. Mex. Física 2012, 58, 348–352. [Google Scholar]
- Machado, J.T.; Kiryakova, V.; Mainardi, F. Recent history of fractional calculus. Commun. Nonlinear Sci. Numer. Simul. 2011, 16, 1140–1153. [Google Scholar] [CrossRef]
- Garcia, J.J.R.; Calderon, M.G.; Ortiz, J.M.; Baleanu, D. Motion of a particle in a resisting medium using fractional calculus approach. Proc. Rom. Acad. Ser. A 2013, 14, 42–47. [Google Scholar]
- Machado, J.T. A fractional approach to the Fermi-Pasta-Ulam problem. Eur. Phys. J. Spec. Top. 2013, 222, 1795–1803. [Google Scholar] [CrossRef]
- Liaqat, M.I.; Akgül, A.; De la Sen, M.; Bayram, M. Approximate and Exact Solutions in the Sense of Conformable Derivatives of Quantum Mechanics Models Using a Novel Algorithm. Symmetry 2023, 15, 744. [Google Scholar] [CrossRef]
- Ebaid, A. Analysis of projectile motion in view of the fractional calculus. Appl. Math. Model. 2011, 35, 1231–1239. [Google Scholar] [CrossRef]
- Ebaid, A.; El-Zahar, E.R.; Aljohani, A.F.; Salah, B.; Krid, M.; Machado, J.T. Analysis of the two-dimensional fractional projectile motion in view of the experimental data. Nonlinear Dyn. 2019, 97, 1711–1720. [Google Scholar] [CrossRef]
- Ahmad, B.; Batarfi, H.; Nieto, J.J.; Oscar, O.-Z.; Shammakh, W. Projectile motion via Riemann-Liouville calculus. Adv. Differ. Equ. 2015, 63. [Google Scholar] [CrossRef]
- Kumar, D.; Singh, J.; Baleanu, D.; Rathore, S. Analysis of a fractional model of the Ambartsumian equation. Eur. Phys. J. Plus 2018, 133, 133–259. [Google Scholar] [CrossRef]
- Ebaid, A.; Cattani, C.; Al Juhani, A.S.; El-Zahar, E.R. A novel exact solution for the fractional Ambartsumian equation. Adv. Differ. Equ. 2021, 2021, 88. [Google Scholar] [CrossRef]
- El-Zahar, E.R.; Alotaibi, A.M.; Ebaid, A.; Aljohani, A.F.; Gómez Aguilar, J.F. The Riemann-Liouville fractional derivative for Ambartsumian equation. Results Phys. 2020, 19, 103551. [Google Scholar] [CrossRef]
- Aljohani, A.F.; Ebaid, A.; Algehyne, E.A.; Mahrous, Y.M.; Cattani, C.; Al-Jeaid, H.K. The Mittag-Leffler Function for Re-Evaluating the Chlorine Transport Model: Comparative Analysis. Fractal Fract. 2022, 6, 125. [Google Scholar] [CrossRef]
- Ebaid, A.; Al-Jeaid, H.K. The Mittag–Leffler Functions for a Class of First-Order Fractional Initial Value Problems: Dual Solution via Riemann–Liouville Fractional Derivative. Fractal Fract. 2022, 6, 85. [Google Scholar] [CrossRef]
- Seddek, L.F.; Ebaid, A.; El-Zahar, E.R.; Aljoufi, M.D. Exact Solution of Non-Homogeneous Fractional Differential System Containing 2n Periodic Terms under Physical Conditions. Mathematics 2023, 11, 3308. [Google Scholar] [CrossRef]
- Algehyne, E.A.; Aldhabani, M.S.; Areshi, M.; El-Zahar, E.R.; Ebaid, A.; Al-Jeaid, H.K. A Proposed Application of Fractional Calculus on Time Dilation in Special Theory of Relativity. Mathematics 2023, 11, 3343. [Google Scholar] [CrossRef]
- Jumarie, G. Fractional partial differential equations and modified Riemann-Liouville derivative new methods for solution. J. Appl. Math. Comput. 2007, 24, 31–48. [Google Scholar] [CrossRef]
- Atangana, A.; Gómez-Aguilar, J.F. Numerical approximation of Riemann-Liouville definition of fractional derivative: From Riemann-Liouville to Atangana-Baleanu. Numer. Methods Partial. Differ. Eq. 2018, 34, 1502. [Google Scholar] [CrossRef]

Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Albidah, A.B. Application of Riemann–Liouville Derivatives on Second-Order Fractional Differential Equations: The Exact Solution. Fractal Fract. 2023, 7, 843. https://doi.org/10.3390/fractalfract7120843
Albidah AB. Application of Riemann–Liouville Derivatives on Second-Order Fractional Differential Equations: The Exact Solution. Fractal and Fractional. 2023; 7(12):843. https://doi.org/10.3390/fractalfract7120843
Chicago/Turabian StyleAlbidah, Abdulrahman B. 2023. "Application of Riemann–Liouville Derivatives on Second-Order Fractional Differential Equations: The Exact Solution" Fractal and Fractional 7, no. 12: 843. https://doi.org/10.3390/fractalfract7120843
APA StyleAlbidah, A. B. (2023). Application of Riemann–Liouville Derivatives on Second-Order Fractional Differential Equations: The Exact Solution. Fractal and Fractional, 7(12), 843. https://doi.org/10.3390/fractalfract7120843








