Parameter Estimation of LFM Signals Based on FOTD-CFRFT under Impulsive Noise
Abstract
1. Introduction
2. Impulsive Noise Model
- (1)
- If , is a real number, then
- (2)
- If , m is a non-zero real number, then
- (3)
- Let and be mutually independent α-stable distribution, thenwhere
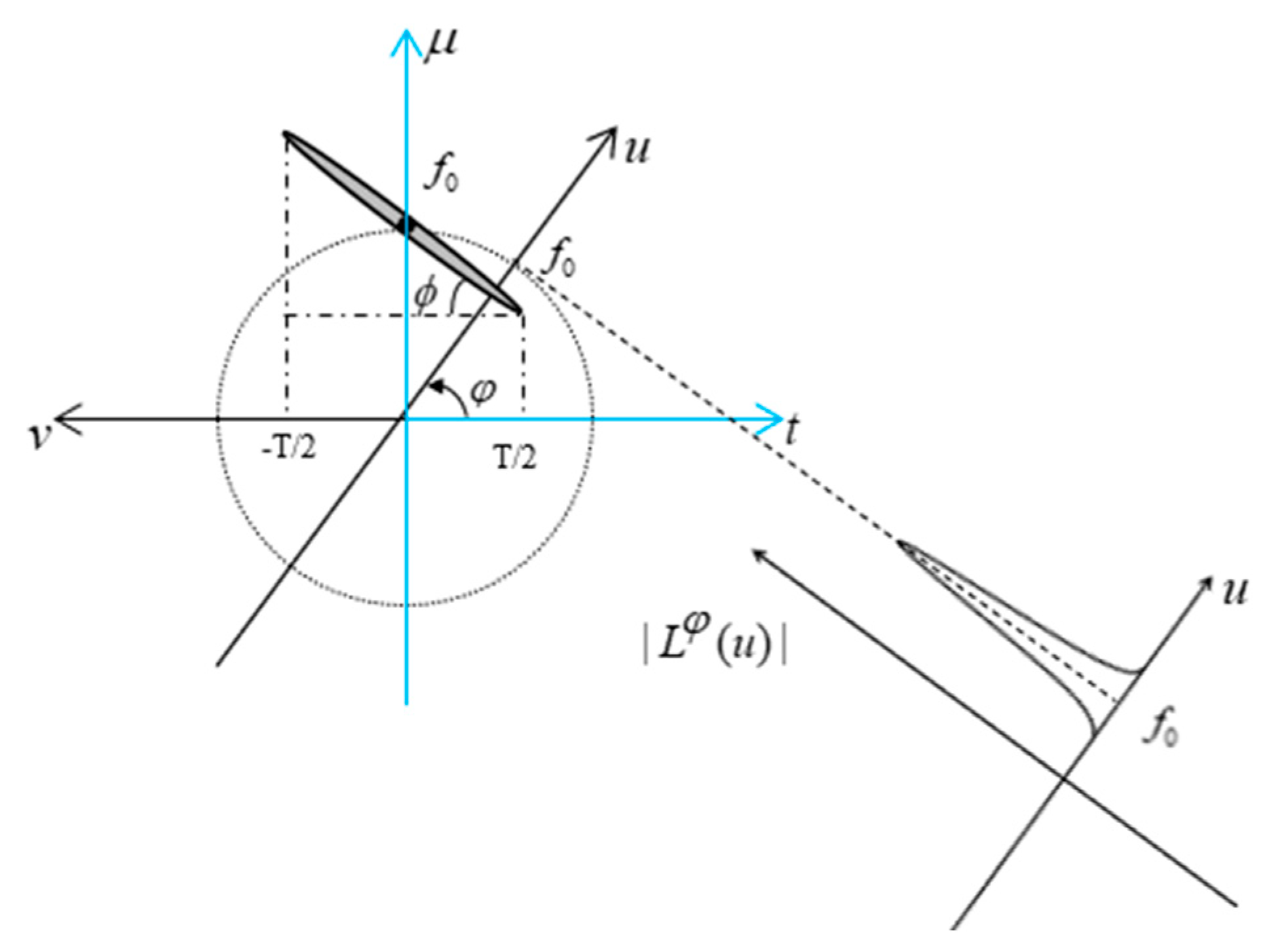
3. Parameter Estimation Method
3.1. Fractional-Order Tracking Differentiator
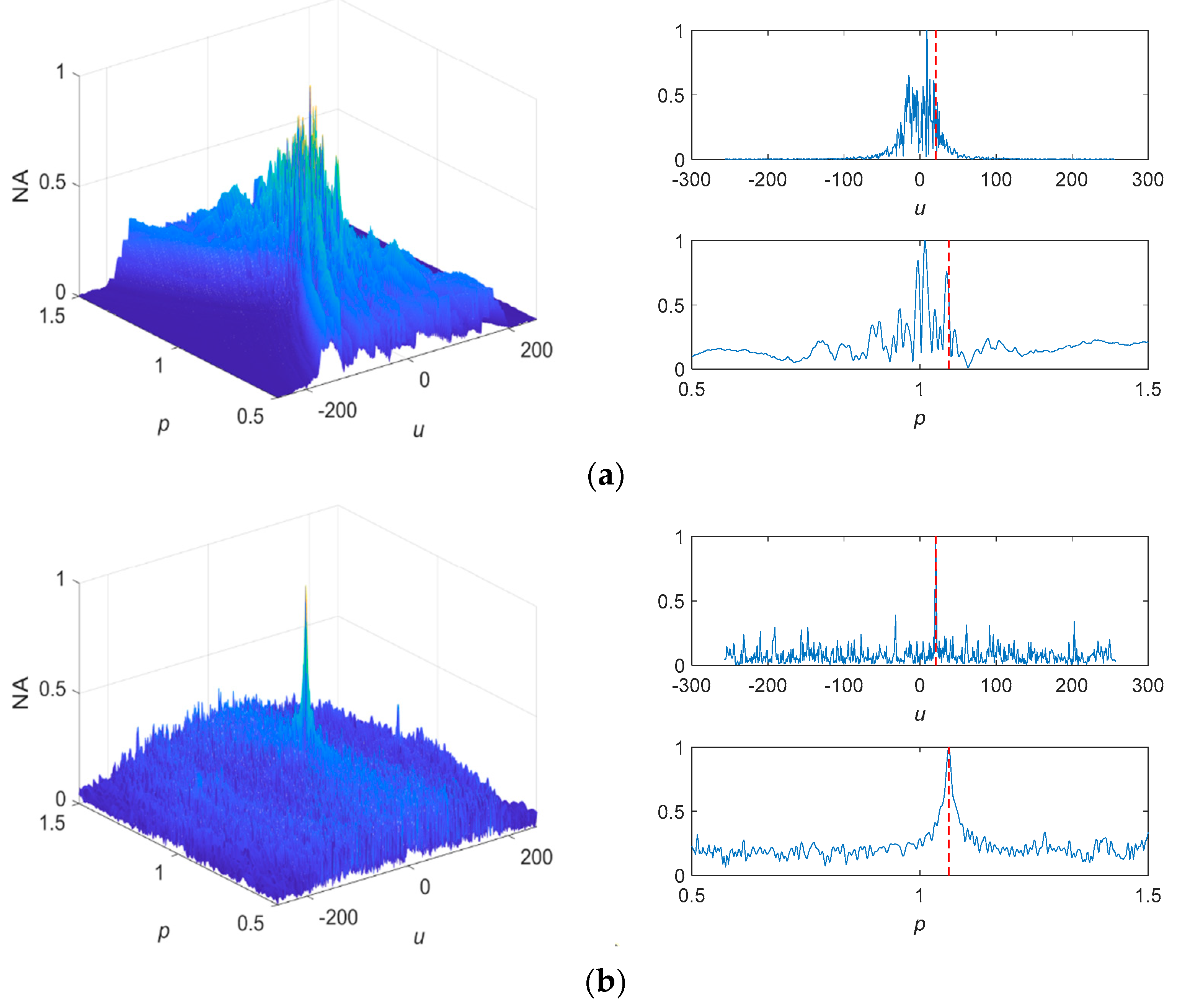
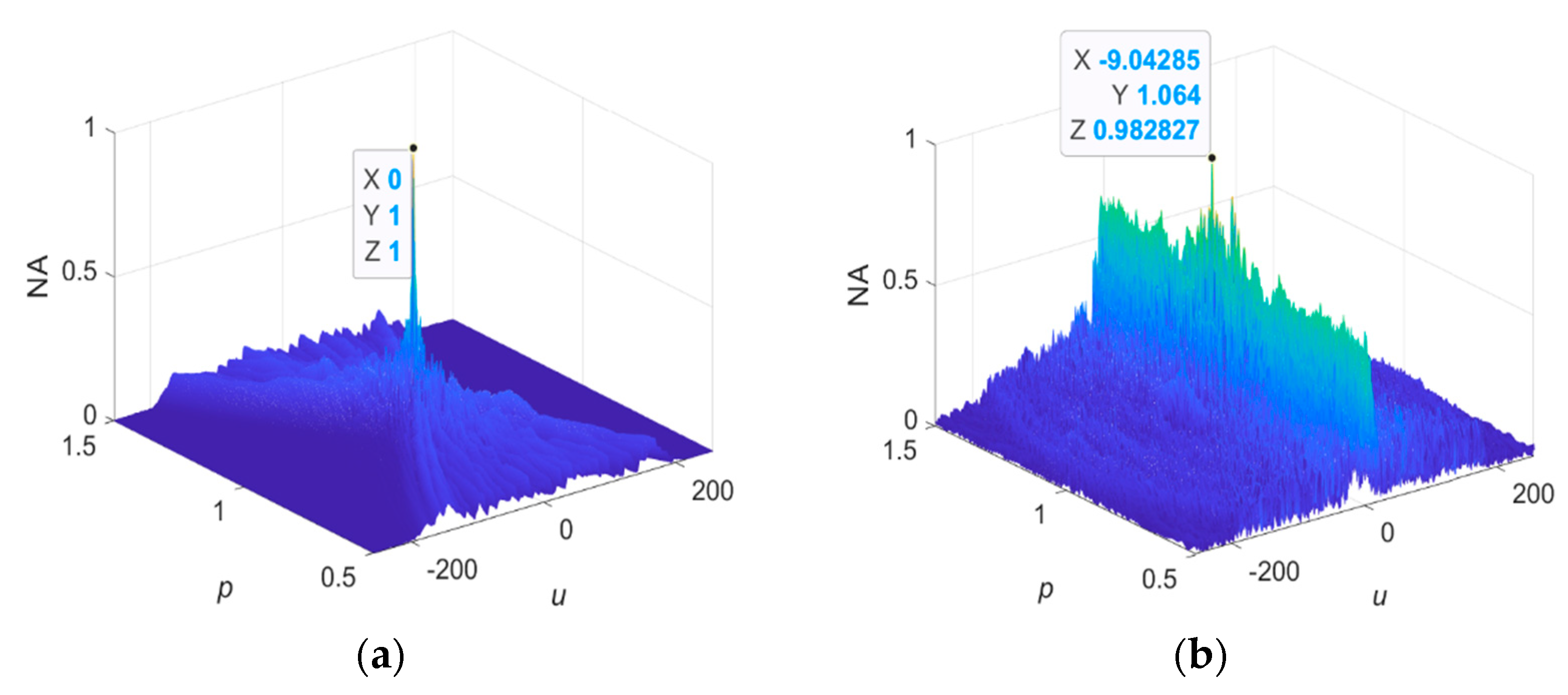
3.2. Parameter Estimation Model
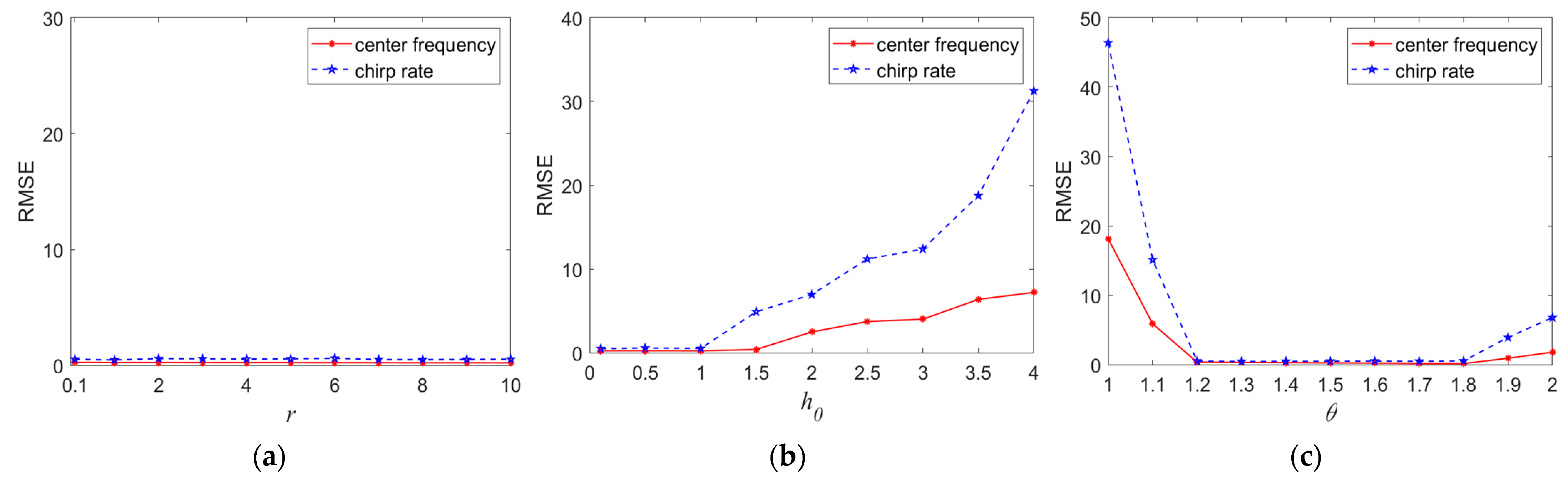
4. Simulation Experiment
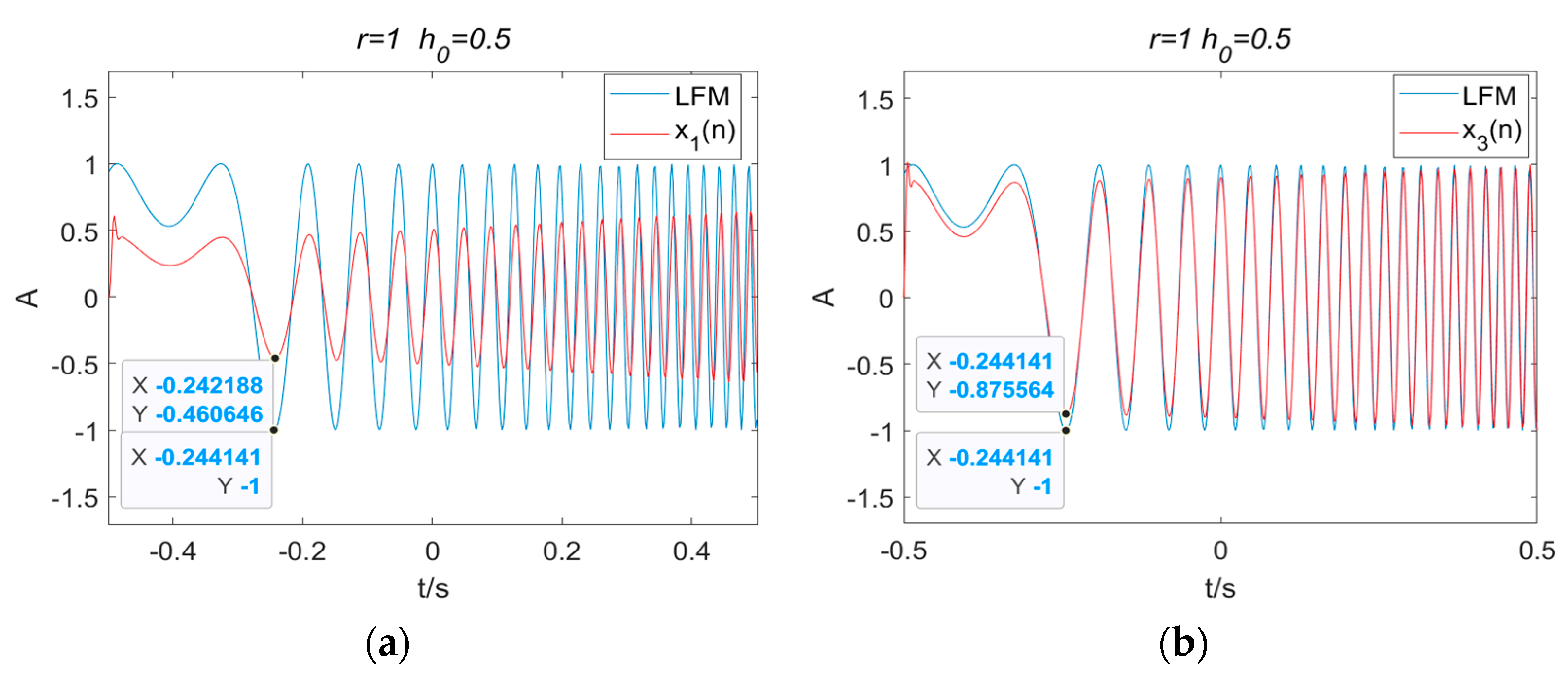
4.1. FOTD Analysis
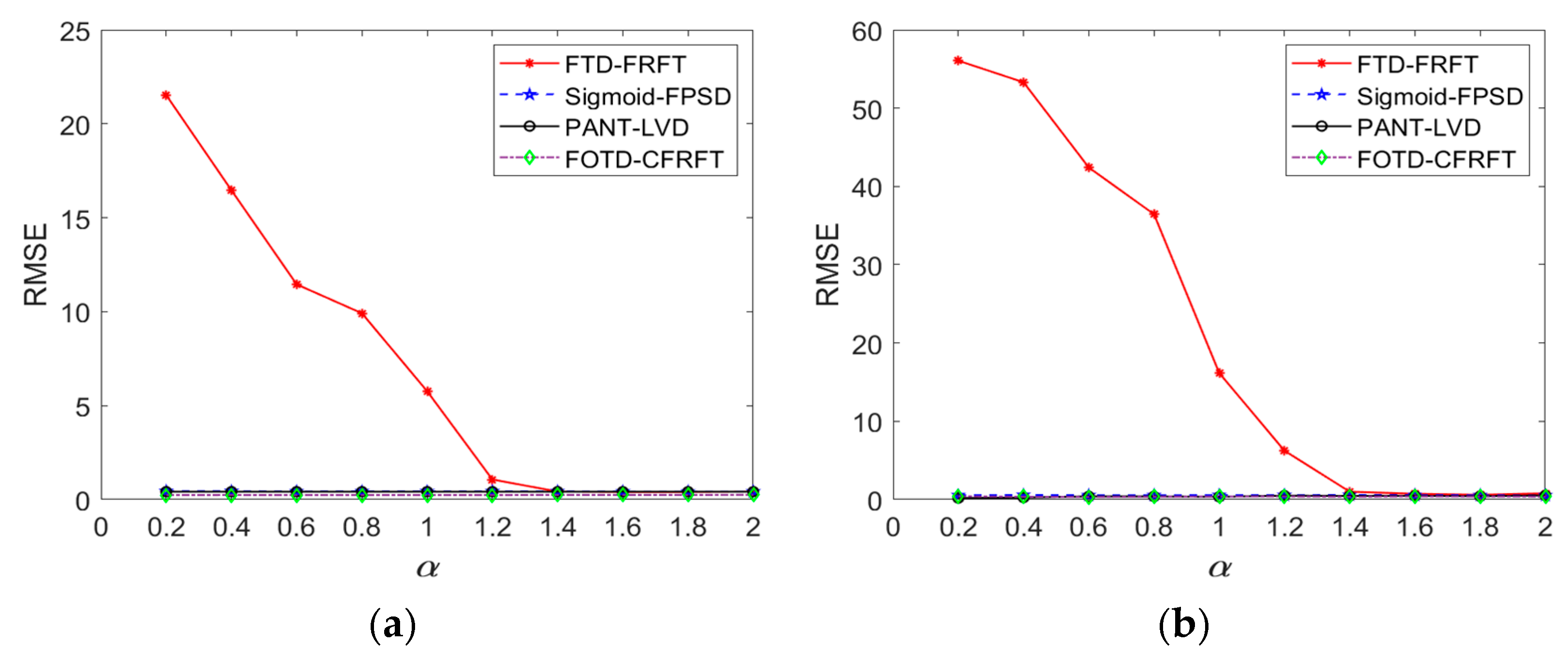
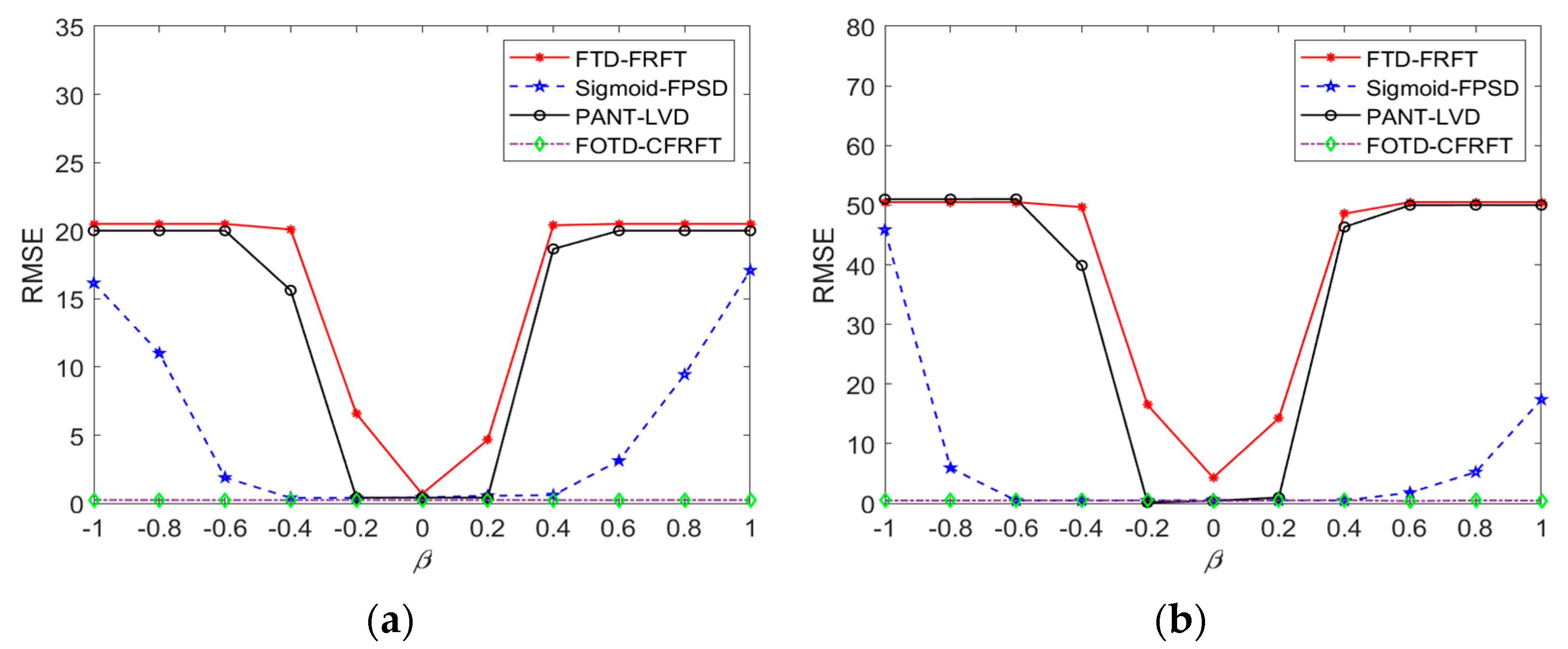
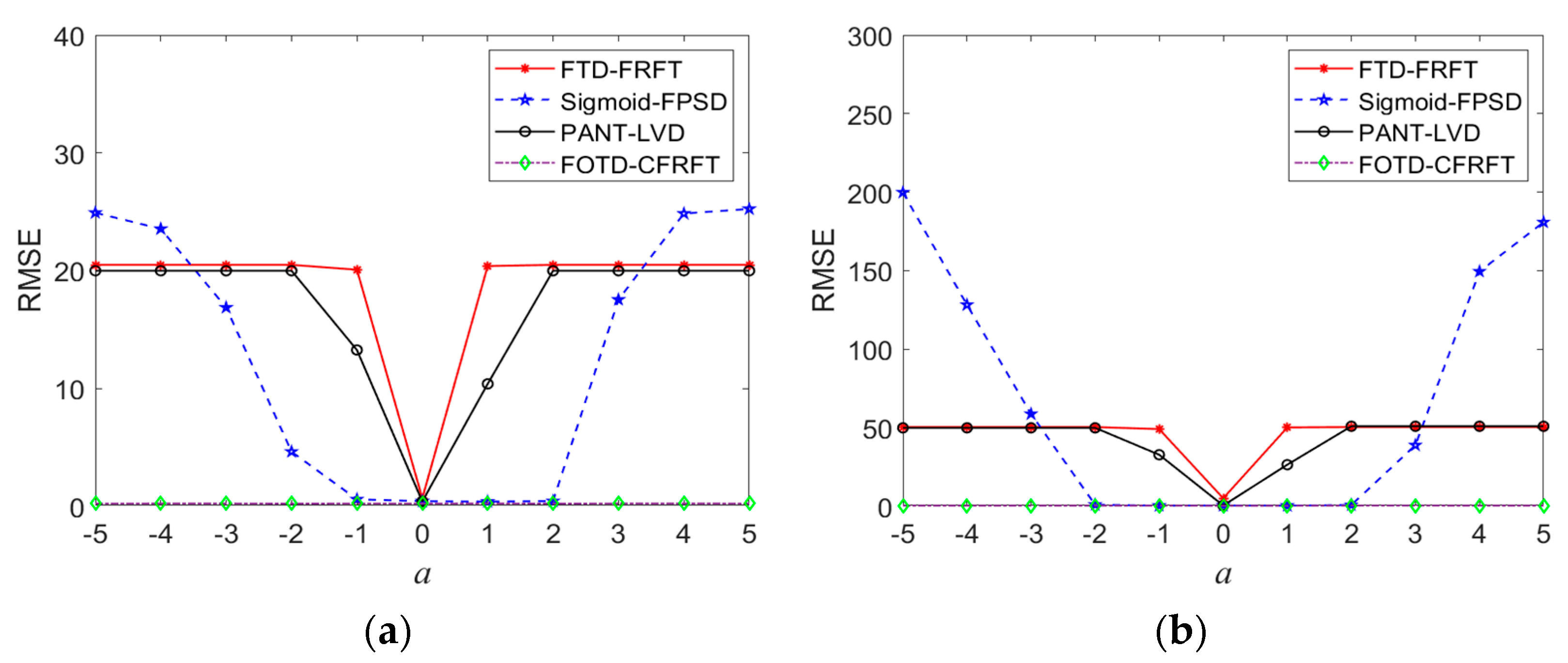
4.2. Comparisons
4.2.1. Standard SαS Distribution Noise
4.2.2. Non-Standard SαS Distribution Noise
- (1)
- When , the correction formula is
- (2)
- When , let , the correction formula is
- (3)
- When , let , the correction formula is
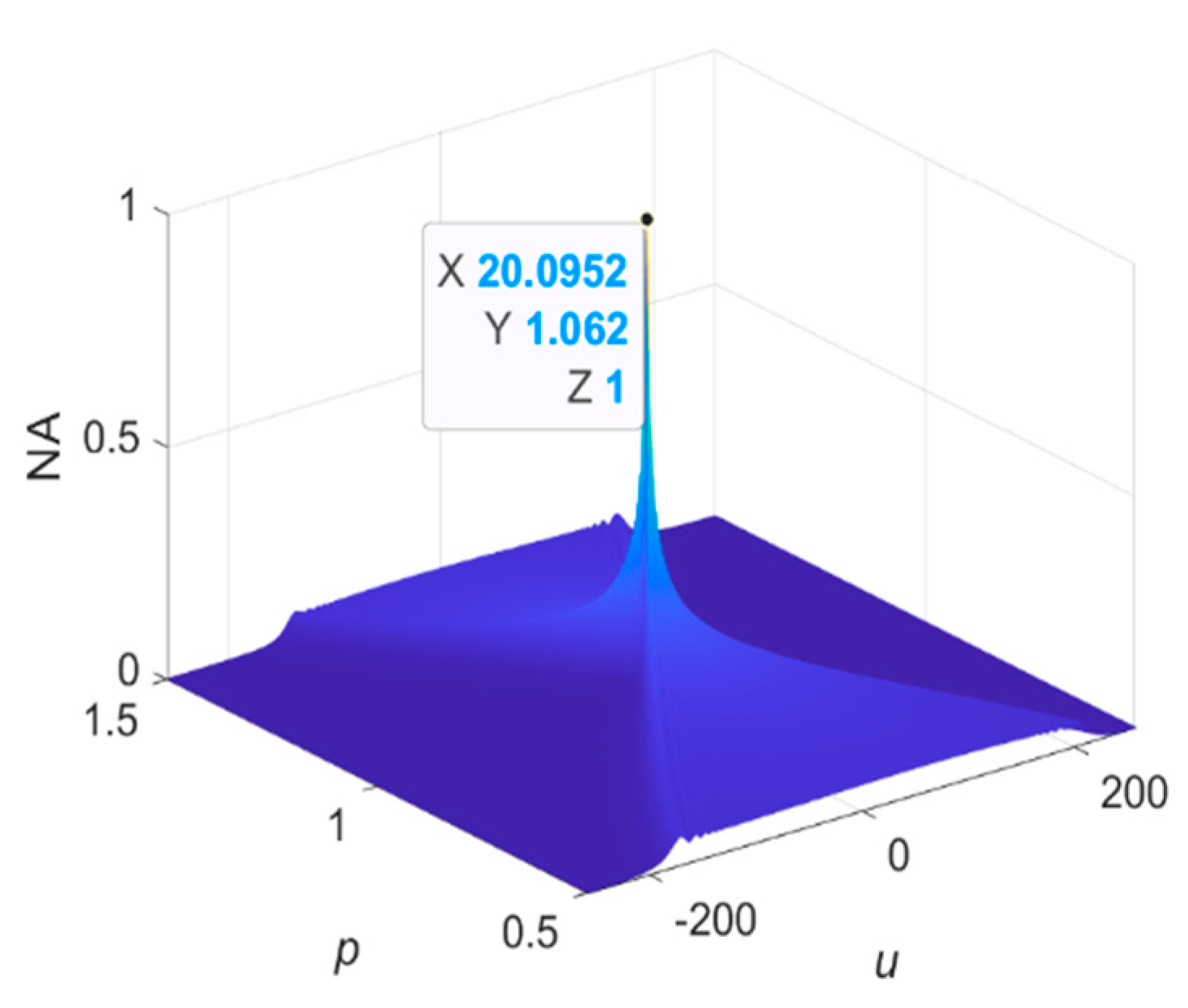
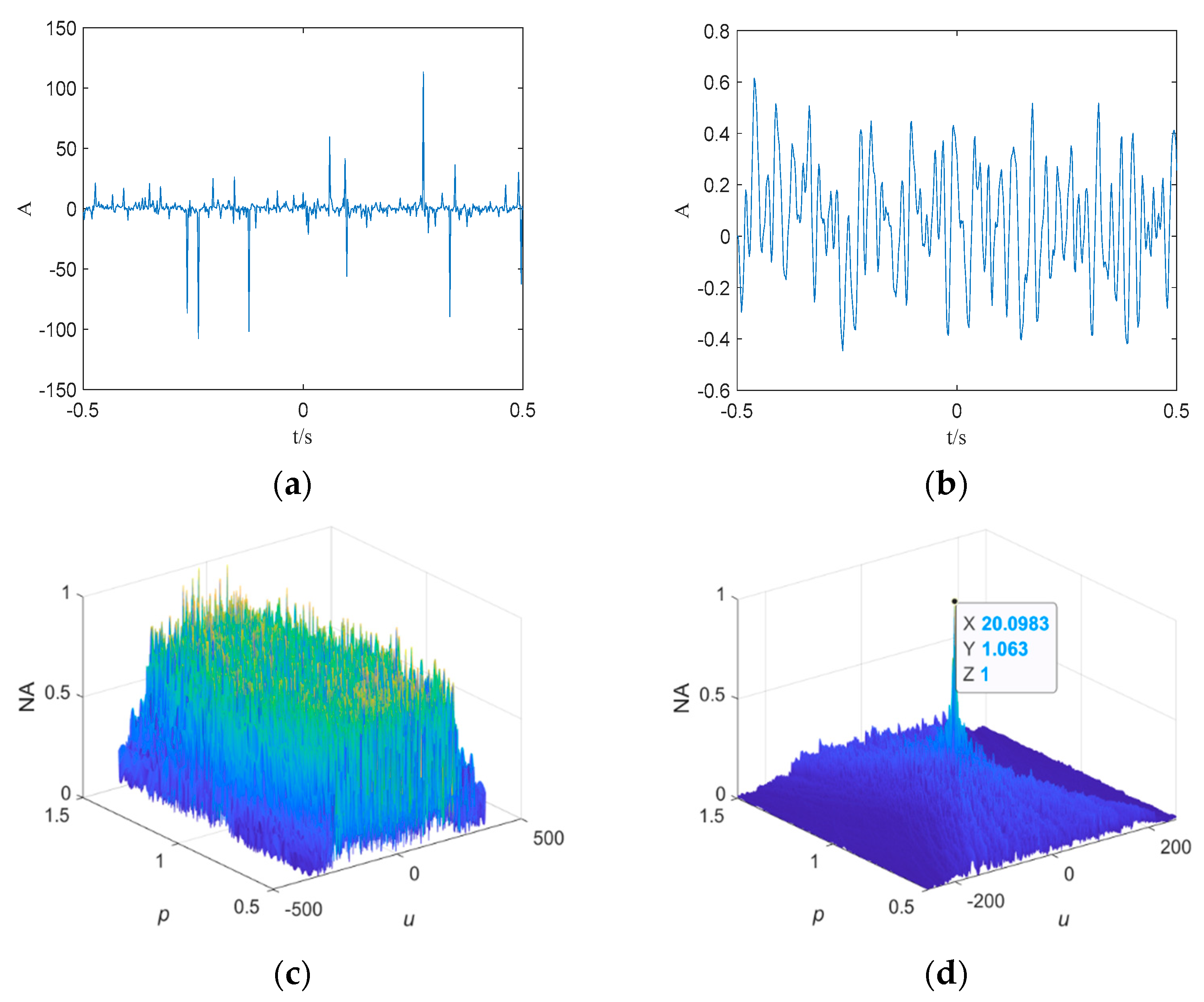
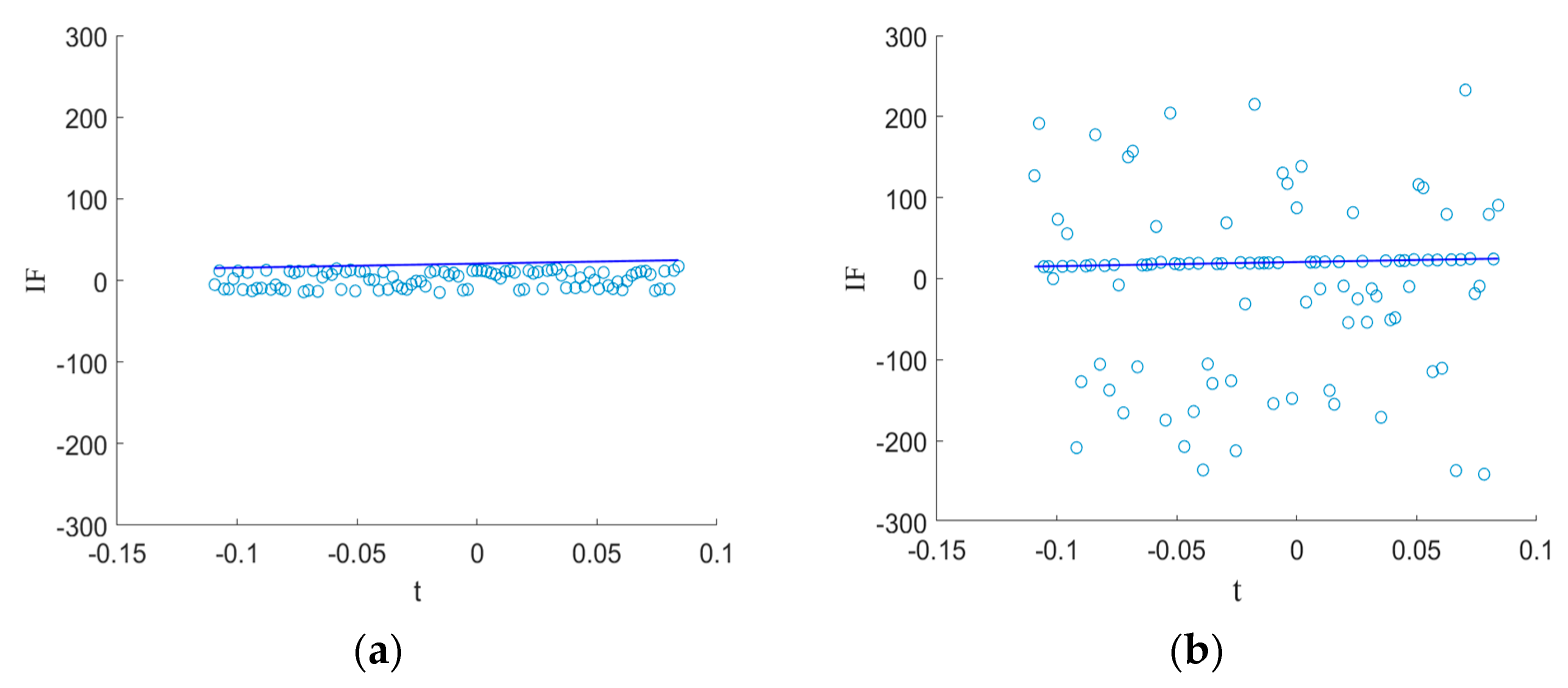
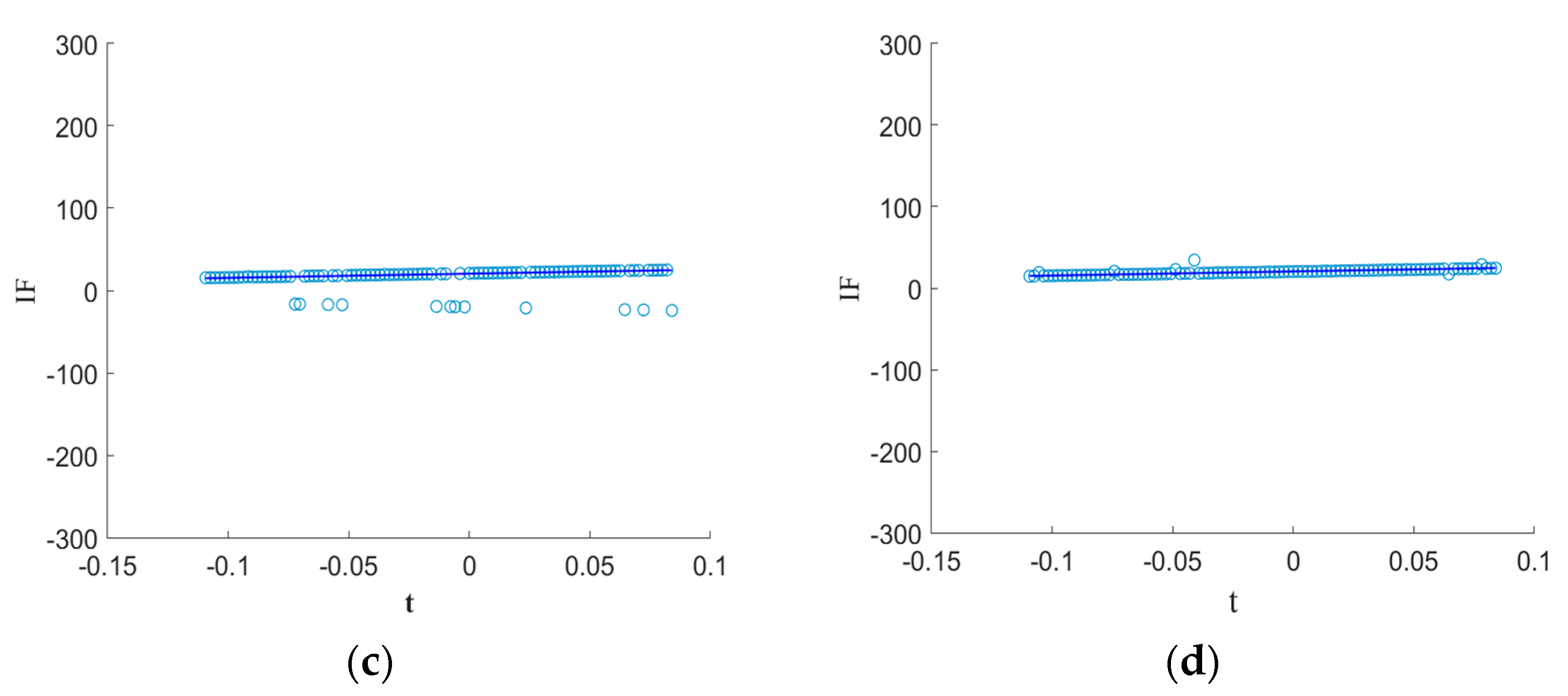
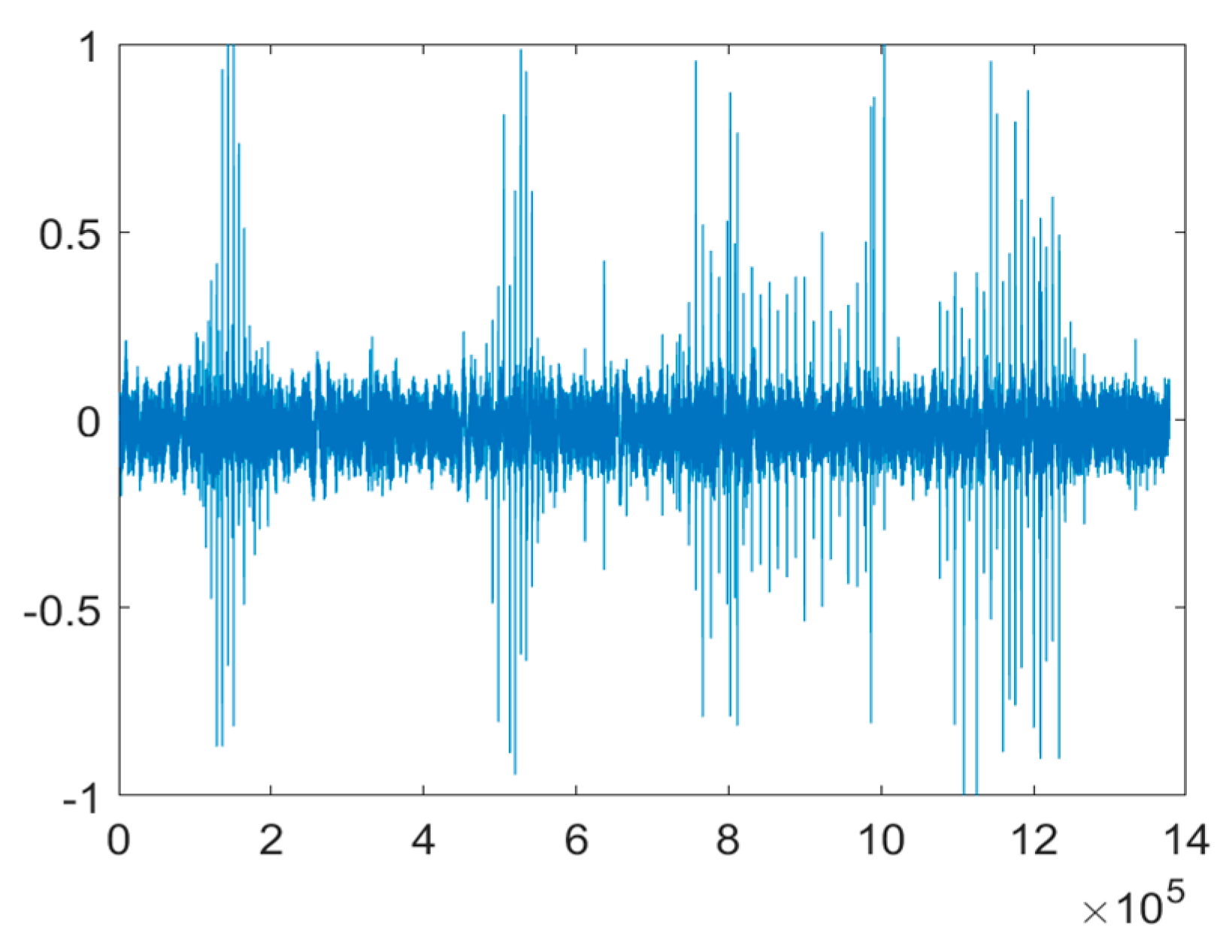
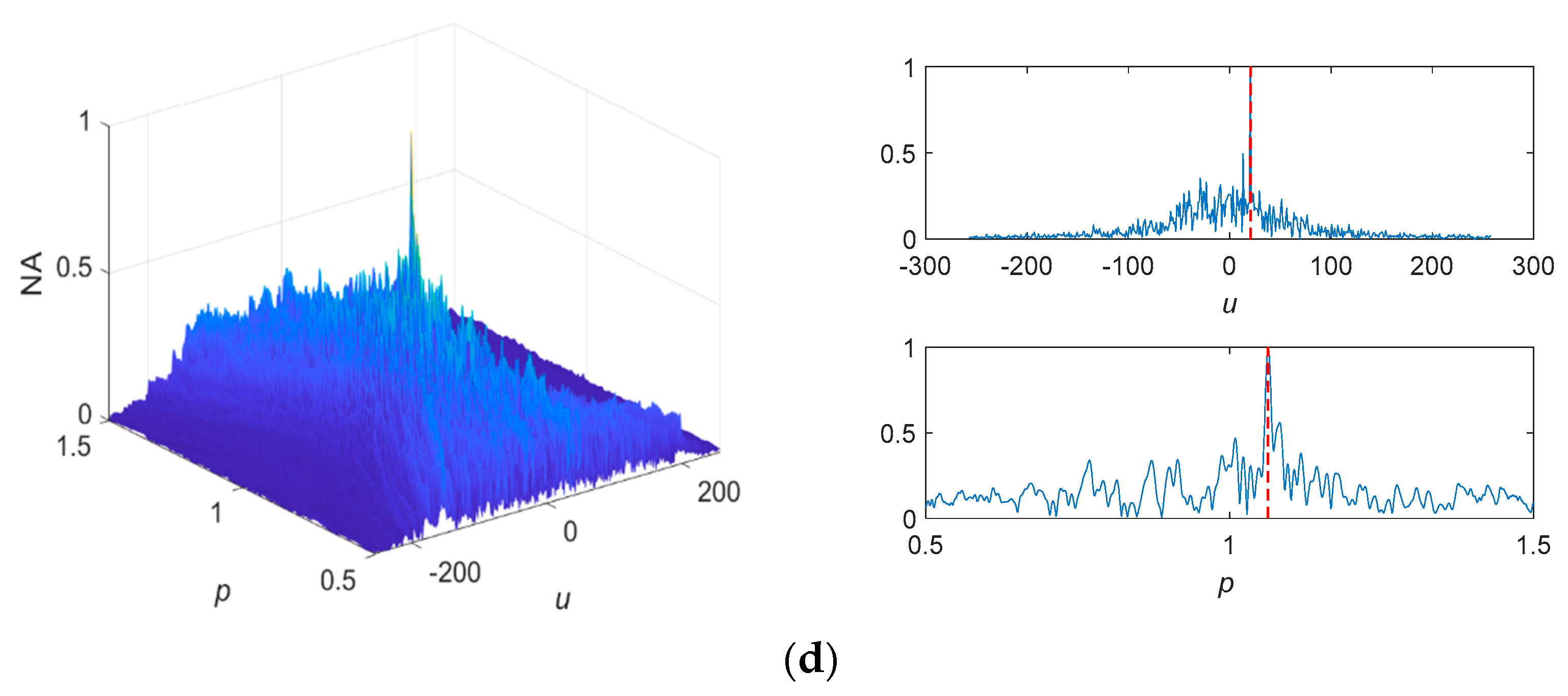
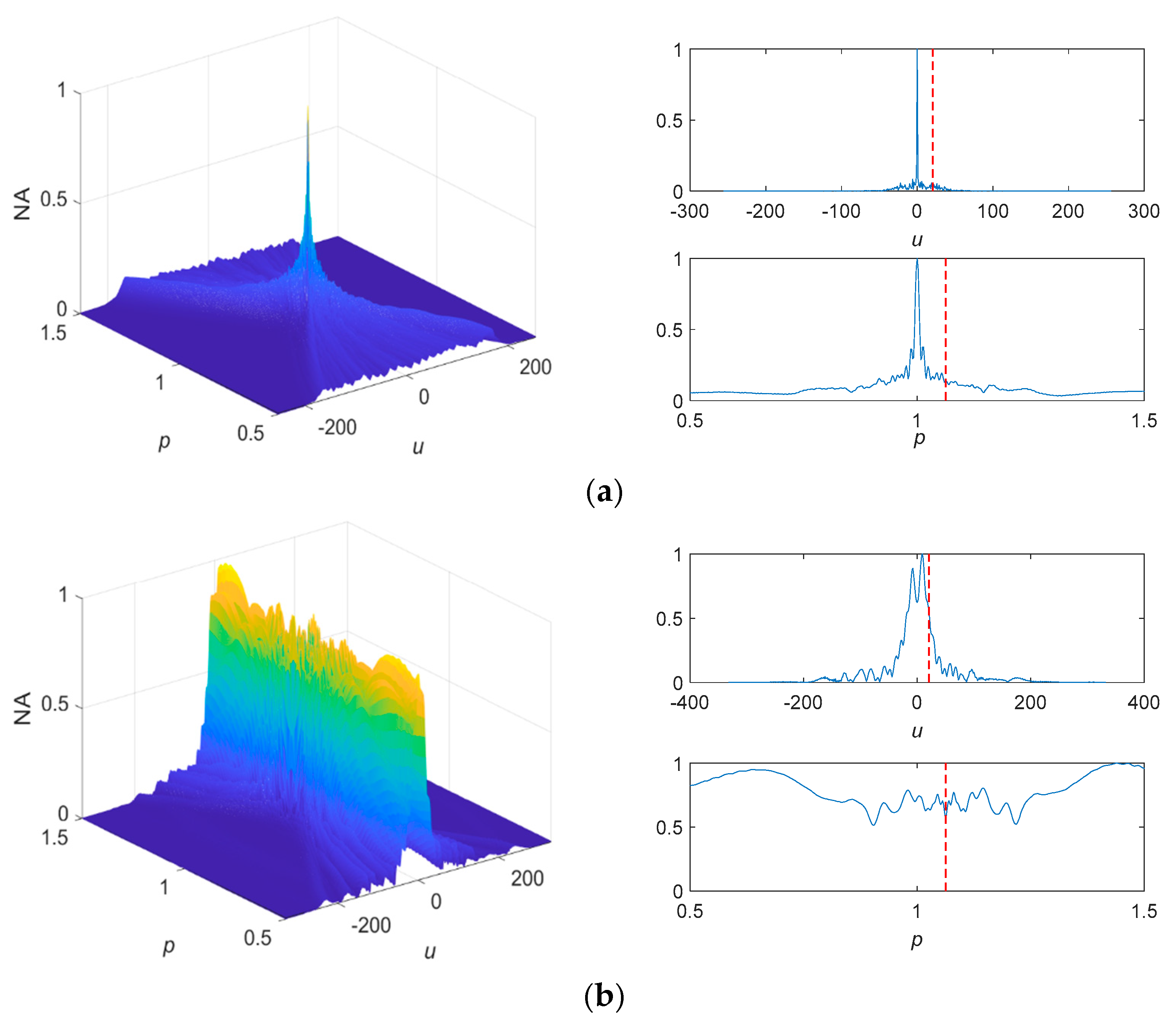
4.3. Measured Noise Experiment
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Bai, G.; Cheng, Y.; Tang, W.; Li, S. Chirp Rate Estimation for LFM Signal by Multiple DPT and Weighted Combination. IEEE Signal Process. Lett. 2019, 26, 149–153. [Google Scholar] [CrossRef]
- Li, T.; Hu, R.; Zhang, Z.; Wang, H. A time delay estimation method of LFM hybrid signals based on hough transform. In Proceedings of the 2021 IEEE 5th Advanced Information Technology, Electronic and Automation Control Conference, Chongqing, China, 12–14 March 2021; pp. 1457–1460. [Google Scholar]
- Jin, Y.; Duan, P.; Ji, H. Estimation of LFM signal parameters based on LVD in complex noise environment. J. Electron. Inf. Technol. 2014, 36, 1106–1112. [Google Scholar]
- Wang, H.; Long, J. Applications of fractional lower order synchrosqueezing transform time frequency technology to machine fault diagnosis. Math. Probl. Eng. 2020, 2020, 3983242. [Google Scholar] [CrossRef]
- Li, L.; Yu, X.; Jiang, Q.; Zang, B.; Jiang, L. Synchrosqueezing transform meets α-stable distribution: An adaptive fractional lower-order SST for instantaneous frequency estimation and non-stationary signal recovery. Signal Process. 2022, 201, 108683. [Google Scholar] [CrossRef]
- Chen, M.; Xing, H.; Wang, H. Multipath delay estimation of LFM signals based on NAT function under impulse noise. J. Electron. Meas. Instrum. 2022, 36, 73–81. [Google Scholar]
- Li, L.; Qiu, T. A robust parameter estimation of LFM signal based on sigmoid transform under the alpha stable distribution noise. Circuits Syst. Signal Process. 2019, 38, 3170–3186. [Google Scholar] [CrossRef]
- Wang, H.; Zhang, Q.; Cheng, W.; Dong, J.; Liu, X. A novel parameter estimation method based on piecewise nonlinear amplitude transform for the LFM signal in impulsive noise. Electronics 2023, 12, 2530. [Google Scholar] [CrossRef]
- Liu, X.; Li, X.; Xiao, B.; Wang, C.; Ma, B. LFM signal parameter estimation via FTD-FRFT in impulse noise. Fractal Fract. 2023, 7, 69. [Google Scholar] [CrossRef]
- Xiao, B.; Liu, X.; Wang, C.; Wang, Y.; Huang, T. Sliding-Window TD-FrFT algorithm for high-precision ranging of LFM signals in the presence of impulse noise. Fractal Fract. 2023, 7, 679. [Google Scholar] [CrossRef]
- Lu, J.; Guo, Y.; Yang, L. Denoising method for LFM signals based on DCNN under pulse noise. Mod. Radar 2023, 7, 1–11. [Google Scholar]
- Razzaq, H.S.; Hussain, Z.M. Instantaneous frequency estimation of FM signals under Gaussian and symmetric α-stable noise: Deep learning versus time–frequency analysis. Information 2022, 14, 18. [Google Scholar] [CrossRef]
- Wei, J.; Gao, Z. Design and analysis on fractional-order tracking differentiator. In Proceedings of the 27th Chinese Control and Decision Conference, Qingdao, China, 23–25 May 2015; pp. 3137–3141. [Google Scholar]
- Wei, Y.; Hu, Y.; Song, L.; Wang, Y. Tracking differentiator based fractional order model reference adaptive control: The 1<α<2 Case. In Proceedings of the 53rd IEEE Conference on Decision and Control, Los Angeles, CA, USA, 15–17 December 2014; pp. 6902–6907. [Google Scholar]
- Park, S.; Han, S. Robust backstepping control combined with fractional-order tracking differentiator and fractional-order nonlinear disturbance observer for unknown quadrotor UAV systems. Appl. Sci. 2022, 12, 11637. [Google Scholar] [CrossRef]
- Huang, X.; Zhang, L.; Chen, Z.; Zhao, R. Robust detection and motion parameter estimation for weak maneuvering target in the alpha-stable noise environment. Digit. Signal Process. 2021, 108, 102885. [Google Scholar] [CrossRef]
- Liu, X.; Wang, C. A novel parameter estimation of chirp signal in α-stable noise. IEICE Electron. Express 2017, 14, 20161053. [Google Scholar] [CrossRef][Green Version]
- Liu, T. Research on Cyclic Stationary Signal Processing Method under Alpha Stable Distributed Noise; Dalian University of Technology: Dalian, China, 2020. [Google Scholar]
- Wei, Y.; Du, B.; Cheng, S.; Wang, Y. Fractional Order Systems Time-Optimal Control and Its Application. J. Optim. Theory Appl. 2017, 174, 122–138. [Google Scholar] [CrossRef]
- Sun, B.; Sun, X. Composite function for optimal control of discrete systems. Control. Decis. 2010, 25, 473–477. [Google Scholar]
- Guo, Y.; Yang, L. Method for parameter estimation of LFM signal and its application. IET Signal Process. 2019, 13, 538–543. [Google Scholar] [CrossRef]
- Eskandar, H.; Sadollah, A.; Bahreininejad, A.; Hamdi, M. Water cycle algorithm—A novel metaheuristic optimization method for solving constrained engineering optimization problems. Comput. Struct. 2012, 110–111, 151–166. [Google Scholar] [CrossRef]
- Sounds Recorded in Glacier Bay. Available online: https://www.nps.gov/glba/learn/nature/soundclips.htm (accessed on 10 July 2023).




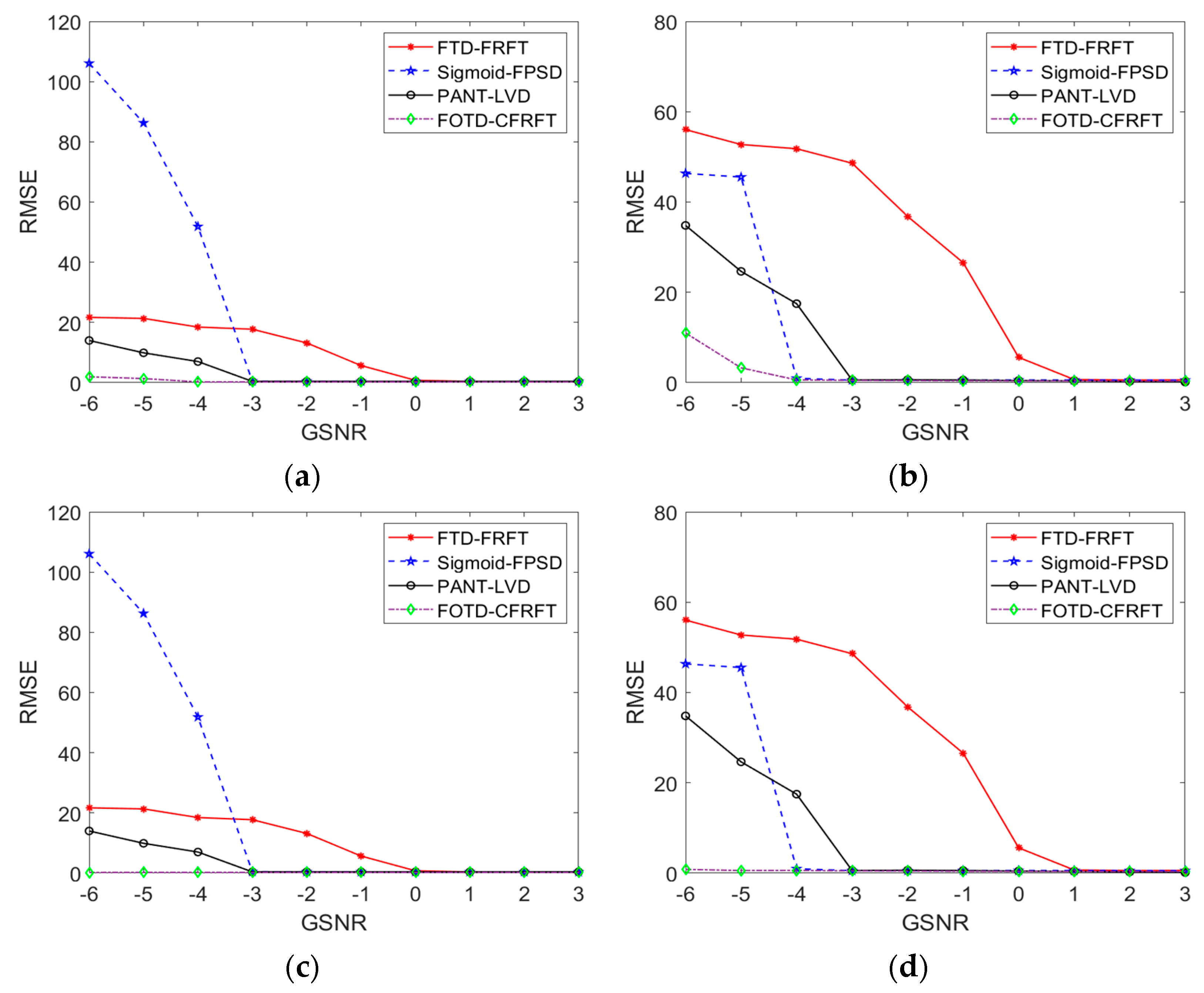




| −6 dB | −5 dB | −4 dB | −3 dB | −2 dB | −1 dB | 0 dB | 1 dB | 2 dB | 3 dB | ||
|---|---|---|---|---|---|---|---|---|---|---|---|
| f0 | FTD-FRFT | 1.2102 | 2.2815 | 5.5838 | 7.6531 | 13.4799 | 18.5058 | 20.0341 | 20.0968 | 20.0952 | 20.0950 |
| Sigmoid-FPSD | −4.7484 | 11.7004 | 10.2649 | 20.2852 | 20.2182 | 20.1562 | 20.1863 | 20.1862 | 20.1058 | 20.1158 | |
| PANT-LVD | 16.0291 | 18.4695 | 19.6947 | 20.9199 | 20.9199 | 20.9199 | 20.9199 | 20.9199 | 20.9199 | 20.9199 | |
| FOTD-CFRFT | 20.2796 | 20.2574 | 20.2608 | 20.2617 | 20.2639 | 20.2652 | 20.2605 | 20.2603 | 20.2649 | 20.2646 | |
| k | FTD-FRFT | −3.5269 | 0.9849 | 1.3671 | 8.1601 | 25.9438 | 40.8245 | 49.4254 | 50.1678 | 50.0054 | 49.9729 |
| Sigmoid-FPSD | 45.4743 | 54.6101 | 50.1517 | 50.1191 | 50.1191 | 50.1678 | 50.1840 | 50.1677 | 50.1516 | 50.1353 | |
| PANT-LVD | 37.9866 | 43.9949 | 47.0189 | 50.1228 | 50.0730 | 50.1329 | 50.2327 | 50.2826 | 50.3425 | 50.3924 | |
| FOTD-CFRFT | 50.0982 | 50.1338 | 50.0889 | 50.1279 | 50.1832 | 50.1652 | 50.1783 | 50.1738 | 50.2006 | 50.1938 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, H.; Guo, Y.; Yang, L. Parameter Estimation of LFM Signals Based on FOTD-CFRFT under Impulsive Noise. Fractal Fract. 2023, 7, 822. https://doi.org/10.3390/fractalfract7110822
Wang H, Guo Y, Yang L. Parameter Estimation of LFM Signals Based on FOTD-CFRFT under Impulsive Noise. Fractal and Fractional. 2023; 7(11):822. https://doi.org/10.3390/fractalfract7110822
Chicago/Turabian StyleWang, Houyou, Yong Guo, and Lidong Yang. 2023. "Parameter Estimation of LFM Signals Based on FOTD-CFRFT under Impulsive Noise" Fractal and Fractional 7, no. 11: 822. https://doi.org/10.3390/fractalfract7110822
APA StyleWang, H., Guo, Y., & Yang, L. (2023). Parameter Estimation of LFM Signals Based on FOTD-CFRFT under Impulsive Noise. Fractal and Fractional, 7(11), 822. https://doi.org/10.3390/fractalfract7110822




