Modeling Long-Distance Forward and Backward Diffusion Processes in Tracer Transport Using the Fractional Laplacian on Bounded Domains
Abstract
:1. Introduction
2. Materials and Methods
2.1. Model Development
2.2. Finite Difference Method Scheme for the Fractional Laplacian-Based Model
3. Results and Discussion
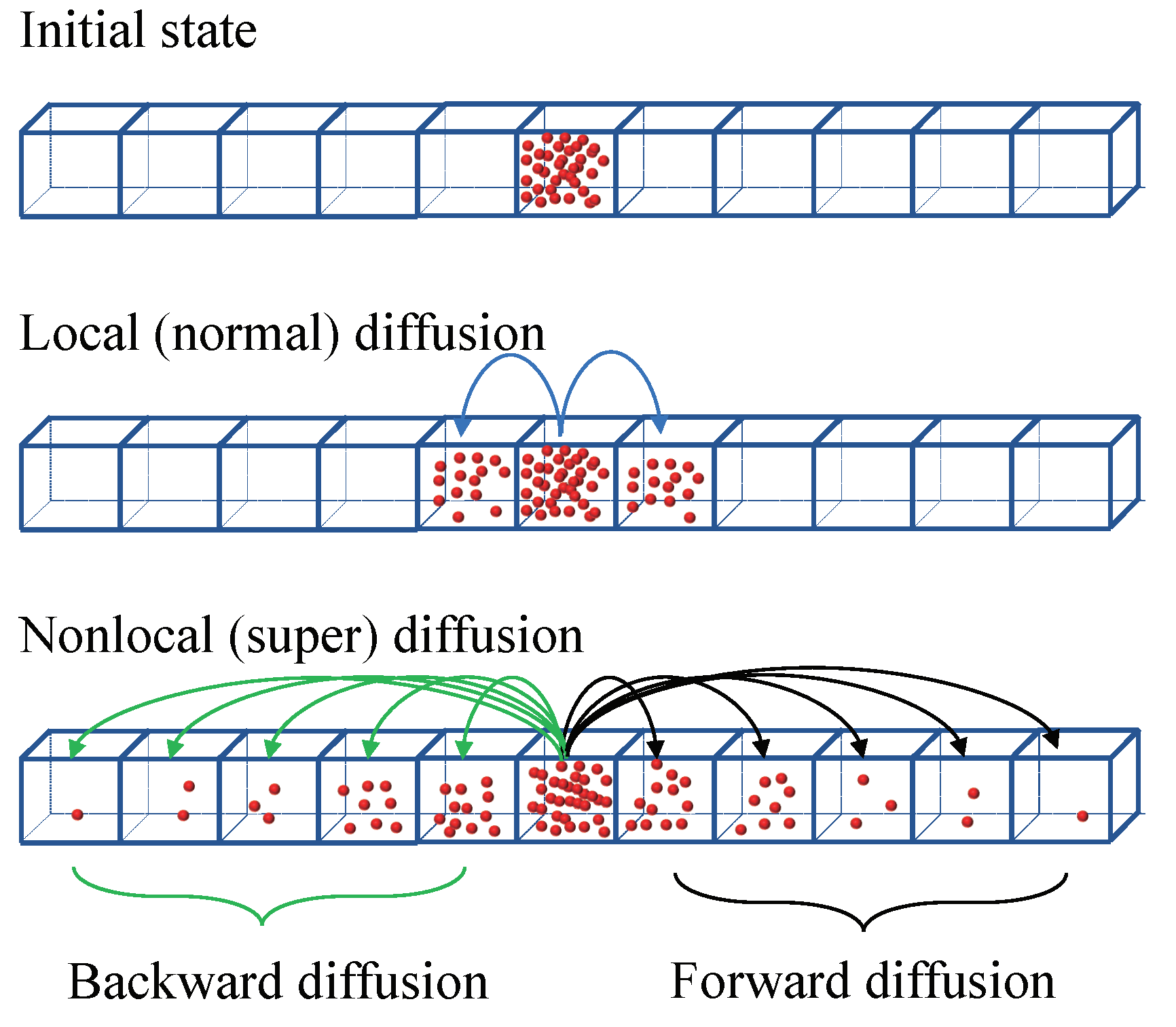
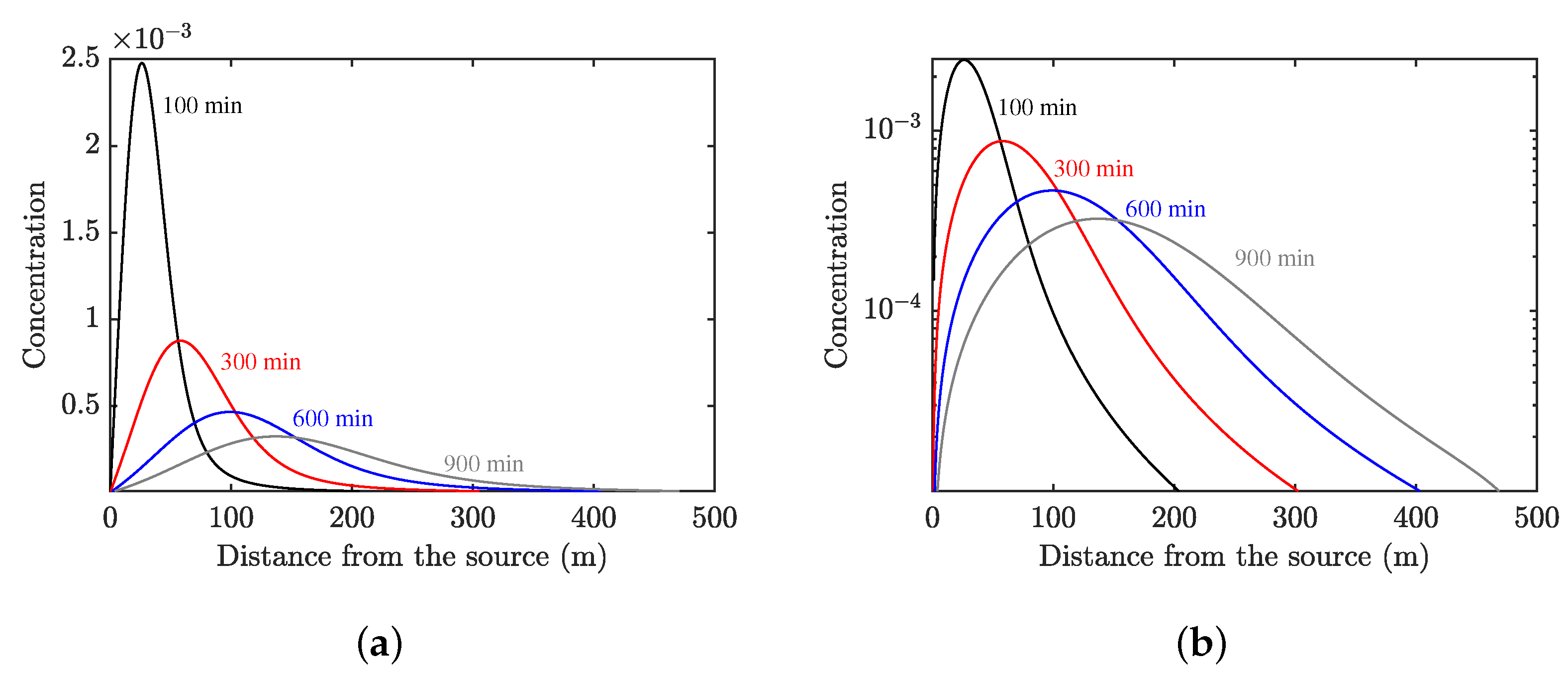
3.1. Diffusion Regimes
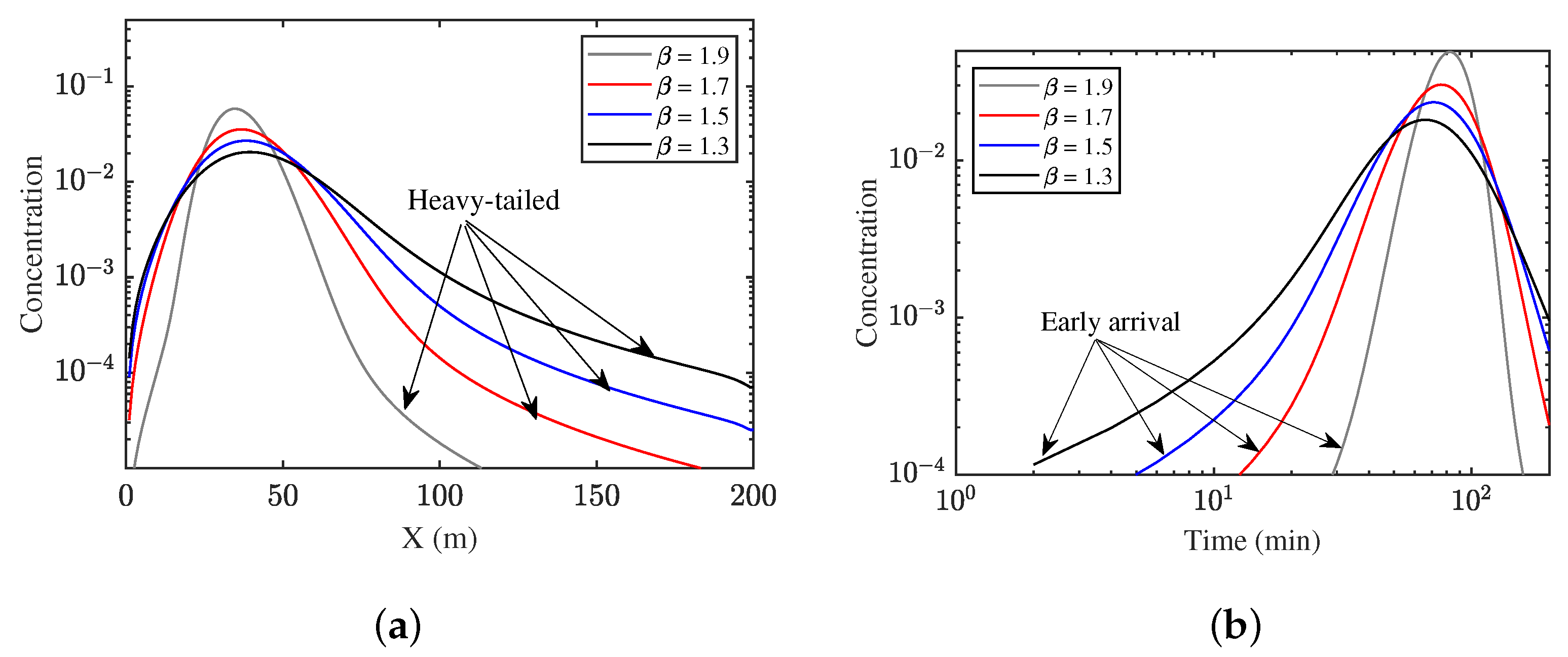
3.2. Sensitivity Analysis of Model Parameters
4. Applications
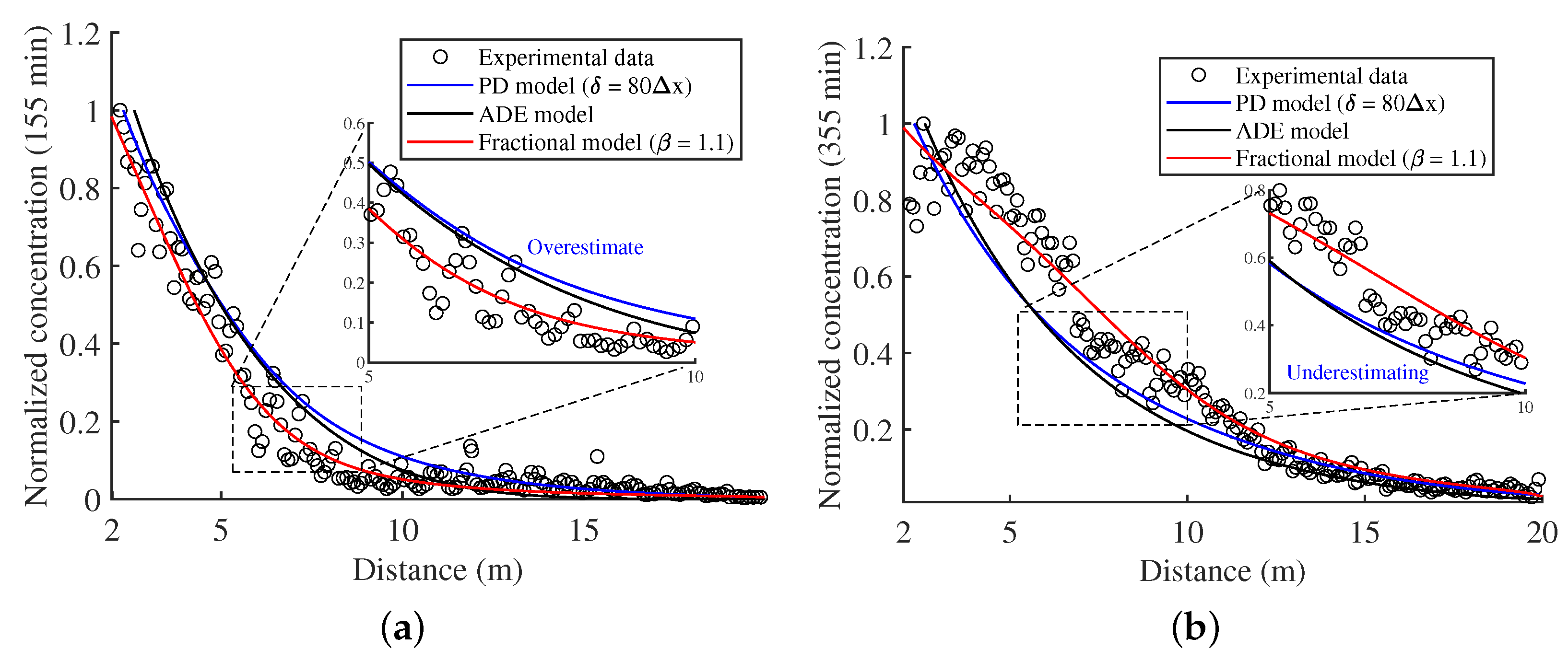
4.1. Case 1: Solute Transport in Groundwater Flow
4.2. Case 2: Intermediate-Scale Flume Experiments of Bedload Sediments
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Bouchaud, J.P.; Georges, A. Anomalous diffusion in disordered media: Statistical mechanisms, models and physical applications. Phys. Rep. 1990, 195, 127–293. [Google Scholar] [CrossRef]
- Berkowitz, B.; Cortis, A.; Dentz, M.; Scher, H. Modeling non-Fickian transport in geological formations as a continuous time random walk. Rev. Geophys. 2006, 44, RG2003. [Google Scholar] [CrossRef]
- Wang, Y.; Sun, H.; Fan, S.; Gu, Y.; Yu, X. A nonlocal fractional peridynamic diffusion model. Fractal Fract. 2021, 5, 76. [Google Scholar] [CrossRef]
- Li, Z.; Yuan, S.; Tang, H.; Zhu, Y.; Sun, H. Quantifying nonlocal bedload transport: A regional-based nonlocal model for bedload transport from local to global scales. Adv. Water Resour. 2023, 177, 104444. [Google Scholar] [CrossRef]
- Hao, X.; Sun, H.; Zhang, Y.; Li, S.; Yu, Z. Co-transport of arsenic and micro/nano-plastics in saturated soil. Environ. Res. 2023, 228, 115871. [Google Scholar] [CrossRef] [PubMed]
- Hatano, Y.; Hatano, N. Dispersive transport of ions in column experiments: An explanation of long-tailed profiles. Water Resour. Res. 1998, 34, 1027–1033. [Google Scholar] [CrossRef]
- Liu, L.; Zhang, S.; Chen, S.; Liu, F.; Feng, L.; Turner, I.; Zheng, L.; Zhu, J. An Application of the Distributed-Order Time-and Space-Fractional Diffusion-Wave Equation for Studying Anomalous Transport in Comb Structures. Fractal Fract. 2023, 7, 239. [Google Scholar] [CrossRef]
- Li, Z.; Kiani Oshtorjani, M.; Chen, D.; Zhang, Y.; Sun, H. Dynamics of Dual-Mode Bedload Transport With Three-Dimensional Alternate Bars Migration in Subcritical Flow: Experiments and Model Analysis. J. Geophys. Res. Earth Surf. 2023, 128, e2022JF006882. [Google Scholar] [CrossRef]
- Adams, E.E.; Gelhar, L.W. Field study of dispersion in a heterogeneous aquifer: 2. Spatial moments analysis. Water Resour. Res. 1992, 28, 3293–3307. [Google Scholar] [CrossRef]
- Zhang, Y.; Benson, D.A.; Reeves, D.M. Time and space nonlocalities underlying fractional-derivative models: Distinction and literature review of field applications. Adv. Water Resour. 2009, 32, 561–581. [Google Scholar] [CrossRef]
- Metzler, R.; Rajyaguru, A.; Berkowitz, B. Modelling anomalous diffusion in semi-infinite disordered systems and porous media. New J. Phys. 2022, 24, 123004. [Google Scholar] [CrossRef]
- Sun, H.; Zhang, Y.; Baleanu, D.; Chen, W.; Chen, Y. A new collection of real world applications of fractional calculus in science and engineering. Commun. Nonlinear Sci. Numer. Simul. 2018, 64, 213–231. [Google Scholar] [CrossRef]
- ten Hagen, B.; van Teeffelen, S.; Löwen, H. Brownian motion of a self-propelled particle. J. Phys. Condens. Matter 2011, 23, 194119. [Google Scholar] [CrossRef]
- Ghosh, P.K.; Misko, V.R.; Marchesoni, F.; Nori, F. Self-propelled Janus particles in a ratchet: Numerical simulations. Phys. Rev. Lett. 2013, 110, 268301. [Google Scholar] [CrossRef] [PubMed]
- Nelissen, K.; Misko, V.; Peeters, F. Single-file diffusion of interacting particles in a one-dimensional channel. Europhys. Lett. 2007, 80, 56004. [Google Scholar] [CrossRef]
- Taloni, A.; Marchesoni, F. Single-file diffusion on a periodic substrate. Phys. Rev. Lett. 2006, 96, 020601. [Google Scholar] [CrossRef]
- Boffetta, G.; De Lillo, F.; Musacchio, S. Anomalous diffusion in confined turbulent convection. Phys. Rev. E 2012, 85, 066322. [Google Scholar] [CrossRef]
- Metzler, R.; Klafter, J. The random walk’s guide to anomalous diffusion: A fractional dynamics approach. Phys. Rep. 2000, 339, 1–77. [Google Scholar] [CrossRef]
- Sun, L.; Qiu, H.; Wu, C.; Niu, J.; Hu, B.X. A review of applications of fractional advection–dispersion equations for anomalous solute transport in surface and subsurface water. Wiley Interdiscip. Rev. Water 2020, 7, e1448. [Google Scholar] [CrossRef]
- Cushman, J.H. The Physics of Fluids in Hierarchical Porous Media: Angstroms to Miles; Springer Science & Business Media: Berlin/Heidelberg, Germany, 2013; Volume 10. [Google Scholar]
- Foufoula-Georgiou, E.; Ganti, V.; Dietrich, W. A nonlocal theory of sediment transport on hillslopes. J. Geophys. Res. Earth Surf. 2010, 115, F00A16. [Google Scholar] [CrossRef]
- Union, J.I.G. Advection diffusion equation models in near-surface geophysical and environmental sciences. J. Indian Geophys. Union 2013, 17, 117–127. [Google Scholar]
- Hilfer, R. Applications of Fractional Calculus in Physics; World Scientific: Singapore, 2000. [Google Scholar]
- Klafter, J.; Lim, S.; Metzler, R. Fractional Dynamics: Recent Advances; World Scientific: Singapore, 2012. [Google Scholar]
- Tawfik, A.M.; Hefny, M.M. Subdiffusive Reaction Model of Molecular Species in Liquid Layers: Fractional Reaction-Telegraph Approach. Fractal Fract. 2021, 5, 51. [Google Scholar] [CrossRef]
- Kim, S.; Kavvas, M.L. Generalized Fick’s law and fractional ADE for pollution transport in a river: Detailed derivation. J. Hydrol. Eng. 2006, 11, 80–83. [Google Scholar] [CrossRef]
- Baeumer, B.; Kovács, M.; Meerschaert, M.M.; Sankaranarayanan, H. Reprint of: Boundary conditions for fractional diffusion. J. Comput. Appl. Math. 2018, 339, 414–430. [Google Scholar] [CrossRef]
- Zhang, Y.; Yu, X.; Li, X.; Kelly, J.F.; Sun, H.; Zheng, C. Impact of absorbing and reflective boundaries on fractional derivative models: Quantification, evaluation and application. Adv. Water Resour. 2019, 128, 129–144. [Google Scholar] [CrossRef]
- Jannelli, A.; Ruggieri, M.; Speciale, M.P. Analytical and numerical solutions of time and space fractional advection–diffusion–reaction equation. Commun. Nonlinear Sci. Numer. Simul. 2019, 70, 89–101. [Google Scholar] [CrossRef]
- Yin, M.; Ma, R.; Zhang, Y.; Chen, K.; Guo, Z.; Zheng, C. A Dual Heterogeneous Domain Model for Upscaling Anomalous Transport With Multi-Peaks in Heterogeneous Aquifers. Water Resour. Res. 2022, 58, e2021WR031128. [Google Scholar] [CrossRef]
- Angstmann, C.N.; Henry, B.I.; Jacobs, B.A.; McGann, A.V. An explicit numerical scheme for solving fractional order compartment models from the master equations of a stochastic process. Commun. Nonlinear Sci. Numer. Simul. 2019, 68, 188–202. [Google Scholar] [CrossRef]
- Furbish, D.J.; Roering, J.J. Sediment disentrainment and the concept of local versus nonlocal transport on hillslopes. J. Geophys. Res. Earth Surf. 2013, 118, 937–952. [Google Scholar] [CrossRef]
- Zhang, Y. Backward Particle Tracking of Anomalous Transport in Multi-Dimensional Aquifers. Water Resour. Res. 2022, 58, e2022WR032396. [Google Scholar] [CrossRef]
- Lischke, A.; Pang, G.; Gulian, M.; Song, F.; Glusa, C.; Zheng, X.; Mao, Z.; Cai, W.; Meerschaert, M.M.; Ainsworth, M.; et al. What is the fractional Laplacian? A comparative review with new results. J. Comput. Phys. 2020, 404, 109009. [Google Scholar] [CrossRef]
- Scherer, R.; Kalla, S.L.; Tang, Y.; Huang, J. The Grünwald–Letnikov method for fractional differential equations. Comput. Math. Appl. 2011, 62, 902–917. [Google Scholar] [CrossRef]
- Li, C.; Qian, D.; Chen, Y. On Riemann-Liouville and caputo derivatives. Discret Dyn. Nat. Soc. 2011, 2011, 562494. [Google Scholar] [CrossRef]
- De Oliveira, E.C.; Tenreiro Machado, J.A. A review of definitions for fractional derivatives and integral. Math. Probl. Eng. 2014, 2014, 238459. [Google Scholar] [CrossRef]
- Zoia, A.; Rosso, A.; Kardar, M. Fractional Laplacian in bounded domains. Phys. Rev. E 2007, 76, 021116. [Google Scholar] [CrossRef]
- D’Elia, M.; Gunzburger, M. The fractional Laplacian operator on bounded domains as a special case of the nonlocal diffusion operator. Comput. Math. Appl. 2013, 66, 1245–1260. [Google Scholar] [CrossRef]
- Zhang, Y.; Zhou, D.; Yin, M.; Sun, H.; Wei, W.; Li, S.; Zheng, C. Nonlocal transport models for capturing solute transport in one-dimensional sand columns: Model review, applicability, limitations and improvement. Hydrol. Process. 2020, 34, 5104–5122. [Google Scholar] [CrossRef]
- Duo, S.; van Wyk, H.W.; Zhang, Y. A novel and accurate finite difference method for the fractional Laplacian and the fractional Poisson problem. J. Comput. Phys. 2018, 355, 233–252. [Google Scholar] [CrossRef]
- Gao, T.; Duan, J.; Li, X.; Song, R. Mean exit time and escape probability for dynamical systems driven by Lévy noises. SIAM J. Sci. Comput. 2014, 36, A887–A906. [Google Scholar] [CrossRef]
- Huang, Y.; Oberman, A. Numerical methods for the fractional Laplacian: A finite difference-quadrature approach. SIAM J. Numer. Anal. 2014, 52, 3056–3084. [Google Scholar] [CrossRef]
- Sun, H.; Li, Z.; Zhang, Y.; Chen, W. Fractional and fractal derivative models for transient anomalous diffusion: Model comparison. Chaos Solitons Fractals 2017, 102, 346–353. [Google Scholar] [CrossRef]
- Yin, M.; Zhang, Y.; Ma, R.; Tick, G.R.; Bianchi, M.; Zheng, C.; Wei, W.; Wei, S.; Liu, X. Super-diffusion affected by hydrofacies mean length and source geometry in alluvial settings. J. Hydrol. 2020, 582, 124515. [Google Scholar] [CrossRef]
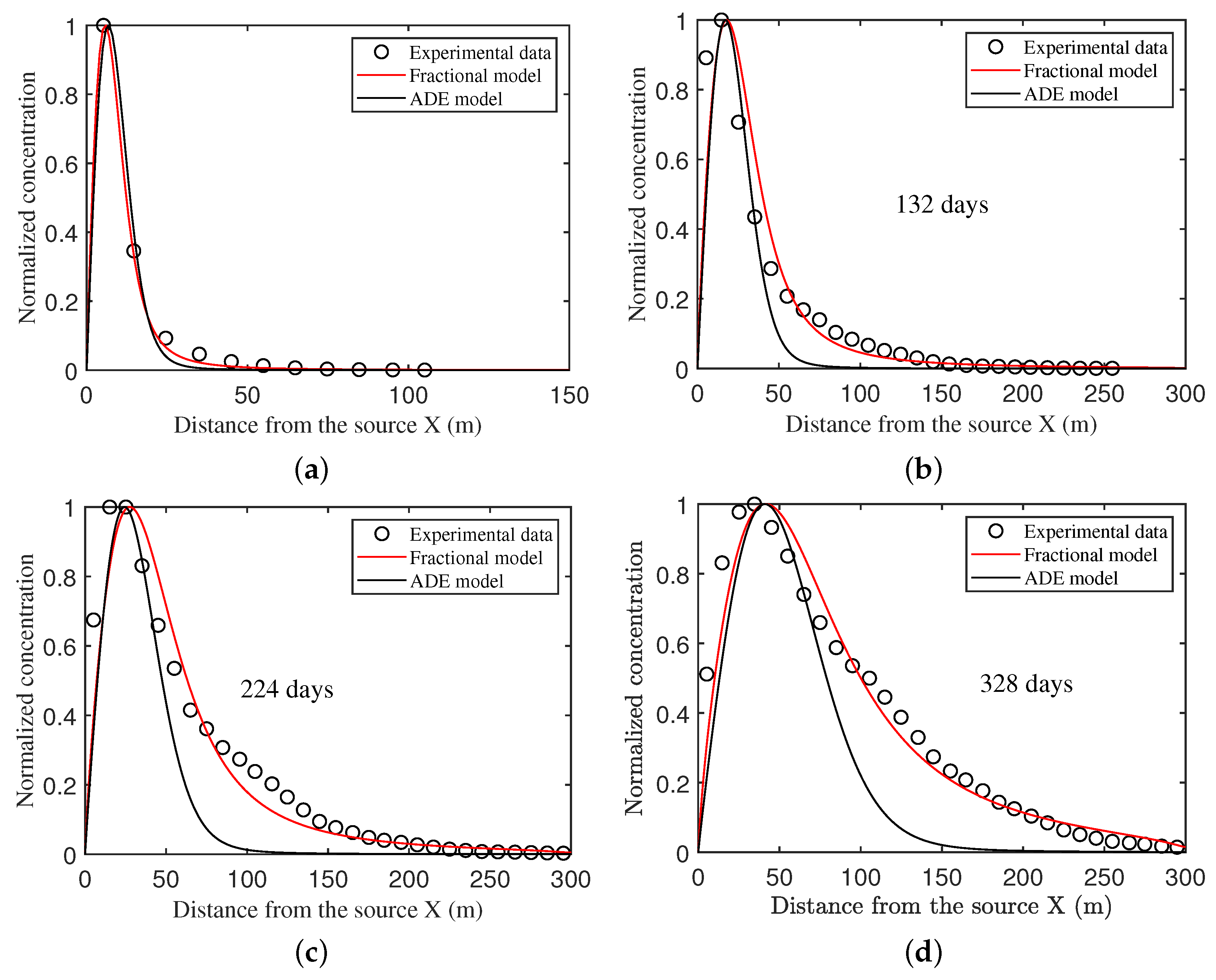
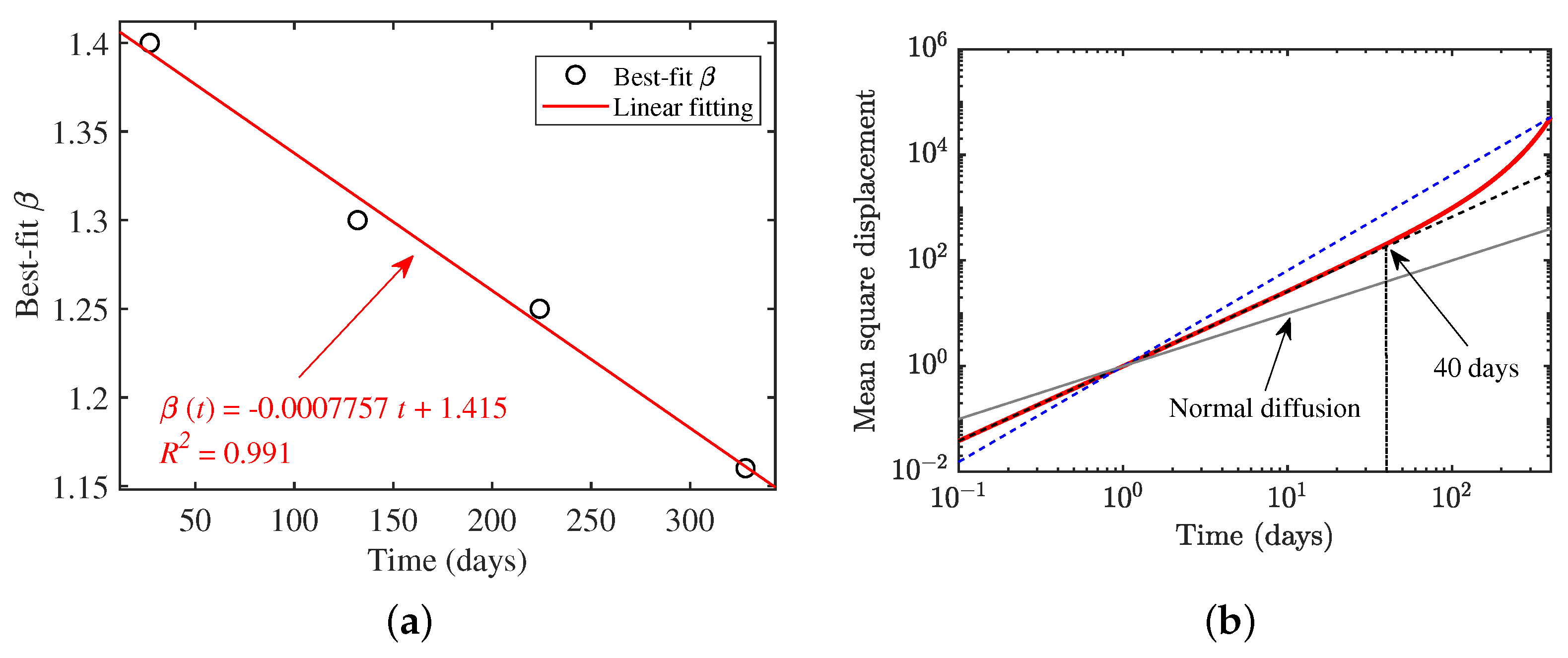
| Time (Days) | v (m/Day) | D (mβ/Day) | R | |
|---|---|---|---|---|
| 27 | 0.018 | 3 | 10 | 1.40 |
| 132 | 1.30 | |||
| 224 | 1.25 | |||
| 328 | 1.16 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, Z.; Tang, H.; Yuan, S.; Zhang, H.; Kong, L.; Sun, H. Modeling Long-Distance Forward and Backward Diffusion Processes in Tracer Transport Using the Fractional Laplacian on Bounded Domains. Fractal Fract. 2023, 7, 823. https://doi.org/10.3390/fractalfract7110823
Li Z, Tang H, Yuan S, Zhang H, Kong L, Sun H. Modeling Long-Distance Forward and Backward Diffusion Processes in Tracer Transport Using the Fractional Laplacian on Bounded Domains. Fractal and Fractional. 2023; 7(11):823. https://doi.org/10.3390/fractalfract7110823
Chicago/Turabian StyleLi, Zhipeng, Hongwu Tang, Saiyu Yuan, Huiming Zhang, Lingzhong Kong, and HongGuang Sun. 2023. "Modeling Long-Distance Forward and Backward Diffusion Processes in Tracer Transport Using the Fractional Laplacian on Bounded Domains" Fractal and Fractional 7, no. 11: 823. https://doi.org/10.3390/fractalfract7110823
APA StyleLi, Z., Tang, H., Yuan, S., Zhang, H., Kong, L., & Sun, H. (2023). Modeling Long-Distance Forward and Backward Diffusion Processes in Tracer Transport Using the Fractional Laplacian on Bounded Domains. Fractal and Fractional, 7(11), 823. https://doi.org/10.3390/fractalfract7110823










