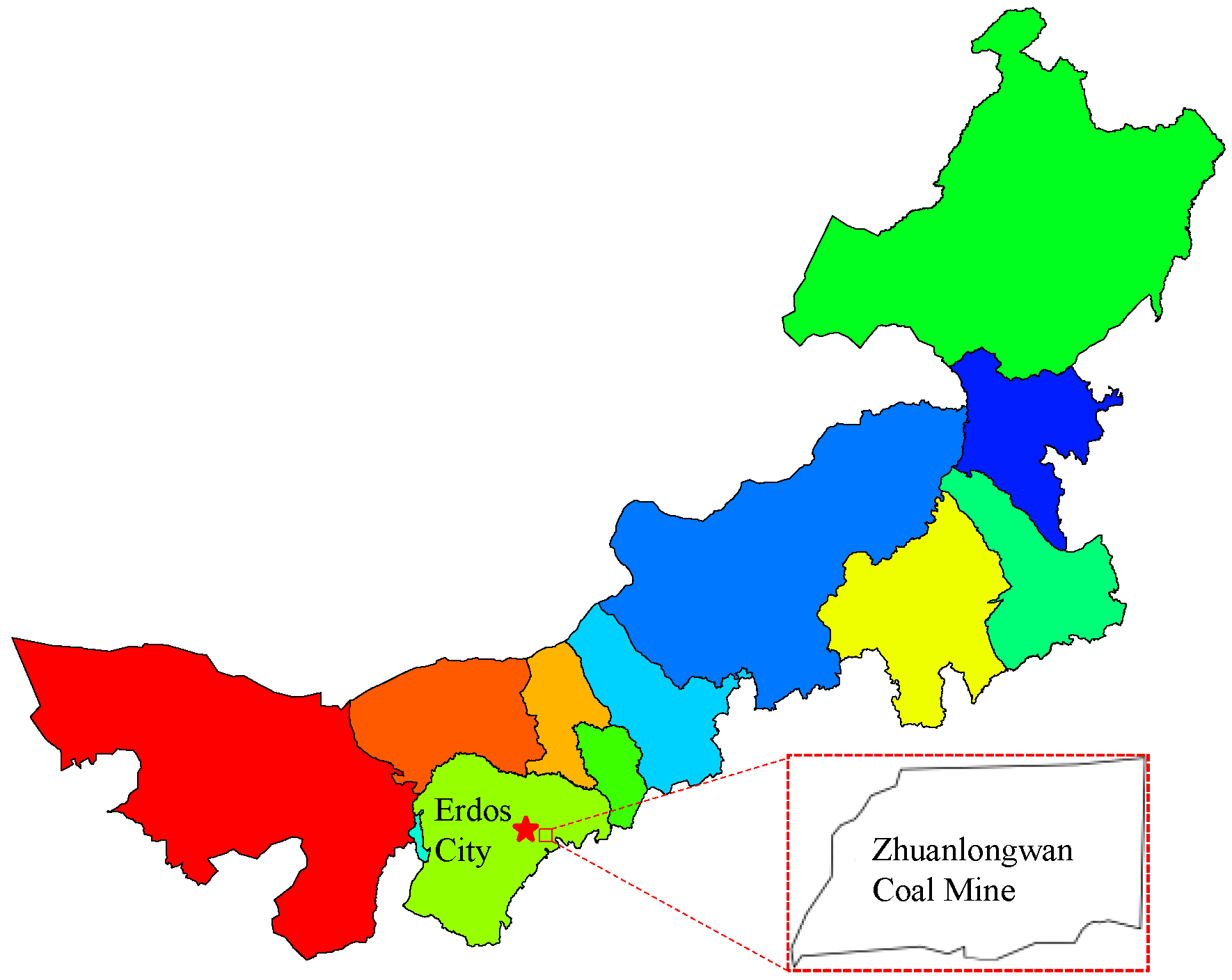
Evolution Law of Shallow Water in Multi-Face Mining Based on Partition Characteristics of Catastrophe Theory

Abstract

It is of great significance for ecological environment protection to clarify the regional evolution characteristics of shallow water under the disturbance of multi-working face mining. In this paper, the catastrophe theory method, GIS spatial analysis function and FEFLOW numerical calculation method were comprehensively used to study the instability risk and evolution law of shallow water systems in the Zhuan Longwan Coal Mine. The results show that: the Zhuan Longwan Coal Mine is divided into five areas (small risk area, light risk area, middle risk area, heavy risk area and special risk area) based on catastrophe theory, among which the middle risk area has the largest area of 16,616,880 m², and the special risk area has the smallest area of 1,769,488 m². Based on the results of catastrophe zoning, the evolution law of shallow water under multi-surface disturbance in different zones is expounded. In the middle-risk area, the water level drop at measuring point 4 is the largest, which is 0.525 m, and the water level drop at measuring point 5 is the smallest, which is 0.116 m. The study aims to provide a basis for regional coal development planning and research on the method of water-retaining coal mining.

1. Introduction

Mining disturbance will inevitably have a negative impact on the groundwater system, resulting in the change of the groundwater system from a stable state to an unstable state [1,2]. As time goes by, the water system will change from a state of instability to a state of stability. However, since the adaptive capacity of the water system is often insufficient to make up for the negative impact caused by mining, it will take a long time to establish a stable state, which will inevitably lead to the loss of more valuable groundwater resources [3,4,5]. Therefore, the study on the determination of the threshold of the main control factors that disturb the change of shallow water systems from a stable state to an unstable state is of great significance for the rational exploitation of coal resources and ensuring the important function of groundwater systems.

Scholars have carried out a great number of studies on two topics: water-retaining coal mining zoning and quantitative assessment of shallow water.

Water-retaining coal mining zoning: Wang Shuangming [6] analyzed the spatial relationship between the thickness of the first coal seam and the water-bearing layer, divided the water-retaining mining conditions in the Yushen mining area and put forward the corresponding regional coal mining method planning scheme. Deng Niandong [7] statistically analyzed the data of 500 boreholes, and based on the occurrence characteristics of the first coal seam and water-bearing and water-resisting layers, divided the Yushen mining area into five types of water-retaining coal mining engineering geological zoning. Li Wenping [8] studied the spatial occurrence structure characteristics of ecological-water-coal measures strata in the study area and divided them into: normal mining mines, level I water-retaining coal mining mines, level II water-retaining coal mining mines and level III water-retaining coal mining mines. Liu Shiliang [9] studied the hydrogeological data such as the thickness of the first coal seam in the Yushenfu mining area, and combined with the residual bedrock and residual soil thickness of mining overburden, studied the zoning of water-retaining coal mining in the mining area.

Evolution law of shallow water: quantitative assessment methods of groundwater disturbance mainly include an analogy method, analytical method and numerical calculation method, among which a numerical calculation method is the most commonly used [10]. Bear [11] analyzed the evolution characteristics of single-phase and multiphase flow under different factors, gave the rigorous derivation process of the most important equations of single-phase and multiphase flow, mass and heat transfer and quantified the evolution characteristics of the hydrodynamic field. Vafai [12] studied and analyzed the changing laws of convection, non-Darcy flow and turbulence, improved the numerical calculation method, and simulated and analyzed the flow, heat and mass transfer in porous media other than hydrogeology and groundwater environments. Mehls et al. [13] put forward the two-dimensional model local calculation unit encryption division method to build a finite difference groundwater calculation model, which improved the accuracy of numerical calculation results to some extent. Mazzia [14] improved the numerical method, which better solved the two-dimensional nonlinear dynamic problem of heavy salt groundwater migration simulation. Wu Qiang et al. [15,16] used spatial data analysis technology to create a good human-computer interaction environment and adopted a groundwater numerical simulation method, which was successfully applied in the water inrush assessment of the coal seam roof and floor [15]. At present, the existing research on the evolution law of zoning and shallow water mostly analyzes the evolution law and zoning characteristics of shallow water from a static perspective. There is little research or no in-depth research on the mutability, dynamics and multifaceted disturbance characteristics of shallow water systems from a stable state to an unstable state.

Based on the analysis of the connotation of water-retaining mining and the influencing factors of the water system, this paper comprehensively took into account of geological system, mining system and water system, exploring the main influencing factors of groundwater system stability. Then, using the catastrophe theory model and normalization method, the risk analysis and grade classification of the Zhuan Longwan Coal Mine were carried out with reference to the risk grade of groundwater development. Finally, based on the risk zoning combined with the catastrophe theory, the paper focused on the characteristics of the influence of mining on the shallow water level of three working faces, namely, the small risk area, the light risk area and the middle-risk area, and revealed the evolution law of shallow water under multi-surface disturbance in different zones, so as to provide a basis for regional coal development planning and research of water-retaining mining method.

2. Main Control Factors of Instability Risk Assessment of Groundwater Systems

There are numerous factors that influence mining on the groundwater system, and it is impractical to analyze them one by one. It is necessary to determine the main control factors that affect the stability of a groundwater system [17,18]. According to the connotation of water-retaining coal mining and the analysis of influencing factors of water system [19,20], after considering the geological system, mining system and water system comprehensively, the following six factors were determined as the main influencing factors of groundwater system stability: the buried depth of coal seam, the space distance between coal and water, the water abundance of water-bearing medium, the permeability coefficient of water-bearing medium, the thickness of effective water-resisting layer and the exploitation quantity [21,22].

The Zhuan Longwan Coal Mine is located in the northeast of the Ejin Horo Banner, Ordos City, Inner Mongolia (as shown in Figure 1). The mine is 10.0 km long from east to west and 5.6 km wide from north to south, covering an area of 43.5 km². At present, No. 2–3 coal seams are mainly mined, with an average thickness of 4.4 m and an average burial depth of 190.2 m. The sedimentary strata from old to new are as follows: the Upper Triassic Yanchang Formation, Yan’an Formation of Middle and Lower Jurassic, Zhiluo Formation and Anding Formation of Middle Jurassic, Ejinhoro Formation of Lower Cretaceous Series, Salawusu Formation of Quaternary Upper Pleistocene Series and Holocene Series strata. The roof is divided into three water-bearing and water-retaining layer groups, namely, the Quaternary sand table water aquifer group, the bedrock fissure confined aquifer group and the bedrock argillaceous water-retaining layer group. The lithology of the Quaternary aquifer is mainly silty sand and sub-sandy soil. The lithology is mainly medium and coarse-grained sandstone in the bedrock fissure-confined aquifer group. The water-retaining layer group is mainly composed of silty mudstone, mudstone, argillaceous siltstone and other lithologic formations.

Based on the original data of the main control factors of groundwater systems in the mining area, the kriging interpolation calculation and processing were performed by GIS technology, and the following thematic map of the main control factors was generated in Figure 2. Here, the instability risk assessment of the groundwater system in the study area was carried out according to the design idea of “fixed production by coal” (mining based on coal resources). The effective water clearance is the thickness of complete rock and earth mass between coal and water, and the exploitation quantity is the thickness of the coal seam at the corresponding position.

3. Risk Assessment of Shallow Water Instability Based on Catastrophe Theory

Mining disturbance causes the groundwater system to change from a stable state to an unstable state [2], and the system often changes from one stable state to another in the catastrophic form. Based on this, catastrophe theory has been widely used in geotechnical engineering [23]. The catastrophe model is used to comprehensively assess the instability risk of groundwater systems under mining disturbance.

3.1. Normalization Process and Assessment Principle

According to the potential function and bifurcation equation of various catastrophe models, the normalization formula of each catastrophe model was deduced, and then the catastrophe theory was used to make a comprehensive assessment decision. Swallowtail, cusp and butterfly catastrophe are three commonly used catastrophe models [23]. The relationship between control variables and state variables in the cusp, swallowtail and butterfly catastrophe models is shown in Figure 3. To distinguish the degree of influence of each control variable on state variables, the main control variable is usually placed at the front, and the secondary control variable is placed at the back.

Taking the swallowtail catastrophe as an example, the effects of the control variables and bifurcation equations of the swallowtail catastrophe on the catastrophe are analyzed. The specific steps are as follows:

The potential function of the swallowtail catastrophe is:

$$V\left(x\right)=\frac{1}{5}{x}^5+\frac{1}{3}a{x}^3+\frac{1}{2}b{x}^2+cx$$

(1)

Wherein: x is the controlled variable, and a, b and c are the controlled variables.

The equilibrium surface of swallowtail catastrophe deduced by potential function is:

$$x^4+a{x}^2+bx+c=0$$

(2)

The singular point set is derived as follows:

$$4x^3-2ax+b=0$$

(3)

Through the above two formulas, x is eliminated. After derivation,

$$4096a^4-46629b^4+4096c^3=0$$

(4)

The equation of bifurcation set obtained by changing the above-mentioned formula:

$$a=-5x^2,\mathrm{b}=8x^3,\mathrm{c}=-3x^4$$

(5)

The above-mentioned equation is further rewritten as:

$$x_a=\sqrt{\frac{a}{-5}},x_b=\sqrt[3]{\frac{b}{8}},x_c=\sqrt[4]{\frac{c}{-3}}$$

(6)

Let the absolute value of x be 1, then a = −6, b = −6, and c = −3. Thus, the range of state variable x and control variables a, b, and c is determined. The corresponding absolute values are divided into x: 0–1, a: 0–5, b: 0–8, and c: 0–3, which is convenient for the subsequent assessment decision-making. The research shows that narrowing the relative range of control variables will not affect the nature of the catastrophe model, and the unification of such range can also make use of the existing data of other methods.

$$x_a=\sqrt{a},x_b=\sqrt[3]{b},x_c=\sqrt[4]{c}$$

(7)

After performing the same derivation process, the normalization equations of the cusp catastrophe and butterfly catastrophe models can be obtained.

Cusp catastrophe:

$$x_a=\sqrt{a},x_b=\sqrt[3]{b}$$

(8)

Butterfly catastrophe:

$$x_a=\sqrt{a},x_b=\sqrt[3]{b},x_c=\sqrt[4]{c}, x_d=\sqrt[5]{d}$$

(9)

The above are the normalization formulas of the three commonly used catastrophe models. The normalization formula is also the basis of comprehensive assessment decision-making by catastrophe theory. It normalizes different states of control variables in a system into the same comparable state, then carries out quantitative recursive operation on the system, derives the system catastrophe membership function value which can represent the system state characteristics and uses this value as the basis of comprehensive assessment decision-making to judge the system state.

3.2. Assessment Principle

When using catastrophe theory to make fuzzy comprehensive assessment decision-making, it is necessary to determine the membership degree of each control variable according to the nature of the actual problem and the degree of influence of each control variable on the decision-making goal. The following three different criteria are commonly used:

1.

Complementarity criterion: when analyzing the influence of each control variable on the state variable, if each variable can mutually make up for shortcomings, the membership degree is determined according to the average value of each control variable. Taking the dovetail catastrophe model as an example,

$$x=\left(\frac{x_a+x_b+x_c}{3}\right)$$

(10)

2.

Non-complementary criterion: when analyzing the influence of each control variable on the state variable, if this influence cannot replace each other, or each other’s deficiencies cannot be mutually made up, the principle of “minimax” should be adopted for value selection, namely:

$$x=\mathrm{m}\mathrm{i}\mathrm{n}\{x_a+x_b+x_c\}$$

(11)

3.

Over-threshold complementarity criterion: each control variable needs to be complementary after reaching a certain threshold.

In view of the nature of practical problems, to make the fuzzy comprehensive analysis and assessment results more scientific and reasonable and avoid the influence of the loss of main control factors on the index at the next higher level, the following two methods can be adopted: (1) ignoring the factors that have little influence on state variables and determining more reasonable control variables; (2) limiting the relative level of data of each control variable, weakening the control variable with small influence and highlighting the control variable that plays a major role.

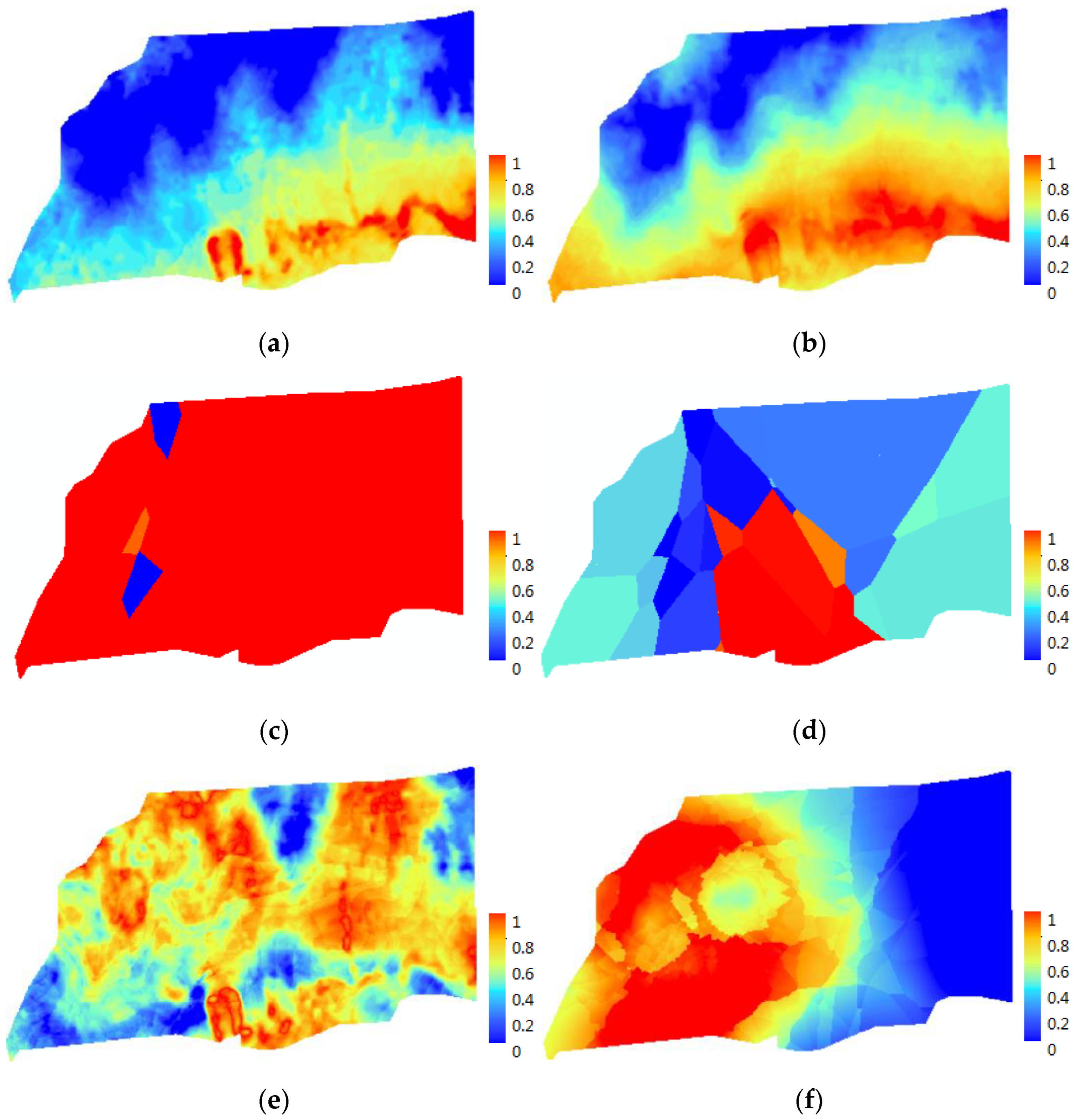
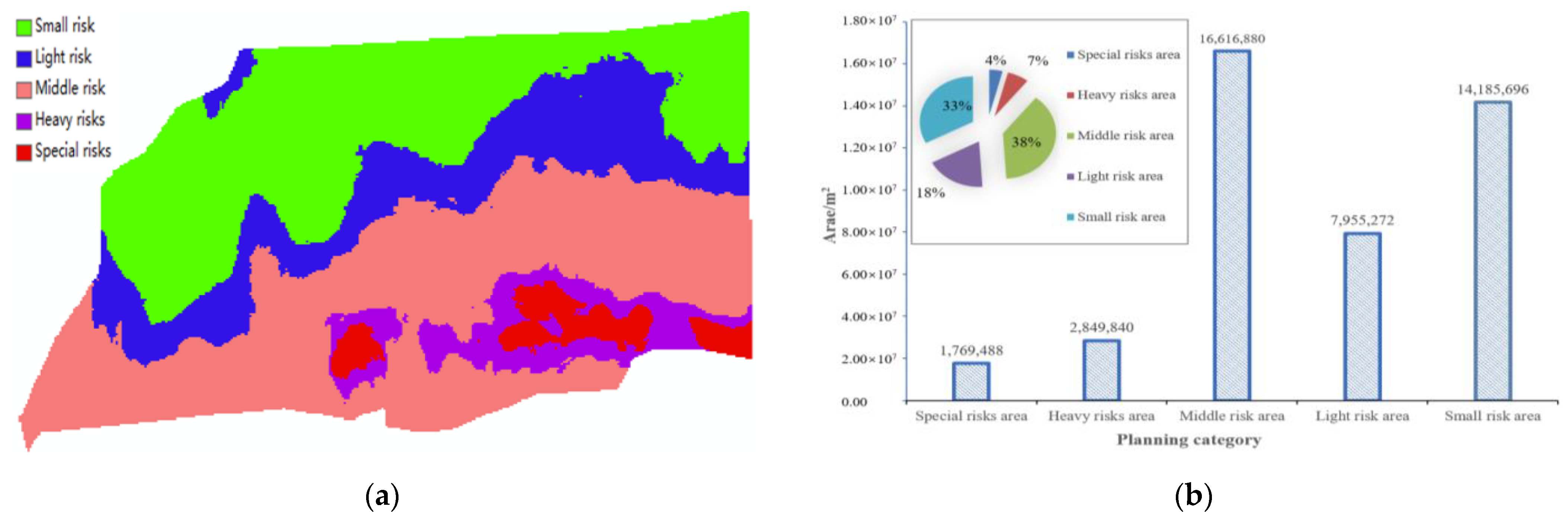
3.3. Risk Analysis of Groundwater System Instability

Determination of catastrophe progression: When using the catastrophe theory to make comprehensive assessments and decisions on the system, it is necessary to deal with various influencing factors to make them comparable. In this paper, fuzzy mathematics was used to determine the membership degree of each influencing factor by the membership function method. The single factor is usually determined by the F distribution method [24]. At present, there are six commonly used F distribution forms, and their corresponding functions include large, medium and small.

In the risk assessment of water system instability, it is necessary to select the corresponding function according to the characteristics of various influencing factors. The specific characteristics are: coal seam thickness, coal-water space distance and effective water-resisting layer thickness. These are positive indexes, and the larger the index of influencing factors, the smaller the risk of system instability. Water-bearing medium’s water abundance and permeability coefficient and exploitation quantity are negative indicators. The smaller the indicators of influencing factors are, the smaller the risk of system instability is. According to the characteristics of the research object, the small and large functions with semi-trapezoidal distribution were selected:

Small function:

$$f\left(x\right)=\left\{\begin{array}{cc}1& x<a\\ \frac{b-x}{b-a}& a\le x\le b\\ 0& x\le b\end{array}\right.$$

(12)

Large function:

$$f\left(x\right)=\left\{\begin{array}{cc}0& x<a\\ \frac{x-a}{b-a}& a\le x\le b\\ 1& x\ge b\end{array}\right.$$

(13)

Moderate function:

$$f\left(x\right)=\left\{\begin{array}{cc}0& x<a\\ \frac{x-a}{b-a}& a\le x\le b\\ 1& b\le x<c\\ \frac{d-x}{d-c}& c\le x<d\end{array}\right.$$

(14)

In the formula, a and b correspond to the upper and lower bounds of the piecewise function. Considering the influence of various influencing factors on the stability of groundwater systems is fuzzy, the approximate estimation method was adopted to quantify them. Each quantitative index can be selected in a certain range, and then the upper and lower bounds of each influencing factor can be determined by reducing its value by 20% based on the maximum and minimum values of each quantitative index, as shown in Figure 4.

After drawing lessons from the risk degree of groundwater development, the grade of risk degree is divided according to the risk value as depicted in

Table 1. Reference table of groundwater development risk state level.

Grade	Special-Risk Area	Heavy-Risk Area	Middle-Risk Area	Light-Risk Area	Small-Risk Area
Risk value	R ≥ 0.95	0.95 ≥ R ≥ 0.85	0.85 ≥ R ≥ 0.50	0.50 ≥ R ≥ 0.30	R ≤ 0.30

.

According to the butterfly catastrophe and cusp catastrophe model in catastrophe theory, the risk analysis of the Zhuan Longwan Coal Mine was carried out, and the risk level of groundwater development was used for reference. According to the risk value, it was classified into five categories, as shown in Figure 5: small risk area, light risk area, middle-risk area, heavy risk area and special risk area. The areas of special risk area, heavy risk area, middle risk area, light risk area and small risk area are 1,769,488 m², 2,849,840 m², 1,661,680 m², 7,944,272 m² and 1,418,5696 m², respectively. Among them, the middle-risk area accounts for the highest proportion (38.32%) and the special-risk area accounts for the lowest proportion (4.1%).

4. Construction of Quantitative Assessment Model of Shallow Water Disturbance

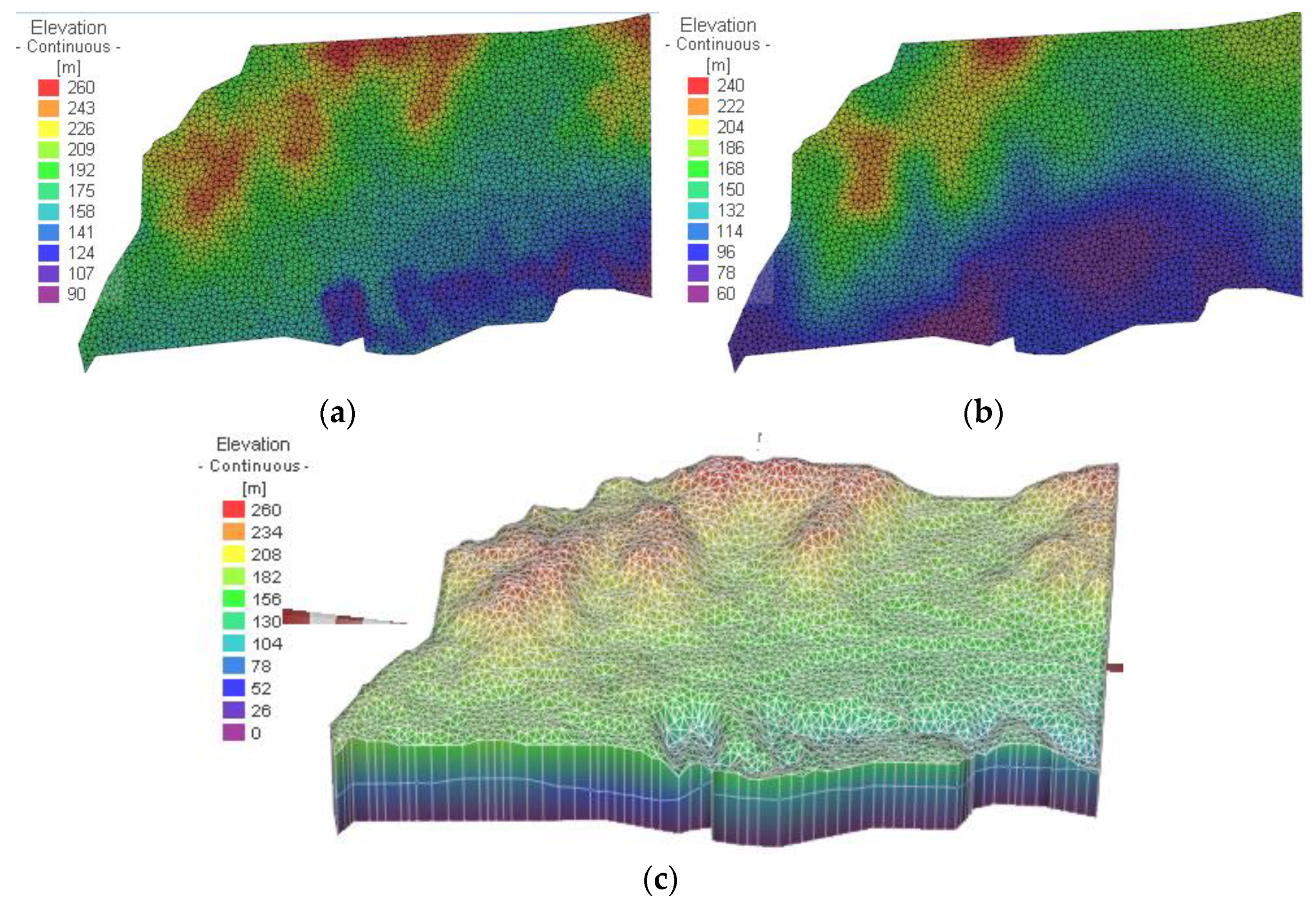
4.1. Model Generalization

(1) Determination of simulation range: this paper took the Zhuan Longwan Mining Area as the research object. The model range is about 12.87 km wide from north to south, and 11.09 km long from east to west, with a total area of about 142.73 km². (2) Generalization of water-bearing (water resisting) layer: The object of this simulation is mainly the Quaternary sand phreatic water-bearing layer. (3) Generalization of boundary conditions: lateral boundary: The flow direction of groundwater in Zhuan Longwan area is from both banks of the Gongniergai ditch to the direction inside the ditch, so the boundary of the first layer of table water aquifer can be generalized into the second type of flow boundary. According to the contour line of water level elevation of the weathered bedrock water-bearing layer, the groundwater flow of shallow water is north to south, as shown in Figure 6. Vertical boundary: The free water surface of the table water aquifer of the sand layer is taken as the upper boundary of the model.

(4) Mathematical model of groundwater flow

According to the generalized heterogeneous and anisotropic three-dimensional unsteady flow model, the following groundwater flow mathematical model is established [25]:

$$f\left(x\right)=\left\{\begin{array}{ll}\frac{\partial }{{\partial }_x}\left(K_x\frac{\partial H}{\partial x}\right)+\frac{\partial }{{\partial }_y}\left(K_y\frac{\partial H}{\partial y}\right)+\frac{\partial }{{\partial }_z}\left(K_z\frac{\partial H}{{\partial }_z}\right)+\epsilon =S_s\frac{\partial H}{\partial t}& x,y,z\in \Omega ,t\ge 0\\ K_x{\left(\frac{\partial H}{\partial x}\right)}^2+K_y{\left(\frac{\partial H}{\partial y}\right)}^2+K_z{\left(\frac{\partial H}{\partial z}\right)}^2-\left(K_z+p\right)+p=\mu \frac{\partial H}{\partial t}& x,y,z\in {\Gamma }_0,t\ge 0\\ H\left(x,y,z\right){\mid }_{t=0}=H_0& x,y,z\in \Omega ,t\ge 0\\ \begin{array}{ll}{K}_n\frac{\partial H}{\partial \overrightarrow{n}}{\mid }_{{\Gamma }_1}=q^{\prime }(x,y,z,t)& \end{array}& x,y,z\in {\Gamma }_0,t\ge 0\end{array}\right.$$

(15)

wherein:

• K_x, K_y, K_z—Permeability coefficient in x, y, z directions (m/d)
• H—Elevation of groundwater level (m);
• t—Time (d);
• ε—Source item (1/d);
• S_s—Unit water storage coefficient of the water-bearing layer below free water surface (1/m);
• p—Precipitation infiltration and evaporation intensity (m/d);
• μ—Specific yield of aquifer;
• $\overrightarrow{n}$—External normal direction vector;
• q′—Class II boundary water inflow or outflow per unit area and per unit time (m/d);
• H₀—t = 0 water level elevation (m);
• Ω—Scope of the simulator;
• Γ₀—The upper boundary of the seepage area, that is, the free surface of groundwater;
• Γ₁—Flow boundary of seepage area.

(5) Regional subdivision of numerical model of the groundwater system

On the basis of the hydrogeological conceptual model and groundwater system mathematical model established above, the established 3D groundwater flow numerical equation is solved by Feflow6.0 finite element software, and the research area is meshed with 3D triangular elements. The automatic encryption technology built into the software is used to automatically encrypt the places where the hydraulic gradient of the mining face development and deployment area changes greatly. The final model is divided into four layers and five slices. The plane is divided into 56,894 elements and 65,765 nodes. The corresponding space is a triangular body based on six nodes. One cell of the plane is about 0.0086 km². After the subdivision, the elevation of each layer of the model should be assigned, to establish the basic model framework, as shown in Figure 7.

(6) Assignment of hydrogeological parameters

For hydrogeological parameters, this study referred to the empirical values of previous studies [26,27], as well as the: hydrogeological conditions and the overall permeability parameters of the stratum in the Report on Classification of Mine Hydrogeological Types. Some of the permeability parameters were selected from the report, while others were from the empirical values. The specific parameters are shown in

Table 2. Stratigraphic hydrogeological parameters of the generalized model.

Rock Stratum Name	Permeability Coefficient (m/d)	Average Permeability Coefficient (Kx/y)	Average Permeability Coefficient (Kz)	Water Storage Coefficient Ss (1/m)	Specific Yield (μ)	Rainfall Infiltration Coefficient
1—water-bearing layer	0.0599–8.433	5.42375	0.542375	2.0 × 10−2	0.25	0.2
2—water-resisting layer	0.0083–0.21	0.0025	0.00025	1.2 × 10−3	0.125	/
3—Water-blocking layer	/	0.00067	0.000067	1.8 × 10−6	0.020	/

:

After coal seam mining, according to the research results of the space-time evolution model of equivalent permeability coefficient [4], the equivalent permeability coefficient of overlying strata driven by coal mining is a function related to time. By adopting the numerical treatment method of water-level geological parameters considering mining disturbance, the equivalent permeability coefficient described by the modified Knothe time function is introduced into the numerical calculation model. This results in the determination of the Figure 8.

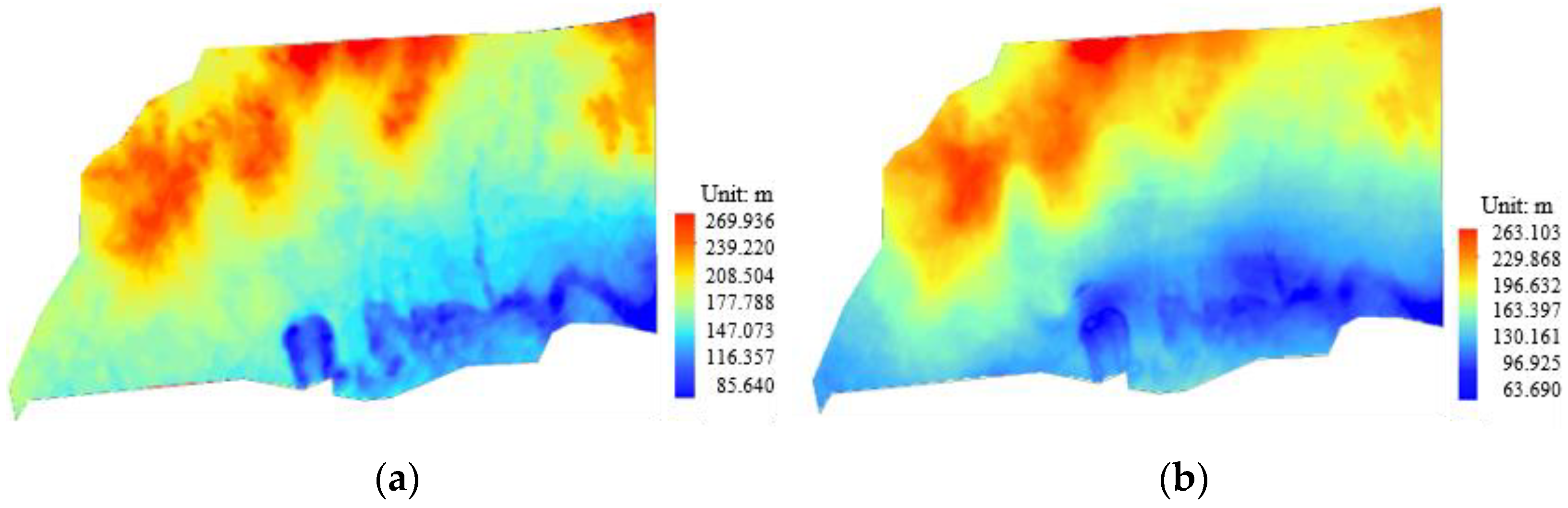
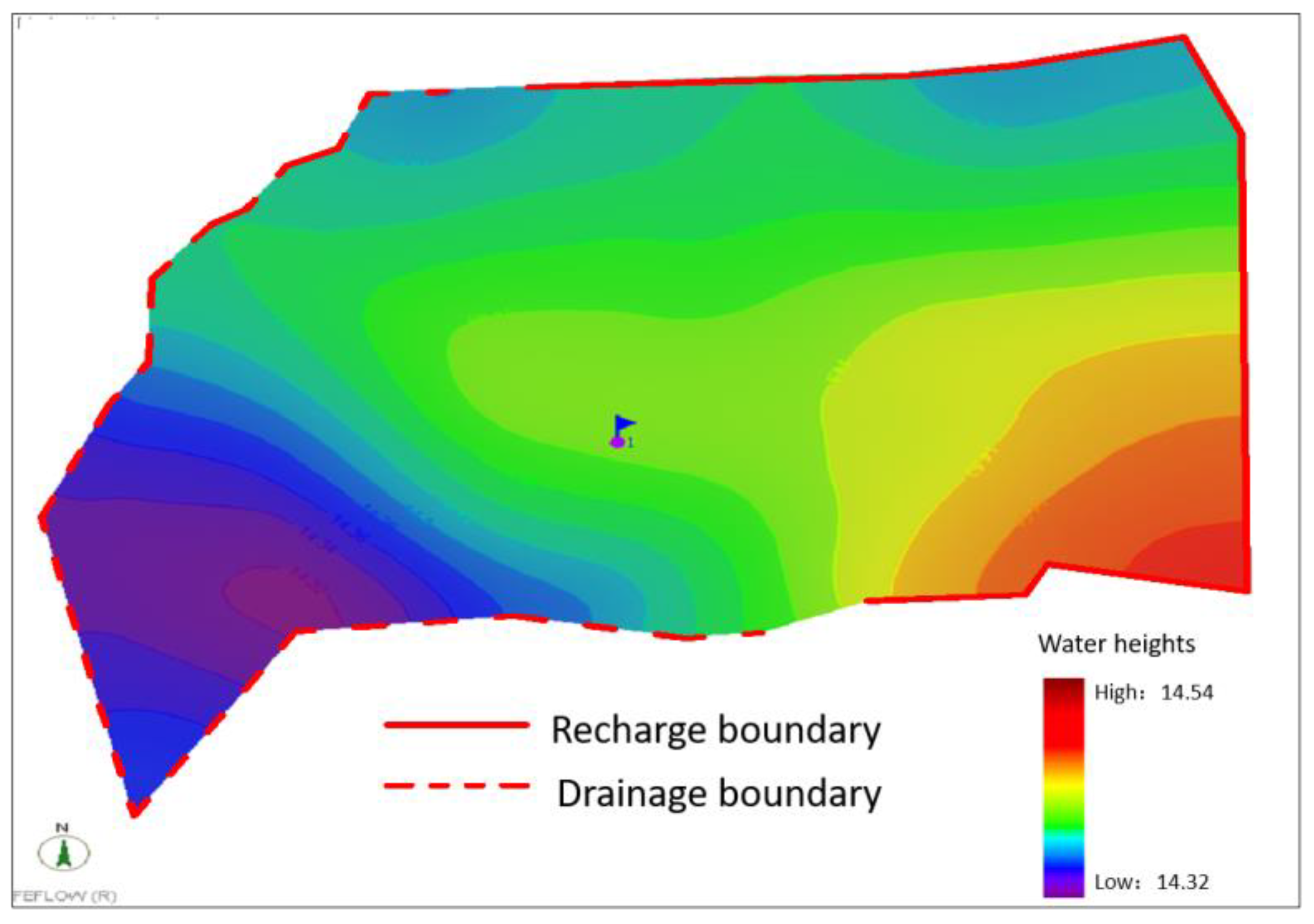
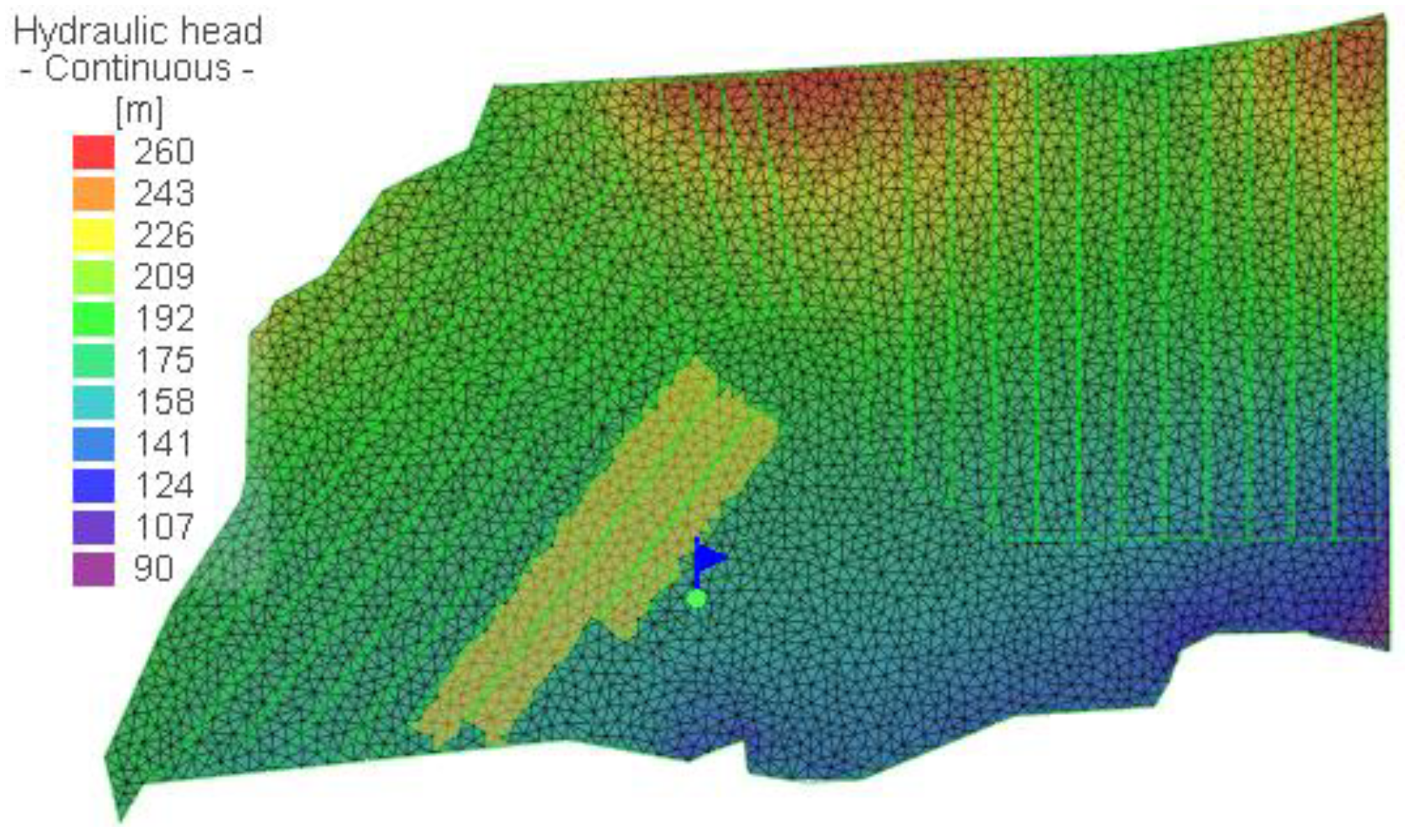
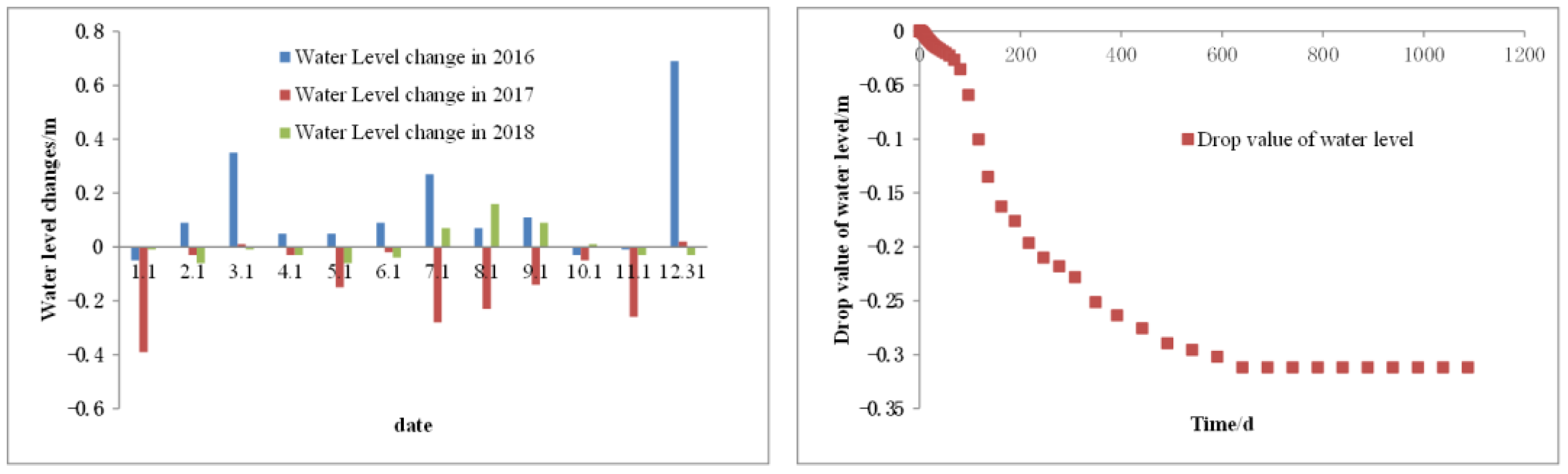
4.2. Verification of Quantitative Assessment Model of Shallow Water Disturbance

To verify the accuracy and reliability of hydrogeological parameters obtained after identification and fitting, the identified calculated flow field was taken as the initial flow field. As shown in Figure 9 and Figure 10, the first mining face in the Zhuan Longwan Coal Mine is 23103 working face, and then the next mining faces are 20102 and 23101. The groundwater monitoring data obtained from January 2016 to December 2018 were selected as the basis for the model test. During the mining period, the monitoring value of the Q1 water level fluctuated, with a maximum water level drop of 0.4 m. The numerical simulation process simulated mining in 23103 working face, mining in 20102 working face and mining in 23101 working face in turn. From the fitting of the groundwater flow field, it can be seen that the calculated value of the water level fits well with the observed value, and the flow direction of the groundwater flow field is roughly the same, which proves that the identified hydrogeological parameters are in line with the actual situation of this area.

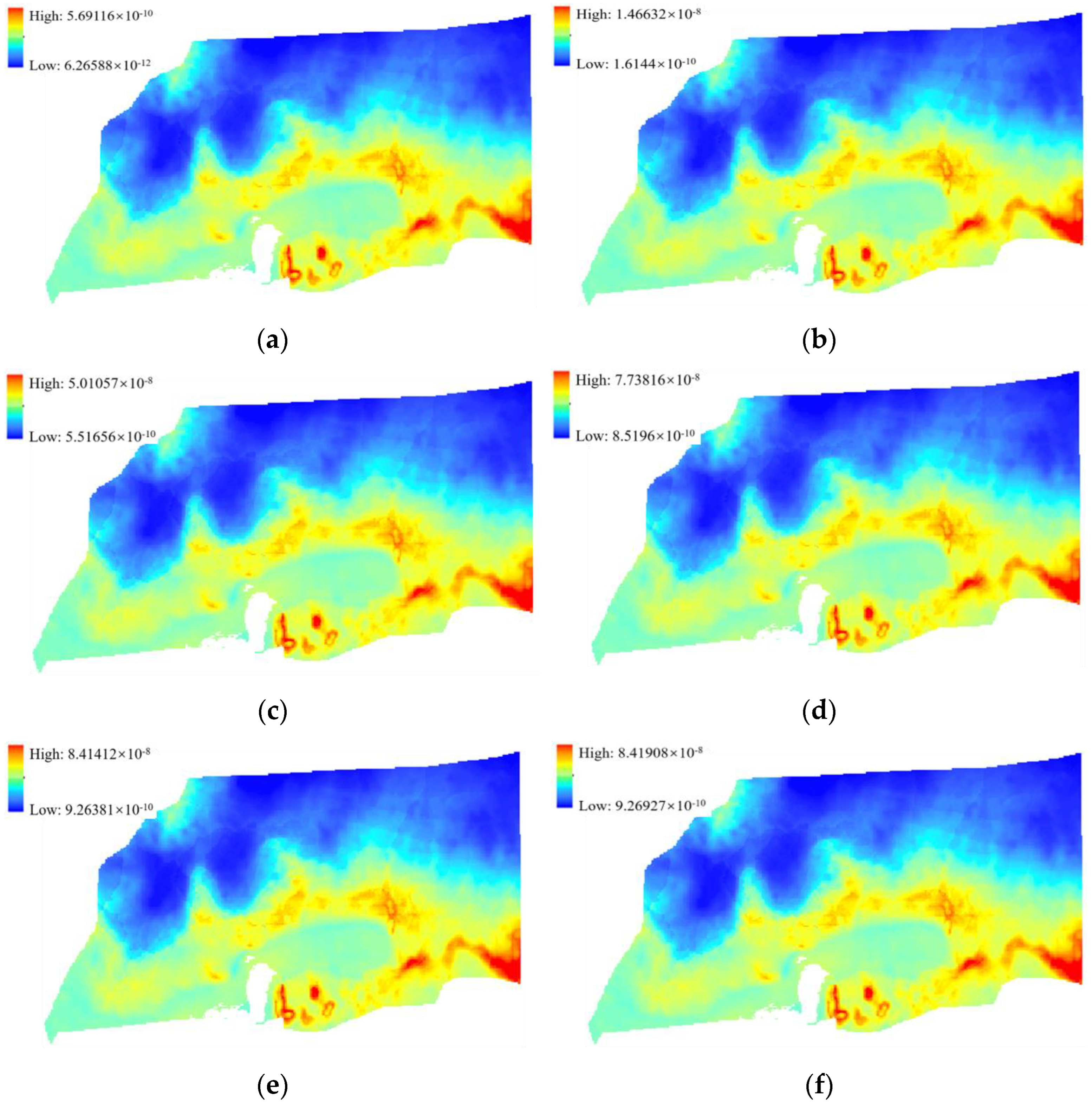
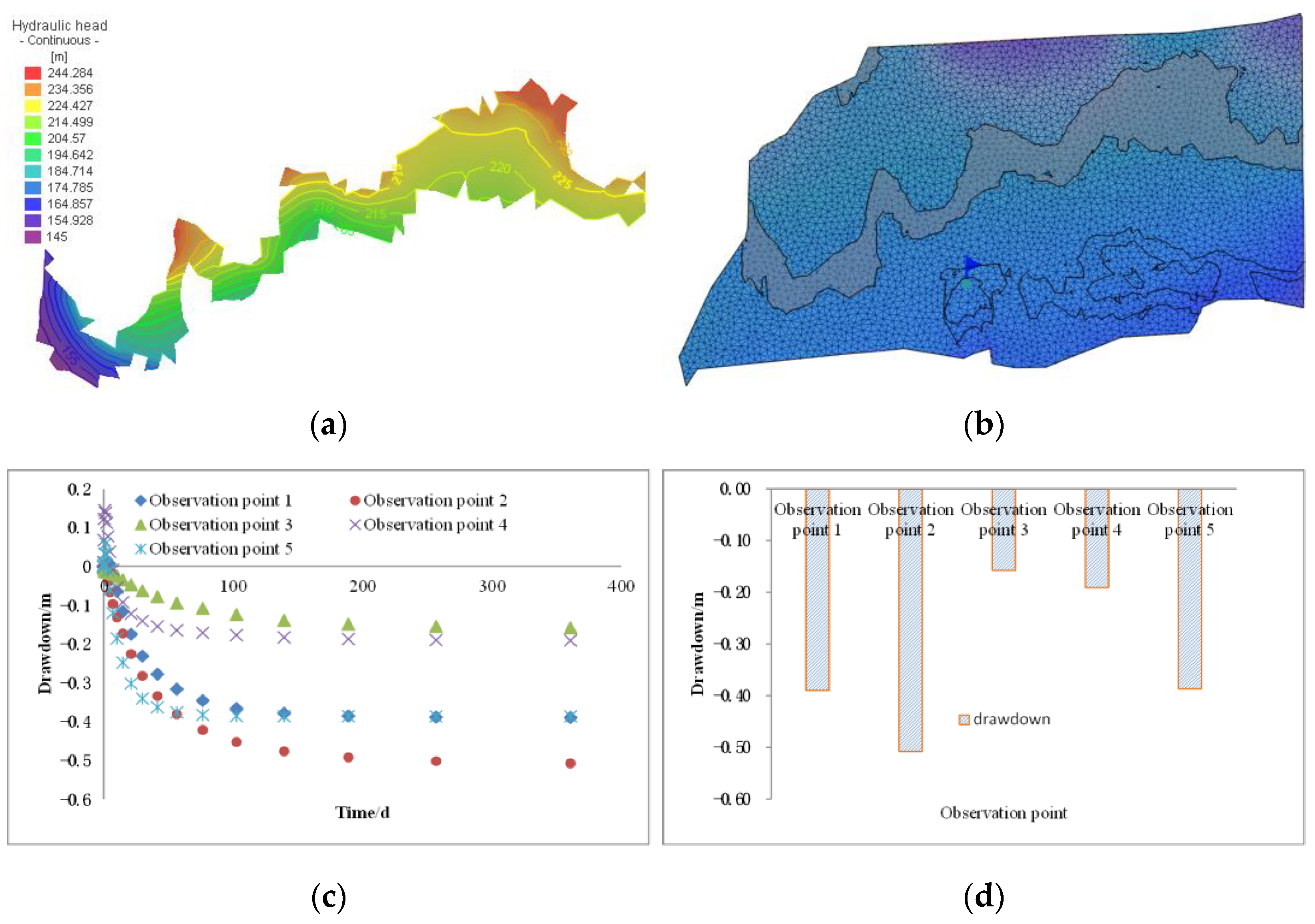
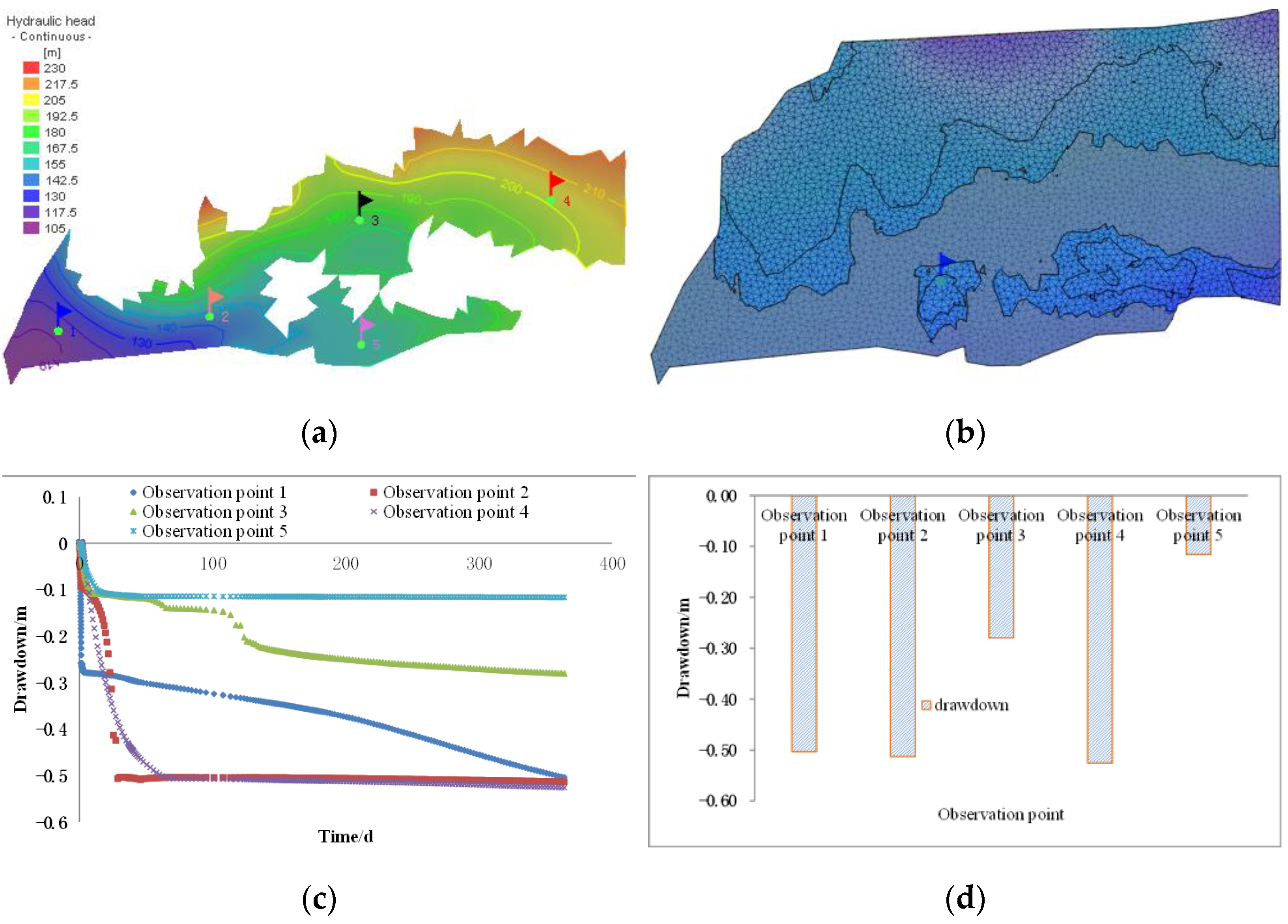
4.3. Evolution Law of Shallow Water in Multi-Working Face Mining Based on Catastrophe Theory Zoning

Combined with the risk zoning of catastrophe theory, this study focused on the characteristics of shallow water levels affected by mining in small-risk areas, light-risk areas and middle-risk areas. This study focused on the response characteristics of shallow water in three continuous mining faces in response areas. In order to reduce the influence of the boundary effect on numerical calculation results, 200 m coal pillars are left at each boundary. The width of the coal pillar is determined according to the horizontal influence radius of mining on shallow water. For example, the length of a working face is 250 m in the Zhuan Longwan Coal Mine and the width of the model corresponding to the three continuous working faces is 1150 m. The regional boundary was set to the fixed head boundary. Based on that, the redistribution characteristics of shallow water resources in three continuous mining faces were simulated.

The variation characteristics of shallow water level after continuous mining of three working faces in a small risk area were simulated. As shown in Figure 11, the head value at the middle of the upper boundary of the model is the largest, and the head value at the lower left boundary of the model is the smallest. With the mining, the head value of measuring points 1, 3, 4 and 5 gradually decreased. The head value of measuring point 2 decreased first, then the water level rose and then remained stable in the area. The water level drop of measuring point 1 is the largest, 0.210 m, followed by that of measuring point 3, 0.158 m. That of measuring point 4 is the smallest, 0.019 m.

The variation characteristics of shallow water level after continuous mining of three working faces in light-risk areas were simulated. As shown in Figure 12, the head value at the upper right boundary of the model is the largest, and the head value at the lower left boundary of the model is the smallest. With the mining, the head value of measuring points 1, 2, 3, 4 and 5 had a small increase at first, and then the water level gradually decreased. After 100 days of mining, the head value remained stable in the area. The water level drop at measuring point 2 is the largest, 0.508. It is followed by those at measuring points 1 and 5, which are 0.390 and 0.386 m, respectively. The water level drop measuring point 3 is the smallest, 0.158 m.

The variation characteristics of shallow water level after continuous mining of three working faces in the middle-risk area were simulated. As shown in Figure 13, the head value at the upper right boundary of the model is the largest, and the head value at the lower left boundary of the model is the smallest. With the mining, the head values at measuring points 2, 4 and 5 first decreased sharply and the head value was stable after mining for about 50 days. With the mining, the head values at measuring points 1 and 3 first dropped sharply. After that, the water level dropped slowly. The largest water level drop of 0.525 m is at measuring point 4, followed by the water level drops of 0.503 m and 0.513 m at measuring points 1 and 2. The smallest water level drop of 0.116 m is at measuring point 5.

The above simulation results show that mining is the most severe in the middle-risk area, followed by the light-risk area, and the small-risk area is the least disturbed. With the decrease in mining height, the influence range and degree of shallow water in the study area gradually decrease.

5. Discussion

Under the disturbance of multi-face mining, the shallow water system often changes from one stable state to another stable state in the form of a catastrophe. Based on this, this paper comprehensively evaluated the instability risk of the groundwater system under mining disturbance by catastrophe model and classified the zones. On the basis of zoning, the evolution law of shallow water under multi-face mining in different areas was studied.

The research shows that the reasonable planning before mining can effectively protect water resources and improve the utilization rate of water resources [4,9,28]. There are 2, 3 and 4 control variables in Cusp catastrophe, Swallowtail catastrophe and Butterfly catastrophe respectively [29]. According to the main control factors of instability risk assessment of groundwater system, the Cusp catastrophe and Butterfly catastrophe were used to classify the instability risk level of the mine water system to find the relative short board in the mine.

The Cannikin Law is also known as the buckets effect [30], as shown in Figure 14, and mining area planning also faces such problems. Under the influence of mining disturbance, the water level drop in the weakest part of hydrogeology is the largest, and the water level drop in the strongest part of hydrogeology is the smallest. Therefore, the upper limit of mining in the study area based on the stability constraint of shallow water systems depends on the weakest part of hydrogeology. Once the shortboard (the first type of water-retaining coal mining area) is mined in the mining area, the shallow water stability will be broken, and the unpredictable negative impact on the ecosystem in the mining area will be caused, which will seriously restrict the economic and social development in the region [31,32]. However, the zoning method of catastrophe theory is also a semi-qualitative and semi-quantitative analysis method, which cannot realize the quantitative analysis of shallow water in each zone.

Focusing on the theme of “water-preserved mining”, experts and scholars have conducted research on the theory and technology of water-preserved mining from various perspectives. However, previous studies have primarily focused on the single-working face-mining process. In this thesis, we address this limitation by combining mutation theory and the FEFLOW numerical simulation method to develop a quantitative evaluation model for shallow water in multi-working face mining across different zones. We then reveal the evolution pattern of shallow water in these mining scenarios. For the constructed hydrogeological calculation model, the accuracy of hydrogeological parameters will directly affect whether the established hydrogeological model can accurately depict the actual hydrogeological conditions in the study area, determine the accuracy of numerical calculation of the model [33], affect the effect of model identification and fitting and ultimately affect whether the whole model can objectively reflect the actual situation and play a practical guiding role [14]. Due to the inhomogeneity of formation media, the actual hydrogeological parameters of water-bearing layers are also different in space, but it is impossible and unrealistic to completely measure the hydrogeological parameters of water-bearing layers [34]. Therefore, it is necessary to generalize the hydrogeological parameters of the water-bearing layer in the study area and generalize the water-bearing layer in a certain range into a homogeneous water-bearing layer, that is, assigning the same hydrogeological parameters. Theoretically, the smaller the zone is, the more accurate it is [35,36]. However, if a zone is too small, it will bring a heavy workload to the identification and adjustment of the model. According to the actual work requirements, proper zoning is carried out, but artificial zoning is subjective and blind to a certain extent.

Based on the above limitations of catastrophe theory model zoning and numerical model calculation, this paper combined the two methods and took the zoning results obtained by catastrophe theory as the basis of numerical model zoning simulation. That is, based on the risk zoning combined with catastrophe theory, it studied the characteristics of the influence of continuous mining on the shallow water level of three working mining faces in different areas, and then revealed the evolution law of shallow water under multi-surface disturbance in different zones. This reduces the difficulty of parameter fitting of numerical models to some extent, avoids the subjectivity and blindness of zoning simulation to a point, and provides a new idea for numerical simulation of shallow water evolution law in large-scale multi-face mining.

6. Conclusions

1.

Based on the connotation of water-retaining mining and the analysis of influencing factors of the water system, this paper determined the main influencing factors of shallow water in the Zhuan Longwan Coal Mine. They are the buried depth of the coal seam, the space distance between coal and water, the water abundance of the water-bearing medium, the permeability coefficient of the water-bearing medium, the thickness of the effective water-resisting layer, and the exploitation quantity. According to the characteristics of the research object, the large and small functions with semi-trapezoidal distribution were selected to normalize them.

2.

According to the butterfly catastrophe model and cusp catastrophe model in catastrophe theory, the risk analysis of the Zhuan Longwan Coal Mine was carried out. The risk level of groundwater development was divided into five categories: small risk, light risk, middle risk, heavy risk and special risk.

3.

According to the research results of the space-time evolution model of equivalent permeability coefficient, the quantitative assessment model of shallow water in the Zhuan longwan Coal Mine was established by adopting the numerical treatment method of water level geological parameters considering mining disturbance. Then, the redistribution characteristics of shallow water resources exploited in three consecutive working faces were simulated.

4.

Under the condition of continuous mining of three working faces, mining had the most intense influence on the middle-risk area, followed by the light-risk area. The small risk area was the least disturbed. With the decrease in mining height, the influence range and degree of the shallow water in the study area gradually decreased. In the middle-risk area, the water level drop at measuring point 4 is the largest, 0.525 m, and that at measuring point 5 is the smallest, 0.116 m.