A Spectral Collocation Method for Solving the Non-Linear Distributed-Order Fractional Bagley–Torvik Differential Equation
Abstract
:1. Introduction
2. Mathematical Preliminaries
3. Spectral Collocation Approach to Solve the Non-Linear DO-FBTEs
3.1. The Initial-Value Problem
3.2. The Boundary-Value Problem
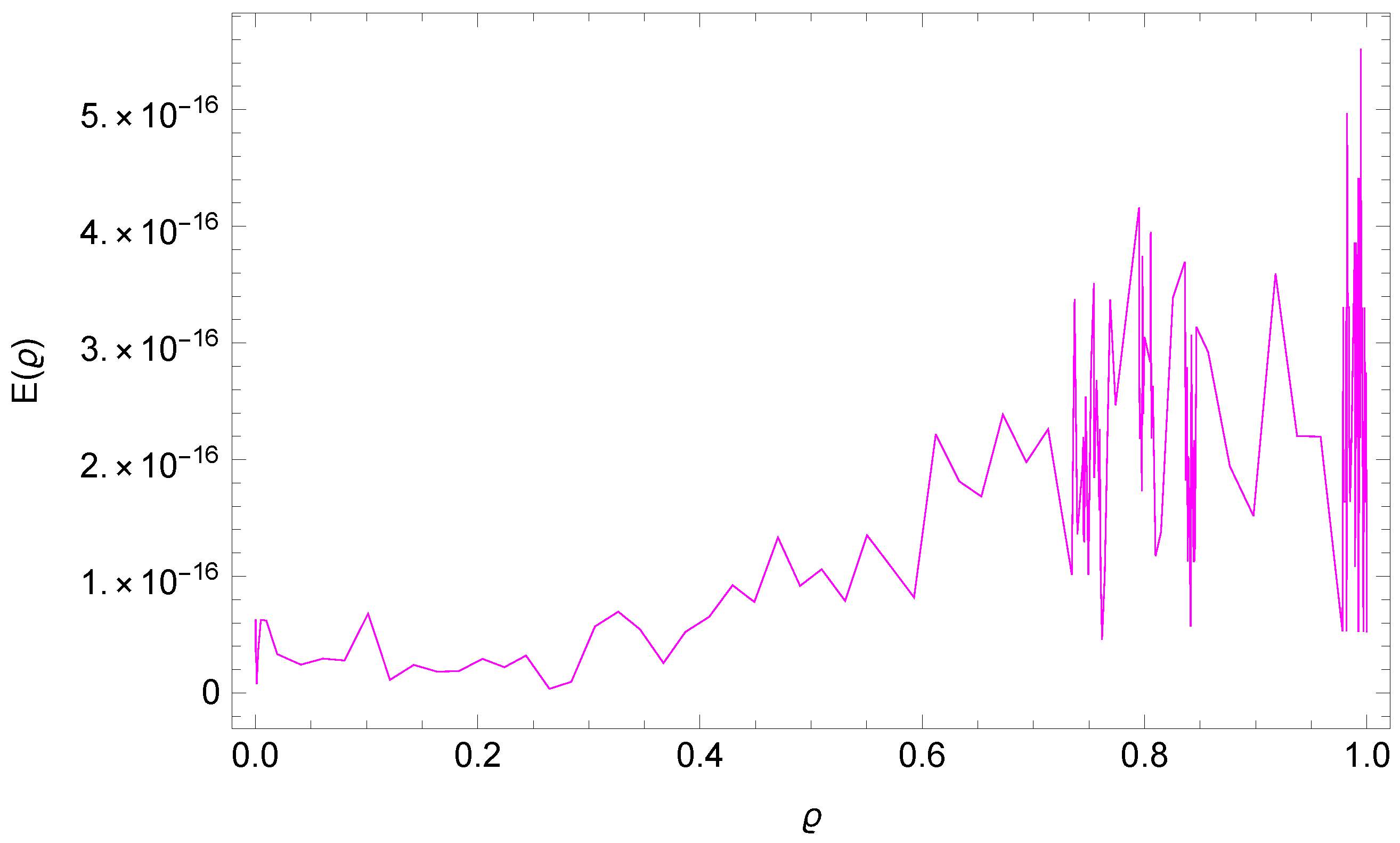
4. Error Analysis
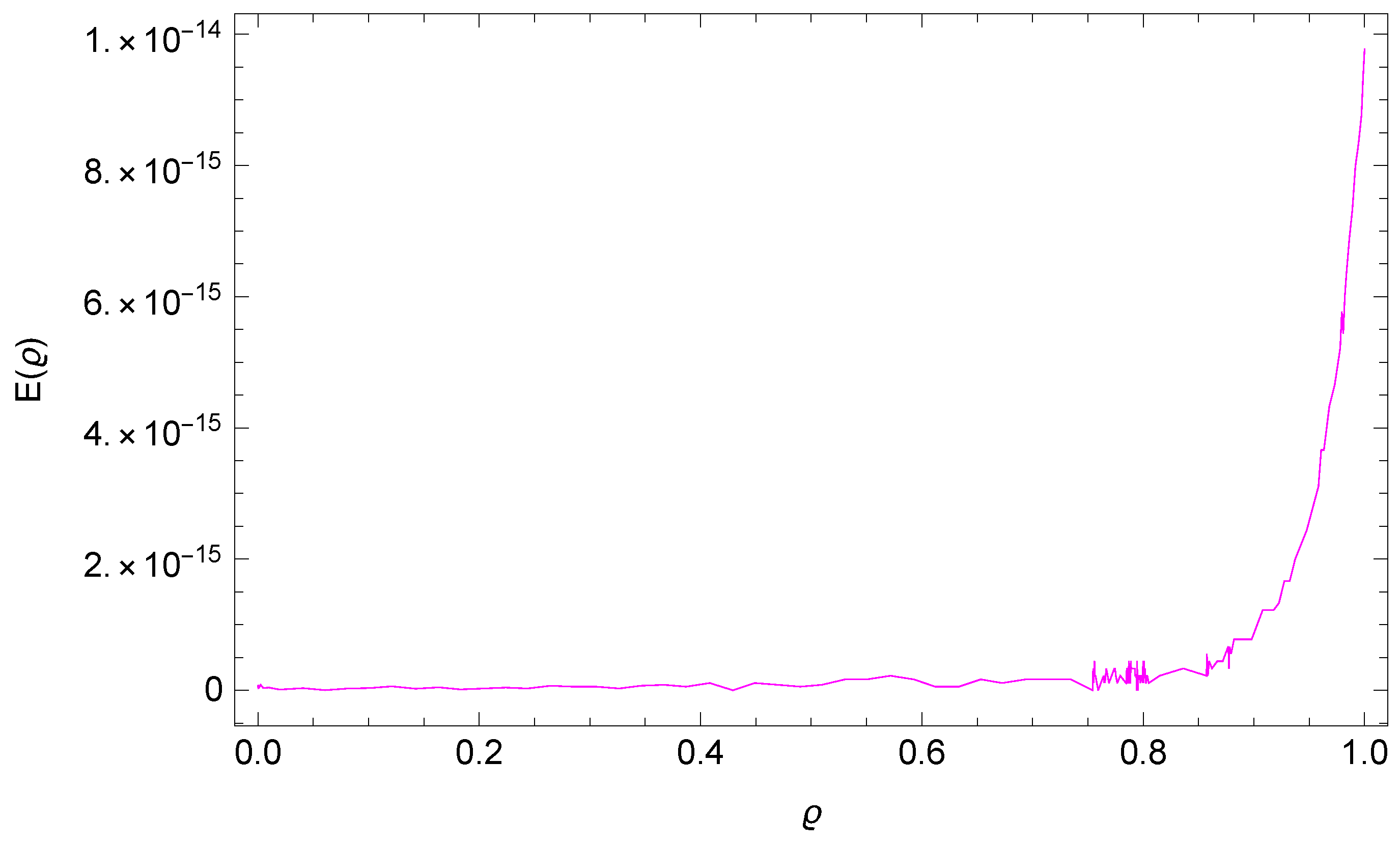
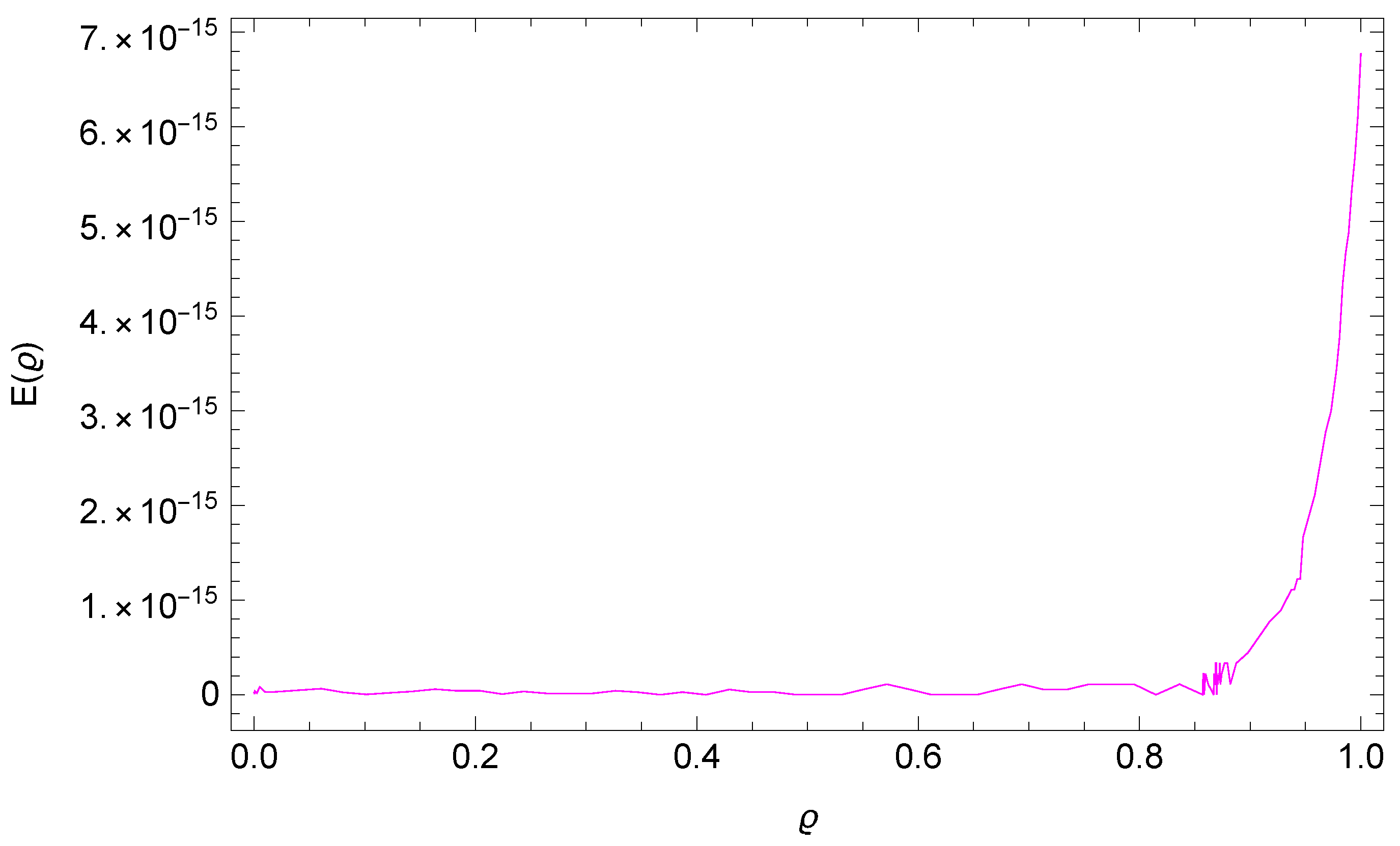
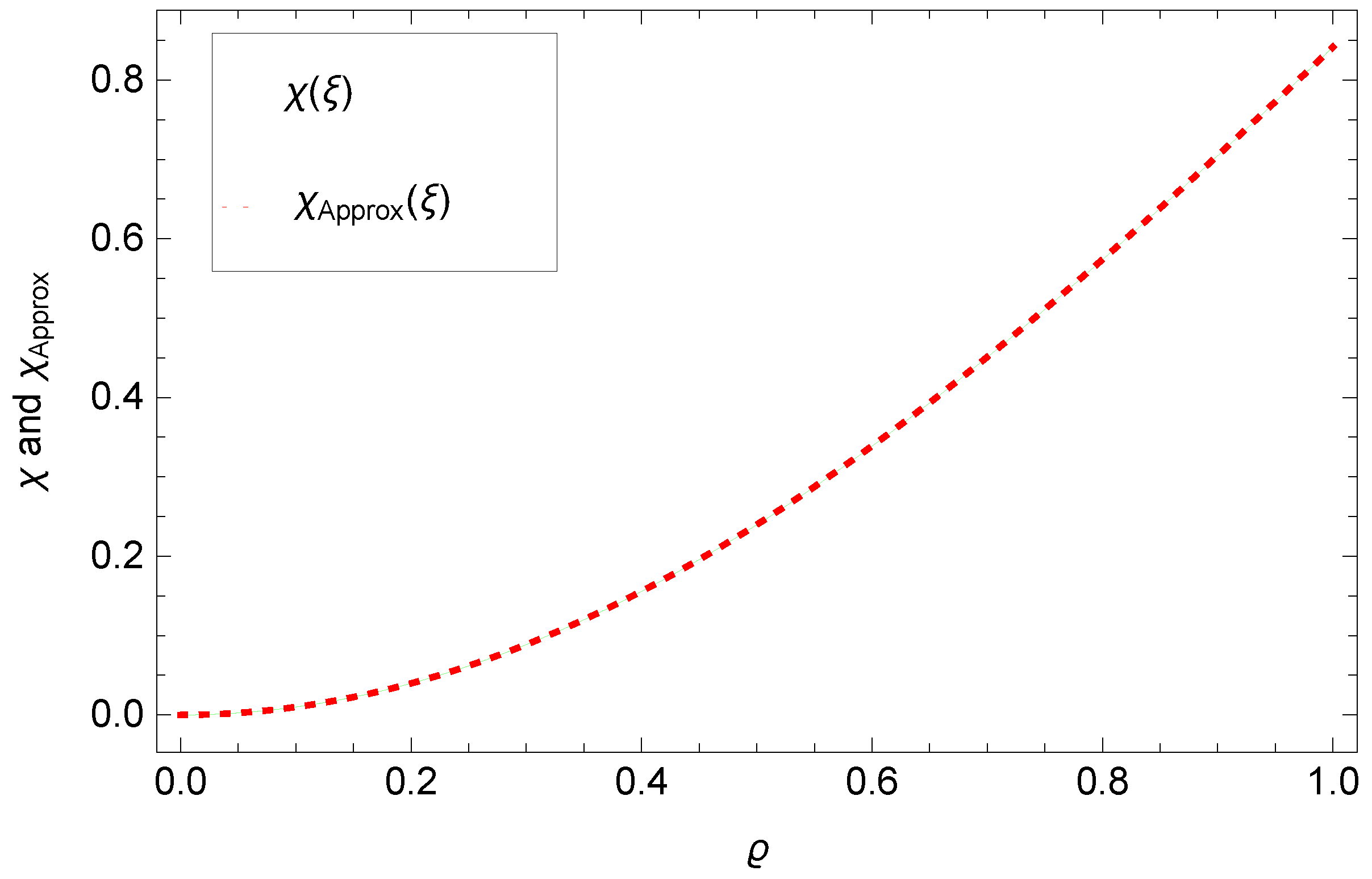
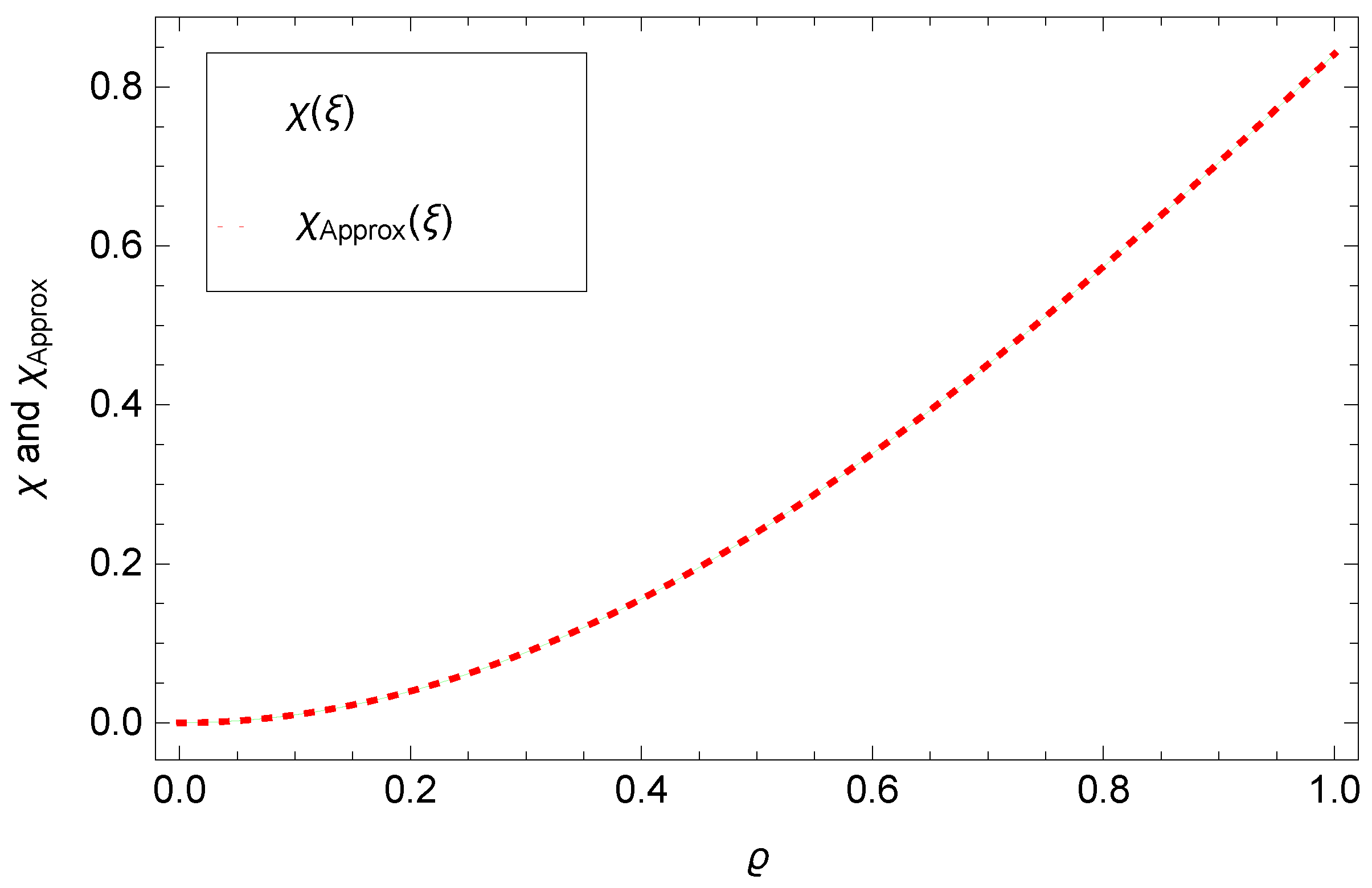
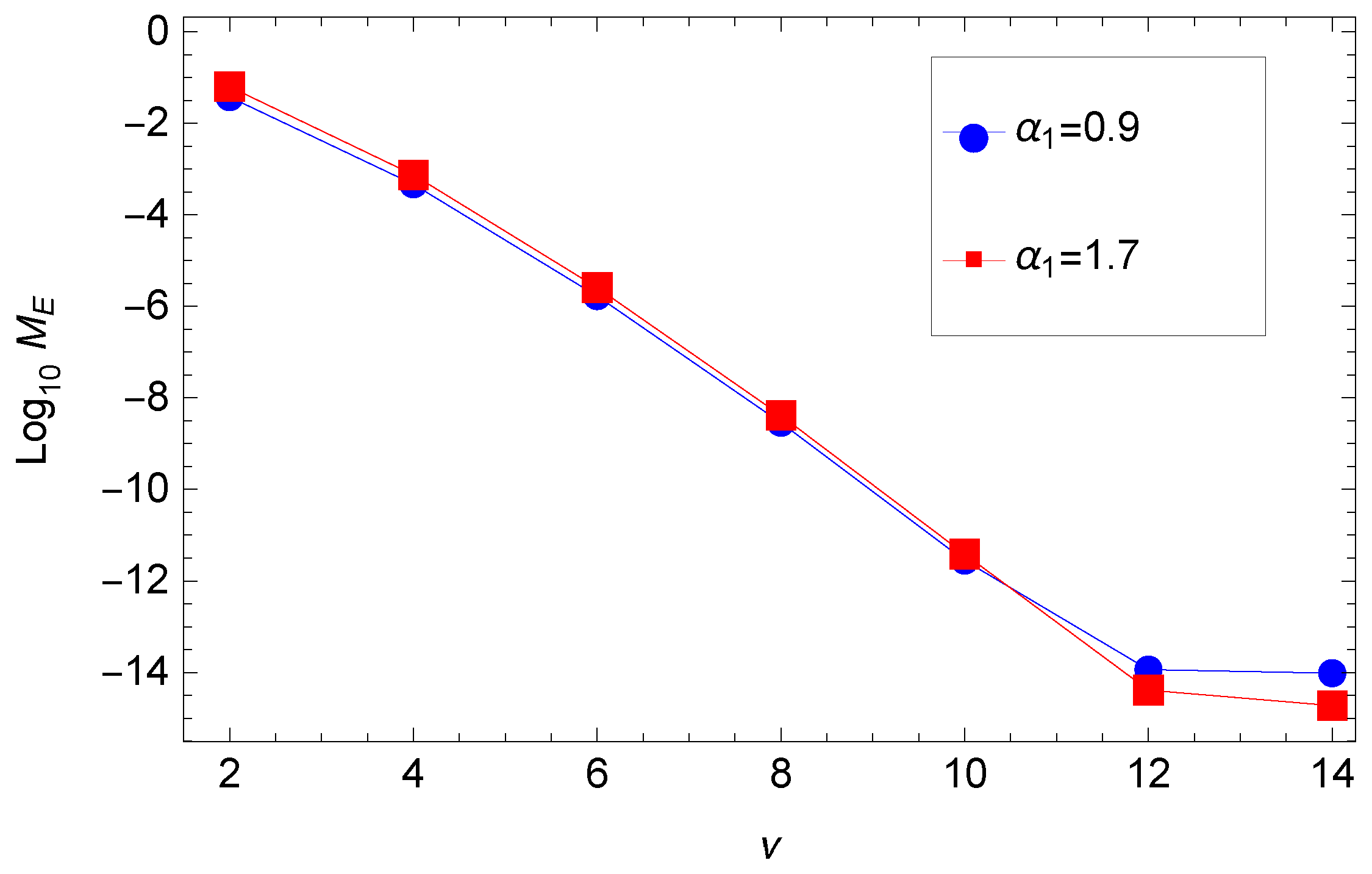
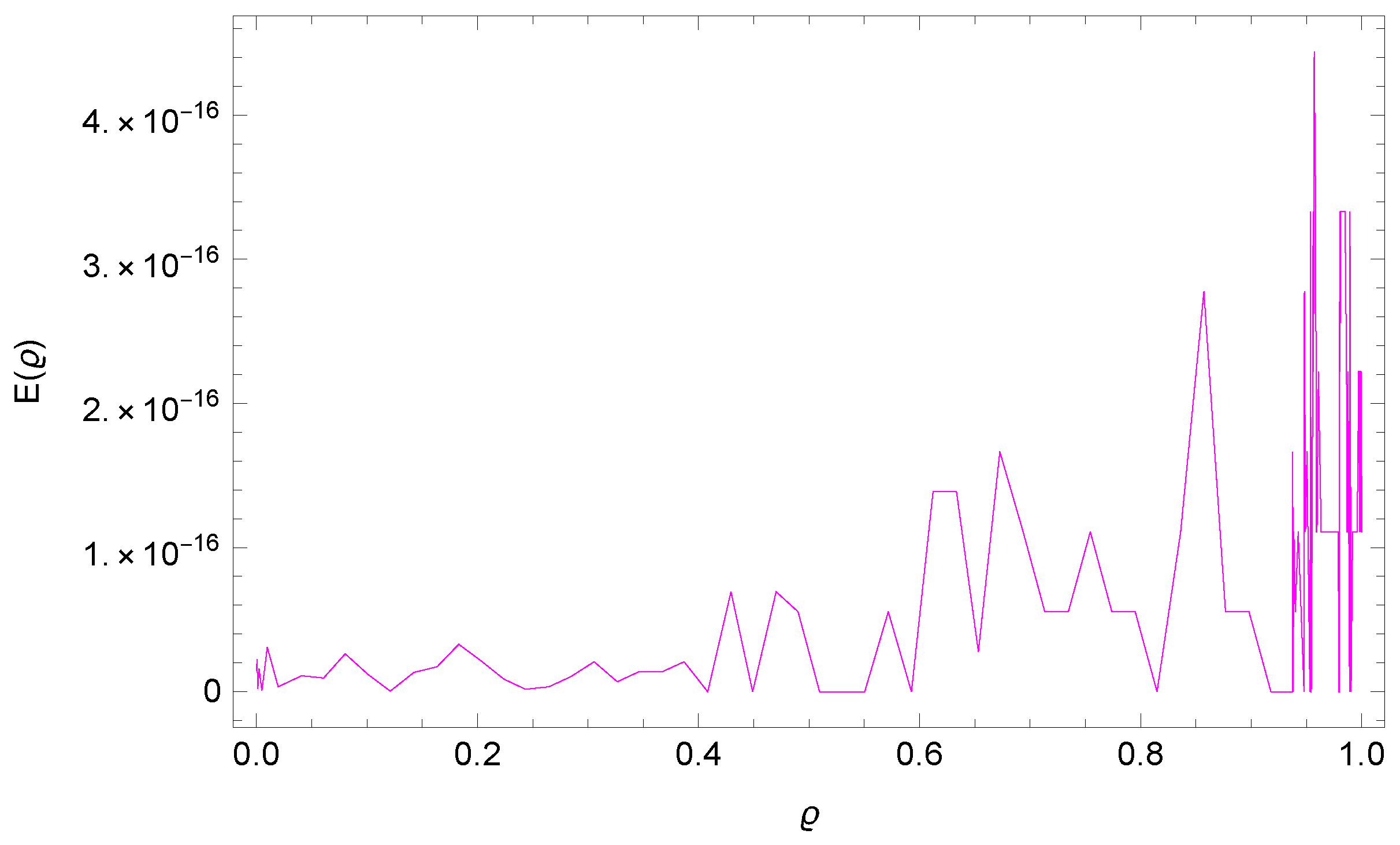
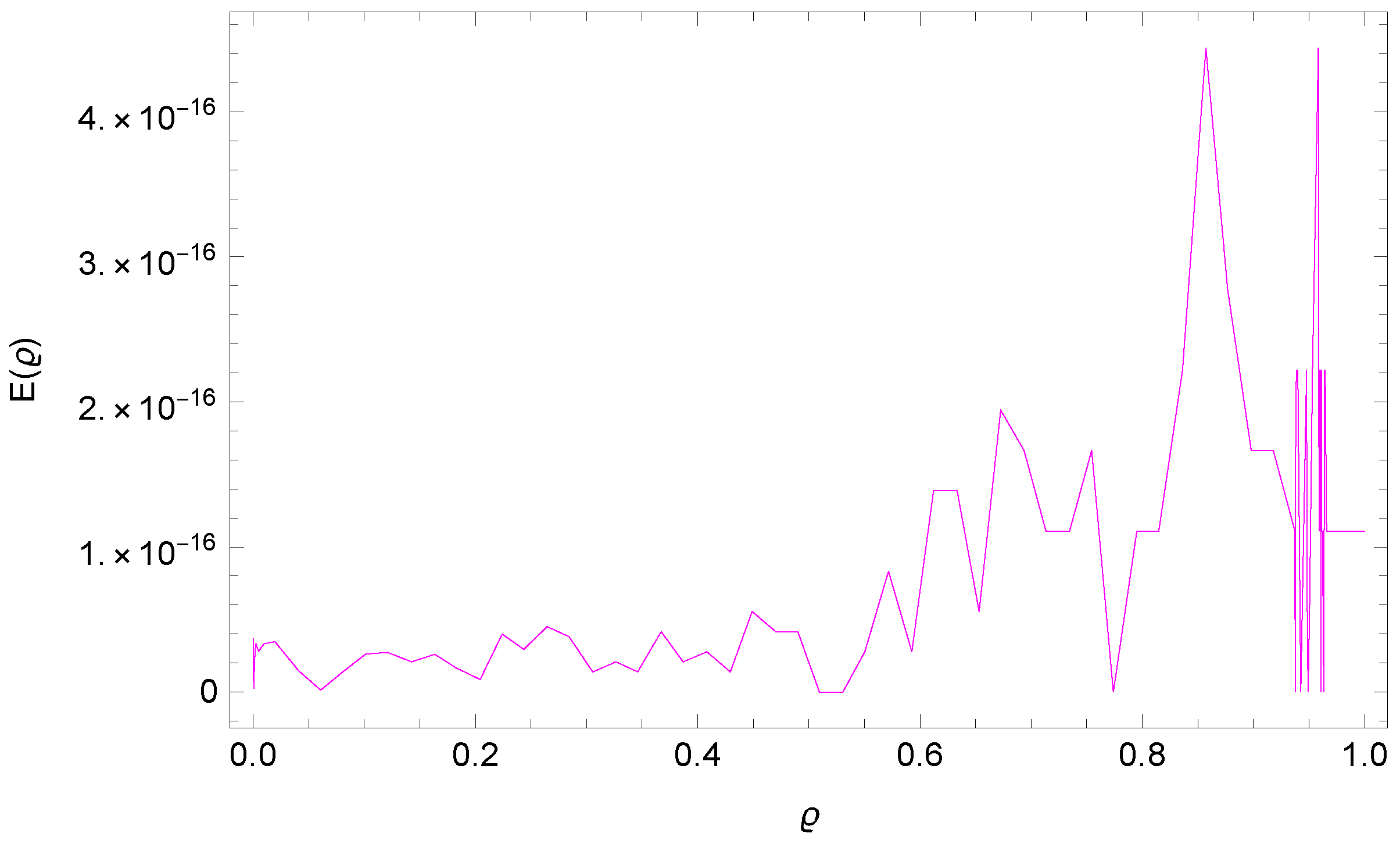
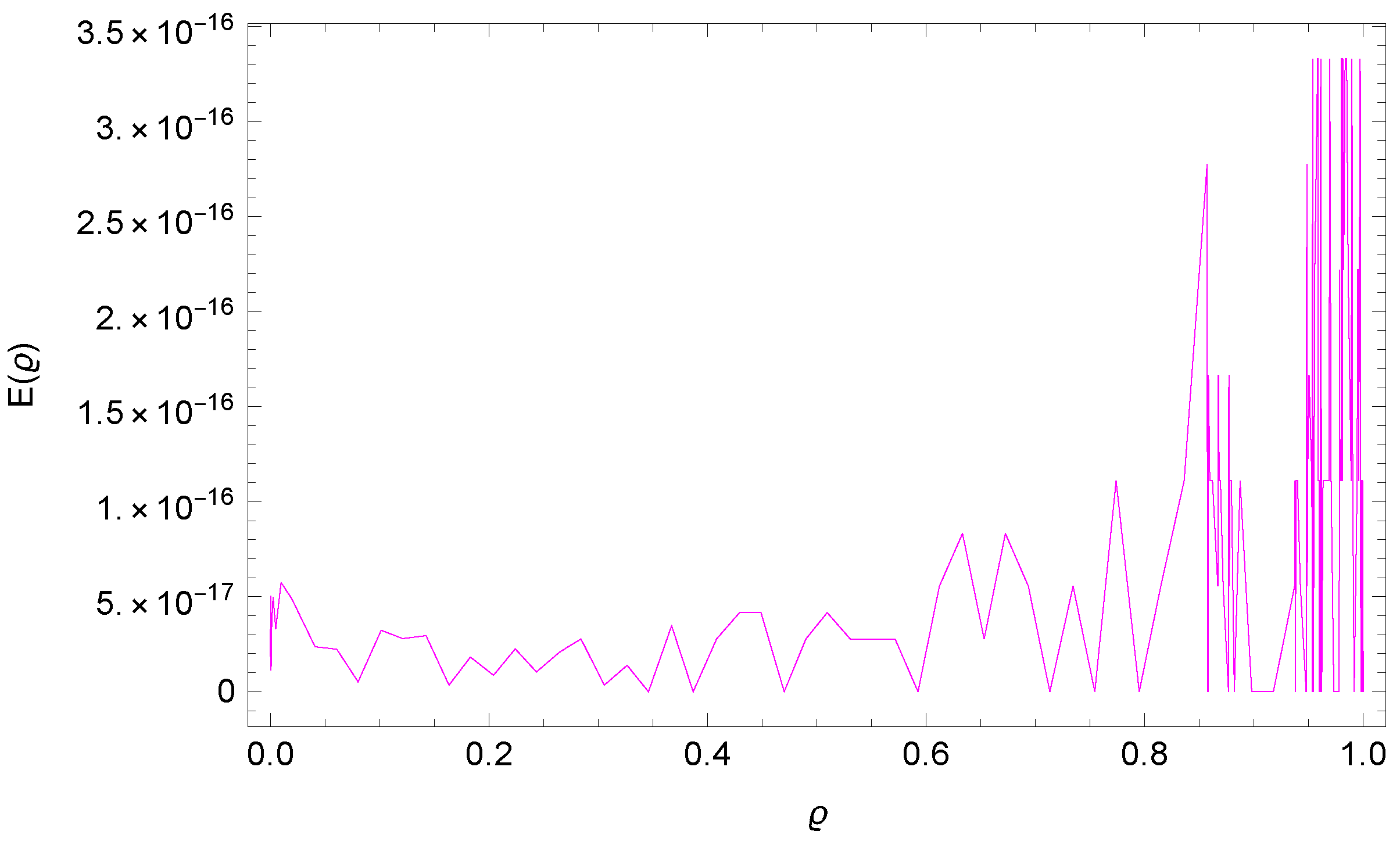
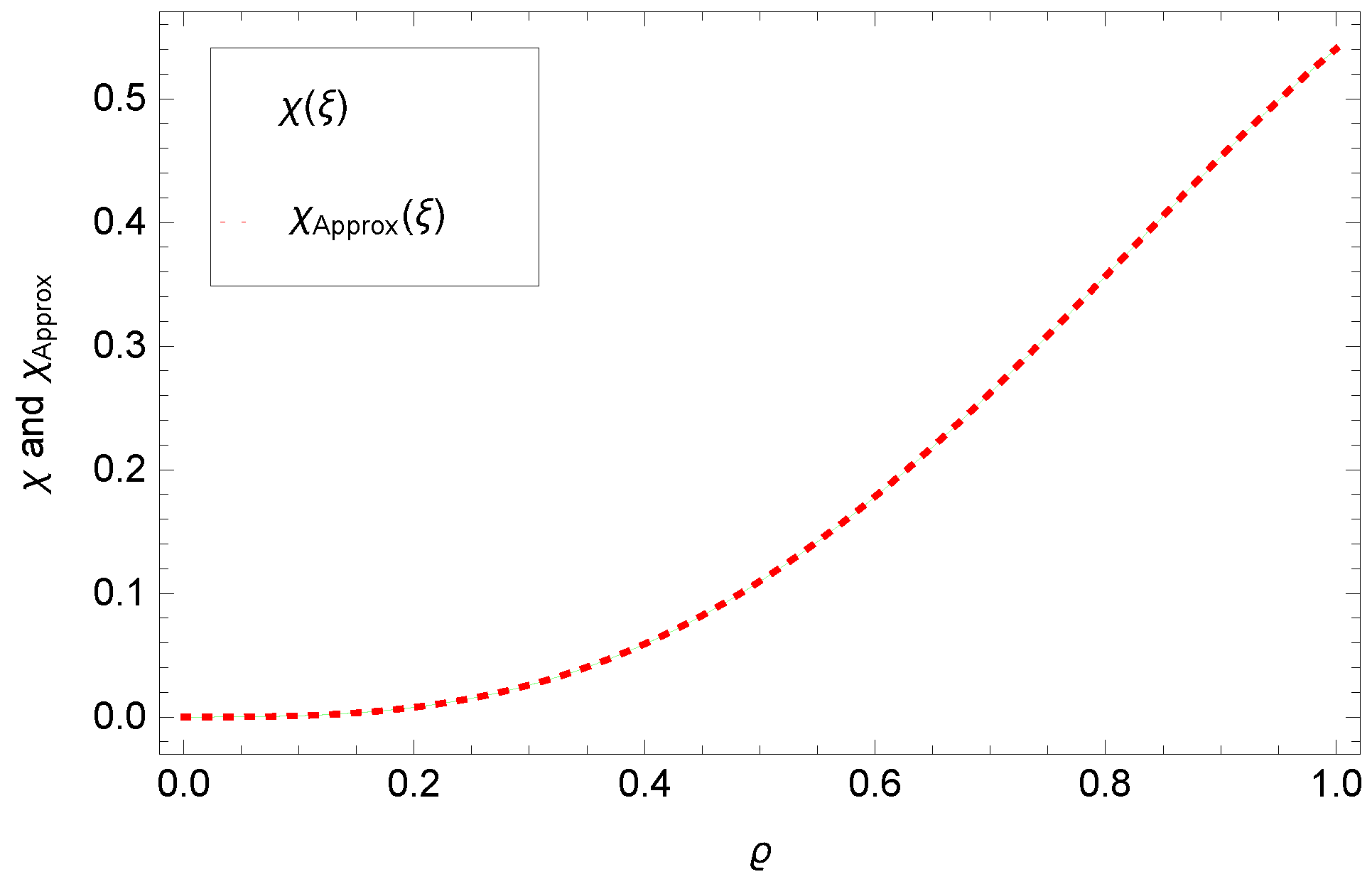
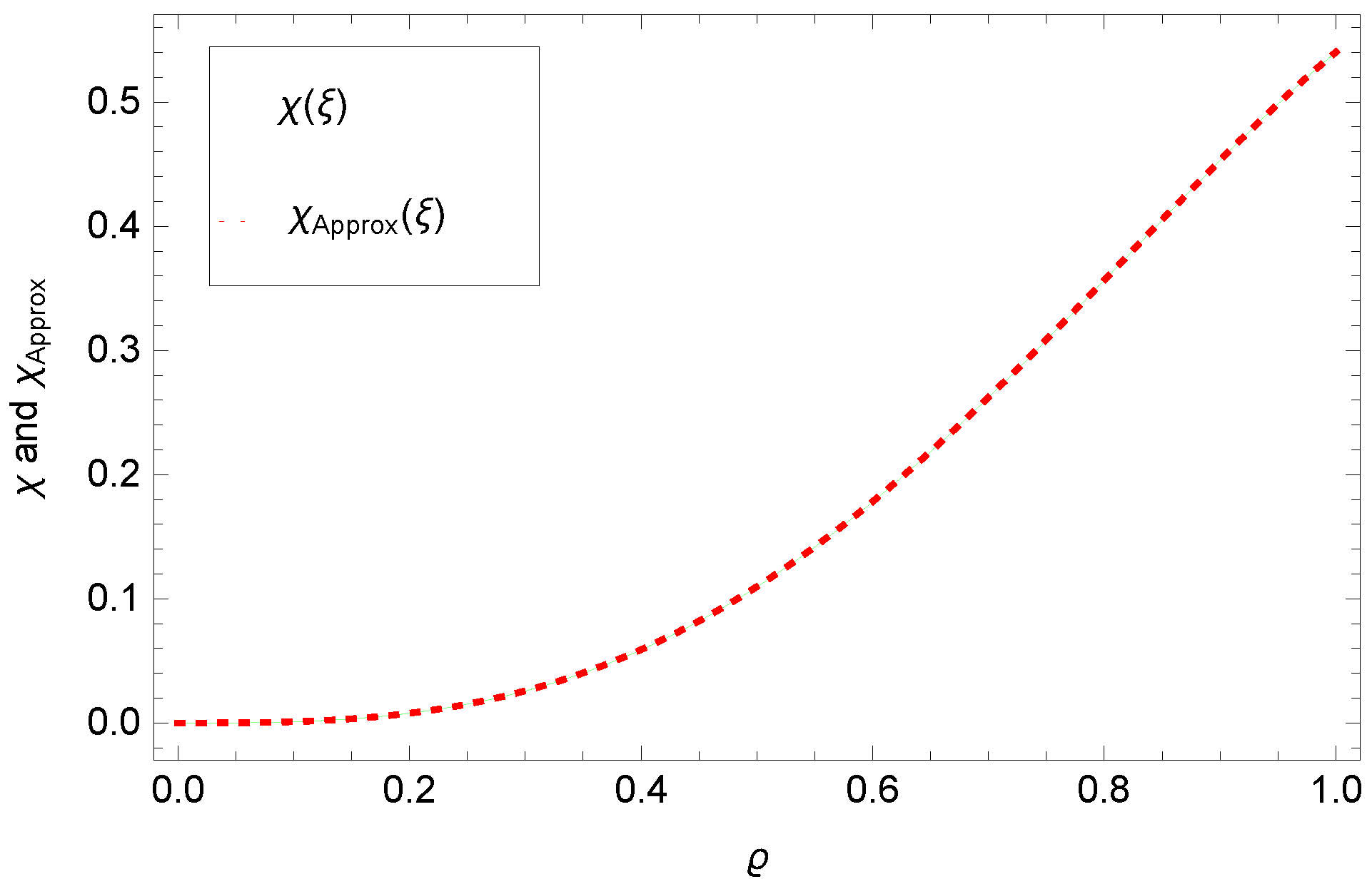
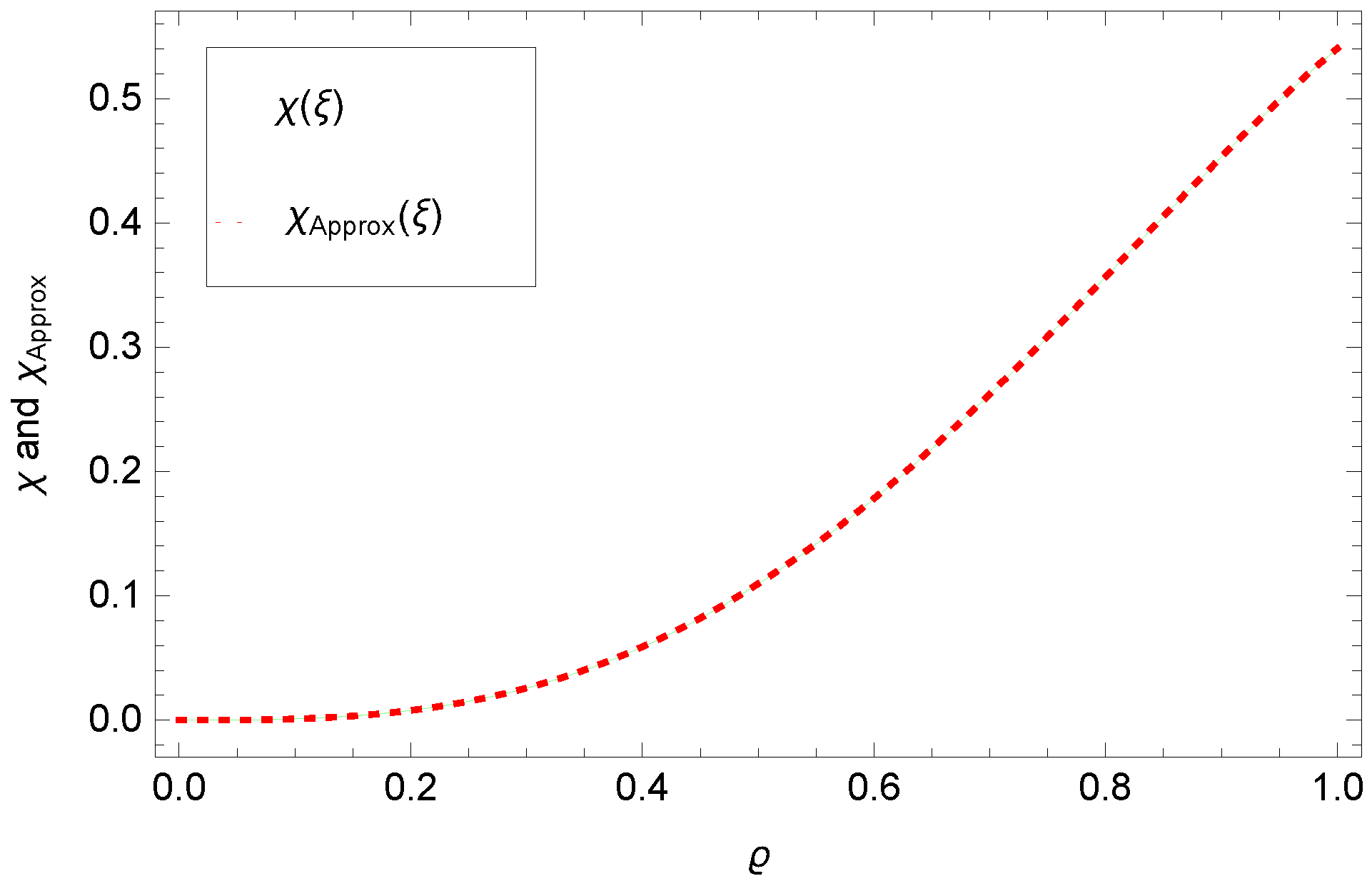
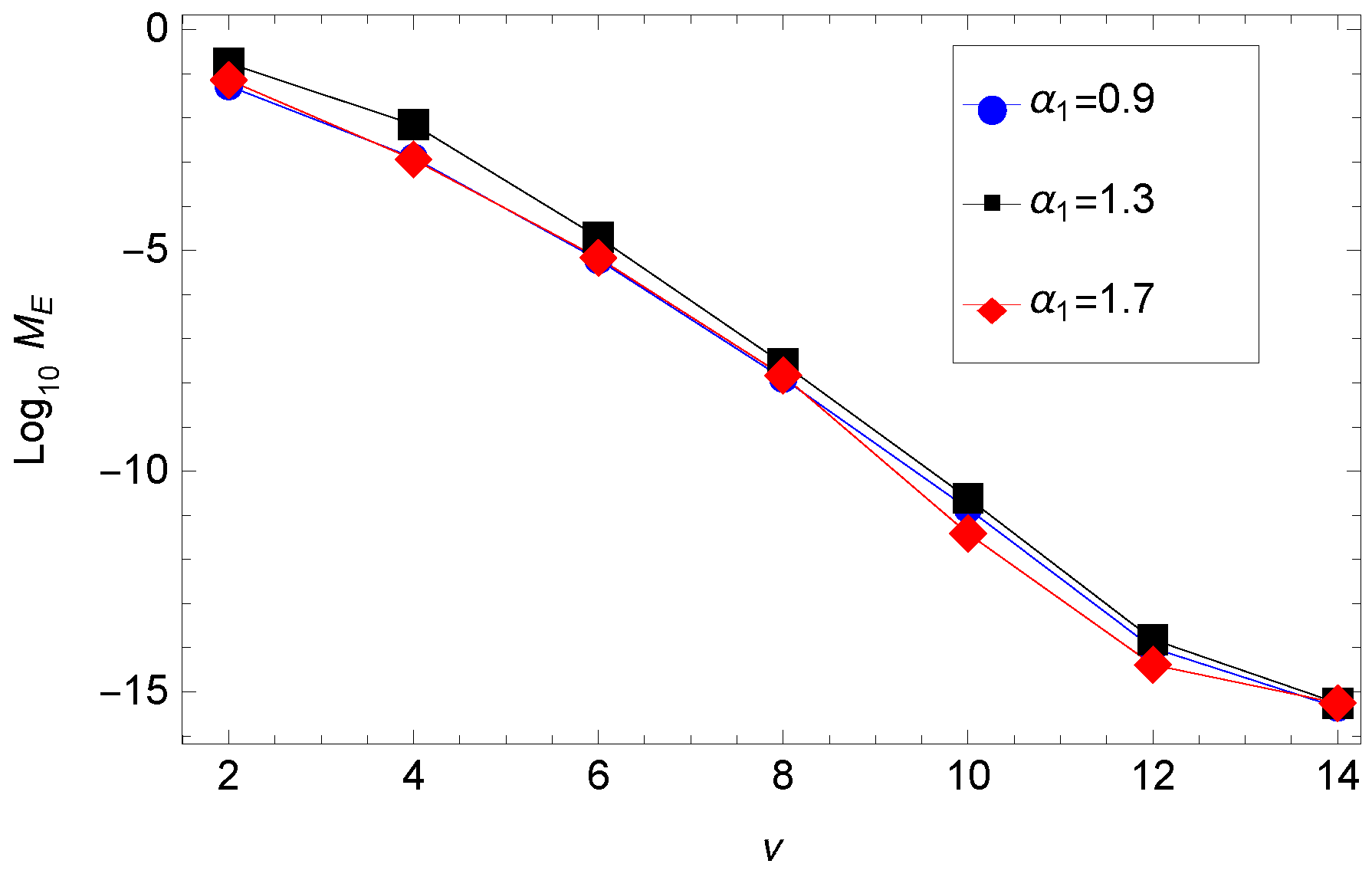
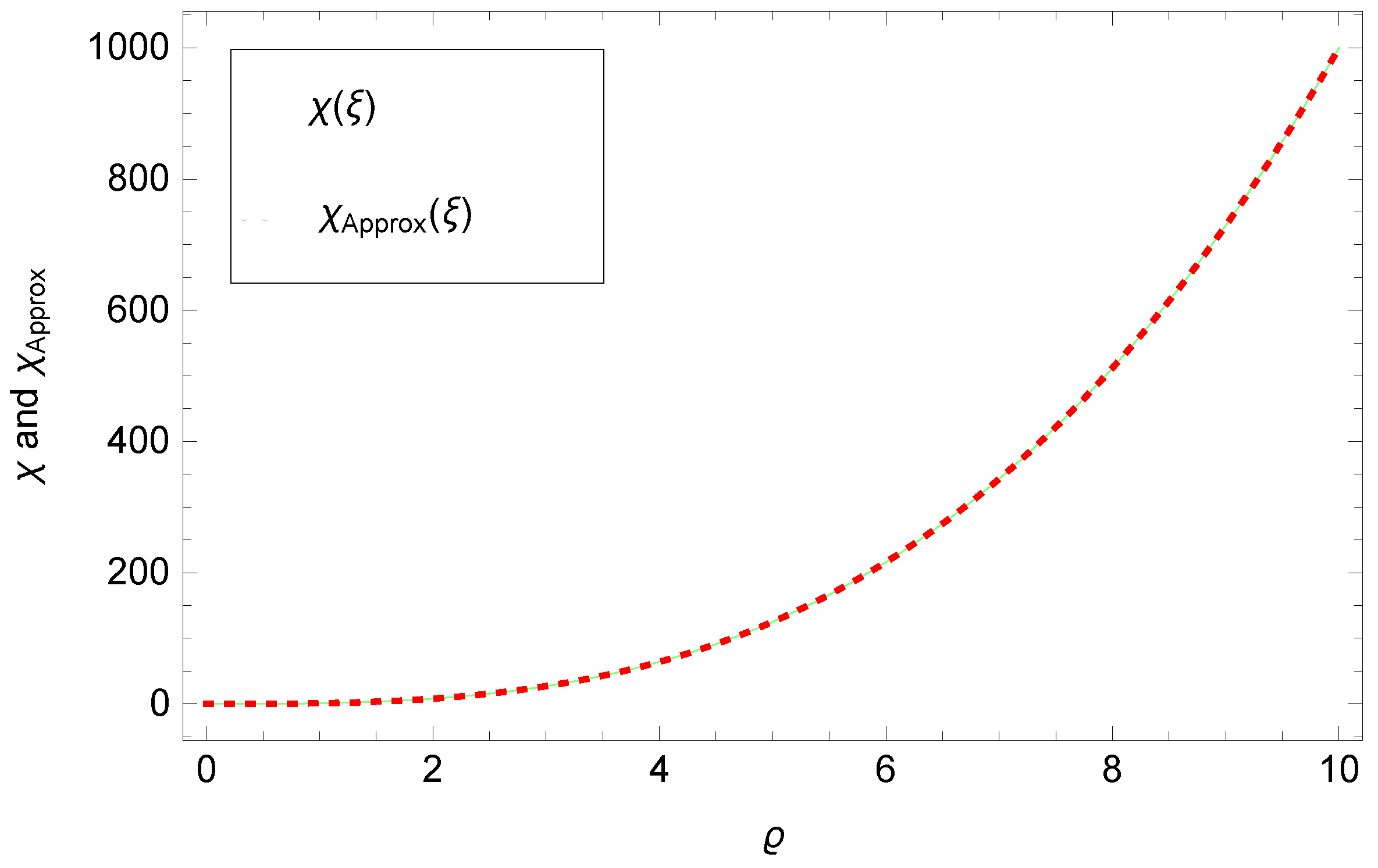
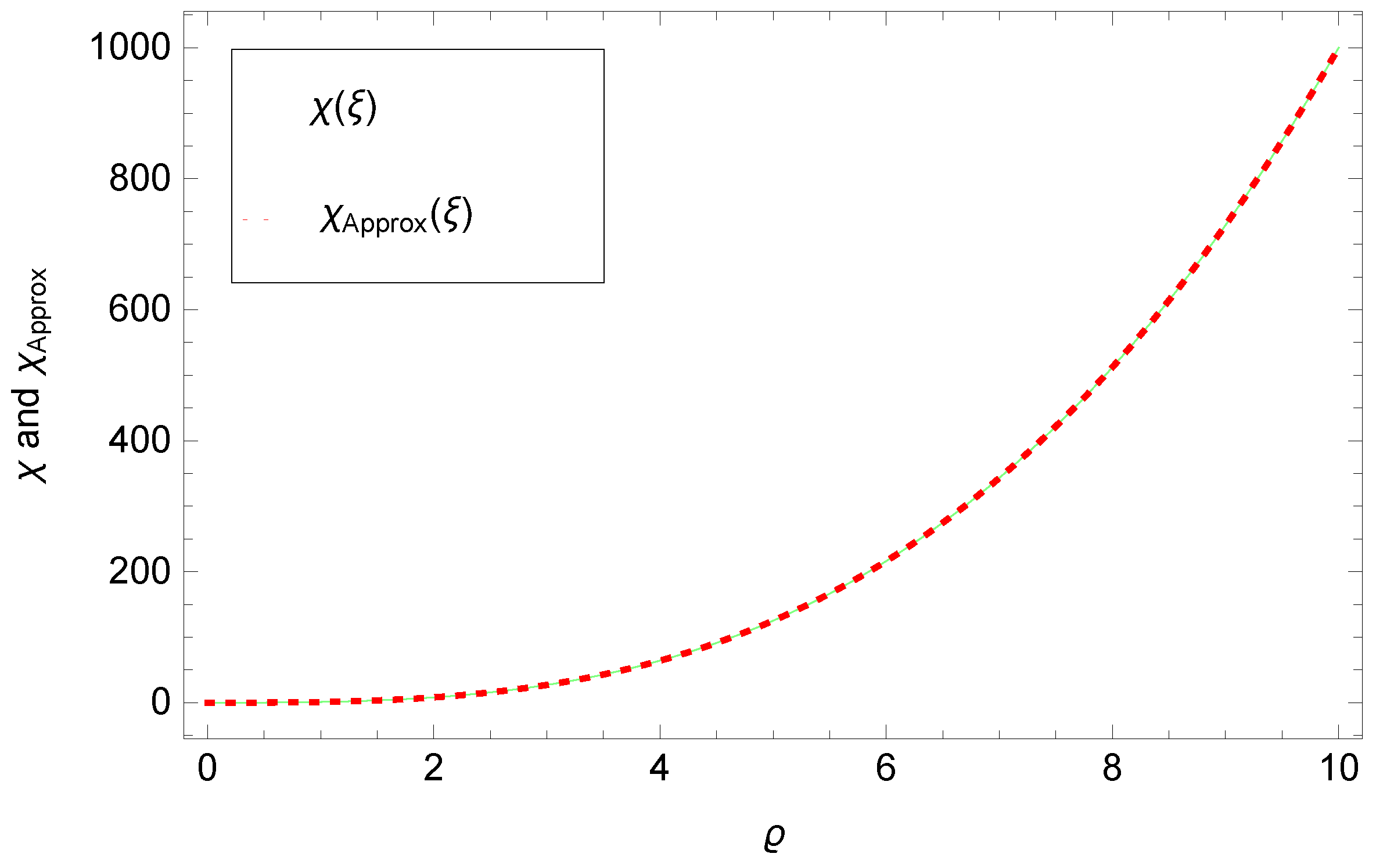
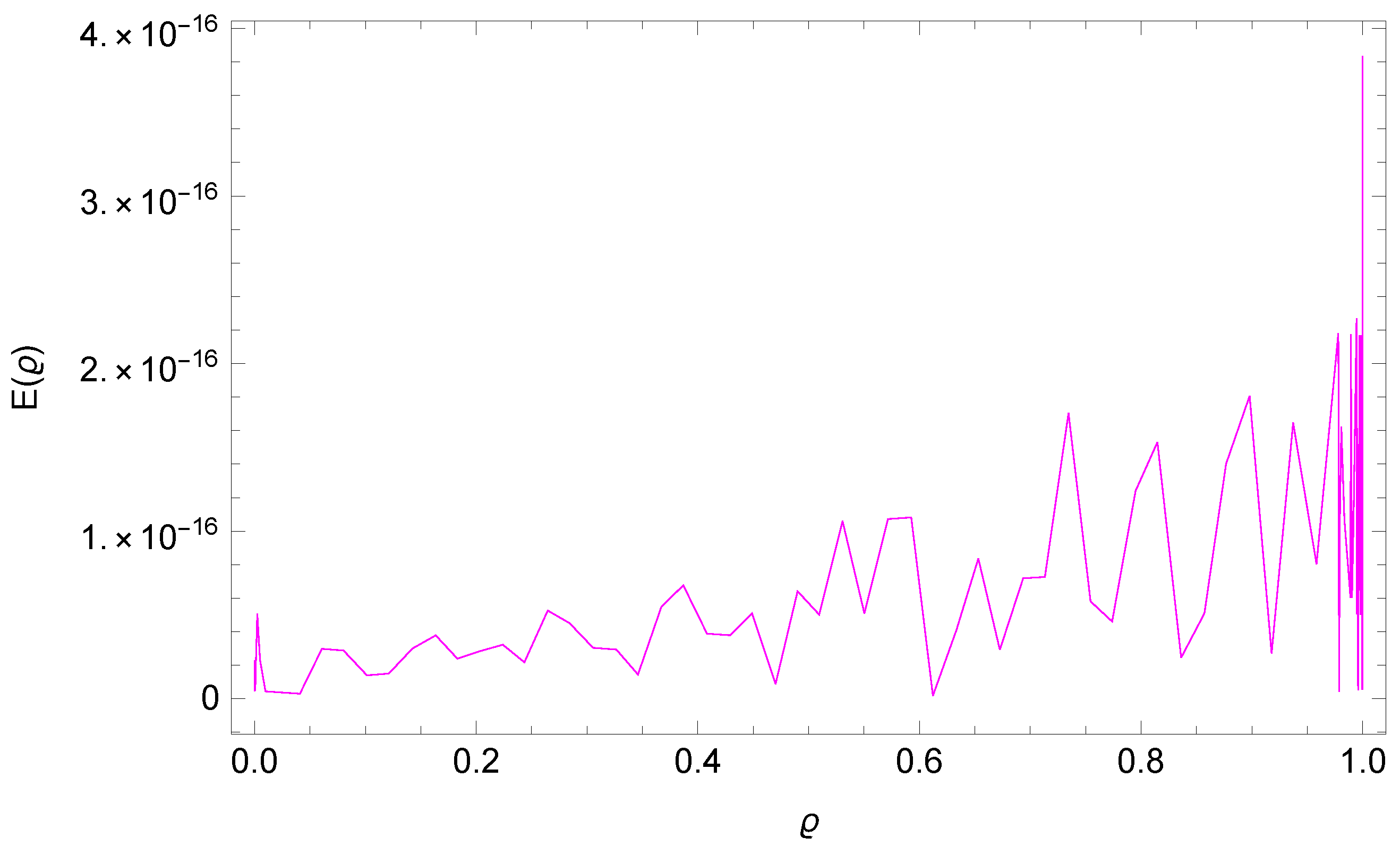
5. Numerical Results
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Guo, L.; Zhao, X.L.; Gu, X.M.; Zhao, Y.L.; Zheng, Y.B.; Huang, T.Z. Three-dimensional fractional total variation regularized tensor optimized model for image deblurring. Appl. Math. Comput. 2021, 404, 126224. [Google Scholar] [CrossRef]
- Miller, K.; Ross, B. An Introduction to the Fractional Calculus and Fractional Differential Equations; Wiley: Hoboken, NJ, USA, 1993. [Google Scholar]
- Ali, H.; Kamrujjaman, M.; Shirin, A. Numerical solution of a fractional-order Bagley–Torvik equation by quadratic finite element method. J. Appl. Math. Comput. 2021, 66, 351–367. [Google Scholar] [CrossRef]
- Ji, T.; Hou, J. Numerical solution of the Bagley–Torvik equation using Laguerre polynomials. SeMA J. 2020, 77, 97–106. [Google Scholar] [CrossRef]
- Mohammadi, F.; Mohyud-Din, S. A fractional-order Legendre collocation method for solving the Bagley-Torvik equations. Adv. Differ. Equ. 2016, 2016, 269. [Google Scholar] [CrossRef]
- Deshi, A.; Gudodagi, G. Numerical solution of Bagley–Torvik, nonlinear and higher order fractional differential equations using Haar wavelet. SeMA J. 2021, 79, 663–675. [Google Scholar] [CrossRef]
- Izadi, M.; Negar, M. Local discontinuous Galerkin approximations to fractional Bagley-Torvik equation. Math. Methods Appl. Sci. 2020, 43, 4798–4813. [Google Scholar] [CrossRef]
- Syam, M.; Alsuwaidi, A.; Alneyadi, A.; Al Refai, S.; Al Khaldi, S. An Implicit Hybrid Method for Solving Fractional Bagley-Torvik Boundary Value Problem. Mathematics 2018, 6, 109. [Google Scholar] [CrossRef]
- Nouri, K.; Elahi-Mehr, S.; Torkzadeh, L. Investigation of the behavior of the fractional Bagley-Torvik and Basset equations via numerical inverse Laplace transform. Rom. Rep. Phys. 2016, 68, 503–514. [Google Scholar]
- Karaaslan, M.; Celiker, F.; Kurulay, M. Approximate solution of the Bagley–Torvik equation by hybridizable discontinuous Galerkin methods. Appl. Math. Comput. 2016, 285, 51–58. [Google Scholar] [CrossRef]
- Torvik, P.J.; Bagley, R.L. On the appearance of the fractional derivative in the behavior of real materials. J. Appl. Mech. 1984, 51, 294–298. [Google Scholar] [CrossRef]
- Morgado, M.; Rebelo, M.; Ferrás, L. Finite Difference Schemes with Non-uniform Time Meshes for Distributed-Order Diffusion Equations. In Proceedings of the International Workshop on Advanced Theory and Applications of Fractional, Calculus, Online, 6–8 September 2021; pp. 239–244. [Google Scholar]
- Aminikhah, H.; Sheikhani, A.H.R.; Houlari, T.; Rezazadeh, H. Numerical solution of the distributed-order fractional Bagley-Torvik equation. IEEE/CAA J. Autom. Sin. 2017, 6, 760–765. [Google Scholar] [CrossRef]
- Yuttanan, B.; Razzaghi, M. Legendre wavelets approach for numerical solutions of distributed order fractional differential equations. Appl. Math. Model. 2019, 70, 350–364. [Google Scholar] [CrossRef]
- Jibenja, N.; Yuttanan, B.; Razzaghi, M. An efficient method for numerical solutions of distributed-order fractional differential equations. J. Comput. Nonlinear Dyn. 2018, 13, 111003. [Google Scholar] [CrossRef]
- Maleknejad, K.; Rashidinia, J.; Eftekhari, T. Numerical solutions of distributed order fractional differential equations in the time domain using the Müntz–Legendre wavelets approach. Numer. Methods Partial Differ. Equ. 2021, 37, 707–731. [Google Scholar] [CrossRef]
- Pourbabaee, M.; Saadatmandi, A. Collocation method based on Chebyshev polynomials for solving distributed order fractional differential equations. Comput. Methods Differ. Equ. 2021, 9, 858–873. [Google Scholar]
- Rashidinia, J.; Eftekhari, T.; Maleknejad, K. A novel operational vector for solving the general form of distributed order fractional differential equations in the time domain based on the second kind Chebyshev wavelets. Numer. Algorithms 2021, 88, 1617–1639. [Google Scholar] [CrossRef]
- Delzanno, G.L. Multi-dimensional, fully-implicit, spectral method for the Vlasov–Maxwell equations with exact conservation laws in discrete form. J. Comput. Phys. 2015, 301, 338–356. [Google Scholar] [CrossRef]
- Chen, Y.; Zhou, J. Error estimates of spectral Legendre–Galerkin methods for the fourth-order equation in one dimension. Appl. Math. Comput. 2015, 268, 1217–1226. [Google Scholar] [CrossRef]
- Abdelkawy, M.; Amin, A.; Lopes, A.M. Fractional-order shifted Legendre collocation method for solving non-linear variable-order fractional Fredholm integro-differential equations. Comput. Appl. Math. 2022, 41, 2. [Google Scholar] [CrossRef]
- Amin, A.; Abdelkawy, M.; Amin, A.K.; Lopes, A.M.; Alluhaybi, A.A.; Hashim, I. Legendre-Gauss-Lobatto collocation method for solving multi-dimensional systems of mixed Volterra-Fredholm integral equations. AIMS Math. 2023, 8, 20871–20891. [Google Scholar] [CrossRef]
- Ezz-Eldien, S.S. On solving systems of multi-pantograph equations via spectral tau method. Appl. Math. Comput. 2018, 321, 63–73. [Google Scholar] [CrossRef]
- Hafez, R.M.; Hammad, M.; Doha, E.H. Fractional Jacobi Galerkin spectral schemes for multi-dimensional time fractional advection–diffusion–reaction equations. Eng. Comput. 2022, 38, 841–858. [Google Scholar] [CrossRef]
- Hammad, M.; Hafez, R.M.; Youssri, Y.H.; Doha, E.H. Exponential Jacobi-Galerkin method and its applications to multidimensional problems in unbounded domains. Appl. Numer. Math. 2020, 157, 88–109. [Google Scholar] [CrossRef]
- Abdelkawy, M.; Alyami, S. Legendre-Chebyshev spectral collocation method for two-dimensional nonlinear reaction-diffusion equation with Riesz space-fractional. Chaos Solitons Fractals 2021, 151, 111279. [Google Scholar] [CrossRef]
- Amin, A.; Amin, A.; Abdelkawy, M.; Alluhaybi, A.; Hashim, I. Spectral technique with convergence analysis for solving one and two-dimensional mixed Volterra-Fredholm integral equation. PLoS ONE 2023, 18, e0283746. [Google Scholar] [CrossRef]
- Doha, E.; Abdelkawy, M.; Amin, A.; Lopes, A. On spectral methods for solving variable-order fractional integro-differential equations. Comput. Appl. Math. 2018, 37, 3937–3950. [Google Scholar] [CrossRef]
- Shen, J.; Tang, T.; Wang, L. Spectral Methods: Algorithms, Analysis and Applications; Springer: Berlin/Heidelberg, Germany, 2011; Volume 41. [Google Scholar]
- Canuto, C.; Hussaini, M.Y.; Quarteroni, A.; Zang, T.A. Spectral Methods: Fundamentals in Single Domains; Springer: Berlin/Heidelberg, Germany, 2007. [Google Scholar]
- Amin, A.Z.; Lopes, A.M.; Hashim, I. A Chebyshev collocation method for solving the non-linear variable-order fractional Bagley–Torvik differential equation. Int. J. Nonlinear Sci. Numer. Simul. 2022, 24, 5. [Google Scholar] [CrossRef]
- Bhrawy, A.; Doha, E.; Alzaidy, J.; Abdelkawy, M. A space-time spectral collocation algorithm for the variable order fractional wave equation. SpringerPlus 2016, 5, 1220. [Google Scholar] [CrossRef]
- Chen, F.; Shen, J. Efficient spectral-Galerkin methods for systems of coupled second-order equations and their applications. J. Comput. Phys. 2012, 231, 5016–5028. [Google Scholar] [CrossRef]
- Yang, Y. Jacobi spectral Galerkin methods for fractional integro-differential equations. Calcolo 2015, 52, 519–542. [Google Scholar] [CrossRef]




| 2 | 6 | 10 | 14 | |
|---|---|---|---|---|
| 2 | 6 | 10 | 14 | |
|---|---|---|---|---|
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Amin, A.Z.; Abdelkawy, M.A.; Solouma, E.; Al-Dayel, I. A Spectral Collocation Method for Solving the Non-Linear Distributed-Order Fractional Bagley–Torvik Differential Equation. Fractal Fract. 2023, 7, 780. https://doi.org/10.3390/fractalfract7110780
Amin AZ, Abdelkawy MA, Solouma E, Al-Dayel I. A Spectral Collocation Method for Solving the Non-Linear Distributed-Order Fractional Bagley–Torvik Differential Equation. Fractal and Fractional. 2023; 7(11):780. https://doi.org/10.3390/fractalfract7110780
Chicago/Turabian StyleAmin, Ahmed Z., Mohamed A. Abdelkawy, Emad Solouma, and Ibrahim Al-Dayel. 2023. "A Spectral Collocation Method for Solving the Non-Linear Distributed-Order Fractional Bagley–Torvik Differential Equation" Fractal and Fractional 7, no. 11: 780. https://doi.org/10.3390/fractalfract7110780
APA StyleAmin, A. Z., Abdelkawy, M. A., Solouma, E., & Al-Dayel, I. (2023). A Spectral Collocation Method for Solving the Non-Linear Distributed-Order Fractional Bagley–Torvik Differential Equation. Fractal and Fractional, 7(11), 780. https://doi.org/10.3390/fractalfract7110780






