Hermite Finite Element Method for Time Fractional Order Damping Beam Vibration Problem

Abstract

In this paper, the vibration problem of a beam with a time fractional damping term is studied by the Hermite finite element method, and its fully discrete scheme is obtained. The stability and error estimation of the scheme are analyzed, and it was proved that it is unconditionally stable and has a convergence order of $O(\tau +{\tau }^{3-\alpha }+h^4)$. The validity of the scheme is verified by numerical examples, the effects of fractional derivative order and damping coefficient on beam vibration are analyzed and the superiority of the fractional order model has been demonstrated by comparing with the traditional damping model.

1. Introduction

In this paper, we consider the following time fractional damping beam vibration problem:

$$\left\{\begin{array}{c}\frac{{\partial }^2}{\partial x^2}(EI\frac{{\partial }^{2}u}{\partial x^2})+\rho A{u}_{tt}+{\mu }_0^C{D}_t^{\alpha }u=f(x,t),x\in (0,L),t\in (0,T],\hfill \\ u(x,0)=\phi (x),u_t(x,0)=\psi (x),x\in [0,L],\hfill \\ u(0,t)=u(L,t)=0,u_x(0,t)=u_x(L,t)=0,t\in [0,T],\hfill \end{array}\right.$$

(1)

where $u(x,t)$ is displacement, $EI$ is the bending stiffness, $\rho$ is density, A is the cross-sectional area, $\mu >0$ is damping coefficient, L is constant, $\phi (x),\psi (x)$ and $f(x,t)$ are smooth functions that are given known. There, ${}_0^C{D}_t^{\alpha }u$ represents the Caputo fractional derivative of order $\alpha (n-1<\alpha <n)$, which is defined as

$${}_0^C{D}_t^{\alpha }u=\frac{1}{\Gamma (n-\alpha )}{\int }_a^b\frac{u^{(n)}ds}{{(t-s)}^{\alpha -n+1}},$$

where $t\in [a,b]$, $\alpha$ is a positive real number. We take the fractional derivative as $1<\alpha <2$.

Fractional calculus is widely used in various related fields of science and engineering, such as mechanics and dynamical systems [1,2], anomalous diffusion [3,4], signal and image processing [5], etc. Fractional calculus provides a better description for analyzing the dynamics of complex systems. In engineering practice, fractional derivatives can be used to describe the viscoelastic properties of advanced materials or the dissipative forces in structural dynamics [6]. The vibration equation of a beam with a damping term can better describe the special properties of an object [7,8,9].

Galucio et al. [10] proposed a finite element method (FEM) based on implicit Newmark scheme for fractional order viscoelastic beams, and numerical examples are given. In [11], the motion equation of a fractional order Timoshenko beam is discretized by FEM and obtained the closed solution of the creep test. In [12], a general model of beams and rods with fractional derivatives is built. Roman et al. [13] proposed the amplitude equation of the fractional order viscoelastic beam by FEM and harmonic balance method. The stability of the steady-state solution is tested. Ehsan et al. [14] studied the vibration problem of a fractional order viscoelastic functionally gradient beam by finite difference method (FDM) and FEM. In [15], the fractional order viscoelastic Timoshenko nanobeams are analyzed by general differential orthogonality (GDQ) technique and FDM. The time response of the system under different boundary conditions is obtained. Oskouie et al. [16] used fractional calculus and Gurtin–Murdoch theory to study the nonlinear vibration of viscoelastic Euler–Bernoulli beams. In [17], FDM and the Galerkin method were combined to solve partial fractional differential equations. The periodic solution of a fractional order microbeam was obtained. The multi-scale method was applied to solve the vibration problem of a fractional order damped beam in [18,19]. Catania et al. [20] used FEM to analyze the vibration of fractional order heterogeneous beams. Xu et al. [21] analyzed the dynamic characteristics and steady-state response of a fractional order viscoelastic beam by wave method and discussed the effects of fractional order on wave propagation, transmission and reflection. Yang et al. [22] established a nonlinear fractional order model of viscoelastic microbeam by a new numerical algorithm, which simplifies the calculation. Cao et al. [23] solved the time fractional diffusion equation optimal control problem by FEM and analyzed the stability and truncation error of the discrete scheme. In [24,25,26], several numerical theories for solving time fractional fourth-order partial differential equations based on mixed finite element method (MFEM) and mixed finite volume element method (MFVM) were presented and analyzed. In [10,11,12,13,14,15,16,17,18,19,20,21,22,23,24,25,26], numerical examples are given and parameterization studies are carried out. The numerical results show that the fractional derivative order, viscoelastic coefficient and various damping coefficient have effects on the vibration of fractional viscoelastic beams under different boundary conditions.

In recent years, fractional order viscoelastic models have been widely used. Compared with classical viscoelastic models, they are more in line with practical situations and can more accurately describe the mechanical properties of viscoelastic materials. Zhang et al. [27] studied the damping characteristics of viscoelastic materials based on the fractional order Kelvin model. Di Paola et al. [28] used a fractional order constitutive model to describe the creep and stress relaxation phenomena of viscoelastic materials. In [29], Bagley et al. obtained the motion equation of a viscoelastic damping structure by using a five-parameter fractional order model. Liu et al. [30] studied the horizontal vibration problem of a single pile in viscoelastic soil layers based on fractional derivative theory. Koeller [31] extended the theory of genetic viscoelasticity to the fractional order and obtained the creep and relaxation functions of various fractional order calculus models by introducing the fractional order spring-pot model. The study of viscoelastic beam vibration is helpful to discover and solve the damage of structural resonance to infrastructure and reduce its negative impact, which is of great significance in the field of engineering mechanics and has a broad application prospect.

The Hermite finite element method ensures that the interpolation function has a continuous first derivative, can directly calculate the stress of the beam problem and has a higher order of convergence. The paper consists of six sections. Section 2 is finite element approximation. Section 3 is the stability analysis of the fully discrete scheme. We estimate the error of the fully discrete scheme by introducing projection in Section 4. In Section 5, four numerical examples are given to verify the validity of the scheme, explore the effect of fractional derivative order and damping coefficient on the vibration of the beam and compare the fractional order model with the classical damping model. Section 6 is the summary of this paper.

2. Finite Element Approximation

We consider $I=[0,L]$ and choose the Sobolev space $H_0^2(I)=\{u|u\in H^2(I),u(0,t)=u(L,t)=0,u_x(0,t)=u_x(L,t)=0\}$ to satisfy the boundary conditions. Multiply both sides of (1) by $v(x)\in H_0^2(I)$ and integrate over 0 to t.

$$\begin{array}{cc}\hfill & (\frac{{\partial }^2}{\partial x^2}(EI\frac{{\partial }^{2}u}{\partial x^2}),v)+(\rho A\frac{{\partial }^{2}u}{\partial t^2},v)+({\mu }_0^C{D}_t^{\alpha }u,v)=(f,v).\hfill \end{array}$$

(2)

Using Green’s formula, we obtain the weak formulation for problem (1): find $u\in H_0^2$, satisfying

$$\left\{\begin{array}{cc}(EI{u}_{xx},v_{xx})+(\rho A{u}_{tt},v)+({\mu }_0^C{D}_t^{\alpha }u,v)=(f,v),\forall v\in H_0^2,\hfill & \\ u(x,0)=\phi (x),u_t(x,0)=\psi (x).\hfill \end{array}\right.$$

(3)

3. Stability of Fully Discrete Finite Element Schemes

For the discretization of time, let $0=t_0<t_1<\cdots <t_N=T$ be a uniform partition of the interval $[0,T]$, $\tau =\frac{T}{N}$, $t_n=n\tau$. $V_h=\{v\in H_0^2(I):v_h\in P_3\}$ is the finite element space composed of piecewise cubic Hermite polynomial on $I_h$. We discretize the second derivative term with the central difference quotient and use the $L1$ approximation formula to discretize the time fractional derivative.

Let $0=x_0<x_1<\cdots <x_M=L$ be the subdivision in the interval $[0,L]$, $h=\frac{L}{M}$. Based on the given finite element space $V_h$, the corresponding finite element full-discrete scheme of (1) is find $u_h^{n+1}\in V_h$ such that

$$\begin{array}{c}(EI{u}_{h,xx}^{n+1},v_{h,xx})+(\rho A\frac{u_h^{n+1}-2u_h^n+u_h^{n-1}}{{\tau }^2},v_h)+(\mu D_t^{\alpha }{u}^{n+1},v_h)=(f^{n+1},v_h),\forall v_h\in V_h.\hfill \end{array}$$

(4)

Define

$${\delta }_t{u}^k=\frac{u_h^k-u_h^{k-1}}{\tau },1\le k\le n+1.$$

The $L1$ approximation formula of the time fractional derivative is as follows, when $1<\alpha <2$,

$$\begin{array}{cc}\hfill {}_0^C{D}_t^{\alpha }{u}^{n+1}& =D_t^{\alpha }{u}^{n+1}+R(u^{n+1})\hfill \\ \hfill & =\frac{{\tau }^{1-\alpha }}{\Gamma (3-\alpha )}\left[b_0^{(\alpha )}{\delta }_t{u}^{n+1}-\sum _{k=1}^n(b_{n-k}^{(\alpha )}-b_{n-k+1}^{(\alpha )}){\delta }_t{u}^k-b_n^{(\alpha )}{u}_t^0\right]+R(u_t^{n+1}),\hfill \end{array}$$

(5)

where $|R(u_t^{n+1})|\le \frac{1}{2\Gamma (2-\alpha )}\left[\frac{1}{4}+\frac{\alpha -1}{(2-\alpha )(3-\alpha )}\right]\underset{t_0\le t\le t_n}{max}|u^{‴}|{\tau }^{3-\alpha }$, $b_l^{\alpha }={(l+1)}^{2-\alpha }-{(l)}^{2-\alpha }$. Next, we will prove the stability of fully discrete finite element scheme.

Theorem 1. 

The fully discrete finite element scheme (4) is unconditionally stable, and there is the stability estimate

$$\begin{array}{cc}\hfill & \rho A\parallel {\delta }_t{u}^{n+1}{\parallel }^2+EI\parallel u_{h,xx}^{n+1}{\parallel }^2\le \rho A\parallel {\delta }_t{u}^1{\parallel }^2+EI{\parallel u_{h,xx}^1\parallel }^2\hfill \\ \hfill & +\frac{\mu t_{n+1}^{2-\alpha }}{\Gamma (3-\alpha )}\parallel u_{h,t}^0{\parallel }^2+\frac{t_{n+1}^{1-\alpha }\Gamma (2-\alpha )\tau }{\mu }\sum _{k=1}^n{\parallel f^{k+1}\parallel }^2.\hfill \end{array}$$

(6)

Proof of Theorem 1. 

Let $v_h={\delta }_t{u}^{n+1}$ in (4); using $(a-b,a)\ge \frac{1}{2}{(\parallel a\parallel }^2-{\parallel b\parallel }^2)$ on the terms of left hand side, we obtain

$$\begin{array}{cc}\hfill & \frac{\rho A}{2\tau }(\parallel {\delta }_t{u}^{n+1}{\parallel }^2-\parallel {\delta }_t{u}^n{\parallel }^2)+\frac{EI}{2\tau }(\parallel u_{h,xx}^{n+1}{\parallel }^2-\parallel u_{h,xx}^n{\parallel }^2)+\mu s{b}_0^{(\alpha )}{\parallel {\delta }_t{u}^{n+1}\parallel }^2\hfill \\ \hfill & \le (\mu s\sum _{k=1}^n(b_{n-k}^{(\alpha )}-b_{n-k+1}^{(\alpha )}){\delta }_t{u}^k,{\delta }_t{u}^{n+1})+\mu s(b_n^{(\alpha )}{u}_{h,t}^0,{\delta }_t{u}^{n+1})+(f^{n+1},{\delta }_t{u}^{n+1}).\hfill \end{array}$$

(7)

Estimating the right hand side terms of (7) by Young inequality, we have

$$\begin{array}{cc}\hfill \mu s\sum _{k=1}^n(b_{n-k}^{(\alpha )}-b_{n-k+1}^{(\alpha )})({\delta }_t{u}^k,{\delta }_t{u}^{n+1})\le \frac{1}{2}\mu s& \sum _{k=1}^n(b_{n-k}^{(\alpha )}-b_{n-k+1}^{(\alpha )}){\parallel {\delta }_t{u}^k\parallel }^2\hfill \\ \hfill & +\frac{1}{2}\mu s\sum _{k=1}^n(b_{n-k}^{(\alpha )}-b_{n-k+1}^{(\alpha )}){\parallel {\delta }_t{u}^{n+1}\parallel }^2,\hfill \end{array}$$

(8)

$$\begin{array}{cc}\hfill & \mu s(b_n^{(\alpha )}{u}_{h,t}^0,{\delta }_t{u}^{n+1})\le \frac{1}{2}\mu s{b}_n^{(\alpha )}\parallel u_{h,t}^0{\parallel }^2+\frac{1}{2}\mu s{b}_n^{(\alpha )}{\parallel {\delta }_t{u}^{n+1}\parallel }^2.\hfill \end{array}$$

(9)

Substituting (8) and (9) into (7), we have

$$\begin{array}{cc}\hfill & \frac{\rho A}{2\tau }(\parallel {\delta }_t{u}^{n+1}{\parallel }^2-\parallel {\delta }_t{u}^n{\parallel }^2)+\frac{EI}{2\tau }(\parallel u_{h,xx}^{n+1}{\parallel }^2-\parallel u_{h,xx}^n{\parallel }^2)+\mu s{b}_0^{(\alpha )}{\parallel {\delta }_t{u}^{n+1}\parallel }^2\hfill \\ \hfill & \le \frac{1}{2}\mu s\sum _{k=1}^n(b_{n-k}^{(\alpha )}-b_{n-k+1}^{(\alpha )})\parallel {\delta }_t{u}^k{\parallel }^2+\frac{1}{2}\mu s\sum _{k=1}^n(b_{n-k}^{(\alpha )}-b_{n-k+1}^{(\alpha )})\parallel {\delta }_t{u}^{n+1}{\parallel }^2+\frac{1}{2}\mu s{b}_n^{(\alpha )}{\parallel u_{h,t}^0\parallel }^2\hfill \\ \hfill & +\frac{1}{2}\mu s{b}_n^{(\alpha )}{\parallel {\delta }_t{u}^{n+1}\parallel }^2+(f^{n+1},{\delta }_t{u}^{n+1}).\hfill \end{array}$$

(10)

Expanding $\frac{1}{2}\mu s{\sum }_{k=1}^n(b_{n-k}^{(\alpha )}-b_{n-k+1}^{(\alpha )})\parallel {\delta }_t{u}^{n+1}{\parallel }^2+\frac{1}{2}\mu s{b}_{n+1}^{(\alpha )}{\parallel {\delta }_t{u}^{n+1}\parallel }^2$, we obtain

$$\begin{array}{c}\hfill \frac{1}{2}\mu s\sum _{k=1}^n(b_{n-k}^{(\alpha )}-b_{n-k+1}^{(\alpha )})\parallel {\delta }_t{u}^{n+1}{\parallel }^2+\frac{1}{2}\mu s{b}_n^{(\alpha )}\parallel {\delta }_t{u}^{n+1}{\parallel }^2=\frac{1}{2}\mu s{b}_0^{(\alpha )}{\parallel {\delta }_t{u}^{n+1}\parallel }^2.\end{array}$$

(11)

Multiplying both sides by $2\tau$ and rearranging provides

$$\begin{array}{cc}\hfill & \rho A\parallel {\delta }_t{u}^{n+1}{\parallel }^2+EI\parallel u_{h,xx}^{n+1}{\parallel }^2+\mu s\tau \sum _{k=1}^n{b}_{n-k+1}^{(\alpha )}{\parallel {\delta }_t{u}^k\parallel }^2\hfill \\ \hfill & \le \rho A\parallel {\delta }_t{u}^n{\parallel }^2+EI\parallel u_{h,xx}^n{\parallel }^2+\mu s\tau \sum _{k=1}^n{b}_{n-k}^{(\alpha )}\parallel {\delta }_t{u}^k{\parallel }^2-\mu s\tau b_0^{(\alpha )}{\parallel {\delta }_t{u}^{n+1}\parallel }^2\hfill \\ \hfill & +\mu s\tau b_n^{(\alpha )}{\parallel u_{h,t}^0\parallel }^2+2\tau (f^{n+1},{\delta }_t{u}^{n+1}).\hfill \end{array}$$

(12)

Denote

$$\begin{array}{c}\hfill F^n=\rho A\parallel {\delta }_t{u}^{n+1}{\parallel }^2+EI\parallel u_{h,xx}^{n+1}{\parallel }^2+\mu s\tau \sum _{k=1}^n{b}_{n-k+1}^{(\alpha )}{\parallel {\delta }_t{u}^k\parallel }^2.\end{array}$$

(13)

We deduce that

$$\begin{array}{cc}\hfill F^n& \le F^{n-1}+\mu s\tau b_n^{(\alpha )}\parallel u_{h,t}^0{\parallel }^2+2\tau (f^{n+1},u_{h,t}^{n+1})-\mu s\tau b_0^{(\alpha )}{\parallel {\delta }_t{u}^{n+1}\parallel }^2\hfill \\ \hfill & \le F^0+\mu s\tau \sum _{k=1}^n{b}_k^{(\alpha )}\parallel u_{h,t}^0{\parallel }^2+2\tau \sum _{k=1}^n(f^{n+1},{\delta }_t{u}^{n+1})-\mu s\tau \sum _{k=1}^n{b}_0^{(\alpha )}{\parallel {\delta }_t{u}^{k+1}\parallel }^2\hfill \\ \hfill & =\rho A\parallel {\delta }_t{u}^1{\parallel }^2+EI\parallel u_{h,xx}^1{\parallel }^2+\mu s\tau \sum _{k=1}^n{b}_k^{(\alpha )}{\parallel u_{h,t}^0\parallel }^2\hfill \\ \hfill & +2\tau \sum _{k=1}^n(f^{k+1},{\delta }_t{u}^{k+1})-\mu s\tau \sum _{k=1}^n{b}_0^{(\alpha )}{\parallel {\delta }_t{u}^{k+1}\parallel }^2.\hfill \\ \end{array}$$

(14)

Using Young inequality, we obtain

$$\begin{array}{cc}\hfill & (f^{k+1},{\delta }_t{u}^{k+1})\le \frac{\mu s{b}_{n-k+1}^{(\alpha )}}{2}\parallel {\delta }_t{u}^{k+1}{\parallel }^2+\frac{1}{2\mu s{b}_{n-k+1}^{(\alpha )}}{\parallel f^{k+1}\parallel }^2.\hfill \end{array}$$

(15)

Thus,

$$\begin{array}{cc}\hfill & \rho A\parallel {\delta }_t{u}^{n+1}{\parallel }^2+EI\parallel u_{h,xx}^{n+1}{\parallel }^2+\mu s\tau \sum _{k=1}^n{b}_{n-k+1}^{(\alpha )}{\parallel {\delta }_t{u}^k\parallel }^2\hfill \\ \hfill & \le \rho A\parallel {\delta }_t{u}^1{\parallel }^2+EI\parallel u_{h,xx}^1{\parallel }^2+\mu s\tau \sum _{k=1}^n{b}_k^{(\alpha )}\parallel u_{h,t}^0{\parallel }^2+\sum _{k=1}^n\frac{\tau }{\mu s{b}_{n-k+1}^{(\alpha )}}{\parallel f^{k+1}\parallel }^2\hfill \\ \hfill & +\mu s\tau \sum _{k=1}^n{b}_{n-k+1}^{(\alpha )}\parallel {\delta }_t{u}^{k+1}{\parallel }^2-\mu s\tau \sum _{k=1}^n{b}_0^{(\alpha )}{\parallel {\delta }_t{u}^{k+1}\parallel }^2.\hfill \end{array}$$

(16)

Subtracting $\mu s\tau {\sum }_{k=1}^n{b}_{n-k+1}^{(\alpha )}{\parallel {\delta }_t{u}^k\parallel }^2$ on both sides of (16), due to $1=b_0^{(\alpha )}>b_1^{(\alpha )}>\cdots >b_n^{(\alpha )}>0$, we deduce

$$\begin{array}{cc}\hfill & \mu s\tau \sum _{k=1}^n{b}_{n-k+1}^{(\alpha )}\parallel {\delta }_t{u}^{k+1}{\parallel }^2-\mu s\tau \sum _{k=1}^n{b}_{n-k+1}^{(\alpha )}{\parallel {\delta }_t{u}^k\parallel }^2\hfill \\ \hfill & =\mu s\tau ((b_n^{(\alpha )}-b_{n-1}^{(\alpha )})\parallel {\delta }_t{u}^2{\parallel }^2+\cdots +(b_2^{(\alpha )}-b_1^{\alpha })\parallel {\delta }_t{u}^n{\parallel }^2-b_n^{\alpha }\parallel {\delta }_t{u}^1{\parallel }^2+b_1^{(\alpha )}\parallel {\delta }_t{u}^{n+1}{\parallel }^2)\hfill \\ \hfill & \le \mu s\tau (b_1^{(\alpha )}\parallel {\delta }_t{u}^{n+1}{\parallel }^2-b_n^{(\alpha )}\parallel {\delta }_t{u}^1{\parallel }^2)\le \mu s\tau b_1^{(\alpha )}{\parallel {\delta }_t{u}^{n+1}\parallel }^2.\hfill \end{array}$$

(17)

Hence,

$$\begin{array}{cc}\hfill & \rho A\parallel {\delta }_t{u}^{n+1}{\parallel }^2+EI{\parallel u_{h,xx}^{n+1}\parallel }^2\hfill \\ \hfill & \le \rho A\parallel {\delta }_t{u}^1{\parallel }^2+EI\parallel u_{h,xx}^1{\parallel }^2+\mu s\tau \sum _{k=1}^n{b}_k^{(\alpha )}\parallel u_{h,t}^0{\parallel }^2+\sum _{k=1}^n\frac{\tau }{\mu s{b}_{n-k+1}^{(\alpha )}}{\parallel f^{k+1}\parallel }^2\hfill \\ \hfill & +\mu s\tau b_1^{(\alpha )}\parallel {\delta }_t{u}^{n+1}{\parallel }^2-\mu s\tau \sum _{k=1}^n{b}_0^{(\alpha )}\parallel {\delta }_t{u}^k{\parallel }^2-\mu s\tau b_0^{(\alpha )}{\parallel {\delta }_t{u}^{n+1}\parallel }^2.\hfill \end{array}$$

(18)

(18) can be written as follows because of $\mu s\tau (b_1^{(\alpha )}-b_0^{(\alpha )}){\parallel {\delta }_t{u}^{n+1}\parallel }^2\le 0$.

$$\begin{array}{cc}\hfill & \rho A\parallel {\delta }_t{u}^{n+1}{\parallel }^2+EI{\parallel u_{h,xx}^{n+1}\parallel }^2\hfill \\ \hfill & \le \rho A\parallel {\delta }_t{u}^1{\parallel }^2+EI\parallel u_{h,xx}^1{\parallel }^2+\mu s\tau \sum _{k=1}^n{b}_k^{(\alpha )}\parallel u_{h,t}^0{\parallel }^2+\sum _{k=1}^n\frac{\tau }{\mu s{b}_{n-k+1}^{(\alpha )}}{\parallel f^{k+1}\parallel }^2.\hfill \end{array}$$

(19)

Note that $b_{n-k+1}\ge (2-\alpha ){(n+1)}^{1-\alpha }$ and ${\sum }_{k=1}^n{b}_k={(n+1)}^{2-\alpha }$; we deduce

$$\begin{array}{cc}\hfill s{b}_{n-k+1}^{\alpha }& =\frac{{\tau }^{1-\alpha }}{\Gamma (3-\alpha )}{b}_{n-k+1}^{(\alpha )}\ge \frac{{\tau }^{1-\alpha }}{\Gamma (3-\alpha )}(2-\alpha ){(n+1)}^{1-\alpha }\hfill \\ \hfill & =\frac{{((n+1)\tau )}^{1-\alpha }}{\Gamma (2-\alpha )}=\frac{t_{n+1}^{1-\alpha }}{\Gamma (2-\alpha )}.\hfill \end{array}$$

(20)

The right hand terms of (19) can be estimated as

$$\begin{array}{cc}\hfill & \sum _{k=1}^n\frac{\tau }{\mu s{b}_{n-k+1}^{(\alpha )}}\parallel f^{n+1}{\parallel }^2\le \frac{t_{n+1}^{1-\alpha }\Gamma (2-\alpha )\tau }{\mu }\sum _{k=1}^n{\parallel f^{k+1}\parallel }^2,\hfill \end{array}$$

(21)

and

$$\begin{array}{cc}\hfill & \mu s\tau \sum _{k=1}^n{b}_k^{(\alpha )}\parallel u_{h,t}^0{\parallel }^2=\mu \tau {(n+1)}^{2-\alpha }\frac{{\tau }^{1-\alpha }}{\Gamma (3-\alpha )}\parallel u_{h,t}^0{\parallel }^2=\frac{\mu t_{n+1}^{2-\alpha }}{\Gamma (3-\alpha )}{\parallel u_{h,t}^0\parallel }^2.\hfill \end{array}$$

(22)

Combining (21) and (22), there holds

$$\begin{array}{cc}\hfill & \rho A\parallel {\delta }_t{u}^{n+1}{\parallel }^2+EI\parallel u_{h,xx}^{n+1}{\parallel }^2\le \rho A\parallel {\delta }_t{u}^1{\parallel }^2+EI{\parallel u_{h,xx}^1\parallel }^2\hfill \\ \hfill & +\frac{\mu t_{n+1}^{2-\alpha }}{\Gamma (3-\alpha )}\parallel u_{h,t}^0{\parallel }^2+\frac{t_{n+1}^{1-\alpha }\Gamma (2-\alpha )\tau }{\mu }\sum _{k=1}^n{\parallel f^{k+1}\parallel }^2.\hfill \end{array}$$

(23)

□

4. Error Estimation of Fully Discrete Finite Element Schemes

We will estimate the error between fully discrete solution and true solution; we introduce the elliptic projection $R_h:H_0^2(I)\to V_h$ such that

$$\begin{array}{cc}(EI{R}_h{u}_{xx},v_{xx})=(EI{u}_{xx},v_{xx}),\forall v\in V_h.\hfill & \end{array}$$

(24)

For projection (24), we have the following Lemma.

Lemma 1 

([32]). $1\le k\le 3$ denotes the degree of finite element space $V_h$; for any $u\in H_0^2\bigcap H^{k+1}$, we have

$$\begin{array}{cc}\parallel u-R_{h}u\parallel +h\parallel u-R_h{u\parallel }_1+h^2\parallel u-R_h{u\parallel }_2\le C{h}^{k+1}{\parallel u\parallel }_{k+1}.\hfill & \end{array}$$

(25)

We present the error estimates for the scheme (4) in Theorem 2.

Theorem 2. 

Let u and $u_h$ be the solutions of (1) and (2), respectively. $u\in H_0^2\bigcap H^4$, and then there exists a constant C independent of T and τ such that

$$\begin{array}{cc}\parallel u^{n+1}-u_h^{n+1}\parallel \le C(\tau +{\tau }^{3-\alpha }+h^4),\hfill & \end{array}$$

(26)

Proof of Theorem 2. 

Taking $t=t_{n+1}$ in Equation (2), tested by $v_h\in V_h$, we obtain

$$\begin{array}{cc}\hfill & (\rho A\frac{u_h^{n+1}-2u_h^n+u_h^{n-1}}{{\tau }^2},v_h)+({\mu }_0^C{D}_t^{\alpha }{u}^{n+1},v_h)+(EI{u}_{xx}^{n+1},v_{h,xx})\hfill \\ \hfill & =(f^{n+1},v_h)-(\rho A(u_{tt}^{n+1}-\frac{u_h^{n+1}-2u_h^n+u_h^{n-1}}{{\tau }^2}),v_h)-(R(u^{n+1}),v_h),\hfill \end{array}$$

(27)

where

$$R(u^{n+1}){=}_0^C{D}_t^{\alpha }{u}^{n+1}-D_t^{\alpha }{u}^{n+1}.$$

Subtracting (27) from (4) to obtain the error equation, we decompose the error as

$$u^{n+1}-u_h^{n+1}=u^{n+1}-R_h{u}^{n+1}+R_h{u}^{n+1}-u_h^{n+1}={\eta }^{n+1}+{\theta }^{n+1},$$

where ${\eta }^{n+1}=u^{n+1}-R_h{u}^{n+1}$ and ${\theta }^{n+1}=R_h{u}^{n+1}-u_h^{n+1}$, and we obtain

$$\begin{array}{cc}\hfill & (EI{\theta }_{xx}^{n+1},v_{h,xx})+(\rho A\frac{{\theta }^{n+1}-2{\theta }^n+{\theta }^{n-1}}{{\tau }^2},v_h)+(\mu D_t^{\alpha }{\theta }^{n+1},v_h)\hfill \\ \hfill & =(\rho A(\frac{u^{n+1}-2u^n+u^{n-1}}{{\tau }^2}-u_{tt}^n),v_h)-(\rho A\frac{{\eta }^{n+1}-2{\eta }^n+{\eta }^{n-1}}{{\tau }^2},v_h)\hfill \\ \hfill & -(\mu D_t^{\alpha }{\eta }^{n+1},v_h)-(\mu R(u^{n+1}),v_h).\hfill \end{array}$$

(28)

Taking $v_h={\delta }_t{\theta }^{n+1}$ in (28), using $(a-b,a)\ge \frac{1}{2}{(\parallel a\parallel }^2-{\parallel b\parallel }^2)$ inequality, we have

$$\begin{array}{cc}\hfill & \frac{EI}{2\tau }(\parallel {\theta }_{xx}^{n+1}{\parallel }^2-\parallel {\theta }_{xx}^n{\parallel }^2)+\frac{\rho A}{2\tau }(\parallel {\delta }_t{\theta }^{n+1}{\parallel }^2-\parallel {\delta }_t{\theta }^n{\parallel }^2)+\mu s{b}_0{\parallel {\delta }_t{\theta }^{n+1}\parallel }^2\hfill \\ \hfill & \le |(\rho A(\frac{u^{n+1}-2u^n+u^{n-1}}{{\tau }^2}-u_{tt}^{n+1}),{\delta }_t{\theta }^{n+1})|+|(\rho A\frac{{\eta }^{n+1}-2{\eta }^n+{\eta }^{n-1}}{{\tau }^2},{\delta }_t{\theta }^{n+1})|\hfill \\ \hfill & +|\mu s(\sum _{k=1}^n(b_{n-k}^{(\alpha )}-b_{n-k+1}^{(\alpha )}){\delta }_t{\theta }^k,{\delta }_t{\theta }^{n+1})|+|\mu s{b}_n^{(\alpha )}({\theta }_t^0,{\delta }_t{\theta }^{n+1})|+|(\mu R(u^{n+1}),{\delta }_t{\theta }^{n+1})|\hfill \\ \hfill & +|\mu s(\sum _{k=1}^n(b_{n-k}^{(\alpha )}-b_{n-k+1}^{(\alpha )}){\delta }_t{\eta }^k,{\delta }_t{\theta }^{n+1})|+|\mu s{b}_n^{(\alpha )}({\eta }_t^0,{\delta }_t{\theta }^{n+1})|+|\mu s{b}_0^{(\alpha )}({\delta }_t{\eta }^{n+1},{\delta }_t{\theta }^{n+1})|.\hfill \end{array}$$

(29)

By Young inequality, we deduce

$$\begin{array}{cc}\hfill (\rho A(\frac{u^{n+1}-2u^n+u^{n-1}}{{\tau }^2}-u_{tt}^{n+1}),{\delta }_t{\theta }^{n+1})\le & \frac{4{\rho }^2{A}^2}{\mu s{b}_0^{(\alpha )}}\parallel \frac{u^{n+1}-2u^n+u^{n-1}}{{\tau }^2}-u_{tt}^{n+1}{\parallel }^2\hfill \\ \hfill & +\frac{\mu s{b}_0^{(\alpha )}}{16}{\parallel {\delta }_t{\theta }^{n+1}\parallel }^2,\hfill \end{array}$$

(30)

$$\begin{array}{cc}\hfill & (\rho A(\frac{{\eta }^{n+1}-2{\eta }^n+{\eta }^{n-1}}{{\tau }^2}),{\delta }_t{\theta }^{n+1})\le \frac{4{\rho }^2{A}^2}{\mu s{b}_0^{(\alpha )}}\parallel \frac{{\eta }^{n+1}-2{\eta }^n+{\eta }^{n-1}}{{\tau }^2}{\parallel }^2+\frac{\mu s{b}_0^{(\alpha )}}{16}{\parallel {\delta }_t{\theta }^{n+1}\parallel }^2,\hfill \end{array}$$

(31)

$$\begin{array}{cc}\hfill & \mu s(\sum _{k=1}^n(b_{n-k}^{(\alpha )}-b_{n-k+1}^{(\alpha )}){\delta }_t{\theta }^k,{\delta }_t{\theta }^{n+1})\le 2\mu s(\sum _{k=1}^n(b_{n-k}^{(\alpha )}-b_{n-k+1}^{(\alpha )})\parallel {\delta }_t{\theta }^k{\parallel }^2+\frac{\mu s}{8}(b_0^{(\alpha )}-b_n^{(\alpha )}){\parallel {\delta }_t{\theta }^{n+1}\parallel }^2,\hfill \end{array}$$

(32)

$$\begin{array}{cc}\hfill & \mu s(\sum _{k=1}^n(b_{n-k}^{(\alpha )}-b_{n-k+1}^{(\alpha )}){\delta }_t{\eta }^k,{\delta }_t{\theta }^{n+1})\le 2\mu s(\sum _{k=1}^n(b_{n-k}^{(\alpha )}-b_{n-k+1}^{(\alpha )})\parallel {\delta }_t{\eta }^k{\parallel }^2+\frac{\mu s}{8}(b_0^{(\alpha )}-b_n^{(\alpha )}){\parallel {\delta }_t{\theta }^{n+1}\parallel }^2,\hfill \end{array}$$

(33)

$$\begin{array}{cc}\hfill & \mu s{b}_n^{(\alpha )}({\theta }_t^0,{\delta }_t{\theta }^{n+1})\le 2\mu s{b}_n^{(\alpha )}\parallel {\theta }_t^0{\parallel }^2+\frac{\mu s{b}_n^{(\alpha )}}{8}{\parallel {\delta }_t{\theta }^{n+1}\parallel }^2,\hfill \end{array}$$

(34)

$$\begin{array}{cc}\hfill & \mu s{b}_n^{(\alpha )}({\eta }_t^0,{\delta }_t{\theta }^{n+1})\le 2\mu s{b}_n^{(\alpha )}\parallel {\eta }_t^0{\parallel }^2+\frac{\mu s{b}_n^{(\alpha )}}{8}{\parallel {\delta }_t{\theta }^{n+1}\parallel }^2,\hfill \end{array}$$

(35)

$$\begin{array}{cc}\hfill & \mu s{b}_0^{(\alpha )}({\delta }_t{\eta }^{n+1},{\delta }_t{\theta }^{n+1})\le 2\mu s{b}_0^{(\alpha )}\parallel {\delta }_t{\eta }^{n+1}{\parallel }^2+\frac{\mu s{b}_0^{(\alpha )}}{8}{\parallel {\delta }_t{\theta }^{n+1}\parallel }^2,\hfill \end{array}$$

(36)

$$\begin{array}{cc}\hfill & (\mu R(u^{n+1}),{\delta }_t{\theta }^{n+1})\le \frac{2\mu }{s{b}_0^{(\alpha )}}\parallel R(u^{n+1}){\parallel }^2+\frac{\mu s{b}_0^{(\alpha )}}{2}{\parallel {\delta }_t{\theta }^{n+1}\parallel }^2.\hfill \end{array}$$

(37)

Substituting (30)–(37) into (29), multiplying both sides by $2\tau$ and rearranging, we obtain

$$\begin{array}{cc}\hfill & EI\parallel {\theta }_{xx}^{n+1}{\parallel }^2+\rho A\parallel {\delta }_t{\theta }^{n+1}{\parallel }^2+4\mu s\tau \sum _{k=1}^n{b}_{n-k+1}^{(\alpha )}\parallel {\delta }_t{\theta }^k{\parallel }^2+4\mu s\tau \sum _{k=1}^n{b}_{n-k+1}^{(\alpha )}{\parallel {\delta }_t{\eta }^k\parallel }^2\hfill \\ \hfill & \le EI\parallel {\theta }_{xx}^n{\parallel }^2+\rho A\parallel {\delta }_t{\theta }^n{\parallel }^2+4\mu s\tau \sum _{k=1}^n{b}_{n-k}^{(\alpha )}\parallel {\delta }_t{\theta }^k{\parallel }^2+4\mu s\tau \sum _{k=1}^n{b}_{n-k}^{(\alpha )}{\parallel {\delta }_t{\eta }^k\parallel }^2\hfill \\ \hfill & +\frac{8\tau {\rho }^2{A}^2}{\mu s{b}_0^{(\alpha )}}\parallel \frac{u^{n+1}-2u^n+u^{n-1}}{{\tau }^2}-u_{tt}^{n+1}{\parallel }^2+\frac{8\tau {\rho }^2{A}^2}{\mu s{b}_0^{(\alpha )}}\parallel \frac{{\eta }^{n+1}-2{\eta }^n+{\eta }^{n-1}}{{\tau }^2}{\parallel }^2+4\mu s\tau b_n^{(\alpha )}{\parallel {\theta }_t^0\parallel }^2\hfill \\ \hfill & +4\mu s\tau b_n^{(\alpha )}\parallel {\eta }_t^0{\parallel }^2+4\mu s\tau b_0^{(\alpha )}\parallel {\delta }_t{\eta }^{n+1}{\parallel }^2+\frac{4\tau \mu }{s{b}_0^{(\alpha )}}{\parallel R(u^{n+1})\parallel }^2.\hfill \end{array}$$

(38)

Denote

$$\begin{array}{c}\hfill G^n=EI\parallel {\theta }_{xx}^{n+1}{\parallel }^2+\rho A\parallel {\delta }_t{\theta }^{n+1}{\parallel }^2+4\mu s\tau \sum _{k=1}^n{b}_{n-k+1}^{(\alpha )}\parallel {\delta }_t{\theta }^k{\parallel }^2+4\mu s\tau \sum _{k=1}^n{b}_{n-k+1}^{(\alpha )}{\parallel {\delta }_t{\eta }^k\parallel }^2.\end{array}$$

(39)

(38) can be written as follows,

$$\begin{array}{cc}\hfill G^n& =G^{n-1}+\frac{8\tau {\rho }^2{A}^2}{\mu s{b}_0^{(\alpha )}}\parallel \frac{u^{n+1}-2u^n+u^{n-1}}{{\tau }^2}-u_{tt}^{n+1}{\parallel }^2+\frac{8\tau {\rho }^2{A}^2}{\mu s{b}_0^{(\alpha )}}\parallel \frac{{\eta }^{n+1}-2{\eta }^n+{\eta }^{n-1}}{{\tau }^2}{\parallel }^2\hfill \\ \hfill & +4\mu s\tau b_n^{(\alpha )}\parallel {\delta }_t{\theta }^0{\parallel }^2+4\mu s\tau b_n^{(\alpha )}\parallel {\delta }_t{\eta }^0{\parallel }^2+4\mu s\tau b_0^{(\alpha )}\parallel {\delta }_t{\eta }^{n+1}{\parallel }^2+\frac{4\tau \mu }{s{b}_0^{\alpha }}{\parallel R(u^{n+1})\parallel }^2\hfill \\ \hfill & =G^0+\frac{8\tau {\rho }^2{A}^2}{\mu s{b}_0^{(\alpha )}}\sum _{k=1}^n\parallel \frac{u^{k+1}-2u^k+u^{k-1}}{{\tau }^2}-u_{tt}^{k+1}{\parallel }^2+\frac{8\tau {\rho }^2{A}^2}{\mu s{b}_0^{(\alpha )}}\sum _{k=1}^n\parallel \frac{{\eta }^{k+1}-2{\eta }^k+{\eta }^{k-1}}{{\tau }^2}{\parallel }^2\hfill \\ \hfill & +4\mu s\tau \sum _{k=1}^n{b}_k^{(\alpha )}\parallel {\theta }_t^0{\parallel }^2+4\mu s\tau \sum _{k=1}^n{b}_k^{(\alpha )}\parallel {\eta }_t^0{\parallel }^2+4\mu s\tau b_0^{(\alpha )}\sum _{k=1}^n\parallel {\delta }_t{\eta }^{k+1}{\parallel }^2+\frac{4\tau \mu }{s{b}_0^{(\alpha )}}\sum _{k=1}^n{\parallel R(u^{n+1})\parallel }^2.\hfill \end{array}$$

(40)

Next, we estimate the the right hand side of (40) one by one,

$$\begin{array}{cc}\hfill \frac{4\tau \mu }{s{b}_0^{(\alpha )}}\sum _{k=1}^n{\parallel R(u^{n+1})\parallel }^2& \le \frac{4\tau \mu }{\frac{{\tau }^{1-\alpha }}{\Gamma (2-\alpha )}{b}_0^{(\alpha )}}{\frac{1}{2\Gamma (2-\alpha )}}^2{(\frac{1}{4}+\frac{\alpha -1}{(2-\alpha )(3-\alpha )})}^2\sum _{k=1}^n\parallel max|u_{ttt}{|{\tau }^{3-\alpha }\parallel }^2\hfill \\ \hfill & =\frac{\mu T^{\alpha }{n}^{1-\alpha }(2-\alpha )}{\Gamma (2-\alpha )}{(\frac{1}{4}+\frac{\alpha -1}{(2-\alpha )(3-\alpha )})}^{2}max{\parallel u_{ttt}\parallel }^2{\tau }^{6-2\alpha }.\hfill \end{array}$$

(41)

By Taylor’s theorem, we deduce

$$\begin{array}{cc}\hfill & \sum _{k=1}^n|\frac{u^{k+1}-2u^k+u^{n-1}}{{\tau }^2}-u_{tt}^{k+1}{|}^2\le \frac{34\tau }{5}{\int }_0^T{|\frac{{\partial }^{3}u}{\partial x^3}|}^{2}ds,\hfill \end{array}$$

(42)

$$\begin{array}{cc}\hfill & \sum _{k=1}^n|\frac{{\eta }^{k+1}-2{\eta }^k+{\eta }^{k-1}}{{\tau }^2}{|}^2\le \frac{C}{{\tau }^2}{\int }_0^T{|{\eta }_t|}^{2}ds.\hfill \end{array}$$

(43)

Then,

$$\begin{array}{cc}\hfill \frac{8\tau {\rho }^2{A}^2}{\mu s{b}_0^{(\alpha )}}\sum _{k=1}^n{\parallel \frac{u^{k+1}-2u^k+u^{k-1}}{{\tau }^2}-u_{tt}^{k+1}\parallel }^2& \le \frac{8\tau {\rho }^2{A}^2}{\mu s{b}_0^{(\alpha )}}\frac{34\tau }{5}{\int }_0^T{\parallel \frac{{\partial }^{3}u}{\partial x^3}\parallel }^{2}ds\hfill \\ \hfill & =\frac{272{\rho }^2{A}^2{\tau }^2}{5\mu {(n+1)}^{1-\alpha }}\Gamma (3-\alpha )t_{n+1}^{\alpha -1}{\int }_0^T{\parallel \frac{{\partial }^{3}u}{\partial x^3}\parallel }^{2}ds,\hfill \end{array}$$

(44)

and

$$\begin{array}{cc}\hfill \frac{8\tau {\rho }^2{A}^2}{\mu s{b}_0^{(\alpha )}}\sum _{k=1}^n{\parallel \frac{{\eta }^{k+1}-2{\eta }^k+{\eta }^{k-1}}{{\tau }^2}\parallel }^2& \le C{h}^8{\int }_0^T{\parallel u_t\parallel }^{2}ds.\hfill \end{array}$$

(45)

We expand $4\mu s\tau b_0^{(\alpha )}{\parallel {\delta }_t{\eta }^{k+1}\parallel }^2$ as follows,

$$\begin{array}{c}\hfill 4\mu s\tau b_0^{(\alpha )}\sum _{k=1}^n\parallel {\delta }_t{\eta }^{k+1}{\parallel }^2=4\mu s\tau b_0^{(\alpha )}\sum _{k=1}^n\parallel {\delta }_t{\eta }^k{\parallel }^2+4\mu s\tau b_0^{(\alpha )}\parallel {\delta }_t{\eta }^{n+1}{\parallel }^2-4\mu s\tau b_0^{(\alpha )}{\parallel {\delta }_t{\eta }^1\parallel }^2.\end{array}$$

(46)

Substituting (41) and (45)–(47) into (40), and dropping nonnegative term $4\mu s\tau b_0^{(\alpha )}{\parallel {\delta }_t{\eta }^1\parallel }^2$, we deduce

$$\begin{array}{cc}\hfill & EI\parallel {\theta }_{xx}^{n+1}{\parallel }^2+\rho A\parallel {\delta }_t{\theta }^{n+1}{\parallel }^2\le EI\parallel {\theta }_{xx}^1{\parallel }^2+\rho A\parallel \frac{{\theta }^1-{\theta }^0}{\tau }{\parallel }^2+C{h}^8{\int }_0^T{\parallel u_t\parallel }^{2}ds\hfill \\ \hfill & +\frac{\mu T^{\alpha }{n}^{1-\alpha }(2-\alpha )}{\Gamma (2-\alpha )}{(\frac{1}{4}+\frac{\alpha -1}{(2-\alpha )(3-\alpha )})}^{2}max\parallel u_{ttt}{\parallel }^2{\tau }^{6-2\alpha }+4\mu s\tau b_0^{(\alpha )}{\parallel {\delta }_t{\eta }^{n+1}\parallel }^2\hfill \\ \hfill & +\frac{272{\rho }^2{A}^2{\tau }^2}{5\mu {(n+1)}^{\alpha -1}}\Gamma (3-\alpha )t_{n+1}^{\alpha -1}{\int }_0^T\parallel \frac{{\partial }^{3}u}{\partial x^3}{\parallel }^{2}ds+4\mu s\tau \sum _{k=1}^n{b}_k^{(\alpha )}\parallel {\theta }_t^0{\parallel }^2+4\mu s\tau \sum _{k=1}^n{b}_k^{(\alpha )}{\parallel {\eta }_t^0\parallel }^2.\hfill \end{array}$$

(47)

Using Gronwall inequality, we obtain

$$\begin{array}{cc}\hfill & EI\parallel {\theta }_{xx}^{n+1}{\parallel }^2+\rho A{\parallel {\delta }_t{\theta }^{n+1}\parallel }^2\hfill \\ \hfill & \le C\left[max\parallel u_{ttt}{\parallel }^2{\tau }^{6-2\alpha }+{\tau }^2{\int }_0^T\parallel \frac{{\partial }^{3}u}{\partial x^3}{\parallel }^{2}ds+h^8{\int }_0^T\parallel u_t{\parallel }^{2}ds+h^8{\parallel u_t\parallel }^2\right].\hfill \end{array}$$

(48)

Applying triangle inequality, we obtain the conclusion that

$$\begin{array}{cc}\hfill \parallel u^{n+1}-u_h^{n+1}\parallel & \le \parallel {\eta }^{n+1}\parallel +\parallel {\theta }^{n+1}\parallel \hfill \\ \hfill & =\parallel {\eta }^{n+1}\parallel +\parallel {\theta }^0\parallel +{\int }_0^t\parallel {\delta }_t{\theta }^{n+1}\parallel ds\hfill \\ \hfill & \le C({\tau }^{3-\alpha }+\tau +h^4).\hfill \end{array}$$

(49)

□

5. Numerical Experiment

In this part, we present four examples: Example 1 verifies Theorem 2, Example 2 shows the effect of fractional derivative variation on beam vibration amplitude and frequency, Example 3 shows the influence of damping coefficient variation on beam vibration amplitude and Example 4 demonstrates the advantages of the fractional order model by comparing with Example 3.

5.1. Example 1

Let variables $\rho ,A,\mu ,E,I,L$ and T in problem (1) be equal to 1. The true solution of the problem is selected as $u(x,t)=x(1-x)sin(\pi x)t^3$, so we consider the following initial boundary value problem:

$$\left\{\begin{array}{c}\frac{{\partial }^{4}u}{\partial x^4}+u_{tt}{+}_0^C{D}_t^{\alpha }u=t^3((12{\pi }^{2}sin(\pi x)+4{\pi }^3(1-2x)cos(\pi x)+{\pi }^4(x-x^2)sin(\pi x)\hfill \\ +6t(x-x^2)sin(\pi x)+6\frac{t^{3-\alpha }}{\Gamma (4-\alpha )}(x-x^2)sin(\pi x).x\in (0,1),t\in (0,1],\hfill \\ u(x,0)=0,u_t(x,0)=0,x\in [0,1],\hfill \\ u(0,t)=u(1,t)=0,u_x(0,t)=u_x(1,t)=0,t\in [0,1],\hfill \end{array}\right.$$

(50)

We keep the space step at $\frac{1}{2^7}$ and change the time step to obtain the $L^{\infty }$, $L^2$ errors and their orders of time convergence. As shown in Table 1, $L^{\infty }$ and $L^2$ order of time convergence reach to the one order for different $\alpha$. In Table 2, taking $\tau =\frac{1}{2^8}$, we obtain the $L^2$, $H^1$ order of space convergence. From the results in Table 2, we find that the $L^2$ order of space convergence reaches four, and the $H^1$ order reaches three. This is consistent with Theorem 2. Figure 1 is a comparison of the function images of the numerical solution and the true solution at $t=1$.

Table 1. Errors and time convergence orders of Example 1.

$\mathit{\alpha }$	$\mathit{\tau }$	${\mathit{L}}^{\mathit{\infty }}$-Error	Order	${\mathit{L}}^2$-Error	Order
$\alpha$ = 1.3	$\frac{1}{8}$	$5.6188\times {10}^{-4}$	-	$5.1524\times {10}^{-1}$	-
	$\frac{1}{16}$	$2.9963\times {10}^{-4}$	0.9070	$2.7477\times {10}^{-1}$	0.9070
	$\frac{1}{32}$	$1.5464\times {10}^{-4}$	0.9543	$1.4182\times {10}^{-1}$	0.9542
	$\frac{1}{64}$	$7.8543\times {10}^{-5}$	0.9774	$7.2033\times {10}^{-2}$	0.9773
$\alpha$ = 1.5	$\frac{1}{8}$	$5.6188\times {10}^{-4}$	-	$5.1524\times {10}^{-1}$	-
	$\frac{1}{16}$	$2.9963\times {10}^{-4}$	0.9070	$2.7477\times {10}^{-1}$	0.9070
	$\frac{1}{32}$	$1.5464\times {10}^{-4}$	0.9543	$1.4182\times {10}^{-1}$	0.9542
	$\frac{1}{64}$	$7.8543\times {10}^{-5}$	0.9774	$7.2032\times {10}^{-2}$	0.9773
$\alpha$ = 1.7	$\frac{1}{8}$	$5.6188\times {10}^{-4}$	-	$5.1524\times {10}^{-1}$	-
	$\frac{1}{16}$	$2.9963\times {10}^{-4}$	0.9070	$2.7477\times {10}^{-1}$	0.9070
	$\frac{1}{32}$	$1.5464\times {10}^{-4}$	0.9543	$1.4181\times {10}^{-1}$	0.9542
	$\frac{1}{64}$	$7.8543\times {10}^{-5}$	0.9774	$7.2031\times {10}^{-2}$	0.9773

Table 2. Errors and spatial convergence orders of Example 1.

$\mathit{\alpha }$	$\mathit{\tau }$	${\mathit{L}}^2$-Error	Order	${\mathit{H}}^1$-Error	Order
$\alpha$ = 1.3	$\frac{1}{4}$	$5.5689\times {10}^{-4}$	-	$1.6552\times {10}^{-2}$	-
	$\frac{1}{8}$	$3.6982\times {10}^{-5}$	3.9125	$2.1556\times {10}^{-3}$	2.9408
	$\frac{1}{12}$	$7.3948\times {10}^{-6}$	3.9699	$6.4312\times {10}^{-4}$	2.9829
	$\frac{1}{16}$	$2.3623\times {10}^{-6}$	3.9666	$2.7199\times {10}^{-4}$	2.9914
$\alpha$ = 1.5	$\frac{1}{4}$	$5.5700\times {10}^{-4}$	-	$1.6553\times {10}^{-2}$	-
	$\frac{1}{8}$	$3.7071\times {10}^{-5}$	3.9093	$2.1563\times {10}^{-3}$	2.9405
	$\frac{1}{12}$	$7.4841\times {10}^{-6}$	3.9462	$6.4361\times {10}^{-4}$	2.9819
	$\frac{1}{16}$	$2.4532\times {10}^{-6}$	3.8772	$2.7241\times {10}^{-4}$	2.9887
$\alpha$ = 1.7	$\frac{1}{4}$	$5.5732\times {10}^{-4}$	-	$1.6558\times {10}^{-2}$	-
	$\frac{1}{8}$	$3.7413\times {10}^{-5}$	3.8969	$2.1590\times {10}^{-3}$	2.9391
	$\frac{1}{12}$	$7.8352\times {10}^{-6}$	3.8558	$6.4386\times {10}^{-4}$	2.9764
	$\frac{1}{16}$	$2.8254\times {10}^{-6}$	3.5455	$2.7287\times {10}^{-4}$	2.9695

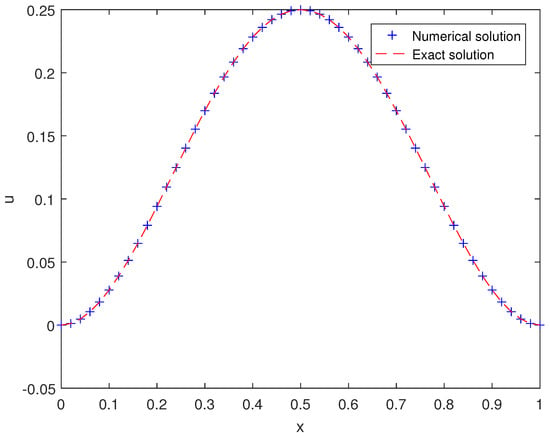
Figure 1. The function images of the numerical solution and the true solution at t = 1 when $\alpha$ = $1.3$.

5.2. Example 2

In this example, we assume the variables $EI=10$, $\rho A=6$, $\mu =1$, $L=1$ and $T=1$. The fractional derivatives are 1.4, 1.5, 1.6, 1.7, 1.8. The initial value $u(x,0)=sin(\pi x)$, and the right end term $f(x,t)=0$.

We take the midpoint of the beam and plot the image. When the fractional derivative $\alpha$ is taken as 1.4, 1.5, 1.6, 1.7, 1.8, the displacement u changes with time t as shown in Figure 2. From the image, we can see that the amplitude of the beam is increasing with the increasing fractional derivative, and the peak value gradually shifts to the right. This indicates that, as the derivative order increases, the vibration frequency of the beam decreases and the vibration attenuation rate slows down.

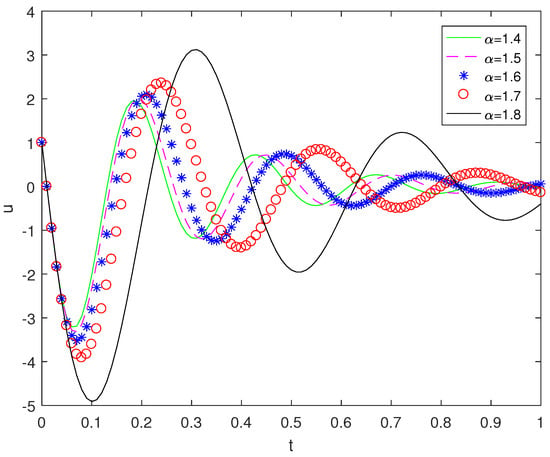
Figure 2. The comparison image of beam vibration amplitude when $\alpha$ takes $1.4$, $1.5$, $1.6$, $1.7$, $1.8$.

5.3. Example 3

We take variables $EI=10$, $\rho A=6$, $L=1$ and $T=1$. The fractional derivatives $\alpha =1.3$. The damping coefficients $\mu$ are 1, 5, 10. The initial value $u(x,0)=sin(\pi x)$, and the right end term $f(x,t)=0$.

We take the midpoint of the beam and plot the image. When the damping coefficient $\mu$ taken as 1, 5, 10, the displacement u changes with time t as shown in Figure 3. From the image, it can be seen that the amplitude of the beam decreases as the damping coefficient increases, and the peak amplitude gradually shifts to the right. It is further shown that the attenuation rate of beam vibration decreases with the increase in damping.

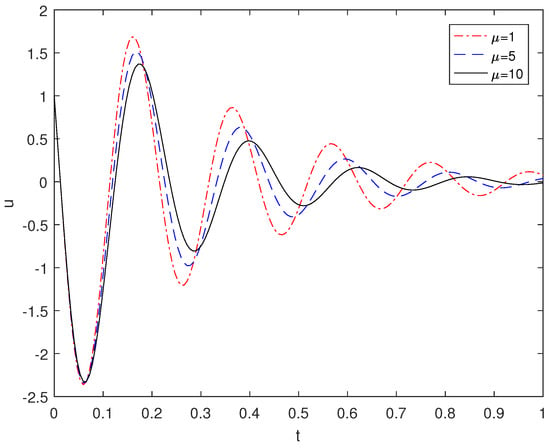
Figure 3. The comparison image of beam vibration amplitude when $\mu$ takes 1, 5, 10.

5.4. Example 4

For the traditional damped beam model, we choose the same true solution, initial value and right end term as in Example 3. Take the midpoint of the beam to draw a graph and we obtain the following image of the displacement u changes with time t when the damping coefficient is 1, 5, 10. As can be seen from Figure 4, the amplitude of the beam decreases as the damping coefficient increases.

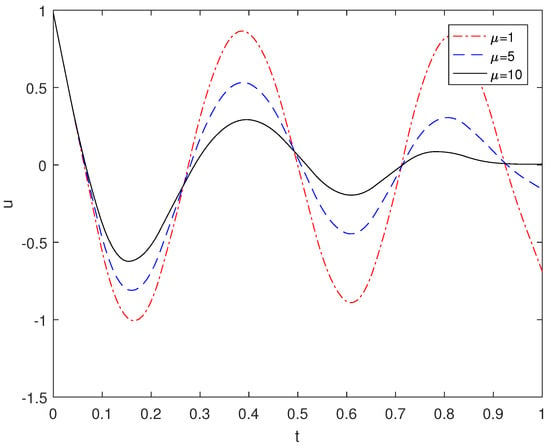
Figure 4. The comparison image of beam vibration amplitude when $\mu$ takes 1, 5, 10.

Combining examples 2, 3, 4, we conclude that the vibration law of the beam in the fractional order damping model is basically the same as the wave characteristics of the classical damping beam, but the order of the fractional derivative has a significant impact on the vibration frequency of the beam. Specifically, the larger the order, the smaller the vibration frequency, and the vibration attenuation rate of the beam gradually decreases. It is shown that the traditional viscoelastic model cannot effectively reflect the long-term effects of damping beam deformation, and the fractional derivative can describe the dynamic characteristics of the structure more flexibly and precisely.

6. Conclusions

In this paper, the Hermite finite element method for solving the vibration problem of a beam with a time fractional damping term is presented. The space is approximated by the finite element method, and the time fractional derivative is approximated by L1 interpolation approximation. The stability and convergence of the fully discrete scheme are analyzed by introducing elliptic projection. The validity of the scheme is verified by numerical examples. It is found that the amplitude of the beam increases and the frequency and the vibration attenuation rate decrease with the increasing fractional derivative, and the amplitude of the beam and the vibration attenuation rate decrease as the damping coefficient increases. The fractional order model describes the vibration attenuation characteristics in the beam more precisely, which has important theoretical and engineering significance.