Conservative Continuous-Stage Stochastic Runge–Kutta Methods for Stochastic Differential Equations
Abstract
1. Introduction
2. CSSRK Methods and Order Conditions
- (I)
- The graph with only one vertex of color k belongs to .
- (II)
- If , then , where denotes the tree formed by joining the subtrees , each by a single branch to a common root of color k.
- (I)
- .
- (II)
- .
- (III)
- If , then
3. Conservative CSSRK Methods
4. Construction of Conservative CSSRK Methods
4.1. Construction of Conservative CSSRK Methods of Order 1
4.2. Construction of Conservative CSSRK Methods of High Order for Single Integrand Conservative SDEs
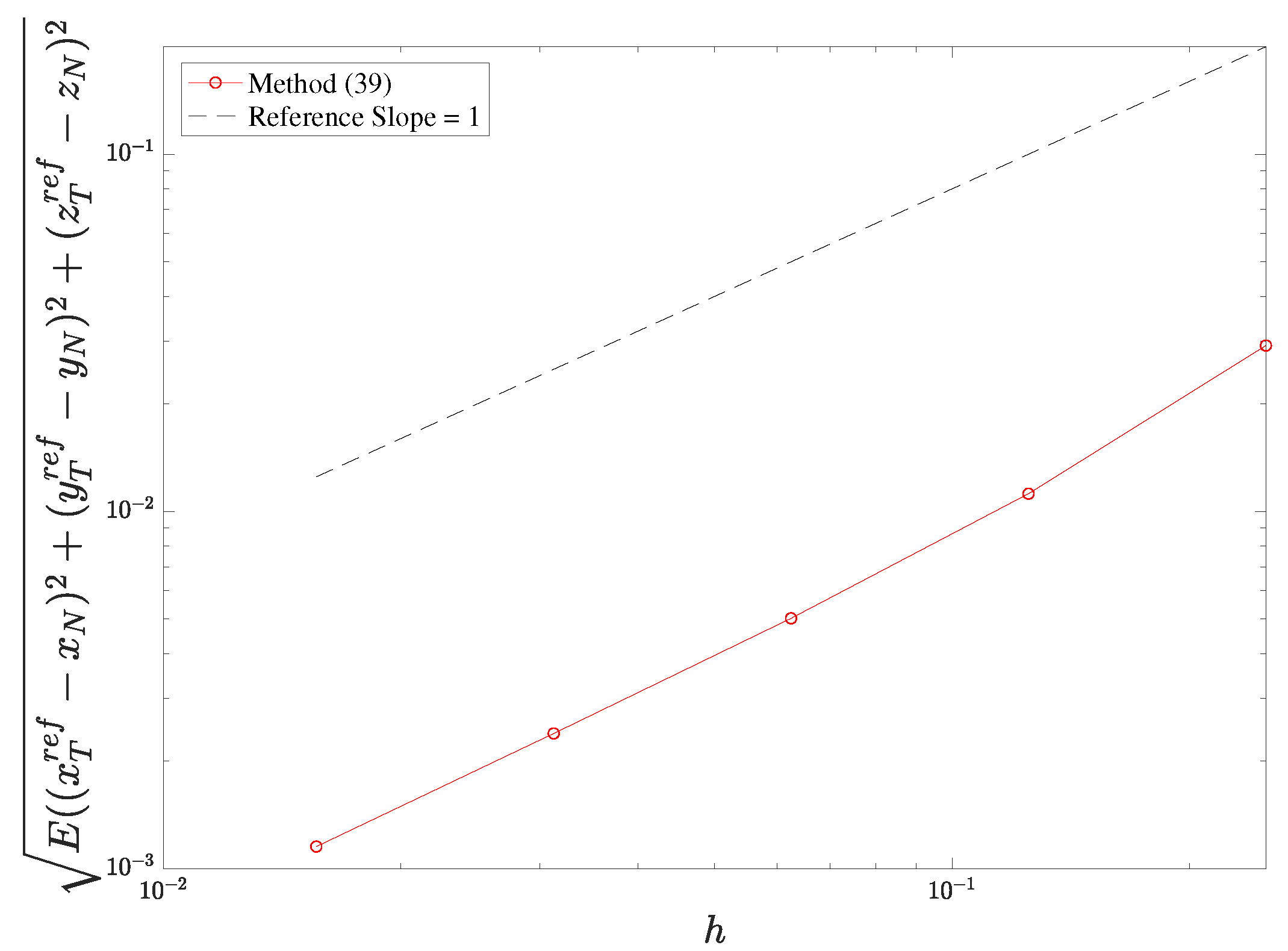
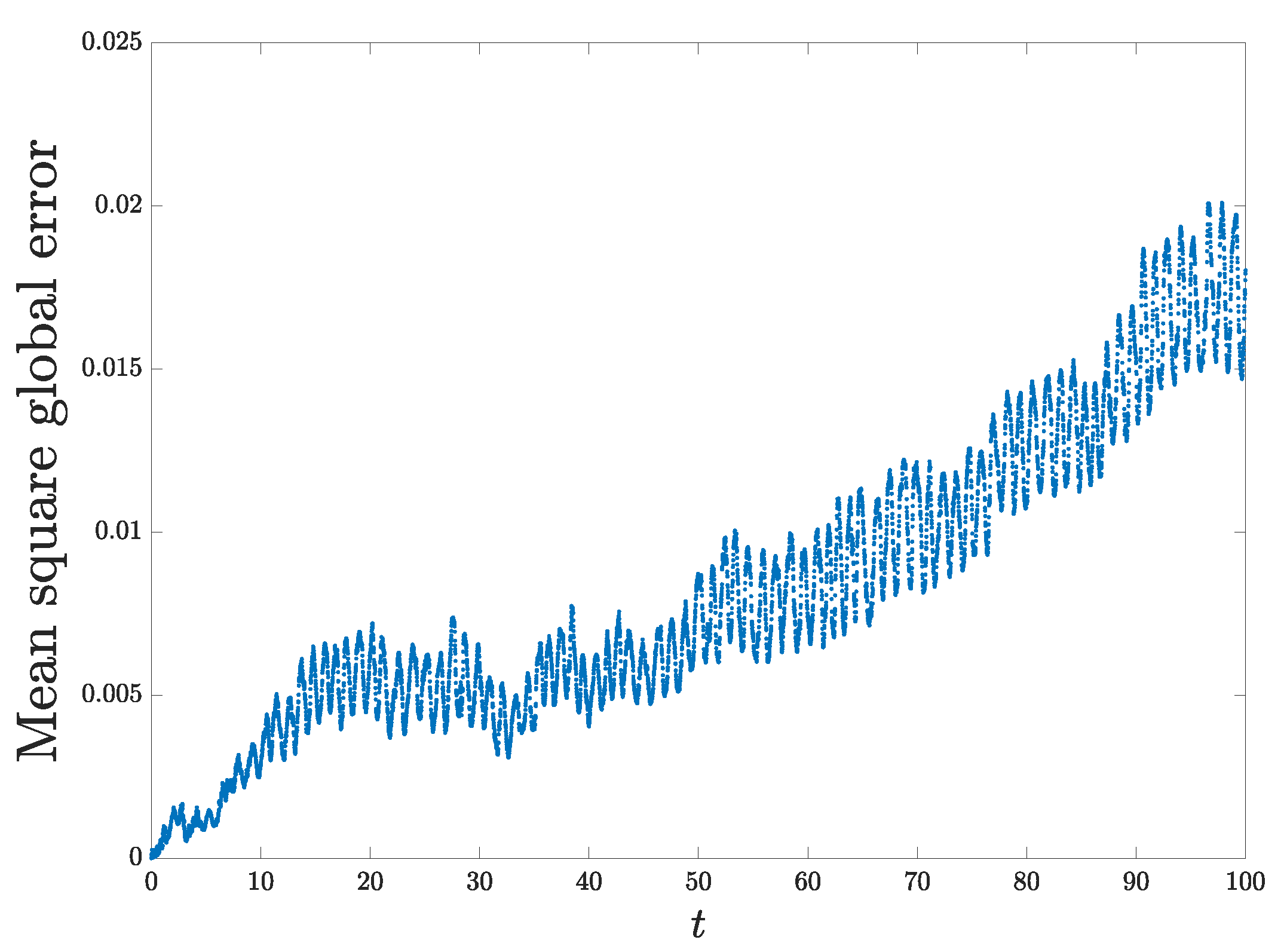
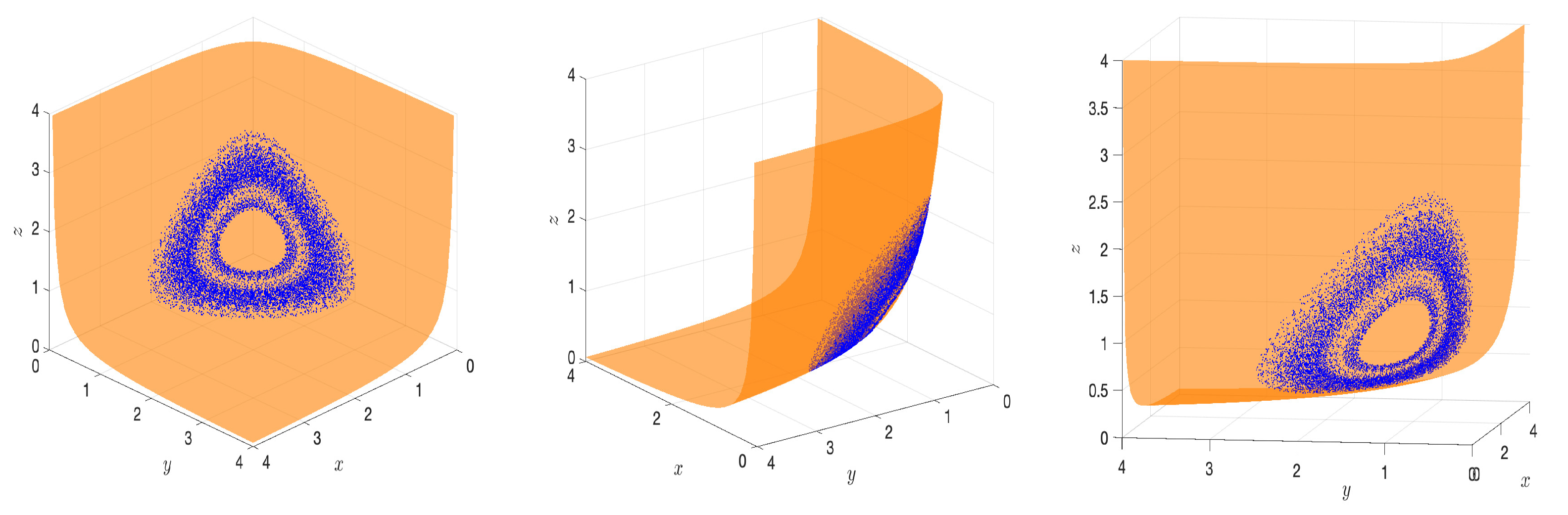
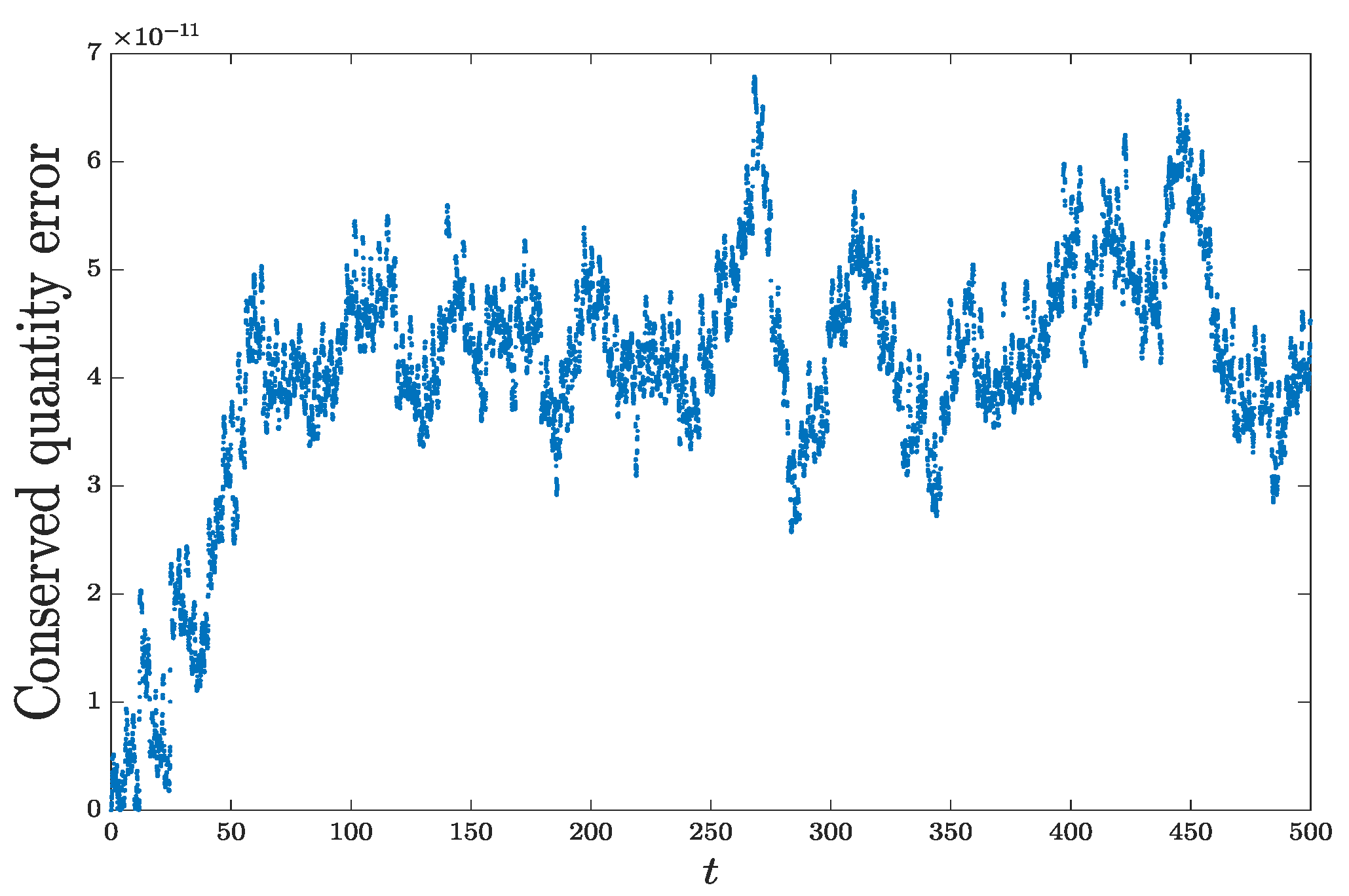
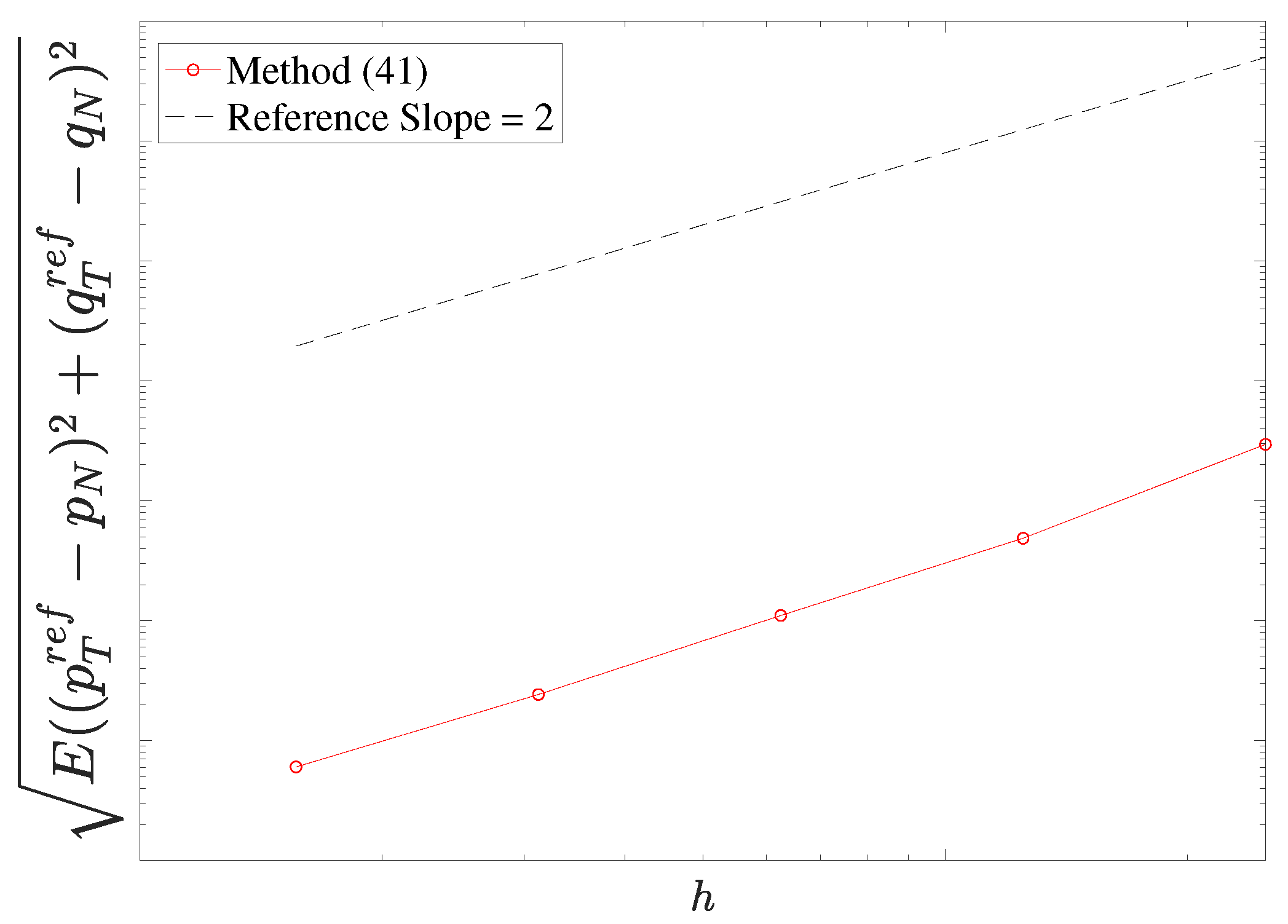
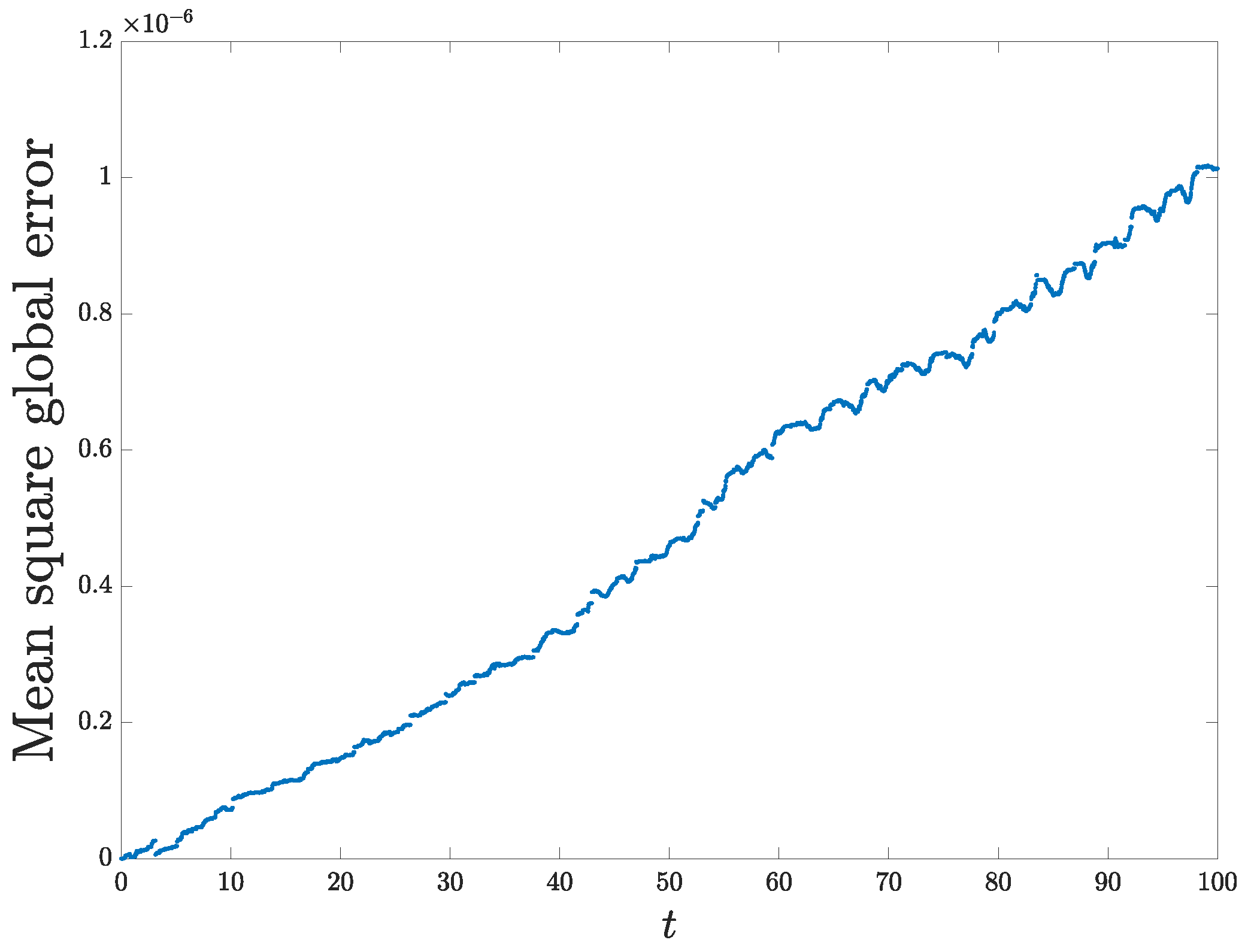
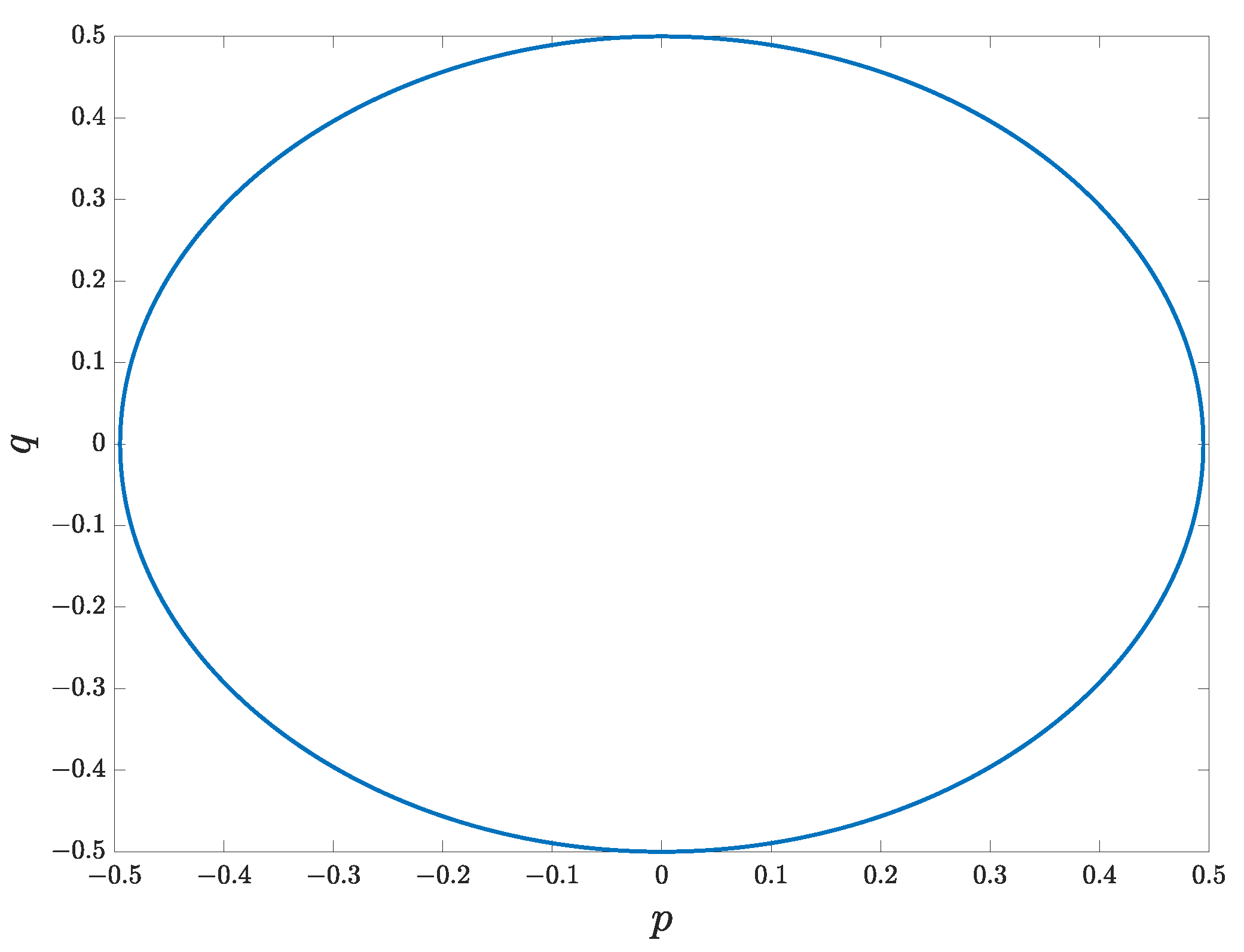
5. Numerical Experiments
6. Conclusions and Remarks
- (i)
- In our construction of conservative CSSRK methods of mean square convergence order 1, we find the known stochastic averaged vector field method is a special case of the derived conservative CSSRK methods. It seems that CSSRK methods may have promising applications in constructing structure-preserving numerical methods.
- (ii)
- It should be pointed out that we restrict ourselves to the case that the degree of is one less than that of in and when proving the conservative conditions for CSSRK methods. A further investigation for other cases is of interest in our future work.
- (iii)
- In this paper, we have only considered conservative SDEs with a single conserved quantity. On the other hand, some SDEs possess multiple conserved quantities. Hence, based on the results in this paper, we would proceed to study CSSRK methods for SDEs, leaving multiple conserved quantities numerically invariant.
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Mao, X. Stochastic Differential Equations and Their Applications; Horwood: New York, NY, USA, 1997. [Google Scholar]
- Milstein, G.N. Numerical Integration of Stochastic Differential Equations; Kluwer Academic Publishers: Dordrecht, The Netherlands, 1995. [Google Scholar]
- Brugnano, L.; Calvo, M.; Montijano, J.I.; Rández, L. Energy-preserving methods for Poisson systems. J. Comput. Appl. Math. 2012, 236, 3890–3904. [Google Scholar] [CrossRef]
- Celledoni, E.; McLachlan, R.I.; McLaren, D.I.; Owren, B.; Quispel, G.R.W.; Wright, W.M. Energy preserving Runge-Kutta methods. ESAIM Math. Model. Numer. Anal. 2008, 43, 645–649. [Google Scholar] [CrossRef]
- Cohen, D.; Hairer, E. Linear energy-preserving integrators for Poisson systems. BIT Numer. Math. 2011, 51, 91–101. [Google Scholar] [CrossRef]
- Hairer, E. Energy-preserving variant of collocation methods. J. Numer. Anal. Indust. Appl. Math. 2010, 5, 73–84. [Google Scholar]
- McLachlan, R.I.; Quispel, G.R.W.; Robidoux, N. Geometric integration using discrete gradients. Phil. Trans. R. Soc. A 1999, 357, 1021–1045. [Google Scholar] [CrossRef]
- Miyatake, Y. An energy-preserving exponentially-fitted continuous stage Runge-Kutta method for Hamiltonian systems. BIT Numer. Math. 2014, 54, 777–799. [Google Scholar] [CrossRef]
- Miyatake, Y.; Butcher, J.C. A characterization of energy-preserving methods and the construction of parallel integrators for Hamiltonian systems. SIAM J. Numer. Anal. 2016, 54, 1993–2013. [Google Scholar] [CrossRef]
- Quispel, G.R.W.; McLaren, D.I. A new class of energy-preserving numerical integration methods. J. Phys. A Math. Theor. 2008, 41, 045206. [Google Scholar] [CrossRef]
- Iavernaro, F.; Pace, B. s-stage trapezoidal methods for the conservation of Hamiltonian functions of polynomial type. AIP Conf. Proc. 2007, 936, 603–606. [Google Scholar]
- Brugnano, L.; Iavernaro, F.; Trigiante, D. Hamiltonian boundary value methods: Energy preserving discrete line integral methods. J. Numer. Anal. Indust. Appl. Math. 2010, 5, 17–37. [Google Scholar]
- Amodio, P.; Brugnano, L.; Iavernaro, F. A note on the continuous-stage Runge-Kutta(-Nyström) formulation of Hamiltonian Boundary Value Methods (HBVMs). Appl. Math. Comput. 2019, 363, 124634. [Google Scholar] [CrossRef]
- Tang, Q.; Chen, C. Continuous finite element methods for Hamiltonian systems. Appl. Math. Mech. 2007, 28, 1071–1080. [Google Scholar] [CrossRef]
- Tang, W.; Sun, Y. Time finite element methods: A unified framework for numerical discretizations of ODEs. Appl. Math. Comput. 2012, 219, 2158–2179. [Google Scholar] [CrossRef]
- Tang, W.; Sun, Y. A new approach to construct Runge-Kutta type methods and geometric numerical integrators. AIP Conf. Proc. 2012, 1479, 1291–1294. [Google Scholar]
- Tang, W.; Sun, Y. Construction of Runge-Kutta type methods for solving ordinary differential equations. Appl. Math. Comput. 2014, 234, 179–191. [Google Scholar] [CrossRef]
- Wu, X.; Wang, B.; Shi, W. Efficient energy-preserving integrators for oscillatory Hamiltonian systems. J. Comput. Phys. 2013, 235, 587–605. [Google Scholar] [CrossRef]
- Mei, L.; Huang, L.; Wu, X. Energy-preserving continuous-stage exponential Runge-Kutta integrators for efficiently solving Hamiltonian systems. SIAM J. Sci. Comput. 2022, 44, A1092–A1115. [Google Scholar] [CrossRef]
- Misawa, T. Energy conservative stochastic difference scheme for stochastic Hamilton dynamical systems. Jpn. J. Ind. Appl. Math. 2000, 17, 119–128. [Google Scholar] [CrossRef]
- Hong, J.; Zhai, S.; Zhang, J. Discrete gradient approach to stochastic differential equations with a conserved quantity. SIAM J. Numer. Anal. 2011, 49, 2017–2038. [Google Scholar] [CrossRef]
- Li, X.; Zhang, C.; Ma, Q.; Ding, X. Discrete gradient methods and linear projection methods for preserving a conserved quantity of stochastic differential equations. Int. J. Comput. Math. 2018, 95, 2511–2524. [Google Scholar] [CrossRef]
- Wang, Z.; Ma, Q.; Ding, X. Numerical simulations of stochastic differential equations with multiple conserved quantities by conservative methods. East Asian J. Appl. Math. 2022, 12, 53–71. [Google Scholar] [CrossRef]
- Zhou, W.; Zhang, L.; Hong, J.; Song, S. Projection methods for stochastic differential equations with conserved quantities. BIT Numer. Math. 2016, 56, 1497–1518. [Google Scholar] [CrossRef]
- Chen, C.; Hong, J.; Jin, D. Modified averaged vector field methods preserving multiple invariants for conservative stochastic differential equations. BIT Numer. Math. 2020, 60, 1–41. [Google Scholar] [CrossRef]
- Cohen, D.; Dujardin, G. Energy-preserving integrators for stochastic Poisson systems. Commun. Math. Sci. 2014, 12, 1523–1539. [Google Scholar] [CrossRef]
- Butcher, J.C. An algebraic theory of integration methods. Math. Comp. 1972, 26, 79–106. [Google Scholar] [CrossRef]
- Butcher, J.C. Coefficients for the study of Runge-Kutta integration processes. J. Austral. Math. Soc. 1963, 3, 185–201. [Google Scholar] [CrossRef]
- Burrage, K.; Burrage, P.M. Order conditions of stochastic Runge-Kutta methods by B-series. SIAM J. Numer. Anal. 2000, 38, 1626–1646. [Google Scholar] [CrossRef]
- Debrabant, K.; Kværnø, A. B-series analysis of stochastic Runge-Kutta methods that use an iterative scheme to compute their internal stage values. SIAM J. Numer. Anal. 2008, 47, 181–203. [Google Scholar] [CrossRef]
- Komori, Y.; Mitsui, T.; Sugiura, H. Rooted tree analysis of the order conditions of ROW-type scheme for stochastic differential equations. BIT Numer. Math. 1997, 37, 43–66. [Google Scholar] [CrossRef]
- Rößler, A. Rooted tree analysis for order conditions of stochastic Runge-Kutta methods for the weak approximation of stochastic differential equations. Stoch. Anal. Appl. 2006, 24, 97–134. [Google Scholar] [CrossRef]
- Debrabant, K.; Kværnø, A. Cheap arbitrary high order methods for single integrand SDEs. BIT Numer. Math. 2017, 57, 153–168. [Google Scholar] [CrossRef]
- Cohen, D.; Debrabant, K.; Rößler, A. High order numerical integrators for single integrand Stratonovich SDEs. Appl. Numer. Math. 2020, 158, 264–270. [Google Scholar] [CrossRef]
- Xin, X.; Qin, W.; Ding, X. Continuous stage stochastic Runge-Kutta methods. Adv. Differ. Equ. 2021, 2021, 61. [Google Scholar] [CrossRef]
- Tang, W. A note on continuous-stage Runge-Kutta methods. Appl. Math. Comput. 2018, 339, 231–241. [Google Scholar] [CrossRef]
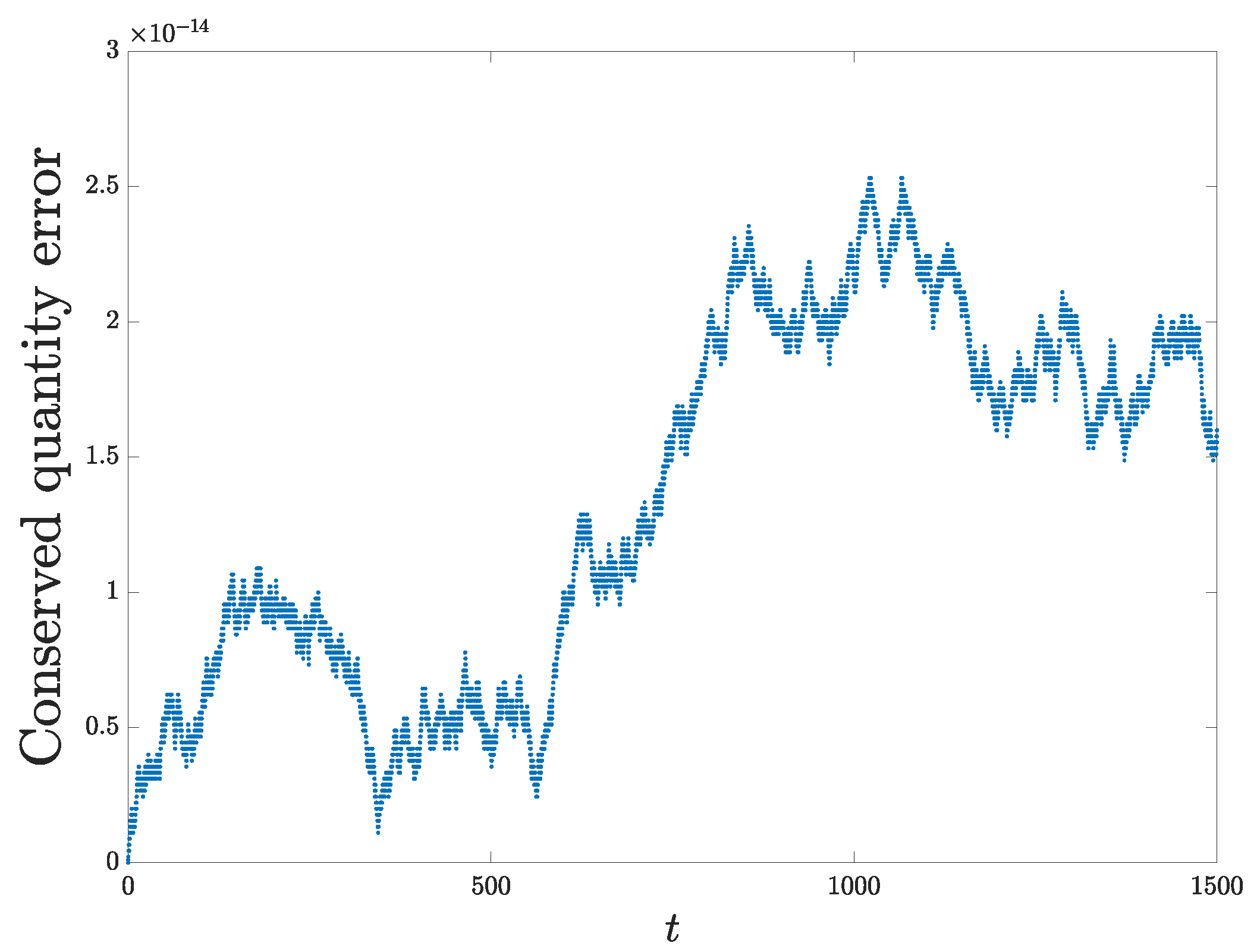
| No. | t | |||
|---|---|---|---|---|
| 1 | • 1 | 0.5 | ||
| 2 | • 0 | 1 | h | |
| 3 |  | 1 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, X.; Wang, Z.; Ma, Q.; Ding, X. Conservative Continuous-Stage Stochastic Runge–Kutta Methods for Stochastic Differential Equations. Fractal Fract. 2023, 7, 83. https://doi.org/10.3390/fractalfract7010083
Li X, Wang Z, Ma Q, Ding X. Conservative Continuous-Stage Stochastic Runge–Kutta Methods for Stochastic Differential Equations. Fractal and Fractional. 2023; 7(1):83. https://doi.org/10.3390/fractalfract7010083
Chicago/Turabian StyleLi, Xiuyan, Zhenyu Wang, Qiang Ma, and Xiaohua Ding. 2023. "Conservative Continuous-Stage Stochastic Runge–Kutta Methods for Stochastic Differential Equations" Fractal and Fractional 7, no. 1: 83. https://doi.org/10.3390/fractalfract7010083
APA StyleLi, X., Wang, Z., Ma, Q., & Ding, X. (2023). Conservative Continuous-Stage Stochastic Runge–Kutta Methods for Stochastic Differential Equations. Fractal and Fractional, 7(1), 83. https://doi.org/10.3390/fractalfract7010083











