Mathematical Modeling of COVID-19 Transmission Using a Fractional Order Derivative
Abstract
1. Introduction
2. Preliminaries
3. Classical Integer Order Model Formulation
4. Model Derivation in the Caputo Operator
5. Analysis of the Model
5.1. Existence Results
5.2. Ulam–Hyers Stability
- (I)
- .
- (II)
5.3. Numerical Algorithm
6. Simulation and Discussion
7. Conclusions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Poutanen, S.M.; Low, D.E.; Henry, B.; Finkelstein, S.; Rose, D.; Green, K.; Tellier, R.; Draker, R.; Adachi, D.; Ayers, M.; et al. Identification of severe acute respiratory syndrome in Canada. N. Engl. J. Med. 2003, 348, 1995–2005. [Google Scholar] [CrossRef] [PubMed]
- De Groot, R.J.; Baker, S.C.; Baric, R.S.; Brown, C.S.; Drosten, C.; Enjuanes, L.; Fouchier, R.A.M.; Galiano, M.; Gorbalenya, A.E.; Memish, Z.A.; et al. Commentary: Middle east respiratory syndrome coronavirus (mers-cov): Announcement of the coronavirus study group. J. Virol. 2013, 87, 7790–7792. [Google Scholar] [CrossRef] [PubMed]
- Read, J.M.; Bridgen, J.R.; Cummings, D.A.; Ho, A.; Jewell, C.P. Novel coronavirus 2019-nCoV: Early estimation of epidemiological parameters and epidemic predictions. medRxiv 2020. [Google Scholar] [CrossRef]
- Shen, M.; Peng, Z.; Xiao, Y.; Zhang, L. Modeling the epidemic trend of the 2019 novel coronavirus outbreak in China. Innovation 2020, 1, 100048. [Google Scholar] [CrossRef]
- Yu, Z.; Zhang, G.; Liu, Q.; Lv, Q. The outbreak assessment and prediction of 2019-nCoV based on time-varying SIR model. J. Univ. Electron. Sci. Technol. China 2020, 49, 357–361. [Google Scholar]
- Asamoah, J.K.K.; Owusu, M.A.; Jin, Z.; Oduro, F.T.; Abidemi, A.; Gyasi, E.O. Global stability and cost-effectiveness analysis of COVID-19 considering the impact of the environment: Using data from Ghana. Chaos Solitons Fractals 2020, 140, 110103. [Google Scholar] [CrossRef]
- Qian, M.; Jiang, J. COVID-19 and social distancing. J. Public Health 2022, 30, 259–261. [Google Scholar] [CrossRef]
- Mwalili, S.; Kimathi, M.; Ojiambo, V.; Gathungu, D.; Mbogo, R. SEIR model for COVID-19 dynamics incorporating the environment and social distancing. BMC Res. Notes 2020, 13, 352. [Google Scholar] [CrossRef]
- Elgazzar, A.S. Simple mathematical models for controlling COVID-19 transmission through social distancing and community awareness. Z. Naturforschung C 2021, 76, 393–400. [Google Scholar] [CrossRef]
- Gao, W.; Veeresha, P.; Prakasha, D.G.; Baskonus, H.M. Novel dynamic structures of 2019-nCoV with nonlocal operator via powerful computational technique. Biology 2020, 9, 107. [Google Scholar] [CrossRef]
- Mandal, M.; Jana, S.; Nandi, S.K.; Khatua, A.; Adak, S.; Kar, T.K. A model based study on the dynamics of COVID-19: Prediction and control. Chaos Solitons Fractals 2020, 136, 109889. [Google Scholar] [CrossRef] [PubMed]
- Khan, M.A.; Atangana, A.; Alzahrani, E. The dynamics of COVID-19 with quarantined and isolation. Adv. Differ. Equ. 2020, 2020, 425. [Google Scholar] [CrossRef] [PubMed]
- Ndaïrou, F.; Area, I.; Nieto, J.J.; Torres, D.F.M. Mathematical modeling of COVID-19 transmission dynamics with a case study of Wuhan. Chaos Solitons Fractals 2020, 135, 109846. [Google Scholar] [CrossRef] [PubMed]
- Li, R.; Pei, S.; Chen, B.; Song, Y.; Zhang, T.; Yang, W.; Shaman, J. Substantial undocumented infection facilitates the rapid dissemination of novel coronavirus (SARS-CoV-2). Science 2020, 368, 489–493. [Google Scholar] [CrossRef]
- Cai, J.; Sun, W.; Huang, J.; Gamber, M.; Wu, J.; He, G. Indirect virus transmission in cluster of COVID-19 cases, Wenzhou, China, 2020. Emerg. Infect. Dis. 2020, 26, 1343. [Google Scholar] [CrossRef]
- Kang, X.; Hu, Y.; Liu, Z.; Sarwar, S. Forecast and evaluation of asymptomatic COVID-19 patients spreading in China. Results Phys. 2022, 34, 105195. [Google Scholar] [CrossRef]
- Xu, C.; Saifullah, S.; Ali, A. Theoretical and numerical aspects of Rubella disease model involving fractal fractional exponential decay kernel. Results Phys. 2022, 34, 105287. [Google Scholar] [CrossRef]
- Haidong, Q.; ur Rahman, M.; Arfan, M. Fractional model of smoking with relapse and harmonic mean type incidence rate under Caputo operator. J. Appl. Math. Comput. 2022, 1–18. [Google Scholar] [CrossRef]
- Atangana, A.; Baleanu, D. New fractional derivatives with nonlocal and non-singular kernel: Theory and application to heat transfer model. arXiv 2016, arXiv:1602.03408. [Google Scholar] [CrossRef]
- Podlubny, I. An introduction to fractional derivatives, fractional differential equations, to methods of their solution and some of their applications. Math. Sci. Eng. 1999, 198, 340. [Google Scholar]
- Zhang, L.; ur Rahman, M.; Arfan, M.; Ali, A. Investigation of mathematical model of transmission co-infection TB in HIV community with a non-singular kernel. Results Phys. 2021, 28, 104559. [Google Scholar] [CrossRef]
- Shen, W.-Y.; Chu, Y.-M.; ur Rahman, M.; Mahariq, I.; Zeb, A. Mathematical analysis of HBV and HCV co-infection model under nonsingular fractional order derivative. Results Phys. 2021, 28, 104582. [Google Scholar] [CrossRef]
- Xu, C.; ur Rahman, M.; Baleanu, D. On fractional-order symmetric oscillator with offset-boosting control. Nonlinear Anal. Model. Control 2022, 27, 994–1008. [Google Scholar] [CrossRef]
- Saifullah, S.; Ali, A.; Khan, Z.A. Analysis of nonlinear time-fractional Klein-Gordon equation with power law kernel. AIMS Math. 2022, 7, 5275–5290. [Google Scholar] [CrossRef]
- Khan, Z.A.; Khan, J.; Saifullah, S.; Ali, A. Dynamics of Hidden Attractors in Four-Dimensional Dynamical Systems with Power Law. J. Funct. Spaces 2022, 2022, 3675076. [Google Scholar] [CrossRef]
- Alqahtani, R.T.; Ahmad, S.; Akgül, A. Dynamical analysis of bio-ethanol production model under generalized nonlocal operator in Caputo sense. Mathematics 2021, 9, 2370. [Google Scholar] [CrossRef]
- Jain, S. Numerical analysis for the fractional diffusion and fractional Buckmaster equation by the two-step Laplace Adam-Bashforth method. Eur. Phys. J. Plus 2018, 133, 19. [Google Scholar] [CrossRef]
- Atangana, A.; Jain, S. A new numerical approximation of the fractal ordinary differential equation. Eur. Phys. J. Plus 2018, 133, 37. [Google Scholar] [CrossRef]
- Saifullah, S.; Ali, A.; Irfan, M.; Shah, K. Time-fractional Klein–Gordon equation with solitary/shock waves solutions. Math. Probl. Eng. 2021, 2021, 6858592. [Google Scholar] [CrossRef]
- Araz, S.İ. Analysis of a COVID-19 model: Optimal control, stability and simulations. Alex. Eng. J. 2021, 60, 647–658. [Google Scholar] [CrossRef]
- Awais, M.; Alshammari, F.S.; Ullah, S.; Khan, M.A.; Islam, S. Modeling and simulation of the novel coronavirus in Caputo derivative. Results Phys. 2020, 19, 103588. [Google Scholar] [CrossRef] [PubMed]
- Ullah, S.; Khan, M.A. Modeling the impact of non-pharmaceutical interventions on the dynamics of novel coronavirus with optimal control analysis with a case study. Chaos Solitons Fractals 2020, 139, 110075. [Google Scholar] [CrossRef] [PubMed]
- Li, B.; Liang, H.; He, Q. Multiple and generic bifurcation analysis of a discrete Hindmarsh-Rose model. Chaos Solitons Fractals 2021, 146, 110856. [Google Scholar] [CrossRef]
- Li, B.; Liang, H.; Shi, L.; He, Q. Complex dynamics of Kopel model with nonsymmetric response between oligopolists. Chaos Solitons Fractals 2022, 156, 111860. [Google Scholar] [CrossRef]
- Eskandari, Z.; Avazzadeh, Z.; Ghaziani, R.K.; Li, B. Dynamics and bifurcations of a discrete-time Lotka–Volterra model using nonstandard finite difference discretization method. Math. Methods Appl. Sci. 2022. [Google Scholar] [CrossRef]
- Baleanu, D.; Abadi, M.H.; Jajarmi, A.; Vahid, K.Z.; Nieto, J.J. A new comparative study on the general fractional model of COVID-19 with isolation and quarantine effects. Alex. Eng. J. 2022, 61, 4779–4791. [Google Scholar] [CrossRef]
- Zhang, L.; Addai, E.; Ackora-Prah, J.; Arthur, Y.D.; Asamoah, J.K.K. Fractional-Order Ebola-Malaria Coinfection Model with a Focus on Detection and Treatment Rate. Comput. Math. Methods Med. 2022, 2022, 6502598. [Google Scholar] [CrossRef]
- Gómez-Aguilar, J.F.; Rosales-García, J.J.; Bernal-Alvarado, J.J.; Córdova-Fraga, T.; Guzmán-Cabrera, R. Fractional mechanical oscillators. Rev. Mex. Física 2012, 58, 348–352. [Google Scholar]
- Afshari, H.; Hosseinpour, H.; Marasi, H.R. Application of some new contractions for existence and uniqueness of differential equations involving Caputo–Fabrizio derivative. Adv. Differ. Equ. 2021, 2021, 321. [Google Scholar] [CrossRef]
- Ulam, S.M. A Collection of Mathematical Problems; Interscience Publishers: New York, NY, USA, 1960; p. 29. [Google Scholar]
- Ulam, S.M. Problem in Modren Mathematics; Courier Corporation: Mineola, NY, USA, 2004. [Google Scholar]

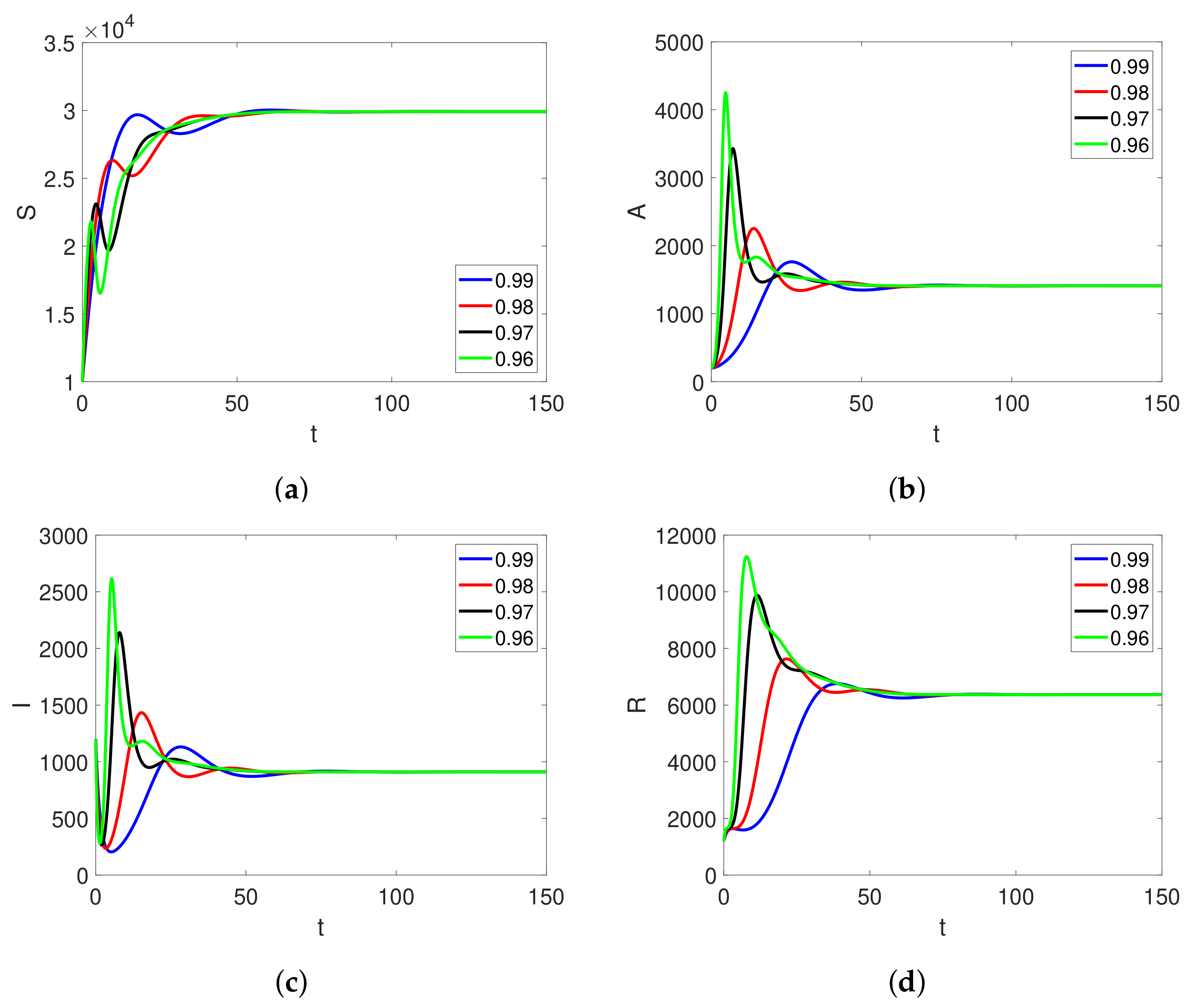
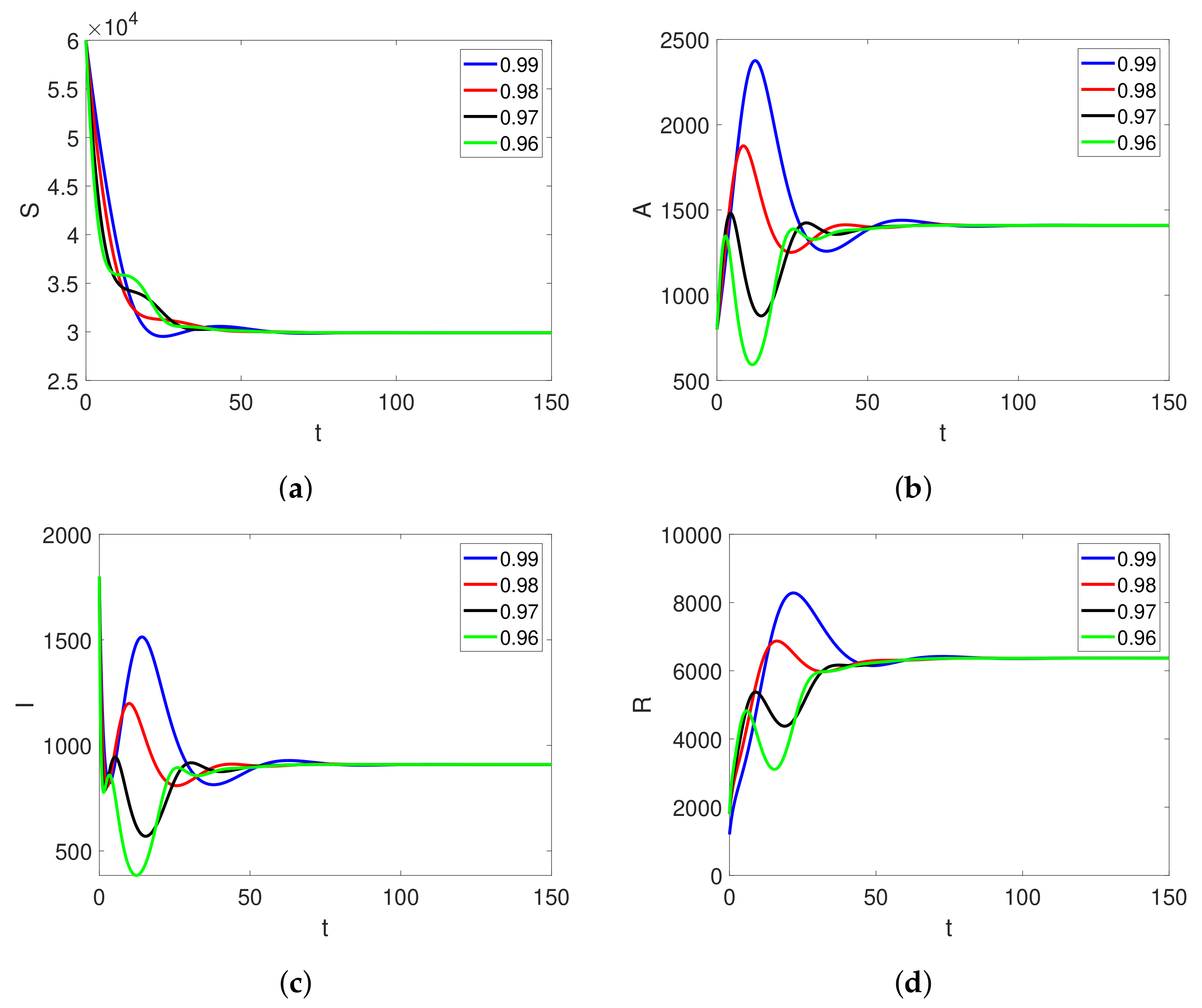
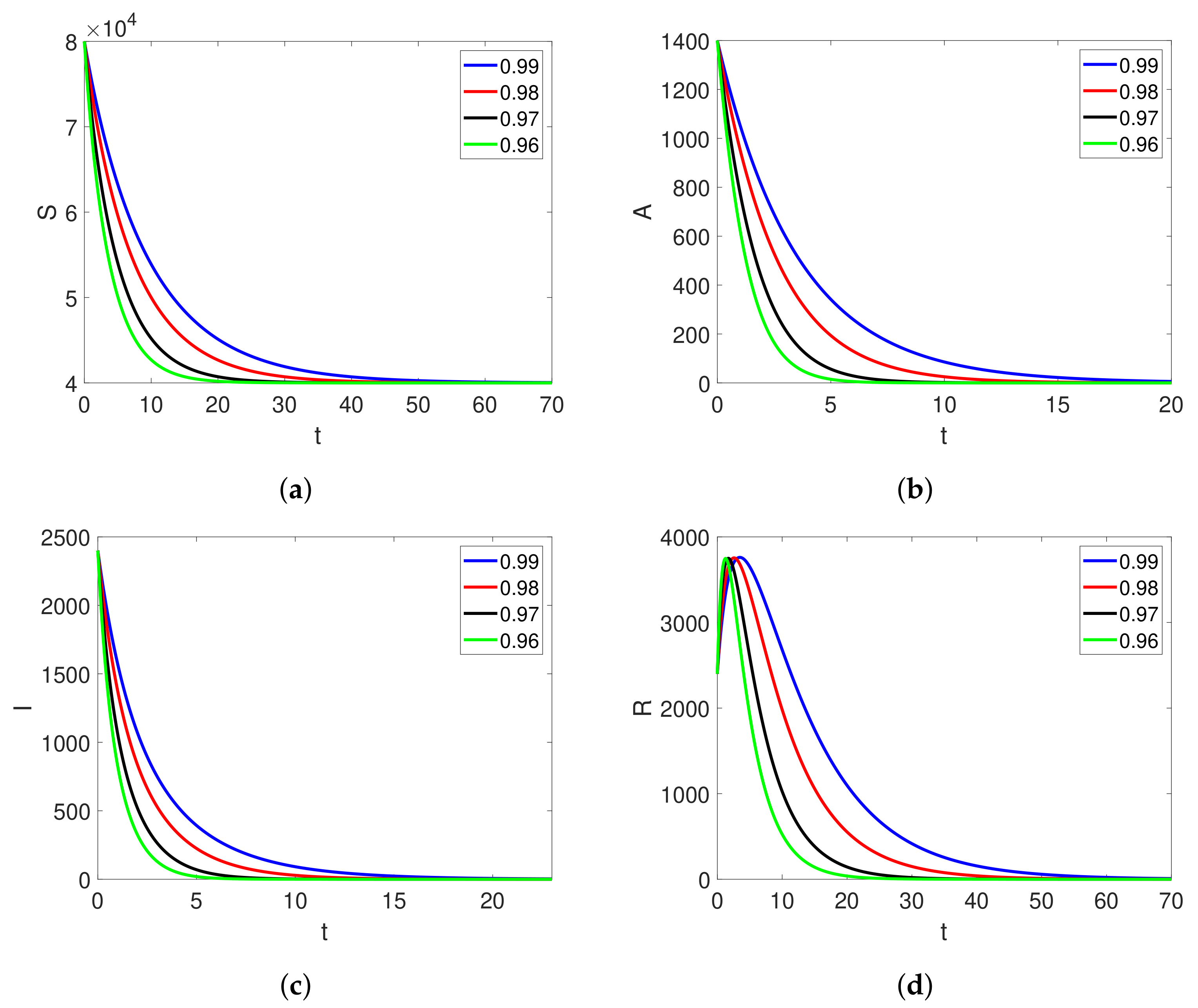
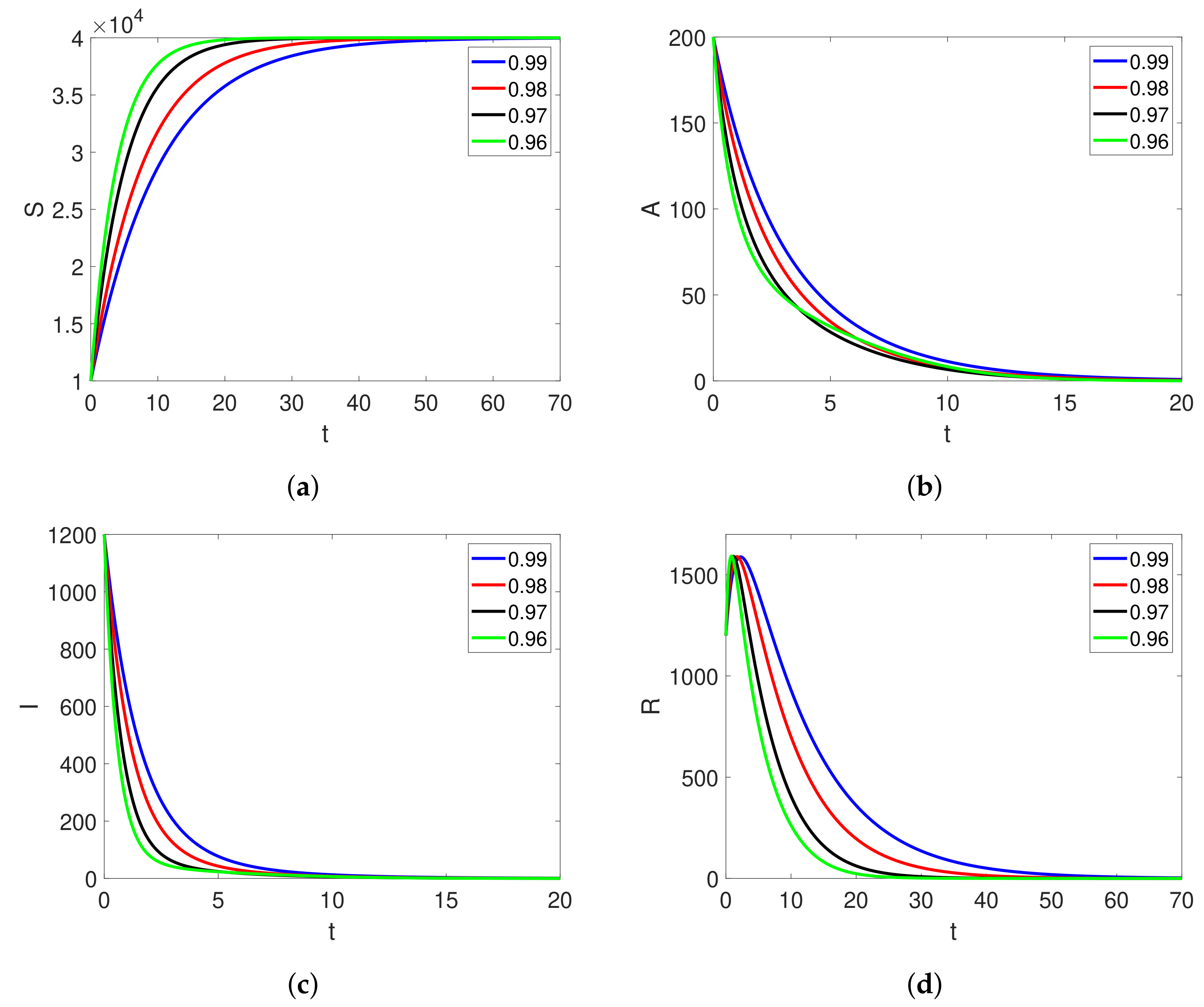

| Parameters | Set 1 | Set 2 |
|---|---|---|
| 2600 | 2600 | |
| ⋏ | 0.6 | 0.3 |
| 0.065 | 0.065 | |
| 0.3 | 0.3 | |
| 0.1 | 0.1 | |
| 0.3 | 0.3 | |
| 0.1 | 0.1 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2022 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Alkahtani, B.S. Mathematical Modeling of COVID-19 Transmission Using a Fractional Order Derivative. Fractal Fract. 2023, 7, 46. https://doi.org/10.3390/fractalfract7010046
Alkahtani BS. Mathematical Modeling of COVID-19 Transmission Using a Fractional Order Derivative. Fractal and Fractional. 2023; 7(1):46. https://doi.org/10.3390/fractalfract7010046
Chicago/Turabian StyleAlkahtani, Badr S. 2023. "Mathematical Modeling of COVID-19 Transmission Using a Fractional Order Derivative" Fractal and Fractional 7, no. 1: 46. https://doi.org/10.3390/fractalfract7010046
APA StyleAlkahtani, B. S. (2023). Mathematical Modeling of COVID-19 Transmission Using a Fractional Order Derivative. Fractal and Fractional, 7(1), 46. https://doi.org/10.3390/fractalfract7010046








