Abstract
In this paper, the shape of the stability domain for a class of difference systems defined by the Caputo forward difference operator of order is numerically analyzed. It is shown numerically that due to of power of the negative base in the expression of the stability domain, in addition to the known cardioid-like shapes, could present supplementary regions where the stability is not verified. The Mandelbrot map of fractional order is considered as an illustrative example. In addition, it is conjectured that for , the shape of does not cover the main body of the underlying Mandelbrot set of fractional order as in the case of integer order.
1. Introduction
In the last decade, fractional calculus has been considered as an important tool in many scientific and engineering fields. The basic theory of fractional calculus modeling and control systems can be found in, e.g., [1,2,3,4,5,6,7]. Studies of their applications are presented in [8,9,10]. Systems with fractional variable orders are analyzed in [11,12]. In terms of the stability analysis of fractional differential equations, one of the important properties that is analysed in order to study the behavior of the considered systems is presented in, e.g., [13,14,15,16], while applications and stability studies of discrete fractional difference equations can be found in [17,18,19].
For commensurate fractional-order systems, several powerful criteria are established. The most well-known Matignon’s stability theorem [20] (see also [21]) determines the system stability by searching for the location of the eigenvalues in the complex plane, which represents a starting point for most research into the stability of fractional-order systems.
In [22], a stability criterion for a fractional difference linear system is presented:
where and is the Caputo forward difference operator (see, e.g., [23,24]).
As shown in [22], the stability criterion for (1) is proved to be fully explicit, also involving the decay rate of the solutions.
The asymptotic stability property of (1) for both scalar and vector cases is stated by the following result:
Theorem 1
([25]). Let and . Then, (1) is asymptotically stable if and only if the isolated zeros, off the non-negative real axis, of lie inside the unit circle.
In [22], the aim is to formulate an alternative stability criterion for the integer difference system:
where is the standard operator here for .
As is well known, the system (2) is asymptotically stable if and only if all the eigenvalues of , where I is the identity matrix, are located inside the unit circle. If one considers the stability set for Equation (2) in the polar form
the stability result can be reformulated in the following form:
Theorem 2
In order to introduce an alternative stability criterion for (1), as a direct extension of Theorem (1), consider the following set:
Note that the second inequality in (3) represents the Matignon criterion.
The main result in [22] is:
Theorem 3
Because of the explicit and convenient form of , drawn in the complex plane for eigenvalues, Theorem 3 became widely used in practical applications.
In this paper, it is shown that for some empirically found values of , the form of might present other unexpected shapes. In addition, a conjecture related to the shape of in the case of the Mandelbrot set of fractional order is introduced.
2. On the Shape of the Stability Area
The parametric equations of the frontier of the stability region for a fixed point, , , can be easily drawn in the following form [22]:
On the other hand, to analyze the shape of in more detail, consider the form (3). As is known, the argument of a complex number , , used in (3), is the angle between the positive real axis and the line joining the origin and the image in the complex plane of z. Usually, the value of the argument is numerically computed as
where the two-argument function atan2 is an available implemented function in the math libraries of many programming languages.
In contrast to the inverse tangent function, (arctan, or atan), the function atan2 computes the principal value of the arctangent of , determining the quadrant of the returned value by using the signs of both arguments. Note that a domain error may occur if both arguments are zero. (Regarding the 1999 ISO C, 1978 ANSI Fortran, or 1982 ISO Pascal Standard standard descriptions and other issues related to atan2 for the case of and , they are referred to on p. 70 [26]). However, as will be shown below, the problem of arg in (3) can be quite complicated, even if both arguments are not zero, as shown next with simple reasoning.
While arctan gives an angle between and , the function atan2 always provides a result within .
Denote, in (3),
and consider the argument of the cos function in as the function , defined as
with a being a parameter (Figure 1). Being determined with atan2, a given by (5) satisfies the following relations: , and . Therefore, because for , , one has
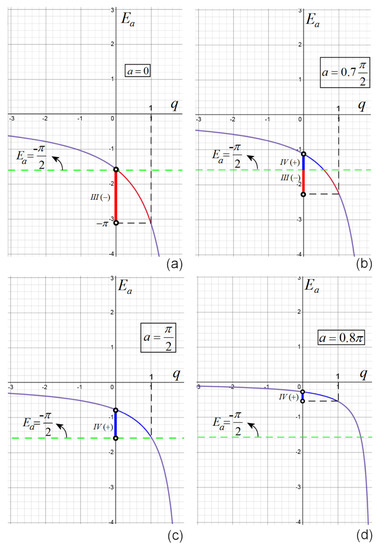
Figure 1.
Graph of the function , for four representative cases: (a) the limit case ; (b) ; (c) ; and (d) .
In order to determine in which quadrant the values of are situated, let us analyze and sketch the graph of the restriction of the function to . The derivative of is . Therefore, from the monotonicity, one deduces that decreases from , for , but to , for . For example, for the limit case of , takes values within the range , i.e., are situated in quadrant III (Figure 1a). For the case of , the values of can be situated in both quadrants III and IV (Figure 1b). For , moves within in the quadrant IV (Figure 1c). The case of is presented in Figure 1d. Therefore, for and , the argument can take values situated in quadrant III and/or IV, where could be either negative or positive.
The relation between q and a on the boundary between the two quadrants III and IV is
To obtain the shape of via relation (3), consider a variable fixed point with the underlying variable eigenvalue, , to be replaced in (3). Denote hereafter by the curve surrounding . The two relations in (3) which define represent the implicit inequalities of two variables x and y that can be drawn with implicit functions plotting commands available in software such as Matlab (e.g., fimplicit), Mathematica (e.g., ContourPlot), or by using the free software Desmos [27]. In Figure 2a, the case of for is presented.
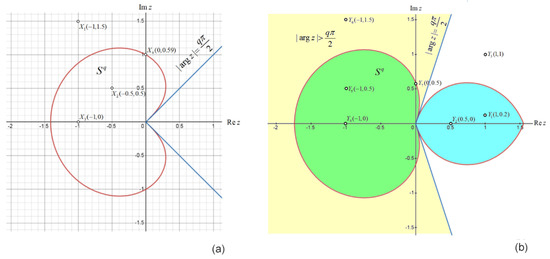
Figure 2.
Graph of (red plot) for two representative cases: (a) ; (b) . Green plot represents the stability domain , surrounded by , delimitated by the inequality , while light blue and white domains do not belong to the stability domain.
Remark 1.
As is known, if in the expression , x is negative and y is not an integer, the mathematical situation is somewhat ambiguous. With infinite numeric precision, the correct result of is mathematically well-defined without ambiguity. Certain values of y yield an imaginary number as a result, while other values of y result in a real-valued result. Specifically, when , the result of is real-valued exactly when y can be written as a fraction, , where m is an integer and n is an odd integer. Furthermore, the result is positive when m is even but negative when m is odd. When y cannot be written as such, the result would be an imaginary number (see, e.g., [28]). For example, in Matlab, for negative base x and non-integer y, the power function returns complex results. A solution could be to use the function nthroot. However, note that in IEEE floating-point computations
Moreover, the log function domain includes negative and complex numbers, which can lead to unexpected results if used unintentionally. Therefore, may be a complex number, if and y is noninteger. In these cases, in some software, such as Matlab, imaginary parts of complex arguments are ignored to the detriment of the shape of .
To summarize, for those values x and y for which , they are situated in quadrant III, and, therefore, is not well-defined. The consequence is that, in addition to the expected area, for some values of q, could present unexpected additional parts. Thus, for , using Desmos, the domain is presented in Figure 2b.
In these cases, the supplementary domain can be determined via the condition (Matignon condition), for , and the lines being tangent to . However, this is not possible in some more complicated cases (Figure 3, Section 2). An animation which shows the variation in the stability domain for , where several such cases appear, is presented as a Supplementary video.
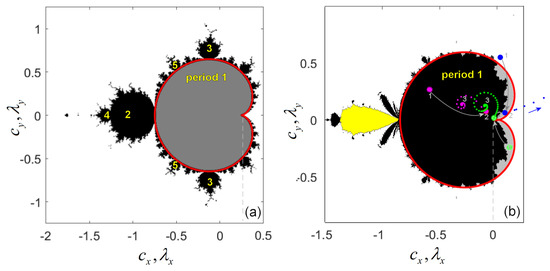
Figure 3.
Mandelbrot sets of IO and FO and their stability domains. (a) IOM set; (b) FOM set and the main cardioid (red plot) surrounding the stability domain for .
To verify if in the considered cases of and contains the stability points, consider the points , (images of the underlying complex numbers) for the case of and, , for the case of , respectively (see Figure 2), and denote
The graph of is the boundary curve and
Therefore, the images of z for which , or are complex values are not points. The values of at the points , and are presented in Table 1 and Table 2, respectively.

Table 1.
Value of at points , , for (see also Figure 2a).

Table 2.
Value of at points , , for (see also Figure 2b).
Regarding the numerical implementation, if in the atan2 function, x and y have different signs, then atan2 and arctan (atan) could have different values. Thus, if in some software the atan2 function is not implemented, it can be emulated with
3. Stability of the Mandelbrot Map of Fractional Order
Next, consider the fractional discretization of the Mandelbrot map
where
and , with c being the complex parameter. For the initial value problems for real fractional discrete systems, see, e.g., [29,30] (in [31], several properties of the complex Mandelbrot map of fractional order and the matlab code to draw the fractal are presented).
The numerical integral of the initial value problem (6) is (see [30] for the solution of real fractional-order systems)
For , one obtains the fractional-order Mandelbrot (FOM) set, presented in Figure 3b. The fractal is obtained with the FO_mandelbrot.m code [32].
To obtain the stability domain of the stable fixed points (period 1) of the FOM map, consider next, for computational reasons, the problem in the Cartesian plane, with , . Contrary to the integer-order case, where the fixed points are found from the equation , here, the fixed points are obtained by solving the equation , i.e., , with the solutions: . For the fixed point , after some calculations, the eigenvalues are obtained as
while, for ,
Consider the eigenvalue , the reasoning for being similar. Then, the useful parametric representation of in coordinates and , defining , are determined from the following equations (see (4)):
The solutions, which represent the parametric equations of the curve , are
In Figure 3a, the integer-order Mandelbrot (IOM) set is drawn together with the main cardioid which has the equation (see, e.g., [33,34,35])
or, in parametric form,
The interior of the curve corresponds to the stable fixed points, obtained from the equation , i.e. .
The curve for the FOM set for , which surrounds the stability domain of the fixed point , , is presented in Figure 3. Note that in both the IO case (Figure 3a) and the FO case (Figure 3b), the Mandelbrot sets (defined on the parametric plane of c in coordinates ) and the stability domains (defined on the eigenvalues in coordinates ) are overplotted.
As detailed in Section 2, to a fixed point , the eigenvalues given by (8) or (9) correspond. For a point , loses its stability, while if , is unstable. If is asymptotically stable, belongs to , and reversely, a point within corresponds to a point c for which is asymptotically stable.
Let us numerically verify this property. Consider (magenta point 1 of coordinates in Figure 3b). Because and , one chooses (9) with right-hand side having signs − and +, respectively. To find the corresponding point c of this value of , one has to solve the problem (8) with unknown and . The solutions are and (magenta point 2 in Figure 3b. To verify the stability of the fixed point corresponding to this value of c, one integrates the system with (7). The orbit starting from point c tends to be point 3 of the coordinates (Figure 3b), which is an approximation with an error of of the fixed stable point .
Interestingly, in comparison with the IO case (Figure 3a), does not fill the entire FOM set (gray fill in Figure 3b). However, points within this gray area of , and similarly for all studied cases of , lead to the same result: the entire domain contains eigenvalues points for which the fixed points are asymptotically stable. Consider, for example, the eigenvalue (green point 1 of coordinates in Figure 3b). By solving system (8), one obtains the point and (green point 2 in Figure 3b), from which the integral (7) generates the orbit tending to point 3 of the coordinates . This, with a precision of , represents the approximation of the fixed point .
On the other hand, points outside of are eigenvalues for which the underlying points c do not belong to the FOM set and, therefore, their fixed points are not stable. Consider, for example, point 1 (blue plot in Figure 3b) of coordinates and . Solving system (8), one obtains , and (point 2 blue outside the FOM set in Figure 3b) from where the orbit diverges in agreement with the definition of the Mandelbrot set of IO or FO.
Among several differences and resemblances between the FOM set and the IOM set [36], one can see that the origin of the so-called “Elephant Valley” (see, e.g., [33]) in the case of the IOM set is located at , while for the FOM set, it is located at (see dotted line in Figure 3).
While for , fills the main body of the FOM set well enough, for , the shape of does not cover the main body. In Figure 4a–c, for , and , the numerically near 0 value, , is chosen instead of , which is not defined. In this case, in order to obtain more fractal details (which look similar to the IOM set), only 30 iterations were used, compared to 1000 iterations for the other cases). One can see that is the ultimate value for q. Thus, for q values below this limit, is shrinking with respect to the main body of the FOM set. Another characteristic is that the shape of obtained with Desmos (Figure 4d) presents an additional part (see also Figure 1b). This image was obtained using both representations: the representation (3) and the parametric form (10).
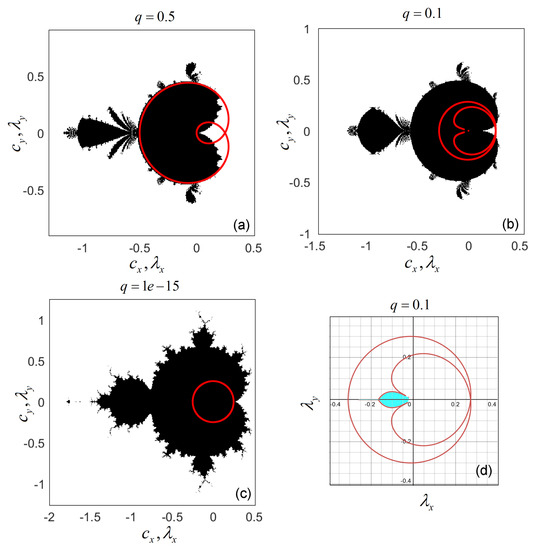
Figure 4.
Mandelbrot sets of FO and their stability domains for three extra cases. (a) The FOM set and for the limit case ; (b) FOM set and for ; (c) FOM set and for ; (d) for , obtained in Desmos software.
Therefore, the following conjecture is numerically sustained (see also [37]):
Conjecture 1.
For , the surface of the stability domain of the fixed points of the FOM shrinks compared to the main body of the fractal set.
Remark 2.
After the first result on the non-periodicity of non-constant solutions of FO, continuous-time systems appeared [38]; this intriguing result has been extended to FO discrete systems too (see, e.g., [39]). Thus, contrary to the IOM set, the head contains points generating two-period stable cycles, and where the bulbs contain the points, generating multiple stable cycles of period 3,4, and so on (Figure 3a). In the case of the FOM set, these apparent periodic orbits do not exist! For example, points in the head (yellow fill in Figure 3b) do not generate periodic orbits. The same situations happen to all bulbs.
4. Conclusions
In this paper, it is shown that drawing the stability domain for empiric values of encounters the problem of the power of negative numbers which could be differently treated by the software used. Therefore, depending on the software used, the graphical results of the stability domain of the linear difference Equation (1) could be unexpected. The power function appearing in is applied to negative values when either the logarithm is a complex number or one obtains an unexpected result (see Remark 1). In addition, the stability domain for the fixed points of an FOM map is determined. The asymptotical stability of the fixed points of the FOM map is verified numerically for . For , the shape of seems not to verify the filling characteristic encountered on the IOM set, a fact that leads to Conjecture 1. Besides several differences between the Mandlebrot sets of IO and FO, such as the shape, the position, and the shape of the stability set, in the FO case, the head of the FOM set does not represent the points that generate stable periodic orbits.
Supplementary Materials
The following supporting information can be downloaded at: https://www.mdpi.com/article/10.3390/fractalfract7010049/s1.
Funding
This research received no external funding.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
Data is contained within the article or Supplementary material.
Conflicts of Interest
The author declares no conflict of interest.
References
- Mozyrska, D.; Wyrwas, M. Stability of linear systems with Caputo fractional-, variable-order difference operator of convolution type. In Proceedings of the 2018 41st International Conference on Telecommunications and Signal Processing (TSP), Athens, Greece, 4–6 July 2018. [Google Scholar]
- Čermáak, J.; Kisela, T.; Nechváatal, L. Stability and asymptotic properties of a linear fractional difference equation. Adv. Differ. Equ. 2012, 2012, 122. [Google Scholar] [CrossRef]
- Hilfer, R. Applications of Fractional Calculus in Physics; World Scientific Publishing Company: Singapore, 2000. [Google Scholar]
- Kilbas, A.A.; Srivastava, H.M.; Trujillo, J.J. Theory and Applications of Fractional Differential Equations; North-Holland Mathematics Studies, 204; Elsevier Science B. V.: Amsterdam, The Netherlands, 2006. [Google Scholar]
- Ortigueira, M.D.; Coito, F.J.; Trujillo, J.J. Discrete-time differential systems. Signal Process. 2015, 107, 198–217. [Google Scholar] [CrossRef]
- Ostalczyk, P. Discrete Fractional Calculus. Applications in Control and Image Processing; Series in Computer Vision 4; World Scientific Publishing Co. Pte Ltd.: Singapore, 2016. [Google Scholar]
- Podlubny, I. Fractional Differential Equations; Academic Press: Cambridge, MA, USA, 1999. [Google Scholar]
- Axtell, M.; Bise, E.M. Fractional calculus applications in control systems. In Proceedings of the IEE 1990 IEEE Conference on Aerospace and Electronics, Dayton, OH, USA, 21–25 May 1990; Volume 311, pp. 536–566. [Google Scholar]
- Bastos, N.R.O.; Ferreira, R.A.C.; Torres, D.F.M. Discrete-time fractional variational problems. Signal Process. 2011, 91, 513–524. [Google Scholar] [CrossRef]
- Vinagre, B.M.; Monje, C.A.; Caldero, A.J. Fractional order systems and fractional order actions. In Proceedings of the Tutorial Workshop#2: Fractional Calculus Applications in Automatic Control and Robotics, Las Vegas, NV, USA, 1 December 2002; pp. 1–23. [Google Scholar]
- Bahaa, G.M. Fractional optimal control problem for variable-order differential systems. Fract. Calc. Appl. Anal. 2017, 20, 1447–1470. [Google Scholar] [CrossRef]
- Mozyrska, D.; Ostalczyk, P. Variable-fractional-order Grünwald-Letnikov backward difference selected properties. In Proceedings of the 39th International Conference on Telecommunications and Signal Processing, Vienna, Austria, 27–29 June 2016. [Google Scholar]
- Brandibur, O.; Garrappa, R.; Kaslik, E. Stability of Systems of Fractional-Order Differential Equations with Caputo Derivatives. Mathematics 2021, 9, 914. [Google Scholar] [CrossRef]
- Čermáak, J.; Kisela, T. Asymptotic stability of dynamic equations with two fractional terms: Continuous versus discrete case. Fract. Calc. Appl. Anal. 2015, 18, 437–458. [Google Scholar] [CrossRef]
- Mozyrska, D.; Wyrwas, M. The Z-transform method and delta type fractional difference operators. Discret. Dyn. Nat. Soc. 2015, 2015, 25. [Google Scholar] [CrossRef]
- Sabatier, J.; Farges, M.M.C. LMI stability conditions for fractional order systems. Comput. Mater. Appl. 2010, 59, 1594–1609. [Google Scholar] [CrossRef]
- Goodrich, C.; Peterson, A.C. Discrete Fractional Calculus; Springer International Publishing: Cham, Switzerland, 2015. [Google Scholar]
- Huang, L.-L.; Wu, G.-C.; Baleanu, D.; Wang, H.Y. Discrete fractional calculus for interval-valued systems. Fuzzy Sets Syst. 2021, 404, 141–158. [Google Scholar] [CrossRef]
- Elsonbaty, A.; Elsadany, A.A. On discrete fractional-order Lotka-Volterra model based on the Caputo difference discrete operator. Math. Sci. 2021, 1–13. [Google Scholar] [CrossRef]
- Matignon, D. Stability results on fractional differential equations with applications to control processing. In Proceedings of the Computational Engineering in Systems and Application Multiconference, IMACS, IEEE-SMC, Lille, France, 9–12 July 1996; Volume 2, pp. 963–968. [Google Scholar]
- Sierociuk, D.; Dzielinski, A. Stability of discrete fractional order state-space systems. J. Vib. Control 2008, 14, 1543–1556. [Google Scholar]
- Čermáak, J.; Györi, I.; Nechvátal, L. On explicit stability conditions for a linear fractional difference system. Fract. Calc. Appl. Anal. 2015, 18, 651–672. [Google Scholar] [CrossRef]
- Abdeljawad, T. On delta and nabla Caputo fractional differences and dual Identities, in Recent Developments and Applications on Discrete Fractional Equations and Related Topic. Hindawi 2013, 2013, 406910. [Google Scholar]
- Anastassiou, G. Principles of delta fractional calculus on time scales and inequalities. Math. Comp. Model. 2010, 52, 556–566. [Google Scholar] [CrossRef]
- Abu-Saris, R.; Al-Mdallal, Q. On the asymptotic stability of linear system of fractional-order difference equations. Fract. Calc. Appl. Anal. 2013, 16, 613–629. [Google Scholar] [CrossRef]
- Beebe, N.H.F. The Mathematical-Function Computation Handbook, Programming Using the MathCW Portable Software Library; Springer: Berlin/Heidelberg, Germany, 2017. [Google Scholar]
- Available online: https://www.desmos.com/calculator/pi5ofejgt0?lang=en (accessed on 12 December 2022).
- Available online: https://wiki.analytica.com/index.php?title=Exponentiation_of_negative_numbers#Exponentiation_operator_.5E (accessed on 12 December 2022).
- Chen, F.; Luo, X.; Zhou, Y. Existence results for nonlinear fractional difference equations. Adv. Differ. Equ. 2011, 2011, 713201. [Google Scholar] [CrossRef]
- Atici, F.M.; Eloe, P.W. Initial value problems in discrete fractional calculus. Proc. Am. Math. Soc. 2009, 137, 981–989. [Google Scholar] [CrossRef]
- Fečkan, M.; Danca, M.-F. Non-periodicity of complex Caputo like fractional differences. In Advances in Fractional-Order Neural Networks; Volume II, submitted.
- Available online: https://www.mathworks.com/matlabcentral/fileexchange/121632-fo_mandelbrot (accessed on 12 December 2022).
- Peitgen, H.-O.; Richter, P.H. The Beauty of Fractals Images of Complex Dynamical Systems; Springer: Berlin/Heidelberg, Germany, 1986. [Google Scholar]
- Branner, B. The Mandelbrot Set. In Chaos and Fractals: The Mathematics behind the Computer Graphics; Devaney, R.L., Keen, L., Eds.; Amer Math Soc: Providence, RI, USA, 1989; pp. 75–105. [Google Scholar]
- Peitgen, H.-O.; Saupe, D. (Eds.) The science of Fractal Images; Springer: New York, NY, USA, 1988; pp. 178–179. [Google Scholar]
- Danca, M.-F.; Fečan, M. Mandelbrot set and Julia sets of fractional order. arXiv 2022, arXiv:2210.02037. [Google Scholar]
- Danca, M.-F. Fractional order logistic map: Numerical approach. Chaos Soliton Fract. 2022, 157, 111851. [Google Scholar] [CrossRef]
- Tavazoei, M.S. A note on fractional-order derivatives of periodic functions. Automatica 2010, 46, 945–948. [Google Scholar] [CrossRef]
- Diblík, J.; Fečkan, M.; Pospíšil, M. Nonexistence of periodic solutions and S-asymptotically periodic solutions in fractional difference equations. Appl. Math. Comput. 2015, 257, 230–240. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2022 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).