Fractal Analysis of Porous Alumina and Its Relationships with the Pore Structure and Mechanical Properties
Abstract
:1. Introduction
2. Materials and Methods
2.1. Raw Materials
2.2. Preparation of Porous Alumina
2.3. Characterization Methods
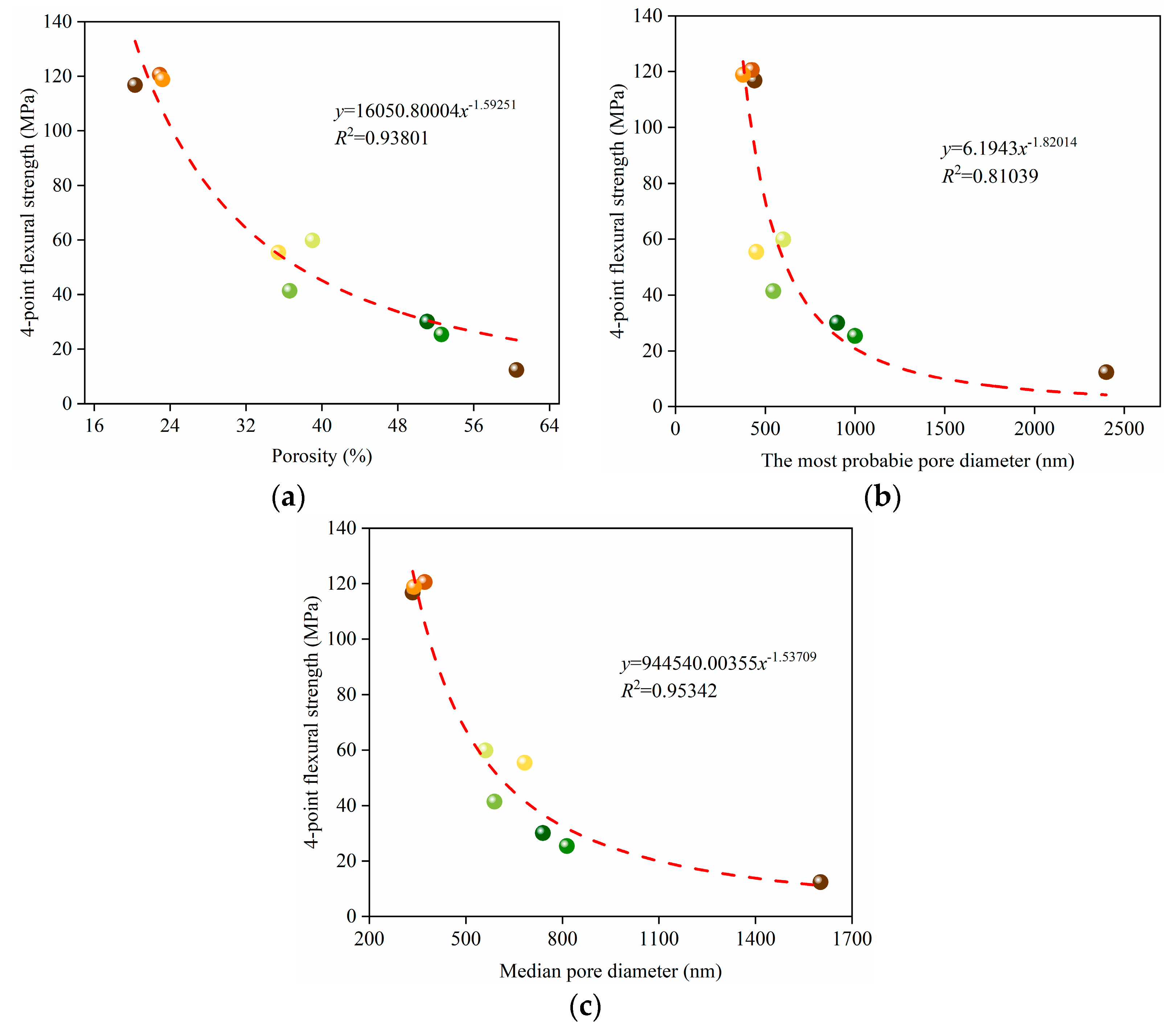
3. Results and Discussion
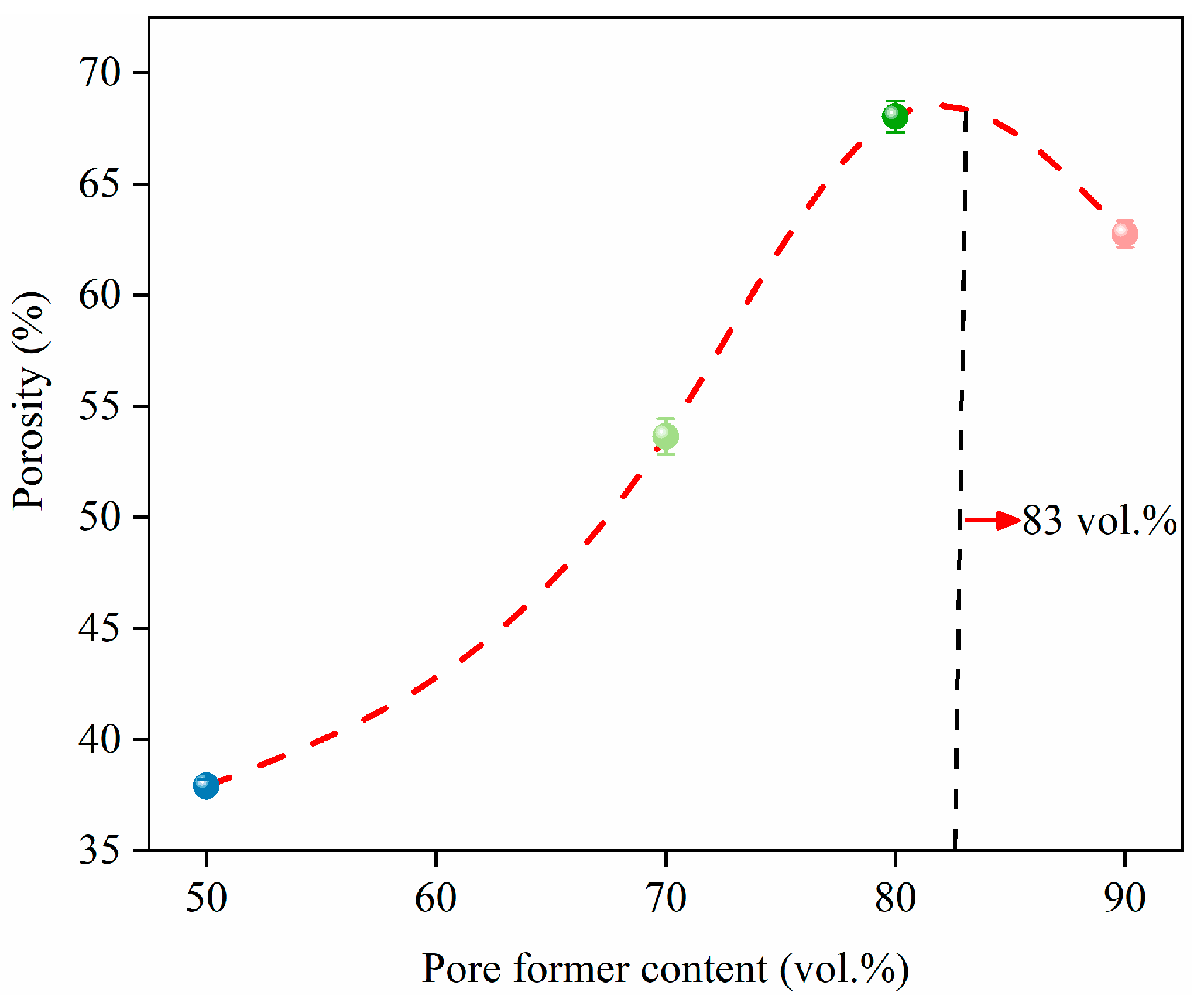
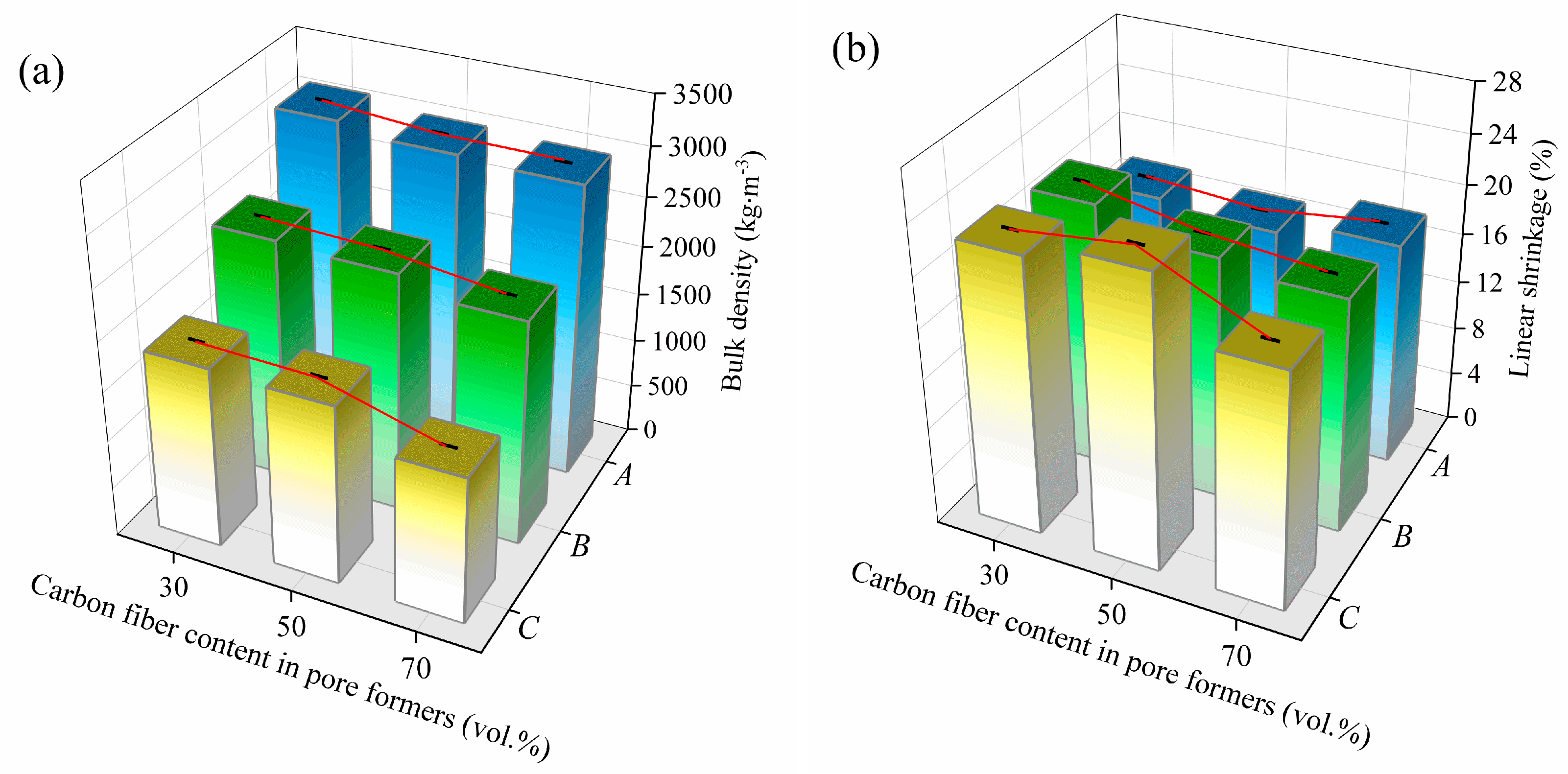
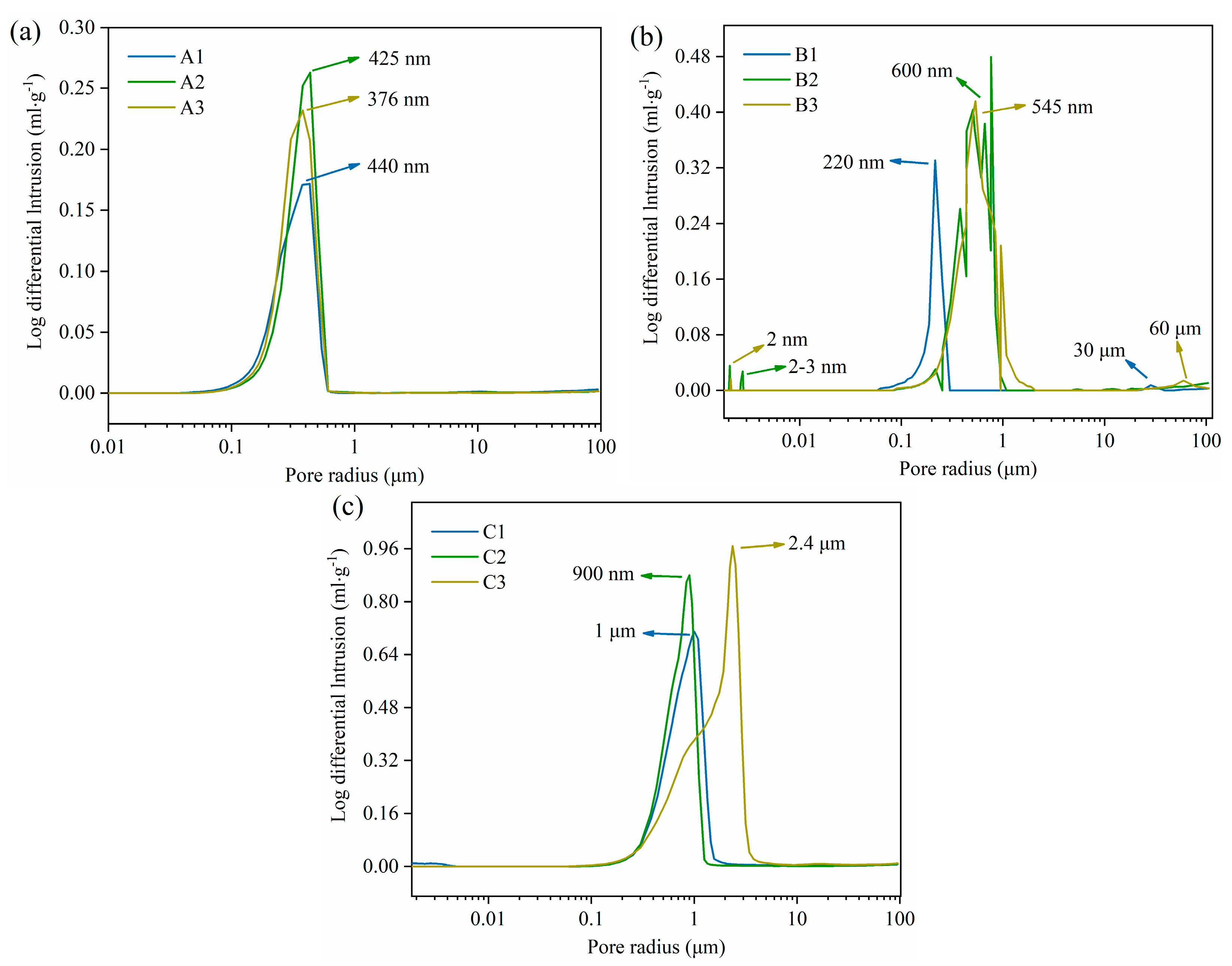
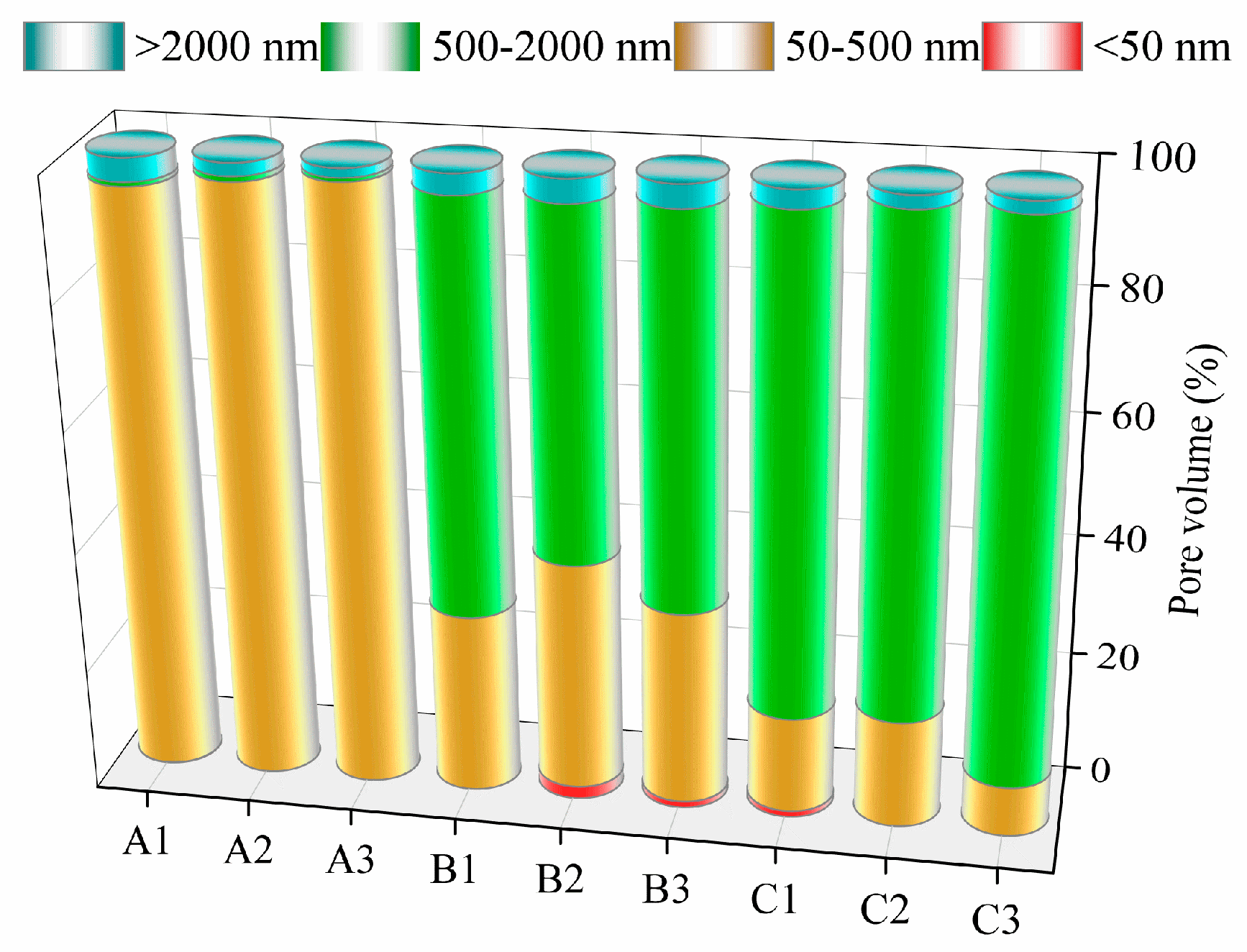
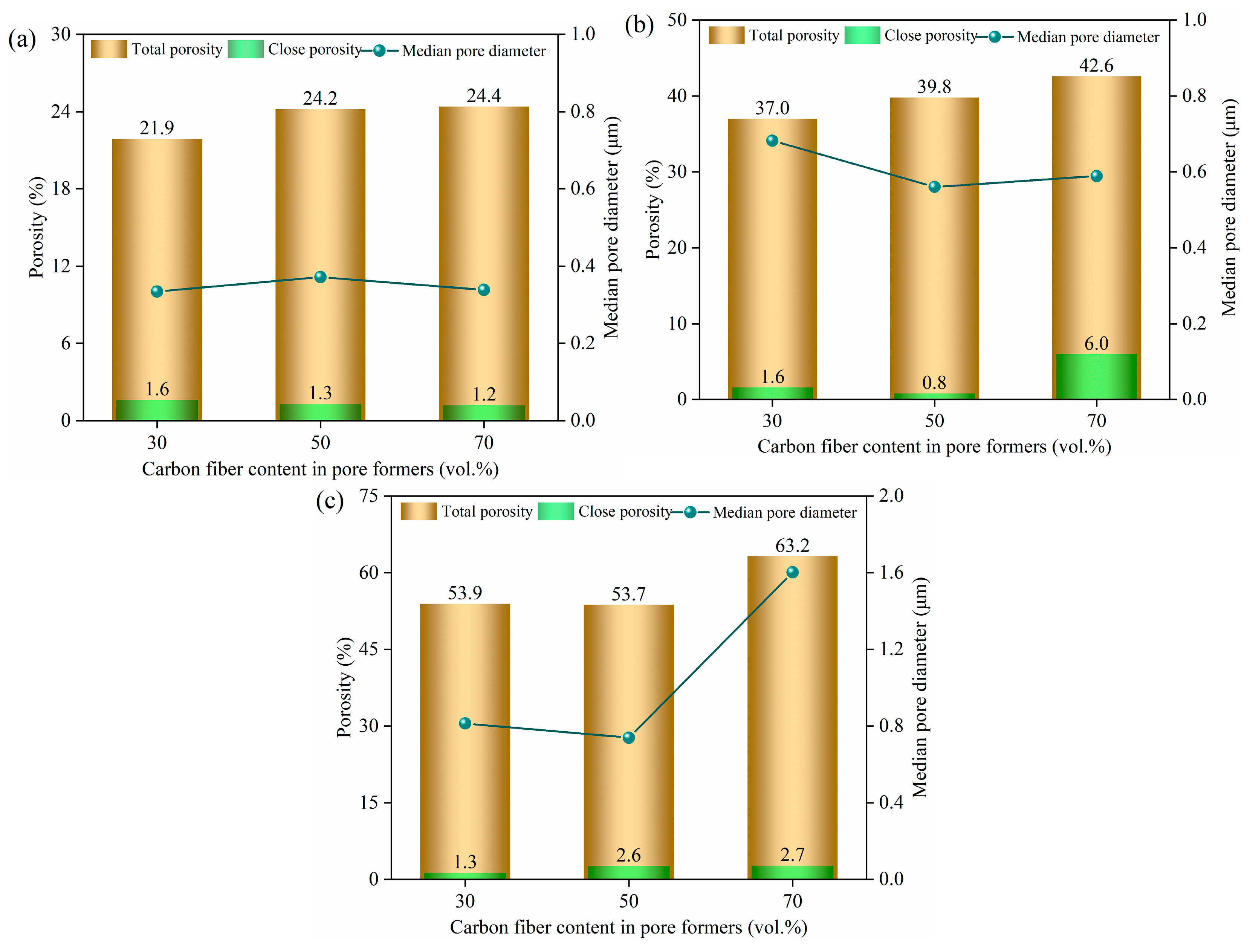
3.1. Effect of Pore Formers on the Bulk Density, Linear Shrinkage, Pore Size Distribution, and Porosity of the Porous Alumina
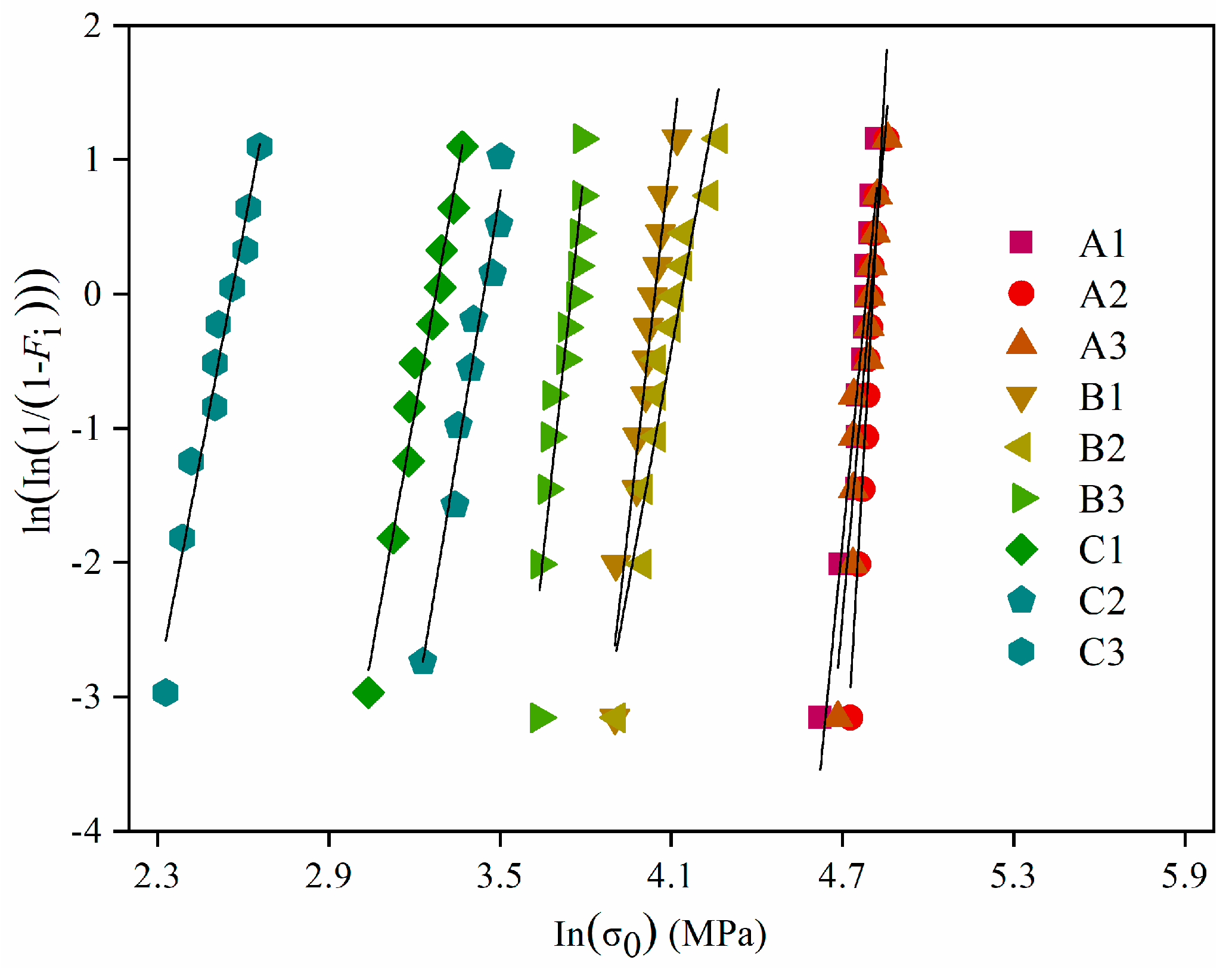
3.2. Mechanical Properties and Weibull Distribution of the Porous Alumina
3.3. Phase Composition and Microstructure of the Porous Alumina
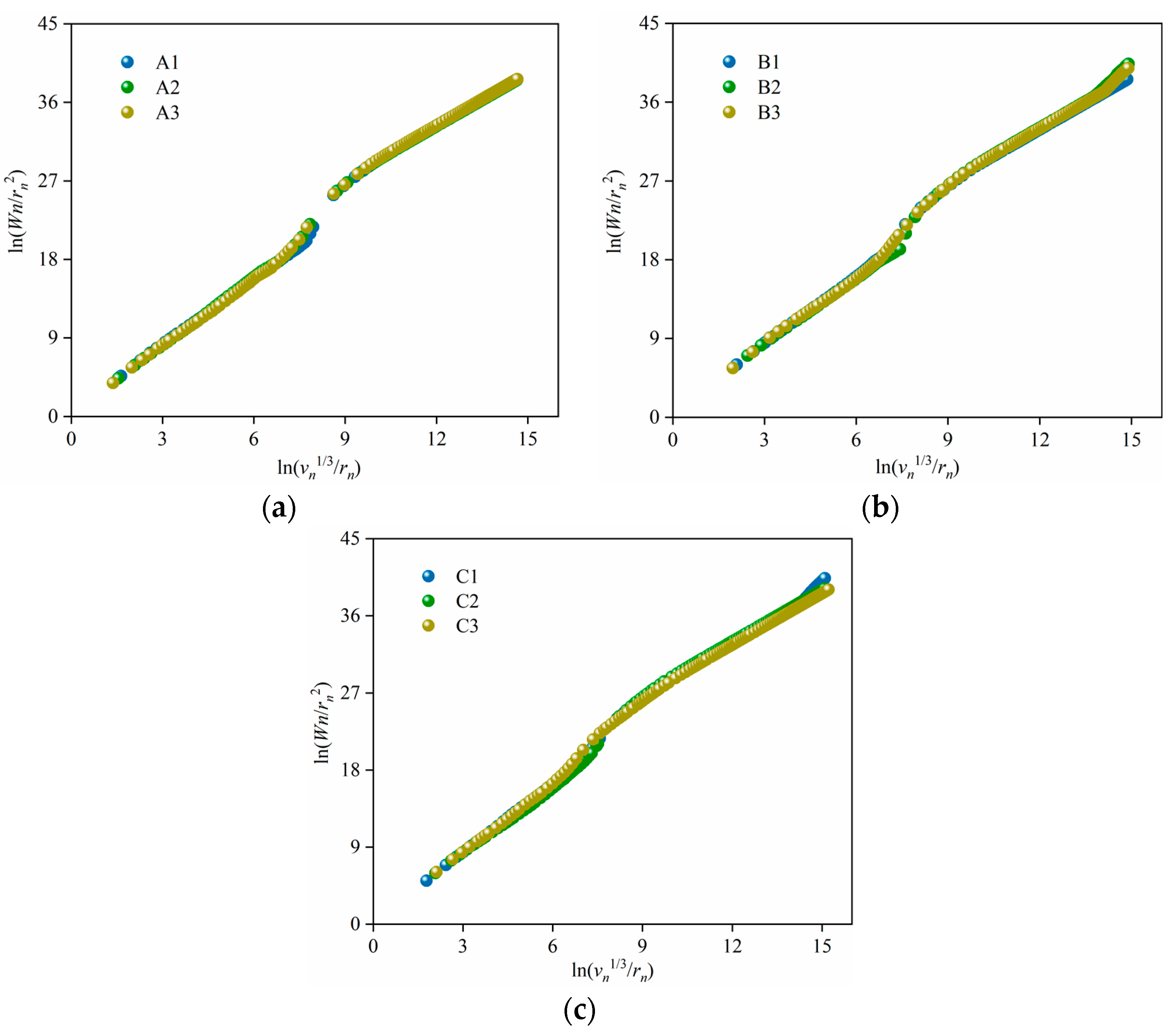
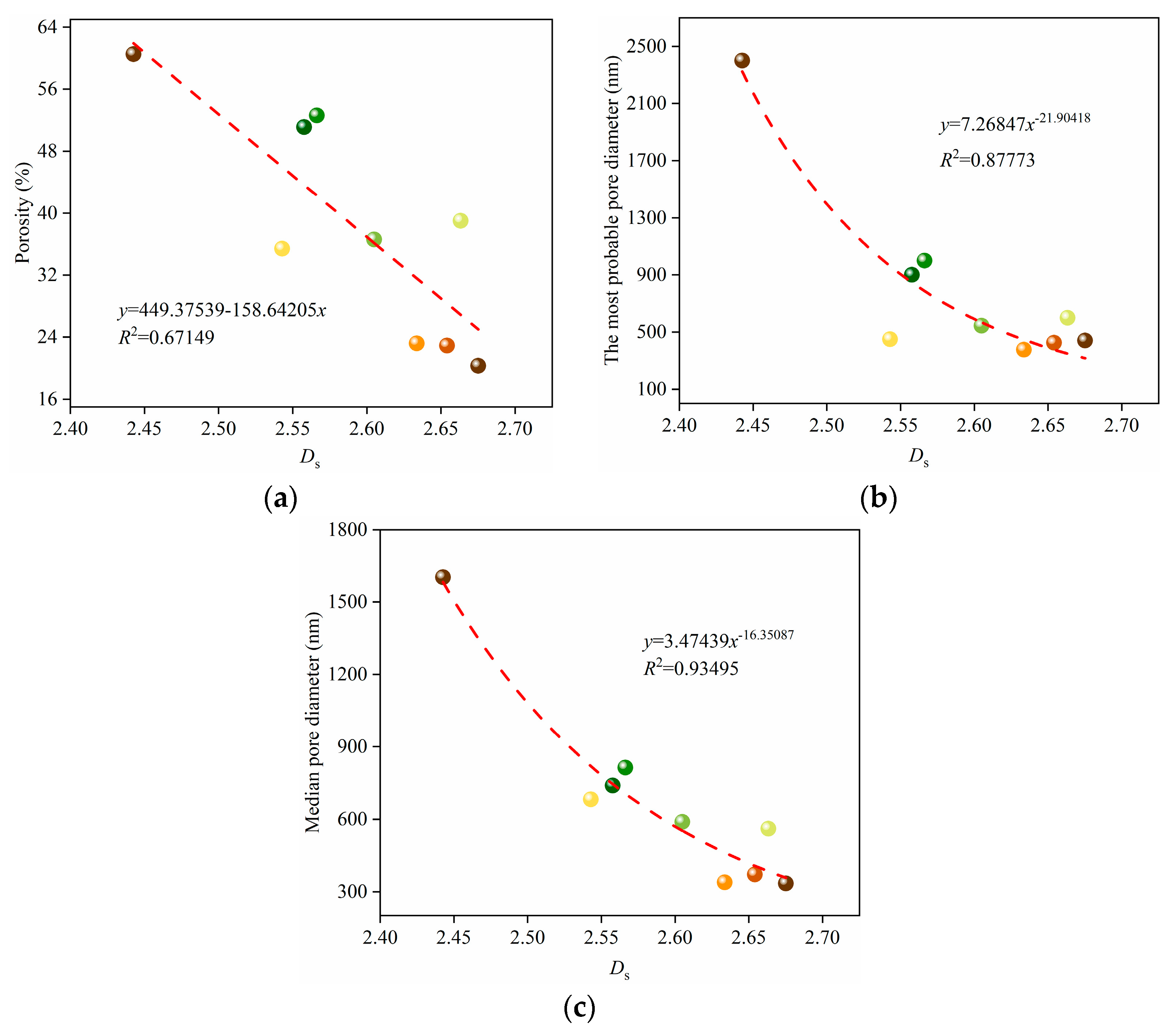
3.4. Fractal Characteristics of the Porous Alumina
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Guzman, I.Y. Certain principles of formation of porous ceramic structures. Properties and applications (A review). Glass Ceram. 2003, 60, 280–283. [Google Scholar] [CrossRef]
- Studart, A.R.; Gonzenbach, U.T.; Tervoort, E.; Gauckler, L.J. Processing routes to macroporous ceramics: A review. J. Am. Ceram. Soc. 2006, 89, 1771–1789. [Google Scholar] [CrossRef]
- Ohji, T.; Fukushima, M. Macro-porous ceramics: Processing and properties. Int. Mater. Rev. 2012, 57, 115–131. [Google Scholar] [CrossRef]
- Pia, G.; Casnedi, L.; Sanna, U. Porous ceramic materials by pore-forming agent method: An intermingled fractal units analysis and procedure to predict thermal conductivity. Ceram. Int. 2015, 41, 6350–6357. [Google Scholar] [CrossRef]
- Yin, S.; Pan, L.; Huang, K.; Qiu, T.; Yang, J. Porous Si3N4 ceramics with hierarchical pore structures prepared by gelcasting using DMAA as gelling agent and PS as pore–forming agent. J. Alloys Compd. 2019, 805, 69–77. [Google Scholar] [CrossRef]
- He, C.; Du, B.; Ma, J.; Xiong, H.; Qian, J.; Cai, M.; Shui, A. Enhanced sound absorption properties of porous ceramics modified by graphene oxide films. J. Am. Ceram. Soc. 2022, 105, 3177–3188. [Google Scholar] [CrossRef]
- Farahani, H.; Wagiran, R.; Hamidon, M.N. Humidity sensors principle, mechanism, and fabrication technologies: A comprehensive review. Sensors 2014, 14, 7881–7939. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Blank, T.A.; Eksperiandova, L.P.; Belikov, K.N. Recent trends of ceramic humidity sensors development: A review. Sens. Actuat. B 2016, 228, 416–442. [Google Scholar] [CrossRef]
- Chen, Y.; Wang, N.; Ola, O.; Xia, Y.; Zhu, Y. Porous ceramics: Light in weight but heavy in energy and environment technologies. Mater. Sci. Eng. R 2021, 143, 100589. [Google Scholar] [CrossRef]
- Raja, M.; Sanjeev, G.; Prem Kumar, T.; Manuel Stephan, A. Lithium aluminate-based ceramic membranes as separators for lithium-ion batteries. Ceram. Int. 2015, 41, 3045–3050. [Google Scholar] [CrossRef]
- Xu, C.; Liu, H.; Yang, H.; Yang, L. A green biocompatible fabrication of highly porous functional ceramics with high strength and controllable pore structures. J. Mater. Sci. Technol. 2016, 32, 729–732. [Google Scholar] [CrossRef]
- Faria, F.P.; Ruellas, T.M.O.; Del Roveri, C.; Donizette Malafatti, J.O.; Paris, E.C.; Giraldi, T.R.; Maestrelli, S.C. Obtaining porous zinc oxide ceramics using replica technique: Application in photocatalysis. Mater. Res.-Ibero-Am. J. 2022, 25, e20210083. [Google Scholar] [CrossRef]
- Wang, S.L.; Zhou, M.; Zeng, L.K.; Dai, W.B. Investigation on the preparation and properties of reticulate porous ceramic for organism carrier in sewage disposal. J. Ceram. Process. Res. 2016, 17, 1095–1099. [Google Scholar]
- Li, Y.; Yang, X.; Liu, D.; Chen, J.; Zhang, D.; Wu, Z. Permeability of the porous Al2O3 ceramic with bimodal pore size distribution. Ceram. Int. 2019, 45, 5952–5957. [Google Scholar] [CrossRef]
- Hedayat, N.; Du, Y.; Ilkhani, H. Review on fabrication techniques for porous electrodes of solid oxide fuel cells by sacrificial template methods. Renew. Sustain. Energ. Rev. 2017, 77, 1221–1239. [Google Scholar] [CrossRef]
- Qu, F.; Yu, Z.; Krol, M.; Chai, N.; Riedel, R.; Graczyk-Zajac, M. Electrochemical performance of carbon-rich silicon carbonitride ceramic as support for sulfur cathode in lithium sulfur battery. Nanomaterials 2022, 12, 1283. [Google Scholar] [CrossRef]
- Wang, L.; He, G.; Yang, Z.C.; Li, J.T. Combustion synthesis of high flexural strength, low linear shrinkage and machinable porous beta-Si3N4 ceramics. J. Eur. Ceram. Soc. 2021, 41, 2395–2399. [Google Scholar] [CrossRef]
- Liu, X.; Yu, C.; Qu, D.L.; Luo, X.D. Preparation of porous beta-SiAlON ceramics using corn starch as pore-forming agent. J. Aust. Ceram. Soc. 2022, 58, 531–537. [Google Scholar] [CrossRef]
- Ternero, F.; Rosa, L.G.; Urban, P.; Montes, J.M.; Cuevas, F.G. Influence of the total porosity on the properties of sintered materials: A review. Metals 2021, 11, 730. [Google Scholar] [CrossRef]
- Dong, Y.; Jiang, H.; Chen, A.; Yang, T.; Zou, T.; Xu, D. Porous Al2O3 ceramics with spontaneously formed pores and enhanced strength prepared by indirect selective laser sintering combined with reaction bonding. Ceram. Int. 2020, 46, 15159–15166. [Google Scholar] [CrossRef]
- Mandelbrot, B.B.; Wheeler, J.A. The fractal geometry of nature. Am. J. Phys. 1983, 51, 286–287. [Google Scholar] [CrossRef]
- Pfeifer, P.; Avnir, D. Chemistry in noninteger dimensions between two and three. I. Fractal theory of heterogeneous surfaces. J. Chem. Phys. 1983, 79, 3558–3565. [Google Scholar] [CrossRef]
- Shenker, O.R. Fractal geometry is not the geometry of nature. Stud. Hist. Philos. Sci. 1994, 25, 967–981. [Google Scholar] [CrossRef]
- Mitic, V.V.; Paunovic, V.; Kocic, L. Fractal approach to BaTiO3-ceramics micro-impedances. Ceram. Int. 2015, 41, 6566–6574. [Google Scholar] [CrossRef]
- Esmonde, H. Fractal and fractional derivative modelling of material phase change. Fractal Fract. 2020, 4, 46. [Google Scholar] [CrossRef]
- Bohaiennko, V.; Bulavatsky, V. Fractional-fractal modeling of filtration-consolidation processes in saline saturated soils. Fractal Fract. 2020, 4, 59. [Google Scholar] [CrossRef]
- Yang, H.M.; Zhang, S.M.; Wang, L.; Chen, P.; Shao, D.K.; Tang, S.W.; Li, J.Z. High-ferrite Portland cement with slag: Hydration, microstructure, and resistance to sulfate attack at elevated temperature. Cem. Concr. Comp. 2022, 130, 104560. [Google Scholar] [CrossRef]
- Meng, Q.; Qin, Q.; Yang, H.; Zhou, H.; Wu, K.; Wang, L. Fractal characteristics of the pore structure of coral powder-cement slurry under different fractal models. Fractal Fract. 2022, 6, 145. [Google Scholar] [CrossRef]
- Wang, L.; Lu, X.; Liu, L.; Xiao, J.; Zhang, G.; Guo, F.; Li, L. Influence of MgO on the hydration and shrinkage behavior of low heat Portland cement-based materials via pore structural and fractal analysis. Fractal Fract. 2022, 6, 40. [Google Scholar] [CrossRef]
- Peng, Y.; Tang, S.; Huang, J.; Tang, C.; Wang, L.; Liu, Y. Fractal analysis on pore structure and modeling of hydration of magnesium phosphate cement paste. Fractal Fract. 2022, 6, 337. [Google Scholar] [CrossRef]
- Wang, L.; Yu, Z.; Liu, B.; Zhao, F.; Tang, S.; Jin, M. Effects of fly ash dosage on shrinkage, crack resistance and fractal characteristics of face slab concrete. Fractal Fract. 2022, 6, 335. [Google Scholar] [CrossRef]
- Wang, L.; Zeng, X.; Yang, H.; Lv, X.; Guo, F.; Shi, Y.; Hanif, A. Investigation and application of fractal theory in cement-based materials: A review. Fractal Fract. 2021, 5, 247. [Google Scholar] [CrossRef]
- Zhang, B.; Li, S. Determination of the surface fractal dimension for porous media by mercury porosimetry. Ind. Eng. Chem. Res. 1995, 34, 1383–1386. [Google Scholar] [CrossRef]
- Yao, D.; Xia, Y.; Zuo, K.H.; Jiang, D.; Günster, J.; Zeng, Y.P.; Heinrich, J.G. The effect of fabrication parameters on the mechanical properties of sintered reaction bonded porous Si3N4 ceramics. J. Eur. Ceram. Soc. 2014, 34, 3461–3467. [Google Scholar] [CrossRef]
- Coble, R.L.; Kingery, W.D. Effect of porosity on physical properties of sintered alumina. J. Am. Ceram. Soc. 1956, 39, 377–385. [Google Scholar] [CrossRef]
- Wang, S.; Yang, Z.; Duan, X.; Jia, D.; Cui, W.; Sun, B.; Zhou, Y. Effects of pore size on microstructure, mechanical and dielectric properties of gel casting BN/Si3N4 ceramics with spherical-shaped pore structures. J. Alloys. Compd. 2013, 581, 46–51. [Google Scholar] [CrossRef]
- Meille, S.; Lombardi, M.; Chevalier, J.; Montanaro, L. Mechanical properties of porous ceramics in compression: On the transition between elastic, brittle, and cellular behavior. J. Eur. Ceram. Soc. 2012, 32, 3959–3967. [Google Scholar] [CrossRef]
- Liu, J.; Li, Y.; Li, Y.; Sang, S.; Li, S. Effects of pore structure on thermal conductivity and strength of alumina porous ceramics using carbon black as pore-forming agent. Ceram. Int. 2016, 42, 8221–8228. [Google Scholar] [CrossRef]






| Samples | Compositions |
|---|---|
| A1 | 9 vol.% carbon fiber + 21 vol.% graphite + 70 vol.% alumina |
| A2 | 15 vol.% carbon fiber + 15 vol.% graphite + 70 vol.% alumina |
| A3 | 21 vol.% carbon fiber + 9 vol.% graphite + 70 vol.% alumina |
| B1 | 15 vol.% carbon fiber + 35 vol.% graphite + 50 vol.% alumina |
| B2 | 25 vol.% carbon fiber + 25 vol.% graphite + 50 vol.% alumina |
| B3 | 35 vol.% carbon fiber + 15 vol.% graphite + 50 vol.% alumina |
| C1 | 21 vol.% carbon fiber + 49 vol.% graphite + 30 vol.% alumina |
| C2 | 35 vol.% carbon fiber + 35 vol.% graphite + 30 vol.% alumina |
| C3 | 49 vol.% carbon fiber + 21 vol.% graphite + 30 vol.% alumina |
| Samples | A1 | A2 | A3 | B2 | B2 | B3 | C1 | C2 | C3 |
|---|---|---|---|---|---|---|---|---|---|
| Weibull (m) | 21.9 | 37.4 | 24.1 | 18.6 | 11.7 | 20.0 | 11.9 | 12.9 | 11.2 |
| Samples | Ds | R2 |
|---|---|---|
| A1 | 2.67513 | 0.99238 |
| A2 | 2.65407 | 0.99291 |
| A3 | 2.63362 | 0.99270 |
| B1 | 2.54288 | 0.99144 |
| B2 | 2.66333 | 0.99302 |
| B3 | 2.60491 | 0.99283 |
| C1 | 2.56622 | 0.99346 |
| C2 | 2.55775 | 0.99045 |
| C3 | 2.44255 | 0.99028 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, X.; Chen, C.; Wang, Y. Fractal Analysis of Porous Alumina and Its Relationships with the Pore Structure and Mechanical Properties. Fractal Fract. 2022, 6, 460. https://doi.org/10.3390/fractalfract6080460
Wang X, Chen C, Wang Y. Fractal Analysis of Porous Alumina and Its Relationships with the Pore Structure and Mechanical Properties. Fractal and Fractional. 2022; 6(8):460. https://doi.org/10.3390/fractalfract6080460
Chicago/Turabian StyleWang, Xufu, Chang Chen, and Yubin Wang. 2022. "Fractal Analysis of Porous Alumina and Its Relationships with the Pore Structure and Mechanical Properties" Fractal and Fractional 6, no. 8: 460. https://doi.org/10.3390/fractalfract6080460
APA StyleWang, X., Chen, C., & Wang, Y. (2022). Fractal Analysis of Porous Alumina and Its Relationships with the Pore Structure and Mechanical Properties. Fractal and Fractional, 6(8), 460. https://doi.org/10.3390/fractalfract6080460






