Abstract
The purpose of this study is to offer a systematic, unified approach to the Mellin-Barnes integrals and associated special functions as Fox H, Aleph ℵ, and Saxena I function, encompassing the fundamental features and important conclusions under natural minimal assumptions on the functions in question. The approach’s pillars are the concept of a Mellin-Barnes integral and the Mellin representation of the given function. A Sinc quadrature is used in conjunction with a Sinc approximation of the function to achieve the numerical approximation of the Mellin-Barnes integral. The method converges exponentially and can handle endpoint singularities. We give numerical representations of the Aleph ℵ and Saxena I functions for the first time.
1. Introduction
In the past 40 years, the field of fractional calculus has undergone extraordinary development. The analytic and numeric approaches in fractional calculus created tremendous progress, especially the analytic side generated diverse directions which increased the improvement tremendously [1]. A large number of methods and approaches were developed, generating a consistent framework for analysis and symbolic computations [1,2]. However, the numeric developments are far behind the analytic achievements especially the numeric representation of special functions like Fox H, Aleph ), and Saxena I functions [3]. Such kinds of functions exist nowadays utilized in the analysis of fractional calculus. The special functions also found its way to applications in physics, engineering, and computer science [4]. It turned out during the years that linear transforms like Laplace-, Fourier-, and Mellin transforms play a vital role to generate special functions like Fox-H, ℵ, and Saxena’s I function [1]. For the generation of such function, it is always essential to use the inverse of linear transforms which analytically exists but finally are difficult to compute numerically. The issue with unknown functions is that they could have previously unknown singularities. Naturally, this affects both the choice of the numerical method and the convergence at these singularities. The convergence of the employed numerical technique itself may also be a concern. This was the case if the approximation was calculated using an inverse Laplace transform, as mentioned in [5,6]. In a recent paper, we demonstrated by using Sinc methods that it becomes pretty efficient when Mittag-Leffler functions, a subset of Fox H functions, are the target in connection with an inverse Laplace transform [7]. Mittag-Leffler functions are frequently used in representing solutions of fractional differential or integral equations [8,9]. However, these functions are only a subset of the analytic functions needed to represent the large assortment of possible solutions to fractional equations.
Generalizations of Fox H functions are ℵ functions which also include the class of Saxena I functions [10]. These exceptional functions, which have been investigated analytically but are difficult to obtain numerically, are still a painstaking foundation for fractional calculus today. We aim to offer a numerical technique that solves most numerical difficulties like convergence and the occurrence of singularities by applying Sinc methods to the computation of these functions. Sinc methods initially introduced by Frank Stenger are a powerful numerical tool that allows representing nearly any calculus operation in an efficient and exponentially converging way [11]. For example, Sinc methods allow for computing of definite or indefinite integrals, convolution integrals, linear integral transforms and their inverse, to solve fractional differential and integral equations, and many other practical computations [12,13]. One essential characteristic of Sinc methods is the use of a small number of computing aids; i.e., small programs, a small number of discretization points, less memory, etc., in connection with a high precision output of numerical results [14]. We shall apply these approaches to the numerical computation of Mellin-Barnes integrals used in the presentation of special functions.
Next, we will introduce the definition of Fox, ℵ, and Saxena I functions. In Section 2, we shall introduce the approximation methods needed for this work. The application of these Sinc methods is demonstrated in Section 3. Section 4 summarizes the results and addresses open problems with the current approach.
1.1. The Fox H Function
The Fox H function was introduced by Charles Fox in connection with dual integral equations in 1965 [15]. As he stated at that time “These H functions contain Bessel functions as special cases and my aim is to show that, with the help of a suitable terminology, it is possible to write down a solution by inspection”. Today we know that Fox H functions are a remarkably broad set of functions and include the elementary as well as special functions. The application of these functions is versatile and permits to derive solutions just by “inspection” as Fox noted. A collection of such applications are comprised in the book by Mathai et al. [4] which extends the classical text by Mathai and Saxena [16]. Both monographs concentrate on the part of getting solutions “by inspection”. However, since then there exists a tremendous need and pressure to boil down the solutions to numbers; i.e., to represent the symbolic Fox H solutions as numerical estimations at least or as accurate numbers. Our aim here is to use the analytic and symbolic ideas of Fox and his successors to evaluate such kinds of solutions numerically. To this end let us introduce some notations for these functions.
A Fox function is defined via a Mellin-Barnes type integral using integers m, n, p, q such that , , for with , the set of complex numbers, and for in the form
with
Here
where represents the natural logarithm of and is not necessarily the principal value. An empty product in (2), if it occurs, is taken to be one, and the poles
of the gamma function and the poles
of the gamma function do not coincide:
The contour in (1) is the infinite contour which separates all the poles in (4) to the left and all the poles in (5) to the right of . In fact there are many ways to define in the complex plane. However, we will concentrate on the cases where is parallel to the imaginary axis in the complex plane. For this reason let , where and are real; then the contour along which the integral of (1) is taken is the straight line whose equation is , where is a constant. This line is parallel to the imaginary axis in the complex s plane and separates the poles.
For numeric integration we take as a contour starting at the point and terminating at the point , where . To simplify the integration we use the substitutions and which delivers
allowing a direct integration to represent the Fox H function at points . Note that the rightmost integral in (7) is a highly oscillating integral. Such kinds of integrals need special care if treated by standard quadrature methods. We will deal with this problem by using the Sinc quadrature discussed in Section 2. The absolute convergence of the integral can be guaranteed under certain conditions on the parameters of the Fox H function; for details see [3].
1.2. The ℵ Function
The ℵ function was introduced by the authors during the examination of fractional differential equations particularly the drift less Fokker-Planck equation [17,18]. The function is a generalization of Fox H function and allows to handle different initial conditions. Today, the ℵ function is well established and in use in several applications [19,20,21,22,23].
An ℵ function is defined via a Mellin-Barnes type integral using integers m, n, , such that , , for with , the set of complex numbers, and for , for k = 1,…,r. The integration path extends from to , and is such that the poles of the gamma functions in the numerator , do not coincide with the poles of the gamma functions , . The parameters and are non-negative integers satisfying , . All the poles of the integrand (8) are often assumed to be simple, and the empty product is interpreted as unity. The ℵ function is defined as follows
with the Mellin representation of the kernel
Here
Note that the Fox H function follows from the ℵ function in case when and . If for the Aleph function reduces to a Saxena I function [10]. According to the definition of we are numerically dealing with a Bromwich integral in the form
The Aleph function in the present form is the result of solving integral and differential equations using linear transform techniques and is now considered the most generalized special function of a function representation [22].
1.3. The Saxena Function
A Saxena I function is similarly defined as an ℵ function via a Mellin-Barnes type integral using integers m, n, , such that , , for with , the set of complex numbers, and for , and [10], in the form
with the Mellin representation of the kernel
Here
The conditions for the contour are the same as for the ℵ function.
2. Approximations
The approaches for approximating using Sinc functions are discussed in this section. First, the basic concepts of Sinc approximations are introduced describing the terms and notion. The second part deals with approximations of definite integrals. Based on these definitions we introduce the approximation of Mellin-Barnes integrals in the next step. We use the properties of Sinc functions allowing a stable and accurate approximation based on Sinc points [24]. For a detailed representation we refer the reader to [11,13].
2.1. Sinc Basis
To start with we first introduce some definitions and theorems allowing us to specify the space of functions, domains, and arcs for a Sinc approximation.
Definition 1.
Domain and Conditions.
Let be a simply connected domain in the complex plane and having a boundary . Let a and b denote two distinct points of and ϕ denote a conformal map of onto , where , such that and . Let denote the inverse conformal map, and let Γ be an arc defined by . Given ϕ, ψ, and a positive number h, let us set , to be the Sinc points, let us also define .
Note the Sinc points are an optimal choice of approximation points in the sense of Lebesgue measures for Sinc approximations [24].
Definition 2.
Function Space.
Let , and let the domains and be given as in Definition 1. If is a number such that , and if the function ϕ provides a conformal map of onto , then . Let α and β denote positive numbers, and let denote the family of functions , for which there exists a positive constant such that, for all . Let be the set of all analytic functions, for which there exists a constant , such that
Now let the positive numbers α and β belong to , and let denote the family of all functions , such that and are finite numbers, where and , and such that where
These definitions directly allow the formulation of an algorithm for a Sinc approximation. Let denote the set of all integers. Select positive integers N and so that . The step length is determined by where , , and d are real parameters. In addition assume there is a conformal map and its inverse such that we can define Sinc points , [25]. The following relations define the basis of a Sinc approximation:
The shifted Sinc is derived from relation (17) by translating the argument by integer steps of length h and applying the conformal map to the independent variable
The approximation of a function results to the representation
using the set of orthogonal functions
where is the conformal map. This type of approximation allows to represent a function on an arc with an exponential decaying accuracy [11]. As proved in [11,13] the approximation works effectively for analytic functions. The approximations (19) allow us to formulate the following theorem for Sinc approximations.
Theorem 1.
Sinc Approximation [25].
Let for and , take M = [β N/α], where [x] denotes the greatest integer in x, and then set . If , and if then there exist positive constants and independent of N, such that
with the base function (see (22)).
The proof of this theorem is given in [13]. Note the choice is close to optimal for an approximation in the space in the sense that the error bound in Theorem 1 cannot be appreciably improved regardless of the basis [25]. It is also optimal in the sense of the Lebesgue measure achieving an optimal value less than Chebyshev approximations [24].
Here are the discrete points based on Sinc points . Note that the discrete shifting allows us to cover the approximation interval in a dense way while the conformal map is used to map the interval of approximation from an infinite range of values to a finite one. Using the Sinc basis we are able to represent the basis functions as a piecewise defined function by
where . This form of the Sinc basis is chosen as to satisfy the interpolation at the boundaries. The basis functions defined in (22) suffice for purposes of uniform−norm approximation over .
This notation allows us to define a row vector of basis functions
with defined as in (22). For a given vector we now introduce the dot product as an approximation of the function by
Based on this notation, we will introduce in the next subsection approximations of definite integrals [13].
2.2. Definite Integral Approximation
In this section, we pose the query of how to approximate definite integrals on a domain over . The approximation will use our basis system introduced in Section 2.1. It turns out that for the basis systems (20), we can get an approximation converging exponentially. Specifically, we are interested in a quadrature formula for definite integrals of the type
where a and b can be finite or infinite. If the function f is approximated by the approximation given in Section 2.1, we write for ,
Scaling the variable and collocating the expression with respect to , we end up with the representation
Equation (28) represents a quadrature formula applicable to different domains. Compared with a Gaussian quadrature formula (28) delivers the weights as well as the function values if the discretization is known by with and . Note since the conformal map depends on the structure of the arc ; i.e., finite, semi-infinite or infinite, the approximation is defined for domains , , or , respectively [11]. The following Theorem summarizes these results.
Theorem 2.
Definite Integrals.
If ϕ denotes a one−to−one transformation of the interval onto the real line , let h denote a fixed positive number, and let the Sinc points be defined on by , , where denotes the inverse function of the conformal map ϕ. Let M and N be positive integers, set , and for a given function f defined on , define the vector , and a vector , then the definite integral is approximated by
and the error of this approximation was estimated in [11] as
where and are constants independent of N.
2.3. Sinc Approximation of Mellin-Barnes Integrals
The Sinc approximation of the Fox H functions needs two discretization steps. Foremost the Sinc discretization of the arc on which the function should be represented finite or semi-infinite and second the Sinc quadrature of the Mellin-Barnes integral at these Sinc points on the arc. The second discretization is a Sinc quadrature on an infinite interval corresponding to the line at parallel to the imaginary axis in . In formulas this means
where , generating a vector which approximates the Fox H function pointwise at on an arc . is selected according to the pole structure of the functions of the numerator in the Mellin representation. Using the basis functions (22) on the arc , we shall approximate the Fox H function by
This approach guarantees that the error will decay as given by (21). Note that a Sinc point based interpolation is able to deal with singularities at the end points of the arc .
Since the ℵ function and the Saxena I functions are similarly defined by Mellin-Barnes integrals as the Fox H function, the procedure for the approximation follows the same line delivering for the ℵ function
and the Saxena I function
All three approximations will satisfy the a priory error formula (21) and converge exponentially to their exact value.
The following section shall demonstrate by a few examples the numerical representation of the three generalized functions.
3. Numerical Examples
This section collects some examples demonstrating the efficient and accurate numerical evaluation of Sinc-based methods applied to Mellin-Barnes integrals, Fox H-, Saxena I-, and ℵ functions. We selected the examples concerning their analytic representation applied to specific physical or engineering problems. Allowing us to compare our results with exact expressions and thus delivering an a priori estimation of the numerical errors. For every comparison in which we calculated local errors, the analytical solution was employed. The following graphics display the analytical answer as a solid line. Over the solid line, the equivalent numerical approximation is displayed as a dashed curve. We may depend on the previously mentioned exponential convergence of the Sinc quadrature and Sinc approximation if no local errors are calculated in the graphs. The analytic Sinc approximations, however, are typically not represented because of their large symbolic representation since we are utilizing a computer algebra system.
3.1. Fox H Functions
In this subsection, we present some examples which are taken from the literature where the symbolic representation was given [1,2,4]. In most of these cases a numerical evaluation of the functions is not offered or discussed. For the first time we will show the numerical evaluation and the a priori error estimation using Sinc methods.
Example 1.
Exponential function
It is well-known that the exponential function is connected with the Mellin transform via the Euler Γ function. The relations between the two functions are as follows
and
where the later of these two expressions is the Mellin transform of the exponential function and the first its inverse given by a Bromwich integral over the vertical line , of the complex s-plane. Whereas the last formula (36) is due to L. Euler who communicated it in two letters of 13 October 1729, and 8 January 1730, to Goldbach. The first formula (35) in a somewhat different form goes back to Pincherle [9,26] as Mellin reported in his paper [27]; but it was Mellin who first realized its great importance.
Let us first numerically examine the representation of the exponential function using the Fox H representation. The exponential function is defined in terms of a Fox H function by
Using the duplication formula for the Γ function in the right most term of (37), we end up with the Mellin representation in (35). The line integral is then calculated by the Mellin-Barnes integral via
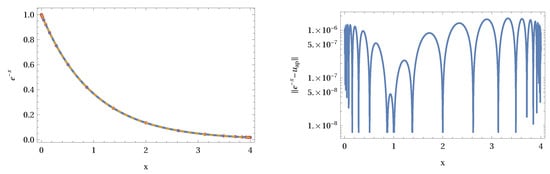
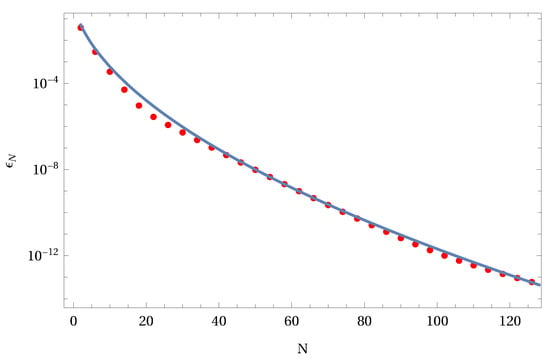
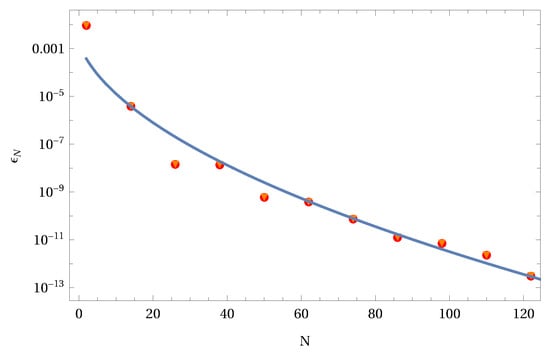
where the path is chosen according to the pole structure of the Γ functions so that γ is a fixed real number. For different z values selected as Sinc points, we compute the numerical values of the integral in the domain for . The set of values is used in a Sinc approximation delivering an analytic representation of the function in terms of the Sinc basis. Results of such an approximation are illustrated in the following Figure 1. Figure 1 shows the exact function (solid line), the Sinc approximation (dashed), and the discrete set of Sinc points (dots). The right panel shows the local error of the approximation. In Figure 2, we depict the error decay of the Sinc approximation as a function of the used number of Sinc points N. A least square fit was used to get the two parameters and which determine the error formula. The example demonstrates that the approximation of the Fox H function is accurate and the precision of the approximation can be a priori estimated using the error decay Formula (30).

Figure 1.
Numerical representation of the Fox H function as a Sinc approximation based on (35) using Sinc points for x. The norm over the local error delivers a value of .

Figure 2.
Error decay with and . The two parameters and are the result of a least square fit.
Example 2.
Mittag-Leffler functions
Over the years it turned out that Mittag-Leffler (ML) functions are of central importance in fractional calculus [5,8,14,28]. This kind of functions are used in many applications and in theoretical work [2]. However, these functions need a special approach when it comes to their numerical representation. Quite recently, we presented an approach to tackle the numerical representation by an inverse Laplace transform [7]. It was shown that a Sinc based approach has some advantages over the standard Talbot or Weideman approach used by Garrappa et al. [6,29,30]. A second approach to numerically represent Mittag-Leffler functions is now available with high accuracy and precision using Fox H functions in connection with Sinc quadrature. We will restrict our discussions to the main three types of Mittag-Leffler functions which are classified as single-, two-, and three-parameter ML functions. The three-parameter ML function is also known as Prabhakar’s function. There are in fact higher parameter ML functions in use which are defined via Fox H functions [28]. We note that these functions are also numerically available with high accuracy. However, due to lack of space, we will not present them here.
The three ML functions we have in mind are defined by the following relations:
and
The line integral is computed by the Mellin-Barnes integral via
where the path is selected according to the pole structure of the Γ functions so that γ is a fixed real number. For different z values selected as Sinc points, we compute the numerical values of the integral in the domain for . The set of values is used in a Sinc approximation.
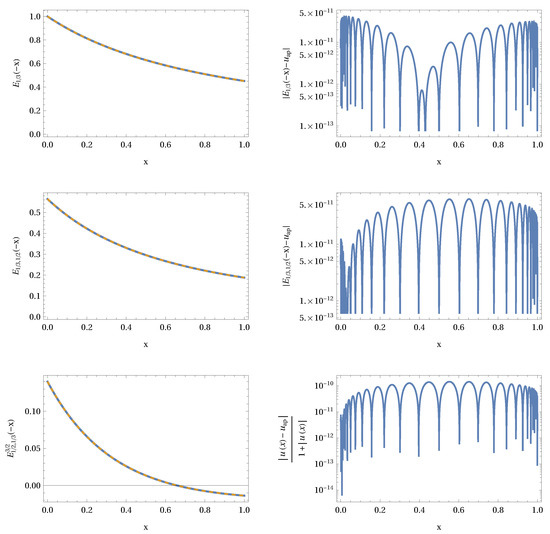
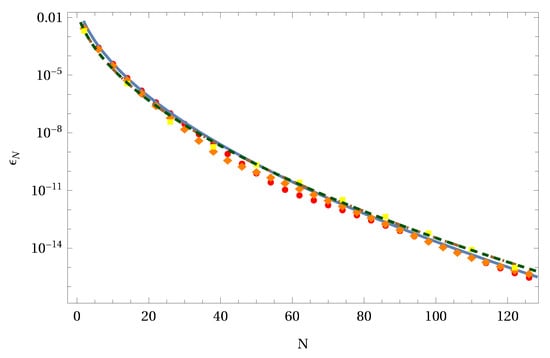
In Figure 3 we graph the solution for the one-, two-, and three-parameter ML function for a specific selection of parameters (left column of Figure 3). The dashed lines correspond to the Sinc approximation while the solid line represents the Mathematica approximation for the first two ML functions and a higher order Sinc approximation with for the Prabhakar ML function. Obviously there is no visible difference for all three types of ML functions. This becomes obvious if we examine the right column of Figure 3. Here the absolute value of the local error is shown for the two first ML functions and a relative error for Prabhakar’s function. The magnitude in all cases is less than . Figure 4 collects the error decay as a function of the number of Sinc points N used in the approximations. It is obvious that for all three types of ML functions nearly the same functional error decay results. This indicates that the upper bound estimation of Equation (30) is satisfied and allows an a priori estimation of the expected error.

Figure 3.
Function representation for , , and from top to bottom, left column with Sinc points. The parameters , , and are indicated in the axis labels, respectively. The local errors are shown in the right column accordingly. For Prabhakar’s function we have to use a relative error because the exact representation is not available. The reference solution was computed with Sinc points.

Figure 4.
Error decay for the three ML functions , , and (dots, solid), (diamond, dot dashed), and (square, dashed), respectively. The least square fit for each function delivered the values , , and .
The least square parameters of the three error decays also indicates that all three functions belong to the same function space introduced in Definition 2.
Example 3.
Krätzel Function
The Krätzel integral was defined by Krätzel [31] as the kernel of an integral transform as follows:
Today we know that the Krätzel function occurs in many fields of applications, such as the study of astrophysical thermonuclear reactions, reaction rate probability integrals in the theory of nuclear reaction rates, in applied analysis, inverse Gaussian distribution, generalized families of distributions in statistical distribution theory, and in statistical mechanics as well as the general pathway model are all shown to be connected to the integral (43) [4]. The generalized Krätzel function was examined by Kilbas and Kumar [32]. Solar radiation data were examined recently in connection with probability distribution functions by Princy [33]. Due to the versatile applications of the Krätzel function, we demonstrate the numerical representation as a density function.
The normalized probability density can be represented as Fox H function by
here , , , and . The corresponding line integral representation is computed by the Mellin-Barnes integral via
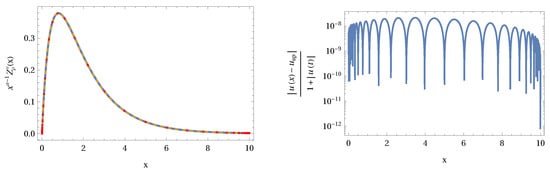
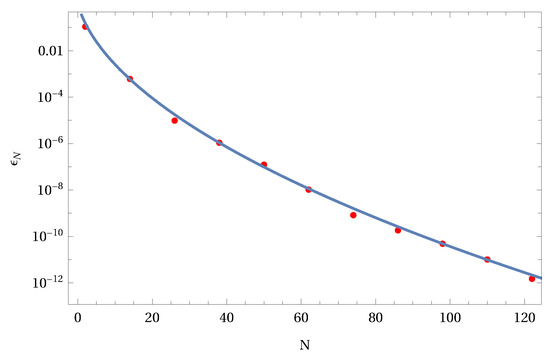
where the path is selected according to the pole structure of the Γ functions, so that γ is a fixed real number. For different discrete z values using Sinc points, we compute the numerical values of the integral in the real domain . The set of values is used in a Sinc approximation. An example using specific parameters and is shown in Figure 5. The left panel of Figure 5 represents the probability density based on and (dashed) Sinc points. The right panel of Figure 5 shows the relative local error of these two versions of the approximation. It is obvious that the local error is small and nearly homogenous on the domain . In Figure 6, we present the error decay of computations with different number of Sinc points used in the approximation. The solid line represents the least square approximation of the two parameter error formula (30). Note that for small numbers of Sinc points we already reach an acceptable small error. If we double the number of Sinc points, we gain more than one decade of accuracy. Figure 6 clearly demonstrates that we have an exponential decay of the error.

Figure 5.
The Krätzel function used as a probability density function for , , and (left panel). The relative local error of the distribution (right panel). Number of Sinc points .

Figure 6.
Error decay for the Krätzel function with , . The least square fit delivered the values .
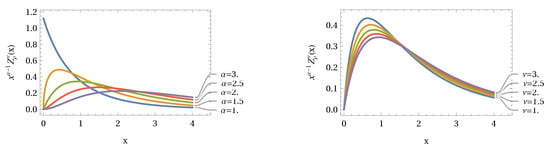
In Figure 7 we demonstrate the variation of the Krätzel function if we change one of the parameters α or ν, respectively.

Figure 7.
The Krätzel function for with variation (left graph) and variation (right graph).
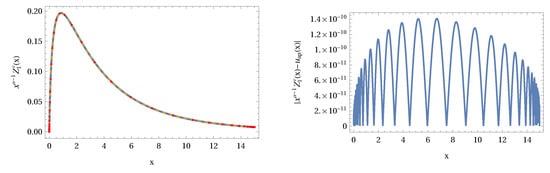
For the special choice , the Krätzel density is reduced to the modified Bessel function with the specific representation
This relation can be used to check the accuracy of our numerical computations shown in Figure 8. For a few number of approximation points , we are able to reach a low level of local errors.

Figure 8.
The Krätzel function for , and (left graph). Right panel local error between the approximation and the Bessel representation. Number of Sinc points .
Example 4.
Abel Equation
In the current example, we will examine the following Abel integral equation
where λ and are real parameters [8,34]. The integral can also be identified as a Riemann-Liouville fractional integral so that (47) can be written as
This in turn opens the connection to the fractional kinetic equation for astrophysical systems examined by Haubold and Mathai [35] using a constant function and . However, such kind of equation was already examined in 1991 by Glöckle and Nonnemacher in connection with viscoelastic materials [36]. We will numerically demonstrate that the use of Fox H functions in connection with a Sinc convolution integral allows a general solution as long as the Laplace transform of exists. In their work on Mittag-Leffler functions, Gorenflow et al. [8] state in Theorem 4.2 the problem based on [37] in which the solution of (47) using convolution integrals are examined. The solution of (47) using two parameter Mittag-Leffler functions [35] reads
This result goes back to the pioneering work of Hille and Tamarkin in 1930 [37]. Introducing new variables in (49) by and using the Fox H representation of the ML function allows us to rewrite the convolution integral as
which can be rewritten by using properties of the Fox H function [4] as
This representation of the solution is suitable for Sinc convolution computations because we already know how to get the discrete Sinc representation of the Fox H function. This data at hand, we only need the Stenger Laplace representation of f to perform the convolution. For details of the numerical approach and implementation see [7,13].
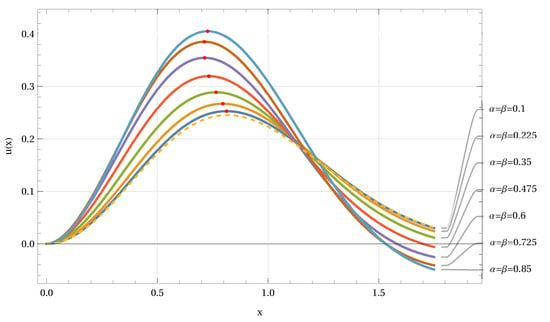
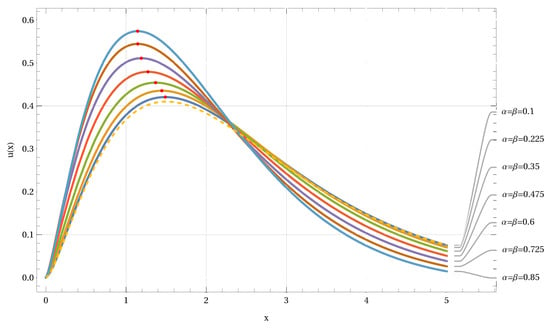
Applying the numerical Sinc methods, we can generate solution approximations for different fractional orders (see Figure 9). The results in Figure 9 demonstrate that the solution starts at like the function f (dashed line). A single peak is observed with varying maximum value and location when is changed. The location of the maximum shifts to the right if the values for become smaller.

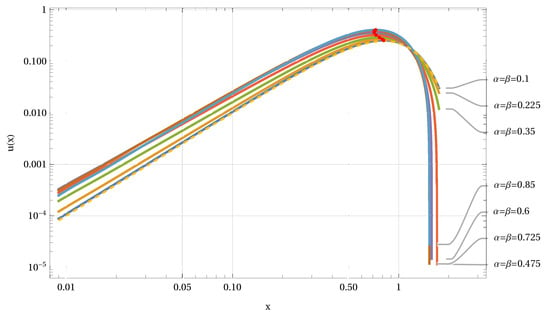
In astrophysical applications, the Maxwell-Boltzmann distribution is used as a standard model for idealized gases. Abel’s Equation (47) can be solved by using a Maxwell-Boltzmann distribution as inhomogeneity. Convolution with the Fox H kernel delivers a shifted distribution as shown in Figure 10 (top graph). The double logarithmic graph (bottom) of Figure 10 for the same computation indicates a similarity observed for the solar neutrino spectrum [38] with a sharp decline on the right side of the function and a linear relation on the left end (in scaled figures).
The examples demonstrate that our approach to represent numerically Fox H functions is highly efficient.
3.2. ℵ Functions
This subsection is discussing numerical representations of different ℵ functions as “simple” functions and advanced applications, as introduced in Equation (8). One characteristic of the ℵ function is the weighted sum of functions in the denominator in Mellin space. We will present different simple and advanced rational expressions of functions to represent functions for which their analytic expressions are unknown. In general, we do not know the specific names of the resulting functions, but we are able to generate analytic representations based on Sinc approximations. The Sinc representation in turn allows generalizations of the Fox H and Saxena I functions. In turn, the Sinc representation allows a numeric computation of function values. Since we do not know what kind of analytic function is represented by the fractions in Mellin space, we shall use a reference representation generated by numerous Sinc points () to estimate a relative error. This approach to estimate the error of the approximation can be used because we know from (21) and (30) that the Sinc approximation converges exponentially. Due to this fact, the error given in the following examples is always a relative error with respect to this large Sinc point approximation.
Recently some applications of ℵ functions to engineering and biomedical applications were discussed in the literature [39,40,41] while applications are discussed in [42,43]. However, the authors stop at the analytical representation of their results and do not generate a numerical verification. We will extend their approaches by going one step further to show that a numerical representation of ℵ functions is possible. Thus, the discussed models can be numerically verified. Due to lack of space, we will restrict ourselves to the function representation only.
Example 5.
Characteristic simple ratio
This example uses a rational expression of Γ functions in such a way that it cannot be reduced to a Fox H or a Saxena I function. The ratio keeps the characteristic of the ℵ function, with a sum of weighted Γ functions in the denominator. We examine the following ratio numerically
by evaluating the following Mellin-Barnes integral on a line parallel to the imaginary axis
A reference approximation using Sinc points is plotted in the same graph as solid line. Obviously there is no visual difference between the low and high approximation. The used Sinc points for approximation are shown as dots in the graph. The right panel of Figure 11 shows the local relative error of the approximation. The reference in this graph is the Sinc approximation with the large number of Sinc points. The right panel reflects a mean error of approximately which is acceptable for applications.

Figure 11.
A true ℵ function using a Mellin representation approximated with Sinc points (left panel). The right panel shows the local relative error where is given by a Sinc approximation with .
First, we verify the accurate representation of the approximation shown in Figure 11. The left panel shows the function approximation using . In Figure 12 we examine the error based on the norm of the relative local error. The error shows an exponential decay if the number of approximation points N is increased. The upper bound of this decay follows the relation (30) which is indicated by the solid line.

Figure 12.
Error decay . The least square fit delivered the values . The • and the ▾ indicate the error estimation based on the relative norm error and the norm, respectively. In the norms, the exact function is replaced by the Sinc approximation using Sinc points. It is obvious that the two error estimations deliver nearly the same numerical values.
We were also curious to see how the ℵ function changes when some Mellin representation elements are changed. As a result, we included four factors at various points in (53). Because the current form in (53) is so straightforward, we modified it to a single parameter representation as follows:
and
The Mellin-Barnes integral yields the equivalent function
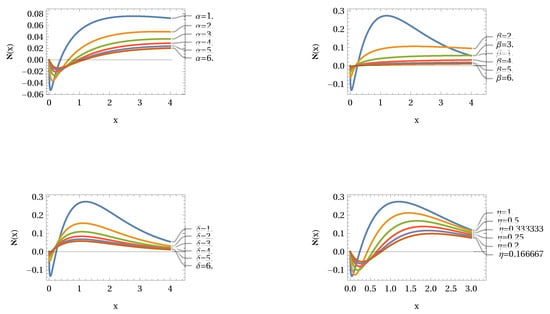
where α, β, δ, and η are all derived from . Variation of the parameters α, β, δ, and η result in distinct variations of the function according to the definition of the ℵ function in (54) and (55). Figure 13 depicts the variation results. We can see that the function behavior varies continuously within a defined region of parameters.

Figure 13.
Variation of parameters (indicated in the panels) for , , , and .
Example 6.
Two parameter weighted Mittag-Leffler (wML) function
It is simple to generalize some types of functions when a tool like the ℵ function is available. In the next example, we will demonstrate this. A Fox H function defines the two-parameter Mittag-Leffler (ML) function, as shown in (40). We may introduce the following representation by following the same line of representation as an ℵ function.
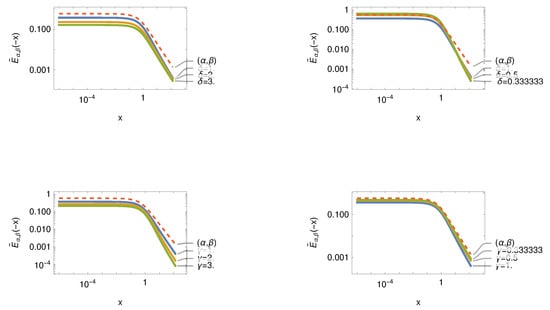
The Mellin representation of the extended Mittag-Leffler function is similar to the two parameter Mittag-Leffler function represented as Fox H function with three Γ terms. The numerator is exactly the same as the Equation (40). The denominator term is weighted by the coefficients δ and γ. The term containing the weight of δ is the same as (40). The difference exists only in the γ weighted term. If we select and , we reproduce the two parameter Mittag-Leffler function . To examine the influence of the two weight parameters δ, , we vary them and represent the results in Figure 14. The Figure indicates that a variation of either of δ or γ in a fractional or integer way will approach the two parameter Mittag-Leffler function from above or below, respectively. In Figure 14 we represent in each row the variation of the parameter δ and γ. The left column of the Figure show changes approaching values larger than one, while the right column shows an approach to smaller values than one. Larger values than one separate the graph of the wML function from the two parameter ML function. Smaller values than one move the graphs of the wML function towards the unweighted ML function, or transpass the ML function in case of δ variation. In addition, we observe that the asymptotic values for larger x values approach a different asymptotic behavior of the ML function. While for (top row) the asymptotic slope is nearly the same for (bottom row) we observe a fanning out of the asymptotic behavior. In general, we can state that the asymptotic behavior of the wML function assumes a different slope than the ML function, which is typically larger than the slope of the ML function.

Figure 14.
Variation of parameters (indicated in the panels) for the weighted Mittag-Leffler function using and . The top row uses and the bottom row . The Mittag-Leffler function is shown as reference (dashed line). The number of Sinc points in all approximations is .
This example demonstrates that well-known functions can be modified straightforwardly if we introduce weights in an ℵ representation in Mellin space. This bears the potential that we can adapt specific functions which do not fit to practical data properly within a well-defined function environment. Such a tool is of utmost practical importance if the data set is of experimental origin.
Example 7.
Solution of Abel’s Integral Equation (47) Generalized
The present example deals with Abel’s equation’s solution (51). We assume that (51) is a function (u(x)) produced by a convolution based on a known function . If we view (51) as a convolution integral, we may alter the restrictions to and/or substitute the ML function with a wML function based on ℵ functions. These modifications will produce a convolution integral representation of the type:
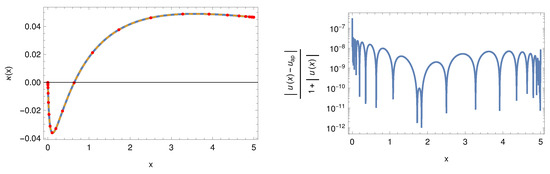
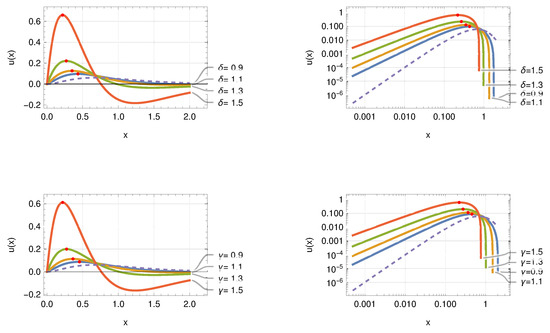
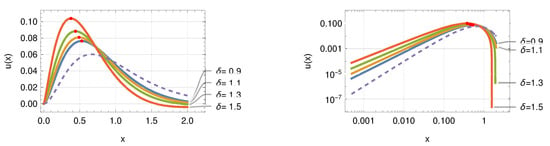
i.e., in the convolution, we replace the Fox H function with an ℵ function. This is a simple assignment in terms of basic arithmetic. The related integral equation, on the other hand, will convert to an unknown equation. We will employ Sinc convolution techniques to produce the function once more, [7,13]. Consider first the case when with and . As previously stated, the weights γ and δ allow for the adaptation of the function to a desired structure, which is more adaptable to a specific instance than the Fox H example. This trait is depicted in Figure 15. The weights allow the curves in the double logarithmic representations to be spread out by approximately four decades in amplitude.

Figure 15.
Variation of parameters (indicated in the panels) for the convolution integral (56) using a weighted Mittag-Leffler function based on ℵ functions. The parameters are and . The top row uses and the bottom row . The number of Sinc points in all approximations is . The inhomogeneity used is (dashed line).
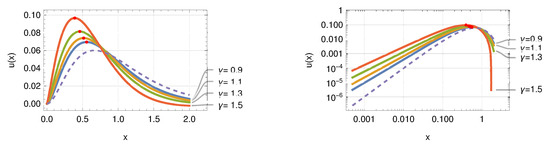
The second situation considered is given by with and . We also modified the weights δ and γ for this set of parameters, resulting in Figure 16. A comparison of Figure 15 and Figure 16 illustrates that changing the relationship between α and β modifies the original function . If pronounced peaks and minima appear, while just a prominent maximum and shallow minima appear in the opposite case. The position of maxima is marked by dots in both Figures.


Figure 16.
Variation of parameters (indicated in the panels) for the convolution integral (56) using a weighted Mittag-Leffler function based on ℵ functions. The parameters are and . The top row uses and the bottom row . The number of Sinc points in all approximations is . The inhomogeneity used is (dashed line).
The examples revealed that we can get numerical values for unknown functions with a few discretization points. The parameter variation allows for a continual modification in the functions, resulting in the desired representation.
3.3. Saxena I Functions
Rather of examining the Saxena I function, we compare the three special functions in this section. As a result, we utilize the case of stable distributions, which Schneider initially looked at in conjunction with Fox H functions [44]. Later, Mainardi and Pagnini used Mellin-Barnes integrals to investigate the Schneider technique [45]. This representation of Fox H functions in Mellin space will be extended to ℵ- and Saxena I functions. We already know that this change in the Mellin model of "stable distributions" leads to various distributions. However, it is fascinating how close some of these functions are to one another. We can use the restrictions on the weights to go back to the Fox H function for the ℵ function. The purpose of this section is to compare these classes of functions graphically by graphing their numerical representations.
Example 8.
Stable Distributions
Schneider established stable one-sided Lévy distributions using a Fourier-Stieltjes transform in conjunction with the Mellin transform [44]. As a result, the density representation in Mellin space is as follows:
where and . In Mellin space, however, relation (60) is nothing more than a Fox H representation. As a result, we may write
which will deliver using the Mellin-Barnes integral the probability density
with . Now we may ask what happens if we replace H with either the ℵ or the Saxena I function in (62); i.e., we set
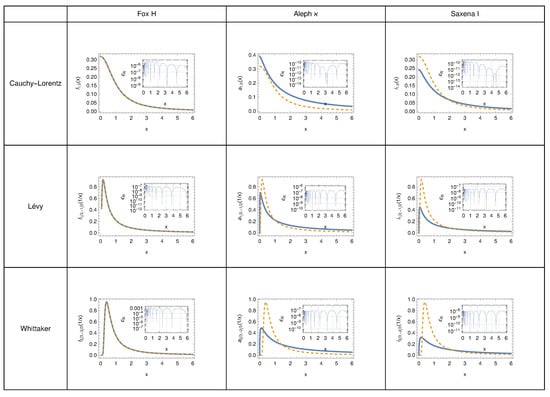
or
as integrand in (62) and get or , respectively. The results are quite interesting and have some similarities with the original definition of the one-sided stable distribution function. The results are collected for a view examples in Figure 17. We depict the Cauchy-Lorentz case with , the Lévy case using , and one of the Whittaker cases using shown in each row, respectively. The Fox column in Figure 17 shows the one-sided stable distribution. The Aleph- and the Saxena columns represent the graphs based on the respective function representation. As a reference, we graph in each row the analytic representation of the function as a dashed line. For Cauchy-Lorentz we have , the Lévy distribution is , and the Whittaker distribution is , where is Whittaker’s W function. The “distributions” based on Aleph or Saxena are graphed as solid lines. We also included an inset to each graph that shows the approximation’s local absolute error. The Aleph and Saxena-based approximations clearly resemble the original distribution in various ways. If the weights are experiencing some limiting process like and , the original distribution can be restored using the Aleph approximation. We don’t have the freedom to adjust the numerical approximation in the Saxena approximation; the numerical approximation is set. The local absolute and relative error is a minor number, as seen in the insets. Furthermore, we may infer from Figure 17 that the asymptotic behavior of the Aleph and Saxena approximations take the values of the Fox H function.

Figure 17.
Three one sided stable distributions and their Aleph and Saxena variants. The number of Sinc points in all approximations is .
The example shows that, in addition to the Fox and Aleph approximations, the Mellin-Barnes representation technique also works for the Saxena I function.
4. Conclusions
We showed that a Sinc approximation of the Mellin-Barnes integral produces acceptable numerical results for three classes of special functions. We were able to construct numerical representations of the Aleph- and Saxena I functions for the first time. The above example demonstrates how simple it is to deal numerically with new and unknown functions. It was observed that the Sinc approximation works effectively with an exponential convergence rate. The calculation benefits greatly from the very small number of discretization points. Furthermore, the approximation approach can handle singularities at the approximation interval’s endpoints. This is only foreseeable by an asymptotic analysis for a certain choice of parameters in the Mellin representation of the functions. In this work, we looked at standard integration pathways parallel to the imaginary axis. However, the Mellin-Barnes contour is not limited to this particular example. In future studies, we are going to investigate alternative contours that may be useful in numerically representing special functions.
Author Contributions
Conceptualization, G.B. and N.S.; methodology, G.B.; software, G.B.; validation, G.B. and N.S.; formal analysis, G.B.; investigation, G.B.; writing—original draft preparation, G.B.; writing—review and editing, G.B. and N.S.; visualization, G.B.; supervision, G.B.; project administration, G.B.; All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Acknowledgments
The authors acknowledge the inspiring discussions and valuable ideas by Frank Stenger.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Kochubei, A.N.; Luchko, Y.F.; Karniadakis, G.; Tarasov, V.E.; Petráš, I.; Baleanu, D.; Lopes, A.M. (Eds.) Handbook of Fractional Calculus with Applications; De Gruyter Reference; De Gruyter: Berlin, Germany; Boston, MA, USA, 2019; ISBN 978-3-11-057081-6. [Google Scholar]
- Beghin, L.; Mainardi, F.; Garrappa, R. (Eds.) Workshop on Nonlocal and Fractional Operators; Nonlocal and Fractional Operators; Springer: Cham, Switzerland, 2021; ISBN 978-3-030-69236-0. [Google Scholar]
- Kilbas, A.A.; Saigo, M. H-Transforms: Theory and Applications; Analytical Methods and Special Functions; Chapman & Hall/CRC: Boca Raton, FL, USA, 2004; ISBN 978-0-415-29916-9. [Google Scholar]
- Mathai, A.M.; Saxena, R.K.; Haubold, H.J. The H-Function: Theory and Applications; Springer: New York, NY, USA, 2010; ISBN 978-1-4419-0915-2. [Google Scholar]
- Garrappa, R. Numerical Evaluation of Two and Three Parameter Mittag-Leffler Functions. SIAM J. Numer. Anal. 2015, 53, 1350–1369. [Google Scholar] [CrossRef]
- Weideman, J.A.C.; Trefethen, L.N. Parabolic and Hyperbolic Contours for Computing the Bromwich Integral. Math. Comp. 2007, 76, 1341–1357. [Google Scholar] [CrossRef]
- Baumann, G. Sinc Based Inverse Laplace Transforms, Mittag-Leffler Functions and Their Approximation for Fractional Calculus. Fractal Fract. 2021, 5, 43. [Google Scholar] [CrossRef]
- Gorenflo, R.; Kilbas, A.A.; Mainardi, F.; Rogosin, S.V. Mittag-Leffler Functions, Related Topics and Applications; Springer Monographs in Mathematics; Springer: Berlin/Heidelberg, Germany, 2014; ISBN 978-3-662-43929-6. [Google Scholar]
- Mainardi, F.; Pagnini, G. Salvatore Pincherle: The Pioneer of the Mellin-Barnes Integrals. J. Comput. Appl. Math. 2003, 153, 331–342. [Google Scholar] [CrossRef]
- Saxena, V.P. Formal Solution of Certain New Pair of Dual Integral Equations Involving H-Functions. Proc. Nat. Acad. Sci. India Sect. A 1982, 52, 366–375. [Google Scholar]
- Stenger, F. Numerical Methods Based on Sinc and Analytic Functions; Springer Series in Computational Mathematics; Springer: New York, NY, USA, 1993; Volume 20, ISBN 978-1-4612-7637-1. [Google Scholar]
- Baumann, G.; Stenger, F. Fractional Calculus and Sinc Methods. Fract. Calc. Appl. Anal. 2011, 14, 568. [Google Scholar] [CrossRef]
- Stenger, F. Handbook of Sinc Numerical Methods; Chapman & Hall/CRC Numerical Analysis and Scientific Computing; CRC Press: Boca Raton, FL, USA, 2011; ISBN 978-1-4398-2158-9. [Google Scholar]
- Baumann, G. New Sinc Methods of Numerical Analysis: Festschrift in Honor of Frank Stenger’s 80th Birthday; Trends in Mathematics; Springer International Publishing: Cham, Switzerland, 2021; ISBN 978-3-030-49715-6. [Google Scholar]
- Fox, C. A Formal Solution of Certain Dual Integral Equations. Trans. Am. Math. Soc. 1965, 119, 389–398. [Google Scholar] [CrossRef]
- Mathai, A.M.; Saxena, R.K. Generalized Hypergeometric Functions with Applications in Statistics and Physical Sciences; Lecture Notes in Mathematics; Springer: Berlin/Heidelberg, Germany; New York, NY, USA, 1973; ISBN 978-3-540-06482-4. [Google Scholar]
- Südland, N.; Baumann, G.; Nonnenmacher, T.F. Open problem: Who knows about the Aleph-functions. Fract. Calc. Appl. Anal. 1998, 1, 401–402. [Google Scholar]
- Südland, N.; Baumann, G.; Nonnenmacher, T.F. Fractional driftless Fokker-Planck equation with power law diffusion coefficients. In Proceedings of the Computer Algebra in Scientific Computing CASC 2001: Proceedings of the Fourth International Workshop on Computer Algebra in Scientific Computing, Konstanz, Germany, 22–26 September 2001; Ganzha, V.G., Mayr, E.W., Vorozhtsov, E.V., Eds.; Springer: Berlin/Heidelberg, Germany, 2001; pp. 513–528. [Google Scholar]
- Saxena, R.K.; Pogány, T.K. On Fractional Integration Formulae for Aleph Functions. Appl. Math. Comput. 2011, 218, 985–990. [Google Scholar] [CrossRef]
- Südland, N.; Volkmann, J.; Kumar, D. Applications to Give an Analytical Solution to the Black Scholes Equation. Integral Transform. Spec. 2019, 30, 205–230. [Google Scholar] [CrossRef]
- Gupta, P.; Shekhawat, A.S. Fractional Calculus Associated with General Polynomials and Aleph Functions. Glob. J. Pure Appl. Math. 2017, 13, 957–966. [Google Scholar]
- Chaurasia, V.B.L.; Singh, Y. Lambert’s Law and Aleph Function. Int. J. Modern Math. Sci. 2012, 4, 84–88. [Google Scholar]
- Khan, Y.; Sharma, P. Some Integral Properties of Aleph Function, General Class of Polynomials Associated with Feynman Integrals. Int. J. Math. Stat. Invent. 2014, 2, 21–27. [Google Scholar]
- Stenger, F.; El-Sharkawy, H.A.M.; Baumann, G. The Lebesgue Constant for Sinc Approximations. In New Perspectives on Approximation and Sampling Theory; Zayed, A.I., Schmeisser, G., Eds.; Applied and Numerical Harmonic Analysis; Springer International Publishing: Cham, Switzerland, 2014; pp. 319–335. ISBN 978-3-319-08800-6. [Google Scholar]
- Stenger, F. Collocating Convolutions. Math. Comp. 1995, 64, 211. [Google Scholar] [CrossRef]
- Pincherle, S. Sulle funzioni ipergeometriche generallizate. Rend. Accad. Naz. Lincei 1888, 4, 792–799. [Google Scholar]
- Mellin, H. Über die fundamentale Wichtigkeit des Satzes von Cauchy für die Theorien der Gamma- und hypergeometrischen Functionen; Acta Societatis Scientiarum Fennicae: Helsinki, Finland, 1896; Volume 21, pp. 1–115. [Google Scholar]
- Haubold, H.J.; Mathai, A.M.; Saxena, R.K. Mittag-Leffler Functions and Their Applications. J. Appl. Math. 2011, 2011, 1–51. [Google Scholar] [CrossRef]
- Talbot, A. The Accurate Numerical Inversion of Laplace Transforms. IMA J. Appl. Math. 1979, 23, 97–120. [Google Scholar] [CrossRef]
- Garrappa, R.; Popolizio, M. Fast methods for the computation of the Mittag-Leffler function. In Handbook of Fractional Calculus with Applications; Kochubei, A.N., Luchko, Y.F., Karniadakis, G., Tarasov, V.E., Petráš, I., Baleanu, D., Lopes, A.M., Eds.; De Gruyter: Berlin, Germany, 2019; pp. 329–346. [Google Scholar]
- Krätzel, E. Integral Transformations of Bessel-Type. In Proceedings of the International Conference on Generalized Functions and Operational Calculus, Varna, Bulgaria, 29 September–6 October 1975; pp. 148–155. [Google Scholar]
- Kilbas, A.A.; Kumar, D. On Generalized Krätzel Function. Integral Transform. Spec. Funct. 2009, 20, 835–846. [Google Scholar] [CrossRef]
- Princy, T. Krätzel Function and Related Statistical Distributions. Commun. Math. Stat. 2014, 2, 413–429. [Google Scholar] [CrossRef]
- Gorenflo, R.; Vessella, S. Abel Integral Equations: Analysis and Applications; Lecture notes in mathematics; Springer: Berlin, Germany; New York, NY, USA, 1991; ISBN 978-3-540-53668-0. [Google Scholar]
- Haubold, H.J.; Mathai, A.M. The Fractional Kinetic Equation and Thermonuclear Functions. Astrophys. Space Sci. 2000, 273, 53–63. [Google Scholar] [CrossRef]
- Glöckle, W.G.; Nonnenmacher, T.F. Fractional Integral Operators and Fox Functions in the Theory of Viscoelasticity. Macromolecules 1991, 24, 6426–6434. [Google Scholar] [CrossRef]
- Hille, E.; Tamarkin, J.D. On the Theory of Linear Integral Equations. Ann. Math. 1930, 31, 479. [Google Scholar] [CrossRef]
- Coraddu, M.; Kaniadakis, G.; Lavagno, A.; Lissia, M.; Mezzorani, G.; Quarati, P. Thermal Distributions in Stellar Plasmas, Nuclear Reactions and Solar Neutrinos. Braz. J. Phys. 1999, 29, 153–168. [Google Scholar] [CrossRef]
- Dubey, R.S. An Application of the Aleph (ℵ)-Function for Detecting Glucose Supply in Human Blood. Int. J. Modern Math. Sci. 2016, 14, 221–226. [Google Scholar]
- Suthar, D.L.; Habenom, H.; Tadesse, H. Certain integrals involving aleph function and wright’s generalized hypergeometric function. Acta Univ. Apulensis Math. Inform. 2017, 52, 1–10. [Google Scholar] [CrossRef]
- Tyagi, S.; Jain, M.; Singh, J. Application of S-Function and the Aleph Function in the Electric Circuit Theory. Int. J. Appl. Comput. Math. 2021, 7, 193. [Google Scholar] [CrossRef]
- Singh, Y.; Gill, V.; Singh, J.; Kumar, D.; Khan, I. Computable Generalization of Fractional Kinetic Equation with Special Functions. J. King Saud Univ.-Sci. 2021, 33, 101221. [Google Scholar] [CrossRef]
- Saxena, R.K.; Daiya, J. Integral Transforms of the S-Functions. Le Mat. 2015, 70, 147–159. [Google Scholar] [CrossRef]
- Schneider, W.R. Stable Distributions: Fox Function Representation and Generalization. In Stochastic Processes in Classical and Quantum Systems; Springer: Berlin/Heidelberg, Germany, 1986; pp. 497–511. [Google Scholar]
- Mainardi, F.; Pagnini, G. Mellin-Barnes Integrals for Stable Distributions and Their Convolutions. Fract. Calc. Appl. Anal. 2008, 11, 443–456. [Google Scholar]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).