Optimizing the Maximum Lyapunov Exponent of Fractional Order Chaotic Spherical System by Evolutionary Algorithms
Abstract
:1. Introduction
- (i)
- Optimizing the chaotic behavior of the 3-D spherical-attractor-generating system by maximizing the MLE with the application of DE, PSO and IWO metaheuristics. The results showed a significantly larger MLEs than the non-optimized system, which is evident in the phase space portraits, time series and the entropy of the optimized systems.
- (ii)
- Construction of a hyperchaotic system of 4-D. The hyperchaotic system was created with a state feedback controller added to the second equation of the original 3-D system. The analyses of the hyperchaotic system revealed that it possesses rich dynamics, exhibiting three different states, namely, hyperchaotic, chaotic, and periodic.
2. Chaotic Dynamical System Considered
3. Novel Hyperchaotic System
4. Optimization Algorithms
4.1. Differential Evolution
4.2. Particle Swarm Optimization
4.3. Invasive Weed Optimization
5. Evaluation of the Lyapunov Exponents
- (i)
- A variational system of the original dynamical system is formed using the Jacobian matrix J of f.
- (ii)
- The original dynamical system is given the initial condition , while the initial condition of the variational system is set to I, an identity matrix.
- (iii)
- The integration of the original and variational systems are done until the orthonormalization period K is reached.
- (iv)
- The variational system is then orthonormalized using the Continuous Gram–Schmidt orthogonalization.
- (v)
- Next, the algorithm obtains and gathers in time the logarithm of the norm of each Lyapunov vector in the variational system.
- (vi)
- The next integration begins with the new orthonormalized vectors as the initial conditions.
- (vii)
- Steps (iii) to (vi) are repeated until the integration period T is reached.
- (viii)
- The n Lyapunov exponents are obtained by evaluating:where , T is the integration period, K is the orthonormalization period, and are the orthonormal vectors. The largest of , is called the maximum Lyapunov exponent.
6. Results
6.1. MLE Optimization
- (i)
- Computer configuration: Intel(R) Core(TM) i7-4790, 3.60 GHz; RAM: 12 GB; Operating System: Windows 10;
- (ii)
- DE: Crossover probability = 0.3;
- (iii)
- PSO: Constriction coefficient ; Damping ratio ;
- (iv)
- IWO: Minimum number of seeds = 0; Maximum number of seeds ; Initial value of standard deviation ; Variance reduction exponent ; Final value of standard deviation .
6.2. Optimized Systems against Hyperchaotic System
7. Discussion
8. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Abbreviations
| 3-D | Three-Dimension |
| 4-D | Four-dimensional |
| ABM | Adams–Bashforth–Moulton |
| CGSO | Continuous Gram–Schmidt Orthogonalization |
| DE | Differential Evolution |
| EA | Evolutionary Algorithm |
| Kolmogorov–Sinai entropy | |
| IWO | Invasive Weed Optimization |
| LE | Lyapunov Exponent |
| MLE | Maximum Lyapunov Exponent |
| ODE | Ordinary Differential Equation |
| PSO | Particle Swarm Optimization |
References
- Lorenz, E.N. Deterministic nonperiodic flow. J. Atmos. Sci. 1963, 20, 130–141. [Google Scholar]
- Carbajal-Gómez, V.H.; Tlelo-Cuautle, E.; Mu noz-Pacheco, J.M.; de la Fraga, L.G.; Sanchez-Lopez, C.; Fernandez-Fernandez, F.V. Optimization and CMOS design of chaotic oscillators robust to PVT variations. Integration 2019, 65, 32–42. [Google Scholar]
- Lü, J.; Chen, G. Generating multiscroll chaotic attractors: Theories, methods and applications. Int. J. Bifurc. Chaos 2006, 16, 775–858. [Google Scholar]
- Yagasaki, K. Melnikov processes and chaos in randomly perturbed dynamical systems. Nonlinearity 2018, 31, 3057. [Google Scholar]
- Marathe, A.; Govindarajan, R. Nonlinear dynamical dystems, their stability, and chaos: Lecture notes from the FLOW-NORDITA Summer School on Advanced Instability Methods for Complex Flows, Stockholm, Sweden, 2013. Appl. Mech. Rev. 2014, 66, 024802. [Google Scholar] [CrossRef]
- Carbajal-Gómez, V.H.; Tlelo-Cuautle, E.; Fernández, F.V. Optimizing the positive Lyapunov exponent in multi-scroll chaotic oscillators with differential evolution algorithm. Appl. Math. Comput. 2013, 219, 8163–8168. [Google Scholar]
- Xu, G.; Shekofteh, Y.; Akgül, A.; Li, C.; Panahi, S. A new chaotic system with a self-excited attractor: Entropy measurement, signal encryption, and parameter estimation. Entropy 2018, 20, 86. [Google Scholar]
- Sahoo, S.; Roy, B.K. Design of multi-wing chaotic systems with higher largest Lyapunov exponent. Chaos Solitons Fractals 2022, 157, 111926. [Google Scholar]
- Miranda-Filho, L.H.; Sobral, T.A.; de Souza, A.J.F.; Elskens, Y.; Romaguera, A.R.d.C. Lyapunov exponent in the Vicsek model. Phys. Rev. E 2022, 105, 014213. [Google Scholar]
- Veeman, D.; Mehrabbeik, M.; Natiq, H.; Rajagopal, K.; Jafari, S.; Hussain, I. A new chaotic system with coexisting attractors. Int. J. Bifurc. Chaos 2022, 32, 2230007. [Google Scholar]
- Hassanaly, M.; Raman, V. Ensemble-LES analysis of perturbation response of turbulent partially-premixed flames. Proc. Combust. Inst. 2019, 37, 2249–2257. [Google Scholar]
- Li, S.; Wu, Y.; Zhang, X. Analysis and synchronization of a new hyperchaotic system with exponential term. Mathematics 2021, 9, 3281. [Google Scholar]
- Thivagar, M.L.; Hamad, A.A.; Tamilarasan, B.; Antony, G.K. A Novel Seven-Dimensional Hyperchaotic. In Proceedings of the Second Doctoral Symposium on Computational Intelligence; Gupta, D., Khanna, A., Kansal, V., Fortino, G., Hassanien, A.E., Eds.; Springer: Singapore, 2022; pp. 329–340. [Google Scholar]
- de la Fraga, L.G.; Tlelo-Cuautle, E.; Carbajal-Gómez, V.H.; Muñoz-Pacheco, J.M. On maximizing positive Lyapunov exponents in a chaotic oscillator with heuristics. Rev. Mex. Fis. 2012, 58, 274–281. [Google Scholar]
- Carbajal-Gómez, V.H.; Tlelo-Cuautle, E.; Fernández, F.V.; de la Fraga, L.G.; Sánchez-López, C. Maximizing Lyapunov Exponents in a Chaotic Oscillator by Applying Differential Evolution. Int. J. Nonlin. Sci. Num. 2014, 15, 11–17. [Google Scholar]
- de la Fraga, L.G.; Tlelo-Cuautle, E. Optimizing the maximum Lyapunov exponent and phase space portraits in multi-scroll chaotic oscillators. Nonlinear Dyn. 2014, 76, 1503–1515. [Google Scholar]
- Núñez-Pérez, J.C.; Adeyemi, V.A.; Sandoval-Ibarra, Y.; Pérez-Pinal, F.J.; Tlelo-Cuautle, E. FPGA realization of spherical chaotic system with application in image transmission. Math. Probl. Eng. 2021, 2021, 5532106. [Google Scholar]
- Elbeltagi, E.; Hegazy, T.; Grierson, D. Comparison among five evolutionary-based optimization algorithms. Adv. Eng. Inform. 2005, 19, 43–53. [Google Scholar]
- Núñez-Pérez, J.C.; Adeyemi, V.A.; Sandoval-Ibarra, Y.; Pérez-Pinal, F.J.; Tlelo-Cuautle, E. Maximizing the chaotic behavior of fractional order Chen system by evolutionary algorithms. Mathematics 2021, 9, 1194. [Google Scholar]
- Rosalie, M. Templates and subtemplates of Rössler attractors from a bifurcation diagram. J. Phys. A-Math. Theor. 2016, 49, 315101. [Google Scholar]
- Shu, Y.; Zhang, F.; Mu, C. Dynamical behaviors of a new hyperchaotic system. Math. Methods Appl. Sci. 2015, 38, 3155–3162. [Google Scholar]
- Yang, Q.; Bai, M. A new 5D hyperchaotic system based on modified generalized Lorenz system. Nonlinear Dyn. 2017, 88, 189–221. [Google Scholar]
- Chen, L.; Tang, S.; Li, Q.; Zhong, S. A new 4D hyperchaotic system with high complexity. Math. Comput. Simul. 2018, 146, 44–56. [Google Scholar]
- Liu, Y.; Tong, X.; Ma, J. Image encryption algorithm based on hyper-chaotic system and dynamic S-box. Multimed. Tools Appl. 2016, 75, 7739–7759. [Google Scholar]
- Xiong, L.; Liu, Z.; Zhang, X. Dynamical analysis, synchronization, circuit design, and secure communication of a novel hyperchaotic system. Complexity 2017, 2017, 4962739. [Google Scholar]
- Ren, H.P.; Bai, C.; Huang, Z.Z.; Grebogi, C. Secure communication based on hyperchaotic Chen system with time-delay. Int. J. Bifurc. Chaos 2017, 27, 1750076. [Google Scholar]
- Hassan, M.F. Synchronization of uncertain constrained hyperchaotic systems and chaos-based secure communications via a novel decomposed nonlinear stochastic estimator. Nonlinear Dyn. 2016, 83, 2183–2211. [Google Scholar]
- Wang, Z.; Sun, Y.; Cang, S. A 3-D spherical chaotic attractor. Acta Phys. Pol. B 2011, 42, 235–247. [Google Scholar]
- Shilnikov, L. A case of the existence of a countable number of periodic motion. Sov. Math. Dokl. 1965, 6, 163–166. [Google Scholar]
- Li, G.; Chen, X. Constructing piecewise linear chaotic system based on the heteroclinic Shil’nikov theorem. Commun. Nonlinear Sci. Numer. Simul. 2009, 14, 194–203. [Google Scholar]
- Storn, R.; Price, K. Differential evolution: A simple and efficient adaptive scheme for global optimization over continuous spaces. J. Glob. Optim. 1997, 11, 341–359. [Google Scholar]
- Hamza, N.; Sarker, R.; Essam, D. Differential evolution with multi-constraint consensus methods for constrained optimization. J. Glob. Optim. 2013, 57, 583–611. [Google Scholar]
- Kennedy, J.; Eberhart, R.C.; Shi, Y. Swarm Intelligence, 1st ed.; Morgan Kaufmann Publishers: Burlington, MA, USA, 2001; p. 512. [Google Scholar]
- Mehrabian, A.R.; Lucas, C. A novel numerical optimization algorithm inspired from weed colonization. Ecol. Inform. 2006, 1, 355–366. [Google Scholar]
- Danca, M.F.; Kuznetsov, N. Matlab code for Lyapunov exponents of fractional order systems. Int. J. Bifurcat. Chaos 2018, 28, 1850067. [Google Scholar]
- Lin, J.; Chen, C. Parameter estimation of chaotic systems by an oppositional seeker optimization algorithm. Nonlinear Dyn. 2014, 76, 509–517. [Google Scholar]
- Zhang, H.; Li, B.; Zhang, J.; Qin, Y.; Feng, X.; Liu, B. Parameter estimation of nonlinear chaotic system by improved TLBO strategy. Soft Comput. 2016, 20, 4965–4980. [Google Scholar]
- Zhou, N.; Pan, S.; Cheng, S.; Zhou, Z. Image compression—Encryption scheme based on hyper-chaotic system and 2D compressive sensing. Opt. Laser Technol. 2016, 82, 121–133. [Google Scholar]
- Ruelle, D. Strange attractors. Math. Intell. 1980, 2, 126. [Google Scholar]
- Takens, F. Detecting strange attractors in turbulence. In Dynamical Systems and Turbulence, Warwick 1980; Rand, D., Young, L.S., Eds.; Springer: Berlin/Heidelberg, Germany, 1981; pp. 366–381. [Google Scholar]
- Vaidyanathan, S. A novel 3-D jerk chaotic system with three quadratic nonlinearities and its adaptive control. Arch. Control Sci. 2016, 26, 19–47. [Google Scholar]
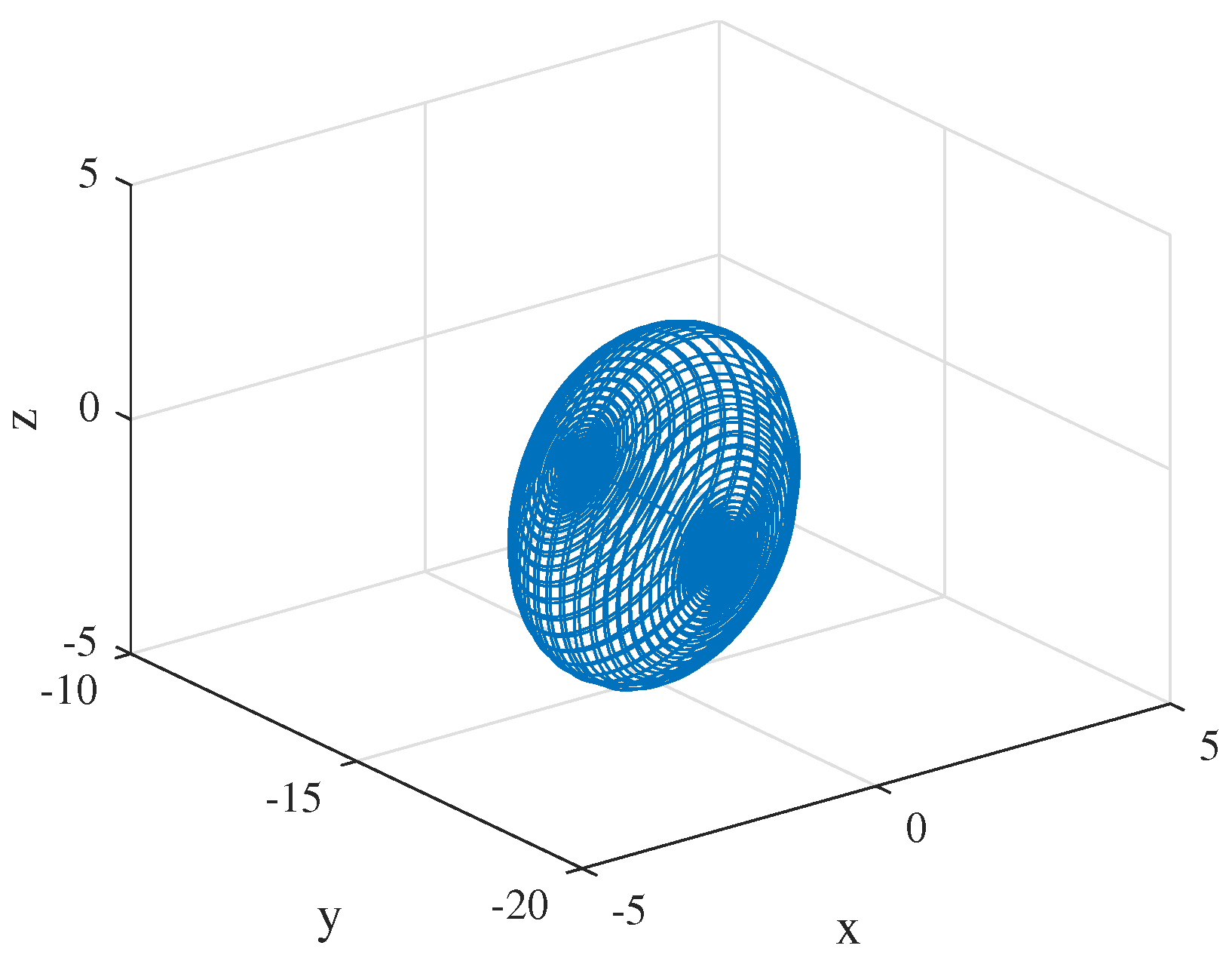
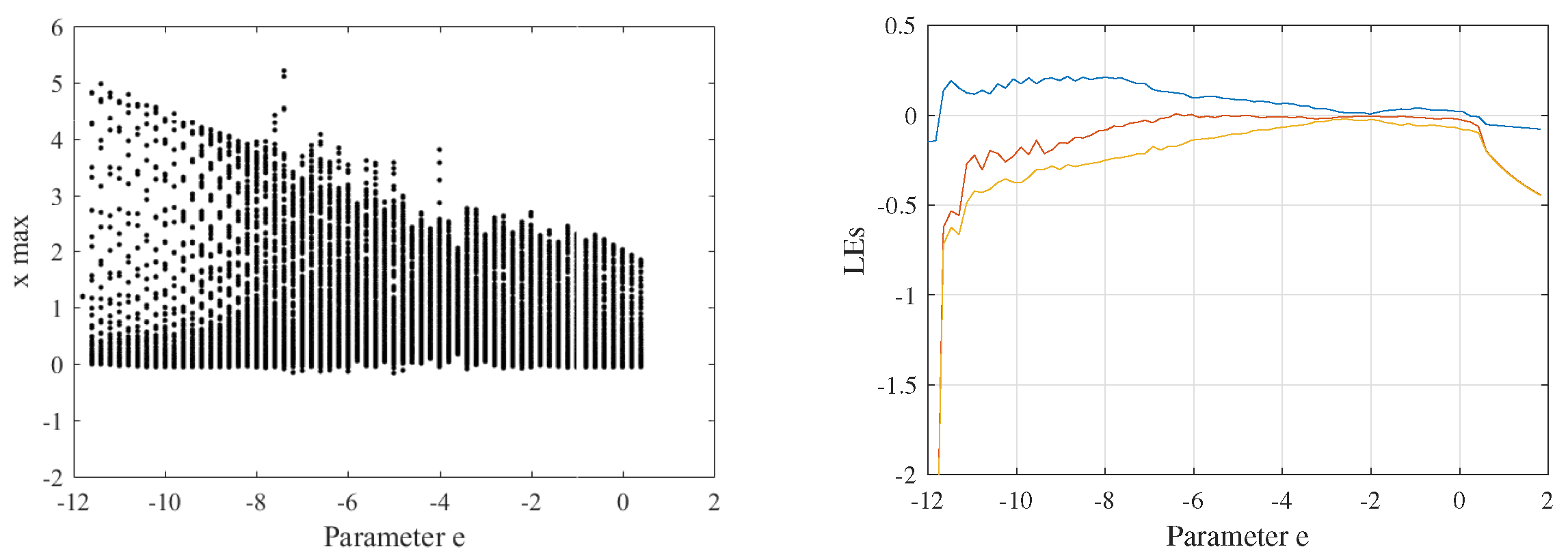
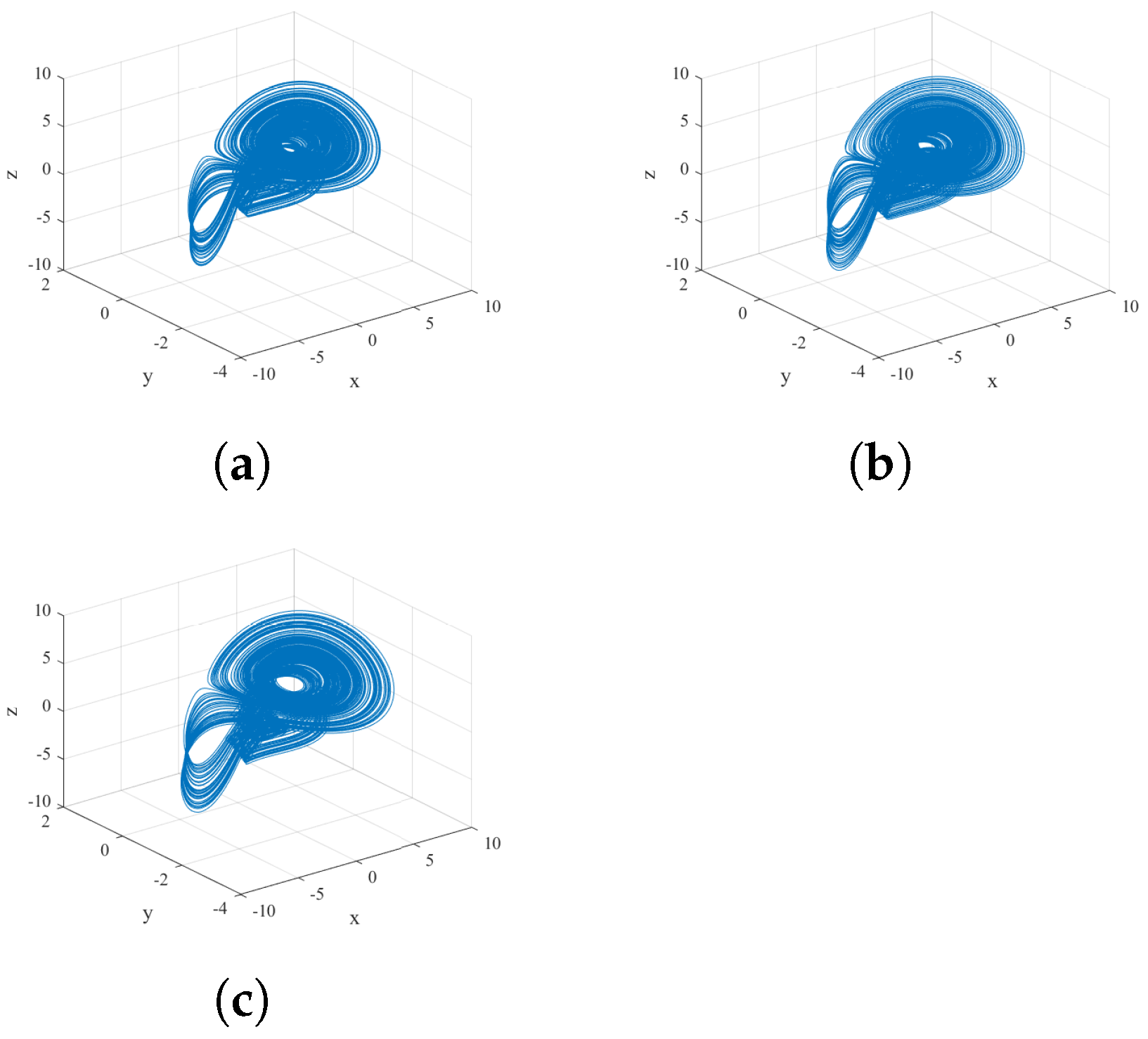
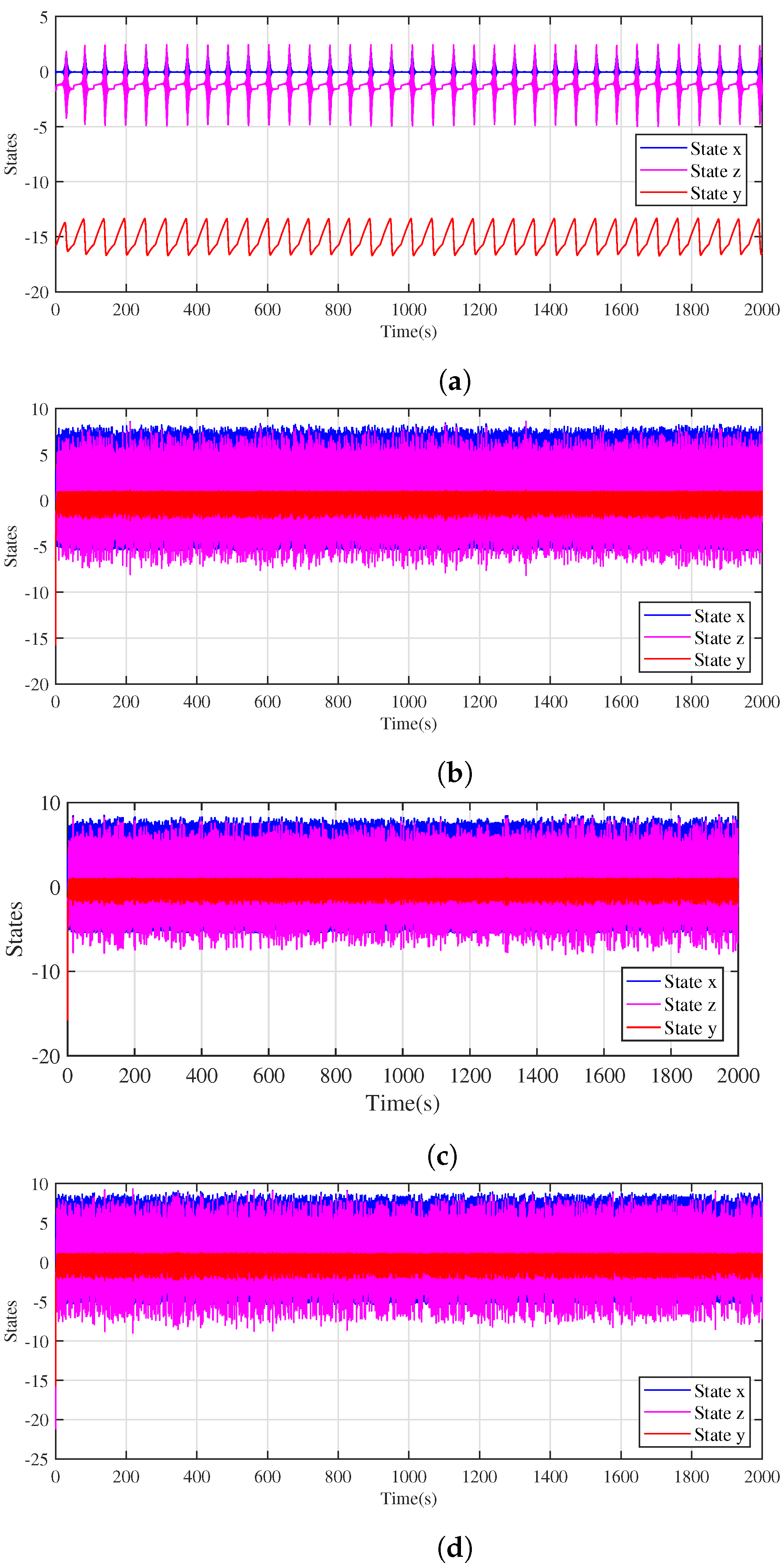

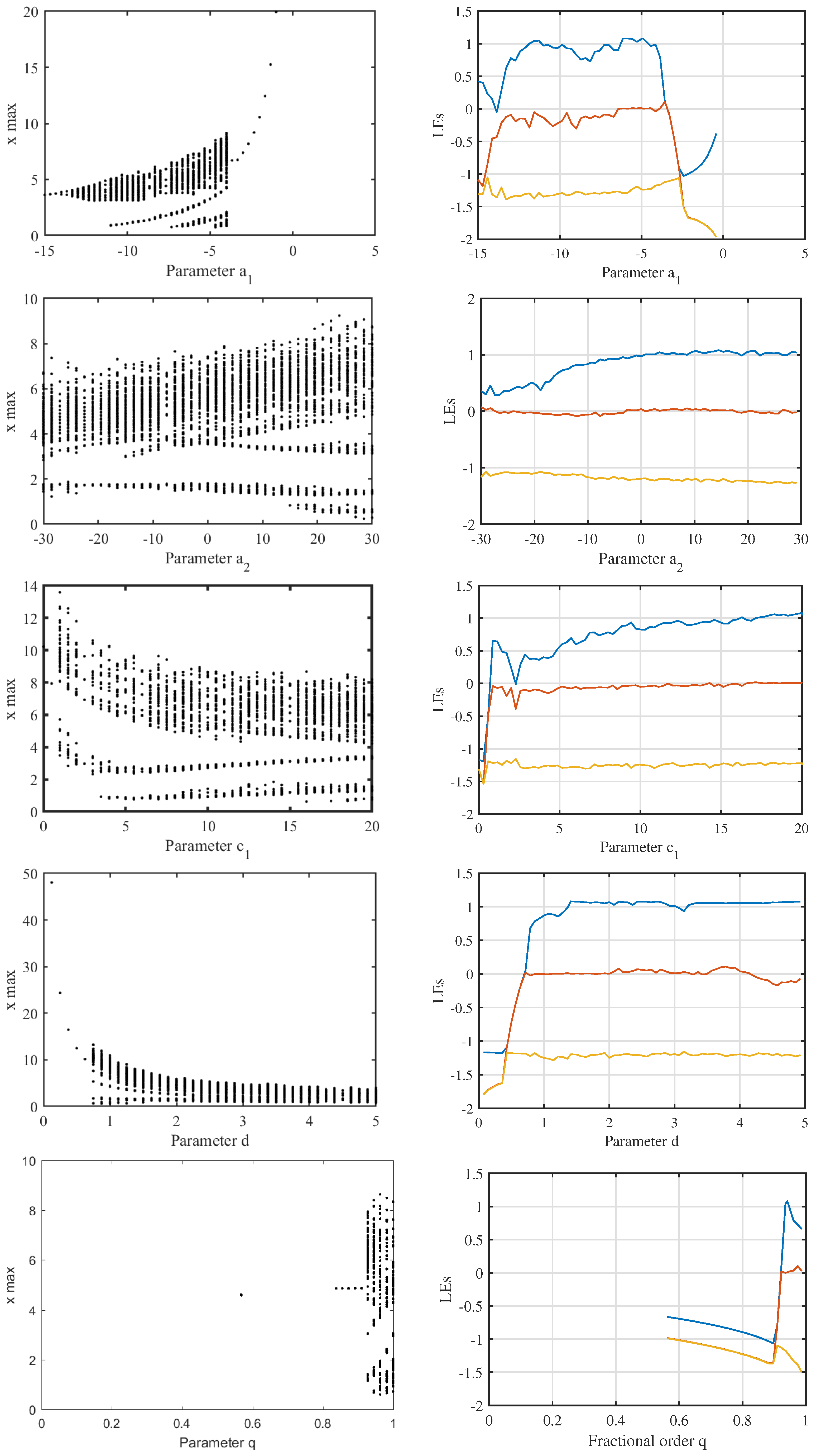
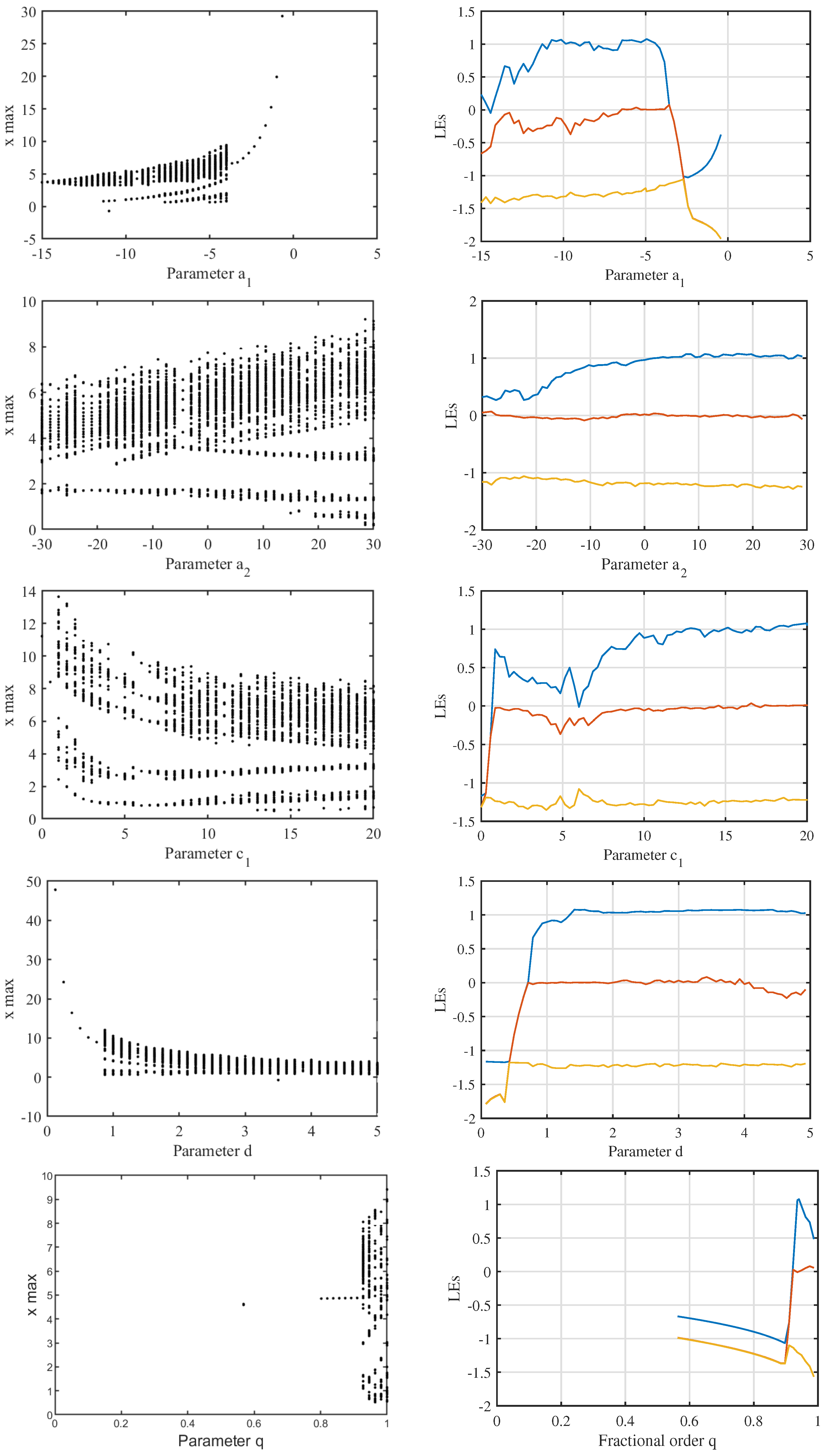


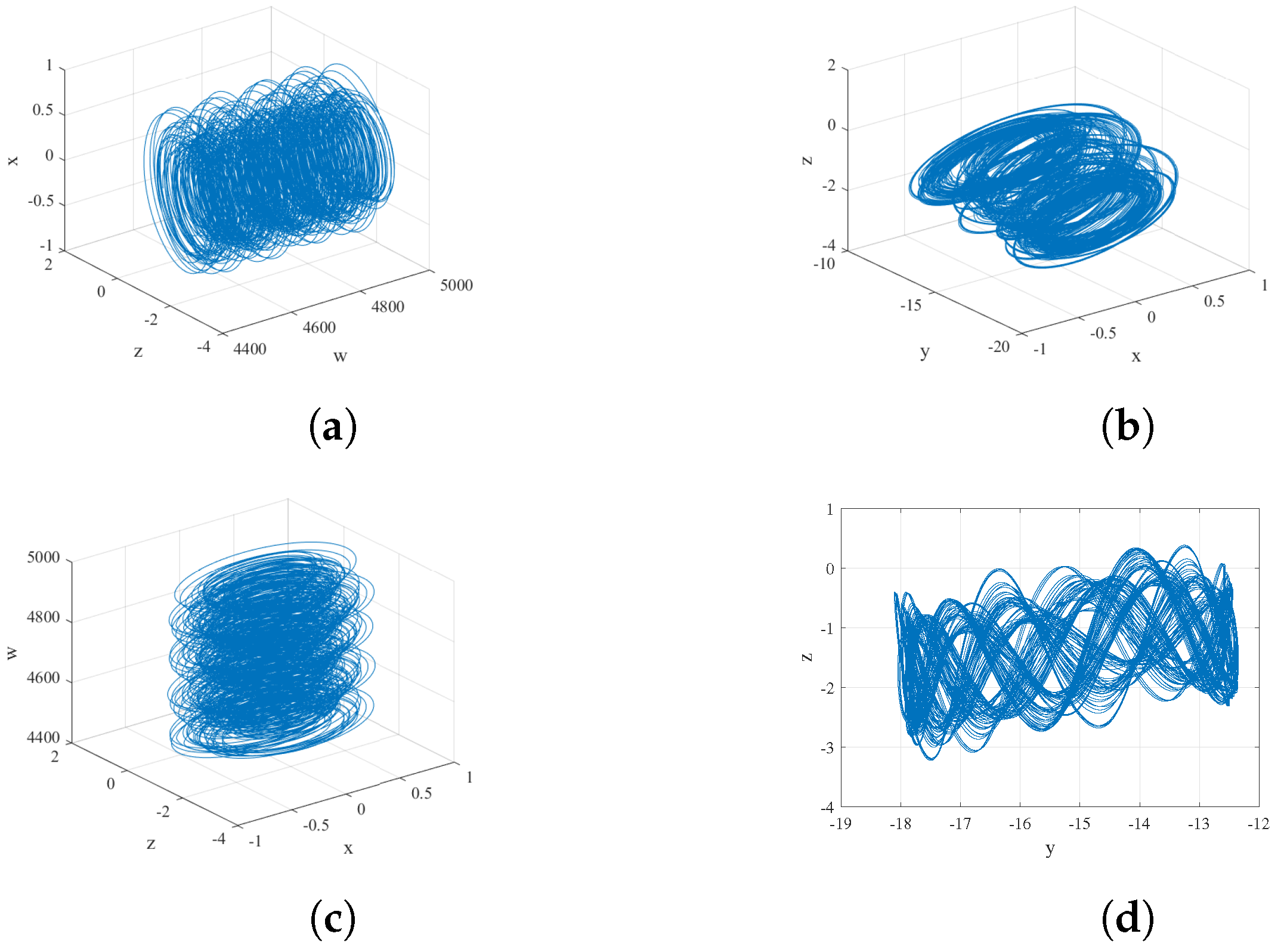
| Parameter | MLE | Equilibrium Point | Eigenvalue , , | Information Entropy | Instability Condition |
|---|---|---|---|---|---|
| Non-optimized Spherical | |||||
| , , , | 0.9772 | ||||
| , , , | |||||
| , , , | |||||
| , | |||||
| DE-optimized Spherical | |||||
| , , , | 6.93343 | ||||
| , , , | |||||
| , , , | |||||
| , | |||||
| PSO-optimized Spherical | |||||
| , , , | 6.8620 | ||||
| , , , | |||||
| , , , | |||||
| , | |||||
| IWO-optimized Spherical | |||||
| , , , | 6.5619 | ||||
| , , , | |||||
| , , , | |||||
| , |
| Parameter g | Parameter r | Dynamical State | ||||
|---|---|---|---|---|---|---|
| 0 | Periodic | |||||
| 0 | Chaotic | |||||
| 0 | Chaotic | |||||
| 0 | Hyperchaotic | |||||
| 0 | Hyperchaotic | |||||
| 0 | Hyperchaotic | |||||
| 0 | Periodic | |||||
| 0 | Chaotic | |||||
| 0 | Hyperchaotic | |||||
| 0 | Periodic | |||||
| 0 | Hyperchaotic | |||||
| 0 | Hyperchaotic | |||||
| 0 | Periodic | |||||
| 0 | Chaotic |
| System | Entropy | Prediction Time |
|---|---|---|
| Non-optimized | 37.8769 | |
| DE-optimized | 0.6413 | |
| PSO-optimized | 0.6433 | |
| IWO-optimized | 0.6501 | |
| Hyperchaotic 1 | ||
| , | 10.1635 | |
| Hyperchaotic 2 | ||
| , | 7.7882 | |
| Hyperchaotic 3 | ||
| , | 10.3455 |
| Reference | Maximum Population | Maximum Iteration | Implementation | Algorithms | Chaotic System |
|---|---|---|---|---|---|
| [6] | 40 | 80 | MATLAB | DE | SNLF |
| [7] | 25 | 50 | N/A | MVO | New Chaotic |
| WOA | oscillator | ||||
| [15] | 40 | 60 | N/A | DE, GA | SNLF |
| [16] | 100 | N/A | N/A | NSGA-II | SNLF, Chua |
| [36] | 40 | 100 | MATLAB | OSOA | Lorenz, Chen |
| [37] | 120 | 100 | MATLAB | TLBO | Lorenz |
| This investigation | 100 | 500 | MATLAB | DE, PSO, IWO | 3-D fractional-order System |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Adeyemi, V.-A.; Tlelo-Cuautle, E.; Perez-Pinal, F.-J.; Nuñez-Perez, J.-C. Optimizing the Maximum Lyapunov Exponent of Fractional Order Chaotic Spherical System by Evolutionary Algorithms. Fractal Fract. 2022, 6, 448. https://doi.org/10.3390/fractalfract6080448
Adeyemi V-A, Tlelo-Cuautle E, Perez-Pinal F-J, Nuñez-Perez J-C. Optimizing the Maximum Lyapunov Exponent of Fractional Order Chaotic Spherical System by Evolutionary Algorithms. Fractal and Fractional. 2022; 6(8):448. https://doi.org/10.3390/fractalfract6080448
Chicago/Turabian StyleAdeyemi, Vincent-Ademola, Esteban Tlelo-Cuautle, Francisco-Javier Perez-Pinal, and Jose-Cruz Nuñez-Perez. 2022. "Optimizing the Maximum Lyapunov Exponent of Fractional Order Chaotic Spherical System by Evolutionary Algorithms" Fractal and Fractional 6, no. 8: 448. https://doi.org/10.3390/fractalfract6080448
APA StyleAdeyemi, V.-A., Tlelo-Cuautle, E., Perez-Pinal, F.-J., & Nuñez-Perez, J.-C. (2022). Optimizing the Maximum Lyapunov Exponent of Fractional Order Chaotic Spherical System by Evolutionary Algorithms. Fractal and Fractional, 6(8), 448. https://doi.org/10.3390/fractalfract6080448









