Existence, Stability and Simulation of a Class of Nonlinear Fractional Langevin Equations Involving Nonsingular Mittag–Leffler Kernel

Abstract

The fractional Langevin equation is a very effective mathematical model for depicting the random motion of particles in complex viscous elastic liquids. This manuscript is mainly concerned with a class of nonlinear fractional Langevin equations involving nonsingular Mittag–Leffler (ML) kernel. We first investigate the existence and uniqueness of the solution by employing some fixed-point theorems. Then, we apply direct analysis to obtain the Ulam–Hyers (UH) type stability. Finally, the theoretical analysis and numerical simulation of some interesting examples show that there is a great difference between the fractional Langevin equation and integer Langevin equation in describing the random motion of free particles.

1. Introduction

To expound the random motion of particles in fluid after colliding with each other, Langevin raised the famous Langevin equation in 1908. Afterward, many random phenomena and processes were found to be described by the Langevin Equation [1,2]. However, the integer-order Langevin equation is unable to meet the accuracy requirements in describing complex viscoelasticity. Thereby, the classical Langevin equation has been extended and modified. Kubo [3,4] put forward a general Langevin equation to simulate the complex viscoelastic anomalous diffusion process. Eab and Lim [5] applied a fractional Langevin equation to describe single-file diffusion. Sandev and Tomovski [6] established a fractional Langevin equation model to study the motion of free particles driven by power-law noise. Furthermore, the stability of the system represents the most important dynamics characteristic. Ulam and Hyers [7,8] proposed a concept of system stability called UH-stability in the 1940s. Over the past decade, there have been many works published (some of which can be found in [9,10,11,12,13,14,15]) on the UH-stability of a fractional system.

It is worth noting that these works on the fractional Langevin system basically involve Caputo or Riemann–Liouville fractional derivatives. In fact, the Caputo or Riemann–Liouville fractional derivatives can produce singularity under some conditions. This makes them difficult to employ as mathematical models of certain physical phenomena. Consequently, a new nonsingular fractional derivative with exponential kernel was raised by Caputo and Febrizio in [16]. Furthermore, another new nonsingular fractional derivative with ML-kernel was put forward by Atangana and Baleanu in [17]. Since their introduction, these nonsingular fractional derivatives have attracted much attention and research in theory [18,19,20,21] and application [22,23,24,25,26,27]. Some new findings on the fractional Langevin equation have been published in recent papers (see [28,29,30,31,32,33,34,35,36]). However, there are a paucity of papers on Ulam–Hyers stability of fractional Langevin system with ML-kernel.

Inspired by the aforementioned research, this manuscript focuses on the following nonlinear fractional Langevin equation with ML-kernel of the form

$$\begin{array}{c}\hfill \left\{\begin{array}{c}{}^{ML}{\mathcal{D}}_{0^{+}}^{\beta }\left[{}^{ML}{\mathcal{D}}_{0^{+}}^{\alpha }-\lambda \right]u\left(t\right)=f(t,u\left(t\right)),t\in (0,T],\hfill \\ u\left(0\right)=A,{}^{ML}{\mathcal{D}}_{0^{+}}^{\alpha }u\left(0\right)=B,\hfill \end{array}\right.\end{array}$$

(1)

where $D=[0,T]$, $T>0$, $0<\alpha ,\beta \le 1$, $\lambda >0$, $A,B\in \mathbb{R}$, $f\in C({\mathbb{R}}^2,\mathbb{R})$, ${}^{ML}{\mathcal{D}}_{0^{+}}^{\alpha }$ and ${}^{ML}{\mathcal{D}}_{0^{+}}^{\beta }$ represent the fractional derivative with ML-kernel.

The remaining structure of the manuscript is as follows. Section 2 introduces some fundamental definitions and lemmas. In Section 3, we obtain some criteria on the existence of solutions to the system (1) by using some fixed-point theorems. The UH-type stabilities of (1) are built in Section 4. As applications, we conduct theoretical analysis and numerical simulation on some examples to verify the correctness and effectiveness of our main results in Section 5. Finally, a brief summary is provided in Section 6.

2. Preliminaries

Definition 1.

[27] For $0<\alpha \le 1$, $T>0$ and $u:[0,T]\to \mathbb{R}$, the left-sided α-order Mittag–Leffler fractional integral of function u is defined by

$$\begin{array}{c}\hfill {}^{ML}{\mathcal{I}}_{0^{+}}^{\alpha }u\left(t\right)=\frac{1-\alpha }{\mathcal{N}\left(\alpha \right)}u\left(t\right)+\frac{\alpha }{\mathcal{N}\left(\alpha \right)\Gamma \left(\alpha \right)}{\int }_0^t{(t-s)}^{\alpha -1}u\left(s\right)ds,\end{array}$$

provided the integral exists, here $\Gamma \left(\alpha \right)$ is the gamma function, $\mathcal{N}\left(\alpha \right)\in C\left(\right[0,1],(0,1\left]\right)$ is a normalization constant satisfying $\mathcal{N}\left(0\right)=\mathcal{N}\left(1\right)=1$.

Definition 2.

[17] For $0<\alpha \le 1$, $T>0$ and $u\in C^1(0,T)$, the left-sided α-order Mittag–Leffler fractional derivative of function u in sense of Caputo is given by

$$\begin{array}{c}\hfill {}^{ML}{\mathcal{D}}_{0^{+}}^{\alpha }u\left(t\right)=\frac{\mathcal{N}\left(\alpha \right)}{(1-\alpha )}{\int }_0^t{\mathbb{E}}_{\alpha }\left[-\frac{\alpha }{1-\alpha }{(t-s)}^{\alpha }\right]u^{\prime }\left(s\right)ds,\end{array}$$

where ${\mathbb{E}}_{\alpha }(·)$ is single parameter Mittag-Leffer function and defined by

$$\begin{array}{c}\hfill {\mathbb{E}}_{\alpha }\left(x\right)=\sum _{k=0}^{\infty }\frac{x^k}{\Gamma (\alpha k+1)}.\end{array}$$

Remark 1.

The Caputo fractional derivative of order $0<\alpha \le 1$ of a continuous function $u:(0,\infty )\to \mathbb{R}$ is defined by

$$\begin{array}{c}\hfill {}^C{\mathcal{D}}_{0^{+}}^{\alpha }u\left(t\right)=\frac{1}{\Gamma (1-\alpha )}{\int }_0^t{(t-s)}^{-\alpha }{u}^{\prime }\left(s\right)ds,\end{array}$$

provided that the right-hand side is pointwise defined on $(0,\infty )$. From Definition 2 and the Caputo fractional derivative, one finds two differences between them. One is that the coefficients are different. The other is that the kernel function is different. The kernel function ${(t-s)}^{-\alpha }$ of Caputo fractional derivative is singular at $s=t$, but the kernel function ${\mathbb{E}}_{\alpha }\left[-\frac{\alpha }{1-\alpha }{(t-s)}^{\alpha }\right]$ of Mittag–Leffler fractional derivative is nonsingular at $s=t$.

Lemma 1.

[37] Assume that $h\in C[0,T]$. Then, the unique solution of fractional differential equation

$$\begin{array}{c}\hfill \left\{\begin{array}{c}{}^{ML}{\mathcal{D}}_{0^{+}}^{\gamma }w\left(t\right)=h\left(t\right),t\in (0,T),0<\gamma \le 1,\hfill \\ w\left(0\right)=w_0,\hfill \end{array}\right.\end{array}$$

is written as

$$\begin{array}{c}\hfill w\left(t\right)=w_0+\frac{1-\gamma }{\mathcal{N}\left(\gamma \right)}[h\left(t\right)-h\left(0\right)]+\frac{\gamma }{\mathcal{N}\left(\gamma \right)\Gamma \left(\gamma \right)}{\int }_0^t{(t-s)}^{\gamma -1}h\left(s\right)ds.\end{array}$$

Remark 2.

It follows from Definition 2 and Lemma 1 that ${}^{ML}{\mathcal{D}}_{0^{+}}^{\alpha }u\left(t\right)\equiv 0$ if and only if $u\left(t\right)\equiv constant$.

Lemma 2.

Let $T>0$, $0<\alpha ,\beta \le 1$, $\lambda >0$, $A,B\in \mathbb{R}$, $f\in C({\mathbb{R}}^2,\mathbb{R})$. If $\delta \triangleq 1-\frac{\lambda (1-\alpha )}{\mathcal{N}\left(\alpha \right)}\ne 0$, then the fractional differential Langevin Equation (1) is equivalent to the following integral equation

$$\begin{array}{cc}\hfill u\left(t\right)=& A+\frac{1}{\delta }\{\frac{B-\lambda A}{\mathcal{N}\left(\alpha \right)\Gamma \left(\alpha \right)}{t}^{\alpha }+\frac{(1-\alpha )(1-\beta )}{\mathcal{N}\left(\alpha \right)\mathcal{N}\left(\beta \right)}[f(t,u\left(t\right))-f(0,A)]\hfill \\ \hfill & +\frac{\lambda \alpha }{\mathcal{N}\left(\alpha \right)\Gamma \left(\alpha \right)}{\int }_0^t{(t-s)}^{\alpha -1}u\left(s\right)ds+\frac{(1-\alpha )\beta }{\mathcal{N}\left(\alpha \right)\mathcal{N}\left(\beta \right)\Gamma \left(\beta \right)}{\int }_0^t{(t-s)}^{\beta -1}f(s,u\left(s\right))ds\hfill \\ \hfill & +\frac{\alpha (1-\beta )}{\mathcal{N}\left(\alpha \right)\mathcal{N}\left(\beta \right)\Gamma \left(\alpha \right)}{\int }_0^t{(t-s)}^{\alpha -1}f(s,u\left(s\right))ds\hfill \\ \hfill & +\frac{\alpha \beta }{\mathcal{N}\left(\alpha \right)\mathcal{N}\left(\beta \right)\Gamma (\alpha +\beta )}{\int }_0^t{(t-s)}^{\alpha +\beta -1}f(s,u\left(s\right))ds\},t\in D.\hfill \end{array}$$

(2)

Proof. 

Assume that the function $u\left(t\right)\in C(0,T)$ is a solution of (1), Then, for $t\in D$, we derive from Lemma 1 that

$$\begin{array}{cc}\hfill & \left[{}^{ML}{\mathcal{D}}_{0^{+}}^{\alpha }-\lambda \right]u\left(t\right)={}^{ML}{\mathcal{D}}_{0^{+}}^{\alpha }u\left(0\right)-\lambda u\left(0\right)+\frac{1-\beta }{\mathcal{N}\left(\beta \right)}[f(t,u\left(t\right))-f(0,u\left(0\right))]\hfill \\ \hfill & +\frac{\beta }{\mathcal{N}\left(\beta \right)\Gamma \left(\beta \right)}{\int }_0^t{(t-\tau )}^{\beta -1}f(\tau ,u\left(\tau \right))d\tau .\hfill \end{array}$$

(3)

(3) gives

$$\begin{array}{cc}\hfill & {}^{ML}{\mathcal{D}}_{0^{+}}^{\alpha }u\left(t\right)=({}^{ML}{\mathcal{D}}_{0^{+}}^{\alpha }u\left(0\right)-\lambda u\left(0\right))+\lambda u\left(t\right)+\frac{1-\beta }{\mathcal{N}\left(\beta \right)}[f(t,u\left(t\right))-f(0,u\left(0\right))]\hfill \\ \hfill & +\frac{\beta }{\mathcal{N}\left(\beta \right)\Gamma \left(\beta \right)}{\int }_0^t{(t-\tau )}^{\beta -1}f(\tau ,u\left(\tau \right))d\tau .\hfill \end{array}$$

(4)

From Lemma 1, $u\left(0\right)=A$ and (4), we yield

$$\begin{array}{cc}\hfill & u\left(t\right)=A+\frac{1-\alpha }{\mathcal{N}\left(\alpha \right)}[\lambda [u\left(t\right)-A]+\frac{1-\beta }{\mathcal{N}\left(\beta \right)}[f(t,u\left(t\right))-f(0,A)]\hfill \\ \hfill & +\frac{\beta }{\mathcal{N}\left(\beta \right)\Gamma \left(\beta \right)}{\int }_0^t{(t-\tau )}^{\beta -1}f(\tau ,u\left(\tau \right))d\tau ]+\frac{\alpha }{\mathcal{N}\left(\alpha \right)\Gamma \left(\alpha \right)}\hfill \\ \hfill & \times {\int }_0^t{(t-s)}^{\alpha -1}[(B-\lambda A)+\lambda u\left(s\right)+\frac{1-\beta }{\mathcal{N}\left(\beta \right)}f(s,u\left(s\right))\hfill \\ \hfill & +\frac{\beta }{\mathcal{N}\left(\beta \right)\Gamma \left(\beta \right)}{\int }_0^s{(s-\tau )}^{\beta -1}f(\tau ,u\left(\tau \right))d\tau ]ds\hfill \\ \hfill =& \left[1-\frac{\lambda (1-\alpha )}{\mathcal{N}\left(\alpha \right)}\right]A+\frac{\lambda (1-\alpha )}{\mathcal{N}\left(\alpha \right)}u\left(t\right)+\frac{(1-\alpha )(1-\beta )}{\mathcal{N}\left(\alpha \right)\mathcal{N}\left(\beta \right)}[f(t,u\left(t\right))-f(0,A)]\hfill \\ \hfill & +\frac{(1-\alpha )\beta }{\mathcal{N}\left(\alpha \right)\mathcal{N}\left(\beta \right)\Gamma \left(\beta \right)}{\int }_0^t{(t-\tau )}^{\beta -1}f(\tau ,u\left(\tau \right))d\tau +\frac{B-\lambda A}{\mathcal{N}\left(\alpha \right)\Gamma \left(\alpha \right)}{t}^{\alpha }\hfill \\ \hfill & +\frac{\lambda \alpha }{\mathcal{N}\left(\alpha \right)\Gamma \left(\alpha \right)}{\int }_0^t{(t-s)}^{\alpha -1}u\left(s\right)ds+\frac{\alpha (1-\beta )}{\mathcal{N}\left(\alpha \right)\mathcal{N}\left(\beta \right)\Gamma \left(\alpha \right)}{\int }_0^t{(t-s)}^{\alpha -1}f(s,u\left(s\right))ds\hfill \\ \hfill & +\frac{\alpha \beta }{\mathcal{N}\left(\alpha \right)\mathcal{N}\left(\beta \right)\Gamma \left(\alpha \right)\Gamma \left(\beta \right)}{\int }_0^t{(t-s)}^{\alpha -1}\left[{\int }_0^s{(s-\tau )}^{\beta -1}f(\tau ,u\left(\tau \right))d\tau \right]ds.\hfill \end{array}$$

(5)

Noting the last integral term of (5), we exchange the order of double integrals to get

$$\begin{array}{cc}\hfill & \frac{\alpha \beta }{\mathcal{N}\left(\alpha \right)\mathcal{N}\left(\beta \right)\Gamma \left(\alpha \right)\Gamma \left(\beta \right)}{\int }_0^t{(t-s)}^{\alpha -1}\left[{\int }_0^s{(s-\tau )}^{\beta -1}f(\tau ,u\left(\tau \right))d\tau \right]ds\hfill \\ \hfill =& \frac{\alpha \beta }{\mathcal{N}\left(\alpha \right)\mathcal{N}\left(\beta \right)\Gamma \left(\alpha \right)\Gamma \left(\beta \right)}{\int }_0^{t}f(\tau ,u\left(\tau \right))\left[{\int }_{\tau }^t{(t-s)}^{\alpha -1}{(s-\tau )}^{\beta -1}ds\right]d\tau \hfill \\ \hfill =& \frac{\alpha \beta }{\mathcal{N}\left(\alpha \right)\mathcal{N}\left(\beta \right)\Gamma (\alpha +\beta )}{\int }_0^t{(t-\tau )}^{\alpha +\beta -1}f(\tau ,u\left(\tau \right))d\tau .\hfill \end{array}$$

(6)

It follows from (5) and (6) that

$$\begin{array}{cc}\hfill u\left(t\right)=& A+\frac{1}{\delta }\{\frac{B-\lambda A}{\mathcal{N}\left(\alpha \right)\Gamma \left(\alpha \right)}{t}^{\alpha }+\frac{(1-\alpha )(1-\beta )}{\mathcal{N}\left(\alpha \right)\mathcal{N}\left(\beta \right)}[f(t,u\left(t\right))-f(0,A)]\hfill \\ \hfill & +\frac{\lambda \alpha }{\mathcal{N}\left(\alpha \right)\Gamma \left(\alpha \right)}{\int }_0^t{(t-s)}^{\alpha -1}u\left(s\right)ds+\frac{(1-\alpha )\beta }{\mathcal{N}\left(\alpha \right)\mathcal{N}\left(\beta \right)\Gamma \left(\beta \right)}{\int }_0^t{(t-\tau )}^{\beta -1}f(\tau ,u\left(\tau \right))d\tau \hfill \\ \hfill & +\frac{\alpha (1-\beta )}{\mathcal{N}\left(\alpha \right)\mathcal{N}\left(\beta \right)\Gamma \left(\alpha \right)}{\int }_0^t{(t-s)}^{\alpha -1}f(s,u\left(s\right))ds\hfill \\ \hfill & +\frac{\alpha \beta }{\mathcal{N}\left(\alpha \right)\mathcal{N}\left(\beta \right)\Gamma (\alpha +\beta )}{\int }_0^t{(t-\tau )}^{\alpha +\beta -1}f(\tau ,u\left(\tau \right))d\tau \}.\hfill \end{array}$$

(7)

Thus, Equation (2) holds, that is, $u\left(t\right)\in C(0,T)$ is also a solution of integral Equation (2). Furthermore, vice versa, if $u\left(t\right)\in C(0,T)$ is a solution of integral Equation (2), then one knows that (4) and (3) hold by finding the fractional derivative ${}^{Ml}{\mathcal{D}}_{0^{+}}^{\alpha }$ at both ends of (2). Next, by finding the fractional derivative ${}^{Ml}{\mathcal{D}}_{0^{+}}^{\beta }$ at both ends of (3), one easily gets the first fractional equation of (1). According to (2) and (3), we have $u\left(0\right)=A$ and ${}^{Ml}{\mathcal{D}}_{0^{+}}^{\alpha }u\left(0\right)=B$. Thus, we verify that $u\left(t\right)\in C(0,T)$ also satisfies system (1). The proof is completed. □

3. Existence of Solutions

In this section, by applying the following important fixed-point theorems, we emphasize to investigate the existence of solutions for system (1).

Lemma 3.

[38] Let $\mathbb{E}$ be a non-empty closed subset of a Banach space $\mathbb{X}$. If $\mathcal{T}:\mathbb{E}\to \mathbb{E}$ is contractive, namely, there is a constant $0<k<1$ such that $\parallel \mathcal{T}u-\mathcal{T}v\parallel \le k\parallel u-v\parallel ,\forall u,v\in \mathbb{E}$, then $\mathcal{T}$ has a unique fixed point $u^{*}\in \mathbb{E}$ such that $\mathcal{T}{u}^{*}=u^{*}$.

Lemma 4.

(Krasnoselskii’s fixed-point theorem [39]) Let$\mathbb{Y}$be a non-empty closed convex subset of a Banach space$\mathbb{X}$. Assume that$\mathcal{P}$and$\mathcal{Q}$are two operators satisfying

(i)

$\mathcal{P}u+\mathcal{Q}v\in \mathbb{Y}$,$\forall u,v\in \mathbb{Y}$.

(ii)

$\mathcal{P}$ is contraction, and $\mathcal{Q}$ is continuous and compact.

Then there is at least a solution $u^{*}\in \mathbb{Y}$ such that $u^{*}=\mathcal{P}{u}^{*}+\mathcal{Q}{u}^{*}$.

By (2), we take $D=[0,T]$, $\mathbb{X}=C(D,\mathbb{R})$. Then $\mathbb{X}$ is a Banach space with the norm $\parallel u\parallel ={sup}_{t\in D}\left|u\left(t\right)\right|$. We shall study the existence and stability of the solution of (1) in $(\mathbb{X},\parallel ·\parallel )$. In the whole paper, we need the following essential assumption.

$\left({\mathrm{H}}_1\right)$

T, $\alpha$, $\beta$, $\lambda$, A and B are some constants and satisfy $T,\lambda >0$, $0<\alpha ,\beta \le 1$, $A,B\in \mathbb{R}$ and $\delta \triangleq 1-\frac{\lambda (1-\alpha )}{\mathcal{N}\left(\alpha \right)}\ne 0$.

Theorem 1.

Assume that$\left({\mathrm{H}}_1\right)$holds, and further assume that$\left({\mathrm{H}}_2\right)$and$\left({\mathrm{H}}_3\right)$are also true.

$\left({\mathrm{H}}_2\right)$$f\in C({\mathbb{R}}^2,\mathbb{R})$, and there is a constant$M>0$such that$\left|f\right(t,u\left)\right|\le M$,$\forall t,u\in \mathbb{R}$.

$\left({\mathrm{H}}_3\right)$$0<\kappa \triangleq \frac{\lambda T^{\alpha }}{\left|\mathcal{N}\right(\alpha )-\lambda (1-\alpha \left)\right|\Gamma \left(\alpha \right)}<1$.

Then, the system (1) has at least one solution $u^{*}\left(t\right)\in \mathbb{X}$.

Proof. 

Based on Lemma 2, for all $u\in \mathbb{X}$, we define two operators $\mathcal{P},\mathcal{Q}:\mathbb{X}\to \mathbb{X}$ as follows:

$$\begin{array}{cc}\hfill \left(\mathcal{P}u\right)\left(t\right)=& A+\frac{1}{\delta }\left\{\frac{B-\lambda A}{\mathcal{N}\left(\alpha \right)\Gamma \left(\alpha \right)}{t}^{\alpha }+\frac{\lambda \alpha }{\mathcal{N}\left(\alpha \right)\Gamma \left(\alpha \right)}{\int }_0^t{(t-s)}^{\alpha -1}u\left(s\right)ds\right\},\forall t\in D,u\in \mathbb{X},\hfill \end{array}$$

(8)

and

$$\begin{array}{cc}\hfill \left(\mathcal{Q}u\right)\left(t\right)=& \frac{1}{\delta }\{\frac{(1-\alpha )(1-\beta )}{\mathcal{N}\left(\alpha \right)\mathcal{N}\left(\beta \right)}[f(t,u\left(t\right))-f(0,A)]+\frac{(1-\alpha )\beta }{\mathcal{N}\left(\alpha \right)\mathcal{N}\left(\beta \right)\Gamma \left(\beta \right)}\hfill \\ \hfill & \times {\int }_0^t{(t-s)}^{\beta -1}f(s,u\left(s\right))ds+\frac{\alpha (1-\beta )}{\mathcal{N}\left(\alpha \right)\mathcal{N}\left(\beta \right)\Gamma \left(\alpha \right)}{\int }_0^t{(t-s)}^{\alpha -1}f(s,u\left(s\right))ds\hfill \\ \hfill & +\frac{\alpha \beta }{\mathcal{N}\left(\alpha \right)\mathcal{N}\left(\beta \right)\Gamma (\alpha +\beta )}{\int }_0^t{(t-s)}^{\alpha +\beta -1}f(s,u\left(s\right))ds\},\forall t\in D,u\in \mathbb{X}.\hfill \end{array}$$

(9)

It is easy to see from (8) and (9) that $\mathcal{P}u+\mathcal{Q}v\in \mathbb{X},\forall u,v\in \mathbb{X}$. Thus, the condition $\left(\mathrm{i}\right)$ in Lemma 4 holds. In addition, for all $t\in D,u,v\in \mathbb{X}$, we have

$$\begin{array}{cc}\hfill & |\left(\mathcal{P}u\right)\left(t\right)-\left(\mathcal{P}v\right)\left(t\right)|=\left|\frac{\lambda \alpha }{\delta \mathcal{N}\left(\alpha \right)\Gamma \left(\alpha \right)}{\int }_0^t{(t-s)}^{\alpha -1}[u\left(s\right)-v\left(s\right)]ds\right|\hfill \\ \hfill \le & \frac{\mathcal{N}\left(\alpha \right)}{\left|\mathcal{N}\right(\alpha )-\lambda (1-\alpha \left)\right|}\times \frac{\lambda \alpha }{\mathcal{N}\left(\alpha \right)\Gamma \left(\alpha \right)}{\int }_0^t{(t-s)}^{\alpha -1}|u\left(s\right)-v\left(s\right)|ds\hfill \\ \hfill \le & \frac{\lambda \alpha }{\left|\mathcal{N}\right(\alpha )-\lambda (1-\alpha \left)\right|\Gamma \left(\alpha \right)}{\int }_0^t{(t-s)}^{\alpha -1}ds·\parallel u-v\parallel =\frac{\lambda t^{\alpha }}{\left|\mathcal{N}\right(\alpha )-\lambda (1-\alpha \left)\right|\Gamma \left(\alpha \right)}\parallel u-v\parallel \hfill \\ \hfill \le & \frac{\lambda T^{\alpha }}{\left|\mathcal{N}\right(\alpha )-\lambda (1-\alpha \left)\right|\Gamma \left(\alpha \right)}\parallel u-v\parallel =\kappa \parallel u-v\parallel .\hfill \end{array}$$

(10)

(10) implies that

$$\begin{array}{c}\hfill \parallel \mathcal{P}u-\mathcal{P}v\parallel \le \frac{\lambda T^{\alpha }}{\left|\mathcal{N}\right(\alpha )-\lambda (1-\alpha \left)\right|\Gamma \left(\alpha \right)}\parallel u-v\parallel =\kappa \parallel u-v\parallel .\end{array}$$

(11)

From $\left({\mathrm{H}}_3\right)$ and (11), we know that $\mathcal{P}:\mathbb{X}\to \mathbb{X}$ is contractive.

Next, we shall show that $\mathcal{Q}:\mathbb{X}\to \mathbb{X}$ is a completely continuous operator by using the Arzelá–Ascoli theorem. Indeed, for all $t\in D,u\in \mathbb{X}$, we derive from $\left({\mathrm{H}}_2\right)$ that

$$\begin{array}{cc}\hfill \left|\right(\mathcal{Q}u\left)\right(t\left)\right|\le & \frac{1}{\left|\delta \right|}\{\frac{(1-\alpha )(1-\beta )}{\mathcal{N}\left(\alpha \right)\mathcal{N}\left(\beta \right)}\left[\right|f(t,u\left(t\right))|+\left|f(0,A)\right|]+\frac{(1-\alpha )\beta }{\mathcal{N}\left(\alpha \right)\mathcal{N}\left(\beta \right)\Gamma \left(\beta \right)}\hfill \\ \hfill & \times {\int }_0^t{(t-s)}^{\beta -1}\left|f(s,u\left(s\right))\right|ds+\frac{\alpha (1-\beta )}{\mathcal{N}\left(\alpha \right)\mathcal{N}\left(\beta \right)\Gamma \left(\alpha \right)}{\int }_0^t{(t-s)}^{\alpha -1}\left|f(s,u\left(s\right))\right|ds\hfill \\ \hfill & +\frac{\alpha \beta }{\mathcal{N}\left(\alpha \right)\mathcal{N}\left(\beta \right)\Gamma (\alpha +\beta )}{\int }_0^t{(t-s)}^{\alpha +\beta -1}\left|f(s,u\left(s\right))\right|ds\}\hfill \\ \hfill \le & \frac{M}{\left|\delta \right|}\{\frac{2(1-\alpha )(1-\beta )}{\mathcal{N}\left(\alpha \right)\mathcal{N}\left(\beta \right)}+\frac{(1-\alpha )\beta }{\mathcal{N}\left(\alpha \right)\mathcal{N}\left(\beta \right)\Gamma \left(\beta \right)}{\int }_0^t{(t-s)}^{\beta -1}ds\hfill \\ \hfill & +\frac{\alpha (1-\beta )}{\mathcal{N}\left(\alpha \right)\mathcal{N}\left(\beta \right)\Gamma \left(\alpha \right)}{\int }_0^t{(t-s)}^{\alpha -1}ds+\frac{\alpha \beta }{\mathcal{N}\left(\alpha \right)\mathcal{N}\left(\beta \right)\Gamma (\alpha +\beta )}{\int }_0^t{(t-s)}^{\alpha +\beta -1}ds\}\hfill \\ \hfill \le & \frac{M}{\left|\delta \right|}\{\frac{2(1-\alpha )(1-\beta )}{\mathcal{N}\left(\alpha \right)\mathcal{N}\left(\beta \right)}+\frac{(1-\alpha )T^{\beta }}{\mathcal{N}\left(\alpha \right)\mathcal{N}\left(\beta \right)\Gamma \left(\beta \right)}+\frac{(1-\beta )T^{\alpha }}{\mathcal{N}\left(\alpha \right)\mathcal{N}\left(\beta \right)\Gamma \left(\alpha \right)}\hfill \\ \hfill & +\frac{\alpha \beta T^{\alpha +\beta }}{\mathcal{N}\left(\alpha \right)\mathcal{N}\left(\beta \right)\Gamma (\alpha +\beta +1)}\}=\varrho M,\hfill \end{array}$$

(12)

where $\varrho =\frac{1}{\left|\delta \right|}\left\{\frac{2(1-\alpha )(1-\beta )}{\mathcal{N}\left(\alpha \right)\mathcal{N}\left(\beta \right)}+\frac{(1-\alpha )T^{\beta }}{\mathcal{N}\left(\alpha \right)\mathcal{N}\left(\beta \right)\Gamma \left(\beta \right)}+\frac{(1-\beta )T^{\alpha }}{\mathcal{N}\left(\alpha \right)\mathcal{N}\left(\beta \right)\Gamma \left(\alpha \right)}+\frac{\alpha \beta T^{\alpha +\beta }}{\mathcal{N}\left(\alpha \right)\mathcal{N}\left(\beta \right)\Gamma (\alpha +\beta +1)}\right\}$. (12) indicates that $\mathcal{Q}:\mathbb{X}\to \mathbb{X}$ is uniformly bounded.

On the other hand, for $\forall u\in \mathbb{X}$, $t_1,t_2\in D$ with $t_1<t_2$, it follows from $f\in C({\mathbb{R}}^2,\mathbb{R})$ and $\left({\mathrm{H}}_2\right)$ that

$$\begin{array}{cc}\hfill & |\left(\mathcal{Q}u\right)\left(t_2\right)-\left(\mathcal{Q}u\right)\left(t_1\right)|=\frac{1}{\left|\delta \right|}|\frac{(1-\alpha )(1-\beta )}{\mathcal{N}\left(\alpha \right)\mathcal{N}\left(\beta \right)}[f(t_2,u\left(t_2\right))-f(t_1,u\left(t_1\right))]\hfill \\ \hfill & +\frac{(1-\alpha )\beta }{\mathcal{N}\left(\alpha \right)\mathcal{N}\left(\beta \right)\Gamma \left(\beta \right)}\left[{\int }_0^{t_2}{(t_2-s)}^{\beta -1}f(s,u\left(s\right))ds-{\int }_0^{t_1}{(t_1-s)}^{\beta -1}f(s,u\left(s\right))ds\right]\hfill \\ \hfill & +\frac{\alpha (1-\beta )}{\mathcal{N}\left(\alpha \right)\mathcal{N}\left(\beta \right)\Gamma \left(\alpha \right)}\left[{\int }_0^{t_2}{(t_2-s)}^{\alpha -1}f(s,u\left(s\right))ds-{\int }_0^{t_1}{(t_1-s)}^{\alpha -1}f(s,u\left(s\right))ds\right]\hfill \\ \hfill & +\frac{\alpha \beta }{\mathcal{N}\left(\alpha \right)\mathcal{N}\left(\beta \right)\Gamma (\alpha +\beta )}[{\int }_0^{t_2}{(t_2-s)}^{\alpha +\beta -1}f(s,u\left(s\right))ds\hfill \\ \hfill & -{\int }_0^{t_1}{(t_1-s)}^{\alpha +\beta -1}f(s,u\left(s\right))ds\left]\right|\hfill \\ \hfill =& \frac{1}{\left|\delta \right|}|\frac{(1-\alpha )(1-\beta )}{\mathcal{N}\left(\alpha \right)\mathcal{N}\left(\beta \right)}[f(t_2,u\left(t_2\right))-f(t_1,u\left(t_1\right))]+\frac{(1-\alpha )\beta }{\mathcal{N}\left(\alpha \right)\mathcal{N}\left(\beta \right)\Gamma \left(\beta \right)}\hfill \\ \hfill & \times \left[{\int }_{t_1}^{t_2}{(t_2-s)}^{\beta -1}f(s,u\left(s\right))ds+{\int }_0^{t_1}\left[{(t_2-s)}^{\beta -1}-{(t_1-s)}^{\beta -1}\right]f(s,u\left(s\right))ds\right]\hfill \\ \hfill & +\frac{\alpha (1-\beta )}{\mathcal{N}\left(\alpha \right)\mathcal{N}\left(\beta \right)\Gamma \left(\alpha \right)}[{\int }_{t_1}^{t_2}{(t_2-s)}^{\alpha -1}f(s,u\left(s\right))ds+{\int }_0^{t_1}\left[{(t_2-s)}^{\alpha -1}-{(t_1-s)}^{\alpha -1}\right]\hfill \\ \hfill & \times f(s,u\left(s\right))ds]+\frac{\alpha \beta }{\mathcal{N}\left(\alpha \right)\mathcal{N}\left(\beta \right)\Gamma (\alpha +\beta )}[{\int }_{t_1}^{t_2}{(t_2-s)}^{\alpha +\beta -1}f(s,u\left(s\right))ds\hfill \\ \hfill & +{\int }_0^{t_1}\left[{(t_2-s)}^{\alpha +\beta -1}-{(t_1-s)}^{\alpha +\beta -1}\right]f(s,u\left(s\right))ds\left]\right|\hfill \\ \hfill \le & \frac{1}{\left|\delta \right|}\{\frac{(1-\alpha )(1-\beta )}{\mathcal{N}\left(\alpha \right)\mathcal{N}\left(\beta \right)}|f(t_2,u\left(t_2\right))-f(t_1,u\left(t_1\right))|+\frac{(1-\alpha )\beta }{\mathcal{N}\left(\alpha \right)\mathcal{N}\left(\beta \right)\Gamma \left(\beta \right)}\hfill \\ \hfill & \times \left[{\int }_{t_1}^{t_2}{(t_2-s)}^{\beta -1}|f(s,u\left(s\right))|ds+{\int }_0^{t_1}|{(t_2-s)}^{\beta -1}-{(t_1-s)}^{\beta -1}|\left|f(s,u\left(s\right))\right|ds\right]\hfill \\ \hfill & +\frac{\alpha (1-\beta )}{\mathcal{N}\left(\alpha \right)\mathcal{N}\left(\beta \right)\Gamma \left(\alpha \right)}[{\int }_{t_1}^{t_2}{(t_2-s)}^{\alpha -1}\left|f(s,u\left(s\right))\right|ds+{\int }_0^{t_1}|{(t_2-s)}^{\alpha -1}-{(t_1-s)}^{\alpha -1}|\hfill \\ \hfill & \times \left|f(s,u\left(s\right))\right|ds]+\frac{\alpha \beta }{\mathcal{N}\left(\alpha \right)\mathcal{N}\left(\beta \right)\Gamma (\alpha +\beta )}[{\int }_{t_1}^{t_2}{(t_2-s)}^{\alpha +\beta -1}\left|f(s,u\left(s\right))\right|ds\hfill \\ \hfill & +{\int }_0^{t_1}|{(t_2-s)}^{\alpha +\beta -1}-{(t_1-s)}^{\alpha +\beta -1}|\left|f(s,u\left(s\right))\right|ds\left]\right\}\hfill \\ \hfill \le & \frac{1}{\left|\delta \right|}\{\frac{(1-\alpha )(1-\beta )}{\mathcal{N}\left(\alpha \right)\mathcal{N}\left(\beta \right)}|f(t_2,u\left(t_2\right))-f(t_1,u\left(t_1\right))|+\frac{M(1-\alpha )\beta }{\mathcal{N}\left(\alpha \right)\mathcal{N}\left(\beta \right)\Gamma \left(\beta \right)}[{\int }_{t_1}^{t_2}{(t_2-s)}^{\beta -1}ds\hfill \\ \hfill & +{\int }_0^T|{(t_2-s)}^{\beta -1}-{(t_1-s)}^{\beta -1}|ds]+\frac{M\alpha (1-\beta )}{\mathcal{N}\left(\alpha \right)\mathcal{N}\left(\beta \right)\Gamma \left(\alpha \right)}[{\int }_{t_1}^{t_2}{(t_2-s)}^{\alpha -1}ds\hfill \\ \hfill & +{\int }_0^T|{(t_2-s)}^{\alpha -1}-{(t_1-s)}^{\alpha -1}|ds]+\frac{M\alpha \beta }{\mathcal{N}\left(\alpha \right)\mathcal{N}\left(\beta \right)\Gamma (\alpha +\beta )}[{\int }_{t_1}^{t_2}{(t_2-s)}^{\alpha +\beta -1}ds\hfill \\ \hfill & +{\int }_0^T|{(t_2-s)}^{\alpha +\beta -1}-{(t_1-s)}^{\alpha +\beta -1}|ds\left]\right\}\hfill \\ \hfill =& \frac{1}{\left|\delta \right|}\{\frac{(1-\alpha )(1-\beta )}{\mathcal{N}\left(\alpha \right)\mathcal{N}\left(\beta \right)}|f(t_2,u\left(t_2\right))-f(t_1,u\left(t_1\right))|+\frac{M(1-\alpha )\beta }{\mathcal{N}\left(\alpha \right)\mathcal{N}\left(\beta \right)\Gamma \left(\beta \right)}[\frac{1}{\beta }{(t_2-t_1)}^{\beta }\hfill \\ \hfill & +{\int }_0^T|{(t_2-s)}^{\beta -1}-{(t_1-s)}^{\beta -1}|ds]+\frac{M\alpha (1-\beta )}{\mathcal{N}\left(\alpha \right)\mathcal{N}\left(\beta \right)\Gamma \left(\alpha \right)}[\frac{1}{\alpha }{(t_2-t_1)}^{\alpha }\hfill \\ \hfill & +{\int }_0^T|{(t_2-s)}^{\alpha -1}-{(t_1-s)}^{\alpha -1}|ds]+\frac{M\alpha \beta }{\mathcal{N}\left(\alpha \right)\mathcal{N}\left(\beta \right)\Gamma (\alpha +\beta )}[\frac{1}{\alpha +\beta }{(t_2-t_1)}^{\alpha +\beta }\hfill \\ \hfill & +{\int }_0^T|{(t_2-s)}^{\alpha +\beta -1}-{(t_1-s)}^{\alpha +\beta -1}|ds\left]\right\}\to 0,\mathrm{as}{t}_2\to t_1.\hfill \end{array}$$

(13)

From (13), we conclude that, $\forall ϵ>0$, $\exists \sigma =\sigma \left(ϵ\right)>0$, for all $t_1,t_2\in D,$$u\in \mathbb{X}$, when $|t_2-t_1|<\sigma$, there is $|\left(\mathcal{Q}u\right)\left(t_2\right)-\left(\mathcal{Q}u\right)\left(t_1\right)|<ϵ$, namely, $\mathcal{Q}:\mathbb{X}\to \mathbb{X}$ is equicontinuous. Thus, we verify that the condition $\left(\mathrm{ii}\right)$ is true. Therefore, according to Lemmas 2 and 4, one knows that there exists at least a fixed point $u^{*}\left(t\right)\in \mathbb{X}$ such that $u^{*}\left(t\right)=\left(\mathcal{P}{u}^{*}\right)\left(t\right)+\left(\mathcal{Q}{u}^{*}\right)\left(t\right)$, which is a solution of system (1). The proof is completed. □

Theorem 2.

Assume that$\left({\mathrm{H}}_1\right)$holds, further assume that$\left({\mathrm{H}}_4\right)$and$\left({\mathrm{H}}_5\right)$are also true.

$\left({\mathrm{H}}_4\right)$$f\in C({\mathbb{R}}^2,\mathbb{R})$, and there is a constant$L>0$such that$\left|f\right(t,u)-f(t,v\left)\right|\le L|u-v|$,$\forall t,u,v\in \mathbb{R}$.

$\left({\mathrm{H}}_5\right)$$0<\rho <1$, here$\rho =\frac{1}{\left|\delta \right|}\left\{\frac{L(1-\alpha )(1-\beta )}{\mathcal{N}\left(\alpha \right)\mathcal{N}\left(\beta \right)}+\frac{L(1-\alpha )T^{\beta }}{\mathcal{N}\left(\alpha \right)\mathcal{N}\left(\beta \right)\Gamma \left(\beta \right)}+\frac{L(1-\beta )T^{\alpha }}{\mathcal{N}\left(\alpha \right)\mathcal{N}\left(\beta \right)\Gamma \left(\alpha \right)}+\frac{L\alpha \beta T^{\alpha +\beta }}{\mathcal{N}\left(\alpha \right)\mathcal{N}\left(\beta \right)\Gamma (\alpha +\beta +1)}+\frac{\lambda T^{\alpha }}{\mathcal{N}\left(\alpha \right)\Gamma \left(\alpha \right)}\right\}$.

Then system (1) has a unique solution $u^{*}\left(t\right)\in \mathbb{X}$.

Proof. 

According to Lemma 2, we define an operator $\mathcal{T}:\mathbb{X}\to \mathbb{X}$ as follows:

$$\begin{array}{cc}\hfill \left(\mathcal{T}u\right)\left(t\right)=& A+\frac{1}{\delta }\{\frac{B-\lambda A}{\mathcal{N}\left(\alpha \right)\Gamma \left(\alpha \right)}{t}^{\alpha }+\frac{(1-\alpha )(1-\beta )}{\mathcal{N}\left(\alpha \right)\mathcal{N}\left(\beta \right)}[f(t,u\left(t\right))-f(0,A)]\hfill \\ \hfill & +\frac{\lambda \alpha }{\mathcal{N}\left(\alpha \right)\Gamma \left(\alpha \right)}{\int }_0^t{(t-s)}^{\alpha -1}u\left(s\right)ds+\frac{(1-\alpha )\beta }{\mathcal{N}\left(\alpha \right)\mathcal{N}\left(\beta \right)\Gamma \left(\beta \right)}{\int }_0^t{(t-s)}^{\beta -1}f(s,u\left(s\right))ds\hfill \\ \hfill & +\frac{\alpha (1-\beta )}{\mathcal{N}\left(\alpha \right)\mathcal{N}\left(\beta \right)\Gamma \left(\alpha \right)}{\int }_0^t{(t-s)}^{\alpha -1}f(s,u\left(s\right))ds\hfill \\ \hfill & +\frac{\alpha \beta }{\mathcal{N}\left(\alpha \right)\mathcal{N}\left(\beta \right)\Gamma (\alpha +\beta )}{\int }_0^t{(t-s)}^{\alpha +\beta -1}f(s,u\left(s\right))ds\}.\hfill \end{array}$$

(14)

Then, for all $u,v\in \mathbb{X}$, we derive from $\left({\mathrm{H}}_4\right)$ and $\left({\mathrm{H}}_5\right)$ that

$$\begin{array}{cc}\hfill & \left|\right(\mathcal{T}u\left)\right(t)-(\mathcal{T}v\left)\right(t\left)\right|\hfill \\ \hfill \le & \frac{1}{\left|\delta \right|}\{\frac{(1-\alpha )(1-\beta )}{\mathcal{N}\left(\alpha \right)\mathcal{N}\left(\beta \right)}|f(t,u\left(t\right))-f(t,v\left(t\right))|+\frac{\lambda \alpha }{\mathcal{N}\left(\alpha \right)\Gamma \left(\alpha \right)}{\int }_0^t{(t-s)}^{\alpha -1}|u\left(s\right)-v\left(s\right)|ds\hfill \\ \hfill & +\frac{(1-\alpha )\beta }{\mathcal{N}\left(\alpha \right)\mathcal{N}\left(\beta \right)\Gamma \left(\beta \right)}{\int }_0^t{(t-s)}^{\beta -1}|f(s,u\left(s\right))-f(s,v\left(s\right))|ds\hfill \\ \hfill & +\frac{\alpha (1-\beta )}{\mathcal{N}\left(\alpha \right)\mathcal{N}\left(\beta \right)\Gamma \left(\alpha \right)}{\int }_0^t{(t-s)}^{\alpha -1}|f(s,u\left(s\right))-f(s,v\left(s\right))|ds\hfill \\ \hfill & +\frac{\alpha \beta }{\mathcal{N}\left(\alpha \right)\mathcal{N}\left(\beta \right)\Gamma (\alpha +\beta )}{\int }_0^t{(t-s)}^{\alpha +\beta -1}|f(s,u\left(s\right))-f(s,v\left(s\right))|ds\}\hfill \\ \hfill \le & \frac{1}{\left|\delta \right|}\{\frac{L(1-\alpha )(1-\beta )}{\mathcal{N}\left(\alpha \right)\mathcal{N}\left(\beta \right)}|u\left(t\right)-v\left(t\right)|+\frac{\lambda \alpha }{\mathcal{N}\left(\alpha \right)\Gamma \left(\alpha \right)}{\int }_0^t{(t-s)}^{\alpha -1}|u\left(s\right)-v\left(s\right)|ds\hfill \\ \hfill & +\frac{L(1-\alpha )\beta }{\mathcal{N}\left(\alpha \right)\mathcal{N}\left(\beta \right)\Gamma \left(\beta \right)}{\int }_0^t{(t-s)}^{\beta -1}|u\left(s\right)-v\left(s\right)|ds\hfill \\ \hfill & +\frac{L\alpha (1-\beta )}{\mathcal{N}\left(\alpha \right)\mathcal{N}\left(\beta \right)\Gamma \left(\alpha \right)}{\int }_0^t{(t-s)}^{\alpha -1}|u\left(s\right)-v\left(s\right)|ds\hfill \\ \hfill & +\frac{L\alpha \beta }{\mathcal{N}\left(\alpha \right)\mathcal{N}\left(\beta \right)\Gamma (\alpha +\beta )}{\int }_0^t{(t-s)}^{\alpha +\beta -1}|u\left(s\right)-v\left(s\right)|ds\}\hfill \\ \hfill \le & \frac{1}{\left|\delta \right|}\{\frac{L(1-\alpha )(1-\beta )}{\mathcal{N}\left(\alpha \right)\mathcal{N}\left(\beta \right)}+\frac{\lambda \alpha }{\mathcal{N}\left(\alpha \right)\Gamma \left(\alpha \right)}{\int }_0^t{(t-s)}^{\alpha -1}ds+\frac{L(1-\alpha )\beta }{\mathcal{N}\left(\alpha \right)\mathcal{N}\left(\beta \right)\Gamma \left(\beta \right)}{\int }_0^t{(t-s)}^{\beta -1}ds\hfill \\ \hfill & +\frac{L\alpha (1-\beta )}{\mathcal{N}\left(\alpha \right)\mathcal{N}\left(\beta \right)\Gamma \left(\alpha \right)}{\int }_0^t{(t-s)}^{\alpha -1}ds+\frac{L\alpha \beta }{\mathcal{N}\left(\alpha \right)\mathcal{N}\left(\beta \right)\Gamma (\alpha +\beta )}{\int }_0^t{(t-s)}^{\alpha +\beta -1}ds\}\parallel u-v\parallel \hfill \\ \hfill =& \frac{1}{\left|\delta \right|}\{\frac{L(1-\alpha )(1-\beta )}{\mathcal{N}\left(\alpha \right)\mathcal{N}\left(\beta \right)}+\frac{\lambda t^{\alpha }}{\mathcal{N}\left(\alpha \right)\Gamma \left(\alpha \right)}+\frac{L(1-\alpha )t^{\beta }}{\mathcal{N}\left(\alpha \right)\mathcal{N}\left(\beta \right)\Gamma \left(\beta \right)}\hfill \\ \hfill & +\frac{L(1-\beta )t^{\alpha }}{\mathcal{N}\left(\alpha \right)\mathcal{N}\left(\beta \right)\Gamma \left(\alpha \right)}+\frac{L\alpha \beta t^{\alpha +\beta }}{\mathcal{N}\left(\alpha \right)\mathcal{N}\left(\beta \right)\Gamma (\alpha +\beta +1)}\}\parallel u-v\parallel \hfill \\ \hfill \le & \frac{1}{\left|\delta \right|}\{\frac{L(1-\alpha )(1-\beta )}{\mathcal{N}\left(\alpha \right)\mathcal{N}\left(\beta \right)}+\frac{\lambda T^{\alpha }}{\mathcal{N}\left(\alpha \right)\Gamma \left(\alpha \right)}+\frac{L(1-\alpha )T^{\beta }}{\mathcal{N}\left(\alpha \right)\mathcal{N}\left(\beta \right)\Gamma \left(\beta \right)}+\frac{L(1-\beta )T^{\alpha }}{\mathcal{N}\left(\alpha \right)\mathcal{N}\left(\beta \right)\Gamma \left(\alpha \right)}\hfill \\ \hfill & +\frac{L\alpha \beta T^{\alpha +\beta }}{\mathcal{N}\left(\alpha \right)\mathcal{N}\left(\beta \right)\Gamma (\alpha +\beta +1)}\}\parallel u-v\parallel =\rho \parallel u-v\parallel .\hfill \end{array}$$

(15)

(15) leads to

$$\begin{array}{c}\hfill \parallel \mathcal{T}u-\mathcal{T}v\parallel \le \rho \parallel u-v\parallel .\end{array}$$

(16)

By (16) and $\left({\mathrm{H}}_5\right)$, we know that $\mathcal{T}:\mathbb{X}\to \mathbb{X}$ is contractive. Thus, it follows from Lemmas 3 and 2 that the operator has a unique fixed point $u^{*}\left(t\right)$, which is a unique solution of system (1). The proof is completed. □

4. Stability of Ulam–Hyers Type

This section mainly discusses the stability of types such as Ulam–Hyers, generalized Ulam–Hyers, Ulam–Hyers–Rassias and generalized Ulam–Hyers–Rassias for system (1).

Let $z\in \mathbb{X}$, $\epsilon >0$, $0<\alpha ,\beta \le 1$ and $\phi \in C(D,{\mathbb{R}}^{+})$ be non-decreasing. Consider the following two inequalities

$$\begin{array}{c}\hfill \left\{\begin{array}{c}|{}^{ML}{\mathcal{D}}_{0^{+}}^{\beta }\left[{}^{ML}{\mathcal{D}}_{0^{+}}^{\alpha }-\lambda \right]z\left(t\right)-f(t,z)|\le \epsilon ,0<t\le T,\hfill \\ z\left(0\right)=A,{}^{ML}{\mathcal{D}}_{0^{+}}^{\alpha }z\left(0\right)=B,\hfill \end{array}\right.\end{array}$$

(17)

and

$$\begin{array}{c}\hfill \left\{\begin{array}{c}|{}^{ML}{\mathcal{D}}_{0^{+}}^{\beta }\left[{}^{ML}{\mathcal{D}}_{0^{+}}^{\alpha }-\lambda \right]z\left(t\right)-f(t,z)|\le \phi \left(t\right)\epsilon ,0<t\le T,\hfill \\ z\left(0\right)=A,{}^{ML}{\mathcal{D}}_{0^{+}}^{\alpha }z\left(0\right)=B.\hfill \end{array}\right.\end{array}$$

(18)

Definition 3.

Assume that for each $\epsilon >0$ and each solution $z\in \mathbb{X}$ of inequality (17), there is a constant $C_1>0$ and a unique solution $u\in \mathbb{X}$ of system (1) such that

$$\begin{array}{c}\hfill \parallel z\left(t\right)-u\left(t\right)\parallel \le C_1\epsilon ,\end{array}$$

then system (1) is called Ulam–Hyers stable (abbreviated as UH-stable).

Definition 4.

Assume that for each $\epsilon >0$ and each solution $z\in \mathbb{X}$ of inequality (17), there is a function $\theta (·)\in C(\mathbb{R},{\mathbb{R}}^{+})$ with $\theta \left(0\right)=0$ and a unique solution $u\in \mathbb{X}$ of system (1) such that

$$\begin{array}{c}\hfill \parallel z\left(t\right)-u\left(t\right)\parallel \le \theta \left(\epsilon \right),\end{array}$$

then system (1) is called generalized Ulam–Hyers (GUH) stable (abbreviated as GUH-stable).

Definition 5.

Assume that for each $\epsilon >0$ and each solution $z\in \mathbb{X}$ of inequality (18), there is a constant $C_2>0$ and a unique solution $u\in \mathbb{X}$ of system (1) such that

$$\begin{array}{c}\hfill \parallel z\left(t\right)-u\left(t\right)\parallel \le C_2\phi \left(t\right)\epsilon ,t\in D,\end{array}$$

then system (1) is called Ulam–Hyers–Rassias stable (abbreviated as UHR-stable).

Definition 6.

Assume that for each $\epsilon >0$ and each solution $z\in \mathbb{X}$ of inequality (18), there is a constant $C_3>0$ and a unique solution $u\in \mathbb{X}$ of system (1) such that

$$\begin{array}{c}\hfill \parallel z\left(t\right)-u\left(t\right)\parallel \le C_3\phi \left(t\right),t\in D,\end{array}$$

then system (1) is called generalized Ulam–Hyers–Rassias stable (abbreviated as GUHR-stable).

Obviously, UH-stable ⇒ GUH-stable, and UHR-stable ⇒ GUHR-stable.

Remark 3.

A function$z\in \mathbb{X}$is a solution of inequality (17) if and only if there exists a function$\varphi \in \mathbb{X}$such that

(1)

$\left|\varphi \right(t\left)\right|\le ϵ$,$0<t\le T$.

(2)

${}^{ML}{\mathcal{D}}_{0^{+}}^{\beta }\left[{}^{ML}{\mathcal{D}}_{0^{+}}^{\alpha }-\lambda \right]z\left(t\right)=f(t,z)+\varphi \left(t\right),0<t\le T$.

Remark 4.

A function$z\in \mathbb{X}$is a solution of inequality (18) if and only if there exists a function$\psi \in \mathbb{X}$such that

(1)

$\left|\psi \right(t\left)\right|\le \phi \left(t\right)ϵ$,$0<t\le T$.

(2)

${}^{ML}{\mathcal{D}}_{0^{+}}^{\beta }\left[{}^{ML}{\mathcal{D}}_{0^{+}}^{\alpha }-\lambda \right]z\left(t\right)=f(t,z)+\psi \left(t\right),0<t\le T$.

Theorem 3.

If all the conditions of Theorem 2 hold, then the system (1) is UH-stable and also GUH-stable.

Proof. 

Based on Lemma 2 and Remark 3, the solution $z\left(t\right)$ of inequality (17) is expressed as

$$\begin{array}{cc}\hfill z\left(t\right)=& A+\frac{1}{\delta }\{\frac{B-\lambda A}{\mathcal{N}\left(\alpha \right)\Gamma \left(\alpha \right)}{t}^{\alpha }+\frac{(1-\alpha )(1-\beta )}{\mathcal{N}\left(\alpha \right)\mathcal{N}\left(\beta \right)}[f(t,z\left(t\right))-f(0,A)+\varphi \left(t\right)-\varphi \left(0\right)]\hfill \\ \hfill & +\frac{\lambda \alpha }{\mathcal{N}\left(\alpha \right)\Gamma \left(\alpha \right)}{\int }_0^t{(t-s)}^{\alpha -1}z\left(s\right)ds+\frac{(1-\alpha )\beta }{\mathcal{N}\left(\alpha \right)\mathcal{N}\left(\beta \right)\Gamma \left(\beta \right)}{\int }_0^t{(t-s)}^{\beta -1}[f(s,z\left(s\right))+\varphi \left(s\right)]ds\hfill \\ \hfill & +\frac{\alpha (1-\beta )}{\mathcal{N}\left(\alpha \right)\mathcal{N}\left(\beta \right)\Gamma \left(\alpha \right)}{\int }_0^t{(t-s)}^{\alpha -1}[f(s,z\left(s\right))+\varphi \left(s\right)]ds\hfill \\ \hfill & +\frac{\alpha \beta }{\mathcal{N}\left(\alpha \right)\mathcal{N}\left(\beta \right)\Gamma (\alpha +\beta )}{\int }_0^t{(t-s)}^{\alpha +\beta -1}[f(s,z\left(s\right))+\varphi \left(s\right)]ds\},t\in D.\hfill \end{array}$$

(19)

By the Theorem 2 and Lemma 2, the unique solution $u^{*}\left(t\right)$ of (1) satisfies

$$\begin{array}{cc}\hfill u^{*}\left(t\right)=& A+\frac{1}{\delta }\{\frac{B-\lambda A}{\mathcal{N}\left(\alpha \right)\Gamma \left(\alpha \right)}{t}^{\alpha }+\frac{(1-\alpha )(1-\beta )}{\mathcal{N}\left(\alpha \right)\mathcal{N}\left(\beta \right)}[f(t,u^{*}\left(t\right))-f(0,A)]\hfill \\ \hfill & +\frac{\lambda \alpha }{\mathcal{N}\left(\alpha \right)\Gamma \left(\alpha \right)}{\int }_0^t{(t-s)}^{\alpha -1}{u}^{*}\left(s\right)ds+\frac{(1-\alpha )\beta }{\mathcal{N}\left(\alpha \right)\mathcal{N}\left(\beta \right)\Gamma \left(\beta \right)}{\int }_0^t{(t-s)}^{\beta -1}f(s,u^{*}\left(s\right))ds\hfill \\ \hfill & +\frac{\alpha (1-\beta )}{\mathcal{N}\left(\alpha \right)\mathcal{N}\left(\beta \right)\Gamma \left(\alpha \right)}{\int }_0^t{(t-s)}^{\alpha -1}f(s,u^{*}\left(s\right))ds\hfill \\ \hfill & +\frac{\alpha \beta }{\mathcal{N}\left(\alpha \right)\mathcal{N}\left(\beta \right)\Gamma (\alpha +\beta )}{\int }_0^t{(t-s)}^{\alpha +\beta -1}f(s,u^{*}\left(s\right))ds\},t\in D.\hfill \end{array}$$

(20)

Similar to (15), it follows from (19) and (20) that

$$\begin{array}{cc}\hfill & |z\left(t\right)-u^{*}\left(t\right)|\le \frac{1}{\left|\delta \right|}\{\frac{(1-\alpha )(1-\beta )}{\mathcal{N}\left(\alpha \right)\mathcal{N}\left(\beta \right)}\left[|f(t,z\left(t\right))-f(t,u^{*}\left(t\right))|+|\varphi \left(t\right)|+|\varphi \left(0\right)|\right]\hfill \\ \hfill & +\frac{\lambda \alpha }{\mathcal{N}\left(\alpha \right)\Gamma \left(\alpha \right)}{\int }_0^t{(t-s)}^{\alpha -1}|z\left(s\right)-u^{*}\left(s\right)|ds+\frac{(1-\alpha )\beta }{\mathcal{N}\left(\alpha \right)\mathcal{N}\left(\beta \right)\Gamma \left(\beta \right)}{\int }_0^t{(t-s)}^{\beta -1}\hfill \\ \hfill & \times \left[|f(s,z\left(s\right))-f(s,u^{*}\left(s\right))|+|\varphi \left(s\right)|\right]ds+\frac{\alpha (1-\beta )}{\mathcal{N}\left(\alpha \right)\mathcal{N}\left(\beta \right)\Gamma \left(\alpha \right)}{\int }_0^t{(t-s)}^{\alpha -1}\hfill \\ \hfill & \times \left[|f(s,z\left(s\right))-f(s,u^{*}\left(s\right))|+|\varphi \left(s\right)|\right]ds+\frac{\alpha \beta }{\mathcal{N}\left(\alpha \right)\mathcal{N}\left(\beta \right)\Gamma (\alpha +\beta )}\hfill \\ \hfill & {\int }_0^t{(t-s)}^{\alpha +\beta -1}\left[|f(s,z\left(s\right))-f(s,u^{*}\left(s\right))|+|\varphi \left(s\right)|\right]ds\}\hfill \\ \hfill \le & \frac{1}{\left|\delta \right|}\{\frac{(1-\alpha )(1-\beta )}{\mathcal{N}\left(\alpha \right)\mathcal{N}\left(\beta \right)}\left[L\parallel z\left(t\right)-u^{*}\left(t\right)\parallel +\epsilon +\epsilon \right]+\frac{\lambda \alpha }{\mathcal{N}\left(\alpha \right)\Gamma \left(\alpha \right)}{\int }_0^t{(t-s)}^{\alpha -1}\hfill \\ \hfill & \times \parallel z\left(s\right)-u^{*}\left(s\right)\parallel ds+\frac{(1-\alpha )\beta }{\mathcal{N}\left(\alpha \right)\mathcal{N}\left(\beta \right)\Gamma \left(\beta \right)}{\int }_0^t{(t-s)}^{\beta -1}\left[L\parallel z\left(s\right)-u^{*}\left(s\right)\parallel +\epsilon \right]ds\hfill \\ \hfill & +\frac{\alpha (1-\beta )}{\mathcal{N}\left(\alpha \right)\mathcal{N}\left(\beta \right)\Gamma \left(\alpha \right)}{\int }_0^t{(t-s)}^{\alpha -1}\left[L\parallel z\left(s\right)-u^{*}\left(s\right)\parallel +\epsilon \right]ds\hfill \\ \hfill & +\frac{\alpha \beta }{\mathcal{N}\left(\alpha \right)\mathcal{N}\left(\beta \right)\Gamma (\alpha +\beta )}{\int }_0^t{(t-s)}^{\alpha +\beta -1}\left[L\parallel z\left(s\right)-u^{*}\left(s\right)\parallel +\epsilon \right]ds\}\hfill \\ \hfill \le & \rho \parallel z\left(t\right)-u^{*}\left(t\right)\parallel +\varrho \epsilon ,\hfill \end{array}$$

which implies that

$$\begin{array}{c}\hfill \parallel z\left(t\right)-u^{*}\left(t\right)\parallel \le \frac{\varrho }{1-\rho }\epsilon .\end{array}$$

(21)

Thus, (21) shows that system (1) is UH-stable and also GUH-stable. The proof is completed. □

Theorem 4.

If all the conditions of Theorem 2 hold, then the system (1) is UHR-stable and also GUHR-stable.

Proof. 

By applying Lemma 2 and Remark 4, the solution $z\left(t\right)$ of inequality (18) is formulated by

$$\begin{array}{cc}\hfill z\left(t\right)=& A+\frac{1}{\delta }\{\frac{B-\lambda A}{\mathcal{N}\left(\alpha \right)\Gamma \left(\alpha \right)}{t}^{\alpha }+\frac{(1-\alpha )(1-\beta )}{\mathcal{N}\left(\alpha \right)\mathcal{N}\left(\beta \right)}[f(t,z\left(t\right))-f(0,A)+\psi \left(t\right)-\psi \left(0\right)]\hfill \\ \hfill & +\frac{\lambda \alpha }{\mathcal{N}\left(\alpha \right)\Gamma \left(\alpha \right)}{\int }_0^t{(t-s)}^{\alpha -1}z\left(s\right)ds+\frac{(1-\alpha )\beta }{\mathcal{N}\left(\alpha \right)\mathcal{N}\left(\beta \right)\Gamma \left(\beta \right)}{\int }_0^t{(t-s)}^{\beta -1}[f(s,z\left(s\right))+\psi \left(s\right)]ds\hfill \\ \hfill & +\frac{\alpha (1-\beta )}{\mathcal{N}\left(\alpha \right)\mathcal{N}\left(\beta \right)\Gamma \left(\alpha \right)}{\int }_0^t{(t-s)}^{\alpha -1}[f(s,z\left(s\right))+\psi \left(s\right)]ds\hfill \\ \hfill & +\frac{\alpha \beta }{\mathcal{N}\left(\alpha \right)\mathcal{N}\left(\beta \right)\Gamma (\alpha +\beta )}{\int }_0^t{(t-s)}^{\alpha +\beta -1}[f(s,z\left(s\right))+\psi \left(s\right)]ds\},t\in D.\hfill \end{array}$$

(22)

Noting that $\phi \ge 0$ is non-decreasing and together with (19) and (22), we have

$$\begin{array}{cc}\hfill & |z\left(t\right)-u^{*}\left(t\right)|\le \frac{1}{\left|\delta \right|}\{\frac{(1-\alpha )(1-\beta )}{\mathcal{N}\left(\alpha \right)\mathcal{N}\left(\beta \right)}\left[|f(t,z\left(t\right))-f(t,u^{*}\left(t\right))|+|\psi \left(t\right)-\psi \left(0\right)|\right]\hfill \\ \hfill & +\frac{\lambda \alpha }{\mathcal{N}\left(\alpha \right)\Gamma \left(\alpha \right)}{\int }_0^t{(t-s)}^{\alpha -1}|z\left(s\right)-u^{*}\left(s\right)|ds+\frac{(1-\alpha )\beta }{\mathcal{N}\left(\alpha \right)\mathcal{N}\left(\beta \right)\Gamma \left(\beta \right)}{\int }_0^t{(t-s)}^{\beta -1}\hfill \\ \hfill & \times \left[|f(s,z\left(s\right))-f(s,u^{*}\left(s\right))|+|\psi \left(s\right)|\right]ds+\frac{\alpha (1-\beta )}{\mathcal{N}\left(\alpha \right)\mathcal{N}\left(\beta \right)\Gamma \left(\alpha \right)}{\int }_0^t{(t-s)}^{\alpha -1}\hfill \\ \hfill & \times \left[|f(s,z\left(s\right))-f(s,u^{*}\left(s\right))|+|\psi \left(s\right)|\right]ds+\frac{\alpha \beta }{\mathcal{N}\left(\alpha \right)\mathcal{N}\left(\beta \right)\Gamma (\alpha +\beta )}\hfill \\ \hfill & {\int }_0^t{(t-s)}^{\alpha +\beta -1}\left[|f(s,z\left(s\right))-f(s,u^{*}\left(s\right))|+|\psi \left(s\right)|\right]ds\}\hfill \\ \hfill \le & \frac{1}{\left|\delta \right|}\{\frac{(1-\alpha )(1-\beta )}{\mathcal{N}\left(\alpha \right)\mathcal{N}\left(\beta \right)}\left[L\parallel z\left(t\right)-u^{*}\left(t\right)\parallel +\phi \left(t\right)\epsilon +\phi \left(t\right)\epsilon |\right]\hfill \\ \hfill & +\frac{\lambda \alpha }{\mathcal{N}\left(\alpha \right)\Gamma \left(\alpha \right)}{\int }_0^t{(t-s)}^{\alpha -1}\parallel z\left(s\right)-u^{*}\left(s\right)\parallel ds+\frac{(1-\alpha )\beta }{\mathcal{N}\left(\alpha \right)\mathcal{N}\left(\beta \right)\Gamma \left(\beta \right)}{\int }_0^t{(t-s)}^{\beta -1}\hfill \\ \hfill & \times \left[L\parallel z\left(s\right)-u^{*}\left(s\right)\parallel +\phi \left(t\right)\epsilon \right]ds+\frac{\alpha (1-\beta )}{\mathcal{N}\left(\alpha \right)\mathcal{N}\left(\beta \right)\Gamma \left(\alpha \right)}{\int }_0^t{(t-s)}^{\alpha -1}\hfill \\ \hfill & \times \left[L\parallel z\left(s\right)-u^{*}\left(s\right)\parallel +\phi \left(t\right)\epsilon \right]ds+\frac{\alpha \beta }{\mathcal{N}\left(\alpha \right)\mathcal{N}\left(\beta \right)\Gamma (\alpha +\beta )}\hfill \\ \hfill & {\int }_0^t{(t-s)}^{\alpha +\beta -1}\left[L\parallel z\left(s\right)-u^{*}\left(s\right)\parallel +\phi \left(t\right)\epsilon \right]ds\}\hfill \\ \hfill \le & \rho \parallel z\left(t\right)-u^{*}\left(t\right)\parallel +\varrho \phi \left(t\right)\epsilon ,t\in D,\hfill \end{array}$$

which implies that

$$\begin{array}{c}\hfill \parallel z\left(t\right)-u^{*}\left(t\right)\parallel \le \frac{\varrho }{1-\rho }\phi \left(t\right)\epsilon ,t\in D.\end{array}$$

(23)

Thus, (23) shows that system (1) is UHR-stable and also GUHR-stable. The proof is completed. □

5. Applications

In this section, we will apply our results to deal with the existence and stability of solutions for two specific systems.

5.1. Theoretical Analysis

Example 1.

Consider the following nonlinear fractional order Langevin equation

$$\begin{array}{c}\hfill \left\{\begin{array}{c}{}^{ML}{\mathcal{D}}_{0^{+}}^{0.3}\left[{}^{ML}{\mathcal{D}}_{0^{+}}^{0.9}-\frac{2}{3}\right]u\left(t\right)=sin\left(t\right)+arctan\left(u\left(t\right)\right),t\in [0,1],\hfill \\ u\left(0\right)=1,{}^{ML}{\mathcal{D}}_{0^{+}}^{0.9}u\left(0\right)=1.\hfill \end{array}\right.\end{array}$$

(24)

Obviously, $T=1>0$, $A=B=1$, $0<\alpha =0.9\le 1$, $0<\beta =0.3\le 1$, $\lambda =\frac{2}{3}>0$, $f(t,u)=sin\left(t\right)+arctan\left(u\right)\in C({\mathbb{R}}^2,\mathbb{R})$. Take $\mathcal{N}\left(x\right)=1-x+\frac{x}{\Gamma \left(x\right)},0<x\le 1$. By a simple calculation, one has $\mathcal{N}\left(0\right)=\mathcal{N}\left(1\right)=1$, $\left|f(t,u)\right|\le M=1+\frac{\pi }{2}$ and

$$\delta =1-\frac{\lambda (1-\alpha )}{\mathcal{N}\left(\alpha \right)}\approx 0.9292>0,0<\kappa =\frac{\lambda T^{\alpha }}{\left|\mathcal{N}\right(\alpha )-\lambda (1-\alpha \left)\right|\Gamma \left(\alpha \right)}\approx 0.7125<1.$$

Thus, the conditions $\left({\mathrm{H}}_1\right)$-$\left({\mathrm{H}}_3\right)$ hold. It follows from Theorem 1 that Equation (24) has at least a solution $u^{*}\left(t\right)\in C^1([0,1],\mathbb{R})$.

Example 2.

Consider the following nonlinear fractional order Langevin equation

$$\begin{array}{c}\hfill \left\{\begin{array}{c}{}^{ML}{\mathcal{D}}_{0^{+}}^{0.8}\left[{}^{ML}{\mathcal{D}}_{0^{+}}^{0.6}-\frac{1}{5}\right]u\left(t\right)=\frac{t^2+2u\left(t\right)}{10},t\in [0,1],\hfill \\ u\left(0\right)=3,{}^{ML}{\mathcal{D}}_{0^{+}}^{0.9}u\left(0\right)=-1.\hfill \end{array}\right.\end{array}$$

(25)

Obviously, $T=1>0$, $A=3$, $B=-1$, $0<\alpha =0.6\le 1$, $0<\beta =0.8\le 1$, $\lambda =\frac{1}{5}>0$, $f(t,u)=\frac{t^2+2u}{10}\in C({\mathbb{R}}^2,\mathbb{R})$. Take $\mathcal{N}\left(x\right)=1-x+\frac{x}{\Gamma \left(x\right)},0<x\le 1$. By a simple calculation, one has $\mathcal{N}\left(0\right)=\mathcal{N}\left(1\right)=1$, $|f(t,u)-f(t,v)|\le \frac{1}{5}|u-v|$, $L=\frac{1}{5}$, $\delta =1-\frac{\lambda (1-\alpha )}{\mathcal{N}\left(\alpha \right)}\approx 0.9004>0$ and

$$\begin{array}{cc}\hfill \rho =& \frac{1}{\left|\delta \right|}\{\frac{L(1-\alpha )(1-\beta )}{\mathcal{N}\left(\alpha \right)\mathcal{N}\left(\beta \right)}+\frac{L(1-\alpha )T^{\beta }}{\mathcal{N}\left(\alpha \right)\mathcal{N}\left(\beta \right)\Gamma \left(\beta \right)}+\frac{L(1-\beta )T^{\alpha }}{\mathcal{N}\left(\alpha \right)\mathcal{N}\left(\beta \right)\Gamma \left(\alpha \right)}\hfill \\ \hfill & +\frac{L\alpha \beta T^{\alpha +\beta }}{\mathcal{N}\left(\alpha \right)\mathcal{N}\left(\beta \right)\Gamma (\alpha +\beta +1)}+\frac{\lambda T^{\alpha }}{\mathcal{N}\left(\alpha \right)\Gamma \left(\alpha \right)}\}\approx 0.3731<1.\hfill \end{array}$$

Thus, we verify that the conditions $\left({\mathrm{H}}_1\right)$, $\left({\mathrm{H}}_4\right)$ and $\left({\mathrm{H}}_5\right)$ are true. From Theorem 2, we know that Equation (24) has a unique solution $u^{*}\left(t\right)\in C^1([0,1],\mathbb{R})$. Meanwhile, according to Theorems 3 and 4, we conclude that Equation (24) is stable in the sense of UH, GUH, UHR and GUHR, respectively.

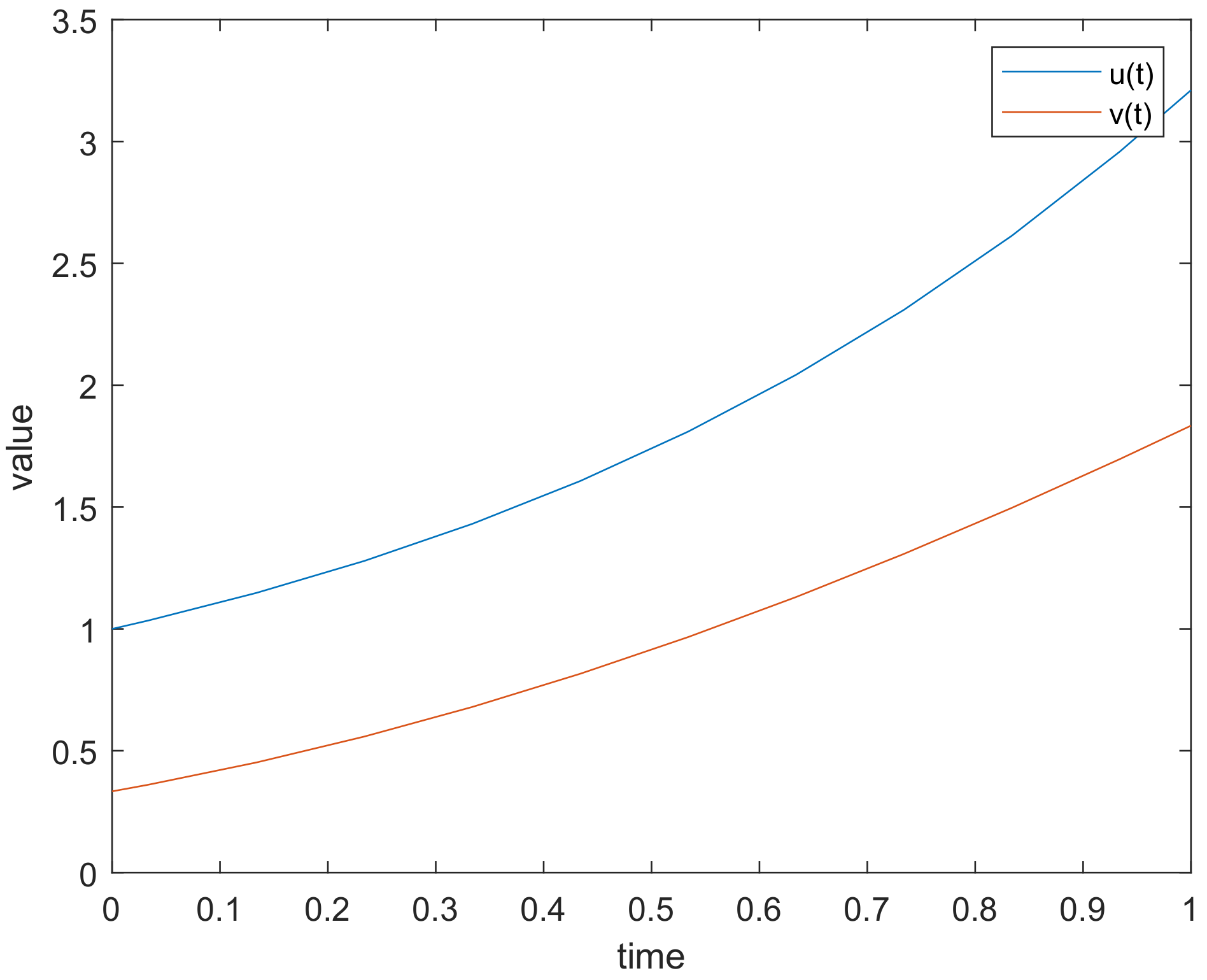
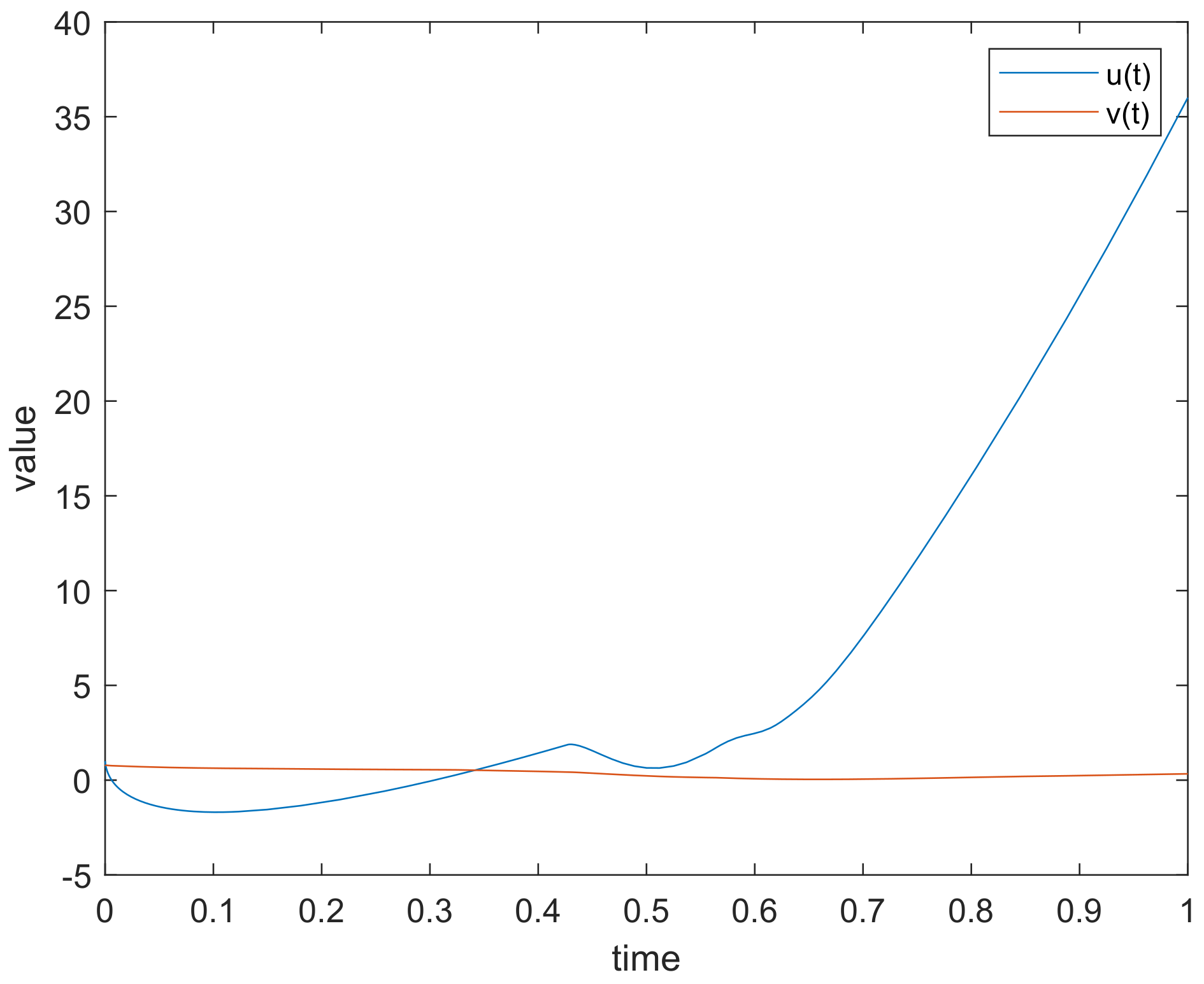
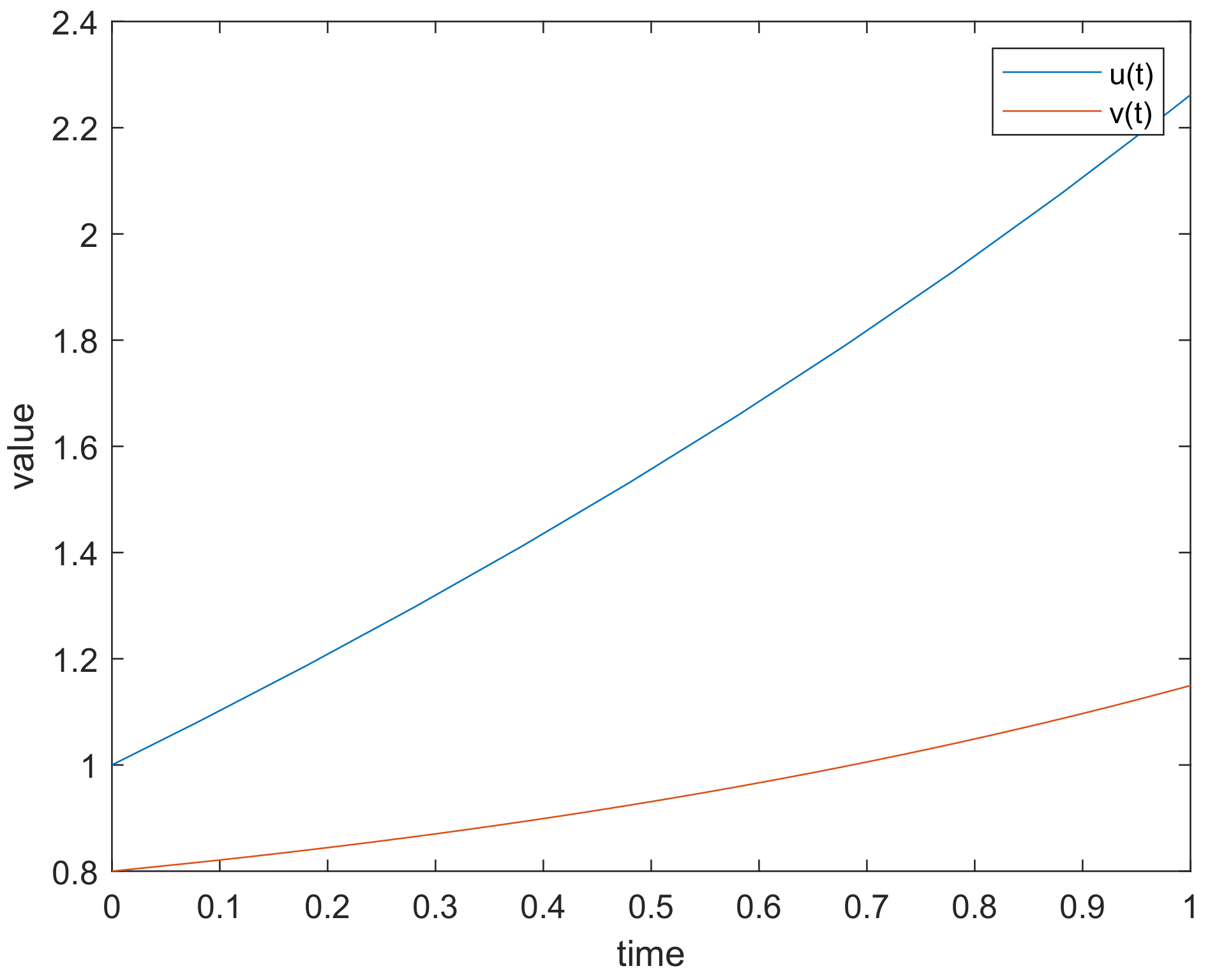
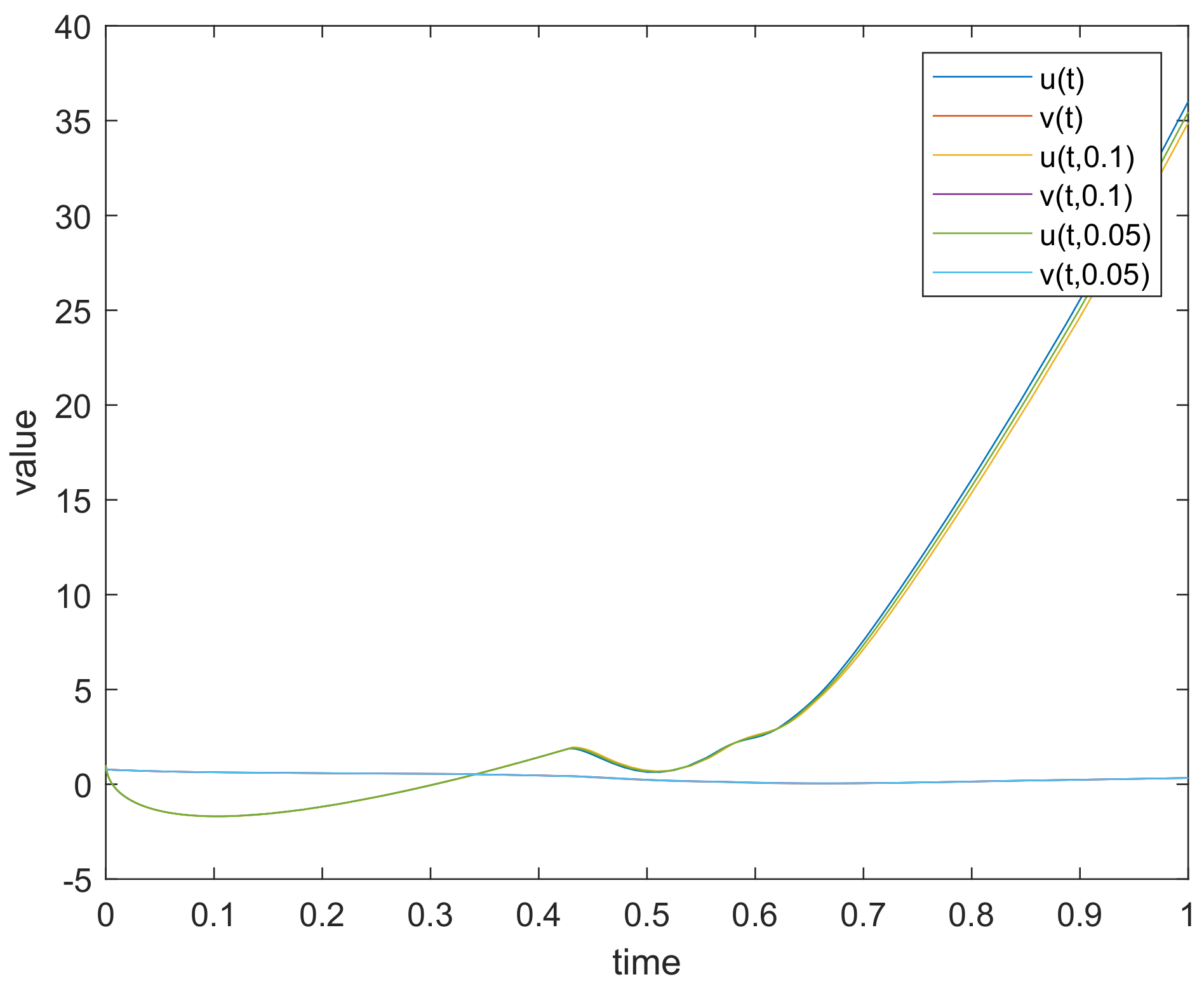
5.2. Numerical Simulation

Let $v\left(t\right)={(}^{ML}{\mathcal{D}}_{0^{+}}^{\alpha }-\lambda )u\left(t\right)$, then Equation (1) is transformed into a system of equations as follows:

$$\begin{array}{c}\hfill \left\{\begin{array}{c}{}^{ML}{\mathcal{D}}_{0^{+}}^{\alpha }u\left(t\right)=\lambda u\left(t\right)+v\left(t\right),t\in (0,T],\hfill \\ {}^{ML}{\mathcal{D}}_{0^{+}}^{\beta }v\left(t\right)=f(t,u\left(t\right)),t\in (0,T],\hfill \\ u\left(0\right)=A,v\left(0\right)=B-\lambda A.\hfill \end{array}\right.\end{array}$$

(26)

When $\alpha =\beta =1$, the fractional Langevin Equation (1) is a classical integer-order differential Langevin equation formulated by

$$\begin{array}{c}\hfill \left\{\begin{array}{c}{\left[u^{\prime }\left(t\right)-\lambda u\left(t\right)\right]}^{\prime }=f(t,u\left(t\right)),t\in (0,T],\hfill \\ u\left(0\right)=A,u^{\prime }\left(0\right)=B.\hfill \end{array}\right.\end{array}$$

(27)

The system of equations equivalent to Equation (27) is formed as

$$\begin{array}{c}\hfill \left\{\begin{array}{c}{u}^{\prime }\left(t\right)=\lambda u\left(t\right)+v\left(t\right),t\in (0,T],\hfill \\ v^{\prime }\left(t\right)=f(t,u\left(t\right)),t\in (0,T],\hfill \\ u\left(0\right)=A,v\left(0\right)=B-\lambda A.\hfill \end{array}\right.\end{array}$$

(28)

The numerical simulation algorithm in this manuscript is briefly stated as follows: Step 1, by applying Lemma 1, it is similar to the proof of Lemma 2 whereby the fractional Langevin equations (26) are transformed into a system of integral equations; Step 2, by calculating the derivative of integer order and simplifying, this system of integral equations becomes a system of delay differential equations of integer order; Step 3, by using ddesd toolbox in MATLAB, this system of delay differential equations of integer order can be numerically simulated. In addition, the corresponding integer-order Langevin Equations (28) are simulated by ode23 toolbox in MATLAB. Next, based on the above algorithm, we numerically simulate and discuss the solutions of (26) and (28) corresponding to Example 1 and Example 2, respectively.

Discussions. (a) Under the condition of the same values of system parameters, the simulations of solutions of Example 1 and its corresponding integer-order differential equation are shown in Figure 1 and Figure 2, respectively. Through the comparison of Figure 1 and Figure 2, $u\left(t\right)$ is very different in two aspects. On the one hand, although the solutions $u\left(t\right)$ of fractional-order and integer-order equations increase monotonically in $t\in [0,1]$, the curvature of $u\left(t\right)$ in Figure 1 is much larger than that in Figure 2. On the other hand, when $t\in [0,1]$, we find that $1\le u\left(t\right)<14$ in Figure 1 and $1\le u\left(t\right)<3.5$ in Figure 2, which is also very different.

(b) Under the condition of the same values of system parameters, the simulations of solutions of Example 2 and the corresponding integer-order differential equation are shown in Figure 3 and Figure 4, respectively. Through the comparison of Figure 3 and Figure 4, $u\left(t\right)$ is greatly different as follows. In Figure 4, the solution $u\left(t\right)$ of integer-order equation increases monotonically in $t\in [0,1]$. However, the solution $u\left(t\right)$ of fractional equation is not monotonous and has maxima and minima in $t\in [0,1]$, shown in Figure 3.

(c) Under the condition of the same values of system parameters, the simulations of Ulam–Hyers stability of Example 2 are shown in Figure 5. It follows from the images of $\epsilon =0.1$ and $\epsilon =0.05$ that, when $\epsilon \to 0^{+}$, the solution curve of the inequality (17) almost coincides with that of Equation (25), which shows that Equation (25) is UH-stable.

6. Conclusions

It is well known that the Langevin equation is a powerful tool in describing the random motion of particles in a fluid. In a particularly complex viscous liquid, the integer-order Langevin equation that describes the motion of particles is no longer accurate. Some scholars have started using the fractional Langevin equation as a model to study this problem, and have achieved good results. However, the research results of these fractional Langevin systems are all centered on Riemann–Liouville or Caputo fractional derivatives. Unfortunately, Riemann–Liouville and Caputo fractional derivatives produce singularities under certain conditions, which renders their application difficult in certain physical fields. Interestingly, the fractional derivative with ML-kernel can eliminate the singularity. In this manuscript, we investigate the existence, uniqueness and UH-stability of solutions for the nonlinear fractional-order Langevin equation with ML-kernel. The theoretical analysis and numerical simulations of two examples verify the correctness and effectiveness of our main conclusions. Furthermore, the mathematical theories and methods employed in this paper can be used as a reference for the study of other fractional differential systems. In addition, considering the fact that the Langevin equation is a classical stochastic differential equation, we can further study the fractional random Langevin equation of nonsingular ML-kernel in future work to reveal the influence of random noise on the motion of free particles.