Stability Analysis on Nabla Discrete Distributed-Order Dynamical System

Abstract

This paper addresses the problems of the stability of a nabla discrete distributed-order dynamical system (NDDS). Firstly, based on a proposed generalized definition of discrete integral, some related definitions of nabla discrete distributed-order calculus are given. Then, several useful inequalities in sense of nabla discrete fractional-order difference are extended to distributed-order cases. Meanwhile, on basis of the proposed inequalities and Lyapunov direct method, some sufficient conditions guaranteeing the asymptotic stability of the origin of NDDS are established under both the Caputo and Riemann–Liouville sense. Finally, some designed simulation examples are given to validate the correctness and practicability of the obtained results.

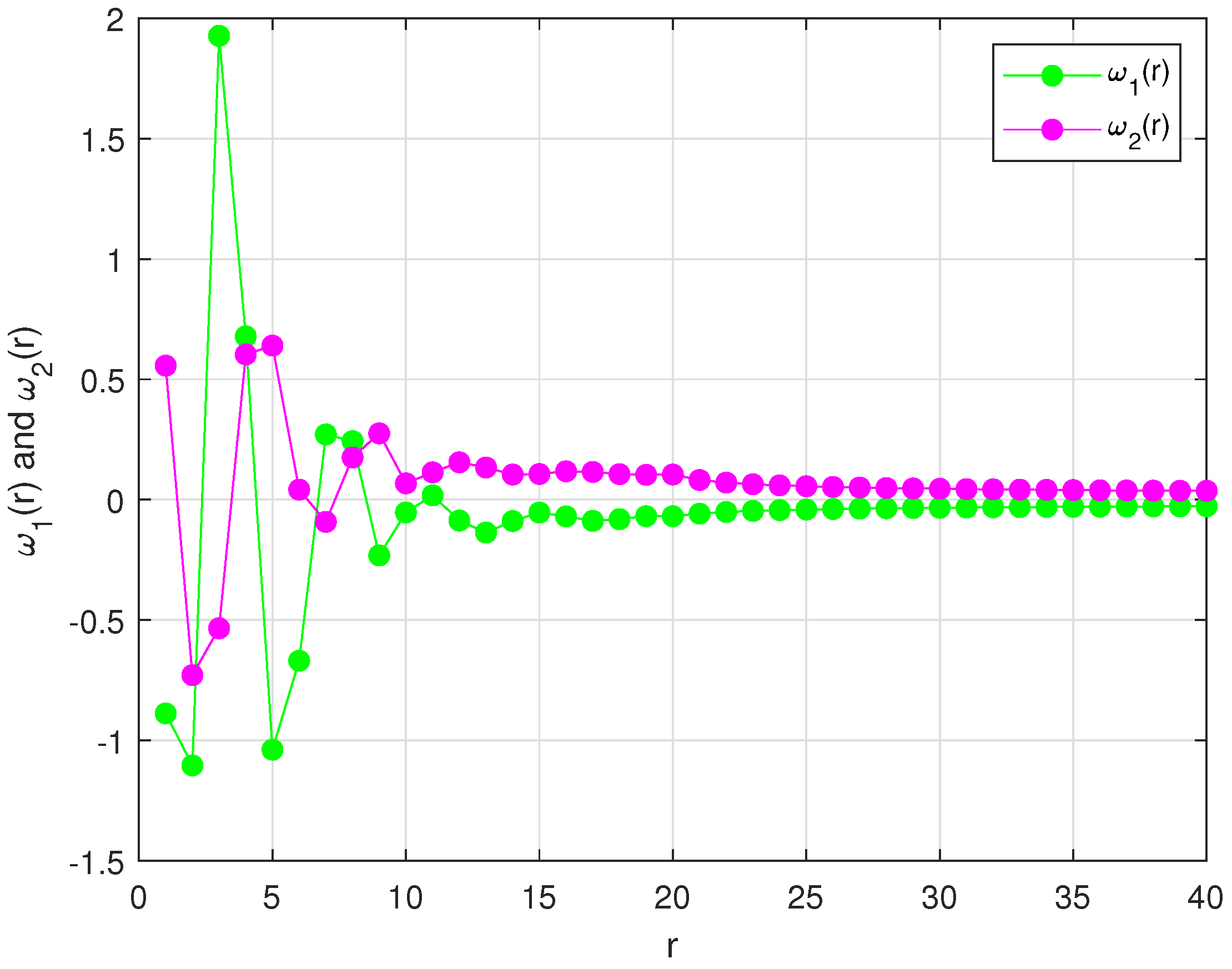
1. Introduction

Fractional-order calculus means that the order of differentiation and integration can be arbitrary non-integer. When the order is taken as an integer, it is integer-order calculus, so fractional-order calculus is said to be a generalization of integer-order calculus. In recent decades, fractional-order calculus has received increasing attention from scholars as it can describe complex dynamics and mechanical processes, such as processes with historical memory and spatial correlation, more precisely and effectively than integer-order calculus [1,2,3].

The distributed-order derivative was first proposed by Caputo in 1995 [4], which can represent any order in a certain range by integrating the weight function $\sigma \left(\theta \right)$ into the fractional-order derivative. Generally speaking, the distributed-order derivative can be recognized as a theoretical extension of the fractional-order derivative, which degenerates to the fractional-order derivative when taking $\sigma \left(\theta \right)=\delta (\theta -{\theta }_1)$. Currently, distributed-order derivatives have appeared in the fields of anomalous diffusion [5,6,7], vibrating systems [8], and so forth. Meanwhile, various results of the dynamical behavior of differential equations of distributed-order have been reported over the past decades [9,10,11,12]. As for the general differential equations of distributed order, numerical methods were given in [9] for solving them. In [12], the shifted Legendre operator matrix of the fractional derivative of a distributed ladder was proposed, which was then applied to the linear equation of the distributed ladder and the diffusion equation of the time-distributed ladder, respectively, in combination with the tau method.

Stability is an important dynamical behavior in the study of control systems and has received a great deal of attention from academics. The classical Lyapunov method plays an important role in the study of system stability as it does not require to solve the solution of the explicit differential equations. In the past few decades, a heated number of Lyapunov stability studies on continuous fractional-order systems have been carried out [13,14,15,16,17,18]. In [13], the Lyapunov stability analysis of continuous frequency distributed models were investigated by employing a novel Lyapunov function, which can be applied to solve the proposed infinite dimensional problem properly. In [14], the authors presented the definition of Mittag–Leffler stability of a fractional-order nonlinear dynamical system and established the fractional-order Lyapunov direct method based on the Lyapunov stability theorem. In [16], a new fractional-order controller was designed to demonstrate the asymptotic pseudo-state stability of the concerned closed-loop system, and several sufficient criteria ensuring the fractional Lyapunov stability of the addressed models were deduced. In [17], the authors considered the Mittag–Leffler stability of a nonlinear fractional-order impulsive system, and several sufficient LMI conditions were derived based on the fractional Lyapunov direct method. Along with the reports for the dynamics of a fractional-order system, numerous stability analysis results concerning the continuous distributed-order system have also been investigated [19,20,21,22]. In [21], several properties concerning the Caputo distributed-order derivative were presented, and the Lyapunov direct method of a distributed-order nonlinear system was established. In [22], the authors proposed a discretization method for a distributed-order dynamical system, and the convergence analysis for the established numberical method was demonstrated. Meanwhile, several stability conditions in relation to the addressed system were presented by utilizing the method of Laplace transformation and the Lyapunov direct method.

For a discrete fractional-order system, there have been some stability results; see [23,24,25,26,27,28,29] and references therein. In [23], the stability theorem for a delta discrete fractional-order difference system and the numerical formulation of the fractional-order difference equation were given. In [24], the fractional-order Mittag–Leffler stability condition was given by using the immobile point technique and the results were applied to a neural network model. In [25], on account of the Lyapunov direct method, several sufficient criteria guaranteeing the uniform stability and uniform asymptotic stability of nabla-Caputo discrete non-autonomous systems were obtained. In [27], the definition of discrete Mittag–Leffler stability was given, and some new criteria for asymptotic stability were proposed by applying Lyapunov stability theory. In [28,29], the authors considered the nabla discrete fractional-order delayed complex-valued neural networks, and several sufficient criteria were derived for quasi-projective synchronization and global Mittag–Leffler synchronization of the addressed models, respectively.

Whether it is an integer-order difference equation, fractional-order difference equation or distributed-order difference equation, it sometimes has obvious advantages compared with the continuous differential equation [30]. For example, some physical processes realized by the difference equation can be more actual and reflect the application backgrounds more applicably, and they can be easily solved by tools of advanced computers. Sometimes, under suitable conditions, the properties of the solution of the difference equations are very close to their continuous counterparts. Generally speaking, it is necessary to discretize the actual systems into difference equation, and sometimes, the proposed problems have always been discrete difference equations.

As for discrete distributed-order difference equation, there are few results on such special problems. Therefore, based on the aforementioned discussions, this paper will study the asymptotic stability of nabla discrete distributed-order systems. First, a more general definition of the discrete integral will be given, and the definition of the sum/difference of the discrete distributed-order will be proposed. Then, some of the lemmas of a nabla discrete fractional-order system will be extended to the case of a nabla discrete distributed-order system. Finally, several results on the Lyapunov stability theorems of both the Caputo discrete distributed-order system and the corresponding Riemann–Liouville cases will be established.

The main contributions of this paper can be summarized as follows:

(i)

A more general definition of the discrete integral is given and the concept of Caputo and Riemann–Liouville nabla discrete distributed-order sum/difference are presented;

(ii)

Several distributed-order difference inequalities in sense of both Caputo and Riemann–Liouville are proposed;

(iii)

Lyapunov stability theorem for Caputo and Riemann–Liouville nabla discrete distributed-order system are established.

2. Preliminaries

Definition 1

([31]). The p-th backwards difference operator (nabla operator) of $\omega \left(r\right):{\mathbb{N}}_{h+1-p}\to \mathbb{R}$ is defined by

$$\begin{array}{c}\hfill {\nabla }^p\omega \left(r\right)=\sum _{\iota =0}^p{(-1)}^{\iota }\left(\genfrac{}{}{0pt}{}{p}{\iota }\right)\omega (r-\iota ),\end{array}$$

(1)

where $p\in {\mathbb{Z}}_{+}$, $h\in \mathbb{R}$, $r\in {\mathbb{N}}_{h+1}$, ${\mathbb{N}}_{h+1}\triangleq \left\{h+1,h+2,h+3,···\right\}$, $\left(\genfrac{}{}{0pt}{}{p}{\iota }\right)\triangleq \frac{\mathrm{\Gamma }(p+1)}{\mathrm{\Gamma }(\iota +1)\mathrm{\Gamma }(p-\iota +1)}$, and $\mathrm{\Gamma }\left(\omega \right)\triangleq {\int }_0^{+\infty }{e}^{-t}{t}^{\omega -1}dt$.

Definition 2

([27]). The θ-th sum of $\omega \left(r\right):{\mathbb{N}}_{h+1}\to \mathbb{R}$ is defined as

$${}_h^{RL}{\nabla }_r^{-\theta }\omega \left(r\right)=\sum _{\iota =0}^{r-h-1}{(-1)}^{\iota }\left(\genfrac{}{}{0pt}{}{-\theta }{\iota }\right)\omega (r-\iota ),$$

(2)

where $\theta \in (p-1,p)$, $p\in {\mathbb{Z}}_{+}$, $h\in \mathbb{R}$, $r\in {\mathbb{N}}_{h+1}$, ${\mathbb{N}}_{h+1}=\left\{h+1,h+2,h+3,···\right\}$. In addition, let ${\theta }^{\overline{\iota }}\triangleq \frac{\mathrm{\Gamma }(\theta +\iota )}{\mathrm{\Gamma }\left(\theta \right)}$, $\theta \notin {\mathbb{Z}}_{-}$, $\iota \in \mathbb{R}$; then, Formula (2) can be rewritten as:

$${}_h^{RL}{\nabla }_r^{-\theta }\omega \left(r\right)=\sum _{\iota =h+1}^r\frac{{(r-\iota +1)}^{\overline{\theta -1}}}{\mathrm{\Gamma }\left(\theta \right)}\omega \left(\iota \right).$$

(3)

Definition 3

([27]). The θ-th nabla Riemann–Liouville and Caputo form of fractional-order backwards difference of $\omega \left(r\right):{\mathbb{N}}_{h+1-p}\to \mathbb{R}$ is defined by

$${}_h^{RL}{\nabla }_r^{\theta }\omega \left(r\right)={\nabla }^p{}_h^{RL}{\nabla }_r^{\theta -p}\omega \left(r\right),$$

(4)

$${}_h^C{\nabla }_r^{\theta }\omega \left(r\right)={}_h^{RL}{\nabla }_r^{\theta -p}{\nabla }^p\omega \left(r\right),$$

(5)

respectively, where $\theta \in (p-1,p)$, $p\in {\mathbb{Z}}_{+}$, $h\in \mathbb{R}$, $r\in {\mathbb{N}}_{h+1}$.

Definition 4

([31]). The shifted forward discrete Dirac pulse function is defined as

$$\delta (r-r_0)=\left\{\begin{array}{cc}1,\hfill & r=r_0,\hfill \\ 0,\hfill & r\ne r_0.\hfill \end{array}\right.$$

(6)

Definition 5

([32]). The discrete nabla integral of $\omega \left(r\right)$ on interval $[h,d]$ is defined as

$${\int }_h^d\omega \left(r\right)\nabla r:=\sum _{r=h+1}^d\omega \left(r\right),$$

(7)

where $\omega \left(r\right):{\mathbb{N}}_{h+1}\to \mathbb{R}$, $d\in {\mathbb{N}}_h$, $r\in N_h$.

In Definition 5, the isometric partition length is required to be 1. However, when the length of the isometric partition is an arbitrary real number, the definition of discrete nabla integral in the existing literature will not be applicable. Therefore, in this paper, in order to introduce the definition of distributed-order sum/difference, we redefine the discrete nabla integral of $\omega \left(r\right)$ on interval $[h,d]$ as follows:

Definition 6.

Let $h={\pi }_0<{\pi }_1<\cdots <{\pi }_p=d$, $\nabla {\pi }_i={\pi }_i-{\pi }_{i-1}=\frac{d-h}{p}$, then ${\pi }_{\iota }=h+\frac{\iota (d-h)}{p}$, $\iota =1,2,...,p$. The discrete nabla integral of $\omega \left(r\right)$ on interval $[d,h]$ is depicted as

$${\int }_h^d\omega \left(r\right)\nabla r:=\frac{d-h}{p}\sum _{\iota =1}^{p}x\left(h+\frac{\iota (d-h)}{p}\right),$$

(8)

where $\omega \left(r\right):\mathbb{R}\to \mathbb{R}$, $h\le d$, $h,d\in \mathbb{R}$, $p\in {\mathbb{Z}}_{+}$, $r\in (h,d]$, $\iota \in {\mathbb{N}}_1$.

Remark 1.

Let $d\in {\mathbb{N}}_h$, and $p=d-h$; then, Definition 6 degenerates into Definition 5.

In the following, based on the continuous distributed-order integral/differential in Caputo sense [4], we will give the definition of the nabla discrete Caputo distributed-order sum/difference.

Definition 7.

The nabla discrete Caputo distributed-order sum/difference is defined as

$${}_h^C{\nabla }_r^{\sigma \left(\theta \right)}\omega \left(r\right)\triangleq {\int }_{d-1}^d\sigma {\left(\theta \right)}_h^C{\nabla }_r^{\theta }\omega \left(r\right)\nabla \theta ,$$

(9)

where $\theta \in (d-1,d)$, $d\in \mathbb{Z}$, $\sigma \left(\theta \right)\ge 0$ denotes the fractional-order weight function.

Actually, by Definition 6, one has

$${\int }_{d-1}^d\sigma {\left(\theta \right)}_h^C{\nabla }_r^{\theta }\omega \left(r\right)\nabla \theta =\frac{1}{p}\sum _{\iota =1}^p\sigma \left(d-1+\frac{\iota }{p}\right){}_h^C{\nabla }_r^{\left(d-1+\frac{\iota }{p}\right)}\omega \left(r\right)=\frac{1}{p}\sum _{\theta =d-1+\frac{1}{p}}^d\sigma {\left(\theta \right)}_h^C{\nabla }_r^{\theta }\omega \left(r\right),$$

(10)

thereupon, (9) can be rewritten as

$${}_h^C{\nabla }_r^{\sigma \left(\theta \right)}\omega \left(r\right):=\frac{1}{p}\sum _{\theta =d-1+\frac{1}{p}}^d\sigma {\left(\theta \right)}_h^C{\nabla }_r^{\theta }\omega \left(r\right),$$

(11)

where $\theta \in (d-1,d)$, $d\in \mathbb{Z}$, $\sigma \left(\theta \right)\ge 0$, $h\in \mathbb{R}$, $r\in {\mathbb{N}}_{h+1}$, $p\in {\mathbb{Z}}_{+}$.

Similarly, for the nabla discrete Riemann–Liouville distributed-order sum/difference, we define the following:

Definition 8.

The nabla discrete Riemann–Liouville distributed-order sum/difference is given as follows:

$${}_h^{RL}{\nabla }_r^{\sigma \left(\theta \right)}\omega \left(r\right):=\frac{1}{p}\sum _{\theta =d-1+\frac{1}{p}}^d\sigma {\left(\theta \right)}_h^{RL}{\nabla }_r^{\theta }\omega \left(r\right),$$

(12)

where $\theta \in (d-1,d)$, $d\in \mathbb{Z}$, $\sigma \left(\theta \right)\ge 0$, $h\in \mathbb{R}$, $r\in {\mathbb{N}}_{h+1}$, $p\in {\mathbb{Z}}_{+}$.

Remark 2.

If $d\in {\mathbb{Z}}_{-}\cup \left\{0\right\}$, Definitions 7 and 8 correspond to the nabla discrete Caputo and Riemann–Liouville distributed-order sum, respectively; if $d\in {\mathbb{Z}}_{+}$, Definitions 7 and 8 correspond to the nabla discrete Caputo and Riemann–Liouville distributed-order difference separately.

Remark 3.

Taking $\sigma \left(\theta \right)=p\delta (\theta -{\theta }_1)$, where ${\theta }_1=d-1+\frac{q}{p}$, $p,q\in {\mathbb{Z}}_{+}$, $p>q$, $\theta \in (d-1,d)$, $d\in \mathbb{Z}$, then the nabla discrete Caputo/Riemann–Liouville distributed-order sum/difference degenerates to the nabla discrete Caputo/Riemann–Liouville fractional-order sum/difference, i.e., ${}_h^{}{\nabla }_r^{\sigma \left(\theta \right)}\omega \left(r\right)={}_h^{}{\nabla }_r^{{\theta }_1}\omega \left(r\right)$.

Definition 9

([32]). The nabla Laplace transform of $\omega :{\mathbb{N}}_{h+1}\to \mathbb{R}$, $h\in \mathbb{R}$ is defined by

$${\mathcal{N}}_h\left\{\omega \left(r\right)\right\}\triangleq \sum _{r=1}^{+\infty }{(1-s)}^{r-1}\omega (r+h),$$

(13)

where the values of s are such that this infinite series converges.

Definition 10

([32]). The discrete Mittag–Leffler function is defined by

$${\mathcal{F}}_{\theta ,\gamma }\left(\lambda ,r,h\right)=\sum _{\iota =0}^{\begin{array}{c}\hfill +\end{array}\infty }{\lambda }^{\iota }\frac{{(r-h)}^{\overline{\iota \theta +\gamma -1}}}{\mathrm{\Gamma }(\iota \theta +\gamma )},$$

(14)

where $\theta >0$, $\gamma \in \mathbb{R}$, $r\in {\mathbb{N}}_h$, $h\in \mathbb{R}$.

Moreover,

$${\mathcal{N}}_h\left\{{\mathcal{F}}_{\theta ,\gamma }\left(\lambda ,r,h\right)\right\}=\frac{s^{\theta -\gamma }}{s^{\theta }-\lambda },$$

(15)

for $\left|1-s\right|<1$, $\left|s^{\theta }\right|>\left|\lambda \right|$.

Definition 11

([33]). A function $\eta :[0,k)\to [0,\infty )$ is referred to belong to class-$\mathcal{K}$ if and only if it is strictly monotonically increasing and $\eta \left(0\right)=0$.

Lemma 1

([34]). If the $\mathcal{N}$-transform of $\omega :{\mathbb{N}}_{h-d}\to \mathbb{R}$ converges for $\left|s-1\right|<\sigma$ for some non-negative σ, then

$${\mathcal{N}}_h\left\{{}_h^C{\nabla }_r^{\theta }\omega \left(r\right)\right\}=s^{\theta }\mathrm{\Omega }\left(s\right)-\sum _{\iota =0}^{d-1}{s}^{\theta -\iota -1}{\left({\nabla }^{\iota }\omega \left(r\right)\right)}_{r=h},$$

(16)

$${\mathcal{N}}_h\left\{{}_h^{RL}{\nabla }_r^{\theta }\omega \left(r\right)\right\}=s^{\theta }\mathrm{\Omega }\left(s\right)-\sum _{\iota =0}^{d-1}{s}^{\iota }{\left({}_h^{RL}{\nabla }_r^{\theta -\iota -1}\omega \left(r\right)\right)}_{r=h},$$

(17)

where $\mathrm{\Omega }\left(s\right)={\mathcal{N}}_h\left\{\omega \left(r\right)\right\}$, $\theta \in (d-1,d)$, $d\in {\mathbb{Z}}_{+}$.

Remark 4.

In line with Definition 7 and Lemma 1, the $\mathcal{N}$-transform of the nabla discrete distributed-order difference can be obtained immediately

$$\begin{array}{cc}\hfill {\mathcal{N}}_h\left\{{}_h^C{\nabla }_r^{\sigma \left(\theta \right)}\omega \left(r\right)\right\}& =\frac{1}{p}\sum _{\theta =d-1+\frac{1}{p}}^d\sigma \left(\theta \right){\mathcal{N}}_h\left\{{}_h^C{\nabla }_r^{\theta }\omega \left(r\right)\right\}\hfill \\ \hfill & =\frac{1}{p}\sum _{\theta =d-1+\frac{1}{p}}^d\sigma \left(\theta \right)s^{\theta }\left(\mathrm{\Omega }\left(s\right)-\sum _{\iota =0}^{d-1}{s}^{-\iota -1}{\left({\nabla }^{\iota }\omega \left(r\right)\right)}_{r=h}\right),\hfill \end{array}$$

(18)

and

$$\begin{array}{cc}\hfill {\mathcal{N}}_h\left\{{}_h^{RL}{\nabla }_r^{\sigma \left(\theta \right)}\omega \left(r\right)\right\}& =\frac{1}{p}\sum _{\theta =d-1+\frac{1}{p}}^d\sigma \left(\theta \right){\mathcal{N}}_h\left\{{}_h^{RL}{\nabla }_r^{\theta }\omega \left(r\right)\right\}\hfill \\ \hfill & =\frac{1}{p}\sum _{\theta =d-1+\frac{1}{p}}^d\sigma \left(\theta \right)\left(s^{\theta }\mathrm{\Omega }\left(s\right)-\sum _{\iota =0}^{d-1}{s}^{\iota }{\left({}_h^{RL}{\nabla }_r^{\theta -\iota -1}\omega \left(r\right)\right)}_{r=h}\right),\hfill \end{array}$$

(19)

where $\mathrm{\Omega }\left(s\right)={\mathcal{N}}_h\left\{\omega \left(r\right)\right\}$, $\sigma \left(\theta \right)\ge 0$, $\theta \in (d-1,d)$, $d\in {\mathbb{Z}}_{+}$, $p\in {\mathbb{Z}}_{+}$.

Lemma 2

([35]). Let $\omega :{\mathbb{N}}_{h+1}\to \mathbb{C}$ and $\mathrm{\Omega }\left(s\right):={\mathcal{N}}_h\left\{\omega \left(r\right)\right\}$; then, all the principal pole of $\mathrm{\Omega }\left(s\right)$ satisfies $|s-1|>1$ if and only if $\omega \left(r\right)$ converges with regard to r and ${lim}_{r\to +\infty }\omega \left(r\right)=0$.

In the following, we extend Theorems 1 and 2 in [26] to the cases of nabla discrete distributed-order.

Lemma 3.

For arbitrary $0<\theta <1$, $\sigma \left(\theta \right)\ge 0$, $p\in Z_{+}$, $u\in Z_{+}$, $v\in Z_{+}$, $2u\ge v$, $\omega \left(r\right)\in \mathbb{R}$, $\phi \left(r\right)\in {\mathbb{R}}^n$, $n\in Z_{+}$, $r\in {\mathbb{N}}_h$, $h\in \mathbb{R}$, and positive definite matrix $S\in {\mathbb{R}}^{n\times n}$; then, the following inequalities hold

$${}_h^C{\nabla }_r^{\sigma \left(\theta \right)}{\omega }^{2u}\left(r\right)\le 2{\omega }^u{\left(r\right)}_h^C{\nabla }_r^{\sigma \left(\theta \right)}{\omega }^u\left(r\right),$$

(20)

$${}_h^C{\nabla }_r^{\sigma \left(\theta \right)}{\omega }^{\frac{2u}{v}}\left(r\right)\le \frac{2u}{2u-v}\omega {\left(r\right)}_h^C{\nabla }_r^{\sigma \left(\theta \right)}{\omega }^{\frac{2u}{v}-1}\left(r\right),$$

(21)

$${}_h^C{\nabla }_r^{\sigma \left(\theta \right)}{\omega }^{\frac{2u}{v}}\left(r\right)\le \frac{2u}{v}{\omega }^{\frac{2u}{v}-1}{\left(r\right)}_h^C{\nabla }_r^{\sigma \left(\theta \right)}\omega \left(r\right),$$

(22)

$${}_h^C{\nabla }_r^{\sigma \left(\theta \right)}{\omega }^{2^u}\left(r\right)\le 2^u{\omega }^{2^u-1}{\left(r\right)}_h^C{\nabla }_r^{\sigma \left(\theta \right)}\omega \left(r\right),$$

(23)

$${}_h^C{\nabla }_r^{\sigma \left(\theta \right)}{\phi }^T\left(r\right)S\phi \left(r\right)\le 2{\phi }^T\left(r\right)S_h^C{\nabla }_r^{\sigma \left(\theta \right)}\phi \left(r\right).$$

(24)

Proof of Lemma 3. 

By employing Definition 7, we have

$$\begin{array}{cc}\hfill & {}_h^C{\nabla }_r^{\sigma \left(\theta \right)}{\omega }^{2u}\left(r\right)-2{\omega }^u{\left(r\right)}_h^C{\nabla }_r^{\sigma \left(\theta \right)}{\omega }^u\left(r\right)\hfill \\ \hfill =& \frac{1}{p}\sum _{\theta =\frac{1}{p}}^1\sigma {\left(\theta \right)}_h^C{\nabla }_r^{\theta }{\omega }^{2u}\left(r\right)-2{\omega }^u\left(r\right)\frac{1}{p}\sum _{\theta =\frac{1}{p}}^1\sigma {\left(\theta \right)}_h^C{\nabla }_r^{\theta }{\omega }^u\left(r\right)\hfill \\ \hfill =& \frac{1}{p}\sum _{\theta =\frac{1}{p}}^1\sigma \left(\theta \right)\left({}_h^C{\nabla }_r^{\theta }{\omega }^{2u}\left(r\right)-2{\omega }^u{\left(r\right)}_h^C{\nabla }_r^{\theta }{\omega }^u\left(r\right)\right),\hfill \end{array}$$

(25)

since $\sigma \left(\theta \right)\ge 0$, $p>0$ and by the similar proof of Theorem 1 in [26], it yields that ${}_h^C{\nabla }_r^{\sigma \left(\theta \right)}{\omega }^{2u}\left(r\right)-2{\omega }^u{\left(r\right)}_h^C{\nabla }_r^{\sigma \left(\theta \right)}{\omega }^u\left(r\right)\le 0$.

The proofs of (21)–(24) are similar; thus, we omit them. □

Lemma 4.

For arbitrary $0<\theta <1$, $\sigma \left(\theta \right)\ge 0$, $p\in Z_{+}$, $u\in Z_{+}$, $v\in Z_{+}$, $2u\ge v$, $\omega \left(r\right)\in \mathbb{R}$, $\phi \left(r\right)\in {\mathbb{R}}^n$, $n\in Z_{+}$, $r\in {\mathbb{N}}_h$, $h\in \mathbb{R}$, and positive definite matrix $S\in {\mathbb{R}}^{n\times n}$, then the following inequalities hold

$${}_h^{RL}{\nabla }_r^{\sigma \left(\theta \right)}{\omega }^{2u}\left(r\right)\le 2{\omega }^u{\left(r\right)}_h^{RL}{\nabla }_r^{\sigma \left(\theta \right)}{\omega }^u\left(r\right),$$

(26)

$${}_h^{RL}{\nabla }_r^{\sigma \left(\theta \right)}{\omega }^{\frac{2u}{v}}\left(r\right)\le \frac{2u}{2u-v}\omega {\left(r\right)}_h^{RL}{\nabla }_r^{\sigma \left(\theta \right)}{\omega }^{\frac{2u}{v}-1}\left(r\right),$$

(27)

$${}_h^{RL}{\nabla }_r^{\sigma \left(\theta \right)}{\omega }^{\frac{2u}{v}}\left(r\right)\le \frac{2u}{v}{\omega }^{\frac{2u}{v}-1}{\left(r\right)}_h^{RL}{\nabla }_r^{\sigma \left(\theta \right)}\omega \left(r\right),$$

(28)

$${}_h^{RL}{\nabla }_r^{\sigma \left(\theta \right)}{\omega }^{2^u}\left(r\right)\le 2^u{\omega }^{2^u-1}{\left(r\right)}_h^{RL}{\nabla }_r^{\sigma \left(\theta \right)}\omega \left(r\right),$$

(29)

$${}_h^{RL}{\nabla }_r^{\sigma \left(\theta \right)}{\phi }^T\left(r\right)S\phi \left(r\right)\le 2{\phi }^T\left(r\right)S_h^{RL}{\nabla }_r^{\sigma \left(\theta \right)}\phi \left(r\right).$$

(30)

Proof of Lemma 4. 

By employing Definition 8, we have

$$\begin{array}{cc}\hfill & {}_h^{RL}{\nabla }_r^{\sigma \left(\theta \right)}{\omega }^{2u}\left(r\right)-2{\omega }^u{\left(r\right)}_h^{RL}{\nabla }_r^{\sigma \left(\theta \right)}{\omega }^u\left(r\right)\hfill \\ \hfill =& \frac{1}{p}\sum _{\theta =\frac{1}{p}}^1\sigma {\left(\theta \right)}_h^{RL}{\nabla }_r^{\theta }{\omega }^{2u}\left(r\right)-2{\omega }^u\left(r\right)\frac{1}{p}\sum _{\theta =\frac{1}{p}}^1\sigma {\left(\theta \right)}_h^{RL}{\nabla }_r^{\theta }{\omega }^u\left(r\right)\hfill \\ \hfill =& \frac{1}{p}\sum _{\theta =\frac{1}{p}}^1\sigma \left(\theta \right)\left({}_h^{RL}{\nabla }_r^{\theta }{\omega }^{2u}\left(r\right)-2{\omega }^u{\left(r\right)}_h^{RL}{\nabla }_r^{\theta }{\omega }^u\left(r\right)\right),\hfill \end{array}$$

(31)

since $\sigma \left(\theta \right)\ge 0$, $p>0$ and by the similar proof of Theorem 2 in [26], it yields that ${}_h^{RL}{\nabla }_r^{\sigma \left(\theta \right)}{\omega }^{2u}\left(r\right)-2{\omega }^u{\left(r\right)}_h^{RL}{\nabla }_r^{\sigma \left(\theta \right)}{\omega }^u\left(r\right)\le 0$.

The proofs of (27)–(30) are similar; thus, we omit them. □

Remark 5.

Taking $\sigma \left(\theta \right)=p\delta (\theta -{\theta }_1)$, where ${\theta }_1=\frac{q}{p}$, $p,q\in {\mathbb{Z}}_{+}$, $p>q$, $\theta \in (0,1)$, the special cases of Lemmas 3 and 4 correspond to Theorems 1 and 2 in [26].

Lemma 5.

${}_h^C{\nabla }_r^{\sigma \left(\theta \right)}\omega \left(r\right)\le {}_h^{RL}{\nabla }_r^{\sigma \left(\theta \right)}\omega \left(r\right)$, $r\in {\mathbb{N}}_{h+1}$ holds for $0<\theta <1$, $\sigma \left(\theta \right)\ge 0$, $p\in Z_{+}$, and $\omega \left(h\right)\ge 0$.

Proof of Lemma 5. 

It follows from (11) and (12) that

$$\begin{array}{cc}\hfill {}_h^{RL}{\nabla }_r^{\sigma \left(\theta \right)}\omega \left(r\right)& =\frac{1}{p}\sum _{\theta =\frac{1}{p}}^1\sigma {\left(\theta \right)}_h^{RL}{\nabla }_r^{\theta }\omega \left(r\right)\hfill \\ \hfill & =\frac{1}{p}\sum _{\theta =\frac{1}{p}}^1\sigma \left(\theta \right)\nabla {}_h^{RL}{\nabla }_r^{\theta -1}\omega \left(r\right)\hfill \\ \hfill & =\frac{1}{p}\sum _{\theta =\frac{1}{p}}^1\sigma \left(\theta \right)\nabla \left(\sum _{\iota =h+1}^r\frac{{(r-\iota +1)}^{\overline{-\theta }}}{\mathrm{\Gamma }(1-\theta )}\omega \left(\iota \right)\right)\hfill \\ \hfill & =\frac{1}{p}\sum _{\theta =\frac{1}{p}}^1\sigma \left(\theta \right)\left(\sum _{\iota =h+1}^r\frac{{(r-\iota +1)}^{\overline{-\theta }}}{\mathrm{\Gamma }(1-\theta )}\omega \left(\iota \right)-\sum _{\iota =h+1}^{r-1}\frac{{(r-\iota )}^{\overline{-\theta }}}{\mathrm{\Gamma }(1-\theta )}\omega \left(\iota \right)\right),\hfill \end{array}$$

(32)

and

$$\begin{array}{cc}\hfill {}_h^C{\nabla }_r^{\sigma \left(\theta \right)}\omega \left(r\right)& =\frac{1}{p}\sum _{\theta =\frac{1}{p}}^1\sigma {\left(\theta \right)}_h^C{\nabla }_r^{\theta }\omega \left(r\right)\hfill \\ \hfill & =\frac{1}{p}\sum _{\theta =\frac{1}{p}}^1\sigma {\left(\theta \right)}_h^{RL}{\nabla }_r^{\theta -1}\nabla \omega \left(r\right)\hfill \\ \hfill & =\frac{1}{p}\sum _{\theta =\frac{1}{p}}^1\sigma \left(\theta \right)\sum _{\iota =h+1}^r\frac{{(r-\iota +1)}^{\overline{-\theta }}}{\mathrm{\Gamma }(1-\theta )}\left(\omega \left(\iota \right)-\omega (\iota -1)\right)\hfill \\ \hfill & =\frac{1}{p}\sum _{\theta =\frac{1}{p}}^1\sigma \left(\theta \right)\left(\sum _{\iota =h+1}^r\frac{{(r-\iota +1)}^{\overline{-\theta }}}{\mathrm{\Gamma }(1-\theta )}\omega \left(\iota \right)-\sum _{\iota =h+1}^r\frac{{(r-\iota +1)}^{\overline{-\theta }}}{\mathrm{\Gamma }(1-\theta )}\omega (\iota -1)\right).\hfill \end{array}$$

(33)

Noting that ${\sum }_{\iota =h+1}^r\frac{{(r-\iota +1)}^{\overline{-\theta }}}{\mathrm{\Gamma }(1-\theta )}\omega (\iota -1)={\sum }_{\iota =h}^{r-1}\frac{{(r-\iota )}^{\overline{-\theta }}}{\mathrm{\Gamma }(1-\theta )}\omega \left(\iota \right)$, therefore

$${}_h^{RL}{\nabla }_r^{\sigma \left(\theta \right)}\omega \left(r\right){=}_h^C{\nabla }_r^{\sigma \left(\theta \right)}\omega \left(r\right)+\frac{1}{p}\sum _{\theta =\frac{1}{p}}^1\sigma \left(\theta \right)\frac{{(r-h)}^{\overline{-\theta }}}{\mathrm{\Gamma }(1-\theta )}\omega \left(h\right),$$

(34)

obviously, $\sigma \left(\theta \right)\frac{{(r-\iota )}^{\overline{-\theta }}}{\mathrm{\Gamma }(1-\theta )}=\sigma \left(\theta \right)\frac{\mathrm{\Gamma }(r-\iota -\theta )}{\mathrm{\Gamma }(1-\theta )\mathrm{\Gamma }(r-\iota )}\ge 0$, hence ${}_h^C{\nabla }_r^{\sigma \left(\theta \right)}\omega \left(r\right)\le {}_h^{RL}{\nabla }_r^{\sigma \left(\theta \right)}\omega \left(r\right)$. □

3. Main Results

In this section, the comparison principle of the nabla discrete distributed-order difference and several Lyapunov stability theorems of the nabla discrete distributed-order dynamical system under some appropriate assumptions will be given.

Theorem 1.

If ${}_h^C{\nabla }_r^{\sigma \left(\theta \right)}\omega \left(r\right)\ge {}_h^C{\nabla }_r^{\sigma \left(\theta \right)}\phi \left(r\right)$, where $\theta \in (0,1)$, $r\in N_h$, taking $\sigma \left(\theta \right)$ so that ${\mathcal{N}}_h^{-1}\left\{\frac{1}{\frac{1}{p}{\sum }_{\theta =\frac{1}{p}}^1\sigma \left(\theta \right)s^{\theta }}\right\}$ is a non-negative function and $\omega \left(h\right)=\phi \left(h\right)$, then $\omega \left(r\right)\ge \phi \left(r\right)$.

Proof of Theorem 1. 

By adding a non-negative function $\xi \left(r\right)$ at the right-hand end of the inequality ${}_h^C{\nabla }_r^{\sigma \left(\theta \right)}\omega \left(r\right)\ge {}_h^C{\nabla }_r^{\sigma \left(\theta \right)}\phi \left(r\right)$, gives

$${}_h^C{\nabla }_r^{\sigma \left(\theta \right)}\omega \left(r\right)={}_h^C{\nabla }_r^{\sigma \left(\theta \right)}\phi \left(r\right)+\xi \left(r\right).$$

(35)

Taking the nabla Laplace transform of formula (35) yields

$$\frac{1}{p}\sum _{\theta =\frac{1}{p}}^1\sigma \left(\theta \right)s^{\theta }\left[\mathrm{\Omega }\left(s\right)-\frac{\omega \left(h\right)}{s}\right]=\frac{1}{p}\sum _{\theta =\frac{1}{p}}^1\sigma \left(\theta \right)s^{\theta }\left[\mathrm{\Phi }\left(s\right)-\frac{\phi \left(h\right)}{s}\right]+\mathsf{\Xi }\left(s\right),$$

(36)

where $\mathrm{\Omega }\left(s\right)={\mathcal{N}}_h\left\{\omega \left(r\right)\right\}$, $\mathrm{\Phi }\left(s\right)={\mathcal{N}}_h\left\{\phi \left(r\right)\right\}$, $\mathsf{\Xi }\left(s\right)={\mathcal{N}}_h\left\{\xi \left(r\right)\right\}$, since $\omega \left(h\right)=\phi \left(h\right)$, we can obtain from Formula (36) that

$$\frac{1}{p}\sum _{\theta =\frac{1}{p}}^1\sigma \left(\theta \right)s^{\theta }\mathrm{\Omega }\left(s\right)=\frac{1}{p}\sum _{\theta =\frac{1}{p}}^1\sigma \left(\theta \right)s^{\theta }\mathrm{\Phi }\left(s\right)+\mathsf{\Xi }\left(s\right),$$

(37)

that is,

$$\mathrm{\Omega }\left(s\right)=\mathrm{\Phi }\left(s\right)+\frac{\mathrm{\Phi }\left(s\right)}{\frac{1}{p}{\sum }_{\theta =\frac{1}{p}}^1\sigma \left(\theta \right)s^{\theta }}.$$

(38)

Taking the inverse nabla Laplace transform of formula (38) yields

$$\omega \left(r\right)=\phi \left(r\right)+\mu \left(r\right)*\xi \left(r\right),$$

(39)

where $\mu \left(r\right)={\mathcal{N}}_h^{-1}\left\{\frac{1}{\frac{1}{p}{\sum }_{\theta =\frac{1}{p}}^1\sigma \left(\theta \right)s^{\theta }}\right\}$. Allowing for the fact that $\mu \left(r\right)$ and $\xi \left(r\right)$ are non-negative functions, then $\mu \left(r\right)*\xi \left(r\right)$ is non-negative function, which implies $\omega \left(r\right)\ge \phi \left(r\right)$. □

In the following, we will study the nabla discrete Caputo/Riemann–Liouville distributed-order non-autonomous system of the form

$${}_h^{}{\nabla }_r^{\sigma \left(\theta \right)}\omega \left(r\right)=f(r,\omega \left(r\right)),$$

(40)

where $0<\theta <1$, $\omega \left(r\right)\in \mathbb{D}\subset {\mathbb{R}}^n$ is the state space incorporating the ${\omega }_e=0$, $h\in \mathbb{R}$, $r\in N_{h+1}$, $f:N_{h+1}\times \mathbb{D}\to {\mathbb{R}}^n$ is locally bounded and satisfies locally the Lipschitz condition in $\omega$, ${}_h^{}{\nabla }_r^{\sigma \left(\theta \right)}$ represents the Caputo/Riemann–Liouville distributed-order operator.

Remark 6.

The function $f(r,\omega (r\left)\right)$ satisfying locally bounded and locally Lipschitz in ω assures the existence and uniqueness of the solution of (40); see Theorem 3.1 in [36].

The equilibrium point for system (40) is depicted as:

Definition 12.

The constant ${\omega }_0$ is an equilibrium point for the discrete distributed-order system (40) if and only if $f(r,{\omega }_0)={}_h^{}{\nabla }_r^{\sigma \left(\theta \right)}{\omega }_0$, $r\in N_{h+1}$.

Remark 7.

Let ${\omega }_1\ne 0$ be an equilibrium point of (40), then by taking $\xi \left(r\right)=\omega \left(r\right)-{\omega }_1$, one has

$${}_h^C{\nabla }_r^{\sigma \left(\theta \right)}\xi \left(r\right)={}_h^C{\nabla }_r^{\sigma \left(\theta \right)}(\omega \left(r\right)-{\omega }_1)=f(r,\xi \left(r\right)+{\omega }_1)=g(r,\xi \left(r\right)),$$

(41)

that is $g(r,0)=0$, which implies that the origin is an equilibrium point for the system (40) with the new variable $\xi \left(r\right)$. Similarly, for the Riemann–Liouville case, it holds that

$$\begin{array}{cc}\hfill {}_h^{RL}{\nabla }_r^{\sigma \left(\theta \right)}\xi \left(r\right)& ={}_h^{RL}{\nabla }_r^{\sigma \left(\theta \right)}(\omega \left(r\right)-{\omega }_1)=f(r,\omega \left(r\right))-{}_h^{RL}{\nabla }_r^{\sigma \left(\theta \right)}{\omega }_1\hfill \\ \hfill =& f(r,\xi \left(r\right)+{\omega }_1)-\frac{1}{p}\sum _{\theta =\frac{1}{p}}^1\sigma \left(\theta \right)\frac{{(r-h)}^{\overline{-\theta }}}{\mathrm{\Gamma }(1-\theta )}{\omega }_1\hfill \\ \hfill =& \overline{g}(r,\xi \left(r\right)),\hfill \end{array}$$

(42)

that is $\overline{g}(r,0)=0$, which means that the origin is an equilibrium point for the system (40) with the new variable $\xi \left(r\right)$. Hence, without loss of generality, we assume that the origin is the equilibrium point of system (40) throughout this paper.

The following assumptions are necessary for the following theorems:

Assumption 1: Taking $\sigma \left(\theta \right)$ so that ${\mathcal{N}}_h^{-1}\left\{\frac{1}{\frac{1}{p}{\sum }_{\theta =\frac{1}{p}}^1\sigma \left(\theta \right)s^{\theta }+{\eta }_3{\eta }_2^{-1}}\right\}\ge 0$, where $\theta \in (0,1)$, $\sigma \left(\theta \right)\ge 0$ and ${\eta }_2$, ${\eta }_3$ > 0;

Assumption 2: All the principal pole of $\frac{\frac{1}{p}{\sum }_{\theta =\frac{1}{p}}^1\sigma \left(\theta \right)s^{\theta -1}}{\frac{1}{p}{\sum }_{\theta =\frac{1}{p}}^1\sigma \left(\theta \right)s^{\theta }+{\eta }_3{\eta }_2^{-1}}$ satisfies $|s-1|>1$, where $\theta \in (0,1)$, $\sigma \left(\theta \right)\ge 0$ and ${\eta }_2$, ${\eta }_3$ > 0.

Theorem 2.

Taking ${}_h^{}{\nabla }_r^{\sigma \left(\theta \right)}={}_h^C{\nabla }_r^{\sigma \left(\theta \right)}$. Let $\mathcal{V}(r,\omega \left(r\right)):N_{h+1}\times \mathbb{D}\to \mathbb{R}$, where $\omega \in \mathbb{D}\subset {\mathbb{R}}^n$ is the state space incorporating the origin. Under Assumptions 1 and 2, supposing that

$${\eta }_1{∥\omega \left(r\right)∥}^{\beta }\le \mathcal{V}(r,\omega \left(r\right))\le {\eta }_2{∥\omega \left(r\right)∥}^{\beta \gamma },$$

(43)

$${}_h^C{\nabla }_r^{\sigma \left(\theta \right)}\mathcal{V}(r,\omega \left(r\right))\le -{\eta }_3{∥\omega \left(r\right)∥}^{\beta \gamma },$$

(44)

where $\theta \in (0,1)$, $\sigma \left(\theta \right)\ge 0$ and β, γ, ${\eta }_1$, ${\eta }_2$, ${\eta }_3$ > 0, then the origin of the system (40) is asymptotically stable.

Proof of Theorem 2. 

Combining (43) with (44) yields

$${}_h^C{\nabla }_r^{\sigma \left(\theta \right)}\mathcal{V}(r,\omega \left(r\right))\le -{\eta }_3{\eta }_2^{-1}\mathcal{V}(r,\omega \left(r\right)).$$

(45)

Subtracting a non-positive function $\xi \left(r\right)$ from the right end of Formula (45)

$${}_h^C{\nabla }_r^{\sigma \left(\theta \right)}\mathcal{V}(r,\omega \left(r\right))=-{\eta }_3{\eta }_2^{-1}\mathcal{V}(r,\omega \left(r\right))-\xi \left(r\right).$$

(46)

Taking the nabla Laplace transform of Formula (46), we can obtain

$$\frac{1}{p}\sum _{\theta =\frac{1}{p}}^1\sigma \left(\theta \right)s^{\theta }\left(\mathcal{V}\left(s\right)-\frac{\mathcal{V}(h,\omega (h\left)\right)}{s}\right)=-{\eta }_3{\eta }_2^{-1}\mathcal{V}\left(s\right)-\mathsf{\Xi }\left(s\right),$$

(47)

where $\mathcal{V}\left(s\right)={\mathcal{N}}_h\left\{\mathcal{V}(r,\omega (r\left)\right)\right\}$, $\mathsf{\Xi }\left(s\right)={\mathcal{N}}_h\left\{\xi \left(r\right)\right\}$, then

$$\mathcal{V}\left(s\right)=\frac{\mathcal{V}(h,\omega \left(h\right))\frac{1}{p}{\sum }_{\theta =\frac{1}{p}}^1\sigma \left(\theta \right)s^{\theta -1}-\mathsf{\Xi }\left(s\right)}{\frac{1}{p}{\sum }_{\theta =\frac{1}{p}}^1\sigma \left(\theta \right)s^{\theta }+{\eta }_3{\eta }_2^{-1}},$$

(48)

and taking the inverse nabla Laplace transform of Formula (48) gives

$$\mathcal{V}(r,\omega (r\left)\right)=\mathcal{V}(h,\omega (h\left)\right)\rho \left(r\right)-\xi \left(r\right)*\mu \left(r\right),$$

(49)

where $\rho \left(r\right)={\mathcal{N}}_h^{-1}\left\{\frac{\frac{1}{p}{\sum }_{\theta =\frac{1}{p}}^1\sigma \left(\theta \right)s^{\theta -1}}{\frac{1}{p}{\sum }_{\theta =\frac{1}{p}}^1\sigma \left(\theta \right)s^{\theta }+{\eta }_3{\eta }_2^{-1}}\right\}$, $\mu \left(r\right)={\mathcal{N}}_h^{-1}\left\{\frac{1}{\frac{1}{p}{\sum }_{\theta =\frac{1}{p}}^1\sigma \left(\theta \right)s^{\theta }+{\eta }_3{\eta }_2^{-1}}\right\}$, $\xi \left(r\right)*\mu \left(r\right)$ represents the convolution of $\xi \left(r\right)$ and $\mu \left(r\right)$. Considering that $\xi \left(r\right)$ is a non-negative function, then $\xi \left(r\right)*\mu \left(r\right)\ge 0$, hence

$$\mathcal{V}(r,\omega (r\left)\right)\le \mathcal{V}(h,\omega (h\left)\right)\rho \left(r\right).$$

(50)

Thereupon, it follows from Assumption 2 and Lemma 2 that

$$\underset{r\to \infty }{lim}\rho \left(r\right)=0.$$

(51)

Then, taking the limit at both ends of (50) yields

$$\underset{r\to \infty }{lim}\mathcal{V}(r,\omega \left(r\right))\le \mathcal{V}(h,\omega \left(h\right))\underset{r\to \infty }{lim}\rho \left(r\right)=0.$$

(52)

Combining (43) with (52), one has

$$\underset{r\to \infty }{lim}{\eta }_1{∥\omega \left(r\right)∥}^{\beta }\le \underset{r\to \infty }{lim}\mathcal{V}(r,\omega \left(r\right))=0,$$

(53)

that is

$$\underset{r\to \infty }{lim}∥\omega \left(r\right)∥=0,$$

(54)

which implies that the origin of the system (40) is asymptotically stable. □

Corollary 1.

Taking ${}_h^{}{\nabla }_r^{\sigma \left(\theta \right)}={}_h^C{\nabla }_r^{\sigma \left(\theta \right)}$. Under Assumptions 1 and 2,

(i)

if ${\omega }^T\left(r\right)f(r,\omega \left(r\right))\le -{\eta }_3{∥\omega \left(r\right)∥}^2$, then the origin of the system (40) is asymptotically stable.

(ii)

if ${}_h^C{\nabla }_r^{\sigma \left(\theta \right)}\omega \left(r\right)\le -\lambda \omega \left(r\right)$, where $\lambda >0$, then the origin of the system (40) is asymptotically stable.

Proof of Corollary 1. 

(i) Suppose the Lyapunov candidate function

$$\mathcal{V}(r,\omega \left(r\right))=\frac{{\omega }^T\left(r\right)\omega \left(r\right)}{2},$$

(55)

using Formula (24) of Lemma 3 in (55) results in

$${}_h^C{\nabla }_r^{\sigma \left(\theta \right)}\mathcal{V}(r,\omega \left(r\right))\le {\omega }^T\left(r\right){}_h^C{\nabla }_r^{\sigma \left(\theta \right)}\omega \left(r\right).$$

(56)

If the hypothesis ${\omega }^T\left(r\right)f(r,\omega \left(r\right))\le -{\eta }_3{∥\omega \left(r\right)∥}^2$ is fulfilled, it follows from (56) that

$${}_h^C{\nabla }_r^{\sigma \left(\theta \right)}\mathcal{V}(r,\omega \left(r\right))\le -{\eta }_3{∥\omega \left(r\right)∥}^2,$$

(57)

since a suitable ${\eta }_1$ can be chosen such that the Lyapunov function meets ${\eta }_1{∥\omega \left(r\right)∥}^2\le \mathcal{V}(r,\omega \left(r\right))\le {∥\omega \left(r\right)∥}^2$, it follows that the origin of system (40) is asymptotically stable using Theorem 2.

(ii) This proof follows directly from the process of proving Theorem 2. □

Corollary 2.

Taking ${}_h^{}{\nabla }_r^{\sigma \left(\theta \right)}={}_h^{RL}{\nabla }_r^{\sigma \left(\theta \right)}$, let $\mathcal{V}(r,\omega \left(r\right)):N_{h+1}\times \mathbb{D}\to \mathbb{R}$, where $\omega \in \mathbb{D}\subset {\mathbb{R}}^n$ is the state space incorporating the origin. Under Assumptions 1 and 2, supposing that

$${\eta }_1{∥\omega \left(r\right)∥}^{\beta }\le \mathcal{V}(r,\omega \left(r\right))\le {\eta }_2{∥\omega \left(r\right)∥}^{\beta \gamma },$$

(58)

$${}_h^{RL}{\nabla }_r^{\sigma \left(\theta \right)}\mathcal{V}(r,\omega \left(r\right))\le -{\eta }_3{∥\omega \left(r\right)∥}^{\beta \gamma },$$

(59)

where $\theta \in (0,1)$, $\sigma \left(\theta \right)\ge 0$ and β, γ, ${\eta }_1$, ${\eta }_2$, ${\eta }_3$ > 0, then the origin of the system (40) is asymptotically stable.

Proof of Corollary 2. 

Considering that $\mathcal{V}(r,\omega (r\left)\right)\ge 0$ and Lemma 5, we can obtain

$${}_h^C{\nabla }_r^{\sigma \left(\theta \right)}\mathcal{V}(r,\omega \left(r\right))\le {}_h^{RL}{\nabla }_r^{\sigma \left(\theta \right)}\mathcal{V}(r,\omega \left(r\right)),$$

(60)

this implies

$${}_h^C{\nabla }_r^{\sigma \left(\theta \right)}\mathcal{V}(r,\omega \left(r\right))\le -{\eta }_3{∥\omega \left(r\right)∥}^{\beta \gamma }.$$

(61)

The following proof is the same as Theorem 2. □

The following assumptions are prerequisites to the following theorems:

Assumption 3: For any given $\alpha >0$, taking $\sigma \left(\theta \right)$ so that ${\mathcal{N}}_h^{-1}\left\{\frac{1}{\frac{1}{m}{\sum }_{\theta =\frac{1}{m}}^1\sigma \left(\theta \right)s^{\theta }+l}\right\}\ge 0$, where $l=\frac{{\eta }_3\left({\eta }_2^{-1}\left(\alpha \right)\right)}{\mathcal{V}(h,\omega (h\left)\right)}$, ${\eta }_2(·)$ and ${\eta }_3(·)$ are discrete class–$\mathcal{K}$ functions;

Assumption 4: For any given $\alpha >0$, all the principal pole of $\frac{\frac{1}{m}{\sum }_{\theta =\frac{1}{m}}^1\sigma \left(\theta \right)s^{\theta -1}}{\frac{1}{m}{\sum }_{\theta =\frac{1}{m}}^1\sigma \left(\theta \right)s^{\theta }+l}$ satisfies $|s-1|>1$, where $l=\frac{{\eta }_3\left({\eta }_2^{-1}\left(\alpha \right)\right)}{\mathcal{V}(h,\omega (h\left)\right)}$, ${\eta }_2(·)$ and ${\eta }_3(·)$ are discrete class–$\mathcal{K}$ functions.

Theorem 3.

Taking ${}_h^{}{\nabla }_r^{\sigma \left(\theta \right)}={}_h^C{\nabla }_r^{\sigma \left(\theta \right)}$. Under Assumptions 3 and 4, assume that there exists a monotonically decrescent and positive definite Lyapunov function $\mathcal{V}(r,\omega (r\left)\right)$ such that

$${\eta }_1\left(∥\omega \left(r\right)∥\right)\le \mathcal{V}(r,\omega \left(r\right))\le {\eta }_2\left(∥\omega \left(r\right)∥\right),$$

(62)

$${}_h^C{\nabla }_r^{\sigma \left(\theta \right)}\mathcal{V}(r,\omega \left(r\right))\le -{\eta }_3\left(∥\omega \left(r\right)∥\right),$$

(63)

where $\theta \in (0,1)$, $\sigma \left(\theta \right)\ge 0$ and ${\eta }_1(·)$, ${\eta }_2(·)$, ${\eta }_3(·)$ are discrete class–$\mathcal{K}$ functions; then, the origin of the system (40) is asymptotically stable.

Proof of Theorem 3. 

Combining Formulae (62) and (63) yields

$${}_h^C{\nabla }_r^{\sigma \left(\theta \right)}\mathcal{V}(r,\omega \left(r\right))\le -{\eta }_3\left({\eta }_2^{-1}\left(\mathcal{V}(r,\omega \left(r\right))\right)\right).$$

(64)

Since $\mathcal{V}(r,\omega (r\left)\right)$ is positive definite and monotonically decreasing, so $\mathcal{V}(r,\omega (r\left)\right)\le \mathcal{V}(h,\omega (h\left)\right)$. Next, we will discuss the classification:

Situation 1: If there exists an integer $\tau \ge a$ satisfing $V(\tau ,\omega (\tau \left)\right)=0$, which implies $\omega \left(\tau \right)=0$. We can obtain that $\omega \left(r\right)=0$ for $r\ge \tau$; then, $\omega =0$ is the equilibrium point.

Situation 2: Supposing that there exists a constant ${\alpha }_0>0$ such that $\mathcal{V}(r,\omega \left(r\right))\ge {\alpha }_0$, for $r>h$, then

$$0<{\alpha }_0\le \mathcal{V}(r,\omega \left(r\right))\le \mathcal{V}(h,\omega \left(h\right)).$$

(65)

Noting that ${\eta }_2^{-1}(·)$ is discrete class–$\mathcal{K}$ function, then

$${\eta }_2^{-1}\left({\alpha }_0\right)\le {\eta }_2^{-1}\left(\mathcal{V}(r,\omega \left(r\right))\right),$$

(66)

and it follows from (66) that

$$\begin{array}{cc}\hfill -{\eta }_3({\eta }_2^{-1}\left(\mathcal{V}(r,\omega \left(r\right))\right)& \le -{\eta }_3\left({\eta }_2^{-1}\left({\alpha }_0\right)\right)\hfill \\ \hfill & =-\frac{{\eta }_3\left({\eta }_2^{-1}\left({\alpha }_0\right)\right)}{\mathcal{V}(h,\omega (h\left)\right)}\mathcal{V}(h,\omega \left(h\right))\hfill \\ \hfill & \le -l\mathcal{V}(r,\omega (r\left)\right),\hfill \end{array}$$

(67)

where $0<l=\frac{{\eta }_3\left({\eta }_2^{-1}\left({\alpha }_0\right)\right)}{\mathcal{V}(h,\omega (h\left)\right)}$. By Formula (64),

$${}_h^C{\nabla }_r^{\sigma \left(\theta \right)}\mathcal{V}(r,\omega \left(r\right))\le -l\mathcal{V}(r,\omega \left(r\right)),$$

(68)

thereupon, under Assumptions 3 and 4, in line with the same proof of Theorem 2, we can obtain that ${lim}_{r\to \infty }\mathcal{V}(r,\omega \left(r\right))=0$, which is contradictory to $\mathcal{V}(r,\omega \left(r\right))\ge {\alpha }_0$.

To sum up, we have

$$\underset{r\to \infty }{lim}\omega \left(r\right)=0,$$

(69)

thus, the origin of the system (40) is asymptotically stable. □

Corollary 3.

Taking ${}_h^{}{\nabla }_r^{\sigma \left(\theta \right)}={}_h^{RL}{\nabla }_r^{\sigma \left(\theta \right)}$. Under Assumptions 3 and 4, assume that there exists a monotonically decrescent and positive definite Lyapunov function $\mathcal{V}(r,\omega (r\left)\right)$ such that

$${\eta }_1\left(∥\omega \left(r\right)∥\right)\le \mathcal{V}(r,\omega \left(r\right))\le {\eta }_2\left(∥\omega \left(r\right)∥\right),$$

(70)

$${}_h^{RL}{\nabla }_r^{\sigma \left(\theta \right)}\mathcal{V}(r,\omega \left(r\right))\le -{\eta }_3\left(∥\omega \left(r\right)∥\right),$$

(71)

where $\theta \in (0,1)$, $\sigma \left(\theta \right)\ge 0$ and ${\eta }_1(·)$, ${\eta }_2(·)$, ${\eta }_3(·)$ are discrete class–$\mathcal{K}$ functions; then, the origin of the system (40) is asymptotically stable.

Proof of Corollary 3. 

It follows from (70) and (71) that

$${}_h^{RL}{\nabla }_r^{\sigma \left(\theta \right)}\mathcal{V}(r,\omega \left(r\right))\le -{\eta }_3\left({\eta }_2^{-1}\left(\mathcal{V}(r,\omega \left(r\right))\right)\right).$$

(72)

Considering that $\mathcal{V}(r,\omega (r\left)\right)\ge 0$ and Lemma 5, we can obtain

$${}_h^C{\nabla }_r^{\sigma \left(\theta \right)}\mathcal{V}(r,\omega \left(r\right))\le {}_h^{RL}{\nabla }_r^{\sigma \left(\theta \right)}\mathcal{V}(r,\omega \left(r\right)),$$

(73)

which implies

$${}_h^C{\nabla }_r^{\sigma \left(\theta \right)}\mathcal{V}(r,\omega \left(r\right))\le -{\eta }_3\left({\eta }_2^{-1}\left(\mathcal{V}(r,\omega \left(r\right))\right)\right).$$

(74)

The following proof is the same as Theorem 3. □

4. Numerical Examples

Example 1.

We extend the continuous Caputo distributed-order system in reference [20] to the discrete case as follows:

$$\left\{\begin{array}{cc}\hfill {}_h^C{\nabla }_r^{\sigma \left(\theta \right)}{\omega }_1\left(r\right)& =-5({\omega }_1\left(r\right)+e^r{\omega }_2\left(r\right)),\hfill \\ \hfill {}_h^C{\nabla }_r^{\sigma \left(\theta \right)}{\omega }_2\left(r\right)& =-5({\omega }_2\left(r\right)-e^r{\omega }_1\left(r\right)),\hfill \end{array}\right.$$

(75)

where $\sigma \left(\theta \right)=4\delta (\theta -\frac{1}{3})+\delta (\theta -\frac{2}{3})$, $\forall \theta \in (0,1)$.

Assume ${\eta }_2=3$, ${\eta }_3=4$,

$$\frac{1}{p}\sum _{\theta =\frac{1}{p}}^1\sigma \left(\theta \right)s^{\theta }+{\eta }_3{\eta }_2^{-1}=\frac{4}{3}{s}^{\frac{1}{3}}+\frac{1}{3}{s}^{\frac{2}{3}}+\frac{4}{3}=\frac{1}{3}{(s^{\frac{1}{3}}+2)}^2=0,$$

(76)

then, the roots $s_{1,2}=-8$ of Equation (76) satisfy $|s-1|>1$. On the basis of (15),

$${\mathcal{N}}_h^{-1}\left\{\frac{1}{\frac{1}{p}{\sum }_{\theta =\frac{1}{p}}^1\sigma \left(\theta \right)s^{\theta }+{\eta }_3{\eta }_2^{-1}}\right\}={\mathcal{N}}_h^{-1}\left\{\frac{1}{\frac{1}{3}{(s^{\frac{1}{3}}+2)}^2}\right\}=3{\mathcal{F}}_{\frac{1}{3},\frac{1}{3}}\left(-2,r,h\right)*{\mathcal{F}}_{\frac{1}{3},\frac{1}{3}}\left(-2,r,h\right),$$

(77)

according to the non-negativity of ${\mathcal{N}}_h^{-1}\left\{\frac{1}{s^{\frac{1}{3}}+2}\right\}={\mathcal{F}}_{\frac{1}{3},\frac{1}{3}}\left(-2,r,h\right)$ (see [37]), so

${\mathcal{N}}_h^{-1}\left\{\frac{1}{\frac{1}{p}{\sum }_{\theta =\frac{1}{p}}^1\sigma \left(\theta \right)s^{\theta }+{\eta }_3{\eta }_2^{-1}}\right\}\ge 0$ is established.

Suppose the Lyapunov candidate function

$$\mathcal{V}(r,\omega \left(r\right))=\frac{1}{2}{\omega }_1^2\left(r\right)+\frac{1}{2}{\omega }_2^2\left(r\right),$$

(78)

let ${\eta }_1=\frac{1}{4}$, then

$${\eta }_1{∥\omega \left(r\right)∥}^2\le \mathcal{V}(r,\omega \left(r\right))=\frac{1}{2}{\omega }_1^2\left(r\right)+\frac{1}{2}{\omega }_2^2\left(r\right)\le {\eta }_2{∥\omega \left(r\right)∥}^2.$$

(79)

Using Formula (24),

$$\begin{array}{cc}\hfill {}_h^C{\nabla }_r^{\sigma \left(\theta \right)}\mathcal{V}(r,\omega \left(r\right))& =\frac{1}{2}{}_h^C{\nabla }_r^{\sigma \left(\theta \right)}{\omega }_1^2\left(r\right)+\frac{1}{2}{}_h^C{\nabla }_r^{\sigma \left(\theta \right)}{\omega }_2^2\left(r\right)\hfill \\ \hfill & \le {\omega }_1{\left(r\right)}_h^C{\nabla }_r^{\sigma \left(\theta \right)}{\omega }_1\left(r\right)+{\omega }_2{\left(r\right)}_h^C{\nabla }_r^{\sigma \left(\theta \right)}{\omega }_2\left(r\right)\hfill \\ \hfill & =-5({\omega }_1^2\left(r\right)+{\omega }_2^2\left(r\right))\hfill \\ \hfill & \le -{\eta }_3{∥\omega \left(r\right)∥}^2.\hfill \end{array}$$

(80)

From Theorem 2, the origin of (75) is asymptotically stable. Figure 1 shows the time responses of state trajectories of (75) with initial values ${\omega }_1\left(0\right)=0.5$, ${\omega }_2\left(0\right)=0.8$.

Figure 1. State responses of the system in (75).

Example 2.

Consider a Caputo distributed-order discrete nonlinear system as follows:

$$\left\{\begin{array}{cc}\hfill {}_h^C{\nabla }_r^{\sigma \left(\theta \right)}{\omega }_1\left(r\right)& =-2({\omega }_1\left(r\right)-{\omega }_2^3\left(r\right)),\hfill \\ \hfill {}_h^C{\nabla }_r^{\sigma \left(\theta \right)}{\omega }_2\left(r\right)& =-2({\omega }_2\left(r\right)+{\omega }_1^3\left(r\right)),\hfill \end{array}\right.$$

(81)

where $\sigma \left(\theta \right)=4\delta (\theta -\frac{1}{3})+\delta (\theta -\frac{2}{3})$, $\forall \theta \in (0,1)$.

Suppose the Lyapunov candidate function

$$\mathcal{V}(r,\omega \left(r\right))={\omega }_1^4\left(r\right)+{\omega }_2^4\left(r\right),$$

(82)

then, in the light of Formula (23)

$$\begin{array}{cc}\hfill {}_h^C{\nabla }_r^{\sigma \left(\theta \right)}\mathcal{V}(r,\omega \left(r\right))& ={}_h^C{\nabla }_r^{\sigma \left(\theta \right)}{\omega }_1^4\left(r\right)+{}_h^C{\nabla }_r^{\sigma \left(\theta \right)}{\omega }_2^4\left(r\right)\hfill \\ \hfill & \le 4{\omega }_1^3{\left(r\right)}_h^C{\nabla }_r^{\sigma \left(\theta \right)}{\omega }_1\left(r\right)+4{\omega }_2^3{\left(r\right)}_h^C{\nabla }_r^{\sigma \left(\theta \right)}{\omega }_2\left(r\right)\hfill \\ \hfill & =-8({\omega }_1^4\left(r\right)+{\omega }_2^4\left(r\right))\hfill \\ \hfill & \le -4/3\mathcal{V}(r,\omega (r\left)\right).\hfill \end{array}$$

(83)

Taking ${\eta }_3{\eta }_2^{-1}=4/3$,

$$\frac{1}{p}\sum _{\theta =\frac{1}{p}}^1\sigma \left(\theta \right)s^{\theta }+{\eta }_3{\eta }_2^{-1}=\frac{4}{3}{s}^{\frac{1}{3}}+\frac{1}{3}{s}^{\frac{2}{3}}+\frac{4}{3}=\frac{1}{3}{(s^{\frac{1}{3}}+2)}^2=0,$$

(84)

then the roots $s_{1,2}=-8$ of Equation (84) satisfy $|s-1|>1$. On the basis of (15),

$${\mathcal{N}}_h^{-1}\left\{\frac{1}{\frac{1}{p}{\sum }_{\theta =\frac{1}{p}}^1\sigma \left(\theta \right)s^{\theta }+{\eta }_3{\eta }_2^{-1}}\right\}={\mathcal{N}}_h^{-1}\left\{\frac{1}{\frac{1}{3}{(s^{\frac{1}{3}}+2)}^2}\right\}=3{\mathcal{F}}_{\frac{1}{3},\frac{1}{3}}\left(-2,r,h\right)*{\mathcal{F}}_{\frac{1}{3},\frac{1}{3}}\left(-2,r,h\right),$$

(85)

according to the non-negativity of ${\mathcal{N}}_h^{-1}\left\{\frac{1}{s^{\frac{1}{3}}+2}\right\}={\mathcal{F}}_{\frac{1}{3},\frac{1}{3}}\left(-2,r,h\right)$ (see [37]), so

${\mathcal{N}}_h^{-1}\left\{\frac{1}{\frac{1}{m}{\sum }_{\theta =\frac{1}{m}}^1\sigma \left(\theta \right)s^{\theta }+{\eta }_3{\eta }_2^{-1}}\right\}\ge 0$ is established. From Theorem 2, the origin of (81) is asymptotically stable. Figure 2 shows the time responses of state trajectories of (81) with initial values ${\omega }_1\left(0\right)=0.5$, ${\omega }_2\left(0\right)=-0.8$.

Figure 2. State responses of the system in (81).

5. Conclusions

In this work, we have concerned the stability analysis of a discrete distributed-order system. By employing a novel definition of discrete integral, the definitions of the Caputo/Riemann–Liouville nabla discrete distributed-order sum/difference have been proposed, and based on these proposed definitions, some relevant generalized inequalities of discrete distributed-order difference have been established. Meanwhile, by utilizing the method of Laplace transformation, Lyapunov direct method and some inequality techniques, several results of Lyapunov stability theorems concerning the discrete Caputo and Riemann–Liouville distributed-order system have been deduced. At last, two examples have been designed to illustrate the validity and feasibility of our theoretical results.

In the future work, we will continue to study the discrete distributed-order neural network system.