A New Fractional Poisson Process Governed by a Recursive Fractional Differential Equation
Abstract
:1. Introduction
2. Main Results
- 1.
- When ,which goes back to a homogeneous Poisson process.
- 2.
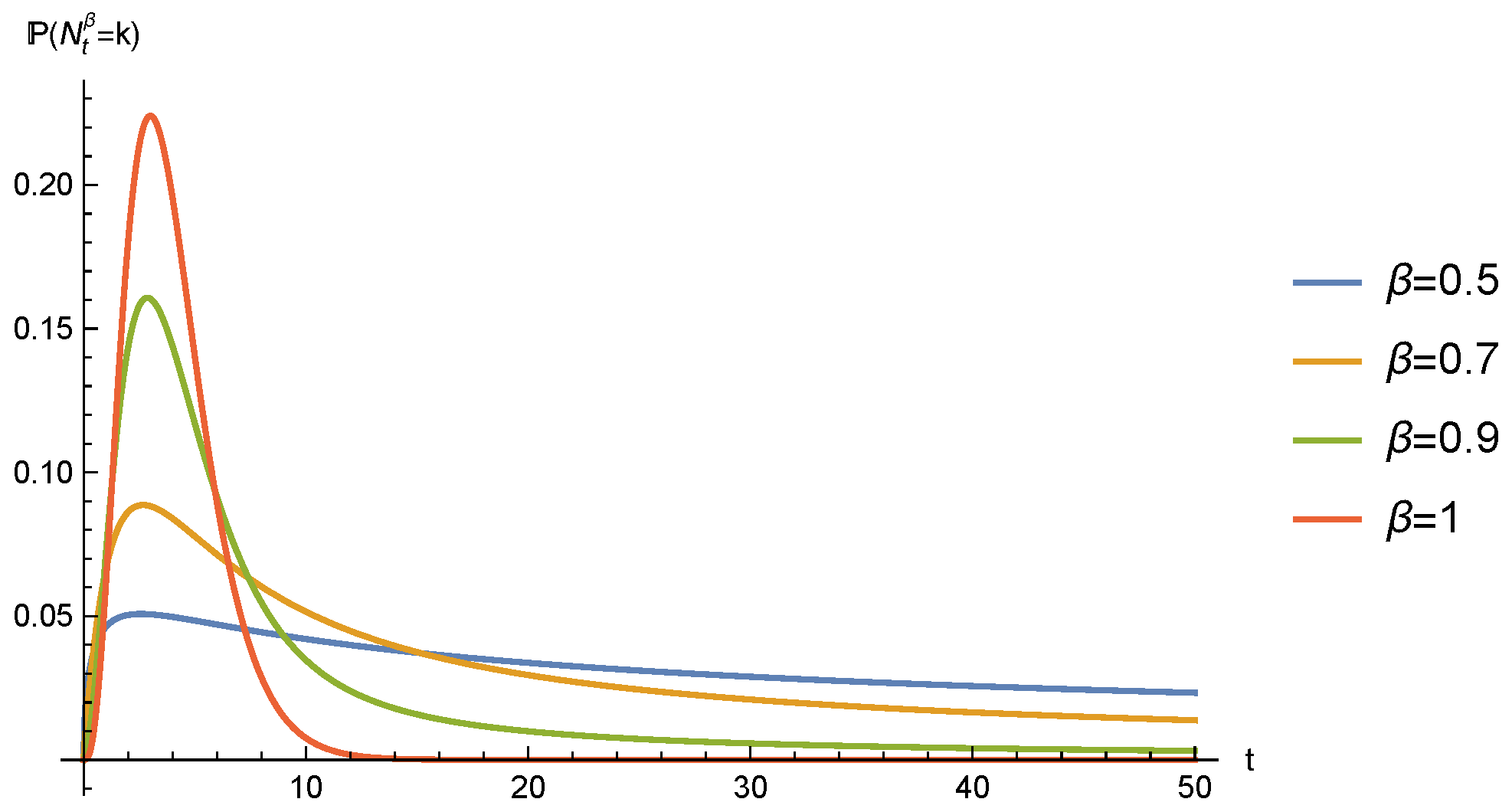
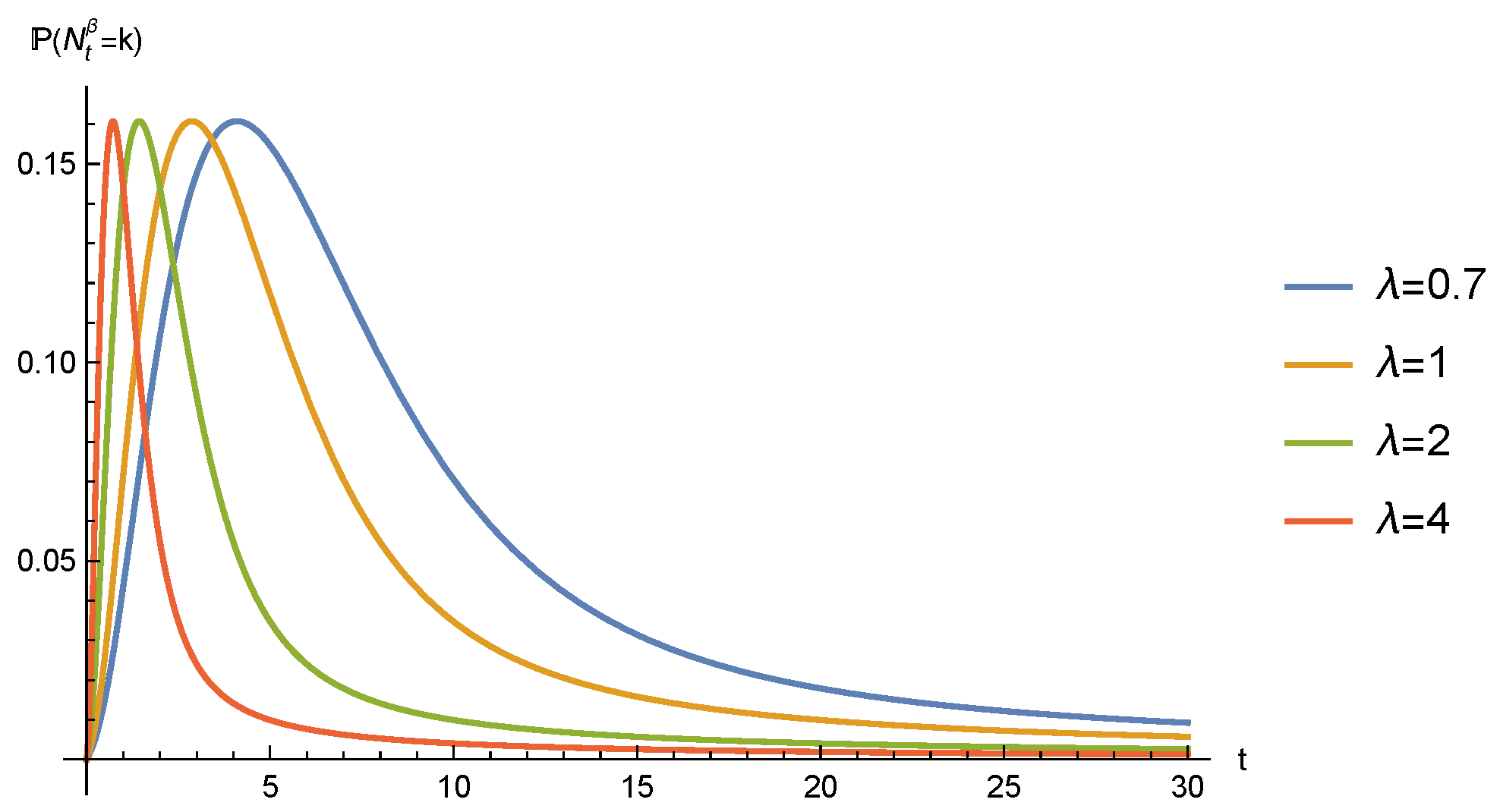
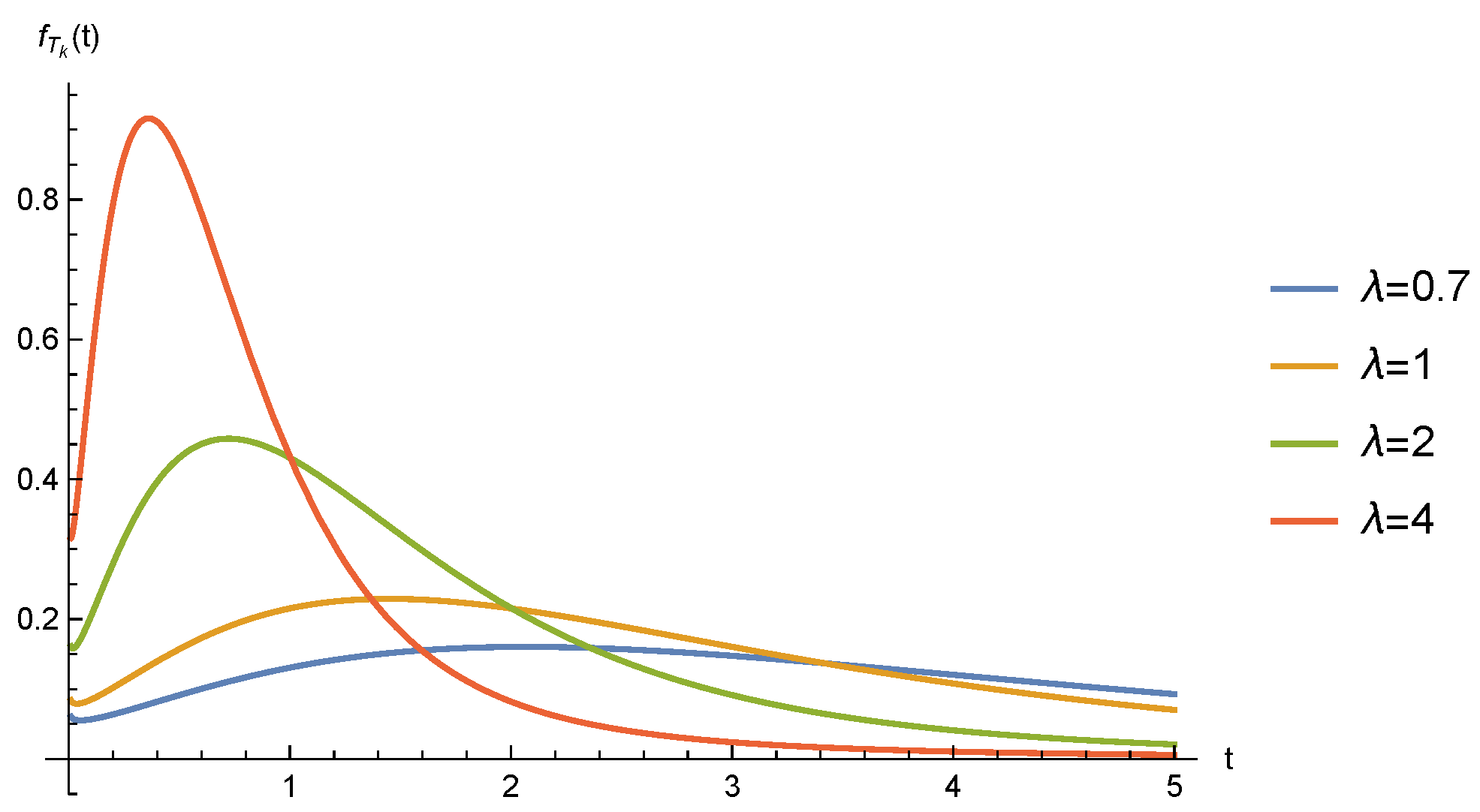
- Since , the integral representation of the Mittag–Leffler function remains [18] (Lemma 2.2.2), and we havewhere is the Fox’s H function. The convergence of this contour integral can be checked by [19] (Equation (1.13)) The integral representation, by closing the contour in two different directions, leads towhich determines the asymptotic behavior of these probability functions.
- 3.
- Equation (8) indicates thati.e., no longer possesses independent increments and therefore loses the lack of memory property of the homogeneous Poisson process.
- 4.
- Sincewhich tends to ∞ as q tends to 0, then does not exist for all , unlike .
- 1.
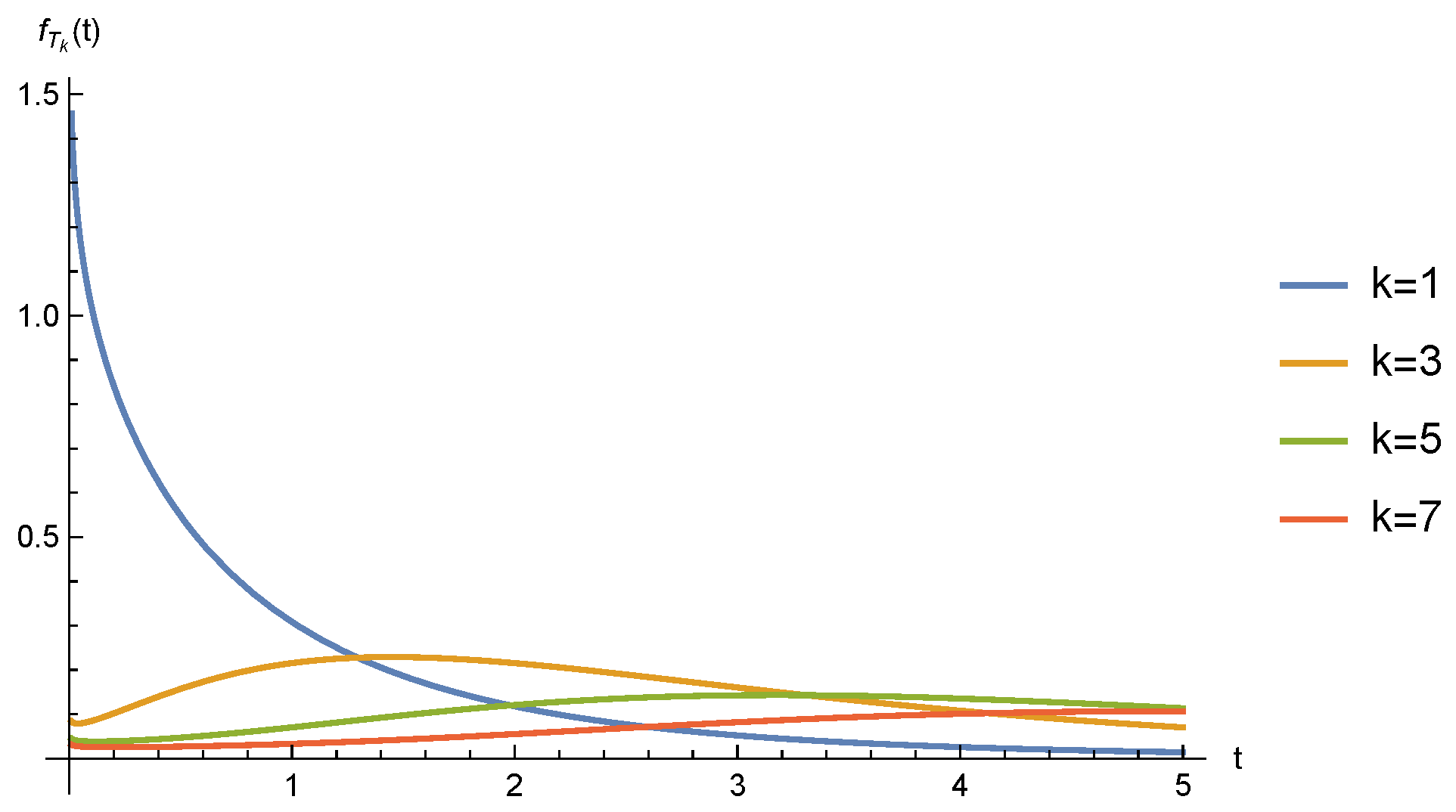
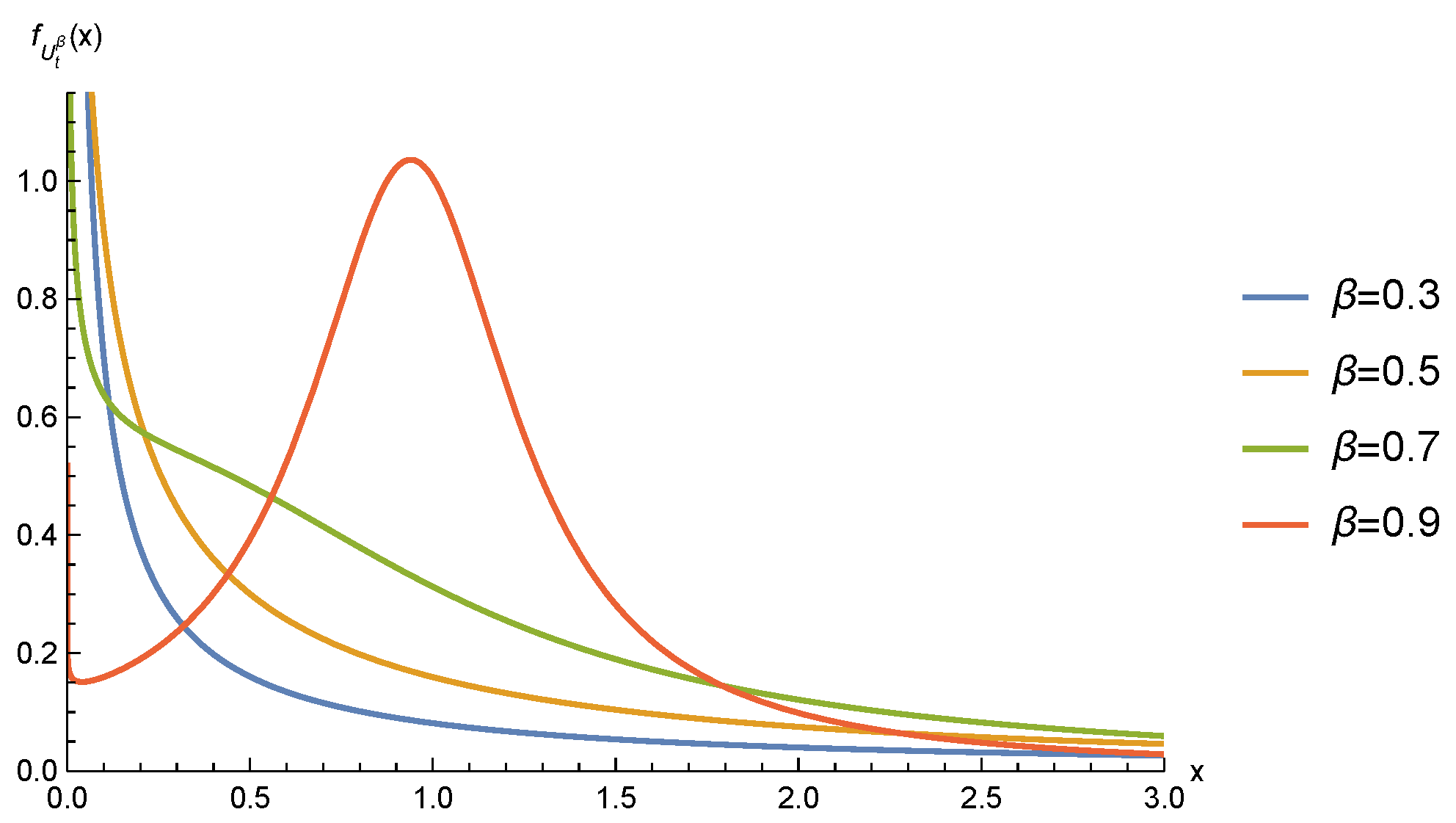
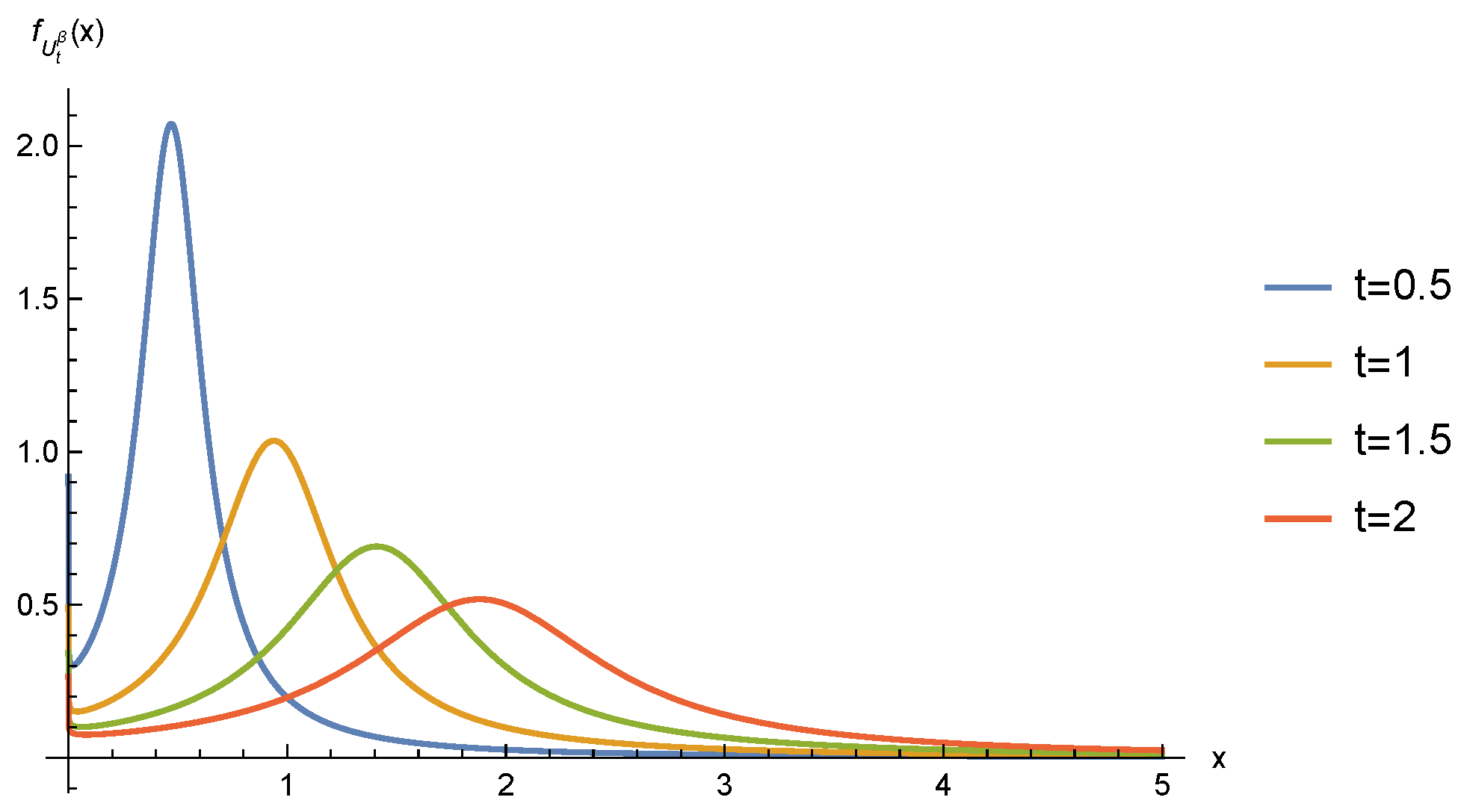
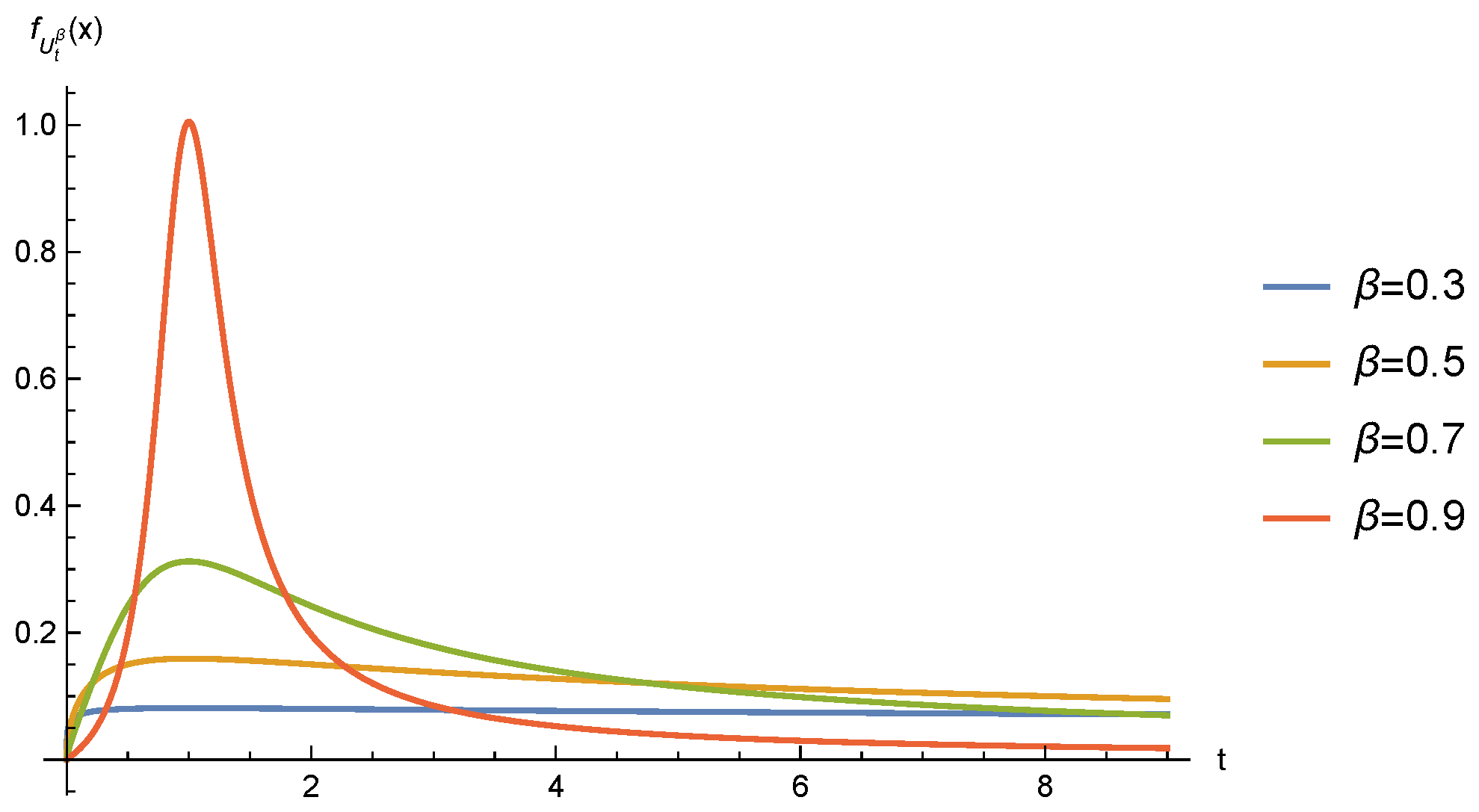
- From Equation (15), does not possess independent and stationary increments.
- 2.
- Comparing Equation (10) and Equation (16), it can be seen thatwhich leads to a simpler form of Equation (13) after a change of variable in Equation (11),Meanwhile, this expression can be seen from Equation (13) directly,With this simplified expression, we can see that when , and when , .
- 3.
- From Equation (16), the Mellin transform only exists for , and therefore does not have the first moment for . This fits our observation in Theorem 1 that does not have the first moment for either.
3. Conclusions and Future Work
Funding
Acknowledgments
Conflicts of Interest
References
- Scalas, E.; Gorenflo, R.; Luckock, H.; Mainardi, F.; Mantelli, M.; Raberto, M. Anomalous waiting times in high-frequency financial data. Quant. Financ. 2004, 4, 695–702. [Google Scholar] [CrossRef] [Green Version]
- Kerss, A.; Leonenko, N.N.; Sikorskii, A. Fractional Skellam processes with applications to finance. Fract. Calc. Appl. Anal. Int. J. Theory Appl. 2014, 17, 532. [Google Scholar] [CrossRef]
- Jumarie, G. Fractional master equation: Non-standard analysis and Liouville–Riemann derivative. Chaos Solitons Fractals 2001, 12, 2577–2587. [Google Scholar] [CrossRef]
- Laskin, N. Fractional Poisson process. Commun. Nonlinear Sci. Numer. Simul. 2003, 8, 201–213. [Google Scholar] [CrossRef]
- Repin, O.N.; Saichev, A.I. Fractional Poisson Law. Radiophys. Quantum Electron. 2000, 43, 738–741. [Google Scholar] [CrossRef]
- Pillai, R.N. On Mittag-Leffler functions and related distributions. Ann. Inst. Stat. Math. 1990, 42, 157–161. [Google Scholar] [CrossRef]
- Mainardi, F.; Gorenflo, R.; Vivoli, A. Beyond the Poisson renewal process: A tutorial survey. J. Comput. Appl. Math. 2007, 205, 725–735. [Google Scholar] [CrossRef] [Green Version]
- Beghin, L.; Orsingher, E. Fractional poisson processes and related planar random motions. Electron. J. Probab. 2009, 14, 1790–1826. [Google Scholar] [CrossRef] [Green Version]
- Beghin, L.; Orsingher, E. Poisson-type processes governed by fractional and higher-order recursive differential equations. Electron. J. Probab. 2010, 15, 684–709. [Google Scholar] [CrossRef]
- Meerschaert, M.; Nane, E.; Vellaisamy, P. The Fractional Poisson Process and the Inverse Stable Subordinator. Electron. J. Probab. 2011, 16, 1600–1620. [Google Scholar] [CrossRef]
- Leonenko, N.; Scalas, E.; Trinh, M. The fractional non-homogeneous Poisson process. Stat. Probab. Lett. 2017, 120, 147–156. [Google Scholar] [CrossRef] [Green Version]
- Uchaikin, V.V.; Sibatov, R.T. Fractional theory for transport in disordered semiconductors. Commun. Nonlin. Sci. Numer. Simul. 2008, 13, 715–727. [Google Scholar] [CrossRef]
- Kumar, A.; Leonenko, N.; Pichler, A. Fractional risk process in insurance. Math. Financ. Econ. 2020, 14, 43. [Google Scholar] [CrossRef] [Green Version]
- Wang, X.T.; Wen, Z.X. Poisson fractional processes. Chaos Solitons Fract. 2003, 18, 169–177. [Google Scholar] [CrossRef]
- Wang, X.T.; Wen, Z.X.; Zhang, S.Y. Fractional Poisson process (II). Chaos Solitons Fract. 2006, 28, 143–147. [Google Scholar] [CrossRef]
- Wang, X.T.; Zhang, S.Y.; Fan, S. Nonhomogeneous fractional Poisson processes. Chaos Solitons Fract. 2007, 31, 236–241. [Google Scholar] [CrossRef]
- Lebedev, N.N. Special Functions and Their Applications; Dover Publications: New York, NY, USA, 1972. [Google Scholar]
- Mathai, A.M.; Haubold, H.J. Special Functions for Applied Scientists; Springer: New York, NY, USA, 2008. [Google Scholar] [CrossRef] [Green Version]
- Mathai, A.; Saxena, R.K.; Haubold, H.J. The H-Function; Springer: New York, NY, USA, 2010. [Google Scholar] [CrossRef]
- Kataria, K.; Vellaisamy, P. On densities of the product, quotient and power of independent subordinators. J. Math. Anal. Appl. 2018, 462, 1627–1643. [Google Scholar] [CrossRef] [Green Version]
- James, L.F. Lamperti-type laws. Ann. Appl. Probab. 2010, 20, 1303–1340. [Google Scholar] [CrossRef] [Green Version]
- Devroye, L.; James, L. On simulation and properties of the stable law. Stat. Methods Appl. 2014, 23, 307–343. [Google Scholar] [CrossRef]
- Lin, G.D. On the Mittag-Leffler distributions. J. Stat. Plan. Inference 1998, 74, 1–9. [Google Scholar] [CrossRef]
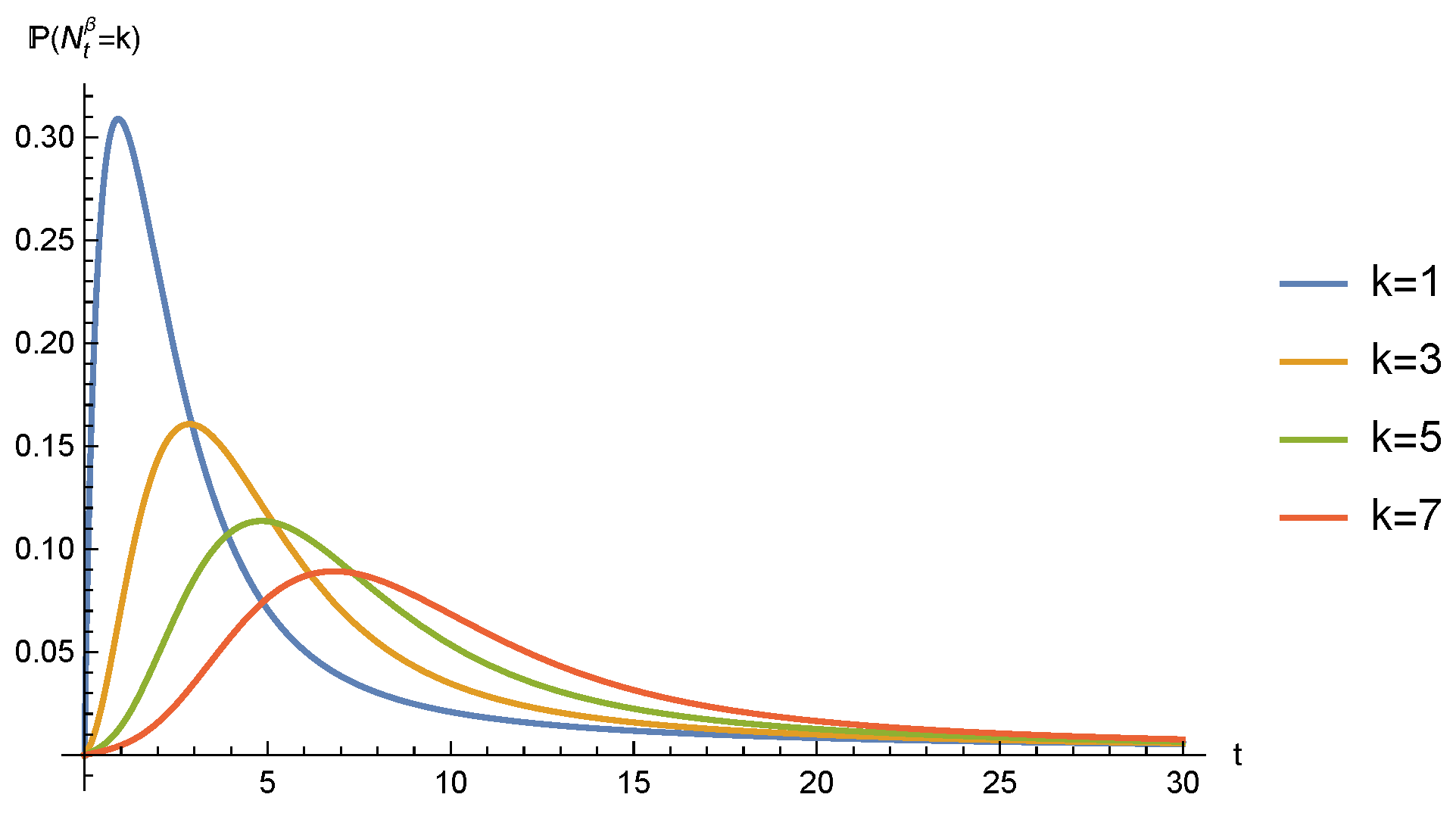

Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, Z. A New Fractional Poisson Process Governed by a Recursive Fractional Differential Equation. Fractal Fract. 2022, 6, 418. https://doi.org/10.3390/fractalfract6080418
Zhang Z. A New Fractional Poisson Process Governed by a Recursive Fractional Differential Equation. Fractal and Fractional. 2022; 6(8):418. https://doi.org/10.3390/fractalfract6080418
Chicago/Turabian StyleZhang, Zhehao. 2022. "A New Fractional Poisson Process Governed by a Recursive Fractional Differential Equation" Fractal and Fractional 6, no. 8: 418. https://doi.org/10.3390/fractalfract6080418
APA StyleZhang, Z. (2022). A New Fractional Poisson Process Governed by a Recursive Fractional Differential Equation. Fractal and Fractional, 6(8), 418. https://doi.org/10.3390/fractalfract6080418





