Discrimination of Microseismic Events in Coal Mine Using Multifractal Method and Moment Tensor Inversion
Abstract
:1. Introduction
2. Site Characterization
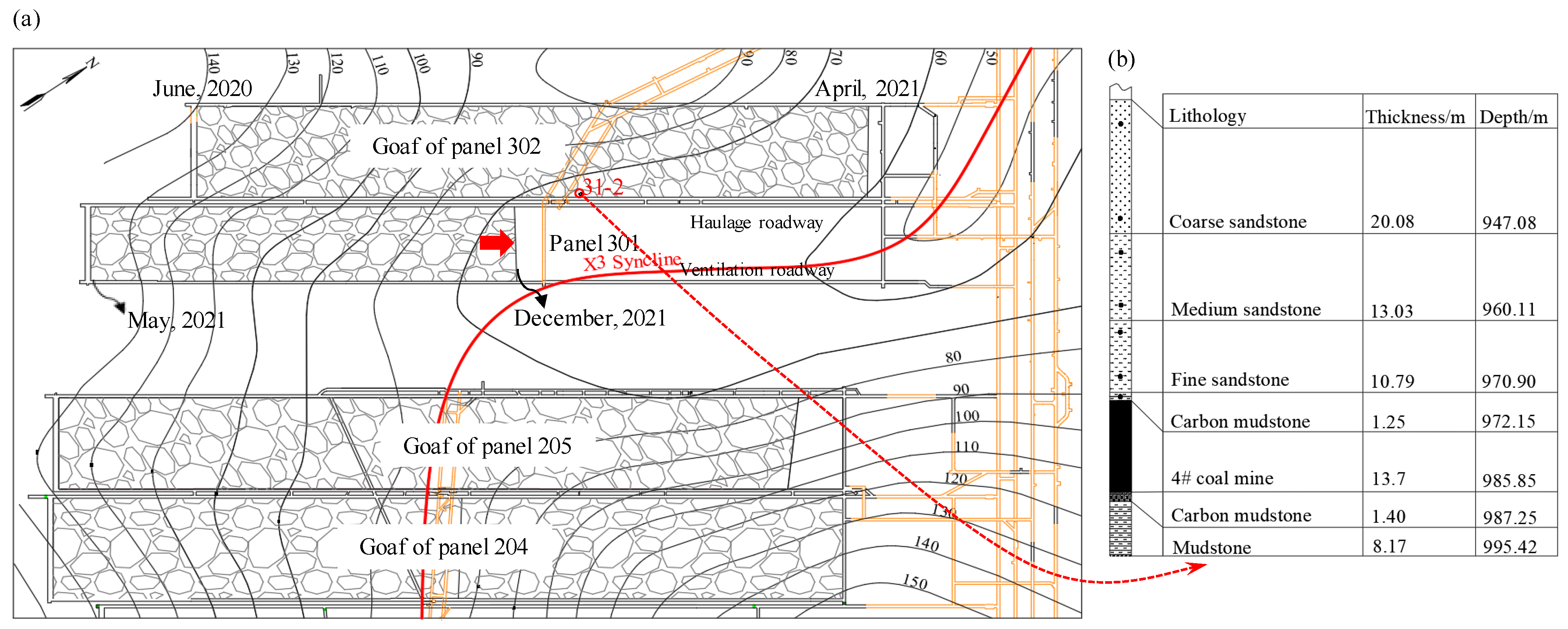
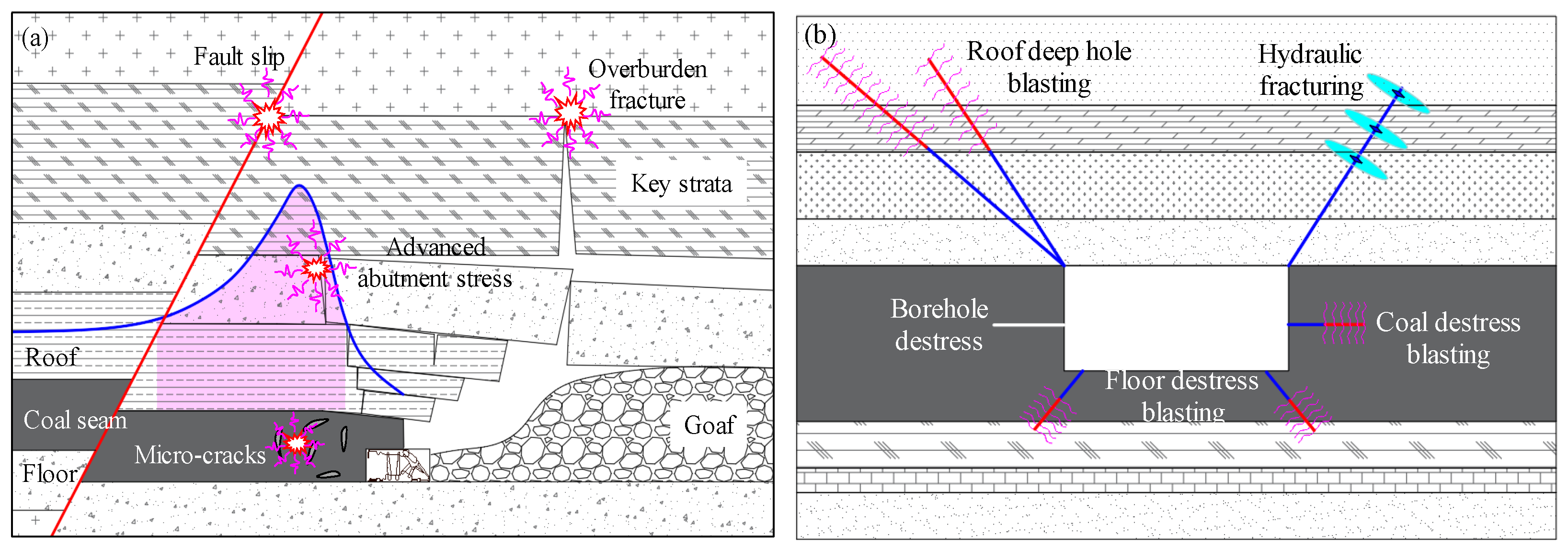
2.1. Geological and Mining Conditions of the Coal Mine
2.2. MS Monitoring System
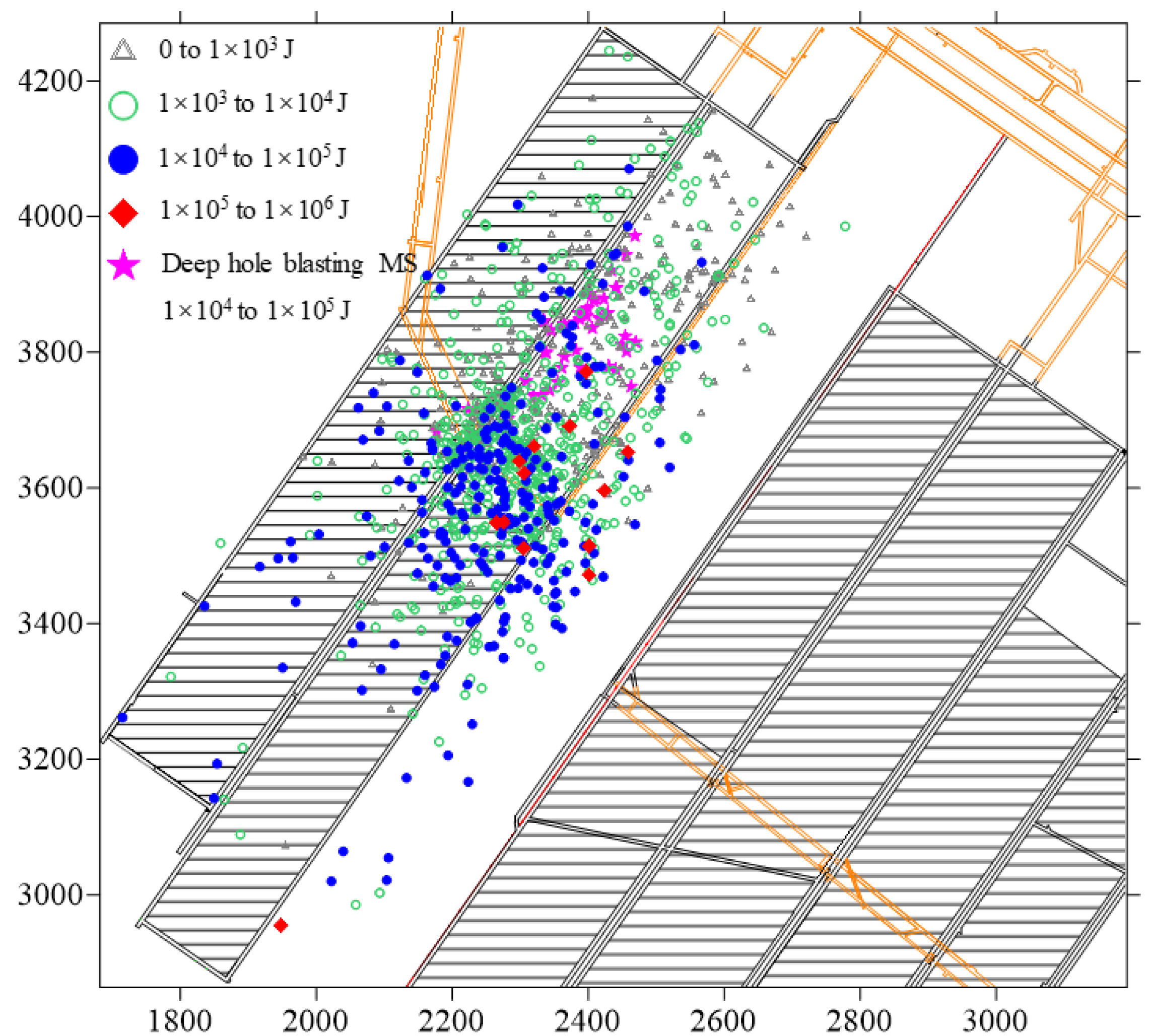
2.3. Data Preparation and Analysis
3. Multifractal Parameters of MS Waveform
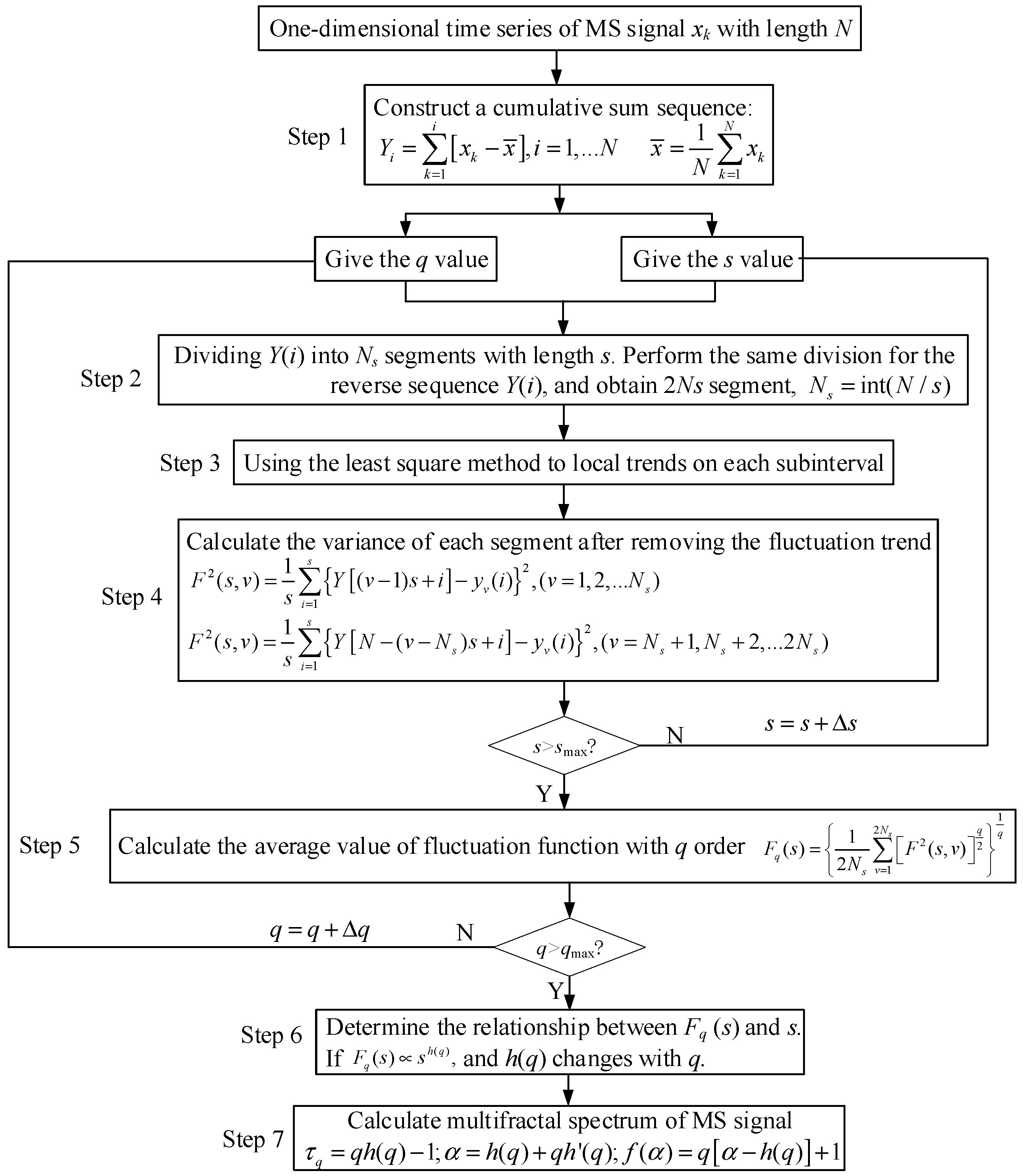
3.1. Multifractal Method
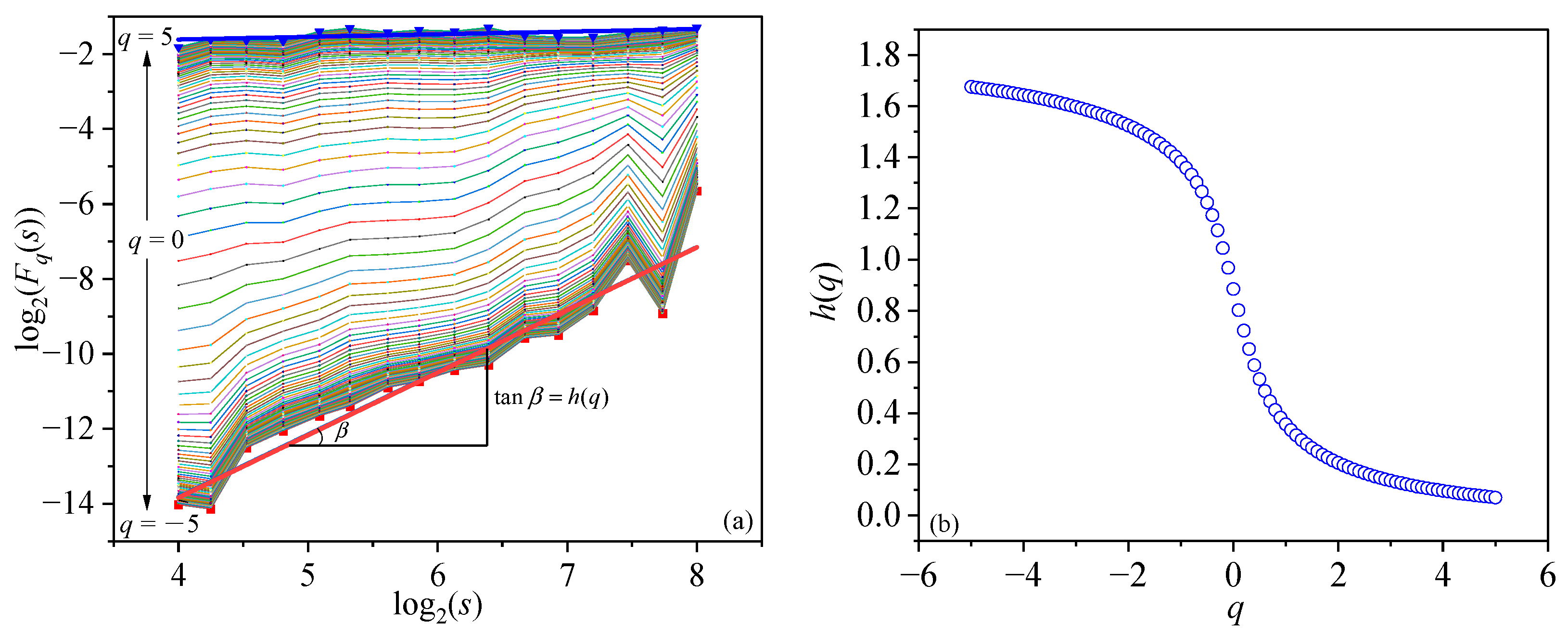
3.2. Key Parameters Setting of MF-DFA Method
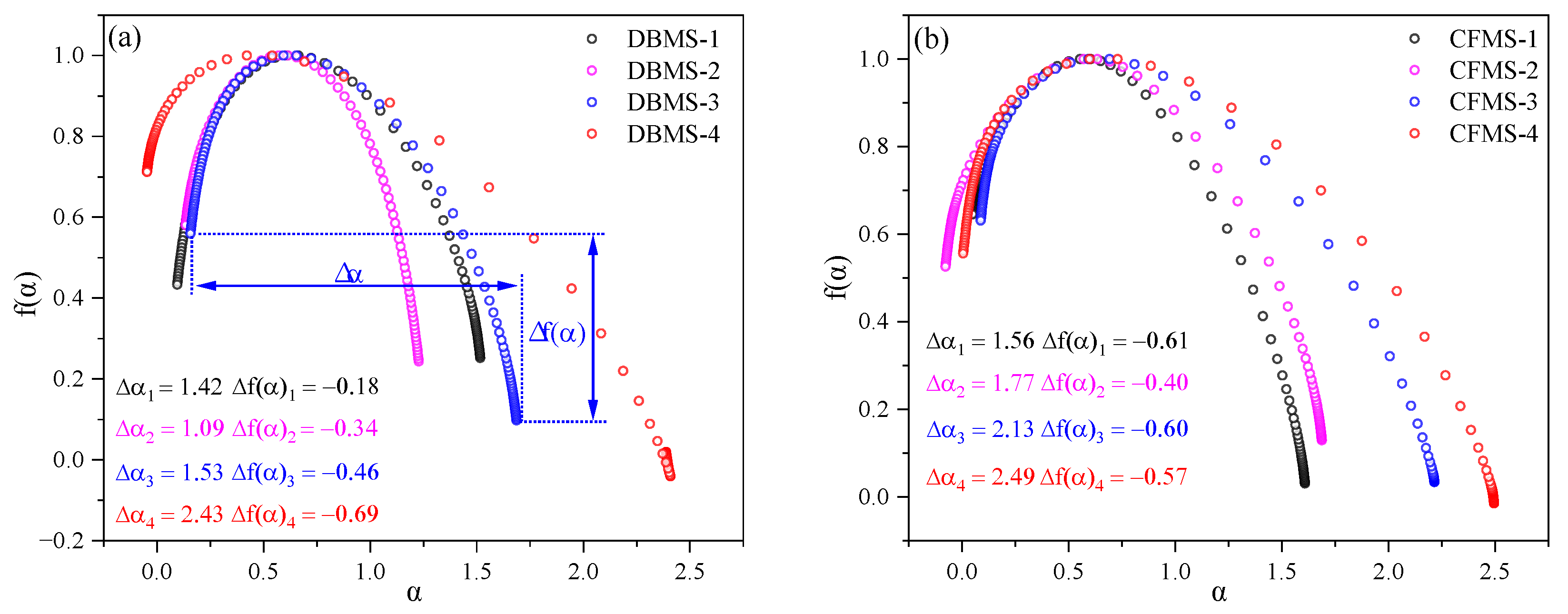
3.3. Results
4. Focal Mechanism of Different Types of MS Events
4.1. Seismic Moment Tensor Inversion
4.2. Results
5. Conclusions
- (1)
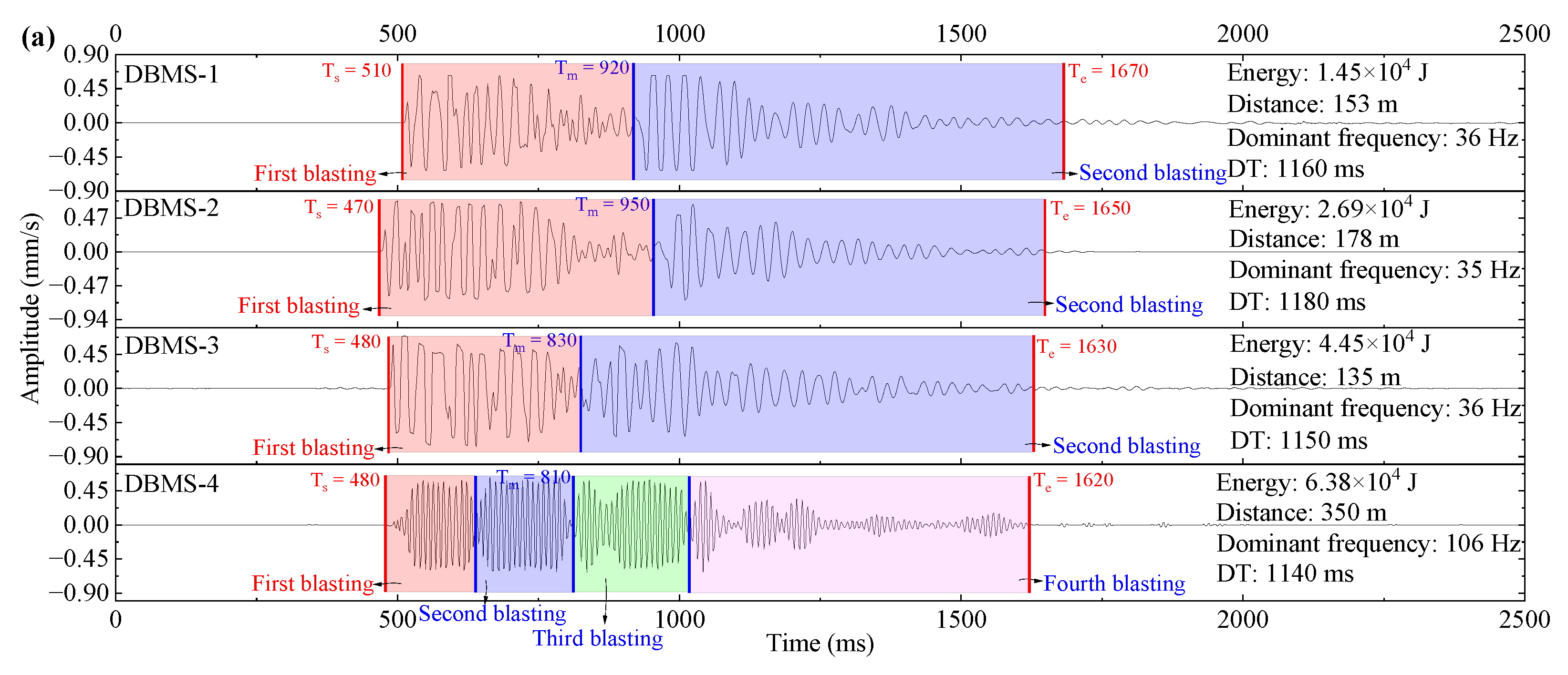
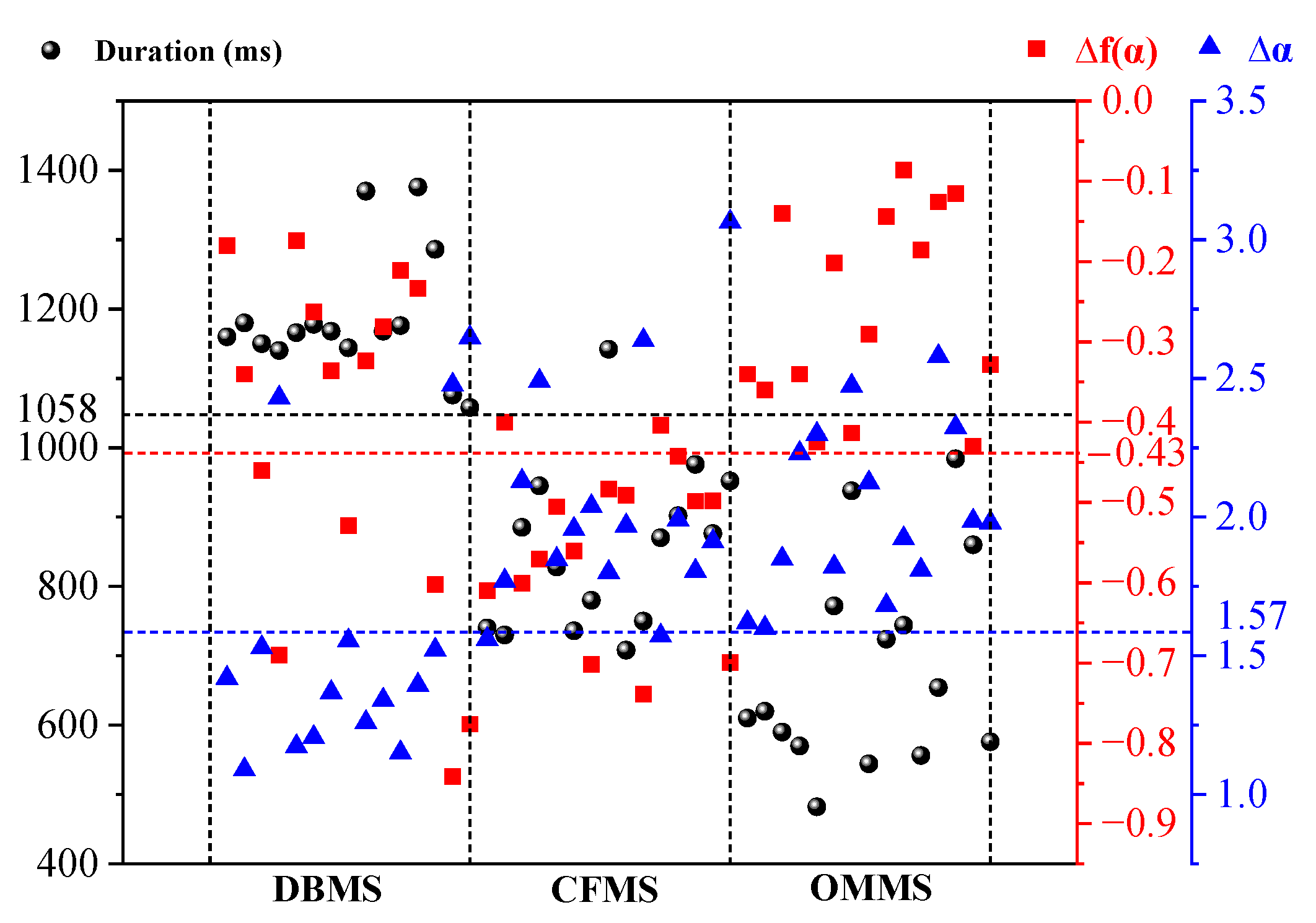
- There are great differences in duration, dominant frequency and wave fluctuation features between different MS waveforms. In general, two obvious fluctuations with similar amplitude can be clearly observed in deep-hole blasting MS waveforms, and they have a longer duration, lower dominant frequency and regular fluctuation compared to mine MS waveforms. In particular, the MS waveforms induced by double hole blasting have more than two strong fluctuations and higher frequency. For mine MS waveforms, only one evident fluctuation with three segments of pre-peak, peak duration and post-peak can be clearly observed, and the amplitude reaches a peak slowly, and its coda wave is developed. Moreover, compared with the overburden movement MS waveform, the pre-peak segment of the coal-rock fracture MS waveform is shorter, while the peak duration is longer, and the coda wave is more prominent.
- (2)
- The multifractal parameters ∆α and ∆f(α) of different MS waveforms were calculated to quantitatively describe the waveform fluctuation characteristics. First, the multifractal parameter ∆α of the deep-hole blasting MS waveform was generally less than 1.57, while that of the mine MS waveform was opposite—it was greater than 1.57. Consequently, parameter ∆α can be used to discriminate the deep-hole blasting and mine MS waveforms. Then, the parameter Δf(α) of the coal-rock fracture MS waveform varies from −0.75 to −0.40, which is lower than that of deep-hole blasting and overburden movement MS waveforms (range from −0.46 to −0.14). Therefore, Δf(α) can be used to discriminate the coal-rock fracture and overburden movement MS waveforms. Especially, the double deep-hole blasting MS waveforms have considerable large ∆α (greater than 2.43) and low Δf(α) (less than −0.69), which is different from the above types of MS waveforms.
- (3)
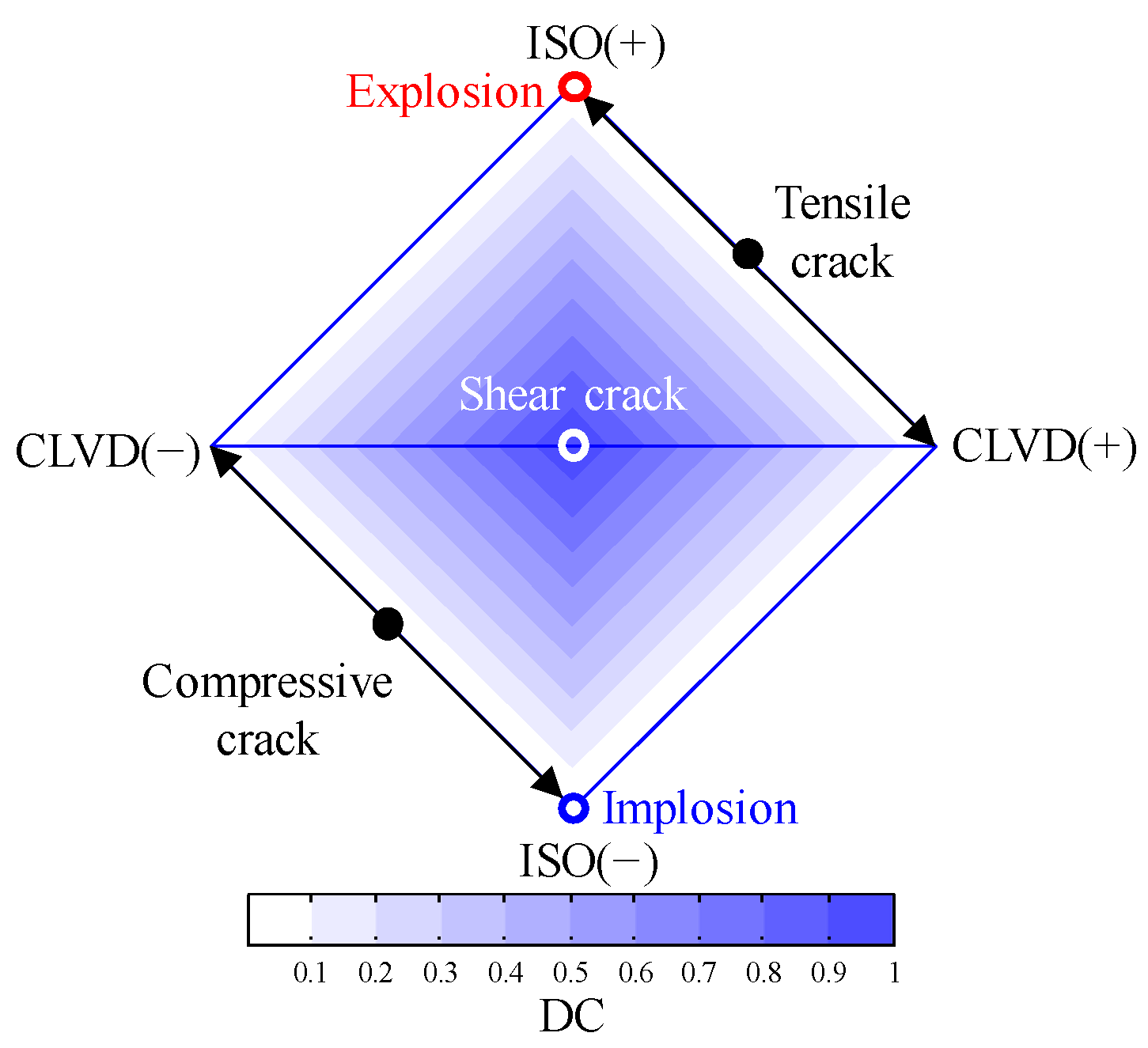
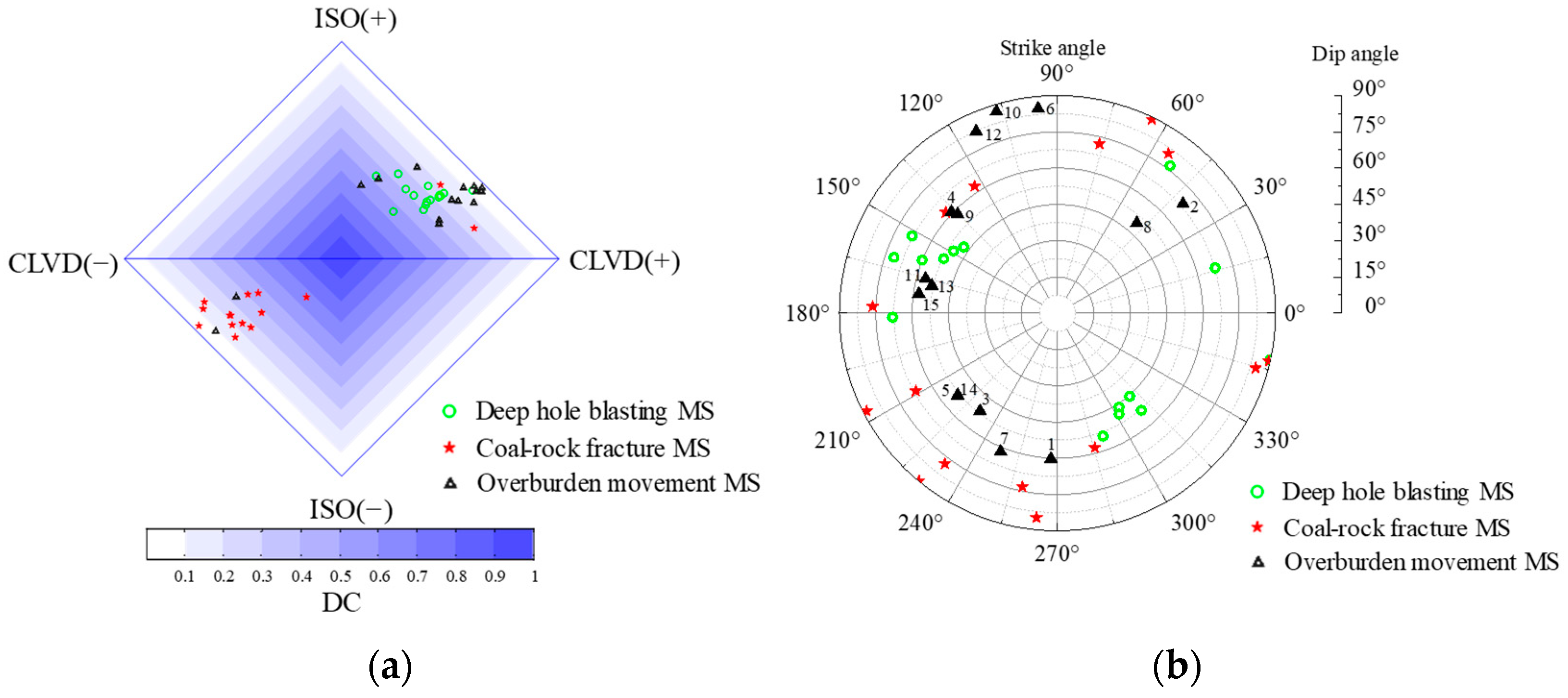
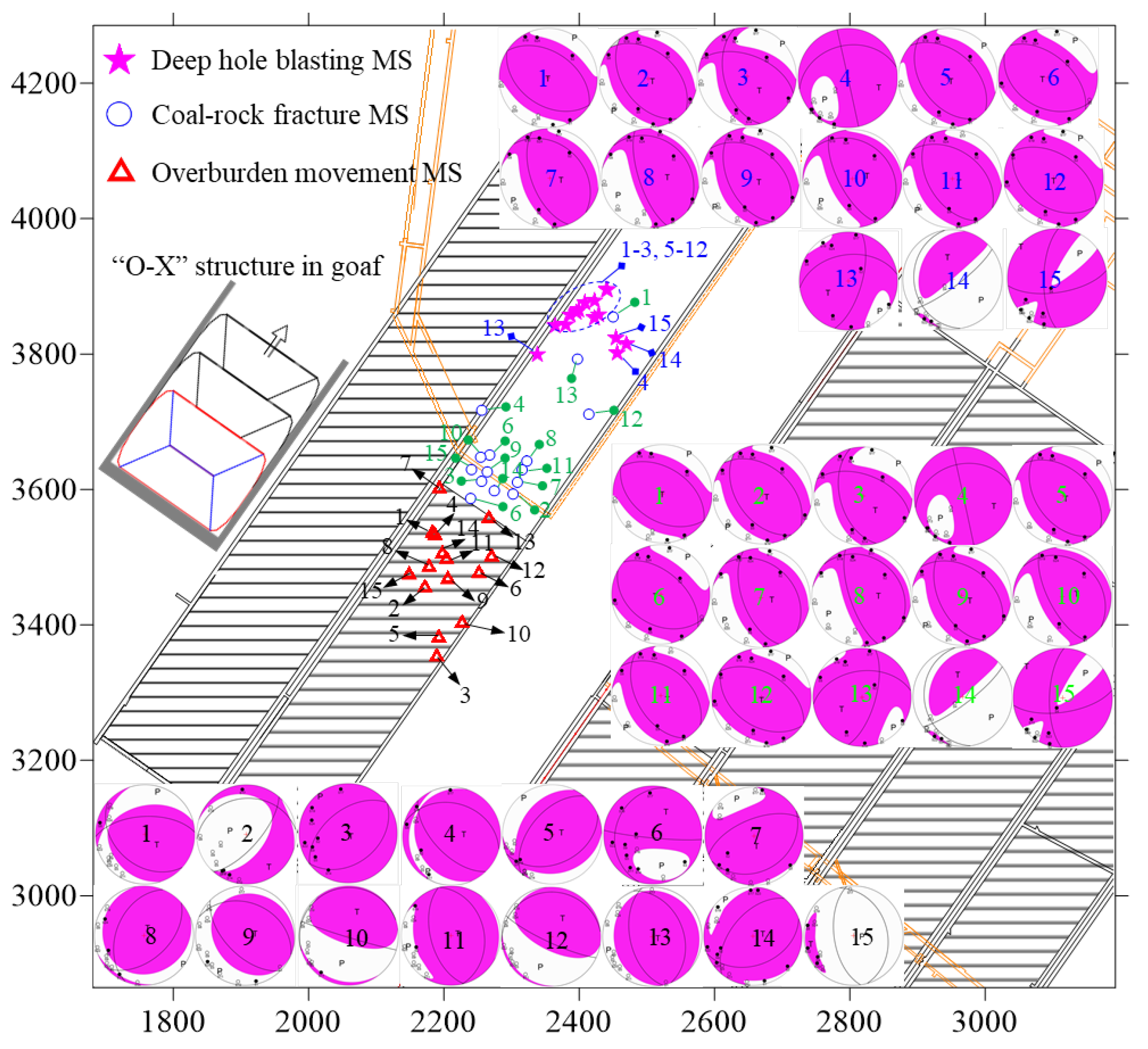
- The moment tensor inversion results indicate that the three types of MS events differ from each other in the focal mechanisms and parameters due to the different fracture modes of coal and rock. For deep-hole blasting MS events, an explosion was not the dominant mechanism, but the CLVD and DC components account for an important proportion. This indicated that some other processes occur during blasting. The moment tensor inversion solution of the mine MS events showed that the CLVD component is the dominant mechanism at the source, while the DC component has a lower percentage. The coal-rock fracture MS events were characterized by compression implosion or compression/shear implosion mixed focal mechanisms, while the overburden movement MS events were tensile explosion or tensile/shear explosion mixed focal mechanisms. The focal mechanisms and nodal plane parameters have close relationships with the inducing factors and occurrence processes of MS events. Moreover, the percentages of individual components of ISO, CLVD and DC and nodal plane parameters can be considered as characteristic parameters for discriminating the three types of MS events.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Tan, L.; Ren, T.; Yang, X.; He, X. A numerical simulation study on mechanical behaviour of coal with bedding planes under coupled static and dynamic load. Int. J. Min. Sci. Technol. 2018, 28, 791–797. [Google Scholar] [CrossRef]
- Cai, W.; Bai, X.; Si, G.; Cao, W.; Gong, S.; Dou, L. A Monitoring Investigation into Rock Burst Mechanism Based on the Coupled Theory of Static and Dynamic Stresses. Rock Mech. Rock Eng. 2020, 53, 5451–5471. [Google Scholar] [CrossRef]
- Tan, L.; Zhou, Z.; Cai, X.; Rui, Y. Analysis of mechanical behaviour and fracture interaction of multi-hole rock mass with DIC measurement. Measurement 2022, 191, 110794. [Google Scholar] [CrossRef]
- Dou, L.; Cai, W.; Cao, A.; Guo, W. Comprehensive early warning of rock burst utilizing microseismic multi-parameter indices. Int. J. Min. Sci. Technol. 2018, 28, 767–774. [Google Scholar] [CrossRef]
- Yu, B.; Zhao, J.; Xiao, H. Case study on overburden fracturing during longwall top coal caving using microseismic monitoring. Rock Mech. Rock Eng. 2017, 50, 507–511. [Google Scholar] [CrossRef]
- Si, G.; Cai, W.; Wang, S.; Li, X. Prediction of relatively high-energy seismic events using spatial–temporal parametrisation of mining-induced seismicity. Rock Mech. Rock Eng. 2020, 53, 5111–5132. [Google Scholar] [CrossRef]
- Luxbacher, K.; Westman, E.; Swanson, P.; Karfakis, M. Three-dimensional time-lapse velocity tomography of an underground longwall panel. Int. J. Rock Mech. Min. Sci. 2008, 45, 478–485. [Google Scholar] [CrossRef]
- Vallejos, J.A.; McKinnon, S.D. Logistic regression and neural network classification of seismic records. Int. J. Rock Mech. Min. Sci. 2013, 62, 86–95. [Google Scholar] [CrossRef]
- Dong, L.J.; Wesseloo, J.; Potvin, Y.; Li, X.B. Discrimination of Mine Seismic Events and Blasts Using the Fisher Classifier, Naive Bayesian Classifier and Logistic Regression. Rock Mech. Rock Eng. 2015, 49, 183–211. [Google Scholar] [CrossRef]
- Dong, L.J.; Wesseloo, J.; Potvin, Y.; Li, X.B. Discriminant models of blasts and seismic events in mine seismology. Int. J. Rock Mech. Min. Sci. 2016, 86, 282–291. [Google Scholar] [CrossRef]
- Dong, L.J.; Tang, Z.; Li, X.B.; Chen, Y.C.; Xue, J.C. Discrimination of mining microseismic events and blasts using convolutional neural networks and original waveform. J. Cent. South Univ. 2020, 27, 3078–3089. [Google Scholar] [CrossRef]
- Zhao, G.-Y.; Ma, J.; Dong, L.-J.; Li, X.-B.; Chen, G.-H.; Zhang, C.-X. Classification of mine blasts and microseismic events using starting-up features in seismograms. Trans. Nonferr. Metals Soc. China 2015, 25, 3410–3420. [Google Scholar] [CrossRef]
- Rao, D.; Shi, X.; Zhou, J.; Yu, Z.; Gou, Y.; Dong, Z.; Zhang, J. An Expert Artificial Intelligence Model for Discriminating Microseismic Events and Mine Blasts. Appl. Sci. 2021, 11, 6474. [Google Scholar] [CrossRef]
- Pu, Y.; Apel, D.B.; Hall, R. Using machine learning approach for microseismic events recognition in underground excavations: Comparison of ten frequently-used models. Eng. Geol. 2020, 268, 105519. [Google Scholar] [CrossRef]
- Zhao, Y.; Xu, H.; Yang, T.; Wang, S.; Sun, D. A hybrid recognition model of microseismic signals for underground mining based on CNN and LSTM networks. Geomat. Nat. Hazards Risk 2021, 12, 2803–2834. [Google Scholar] [CrossRef]
- Wei, H.; Shu, W.; Dong, L.; Huang, Z.; Sun, D. A Waveform Image Method for Discriminating Micro-Seismic Events and Blasts in Underground Mines. Sensors 2020, 20, 4322. [Google Scholar] [CrossRef]
- Song, G.; Cheng, J.; Grattan, K.T.V. Recognition of Microseismic and Blasting Signals in Mines Based on Convolutional Neural Network and Stockwell Transform. IEEE Access 2020, 8, 45523–45530. [Google Scholar] [CrossRef]
- Li, B.; Wang, E.; Li, Z.; Niu, Y.; Li, N.; Li, X. Discrimination of different blasting and mine microseismic waveforms using FFT, SPWVD and multifractal method. Environ. Earth Sci. 2021, 80, 36. [Google Scholar] [CrossRef]
- Kan, J.; Dou, L.; Li, J.; Li, X.; Bai, J.; Wang, M. Characteristics of Microseismic Waveforms Induced by Underground Destress Blasting: Comparison with Those Induced by Ground Blasting and Coal Mining. Front. Earth Sci. 2022, 10, 188–198. [Google Scholar] [CrossRef]
- Li, N.; Li, B.; Chen, D.; Wang, E.; Tan, Y.; Qian, J.; Jia, H. Waveform Characteristics of Earthquakes Induced by Hydraulic Fracturing and Mining Activities: Comparison with Those of Natural Earthquakes. Nat. Resour. Res. 2020, 29, 3653–3674. [Google Scholar] [CrossRef]
- Li, X.; Li, Z.; Wang, E.; Feng, J.; Chen, L.; Li, N.; Kong, X. Extraction of Microseismic Waveforms Characteristics Prior to Rock Burst Using Hilbert-Huang Transform. Measurement 2016, 91, 101–113. [Google Scholar] [CrossRef]
- Ma, J.; Zhao, G.Y.; Dong, L.J.; Chen, G.H.; Zhang, C.X. A Comparison of mine seismic discriminators based on features of source parameters to waveform characteristics. Shock Vib. 2015, 2015, 919143. [Google Scholar] [CrossRef] [Green Version]
- Chen, D.; Wang, E.-Y.; Li, N. Study on the rupture properties and automatic identification model of micro-earthquakes and blasting events in a coal mine. Soil Dyn. Earthq. Eng. 2021, 146, 106759. [Google Scholar] [CrossRef]
- Ma, J.; Dong, L.; Zhao, G.; Li, X. Discrimination of seismic sources in an underground mine using full waveform inversion. Int. J. Rock Mech. Min. Sci. 2018, 106, 213–222. [Google Scholar] [CrossRef]
- Cesca, S.; Rohr, A.; Dahm, T. Discrimination of induced seismicity by full moment tensor inversion and decomposition. J. Seismol. 2012, 17, 147–163. [Google Scholar] [CrossRef]
- Wojtecki, Ł.; Konicek, P.; Mendecki, M.J.; Zuberek, W.M. Evaluation of Destress Blasting Effectiveness Using the Seismic Moment Tensor Inversion and Seismic Effect Methods. Int. J. Geomech. 2022, 22, 04022010. [Google Scholar] [CrossRef]
- Zhu, J.; Ma, B.; Xie, H.; Gao, F.; Zhou, H.; Zhou, C.; Zheng, F. The Differences and Connections between Mining Seismicity and Coal Bursts in Coal Mines and Preliminary Study on Coal Bursts Induced by Mining Seismicity. J. China Coal Soc. 2022, 10, 1027–1039. [Google Scholar] [CrossRef]
- Pan, Y.S.; Gu, B.X.; Wang, S.; Guo, Y. Three-dimension of model and its application mines seismic wave propagation. J. China Coal Soc. 2012, 37, 1810–1814. [Google Scholar]
- He, J.; Dou, L.; Gong, S.; Li, J.; Ma, Z. Rock burst assessment and prediction by dynamic and static stress analysis based on micro-seismic monitoring. Int. J. Rock Mech. Min. Sci. 2017, 93, 46–53. [Google Scholar] [CrossRef]
- Fan, C.; Li, L. Characteristics analysis of nonstationary signals based on multifractal detrended fluctuation analysis method. In Proceedings of the 27th Chinese Control and Decision Conference (2015 CCDC), Qingdao, China, 23–25 May 2015; pp. 1614–1618. [Google Scholar]
- Laudani, R.; Zhang, D.; Faouzi, T.; Porcu, E.; Ostoja-Starzewski, M.; Chamorro, L.P. On streamwise velocity spectra models with fractal and long-memory effects. Phys. Fluids 2021, 33, 035116. [Google Scholar] [CrossRef]
- Laudani, R.; Ostoja-Starzewski, M. Fracture of beams with random field properties: Fractal and Hurst effects. Int. J. Solids Struct. 2020, 191, 243–253. [Google Scholar] [CrossRef]
- Kantelhardt, J.W.; Zschiegner, S.A.; Koscielny-Bunde, E.; Havlin, S.; Bunde, A.; Stanley, H.E. Multifractal detrended fluctuation analysis of nonstationary time series. Physica A 2002, 316, 87–114. [Google Scholar] [CrossRef] [Green Version]
- Xu, F.L.; Wang, E.Y.; Song, D.Z.; Song, X.Y.; Wei, M.Y. Long-range correlation and multifractal distribution of acoustic emission of coal-rock. Rock Soil Mech. 2011, 32, 2111–2116. [Google Scholar]
- Fu, X.Q.; Yang, R.S.; Cui, X.Q.; Liu, X.; Liu, J.F.; Lei, Z. Multi-fractal detrended fluctuation analysis of the blasting vibration signal in a frozen shaft. J. Vib. Shock 2020, 39, 51–58. [Google Scholar]
- Telesca, L.; Colangelo, G.; Lapenna, V.; Macchiato, M. Fluctuation dynamics in geoelectrical data: An investigation by using multifractal detrended fluctuation analysis. Phys. Lett. A 2004, 332, 398–404. [Google Scholar] [CrossRef]
- Mao, H.; Zhang, M.; Jiang, R.; Li, B.; Xu, J.; Xu, N. Study on deformation pre-warning of rock slopes based on multi-fractal characteristics of microseismic signals. Chin. J. Rock Mech. Eng. 2020, 39, 560–571. [Google Scholar]
- Khandelwal, M.; Singh, T.N. Prediction of blast induced ground vibrations and frequency in opencast mine: A neural network approach. J. Sound Vib. 2006, 289, 711–725. [Google Scholar] [CrossRef]
- Jost, M.U.; Herrmann, R.B. A student’s guide to and review of moment tensors. Seismol. Res. Lett. 1989, 60, 37–57. [Google Scholar] [CrossRef]
- Knopoff, L.; Randall, M.J. The compensated linear-vector dipole: A possible mechanism for deep earthquakes. J. Geophys. Res. 1970, 75, 4957–4963. [Google Scholar] [CrossRef]
- Vavryčuk, V. Moment tensor decompositions revisited. J. Seismol. 2014, 19, 231–252. [Google Scholar] [CrossRef] [Green Version]
- Kwiatek, G.; Martínez-Garzón, P.; Bohnhoff, M. HybridMT: A MATLAB/shell environment package for seismic moment tensor inversion and refinement. Seismol. Res. Lett. 2016, 87, 964–976. [Google Scholar] [CrossRef] [Green Version]
- Vavrycuk, V. Inversion for parameters of tensile earthquakes. J. Geophys. Res. 2001, 106, 16339–16355. [Google Scholar] [CrossRef]
- Tan, L.; Ren, T.; Dou, L.; Yang, X.; Qiao, M.; Peng, H. Analytical stress solution and mechanical properties for rock mass containing a hole with complex shape. Theor. Appl. Fract. Mech. 2021, 114, 103002. [Google Scholar] [CrossRef]
- Dou, L.; He, H. Study of OX-F-T spatial structure evolution of overlying strata in coal mines. Chin. J. Rock Mech. Eng. 2012, 31, 453–460. [Google Scholar]



Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kan, J.; Dou, L.; Li, J.; Song, S.; Zhou, K.; Cao, J.; Bai, J. Discrimination of Microseismic Events in Coal Mine Using Multifractal Method and Moment Tensor Inversion. Fractal Fract. 2022, 6, 361. https://doi.org/10.3390/fractalfract6070361
Kan J, Dou L, Li J, Song S, Zhou K, Cao J, Bai J. Discrimination of Microseismic Events in Coal Mine Using Multifractal Method and Moment Tensor Inversion. Fractal and Fractional. 2022; 6(7):361. https://doi.org/10.3390/fractalfract6070361
Chicago/Turabian StyleKan, Jiliang, Linming Dou, Jiazhuo Li, Shikang Song, Kunyou Zhou, Jinrong Cao, and Jinzheng Bai. 2022. "Discrimination of Microseismic Events in Coal Mine Using Multifractal Method and Moment Tensor Inversion" Fractal and Fractional 6, no. 7: 361. https://doi.org/10.3390/fractalfract6070361
APA StyleKan, J., Dou, L., Li, J., Song, S., Zhou, K., Cao, J., & Bai, J. (2022). Discrimination of Microseismic Events in Coal Mine Using Multifractal Method and Moment Tensor Inversion. Fractal and Fractional, 6(7), 361. https://doi.org/10.3390/fractalfract6070361





