Chaos Suppression of a Fractional-Order Modificatory Hybrid Optical Model via Two Different Control Techniques

Abstract

In this current manuscript, we study a fractional-order modificatory hybrid optical model (FOMHO model). Experiments manifest that under appropriate parameter conditions, the fractional-order modificatory hybrid optical model will generate chaotic behavior. In order to eliminate the chaotic phenomenon of the (FOMHO model), we devise two different control techniques. First of all, a suitable delayed feedback controller is designed to control chaos in the (FOMHO model). A sufficient condition ensuring the stability and the occurrence of Hopf bifurcation of the fractional-order controlled modificatory hybrid optical model is set up. Next, a suitable delayed mixed controller which includes state feedback and parameter perturbation is designed to suppress chaos in the (FOMHO model). A sufficient criterion guaranteeing the stability and the onset of Hopf bifurcation of the fractional-order controlled modificatory hybrid optical model is derived. In the end, software simulations are implemented to verify the accuracy of the devised controllers. The acquired results of this manuscript are completely new and have extremely vital significance in suppressing chaos in physics. Furthermore, the exploration idea can also be utilized to control chaos in many other differential chaotic dynamical models.

1. Introduction

Chaos widely exists in many areas, such as astronomy, quantum mechanics, economy and finance, weather, climate, network science, thermodynamics, chemistry, probabilistic mathematics, fluid mechanics and so on [1,2,3,4,5,6,7]. The study indicates that chaos has a very important application value in power system protection, flow dynamics, biomedicine, computer technique, information science, cryptology, communication engineering and so on [8]. However, in many cases, chaotic behavior is undesirable in physical science, life science, economic system, network science, safety information and engineering technology. Thus, how to eliminate chaos and obtain the dynamic behavior we need is a major theme of the present era. During the past decades, a great number of chaos control techniques were proposed, and a series of excellent achievements have been reported. For example, Aqeel et al. [9] applied the state-space linearization method to control chaos in the Krause and Roberts geomagnetic chaotic model. Kaur et al. [10] controlled the chaos in the chaotic plankton system by virtue of a delayed feedback controller. Li et al. [11] suppressed the chaos in a brushless DC motor model by applying a nonlinear state feedback controller. Yin et al. [12] controlled the chaotic behavior of a permanent-magnet synchronous-motor drive system by making use of an equivalent-input-disturbance-based control approach. Ott et al. [13] proposed the OGY (it is proposed by E. Ott, C. Grebogi and J.A. Yorke) method to eliminate chaos in a chaotic dynamical model. Du et al. [14] dealt with the chaotic phenomenon of an economic system via phase-space compression. Zheng [15] explored the chaos and hyperchaos control of a chaotic model by applying an adaptive feedback controller. For more detailed publications on this aspect, one can see [16,17,18,19,20,21].

In particular, there exist many chaotic dynamical models in physics. In 1994, Mitschke and Flüggen [22] set up an electrooptical chaotic hybrid model. The basic structure of this model can be described as the following form:

$$\begin{array}{ccc}& & \frac{d^3\mathcal{U}\left(t\right)}{dt}=\frac{d^2\mathcal{U}\left(t\right)}{dt}\left(\frac{\mathcal{L}}{\mathcal{R}}+{\mathcal{R}}_m\mathcal{C}\right)-\frac{d\mathcal{U}\left(t\right)}{dt}\left(\frac{{\mathcal{R}}_m}{\mathcal{R}}+\frac{\mathcal{C}}{{\mathcal{C}}_m}+1\right)\hfill \\ & & -\frac{1}{\mathcal{R}{\mathcal{C}}_m}\mathcal{U}+\frac{{\theta }^2}{\mathcal{R}{\mathcal{C}}_m}{(\mathcal{U}-\nu )}^2,\hfill \end{array}$$

(1)

where $\mathcal{U}$ denotes the voltage in the capacitor; ${\mathcal{R}}_m$ stands for the variable resistance; $\mathcal{R}$ stands for the resistance; ${\mathcal{C}}_m,\mathcal{C}$ represent the capacitor; $\mathcal{L}$ stands for the inductivity; $\theta$ denotes the gain; $\nu$ is bias. By suitable transformation, we can obtain the following system:

$$\left\{\begin{array}{c}{\displaystyle \frac{d{v}_1\left(t\right)}{dt}=v_2\left(t\right),}\hfill \\ {\displaystyle \frac{d{v}_2\left(t\right)}{dt}=v_3\left(t\right),}\hfill \\ {\displaystyle \frac{d{v}_3\left(t\right)}{dt}=-a{v}_3\left(t\right)-v_2\left(t\right)-g\left(v_1\left(t\right)\right),}\hfill \end{array}\right.$$

(2)

where $a>0,b>0$ represent two real numbers and $g\left(v_1\left(t\right)\right)$ stands for the logistic function described by

$$g\left(v_1\left(t\right)\right)=b{v}_1\left(t\right)(1-v_1\left(t\right)).$$

(3)

In this paper, we replace the quadratic logistic function g in model (2) with the following cubic logistic function:

$$g\left(v_1\left(t\right)\right)=b{v}_1\left(t\right)(1-v_1^2\left(t\right)),$$

(4)

then, we obtain

$$\left\{\begin{array}{c}{\displaystyle \frac{d{v}_1\left(t\right)}{dt}=v_2\left(t\right),}\hfill \\ {\displaystyle \frac{d{v}_2\left(t\right)}{dt}=v_3\left(t\right),}\hfill \\ {\displaystyle \frac{d{v}_3\left(t\right)}{dt}=-a{v}_3\left(t\right)-v_2\left(t\right)-b{v}_1\left(t\right)(1-v_1^2\left(t\right)).}\hfill \end{array}\right.$$

(5)

A fractional-order dynamical system is a contemporary concept and can be regarded as a vital part of abstract mathematics [23]. A fractional-order dynamical system owns the influence of time memory which is absent for its integer-order counterparts. A fractional-order derivative can describe the whole time domain of the dynamical process, but an integer-order derivative can only describe the variation of a certain peculiarity at a given point in time [23]. The investigation indicates that a fractional-order dynamical system is a more effective tool to describe the actual natural phenomenon than the integer-order dynamical system. The reason lies in the memory trait and hereditary peculiarity of the fractional-order dynamical system [24,25,26,27]. Recently, fractional-order dynamical systems have been found to be an enormous application prospect in numerous areas, such as control technology, artificial intelligence, network science, mechanics, physical science, economics, biological medical treatment, all sorts of physical waves and so on [28,29,30,31,32]. In recent years, a great deal of work on fractional-order dynamical models has been published. For example, Kaslik and Rădulescu [33] discussed the Hopf bifurcation of fractional-order gene regulatory networks. Yuan et al. [34] dealt with the bifurcation behavior of a fractional-order delayed prey–predator system. Xue et al. [35] applied command-filtering and a sliding mode technique to investigate the adaptive fuzzy finite-time backstepping control of a fractional nonlinear model. Djilali et al. [36] explored the Turing–Hopf bifurcation of a fractional mussel-algae system. In particular, the study on chaos control of a fractional order has also attracted great interest from many scholars in engineering and mathematics circles (e.g., see [37,38,39,40]). For different fractional-order chaotic dynamical systems, how to control the chaos of fractional-order chaotic dynamical systems is still a hot issue. Inspired by the analysis above and on the basis of model (5), we propose and explore the following (FOMHO model):

$$\left\{\begin{array}{c}{\displaystyle \frac{d^{\rho }{v}_1\left(t\right)}{d{t}^{\rho }}=v_2\left(t\right),}\hfill \\ {\displaystyle \frac{d^{\rho }{v}_2\left(t\right)}{d{t}^{\rho }}=v_3\left(t\right),}\hfill \\ {\displaystyle \frac{d^{\rho }{v}_3\left(t\right)}{d{t}^{\rho }}=-a{v}_3\left(t\right)-v_2\left(t\right)-b{v}_1\left(t\right)(1-v_1^2\left(t\right)),}\hfill \end{array}\right.$$

(6)

where $\rho \in (0,1]$. The investigation manifests that the fractional-order modificatory hybrid optical model (6) displays chaotic phenomenon under the parameter conditions $a=0.94,b_1=2.$ The numerical simulation plots are presented in Figure 1.

In this current manuscript, we will explore two aspects as follows:

(i)

Taking advantage of a delayed feedback controller to eliminate chaos in model (6) and explore the stability and generation of Hopf bifurcation of a fractional-order controlled modificatory hybrid optical model.

(ii)

Making use of a suitable mixed controller including state feedback and parameter perturbation to suppress chaos in model (6) and investigate the stability and generation of Hopf bifurcation of a fractional-order controlled modificatory hybrid optical model.

The primary contribution of this manuscript is stated as follows:

• A proper delayed feedback controller is effectively devised to control the chaotic phenomenon of model (6).
• A proper mixed controller including state feedback and parameter perturbation is resoundingly designed to suppress the chaotic phenomenon of model (6).
• The exploration way can also be utilized to probe into the chaos control of lots of other fractional-order dynamical models.

The fabric of this manuscript is as follows. Some requisite knowledge on the fractional-order differential system is prepared in Section 2. In Section 3, the chaotic phenomenon of model (6) is controlled by using a suitable delayed feedback controller. In Section 4, the chaotic phenomenon of model (6) is controlled by virtue of a proper mixed controller including state feedback and parameter perturbation. In Section 5, computer simulations are put into effect to verify the established assertions. Section 6 completes this manuscript.

2. Preliminaries

In this part, we present some requisite definitions and lemmas on fractional-order differential system.

Definition 1

([41]). The Riemann–Liouville fractional integral of order ρ of the function $h\left(ϵ\right)$ is defined as follows:

$${\mathcal{I}}^{\rho }h\left(\epsilon \right)=\frac{1}{\mathsf{\Gamma }\left(\rho \right)}{\int }_{{\epsilon }_0}^{\epsilon }{(\epsilon -\zeta )}^{\rho -1}h\left(\zeta \right)d\zeta ,$$

where $\epsilon >{\epsilon }_0,\rho >0$ and $\mathsf{\Gamma }\left(\zeta \right)={\int }_0^{\infty }{s}^{\zeta -1}{e}^{-s}ds$.

Definition 2

([41]). The Caputo fractional-order derivative of order ρ of the function $h\left(\epsilon \right)\in ([{\epsilon }_0,\infty ),R)$ is defined as follows:

$${\mathcal{D}}^{\rho }h\left(\epsilon \right)=\frac{1}{\mathsf{\Gamma }(\iota -\rho )}{\int }_{{\epsilon }_0}^{\epsilon }\frac{h^{\left(\iota \right)}\left(s\right)}{{(\epsilon -s)}^{\rho -\iota +1}}ds,$$

where $\epsilon \ge {\epsilon }_0$ and ι represents a positive integer ($\rho \in [\iota -1,\iota ))$. In particular, if $\rho \in (0,1)$, then

$${\mathcal{D}}^{\rho }h\left(\epsilon \right)=\frac{1}{\mathsf{\Gamma }(1-\rho )}{\int }_{{\epsilon }_0}^{\epsilon }\frac{h^{{}^{\prime }}\left(s\right)}{{(\epsilon -s)}^{\rho }}ds.$$

Lemma 1

([42]). Consider the following fractional-order model: ${\mathcal{D}}^{\rho }v=\mathcal{H}v,v\left(0\right)=v_0$ where $\rho \in (0,1),v\in R^m,\mathcal{H}\in R^{m\times m}.$ Denote ${\nu }_k(k=1,2,\cdots ,m)$ the root of the characteristic equation of ${\mathcal{D}}^{\rho }v=\mathcal{H}v$, then the equilibrium point of model ${\mathcal{D}}^{\rho }v=\mathcal{H}v$ is locally asymptotically stable if $|arg\left({\nu }_k\right)|>\frac{\rho \pi }{2}(k=1,2,\cdots ,m)$ and the equilibrium point of model ${\mathcal{D}}^{\rho }v=\mathcal{H}v$ is stable if $|arg\left({\nu }_k\right)|>\frac{\rho \pi }{2}(k=1,2,\cdots ,m)$ and every critical eigenvalue which obeys $|arg\left({\nu }_k\right)|=\frac{\rho \pi }{2}$$(k=1,2,\cdots ,m)$ owns geometric multiplicity one.

3. Chaos Suppression via Delayed Feedback Controller

In this part, we are to apply an appropriate delayed feedback controller to eliminate the chaotic phenomenon of the fractional-order modificatory hybrid optical model (6). Obeying the way of Yu and Chen [43], we propose the following delayed feedback controller:

$$\zeta \left(t\right)=\delta [v_1(t-\theta )-v_1\left(t\right)],$$

(7)

where $\delta$ stands for feedback gain coefficient and $\theta$ denotes a delay. Adding the delayed feedback controller (7) to the first equation of model (6), we obtain

$$\left\{\begin{array}{c}{\displaystyle \frac{d^{\rho }{v}_1\left(t\right)}{d{t}^{\rho }}=v_2\left(t\right)+\delta [v_1(t-\theta )-v_1\left(t\right)],}\hfill \\ {\displaystyle \frac{d^{\rho }{v}_2\left(t\right)}{d{t}^{\rho }}=v_3\left(t\right),}\hfill \\ {\displaystyle \frac{d^{\rho }{v}_3\left(t\right)}{d{t}^{\rho }}=-a{v}_3\left(t\right)-v_2\left(t\right)-b{v}_1\left(t\right)(1-v_1^2\left(t\right)).}\hfill \end{array}\right.$$

(8)

Obviously, model (8) has three equilibrium points $V_1(0,0,0),V_2(1,0,0),V_3(-1,0,0)$. In this manuscript, we merely consider the equilibrium point $V_2(1,0,0).$ For another two equilibrium points $V_1(0,0,0),V_3(-1,0,0)$, we can deal with them in a similar way. Here, we omit it. The linear system of (8) around the equilibrium point $V_2(1,0,0)$ is given by

$$\left\{\begin{array}{c}{\displaystyle \frac{d^{\rho }{v}_1\left(t\right)}{d{t}^{\rho }}=-\delta v_1\left(t\right)+v_2\left(t\right)+\delta v_1(t-\theta ),}\hfill \\ {\displaystyle \frac{d^{\rho }{v}_2\left(t\right)}{d{t}^{\rho }}=v_3\left(t\right),}\hfill \\ {\displaystyle \frac{d^{\rho }{v}_3\left(t\right)}{d{t}^{\rho }}=-2b{v}_1\left(t\right)-v_2\left(t\right)-a{v}_3\left(t\right).}\hfill \end{array}\right.$$

(9)

The characteristic equation of (9) can be expressed as

$$det\left[\begin{array}{ccc}{s}^{\rho }+\delta -\delta e^{-s\theta }& -1& 0\\ 0& s^{\rho }& -1\\ 2b& 1& s^{\rho }+a\end{array}\right]=0.$$

(10)

Then

$${\mathcal{U}}_1\left(s\right)+{\mathcal{U}}_2\left(s\right)e^{-s\theta }=0,$$

(11)

where

$$\left\{\begin{array}{c}{\displaystyle {\mathcal{U}}_1\left(s\right)=s^{3\rho }+a_1{s}^{2\rho }+a_2{s}^{\rho }+a_3,}\hfill \\ {\displaystyle {\mathcal{U}}_2\left(s\right)=a_4{s}^{2\rho }+a_5{s}^{\rho }+a_4,}\hfill \end{array}\right.$$

(12)

where

$$\left\{\begin{array}{c}{\displaystyle a_1=a+\delta ,}\hfill \\ {\displaystyle a_2=a\delta +1,}\hfill \\ {\displaystyle a_3=2b+\delta ,}\hfill \\ {\displaystyle a_4=-\delta ,}\hfill \\ {\displaystyle a_5=-a\delta .}\hfill \end{array}\right.$$

(13)

Assume that $\theta =0,$ then (11) has the following form:

$${\lambda }^3+(a_1+a_4){\lambda }^2+(a_2+a_5)\lambda +a_3+a_4=0.$$

(14)

Assume that

$$\left({\mathcal{H}}_1\right)\left\{\begin{array}{c}{\displaystyle a_1+a_4>0,}\hfill \\ {\displaystyle (a_1+a_4)(a_2+a_5)>a_3+a_4,}\hfill \\ {\displaystyle (a_3+a_4)[(a_1+a_4)(a_2+a_5)-(a_3+a_4)]>0}\hfill \end{array}\right.$$

is fulfilled, then all the roots ${\lambda }_1,{\lambda }_2,{\lambda }_3$ of Equation (14) satisfy $|\arg \left({\lambda }_1\right)|>\frac{\rho \pi }{2}$, $|\arg \left({\lambda }_2\right)|>\frac{\rho \pi }{2}$ and $|\arg \left({\lambda }_3\right)|>\frac{\rho \pi }{2}$. Using Lemma 1, one can easily know that the equilibrium point $V_2(1,0,0)$ of model (8) is locally asymptotically stable when $\theta =0$.

Suppose that $s=i\varphi =\varphi \left(cos\frac{\pi }{2}+isin\frac{\pi }{2}\right)$ is the root of Equation (11). Then, (11) becomes

$$\begin{array}{ccc}& & {\varphi }^{3\rho }\left(cos\frac{3\rho \pi }{2}+isin\frac{3\rho \pi }{2}\right)+a_1{\varphi }^{2\rho }(cos\rho \pi +isin\rho \pi )+a_2{\varphi }^{\rho }\left(cos\frac{\rho \pi }{2}+isin\frac{\rho \pi }{2}\right)\hfill \\ & & +a_3+\left[a_4{\varphi }^{2\rho }(cos\rho \pi +isin\rho \pi )+a_5{\varphi }^{\rho }\left(cos\frac{\rho \pi }{2}+isin\frac{\rho \pi }{2}\right)+a_4\right]e^{-i\varphi \theta }=0,\hfill \end{array}$$

(15)

which leads to

$$\left\{\begin{array}{c}{\displaystyle {\mathcal{Q}}_{1}cos\varphi \theta +{\mathcal{Q}}_{2}sin\varphi \theta ={\mathcal{S}}_1,}\hfill \\ {\displaystyle {\mathcal{Q}}_{2}cos\varphi \theta -{\mathcal{Q}}_{1}sin\varphi \theta ={\mathcal{S}}_2,}\hfill \end{array}\right.$$

(16)

where

$$\left\{\begin{array}{c}{\displaystyle {\mathcal{Q}}_1={\sigma }_1{\varphi }^{2\rho }+{\sigma }_2{\varphi }^{\rho }+{\sigma }_3,}\hfill \\ {\displaystyle {\mathcal{Q}}_2={\sigma }_4{\varphi }^{2\rho }+{\sigma }_5{\varphi }^{\rho },}\hfill \\ {\displaystyle {\mathcal{S}}_1={\sigma }_6{\varphi }^{3\rho }+{\sigma }_7{\varphi }^{2\rho }+{\sigma }_8{\varphi }^{\rho }+{\sigma }_9,}\hfill \\ {\displaystyle {\mathcal{S}}_2={\sigma }_{10}{\varphi }^{3\rho }+{\sigma }_{11}{\varphi }^{2\rho }+{\sigma }_{12}{\varphi }^{\rho },}\hfill \end{array}\right.$$

(17)

where

$$\left\{\begin{array}{c}{\displaystyle {\sigma }_1=a_{4}cos\rho \pi ,}\hfill \\ {\displaystyle {\sigma }_2=a_{5}cos\frac{\rho \pi }{2},}\hfill \\ {\displaystyle {\sigma }_3=a_4,}\hfill \\ {\displaystyle {\sigma }_4=a_{4}sin\rho \pi ,}\hfill \\ {\displaystyle {\sigma }_5=a_{5}sin\frac{\rho \pi }{2},}\hfill \\ {\displaystyle {\sigma }_6=-cos\frac{3\rho \pi }{2},}\hfill \\ {\displaystyle {\sigma }_7=-a_{1}cos\rho \pi ,}\hfill \\ {\displaystyle {\sigma }_8=-a_{2}cos\frac{2\rho \pi }{2},}\hfill \\ {\displaystyle {\sigma }_9=-a_3,}\hfill \\ {\displaystyle {\sigma }_{10}=-sin\frac{3\rho \pi }{2},}\hfill \\ {\displaystyle {\sigma }_{11}=-a_{1}sin\rho \pi ,}\hfill \\ {\displaystyle {\sigma }_{12}=-a_{2}sin\frac{2\rho \pi }{2}.}\hfill \end{array}\right.$$

(18)

Making use of (16), one derives

$$cos\varphi \theta =\frac{{\mathcal{S}}_1{\mathcal{Q}}_1+{\mathcal{S}}_2{\mathcal{Q}}_2}{{\mathcal{Q}}_1^2+{\mathcal{Q}}_2^2}$$

(19)

and

$${\mathcal{Q}}_1^2+{\mathcal{Q}}_2^2={\mathcal{S}}_1^2+{\mathcal{S}}_2^2.$$

(20)

By (20), one has

$${\kappa }_1{\varphi }^{6\rho }+{\kappa }_2{\varphi }^{5\rho }+{\kappa }_3{\varphi }^{4\rho }+{\kappa }_4{\varphi }^{3\rho }+{\kappa }_5{\varphi }^{2\rho }+{\kappa }_6{\varphi }^{\rho }+{\kappa }_7=0,$$

(21)

where

$$\left\{\begin{array}{c}{\displaystyle {\kappa }_1={\sigma }_6^2+{\sigma }_{10}^2,}\hfill \\ {\displaystyle {\kappa }_2=2({\sigma }_6{\sigma }_7+{\sigma }_{10}{\sigma }_{11}),}\hfill \\ {\displaystyle {\kappa }_3={\sigma }_7^2+{\sigma }_{11}^2-{\sigma }_1^2-{\sigma }_4^2+2({\sigma }_6{\sigma }_8+{\sigma }_{10}{\sigma }_{12}),}\hfill \\ {\displaystyle {\kappa }_4=2({\sigma }_6{\sigma }_9+{\sigma }_7{\sigma }_8+{\sigma }_{11}{\sigma }_{12}-{\sigma }_1{\sigma }_2+{\sigma }_4{\sigma }_5),}\hfill \\ {\displaystyle {\kappa }_5={\sigma }_8^2+{\sigma }_{12}^2-{\sigma }_2^2-{\sigma }_5^2+2({\sigma }_7{\sigma }_9-{\sigma }_1{\sigma }_3),}\hfill \\ {\displaystyle {\kappa }_6=2({\sigma }_8{\sigma }_9-{\sigma }_2{\sigma }_3),}\hfill \\ {\displaystyle {\kappa }_7={\sigma }_9^2-{\sigma }_3^2.}\hfill \end{array}\right.$$

(22)

Denote

$$\mathsf{\Xi }\left(\varphi \right)={\kappa }_1{\varphi }^{6\rho }+{\kappa }_2{\varphi }^{5\rho }+{\kappa }_3{\varphi }^{4\rho }+{\kappa }_4{\varphi }^{3\rho }+{\kappa }_5{\varphi }^{2\rho }+{\kappa }_6{\varphi }^{\rho }+{\kappa }_7.$$

(23)

If

$$\left({\mathcal{A}}_2\right)|{\sigma }_9|<|{\sigma }_3|$$

is fulfilled, notice that ${lim}_{\varphi \to +\infty }\mathsf{\Xi }\left(\varphi \right)=+\infty$, then Equation (21) owns at least one positive real root. Thus, Equation (11) owns at least one pair of purely roots. In view of Sun et al. [44], the following assertion can be built.

Lemma 2.

(1) Suppose that ${\kappa }_k>0(k=1,2,\cdots ,7)$, then Equation (11) owns no root with zero real parts for $\theta \ge 0$. (2) Suppose that $\left({\mathcal{A}}_2\right)$ is satisfied and ${\kappa }_k>0(k=1,2,\cdots ,6)$, then Equation (11) owns a pair of purely imaginary roots $\pm i{\varphi }_0$ if $\theta ={\theta }_0^{\left(j\right)}(j=1,2,\cdots ,)$ where

$${\theta }_0^{\left(j\right)}=\frac{1}{{\varphi }_0}\left[arccos\left(\frac{{\mathcal{S}}_1{\mathcal{Q}}_1+{\mathcal{S}}_2{\mathcal{Q}}_2}{{\mathcal{Q}}_1^2+{\mathcal{Q}}_2^2}\right)+2j\pi \right],$$

(24)

where $j=0,1,2,\cdots ,$ and ${\varphi }_0>0$ denotes the unique zero of $\mathsf{\Xi }\left(\varphi \right).$

Let ${\theta }_0={\theta }_0^{\left(0\right)}$. Assume that

$$\left({\mathcal{A}}_3\right){\mathcal{C}}_{1R}{\mathcal{C}}_{2R}+{\mathcal{C}}_{1I}{\mathcal{C}}_{2I}>0,$$

where

$$\left\{\begin{array}{c}{\displaystyle {\mathcal{C}}_{1R}=3\rho {\varphi }_0^{2\rho -1}cos\frac{(2\rho -1)\pi }{2}+2\rho a_1{\varphi }_0^{2\rho -1}cos\frac{(2\rho -1)\pi }{2}}\hfill \\ {\displaystyle +\rho a_2{\varphi }_0^{\rho -1}cos\frac{(\rho -1)\pi }{2}+\left[2\rho a_4{\varphi }_0^{2\rho -1}cos\frac{(2\rho -1)\pi }{2}\right.}\hfill \\ {\displaystyle \left.+\rho a_{5}cos\frac{(\rho -1)\pi }{2}\right]cos{\varphi }_0{\theta }_0+\left[2\rho a_4{\varphi }_0^{2\rho -1}sin\frac{(2\rho -1)\pi }{2}\right.}\hfill \\ {\displaystyle \left.+\rho a_{5}sin\frac{(\rho -1)\pi }{2}\right]sin{\varphi }_0{\theta }_0,}\hfill \\ {\displaystyle {\mathcal{C}}_{1I}=3\rho {\varphi }_0^{2\rho -1}sin\frac{(2\rho -1)\pi }{2}+2\rho a_1{\varphi }_0^{2\rho -1}sin\frac{(2\rho -1)\pi }{2}}\hfill \\ {\displaystyle +\rho a_2{\varphi }_0^{\rho -1}sin\frac{(\rho -1)\pi }{2}-\left[2\rho a_4{\varphi }_0^{2\rho -1}cos\frac{(2\rho -1)\pi }{2}\right.}\hfill \\ {\displaystyle \left.+\rho a_{5}cos\frac{(\rho -1)\pi }{2}\right]sin{\varphi }_0{\theta }_0+\left[2\rho a_4{\varphi }_0^{2\rho -1}sin\frac{(2\rho -1)\pi }{2}\right.}\hfill \\ {\displaystyle \left.+\rho a_{5}sin\frac{(\rho -1)\pi }{2}\right]cos{\varphi }_0{\theta }_0,}\hfill \\ {\displaystyle {\mathcal{C}}_{2R}=\left(a_4{\varphi }_0^{2\rho }cos\rho \pi +a_{5}cos\frac{\rho \pi }{2}+a_5\right){\varphi }_{0}sin{\varphi }_0{\theta }_0}\hfill \\ {\displaystyle -\left(a_4{\varphi }_0^{2\rho }sin\rho \pi +a_{5}sin\frac{\rho \pi }{2}\right){\varphi }_{0}cos{\varphi }_0{\theta }_0,}\hfill \\ {\displaystyle {\mathcal{C}}_{2I}=\left(a_4{\varphi }_0^{2\rho }cos\rho \pi +a_{5}cos\frac{\rho \pi }{2}+a_5\right){\varphi }_{0}cos{\varphi }_0{\theta }_0}\hfill \\ {\displaystyle +\left(a_4{\varphi }_0^{2\rho }sin\rho \pi +a_{5}sin\frac{\rho \pi }{2}\right){\varphi }_{0}sin{\varphi }_0{\theta }_0.}\hfill \end{array}\right.$$

(25)

Lemma 3.

Let $s\left(\theta \right)={ϵ}_1\left(\theta \right)+i{ϵ}_2\left(\theta \right)$ be the root of (11) at $\theta ={\theta }_0$ obeying ${ϵ}_1\left({\theta }_0\right)=0,$${ϵ}_2\left({\theta }_0\right)={\varphi }_0$, then $Re\left(\frac{ds}{d\theta }\right){|}_{\theta ={\theta }_0,\varphi ={\varphi }_0}>0.$

Proof. 

Applying (11), one obtains

$${\left(\frac{ds}{d\theta }\right)}^{-1}=\frac{{\mathcal{C}}_1\left(s\right)}{{\mathcal{C}}_2\left(s\right)}-\frac{\theta }{s},$$

(26)

where

$$\left\{\begin{array}{c}{\displaystyle {\mathcal{C}}_1\left(s\right)=3\rho s^{3\rho -1}+2\rho a_1{s}^{2\rho -1}+\rho a_2{s}^{\rho -1}+(2\rho a_4{s}^{2\rho -1}+\rho a_5{s}^{\rho -1})e^{-s\theta },}\hfill \\ {\displaystyle {\mathcal{C}}_2\left(s\right)=s{e}^{-s\theta }\left(a_4{s}^{2\rho }+a_5{s}^{\rho }+a_4\right).}\hfill \end{array}\right.$$

(27)

Using (26), one obtains

$$\mathsf{Re}\mathsf{e}{\left[{\left(\frac{ds}{d\vartheta }\right)}^{-1}\right]}_{\theta ={\theta }_0,\varphi ={\varphi }_0}=\mathrm{Re}{\left[\frac{{\mathcal{C}}_1\left(s\right)}{{\mathcal{C}}_2\left(s\right)}\right]}_{\theta ={\theta }_0,\varphi ={\varphi }_0}=\frac{{\mathcal{C}}_{1R}{\mathcal{C}}_{2R}+{\mathcal{C}}_{1I}{\mathcal{C}}_{2I}}{{\mathcal{C}}_{2R}^2+{\mathcal{C}}_{2I}^2}.$$

(28)

Applying $\left({\mathcal{A}}_3\right)$, one derives

$$\mathrm{Re}{\left[{\left(\frac{ds}{d\theta }\right)}^{-1}\right]}_{\theta ={\theta }_0,\varphi ={\varphi }_0}>0.$$

The proof finishes. □

Making use of Lemma 1, the following assertion is easily built.

Theorem 1.

Assume that $\left({\mathcal{A}}_1\right)$–$\left({\mathcal{A}}_3\right)$ are fulfilled, then the equilibrium point $V_2(1,0,0)$ of model (8) is locally asymptotically stable if θ falls into the interval $[0,{\theta }_0)$ and model (8) generates a Hopf bifurcation near the equilibrium point $V_2(1,0,0)$ when $\theta ={\theta }_0.$

Remark 1.

Of course, we can add the delayed feedback controller to the second or third equation of model (3). Whether this control method is feasible or not requires similar analysis as Section 3.

4. Chaos Suppression via Delayed Mixed Controller

In this part, we will apply a suitable delayed mixed controller which includes state feedback and parameter perturbation to control the chaos of the fractional-order modificatory hybrid optical model (6). Following the idea of [45,46], we obtain the following fractional-order controlled modificatory hybrid optical model

$$\left\{\begin{array}{c}{\displaystyle \frac{d^{\rho }{v}_1\left(t\right)}{d{t}^{\rho }}=v_2\left(t\right),}\hfill \\ {\displaystyle \frac{d^{\rho }{v}_2\left(t\right)}{d{t}^{\rho }}=v_3\left(t\right),}\hfill \\ {\displaystyle \frac{d^{\rho }{v}_3\left(t\right)}{d{t}^{\rho }}={\alpha }_1[-a{v}_3\left(t\right)-v_2\left(t\right)-b{v}_1\left(t\right)(1-v_1^2\left(t\right))]+{\alpha }_2[v_3(t-\theta )-v_3\left(t\right)],}\hfill \end{array}\right.$$

(29)

where ${\alpha }_1,{\alpha }_2$ are feedback gain parameters. Clearly, model (29) has the same equilibrium points as those in model (6). In this manuscript, we merely consider the equilibrium point $V_2(1,0,0).$ For another two equilibrium points $V_1(0,0,0),V_3(-1,0,0)$, we can deal with them in a similar way. Here, we omit it. The linear system of (29) near the equilibrium point $V_2(1,0,0)$ reads

$$\left\{\begin{array}{c}{\displaystyle \frac{d^{\rho }{v}_1\left(t\right)}{d{t}^{\rho }}=v_2\left(t\right),}\hfill \\ {\displaystyle \frac{d^{\rho }{v}_2\left(t\right)}{d{t}^{\rho }}=v_3\left(t\right),}\hfill \\ {\displaystyle \frac{d^{\rho }{v}_3\left(t\right)}{d{t}^{\rho }}=-2b{\alpha }_1{v}_1\left(t\right)-{\alpha }_1{v}_2\left(t\right)-({\alpha }_{1}a+{\alpha }_2)v_3\left(t\right)+{\alpha }_2{v}_3(t-\theta ).}\hfill \end{array}\right.$$

(30)

The characteristic equation of (30) takes the following form:

$$det\left[\begin{array}{ccc}{s}^{\rho }& -1& 0\\ 0& s^{\rho }& -1\\ 2b{\alpha }_1& {\alpha }_1& s^{\rho }+({\alpha }_{1}a+{\alpha }_2)-{\alpha }_2{e}^{-s\theta }\end{array}\right]=0.$$

(31)

Then

$${\mathcal{V}}_1\left(s\right)+{\mathcal{V}}_2\left(s\right)e^{-s\theta }=0,$$

(32)

where

$$\left\{\begin{array}{c}{\displaystyle {\mathcal{V}}_1\left(s\right)=s^{3\rho }+b_1{s}^{2\rho }+b_2{s}^{\rho }+b_3,}\hfill \\ {\displaystyle {\mathcal{V}}_2\left(s\right)=b_4{s}^{2\rho }.}\hfill \end{array}\right.$$

(33)

where

$$\left\{\begin{array}{c}{\displaystyle b_1=a{\alpha }_1+{\alpha }_2,}\hfill \\ {\displaystyle b_2={\alpha }_1,}\hfill \\ {\displaystyle b_3=2b{\alpha }_1,}\hfill \\ {\displaystyle b_4=-{\alpha }_2.}\hfill \end{array}\right.$$

(34)

If $\theta =0,$ then (32) becomes

$${\lambda }^3+(b_1+b_4){\lambda }^2+b_2\lambda +b_3=0.$$

(35)

If

$$\left({\mathcal{A}}_4\right)\left\{\begin{array}{c}{\displaystyle b_1+b_4>0,}\hfill \\ {\displaystyle (b_1+b_4)b_2>b_3,}\hfill \\ {\displaystyle b_3[(b_1+b_4)b_2-b_3]>0}\hfill \end{array}\right.$$

holds, then all the roots ${\lambda }_1,{\lambda }_2,{\lambda }_3$ of (35) satisfy $|\arg \left({\lambda }_1\right)|>\frac{\rho \pi }{2},\left|\arg \left({\lambda }_2\right)\right|>\frac{\rho \pi }{2}$ and $|\arg \left({\lambda }_3\right)|>\frac{\rho \pi }{2}$. By virtue of Lemma 1, one obtains that the equilibrium point $V_2(1,0,0)$ of model (29) is locally asymptotically stable when $\theta =0$.

Assume that $s=i\phi =\phi \left(cos\frac{\pi }{2}+isin\frac{\pi }{2}\right)$ is the root of Equation (32). Then, (32) becomes

$$\begin{array}{ccc}& & {\phi }^{3\rho }\left(cos\frac{3\rho \pi }{2}+isin\frac{3\rho \pi }{2}\right)+b_1{\phi }^{2\rho }(cos\rho \pi +isin\rho \pi )\hfill \\ & & +b_2{\phi }^{\rho }\left(cos\frac{\rho \pi }{2}+isin\frac{\rho \pi }{2}\right)+b_3+b_4{\phi }^{2\rho }(cos\rho \pi +isin\rho \pi )e^{-i\phi \theta }=0,\hfill \end{array}$$

(36)

which leads to

$$\left\{\begin{array}{c}{\displaystyle {\mathcal{G}}_{1}cos\phi \theta +{\mathcal{G}}_{2}sin\phi \theta ={\mathcal{J}}_1,}\hfill \\ {\displaystyle {\mathcal{G}}_{2}cos\phi \theta -{\mathcal{G}}_{1}sin\phi \theta ={\mathcal{J}}_2,}\hfill \end{array}\right.$$

(37)

where

$$\left\{\begin{array}{c}{\displaystyle {\mathcal{G}}_1=e_1{\phi }^{2\rho },}\hfill \\ {\displaystyle {\mathcal{G}}_2=e_2{\phi }^{2\rho },}\hfill \\ {\displaystyle {\mathcal{J}}_3=e_3{\phi }^{3\rho }+e_4{\phi }^{2\rho }+e_5{\phi }^{\rho }+e_6,}\hfill \\ {\displaystyle {\mathcal{J}}_1=e_7{\phi }^{3\rho }+e_8{\phi }^{2\rho }+e_9{\phi }^{\rho },}\hfill \end{array}\right.$$

(38)

where

$$\left\{\begin{array}{c}{\displaystyle e_1=b_{4}cos\rho \pi ,}\hfill \\ {\displaystyle e_2=b_{4}sin\rho \pi ,}\hfill \\ {\displaystyle e_3=-cos\frac{3\rho \pi }{2},}\hfill \\ {\displaystyle e_4=-b_{1}cos\rho \pi ,}\hfill \\ {\displaystyle e_5=-b_{2}cos\frac{\rho \pi }{2},}\hfill \\ {\displaystyle e_6=-b_3,}\hfill \\ {\displaystyle e_7=-sin\frac{3\rho \pi }{2},}\hfill \\ {\displaystyle e_8=-b_{1}sin\rho \pi ,}\hfill \\ {\displaystyle e_9=-b_{2}sin\frac{\rho \pi }{2}.}\hfill \end{array}\right.$$

(39)

It follows from (37) that

$${\mathcal{G}}_1^2+{\mathcal{G}}_2^2={\mathcal{J}}_1^2+{\mathcal{J}}_2^2,$$

(40)

which leads to

$${\eta }_1{\phi }^{6\rho }+{\eta }_2{\phi }^{5\rho }+{\eta }_3{\phi }^{4\rho }+{\eta }_4{\phi }^{3\rho }+{\eta }_5{\phi }^{2\rho }+{\eta }_6{\phi }^{\rho }+{\eta }_7=0,$$

(41)

where

$$\left\{\begin{array}{c}{\displaystyle {\eta }_1=e_3^2+e_7^2,}\hfill \\ {\displaystyle {\eta }_2=2(e_3{e}_4+e_7{e}_8),}\hfill \\ {\displaystyle {\eta }_3=e_4^2+e_8^2-e_1^2-e_2^2+2(e_3{e}_5+e_7{e}_9),}\hfill \\ {\displaystyle {\eta }_4=2(e_3{e}_6+e_4{e}_5+e_8{e}_9),}\hfill \\ {\displaystyle {\eta }_5=e_5^2+e_9^2+2e_4{e}_6,}\hfill \\ {\displaystyle {\eta }_6=2e_5{e}_6,}\hfill \\ {\displaystyle {\eta }_7=e_6^2.}\hfill \end{array}\right.$$

(42)

We assume that Equation (41) has six roots (say ${\phi }_k,h=1,2,3,4,5,6)$. Then, by

$${\theta }_h^{\left(k\right)}=\frac{1}{{\phi }_h}\left[arccos\left(\frac{{\mathcal{J}}_1{\mathcal{G}}_1+{\mathcal{J}}_2{\mathcal{G}}_2}{{\mathcal{G}}_1^2+{\mathcal{G}}_2^2}\right)+2k\pi \right],$$

(43)

where $k=1,2,\cdots ,h=1,2,3,4,5,6.$ Set ${\theta }_{0ȡ}={min}_{k=1,2,\cdots ,h=1,2,3,4,5,6}\left\{{\theta }_h^{\left(k\right)}\right\}.$ In this case, we assume that Equation (41) has the root ${\phi }_0$.

Next, the following assumption is presented.

$$\left({\mathcal{A}}_5\right){\mathcal{N}}_{1R}{\mathcal{N}}_{2R}+{\mathcal{N}}_{1I}{\mathcal{N}}_{2I}>0,$$

where

$$\left\{\begin{array}{c}{\displaystyle {\mathcal{N}}_{1R}=3\rho {\phi }_0^{2\rho -1}cos\frac{(2\rho -1)\pi }{2}+2\rho b_1{\phi }_0^{2\rho -1}cos\frac{(2\rho -1)\pi }{2}}\hfill \\ {\displaystyle +\rho b_2{\phi }_0^{\rho -1}cos\frac{(\rho -1)\pi }{2}+2\rho b_4{\varphi }_0^{2\rho -1}cos\frac{(2\rho -1)\pi }{2}cos{\phi }_0{\theta }_{0\ast }}\hfill \\ {\displaystyle +2\rho b_4{\varphi }_0^{2\rho -1}sin\frac{(2\rho -1)\pi }{2}sin{\phi }_0{\theta }_{0\ast },}\hfill \\ {\displaystyle {\mathcal{N}}_{1I}=3\rho {\phi }_0^{2\rho -1}sin\frac{(2\rho -1)\pi }{2}+2\rho b_1{\phi }_0^{2\rho -1}sin\frac{(2\rho -1)\pi }{2}}\hfill \\ {\displaystyle +\rho b_2{\phi }_0^{\rho -1}sin\frac{(\rho -1)\pi }{2}-2\rho b_4{\varphi }_0^{2\rho -1}cos\frac{(2\rho -1)\pi }{2}sin{\phi }_0{\theta }_{0\ast }}\hfill \\ {\displaystyle +2\rho b_4{\varphi }_0^{2\rho -1}sin\frac{(2\rho -1)\pi }{2}cos{\phi }_0{\theta }_{0\ast },}\hfill \\ {\displaystyle {\mathcal{N}}_{2R}=b_4{\phi }_0^{2\rho }cos\rho \pi {\phi }_{0}sin{\phi }_0{\theta }_{0\ast }-b_4{\phi }_0^{2\rho }sin\rho \pi {\phi }_{0}cos{\phi }_0{\theta }_{0\ast },}\hfill \\ {\displaystyle {\mathcal{N}}_{2I}=b_4{\phi }_0^{2\rho }cos\rho \pi {\phi }_{0}cos{\phi }_0{\theta }_{0\ast }-b_4{\phi }_0^{2\rho }sin\rho \pi {\phi }_{0}sin{\phi }_0{\theta }_{0\ast }.}\hfill \end{array}\right.$$

(44)

Lemma 4.

Suppose that $s\left(\theta \right)=f_1\left(\theta \right)+i{f}_2\left(\theta \right)$ is the root of (32) at $\theta ={\theta }_{0\ast }$ satisfying $f_1\left({\theta }_{0\ast }\right)=0$, $f_2\left({\theta }_{0\ast }\right)={\theta }_0$, then $Re\left(\frac{ds}{d\theta }\right){|}_{\theta ={\theta }_{0\ast },\phi ={\phi }_0}>0.$

Proof. 

Making use of (32), one derives

$${\left(\frac{ds}{d\theta }\right)}^{-1}=\frac{{\mathcal{N}}_1\left(s\right)}{{\mathcal{N}}_2\left(s\right)}-\frac{\theta }{s},$$

(45)

where

$$\left\{\begin{array}{c}{\displaystyle {\mathcal{N}}_1\left(s\right)=3\rho s^{3\rho -1}+2\rho b_1{s}^{2\rho -1}+\rho b_2{s}^{\rho -1}+2\rho b_4{s}^{2\rho -1}{e}^{-s\theta },}\hfill \\ {\displaystyle {\mathcal{N}}_2\left(s\right)=-s{e}^{-s\theta }{b}_4{s}^{2\rho }.}\hfill \end{array}\right.$$

(46)

Then

$$\mathrm{Re}{\left[{\left(\frac{ds}{d\theta }\right)}^{-1}\right]}_{\theta ={\theta }_{0\ast },\phi ={\phi }_0}=\mathrm{Re}{\left[\frac{{\mathcal{N}}_1\left(s\right)}{{\mathcal{N}}_2\left(s\right)}\right]}_{\theta ={\theta }_{0\ast },\phi ={\phi }_0}=\frac{{\mathcal{N}}_{1R}{\mathcal{N}}_{2R}+{\mathcal{N}}_{1I}{\mathcal{N}}_{2I}}{{\mathcal{N}}_{2R}^2+{\mathcal{N}}_{2I}^2}.$$

(47)

By $\left({\mathcal{A}}_5\right)$, we derive

$$\mathrm{Re}{\left[{\left(\frac{ds}{d\theta }\right)}^{-1}\right]}_{\theta ={\theta }_{0\ast },\phi ={\phi }_0}>0.$$

The proof ends. □

Using Lemma 1, we obtain the following result.

Theorem 2.

Suppose that $\left({\mathcal{A}}_4\right)$ and $\left({\mathcal{A}}_5\right)$ hold, then the equilibrium point $V_2(1,0,0)$ of model (29) is locally asymptotically stable if $\theta \in [0,{\theta }_{0\ast })$ and model (29) generates a Hopf bifurcation around the equilibrium point $V_2(1,0,0)$ when $\theta ={\theta }_{0\ast }.$

Remark 2.

Of course, we can add the delayed mixed controller which includes state feedback and parameter perturbation to the first or second equation of model (3). Whether this control method is feasible or not requires similar analysis as Section 4.

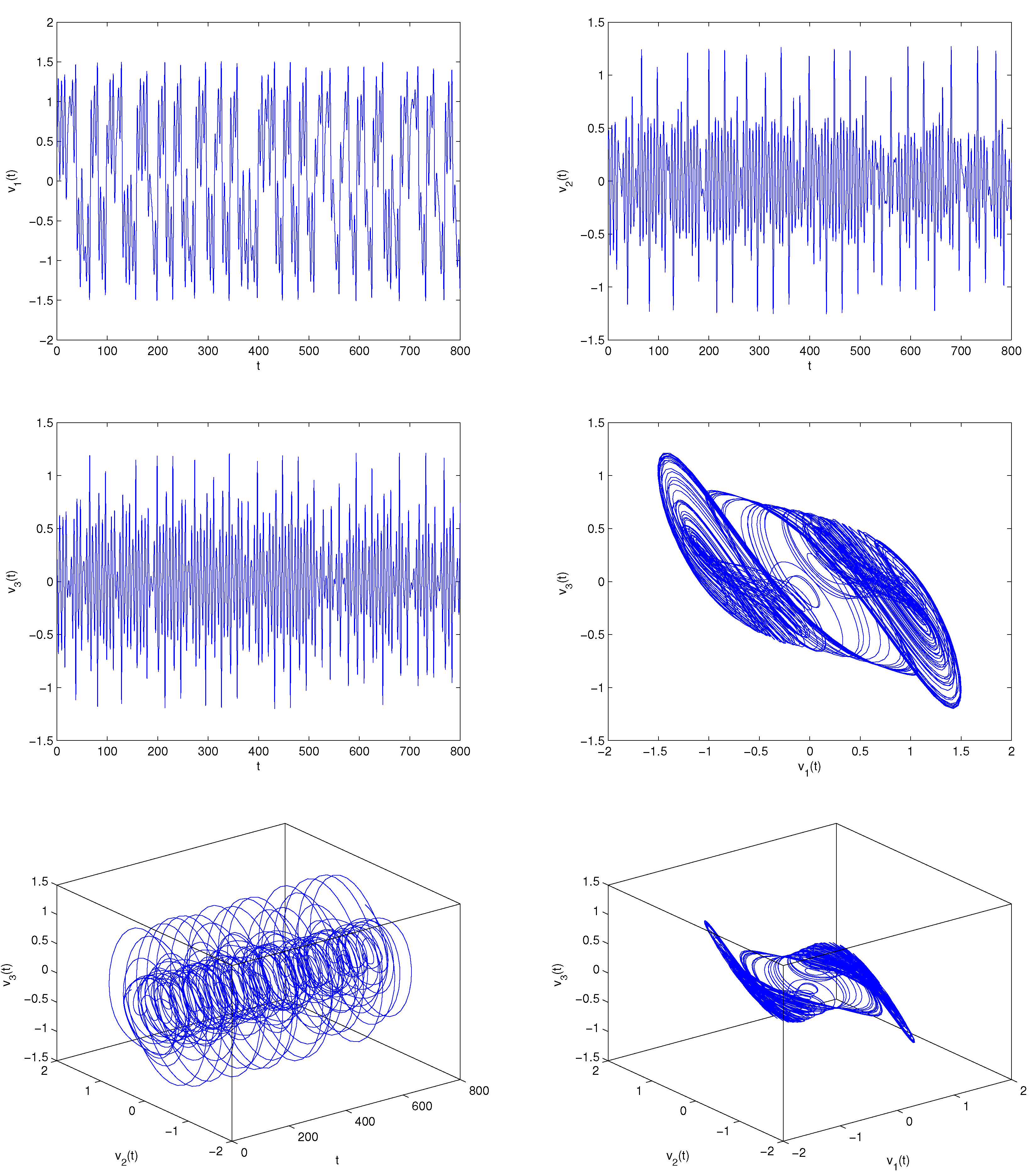
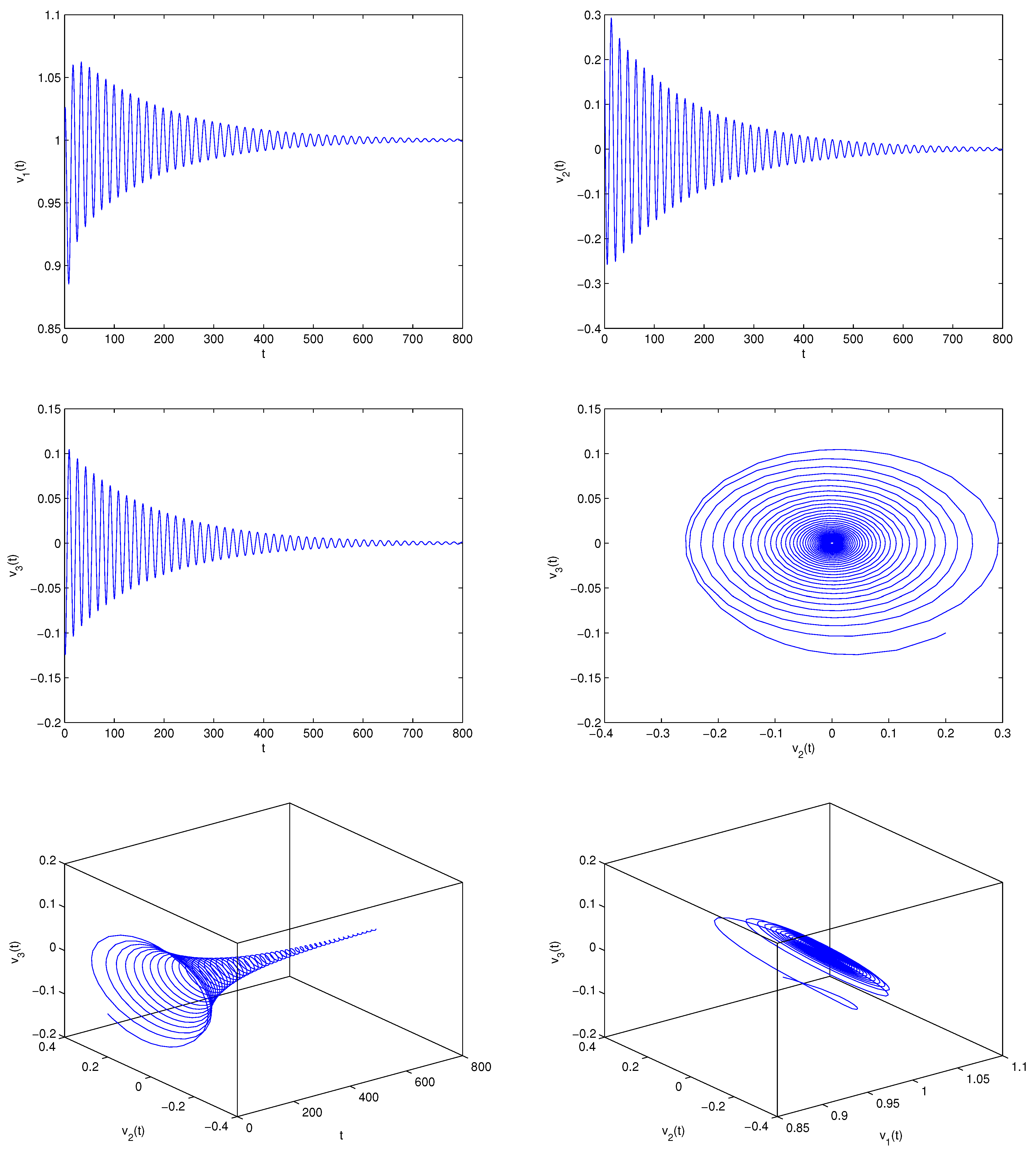
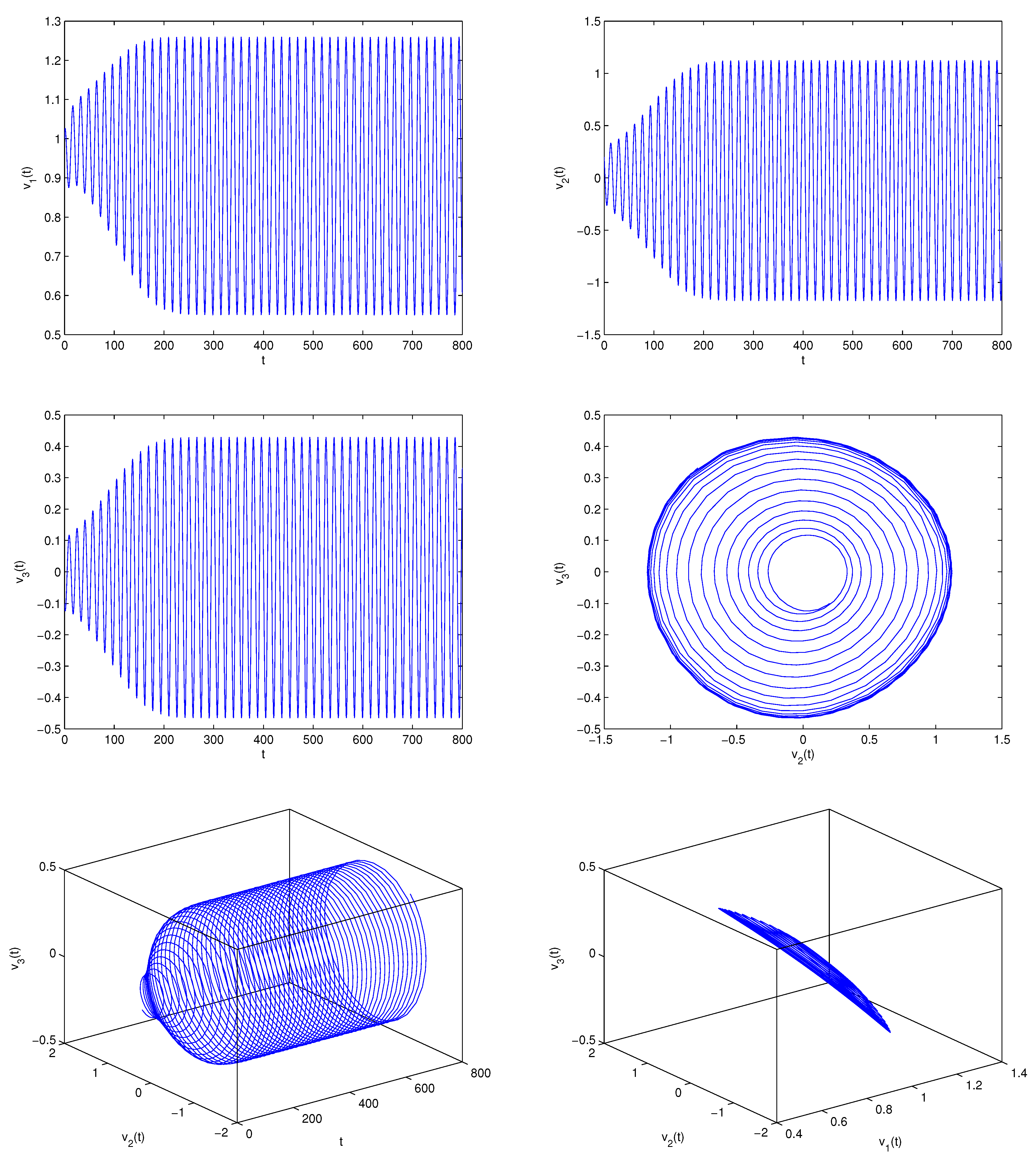
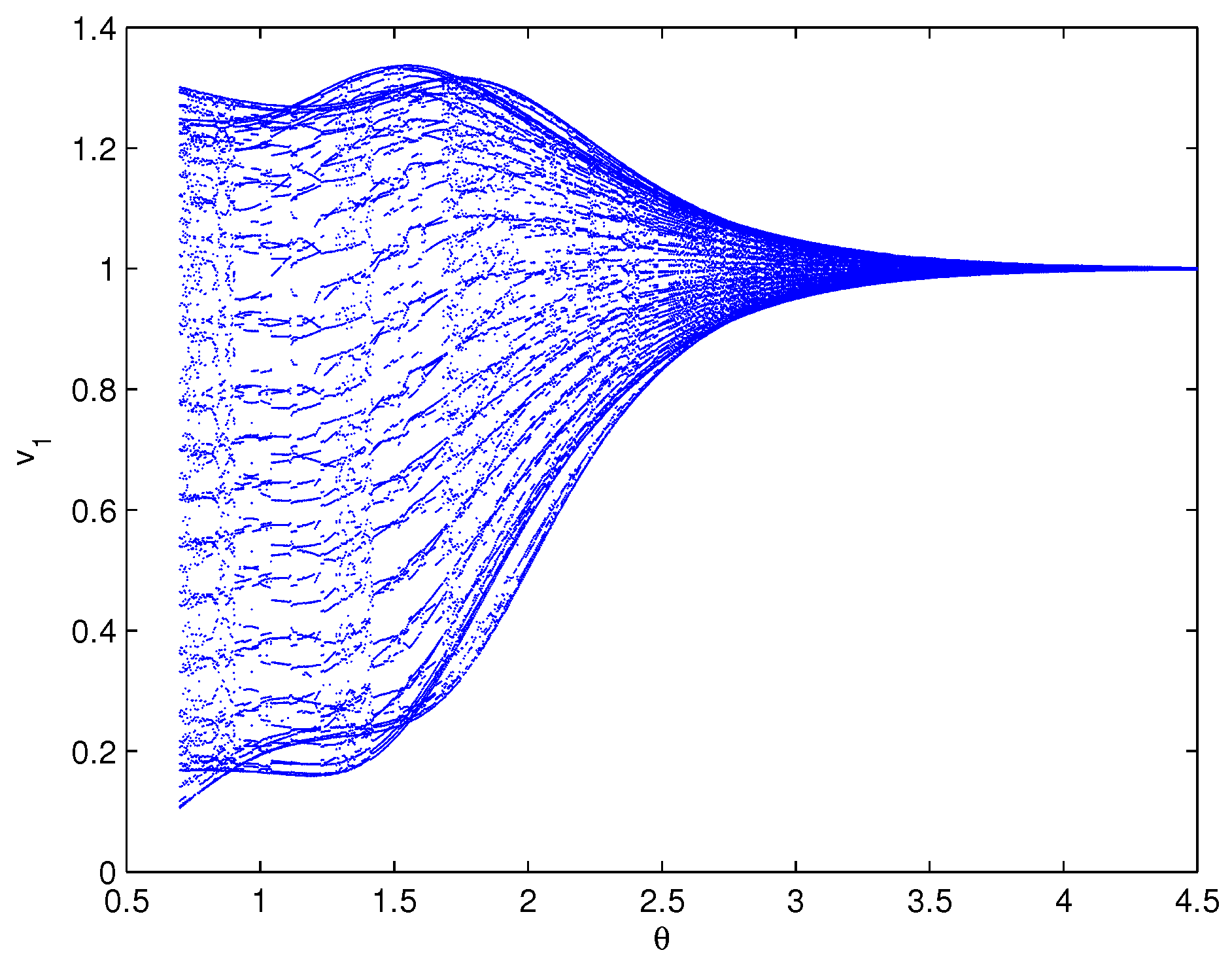
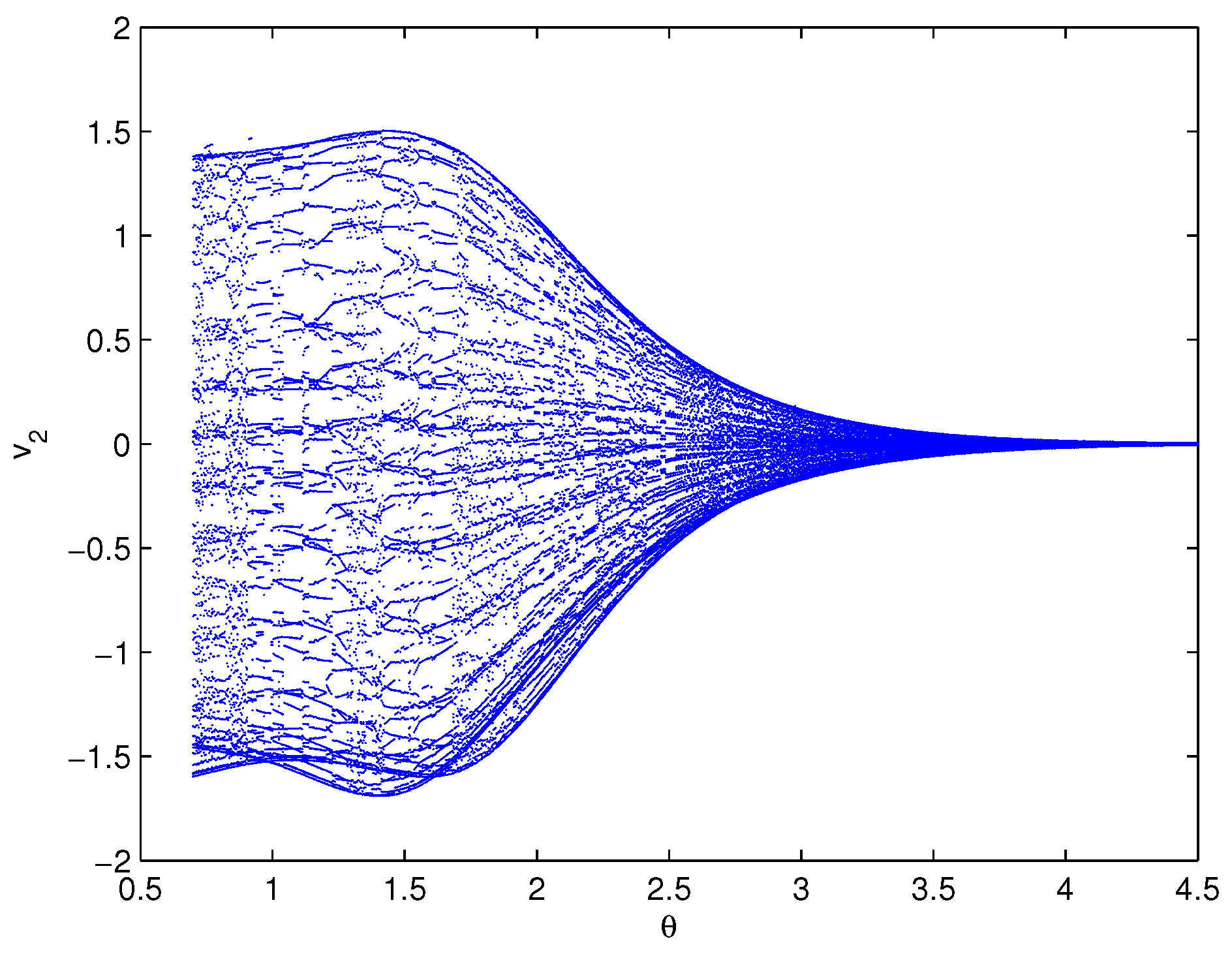
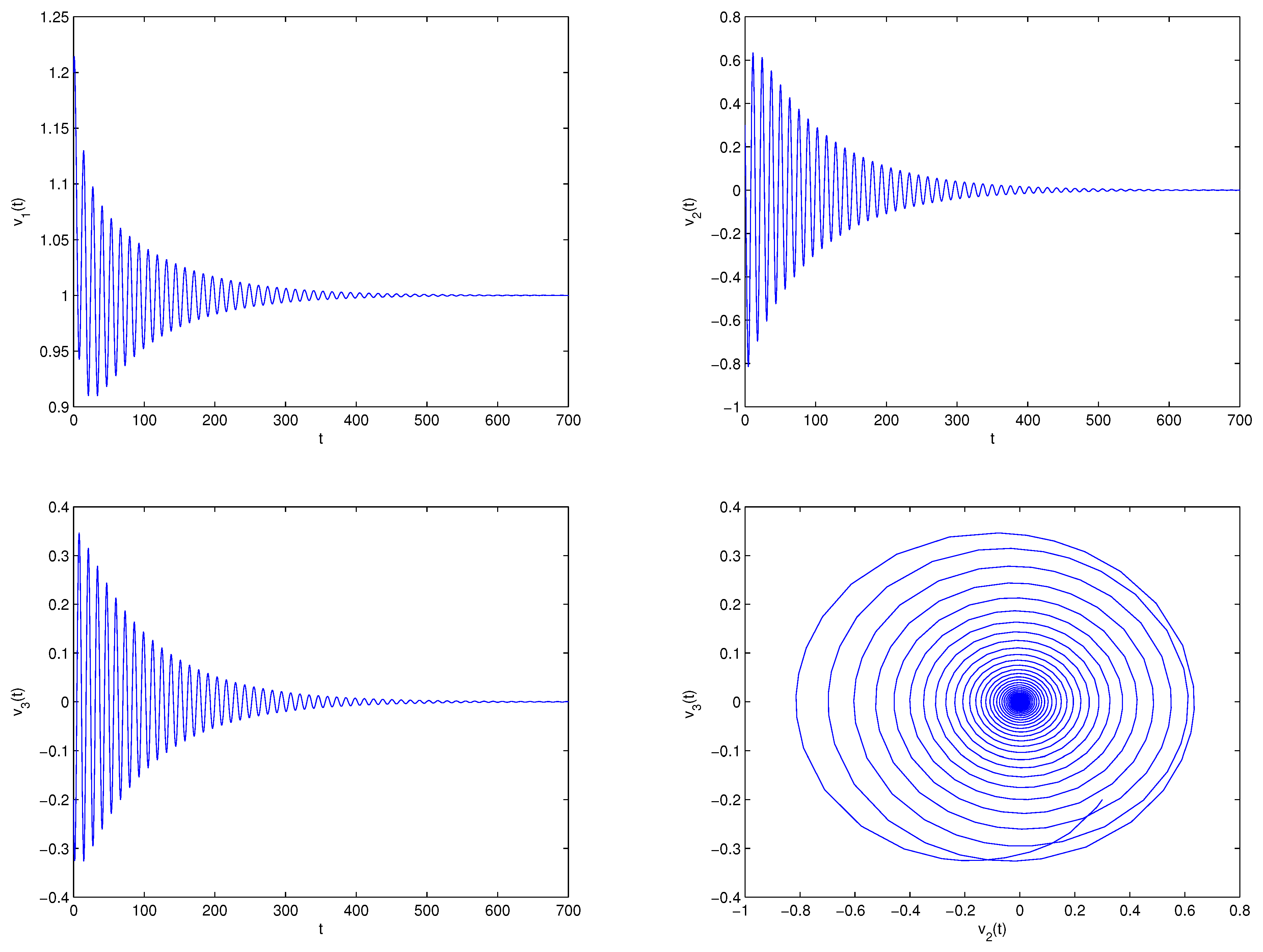
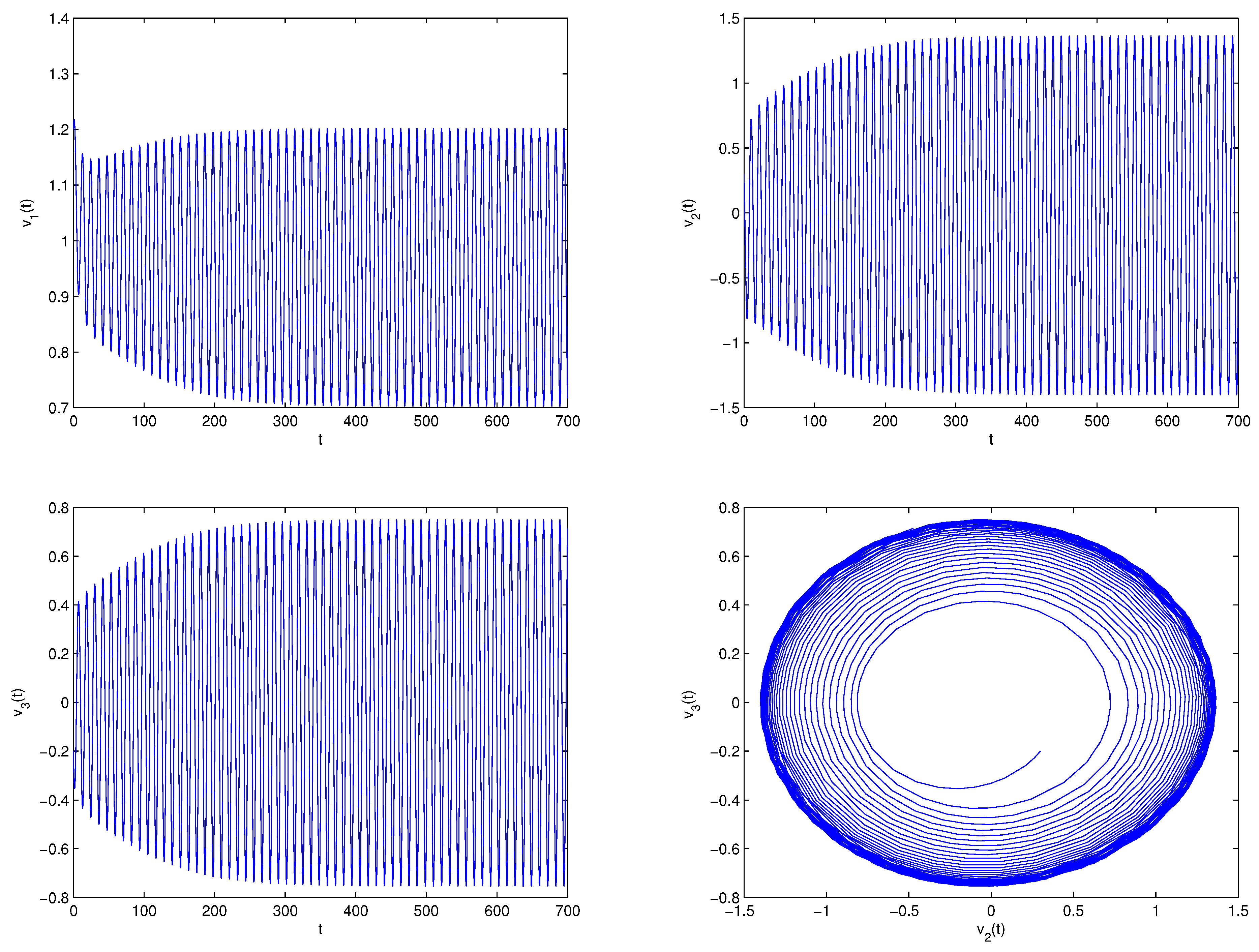
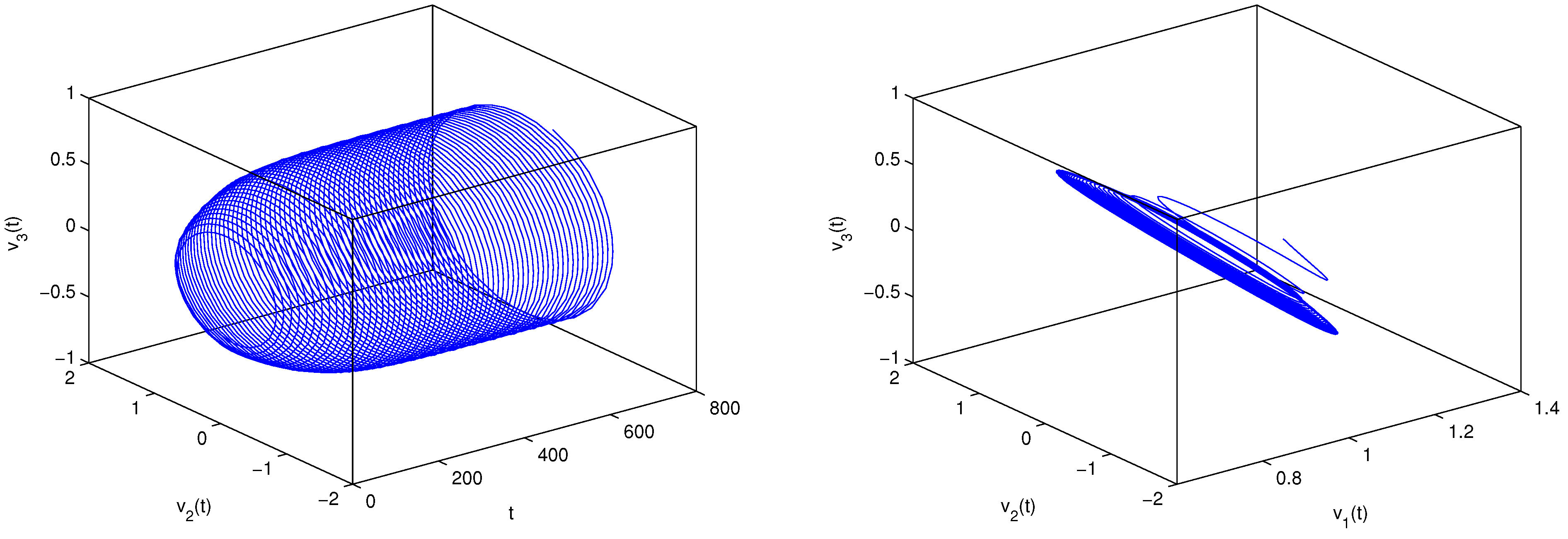
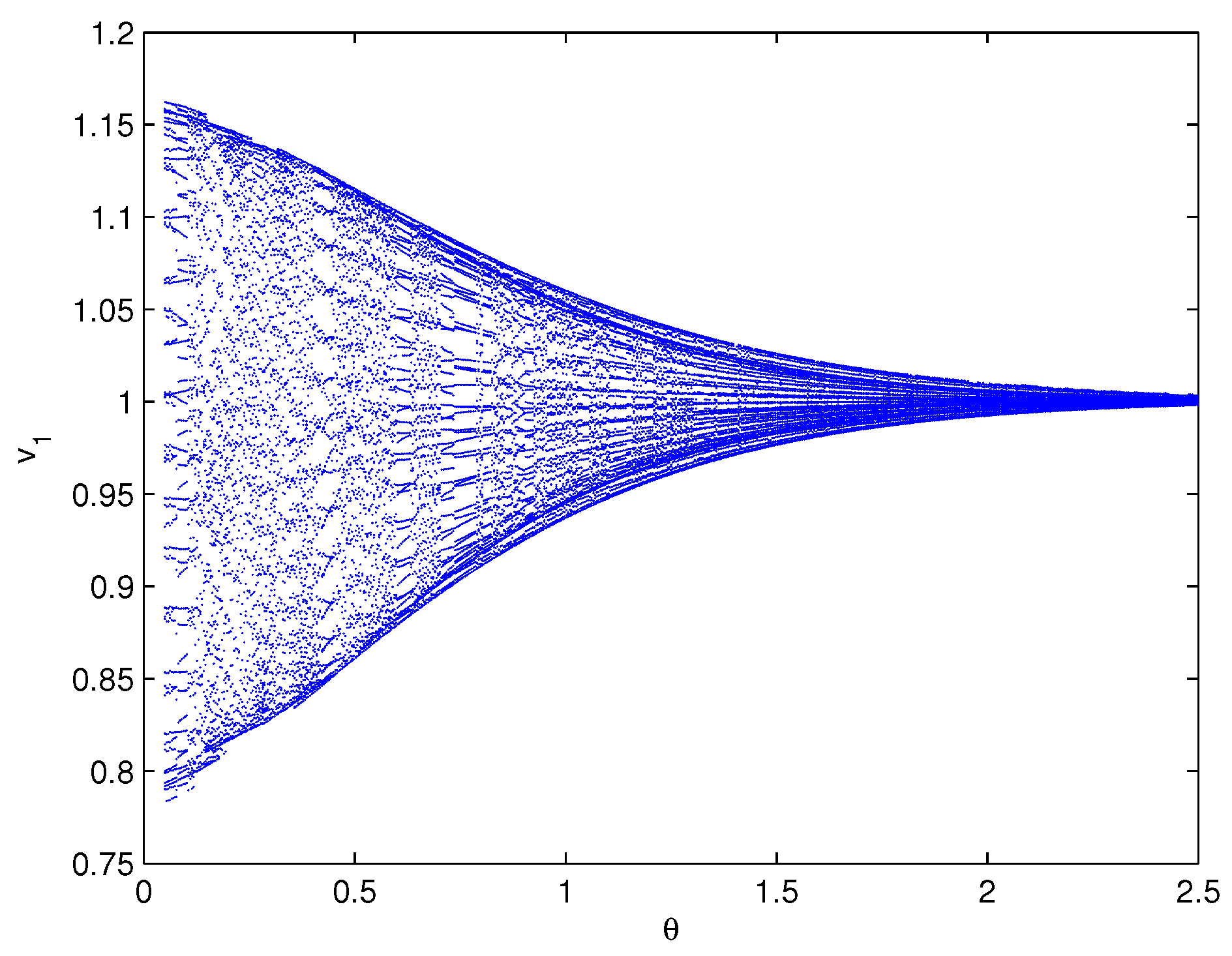
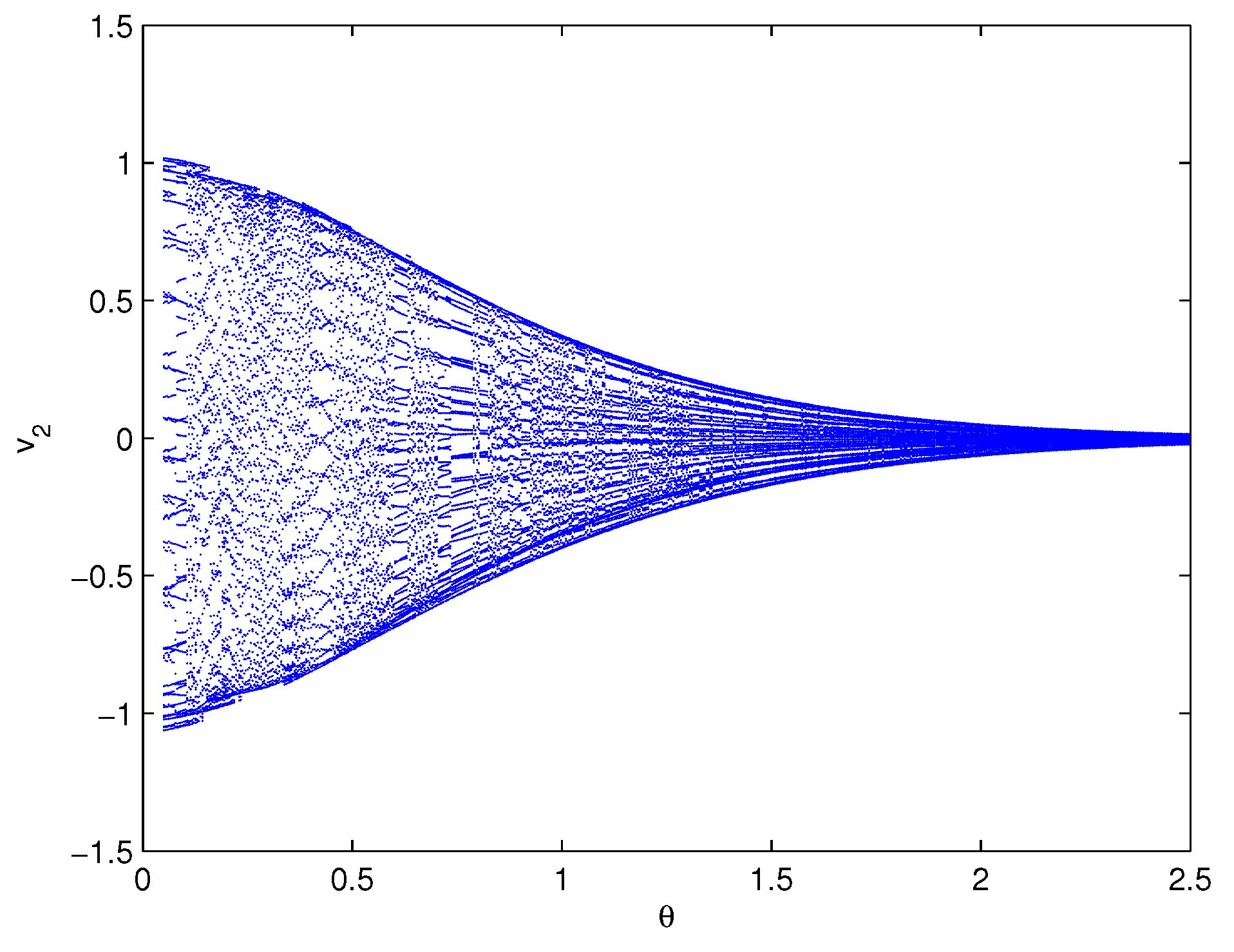
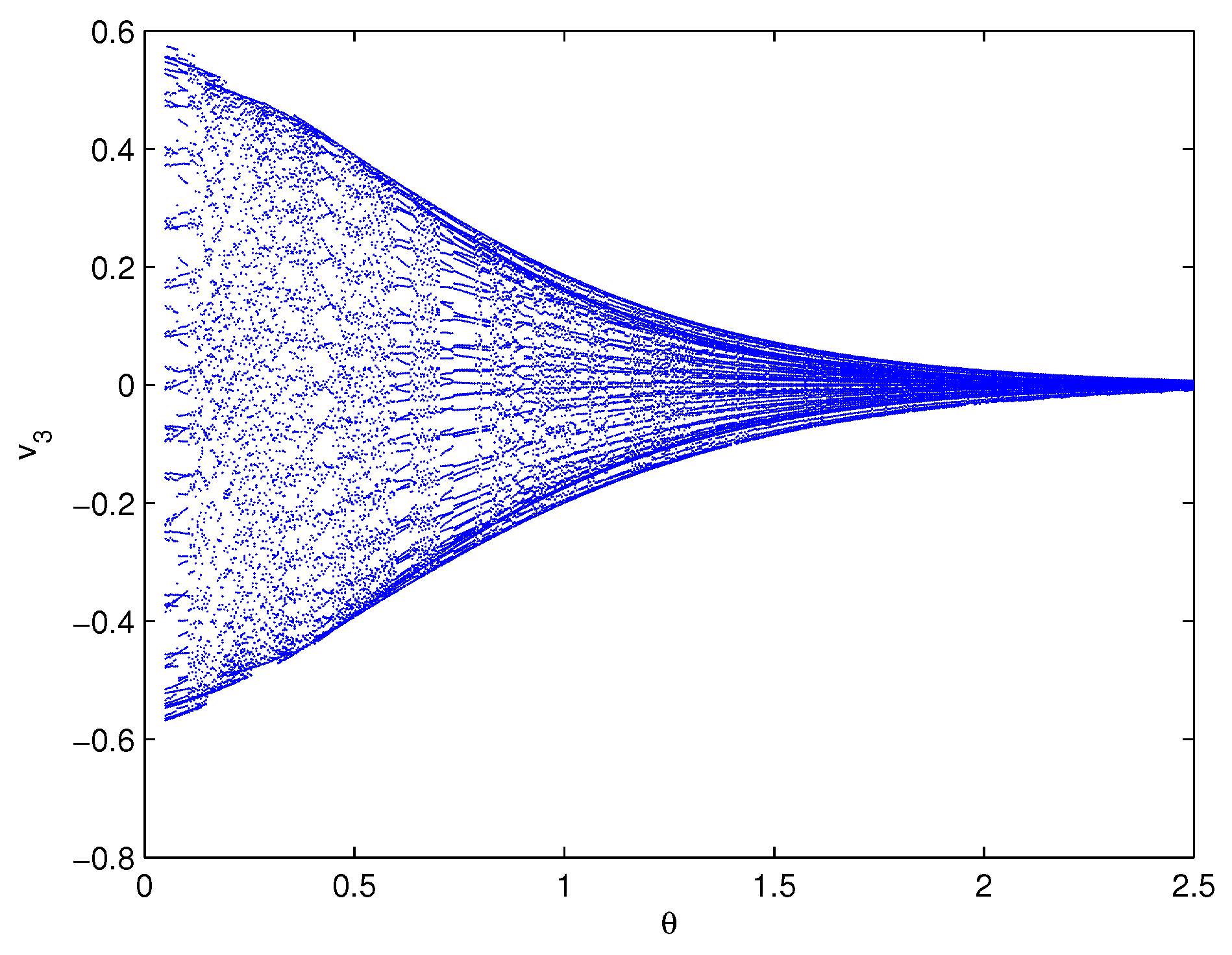
5. Examples

Example 1.

Consider the following fractional-order controlled modificatory hybrid optical model:

$$\left\{\begin{array}{c}{\displaystyle \frac{d^{0.97}{v}_1\left(t\right)}{d{t}^{0.97}}=v_2\left(t\right)+\delta [v_1(t-\theta )-v_1\left(t\right)],}\hfill \\ {\displaystyle \frac{d^{0.97}{v}_2\left(t\right)}{d{t}^{0.97}}=v_3\left(t\right),}\hfill \\ {\displaystyle \frac{d^{0.97}{v}_3\left(t\right)}{d{t}^{0.97}}=-0.94v_3\left(t\right)-v_2\left(t\right)-2v_1\left(t\right)(1-v_1^2\left(t\right)).}\hfill \end{array}\right.$$

(48)

One can easily know that model (48) owns three equilibrium points $V_1(0,0,0),$$V_2(1,0,0),V_3(-1,0,0)$. In this numerical simulation, we only focus on the equilibrium point $V_2(1,0,0).$ Making use of the computer, one can determine ${\varphi }_0=2.0912,{\theta }_0=1.3$. The assumptions $\left({\mathcal{A}}_1\right)$–$\left({\mathcal{A}}_3\right)$ of Theorem 1 hold true. Select $\theta =3.2<{\theta }_0=3.5$, which shows that $\theta$ falls into the interval range $[0,3.5)$. The homologous numerical simulation plots are presented in Figure 2. It follows from Figure 2 that the three state variables $v_1,v_2,v_3$ will get close to $1,0,0$, respectively, as $t\to \infty .$ Select $\theta =3.8>{\theta }_0=3.5$, which indicates that $\theta$ passes through the critical delay value $3.5$. The homologous numerical simulation plots are provided in Figure 3. It follows from Figure 3 that the three state variables $v_1,v_2,v_3$ will maintain a periodic vibratory level near $1,0,0$, respectively, as $t\to \infty .$ Two situations clearly manifest the vanishing of the chaos of fractional-order chaotic modificatory hybrid optical model (6). Additionally, the bifurcation plots are given in Figure 4, Figure 5 and Figure 6 to manifest that the bifurcation value (with respect to the delay $\theta$) of model (48) is about $3.5$. The simulation results powerfully illustrate the scientificity of the designed delayed feedback controller in this manuscript.

Example 2.

Consider the following fractional-order controlled modificatory hybrid optical model:

$$\left\{\begin{array}{c}{\displaystyle \frac{d^{0.97}{v}_1\left(t\right)}{d{t}^{0.97}}=v_2\left(t\right),}\hfill \\ {\displaystyle \frac{d^{0.97}{v}_2\left(t\right)}{d{t}^{0.97}}=v_3\left(t\right),}\hfill \\ {\displaystyle \frac{d^{0.97}{v}_3\left(t\right)}{d{t}^{0.97}}={\alpha }_1[-0.94v_3\left(t\right)-v_2\left(t\right)-2v_1\left(t\right)(1-v_1^2\left(t\right))]+{\alpha }_2[v_3(t-\theta )-v_3\left(t\right)].}\hfill \end{array}\right.$$

(49)

One can easily know that model (49) owns three equilibrium points $V_1(0,0,0),$$V_2(1,0,0),V_3(-1,0,0)$. In this numerical simulation, we only focus on the equilibrium point $V_2(1,0,0).$ Let ${\alpha }_1=0.3,{\alpha }_2=0.3.$ Making use of the computer, one can determine ${\phi }_0=4.2311,{\theta }_{0\ast }=2.1$. The assumptions $\left({\mathcal{A}}_4\right)$ and $\left({\mathcal{A}}_5\right)$ of Theorem 2 hold true. Select $\theta =1.8<{\theta }_{0\ast }=2.1$, which shows that $\theta$ falls into the interval range $[0,2.1)$. The homologous numerical simulation plots are presented in Figure 7. It follows from Figure 7 that the three state variables $v_1,v_2,v_3$ will get close to $1,0,0$, respectively, as $t\to \infty .$ Select $\theta =2.8>{\theta }_{0\ast }=2.1$, which indicates that $\theta$ passes through the critical delay value $2.1$. The homologous numerical simulation plots are provided in Figure 8. It follows from Figure 8 that the three state variables $v_1,v_2,v_3$ will maintain a periodic vibratory level near $1,0,0$, respectively, as $t\to \infty .$ Two situations clearly manifest the vanishing of the chaos of fractional-order chaotic modificatory hybrid optical model (6). Additionally, the bifurcation plots are given in Figure 9, Figure 10 and Figure 11 to manifest that the bifurcation value (with respect to the delay $\theta$) of model (49) is about $2.1$. The simulation results powerfully illustrate the scientificity of the designed mixed controller in this manuscript.

Remark 3.

It follows from the computer simulation results of Examples 1 and 2, one can easily know that the stability domain of fractional-order controlled modificatory hybrid optical model (48) is enlarged and the time of occurrence of Hopf bifurcation of model (48) is postponed. (In controlled model (48), ${\theta }_0=3.5$, but in controlled model (49), ${\theta }_{0\ast }=2.1$).

6. Conclusions

For a long time, chaos suppression, which is an old and classic topic, has attracted great attention from many scholars in engineering circles. During the past several decades, plenty of chaos control techniques were proposed and very rich results have been achieved. In this present manuscript, we deal with the chaos suppression of a (FOMHO model) by virtue of two different control controllers. Taking advantage of an apposite delayed feedback controller, we effectively suppress the chaos of the (FOMHO model). A sufficient condition ensuring the stability and occurrence of Hopf bifurcation of the fractional-order controlled modificatory hybrid optical model is set up. By virtue of a proper delayed mixed controller that consists of state feedback and parameter perturbation, we successfully eliminate the chaotic behavior of the (FOMHO model). A sufficient condition which guarantees the stability and occurrence of Hopf bifurcation of the fractional-order controlled modificatory hybrid optical model is built. The exploration shows that the delay in the two controllers has a vital effect on the chaotic behavior. The acquired results of this manuscript are perfectly new, and the exploration idea of this manuscript can also be utilized to inquire into numerous chaos control aspects of fractional-order dynamical models in plentiful fields.