The Hausdorff Dimension and Capillary Imbibition

Abstract

The time scaling exponent for the analytical expression of capillary rise $\ell \sim t^{\delta }$ for several theoretical fractal curves is derived. It is established that the actual distance of fluid travel in self-avoiding fractals at the first stage of imbibition is in the Washburn regime, whereas at the second stage it is associated with the Hausdorff dimension $d_{\mathcal{H}}$. Mapping is converted from the Euclidean metric into the geodesic metric for linear fractals $\mathcal{F}$ governed by the geodesic dimension $d_g=d_{\mathcal{H}}/d_{\ell }$, where $d_{\ell }$ is the chemical dimension of $\mathcal{F}$. The imbibition measured by the chemical distance ${\ell }_g$ is introduced. Approximate spatiotemporal maps of capillary rise activity are obtained. The standard differential equations proposed for the von Koch fractals are solved. Illustrative examples to discuss some physical implications are presented.

1. Introduction

Fractal geometry studies shapes, which are scale invariant, have fractional dimensions and self-similar properties, so their Hausdorff dimensions exceed the corresponding topological dimensions, i.e., $d_{\mathcal{H}}>d_t$ [1]. Fractal theory is widely applied to the fields of physics, chemistry, biology, medicine, geology and computer science (see Refs. [2,3,4,5,6]). Specifically, it is used to model transport phenomena in porous media [7,8,9,10,11,12] due to the fractal features [13,14].

Capillary-driven fluid flow is the main transport mechanism in many natural systems. Capillarity was observed for the first time by Leonardo da Vinci [15]. Washburn [16] derived a relation for the fluid moving through a small cylindrical capillary or porous medium, which showed a time dependence of the imbibing fluid distance as $\ell \sim t^{1/2}$.

The complexity of pore structure plays an important role for the determination of the properties of porous media. This heterogeneity is related to the value of the time exponent, so that the imbibition speed is slower than for the Washburn regime, as the imbibition path is not a straight line as in the Washburn capillary tubes. Therefore, the capillary rise can be estimated as:

$$\begin{array}{c}\hfill \ell \sim t^{\delta },\end{array}$$

(1)

where $\delta <0.5$ is the time scaling exponent. In this sense, Launghlin and Davies reported an exponent $\delta =0.41$ for capillary imbibition in fibrous textile [17]. The effect of the capillary’s roughened path was shown in [18] by making experimental tests on glass bed, where $\delta =0.25$. Lam and Horváth carried out their capillary imbibition studies on paper as the porous media and they obtained an exponent $\delta =0.382$ [19]. Whereas in 2006, Li [20] and Balankin et al. [21] reported exponents equal to $0.32$ and $0.38$ on chalk and paper studies, respectively. In [22] it was proved that the capillary rise does not behave according to the Washburn law, and concluded that the time exponent $\delta =0.49$ for a newspaper sheet depends on the swelling of paper fibers and the non-Newtonian character of the liquid. Paper wetting experiments using displacement of air by black Chinese ink was developed in [23] and introduced a new time exponent with the value of $\delta =0.41$. Recently, Zhu et al. [11] reported values of $\delta =0.34,0.38,0.42$ in several tight reservoirs. However, none of the above-mentioned references provide details regarding the fluctuations of the time exponent $\delta <0.5$ or the relations that explain the anomaly of $\delta$.

On the other hand, it has been proved that the pore and fracture networks are almost always fractal [24,25,26,27] and they are well-described by fractal geometry rather than traditional geometry [28,29,30]. Therefore, many approximate models of spontaneous imbibition are based on the fractal ramification of pores and channels that form tortuous capillaries through which liquid is imbibed.

Thereby, Li and Zhao [31] proposed a fractal model for the prediction of spontaneous imbibition where the time exponent is linked to the Hausdorff dimension of the porous matrix using different core samples (glass-bed pack, chalk, Geyser rock and Berea sandstone), such that $\delta =d_{\mathcal{H}}-2$. This model is efficient for a fractal reservoir of the three-dimensional Cantor tartan type and later it was modified in [32] as $\delta =d_{t\mathcal{H}}-2$, where $d_{t\mathcal{H}}$ is the topological Hausdorff dimension of the medium, which quantifies the ramification of a fractal matrix and its transport properties. Thereafter, a revolutionary method to compute the time exponent was deduced by Cai [33], which explains the anomality of $\delta$ with respect to the Washburn model. The model establishes the relation between the tortuosity path of the capillary tube and the fractality of a porous medium. At first, the concept of the fractal dimension of tortuosity of capillary $d_{\tau }$ is introduced, so that $\delta =1/2d_{\tau }$. It is well-known that, $d_{\tau }$ can be obtained both for a single capillary using the box count method [34], and for tortuous streamtubes in porous media using Equation (8) from Ref. [6].

In this work we introduce a relation that allows the determination of the time exponent in order to compute the prediction of the imbibed volume in fractal capillaries for any fractal curve such that it is only necessary to calculate the Hausdorff dimension of the capillary. It also allows to understand the physical nature of the fluctuations of the time exponent ($0.25\le \delta \le 0.5$) given in [11,17,18,19,20,21,22,23]

The tortuous flow paths may be similar to the triadic Koch curve, which is a self-similar fractal [35,36]. In this regard, the standard von Koch curve plays an important role to model processes with fractal structures, such as: diffusion [37,38], stresses and strains [39], motion and vibrations [40,41], antenna design [42], stationary heat equation [43], among others.

The 3-adic von Koch curve can be constructed as follows. The initiator ${\mathcal{F}}_0$, is a straight line that is partitioned into three equal parts. The middle part is replaced by an equilateral triangle. This is the basic step and the reduced figure has four equal lines joined with each other. This new figure is known as a generator denoted by ${\mathcal{F}}_1$. We construct ${\mathcal{F}}_2$ by applying the same operation to each of the four lines in ${\mathcal{F}}_1$ and so on. Its Hausdorff dimension is defined as: [44]

$$\begin{array}{c}\hfill d_{\mathcal{H}}=\frac{log4}{log3}.\end{array}$$

(2)

The path-connected Koch curve is a finitely ramified fractal whose fractal features are characterized by a set of dimension numbers [36,45,46]. The Hausdorff dimension $d_{\mathcal{H}}$ characterizes the degree to which a set fills the Euclidean space in which it is embedded [47], so that $d_{\mathcal{H}}$ is associated to a measure with respect to the Euclidean metric; while the chemical dimension $d_{\ell }$ characterizes the fractal topology, which is measured with respect to the geodesic metric on the fractal [36,45,46]. In addition, the geodesic dimension is given by $d_g=d_{\mathcal{H}}/d_{\ell }$ [36]. It is known that $d_{\ell }=1$ on self-avoiding curves [48], so for the von Koch fractal we have $d_g=d_{\mathcal{H}}$.

Therefore, the analytical expression of the time scaling exponent $\delta$ for capillary rise on fractal curves can be obtained by mapping from the Euclidean metric to the geodesic metric on the von Koch curve using the ordinary calculus, and we obtain ${\ell }_g\sim {\ell }^{d_{\mathcal{H}}}$. This allows us to establish the lower and upper bounds for the time scaling exponent characterizing the capillary rise. Thereafter, the exact values of distances of fluid travel ℓ, ${\ell }_g$ and Euclidean distance (${\ell }_{ϵ}$) are obtained.

The manuscript consists of five sections: following the “Introduction”, we review the geodesic metric ${\ell }_g$ and the basic tools required in Section 2. In Section 3, we apply ${\ell }_g$ for the von Koch curves and the standard differential equations of spontaneous imbibition as geodesic distance function are introduced. In Section 4 the capillary rise activity on Koch fractal is studied. In Section 5 the main findings and conclusions are outlined.

2. Terminology and Notations

In this section, some theoretical considerations about spontaneous imbibition and concepts of self-avoiding fractal curves are reviewed and defined.

2.1. Classical Differential Equation for Immiscible Imbibition

In spontaneous imbibition the pressure is similar at both ends of the capillary and the penetration of a wetting liquid into the capillary or porous media is influenced by the interface curvature, which takes place due to the capillary pressure, illustrated by the following equation:

$$\begin{array}{c}\hfill p_c=\frac{2\sigma cos\theta }{r_c},\end{array}$$

(3)

where $\sigma$ is the surface tension, and $r_c$ is the capillary radius. Many methods have been developed to investigate the capillary effects in unconventional reservoirs in order to characterize the capillary pressure (see for example [49,50,51,52] and references therein).

Imbibition arises when the contact angle ($\theta$) between the liquid and the capillary surface is less than $\mathsf{\pi }/2$. The physics of imbibition is governed by the Bond and capillary numbers [53,54]. The first of them is $\mathit{Bo}=\left({\rho }_w-{\rho }_g\right)\mathit{g}{r}_c^2/\sigma$ that represents the ratio of gravity and capillary forces, and the second one is $\mathit{Ca}=\mu \mathit{v}/\sigma$, which is the ratio of viscous and capillary forces; where $\mathit{g}$ is the gravity constant, ${\rho }_w$ is the wetting liquid density, ${\rho }_0$ is the gas density, $\mu$ is the fluid dynamic viscosity and $\mathit{v}$ is the fluid velocity.

Furthermore, the viscosity ratio $M={\mu }_w/{\mu }_0$ is an important parameter since the viscous forces can either stabilize or destabilize the fluid–fluid interface. Depending on the flow conditions and pore radius, extremely different flow regimes occur. When $M\gg 1$, $\mathrm{Bo}\ll 1$ and $\mathrm{Ca}\ll 1$, the capillary forces are dominant, and the inertial effects can be neglected. If in the capillary tube only the laminar flow exists, the liquid penetration is governed by the balance of the capillary, viscous ($(8\mu \ell /r_c^2)(d\ell /dt)$ ) and hydrostatic (${\rho }_w\mathit{g}\ell$) effects as $p_c=p_{\mu }+p_g$, with ℓ being the straight-line distance (vertical) of fluid penetration (see the iteration $k=0$ of von Koch curve in Figure 1). Therefore, the capillary rise is given as:

$$\begin{array}{c}\hfill \frac{d\ell }{d\mathit{t}}=\frac{\kappa }{\mu }{\rho }_w\mathit{g}\left(\frac{{\ell }_{eq}}{\ell }-1\right),\end{array}$$

(4)

where $\kappa =r_c^2/8$ is the intrinsic permeability of the tube and ${\ell }_{eq}=p_c/{\rho }_w\mathit{g}$ is the equilibrium height of the liquid–air interface, at which the capillary and hydrostatic pressures are balanced.

The solution of Equation (4) has two stages determined by the equilibration time $t_{eq}={\ell }_{eq}\mu /\kappa g{\rho }_w^2$ [55]. On the one hand, for $t\ll t_{eq}$, which corresponds to $\ell \ll {\ell }_{eq}$ or to the absence of gravity (a horizontal cylindrical capillary) when ${\ell }_{eq}=\infty$, the advancing liquid is given by the Washburn regime:

$$\begin{array}{c}\hfill \ell \left(t\right)=\Omega t^{\frac{1}{2}},\end{array}$$

(5)

where $\Omega ={\left(2\kappa p_c/\mu \right)}^{1/2}$. On the other hand, when $t\gg t_{eq}$ the equilibrium height is approached exponentially as:

$$\begin{array}{c}\hfill \ell \left(t\right)\sim {\ell }_{eq}\left(1-e^{-t/t_{eq}}\right).\end{array}$$

(6)

2.2. Euclidean and Geodesic Metric on Fractal Curves

The Hausdorff dimension is defined with respect to the Euclidean metric in the embedding Euclidean space via the scaling relation [56]

$$\begin{array}{c}\hfill N_{ϵ}\sim {ϵ}^{d_{\mathcal{H}}},\end{array}$$

(7)

where $N_{ϵ}$ is the number of n-dimensional covering elements of size $ϵ$ needed to cover the fractal. The Hausdorff dimension can be treated as the degree to which a set “fills” the Euclidean space in which it is embedded. Note that for d-dimensional Euclidean patterns, the Hausdorff dimension defined by Equation (7) is equal to the topological dimension $d_t$. On the other hand, for fractals living in n-dimensional space $d_t<d_{\mathcal{H}}\le n$.

Nevertheless, there always exists the intrinsic geodesic metric associated with the fractal topology [57,58] characterized by the chemical dimension $d_{\ell }$, which is independent of the embedding [36]. The chemical dimension of a fractal $\mathcal{F}$ is defined as [48] the Hausdorff dimension with respect to the intrinsic geodesic metric on the fractal by fractal covering for the $d_{\ell }$-dimensional balls with diameter not smaller than ${ϵ}_{\ell }$, such that [48]

$$\begin{array}{c}\hfill N_{\ell }\sim {ϵ}_{\ell }^{d_{\ell }}.\end{array}$$

(8)

It is a straightforward matter to see that the mass of fractal scales with the ball’s diameter is

$$\begin{array}{c}\hfill \mathcal{M}\sim {ϵ}_{\ell }^{d_{\ell }}\sim {ϵ}^{d_{\mathcal{H}}},\end{array}$$

(9)

where ${ϵ}_{\ell }$ and $ϵ$ denote the ball diameter with respect to the geodesic and Euclidean metrics, respectively [36]. The mapping from the geodesic metric on the fractal into the Euclidean metric in the embedding space implies that the geodesic distances between two points on the fractal denoted by ${\ell }_g={\ell }_{{ϵ}_{\ell }}$ scales with the Euclidean distance between these points in the embedding Euclidean space ${\ell }_{ϵ}$ as follow

$$\begin{array}{c}\hfill {\ell }_g\sim {\ell }_{ϵ}^{d_{\mathcal{H}}/d_{\ell }}\sim {\ell }_{ϵ}^{d_g},\end{array}$$

(10)

where $d_g=d_{\mathcal{H}}/d_{\ell }\ge 1$ is the geodesic dimension. Note that the geodesic dimension is equal to the Hausdorff dimension of the minimum path $d_{min}$ on the fractal.

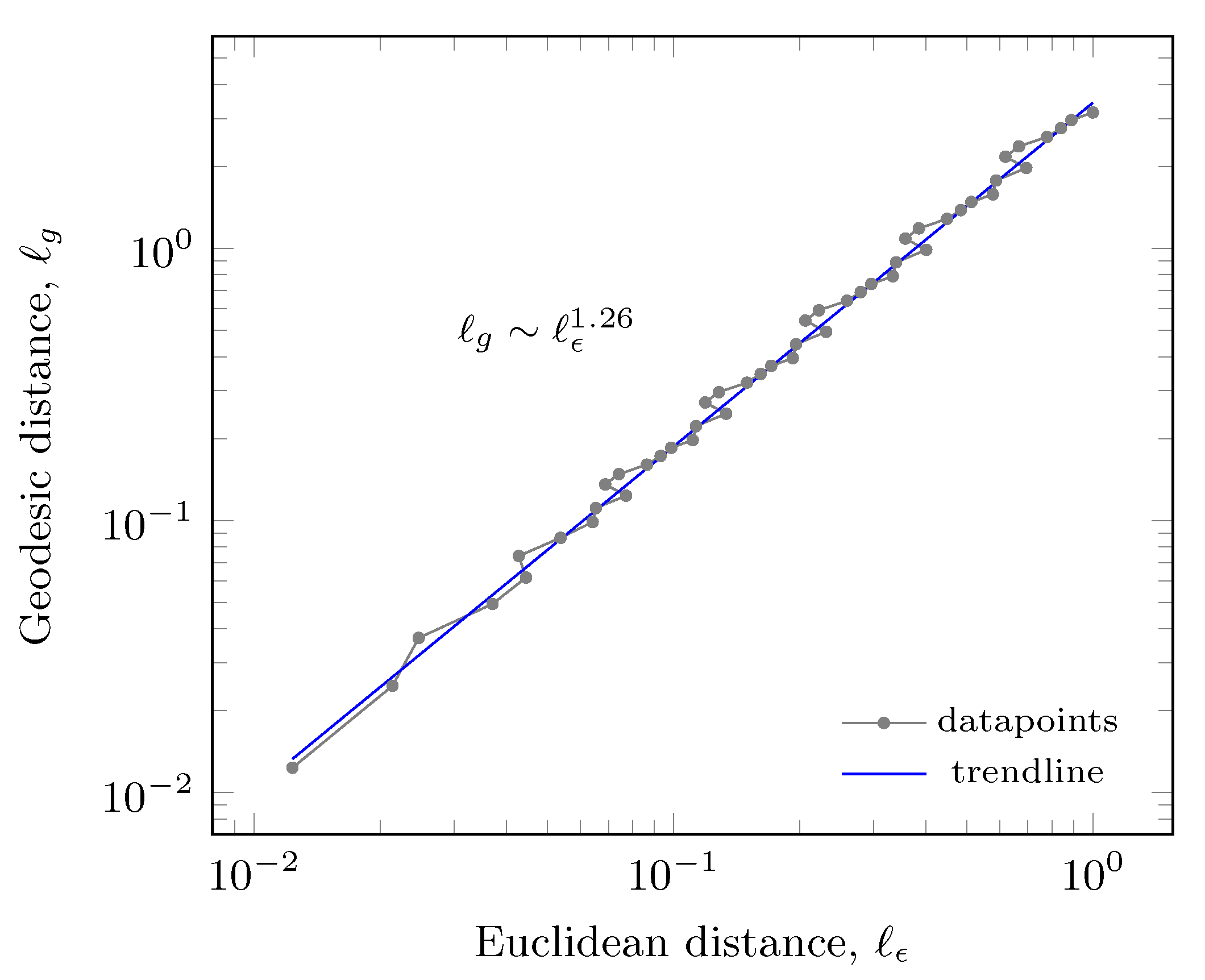
2.3. Geodesic Dimension $D_g$ and Distances on Self-Avoiding Fractals

It was established that the Hausdorff dimension of the minimum path for self-avoiding Koch curves is equal to the Hausdorff dimension, i.e., [36,48]

$$\begin{array}{c}\hfill d_{min}=d_g=d_{\mathcal{H}},\end{array}$$

(11)

meanwhile the chemical dimension is equal to one ($d_{\ell }=1$) [36,45,46]. The geodesic distance from the origin of fractal $\mathcal{F}$ to an arbitrary point x (see Figure 1) can be obtained as: [59]

$$\begin{array}{c}\hfill {\ell }_g=m_1{\left({\ell }_{ϵ}\right)}^{d_{\mathcal{H}}},\end{array}$$

(12)

where $1\le d_{\mathcal{H}}<2$ and $m_1$ is a proportionality constant. The values of $m_1$ are discussed in detail in Ref. [59]. At Figure 2 the relation between chemical and Euclidean distances for the standard von Koch curve is presented.

Figure 1. First four iterations of classical von Koch curve [44]. The initiator is equal to Washburn capillary with $d_{\mathcal{H}}=1$ [16]. The last drawing (blue color) shows the three travel distances of the fluid (for an example of the experimental setup in a vertically straight capillary see [55]).

Figure 1. First four iterations of classical von Koch curve [44]. The initiator is equal to Washburn capillary with $d_{\mathcal{H}}=1$ [16]. The last drawing (blue color) shows the three travel distances of the fluid (for an example of the experimental setup in a vertically straight capillary see [55]).

Moreover, in [60] it was established that for statistical fractals or single-valued functions, the geodesic distance ${\ell }_g$ is the actual distance that fluid travels in a heterogeneous porous medium, which is as a function of the straight-line distance ℓ, between the starting and ending points of the fractal path given by the following equation:

$$\begin{array}{c}\hfill {\ell }_g=m_2{\ell }^{d_{\mathcal{H}}},\end{array}$$

(13)

where

$$\begin{array}{c}\hfill m_2={ϵ}^{1-d_{\mathcal{H}}}\end{array}$$

(14)

being $ϵ$ the lower cutoff of fractal $\mathcal{F}$ (for the standard von Koch curve $ϵ=1/3^k$, where k is the iteration number).

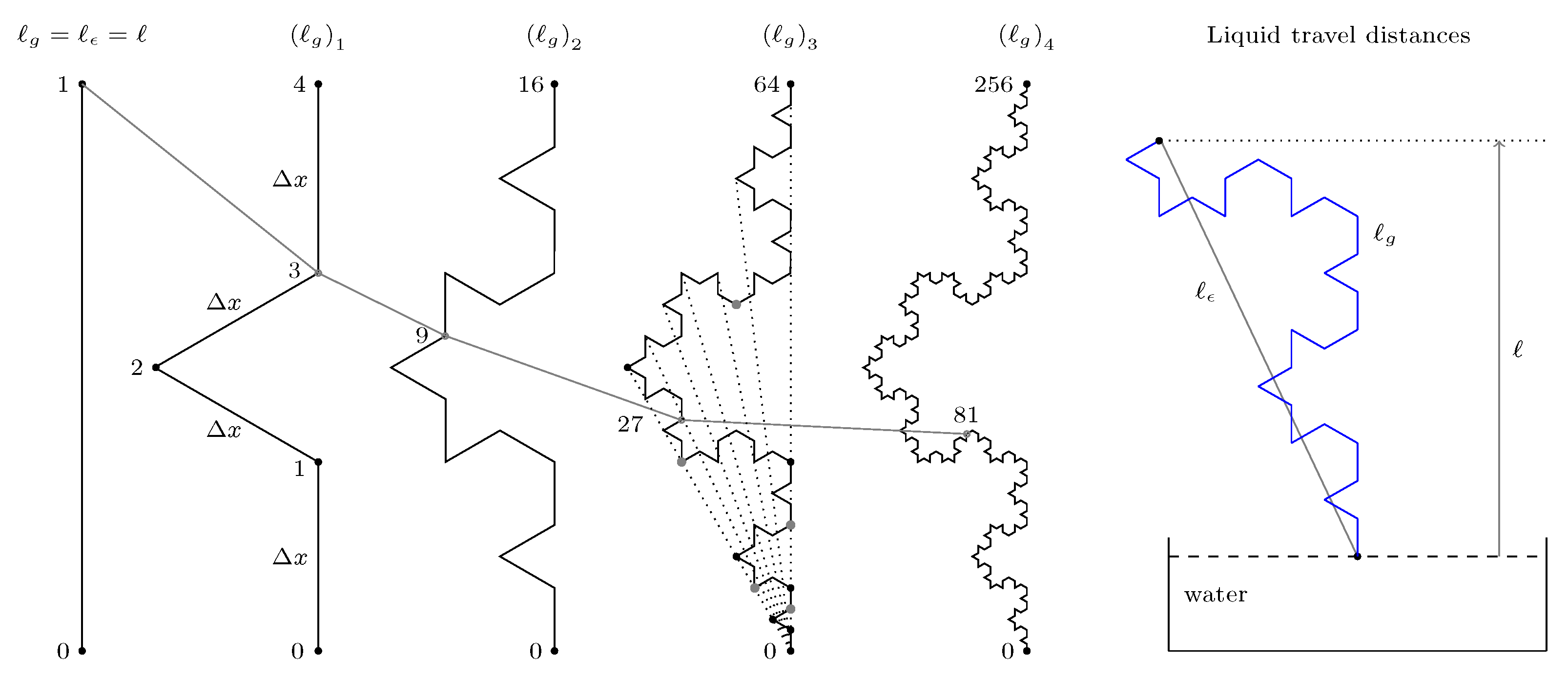
3. Standard Differential Equation of Capillary Rise with Geodesic Metric

In this section, differential equations of capillary rise for capillaries with fractal path are suggested, denoted by $\mathcal{F}$ in order to describe the fractal imbibition under the analogous assumptions to those in Ref. [33].

Differentiating Equation (13) with respect to the time t for a single capillary results in:

$${\mathit{v}}_g=m_2{d}_{\mathcal{H}}{\ell }^{d_{\mathcal{H}}-1}\mathit{v},$$

(15)

where ${\mathit{v}}_g=d{\ell }_g/dt$ is the actual velocity of liquid traveling through the geodesic pass of a capillary; $\mathit{v}=d\ell /dt$ is the imbibition velocity for the Euclidean pass (straight-line ℓ); where the Euclidian distance ℓ is such that $d_{\mathcal{H}}=1$, and we have that ${\mathit{v}}_g=\mathit{v}$. The scaling ratio between both velocities can be rewritten as:

$$\begin{array}{c}\hfill \frac{d{\ell }_g}{dt}=m_2{d}_{\mathcal{H}}{\ell }^{d_{\mathcal{H}}-1}\frac{d\ell }{dt}.\end{array}$$

(16)

In [61] it was shown that when a wetting liquid contacts with a capillary of any shape (Euclidean or fractal), the capillary rise is described as:

$$\begin{array}{c}\hfill \frac{d{\ell }_g}{dt}=\frac{\kappa }{\mu }\frac{\ell }{{\ell }_g}{\rho }_w\mathit{g}\left(\frac{{\ell }_{eq}}{\ell }-1\right).\end{array}$$

(17)

The capillary rise in fractal curves is obtained substituting Equations (13) and (16) in (17), and we obtain:

$$\begin{array}{c}\hfill \frac{d\ell }{dt}=\frac{\kappa }{\mu m_2^2}\frac{{\rho }_w\mathit{g}}{{\ell }^{2(d_{\mathcal{H}}-1)}{d}_{\mathcal{H}}}\left(\frac{{\ell }_{eq}}{\ell }-1\right).\end{array}$$

(18)

Integrating Equation (18) neglecting the gravitational force, we obtain the capillary rise in the first stage of imbibition as:

$$\begin{array}{c}\hfill \ell \left(t\right)={\Omega }_{\mathcal{F}}{t}^{\frac{1}{2d_{\mathcal{H}}}}\end{array}$$

(19)

where ${\Omega }_{\mathcal{F}}={\left(2\kappa p_c/\mu m_2^2\right)}^{1/2d_{\mathcal{H}}}$, and the time scaling exponent is bounded as $0.25\le \delta =1/2d_{\mathcal{H}}\le 0.5$. Equation (19) implies that the real travel distance of a fluid during the capillary rise in a porous media is a power law time function that depends on the Hausdorff dimension of the fractal capillary (which can be estimated more easely than the tortuosity dimension as in [61]). The behavior of Equation (19), shown in Figure 3, matches with previous experimental tests (see Refs. [62,63,64]) Meanwhile, when $d_{\mathcal{H}}=1$, the fractal curve is a straight line and the axial (or unidirectional) imbibition into a cylinder is obtained (see Equation (5)), as for $d_{\mathcal{H}}=2$ the fractal curve is a highly tortuous line, so irregular that it fills a two-dimensional space.

The second stage of imbibition can be modeled according to Equation (18). The equilibrium height is reached at different times (Figure 3a), which depends on the Hausdorff dimension of the capillary (exponential trendline shown in Figure 3b).

Moreover, the geodesic distance that corresponds to the real path that a fluid travels during a capillary rise is governed by the following equation:

$$\begin{array}{c}\hfill \frac{d{\ell }_g}{dt}=\frac{r_c^2}{8\mu }\frac{1}{{\ell }_g}\left(\frac{2\sigma cos\theta }{r_c}-{\rho }_w\mathit{g}{\left(\frac{{\ell }_g}{m_2}\right)}^{\frac{1}{d_{\mathcal{H}}}}\right),\end{array}$$

(20)

and for the first stage of imbibition the expression for ${\ell }_g$ is:

$$\begin{array}{c}\hfill {\ell }_g\left(t\right)={\Omega }_g{t}^{\frac{1}{2}},\end{array}$$

(21)

where ${\Omega }_g={\left(2\kappa p_c/\mu m_2^2\right)}^{1/2}$. Therefore, the geodesic distance of fluid in the first stage of imbibition is in the Washburn regime (see the upper red curve in Figure 3).

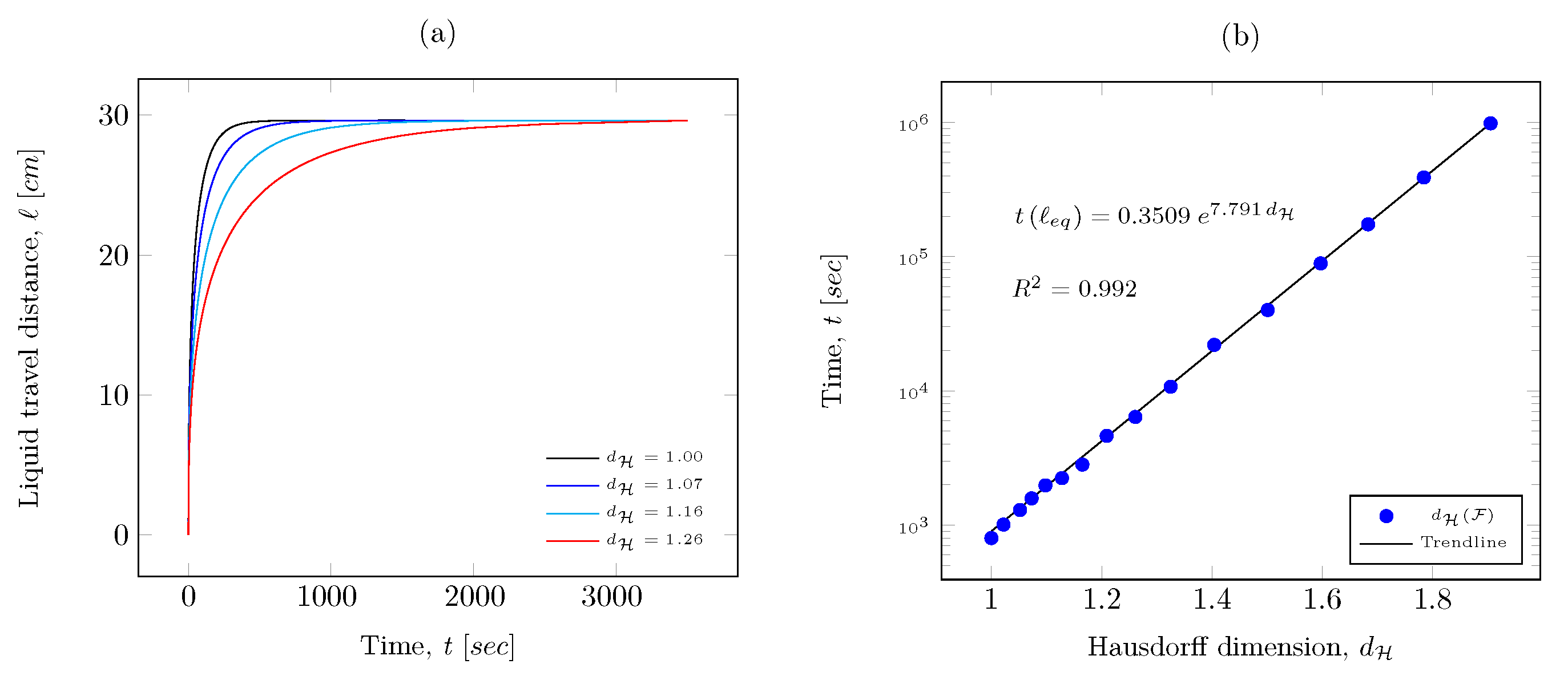
4. Results Obtained on Capillary Rise on Von Koch Curves

In this Section we describe the capillary rise on standard von Koch fractal in order to show some physical implications.

Consider a rough capillary triadic Koch’s type curve presented in Figure 1, whose geodesic distance is:

$$\begin{array}{c}\hfill {\ell }_g=n\Delta x,\end{array}$$

(22)

for

$$\begin{array}{c}\hfill \Delta x={\left(\frac{1}{3}\right)}^k,\end{array}$$

(23)

where n is the site number on the fractal and ${\ell }_{ϵ}=1$ is the Euclidean distance. We study the capillary rise for a glass capillary and distilled water with the following properties $\theta =0^{\circ }$, $\rho =0.998{\mathrm{g}/\mathrm{cm}}^3$, $\mu =0.01\mathrm{dina}{\mathrm{s}/\mathrm{cm}}^2$, $\sigma =724\mathrm{dina}/\mathrm{cm}$ and $\ell =64\mathrm{cm}$.

The capillary rise activity for the first stage of spontaneous imbibition is presented in Figure 3. Note that the imbibition height (ℓ) depends on the Hausdorff dimension of capillary $\mathcal{F}$ (Equation (19)) and the geodesic distance of imbibition is in the Washburn regime $\delta =0.5$ given by Equation (21), so that $\delta \left({\ell }_g\right)>\delta (\ell )$ as is shown in Figure 3a.

The values of $\delta$ in Figure 3a are in the range of $[0.25,0.5]$ and correspond to all possible values of the capillary rise $\ell \left(t\right)\sim t^{\delta }$ as a function of time exponent, which in its turn depends on the Hausdorff dimension $\delta =1/2d_{\mathcal{H}}$ of the fractal capillary. Therefore, $\delta$ has the following range:

$$\begin{array}{c}\hfill \frac{1}{4}\le \delta \le \frac{1}{2}.\end{array}$$

(24)

The above mentioned result follows from the fact that $d_{\mathcal{H}}$ characterizes the capacity of the fractal to fill the embedded space, so that for self-avoiding curves embedded in ${\Re }^2$ the Hausdorff dimension $d_{\mathcal{H}}$ is such that $1\le d_{\mathcal{H}}<2$. In the case when $d_{\mathcal{H}}=1$ the capillary tube is straight (one-dimensional Euclidean case), and the exact Washburn regime with $\delta =1/2d_{\mathcal{H}}=0.5$ is obtained. Meanwhile for $d_{\mathcal{H}}=2$ the capillary tube is a highly tortuous line so irregular that fills a two-dimensional space and $\delta =1/2d_{\mathcal{H}}=0.25$.

If a generic von Koch capillary is analyzed with several Hausdorff dimensions $1\le d_{\mathcal{H}}\left(\mathcal{F}\right)\le 2$, so that [65]:

$$\begin{array}{c}\hfill d_{\mathcal{H}}=\frac{log4}{log2\left(1+cos\gamma \right)},\end{array}$$

(25)

where $\gamma$ is the indentation angle ($\gamma ={60}^{\circ }$ for 3-adic von Koch fractal), then it is possible to find the time scaling exponent for any tortuous capillaries in the range given by Equation (24).

Many experimental results of capillary rises obtained for different porous media proved that they do not have the behavior given by the Washburn equation $\ell \left(t\right)\sim t^{1/2}$. Experimental works showed that the imbibition speed for some porous media can be slower than that of the Washburn regime, i.e., $\delta <0.5$ as it is plotted in Figure 3b. This anomaly of the time scaling exponent cannot be explained by the gravity or inertial effects. Some researchers have suggested that this phenomenon is attributed to the fractality of the porous medium [21], explaining it with different approaches [31,61].

However, the above-mentioned anomaly is explained by Equations (19) and (24) obtained in the previous section, which characterize the irregular path of a liquid through a porous medium such as a fractal curve using its Hausdorff dimension that defines the value of the scaling exponent. Thus, the delta values can be found once the Hausdorff dimension of the porous medium is calculated.

The calculated Hausdorff dimensions of porous media corresponding to the previous works are shown in Figure 3b and they are in the range given by Equation (24).

The following remarks and outlooks may be drawn based on the results obtained:

1

The validation of the introduced formulation was performed by comparison of the calculated theoretical values with the experimental results of other authors mentioned above.

2

The formulation can be applied to highly tortuous capillaries. It is adaptable to fractal-curve-like capillaries and it does not depend on their tortuosity (for example, in the case when the capillary is a generalized fractal Koch curve, Weierstrass curve, or any linear fractal with Hausdorff dimension between 1 and 2).

3

The “effective” volume of imbibed liquid can be computed directly using the geodesic distance instead of the imbibition height distance.

4

The developed method is an optimization of the formulation proposed in [61], where $\delta =1/2d_{\tau }$. In the proposed method, it is not necessary to calculate neither the tortuosity nor the tortuosity fractal dimension of capillary tubes, it is enough to simply determine their Hausdorff dimension.

5

The time scaling exponent deduced by Li and Zhao $\delta =d_{\mathcal{H}}-2$ [31] is highly accurate in fractal matrix-type three-dimensional Cantor tartan. However, Equation (24) can be used to fit the experimental data once its $d_{\mathcal{H}}$ is determined (by its porosity rate [13]) instead of the Li–Zhao formulation.

From Equation (18) follows that the equilibrium distance ${\ell }_{eq}$ for several Hausdorff dimensions of von Koch curves in the second stage of imbibition are plotted in Figure 4a, and the corresponding time data versus Hausdorff dimension of $\mathcal{F}$ are presented in Figure 4b.

Note that, the time that fluid requires to reach the equilibrium height ${\ell }_{eq}$ directly depends on the Hausdorff dimension as:

$$\begin{array}{c}\hfill t\left({\ell }_{eq}\right)\sim e^{7.791d_{\mathcal{H}}}.\end{array}$$

(26)

Moreover, the geodesic length ${\ell }_g$ in the second stage of imbibition is a function of the Hausdorff dimension of the capillary tube (see Figure 5a). These lengths exceed the Euclidean and vertical distances, ${\ell }_g>{\ell }_{ϵ}>\ell$ (see Figure 4 and Figure 5). The equilibrium distances calculated using Equation (20) (see Figure 5b), imply that, for a capillar with any Hausdorff dimension, the geodesic distance can be computed as:

$$\begin{array}{c}\hfill {\left({\ell }_g\right)}_{eq}\sim t^{\eta },\end{array}$$

(27)

where $\eta =0.36$, and it is bounded by the indentation angles from Equation (25) as $0^{\circ }\le \gamma \le {90}^{\circ }$ (see Figure 5b).

5. Conclusions

Analytical expressions (Equations (18) and (20)) in standard calculus sense that characterize the capillary rise for spontaneous imbibition on generic Koch’s curve-like capillary tubes were derived.

It was established that the geodesic ${\ell }_g$ and Euclidean ${\ell }_{ϵ}$ travel distances of fluid on capillary type self-avoiding fractals are linked to their Hausdorff dimensions. Specifically, the time scaling exponent in the first stage of imbibition is a function of the Hausdorff dimension $\ell \left(t\right)\sim t^{1/2d_{\mathcal{H}}}$ and its fluctuation range is given by Equation (24). By contrast, in the second stage of imbibition, it was found that the time a fluid needs to reach the equilibrium height ${\ell }_{eq}$ on fractal curves is a function of the Hausdorff dimension and the equilibrium geodesic distance of fluid travel is a time function given by Equations (26) and (27), respectively.

Comparing the estimations of capillary rise derived using the developed approach versus the experimental data obtained by different researchers (see Figure 3b), it can be concluded that the formulation obtained can reproduce the global trend of variation of the time exponent with respect to the fractal capillary path.

New analytical expressions involving generalized von Koch fractal curves have been suggested, which can be used as mathematical models for many physical problems such as: fluid–fluid displacement in petroleum engineering, water penetration into cement pastes in construction industry, behavior of garments in the presence of liquids in textile production, among others.

We expect that the results obtained in this study will provide useful information for further experimental studies of porous media, for example, samples with capillary tube types of von Koch or Weierstrass fractals and, as a future work, we plan to perform the sensitivity analysis of the model.