A Fractal Permeability Model of Tight Oil Reservoirs Considering the Effects of Multiple Factors
Abstract
:1. Introduction
2. Fractal Geometry Theory
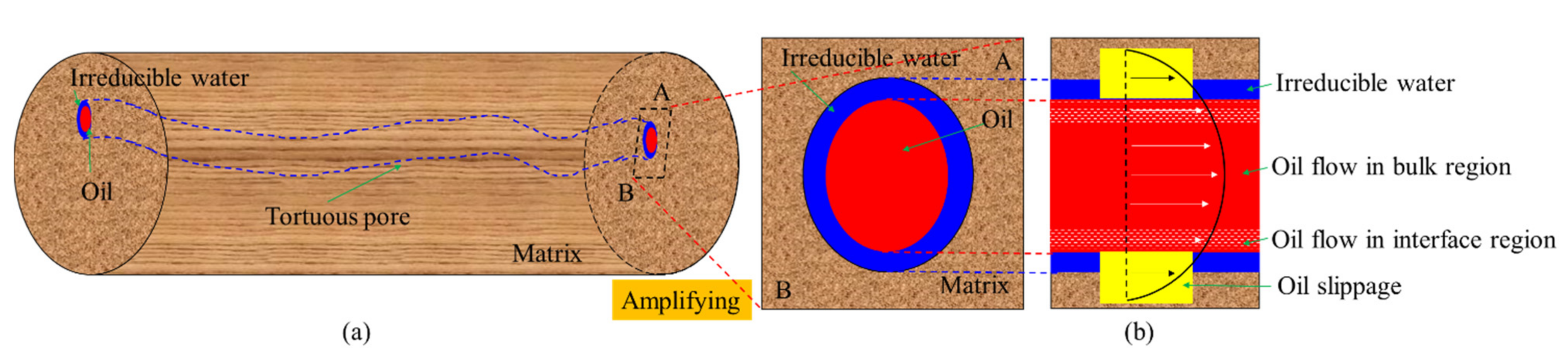
3. Fractal Permeability Model of Tight Oil Reservoirs
4. Model Verifications and Analysis
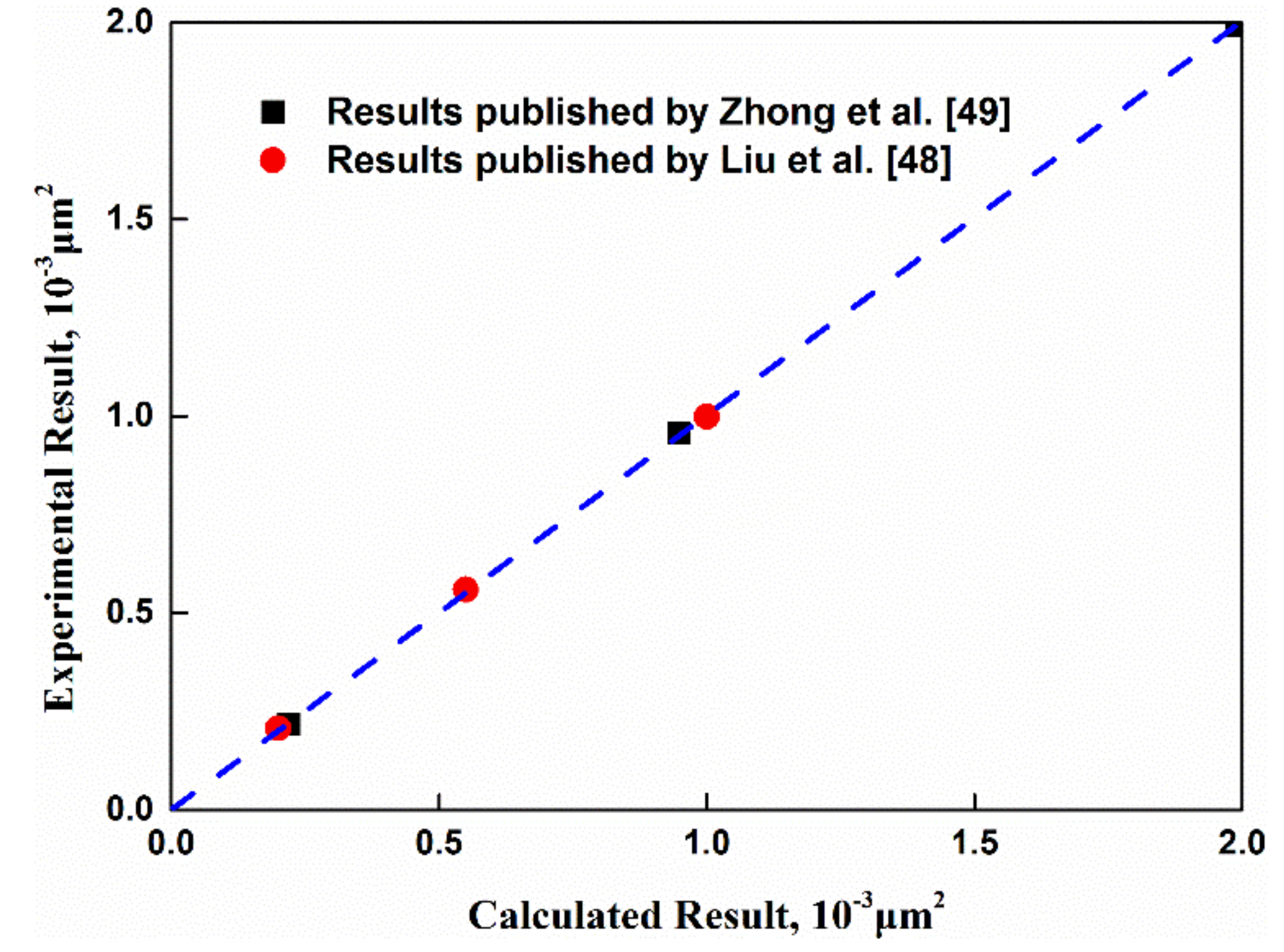
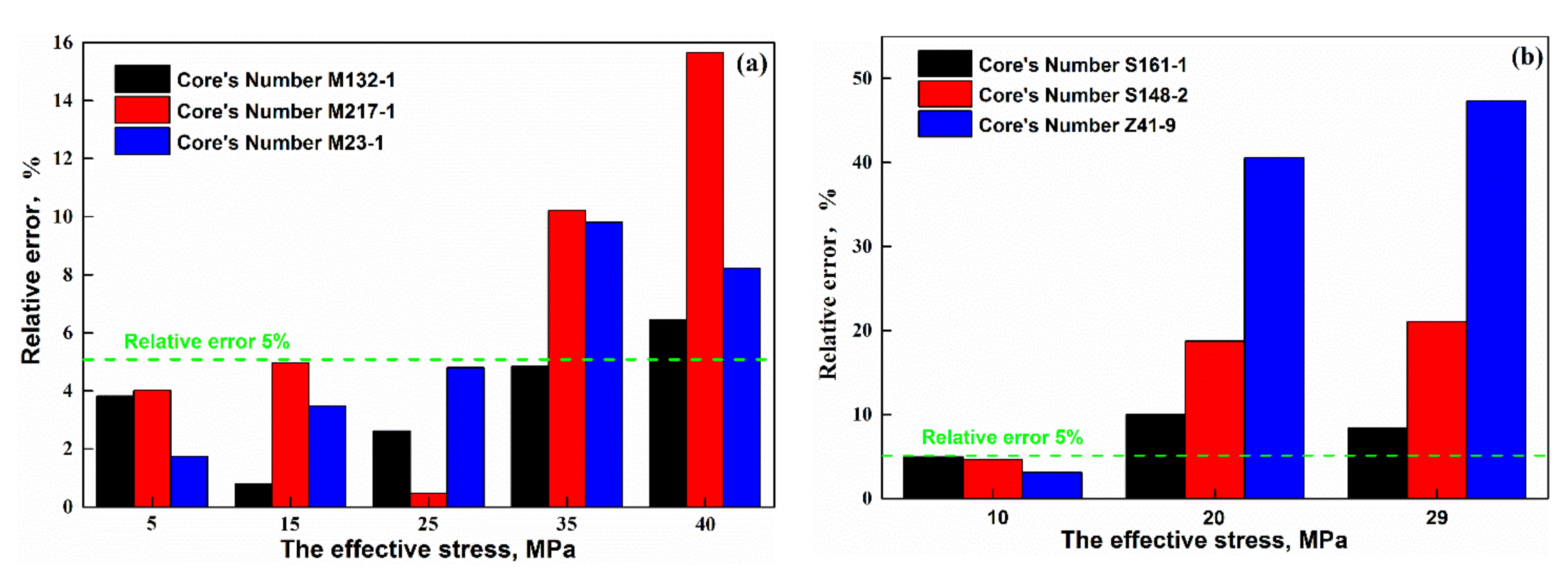
4.1. Fractal Permeability Model Verification
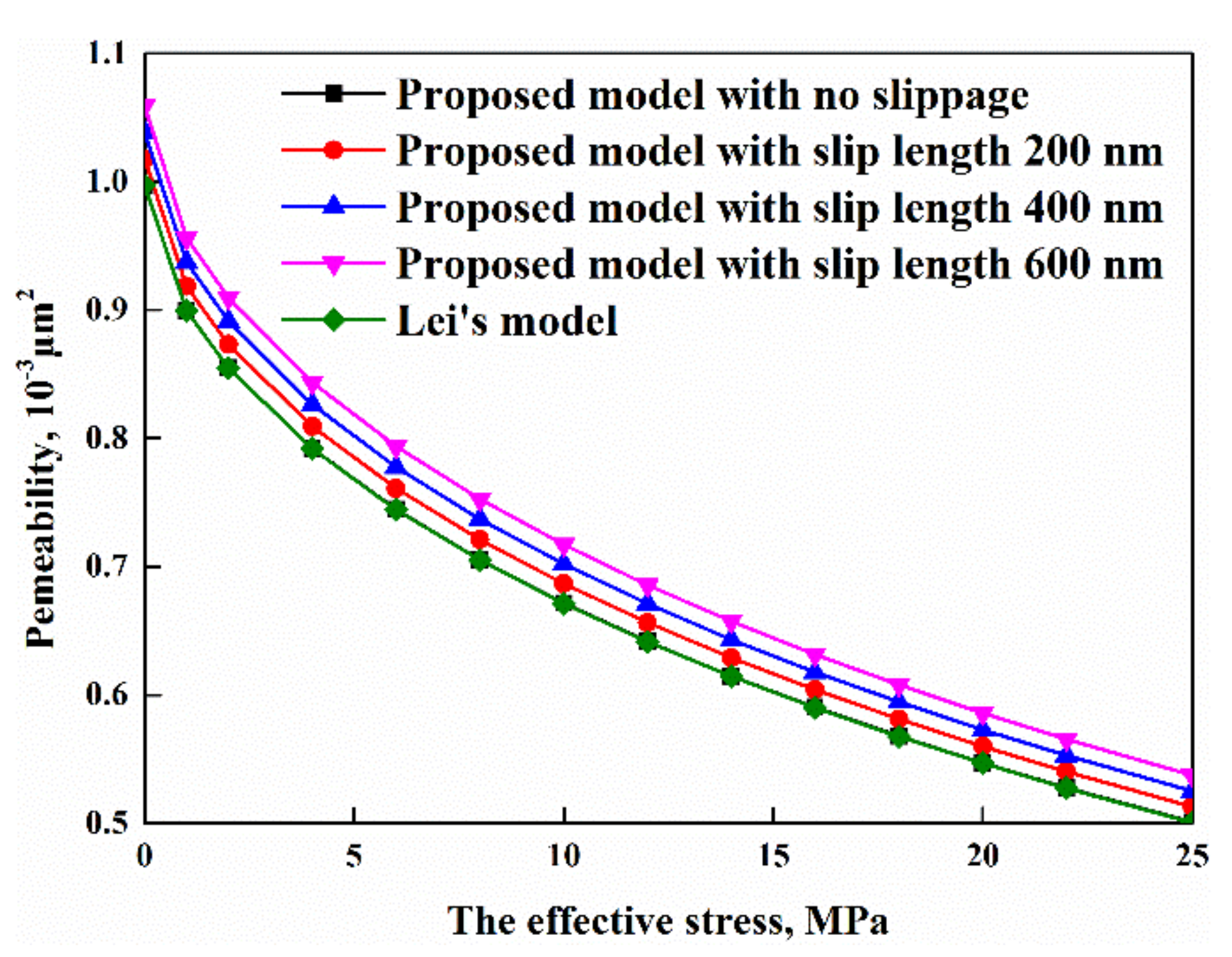
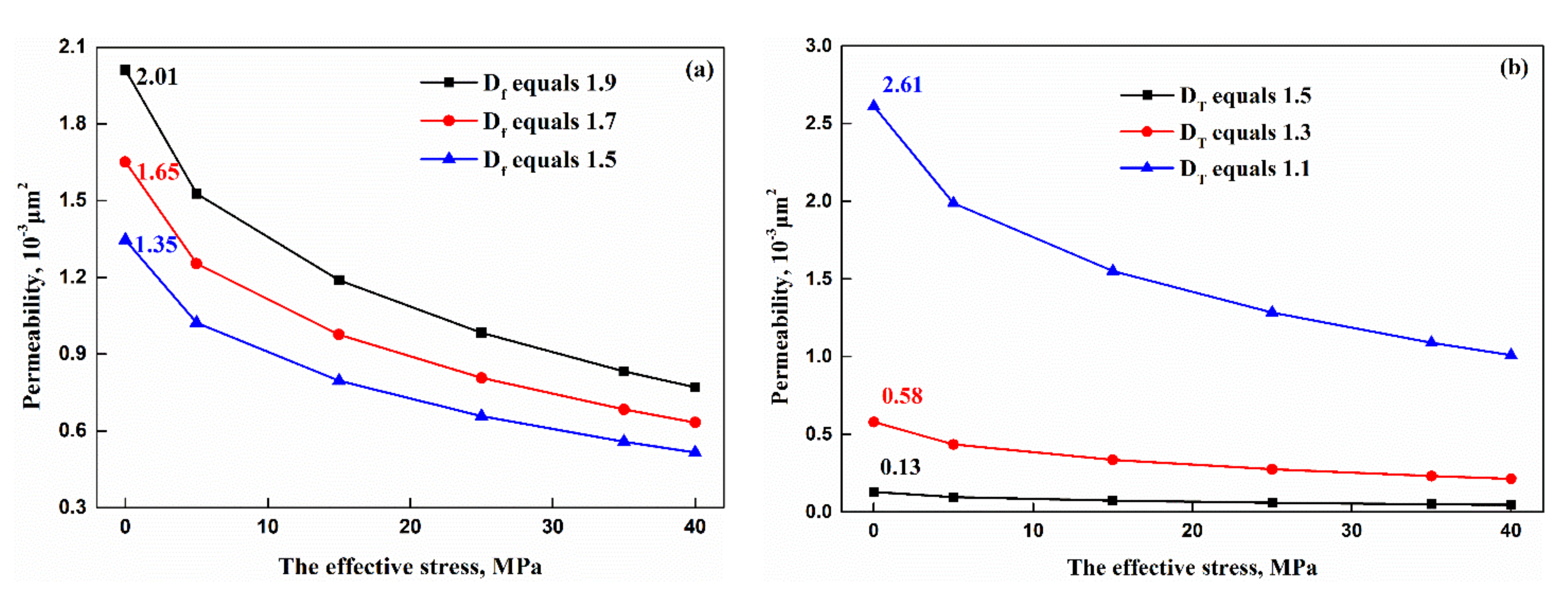
4.2. The Effects of Multiple Factors on Tight Reservoir Permeability
5. Conclusions
- (1)
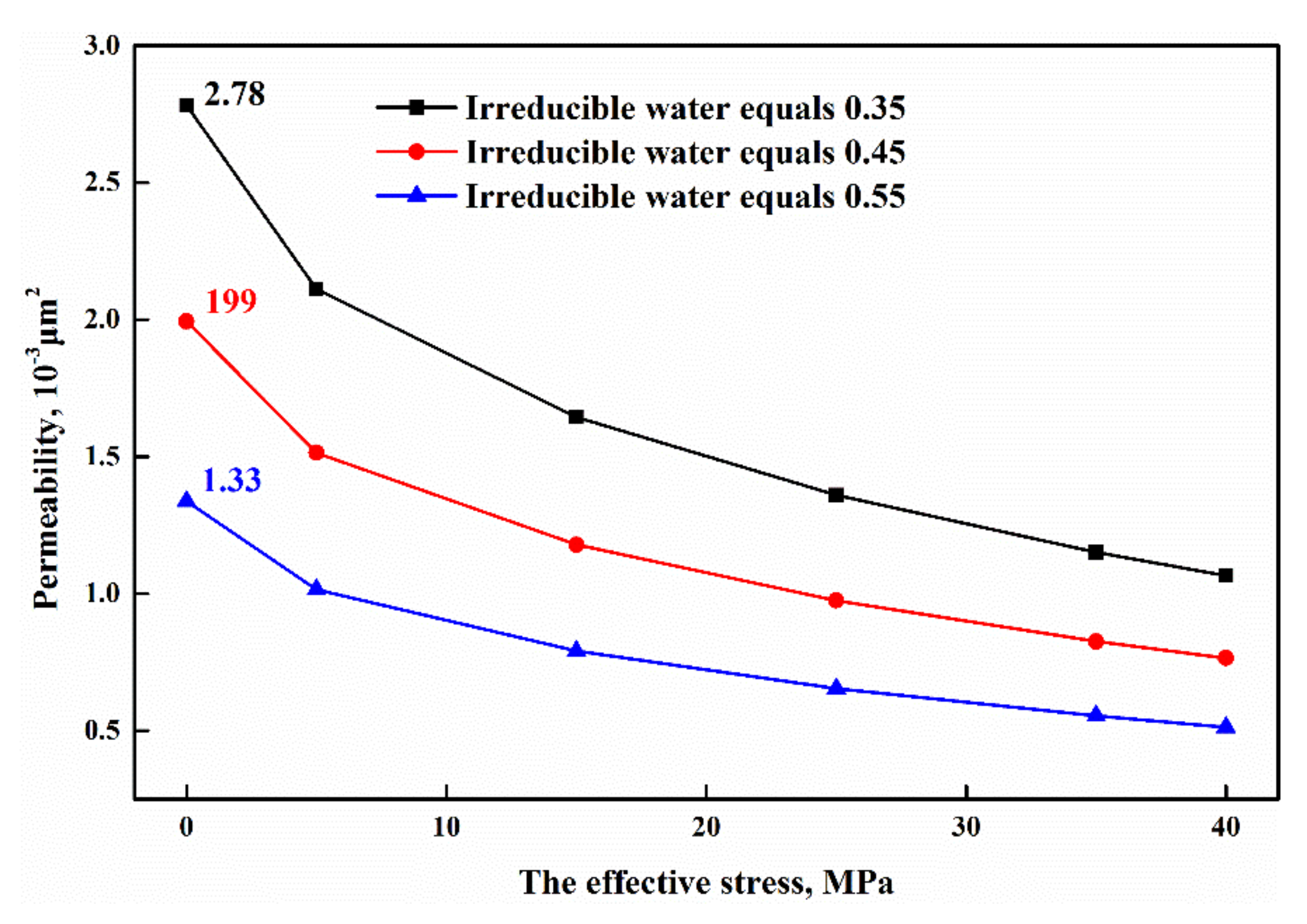
- A decreasing porous fractal dimension results in a decrease in permeability. The permeability decreases with the increase in tortuosity fractal dimension and irreducible water. When the irreducible water increased from 0.35 to 0.55, the permeability decreased from 2.78 × 10−3 μm2 to 1.33 × 10−3 μm2, and reduced by more than half the permeability.
- (2)
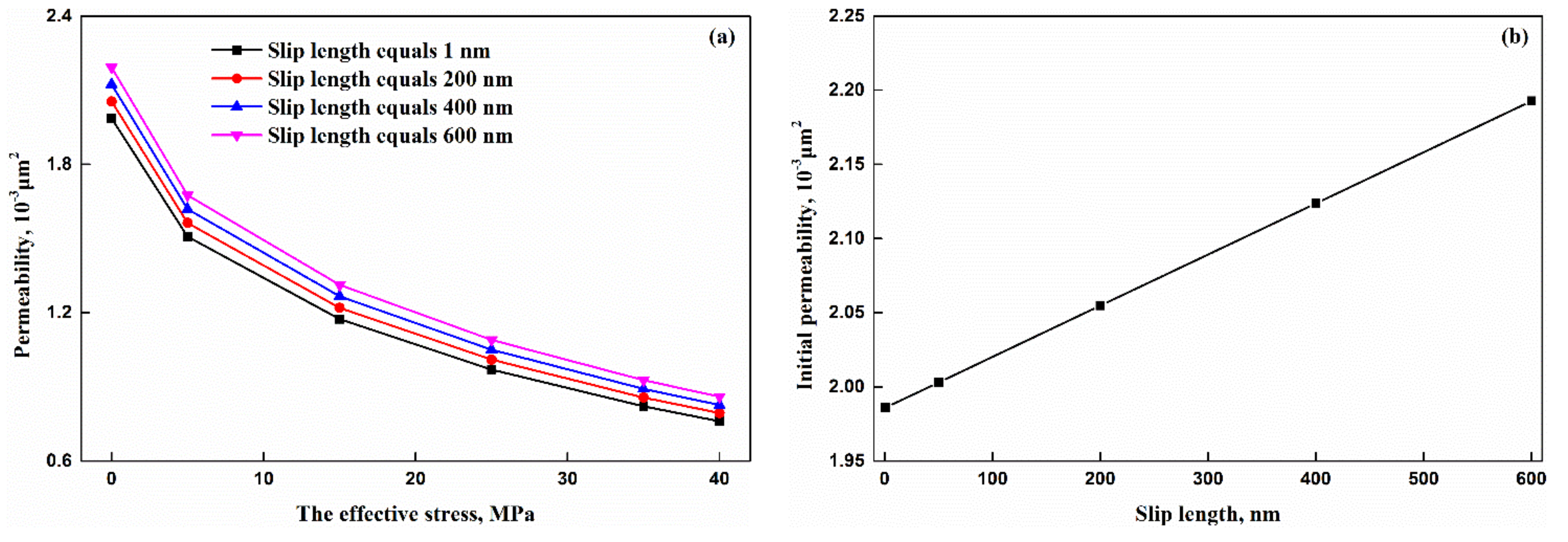
- An increase in slip length results in an increasing actual flow channel, which makes permeability increase. The initial permeability linear increases with an increasing slip lengths. When the slip length increased from 1 nm to 600 nm, the initial permeability increased from 1.98 × 10−3 μm2 to 2.19 × 10−3 μm2, and the increase rate was 10%.
- (3)
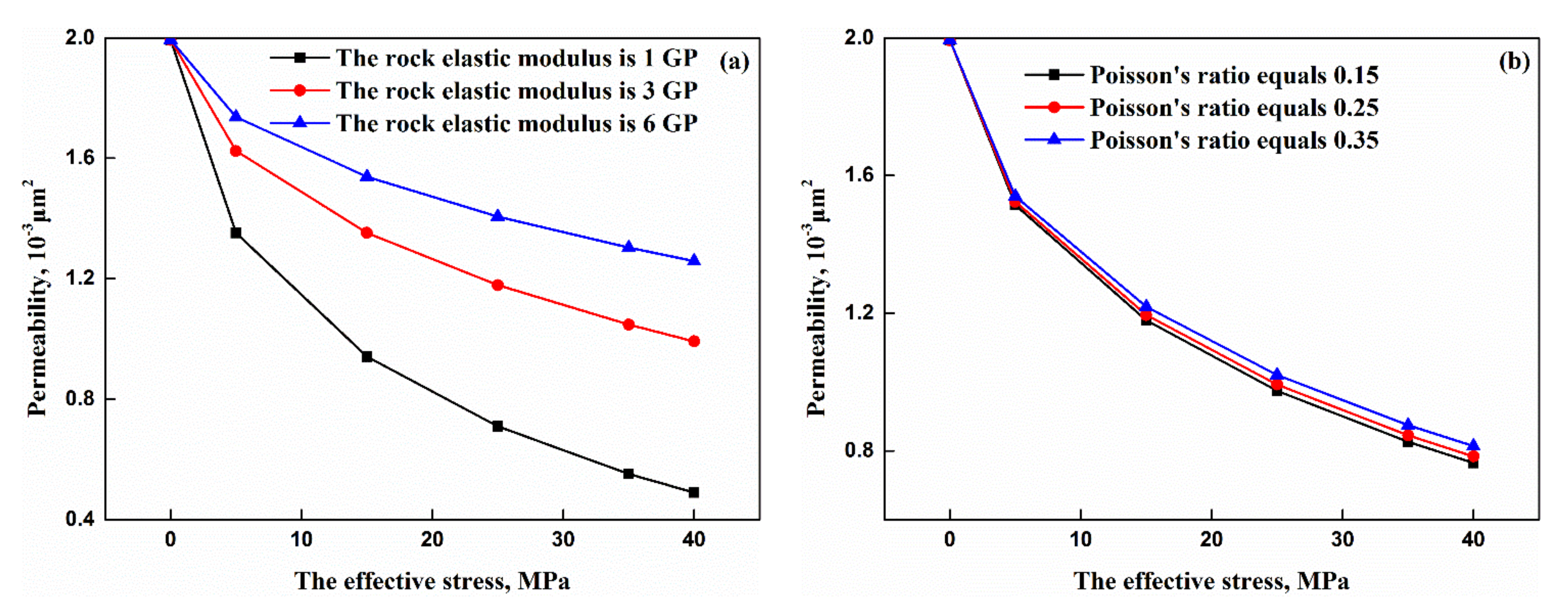
- The permeability decreases with the increase of effective stress. The porous fractal dimension, tortuosity fractal dimension, slip length, and irreducible water have a tiny effect on the permeability changing rate with effective stress. When the parameters of the rock’s mechanical property (the rock elastic modulus and Poisson’s ratio) increased, the permeability’s decreasing rate with effective stress became small.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A. The Flow Rate of Fluid Flowing through a Pore considering Multiple Factors’ Effects
Appendix B. The Detailed Derivation of the Flow Rate of Fluid Flowing through a Core considering the Effects of Multiple Factors
References
- Wu, Z.; Cui, C.; Ye, Y.; Cheng, X.; Trivedi, J. A fractal model for quantitative evaluating the effects of spontaneous imbibition and displacement on the recovery of tight reservoirs. J. Petrol. Sci. Eng. 2021, 198, 108120. [Google Scholar] [CrossRef]
- Wu, Z.; Cui, C.; Ye, Y.; Cheng, X.; Trivedi, J. A novel model for the proppant equilibrium height in hydraulic fractures for low-viscosity fracturing fluid treatment. Petrol. Sci. 2021, online. [Google Scholar] [CrossRef]
- Peng, Y.; Liu, J.; Zhang, G.; Pan, Z.; Ma, Z.; Wang, Y.; Hou, Y. A pore geometry-based permeability model for tight rocks and new sight of impact of stress on permeability. J. Nat. Gas Sci. Eng. 2021, 91, 103958. [Google Scholar] [CrossRef]
- Wu, Z.; Cui, C.; Lv, G.; Bing, S.; Cao, G. A multi-linear transient pressure model for multistage fractured horizontal well in tight oil reservoirs with considering threshold pressure gradient and stress sensitivity. J. Petrol. Sci. Eng. 2019, 172, 839–854. [Google Scholar] [CrossRef]
- Wu, Y.; Cheng, L.; Huang, S.; Bai, Y.; Jia, P.; Wang, S.; Xu, B.; Chen, L. An approximate semianalytical method for two-phase flow analysis of liquid-rich shale gas and tight light-oil wells. J. Petrol. Sci. Eng. 2019, 176, 562–572. [Google Scholar] [CrossRef]
- Wang, H.; Wu, W.; Chen, T.; Yu, J.; Pan, J. Pore structure and fractal analysis of shale oil reservoirs: A case study of the Paleogene Shahejie Formation in the Dongying Depression, Bohai Bay, China. J. Petrol. Sci. Eng. 2019, 177, 711–723. [Google Scholar] [CrossRef]
- Zhang, S.; Yan, J.; Hu, Q.; Wang, J.; Tian, T.; Chao, J.; Wang, M. Integrated NMR and FE-SEM methods for pore structure characterization of Shahejie shale from the Dongying Depression, Bohai Bay Basin. Mar. Petrol. Geol. 2019, 100, 85–94. [Google Scholar] [CrossRef]
- Wang, Y.; Gao, Y.; Fang, Z. Pore throat structure and classification of Paleogene tight reservoirs in Jiyang depression, Bohai Bay Basin, China. Petrol. Explor. Dev. 2021, 45, 208–322. [Google Scholar] [CrossRef]
- Wang, F.; Yang, K.; Zai, Y. Multifractal characteristics of shale and tight sandstone pore structures with nitrogen adsorption and nuclear magnetic resonance. Petrol. Sci. 2020, 17, 1209–1220. [Google Scholar] [CrossRef]
- Yin, X.; Shu, J.; Chen, S.; Wu, P.; Gao, W.; Gao, J.; Shi, X. Impact of rock type on the pore structures and physical properties within a tight sandstone reservoir in the Ordos Basin, NW China. Petrol. Sci. 2020, 17, 896–991. [Google Scholar] [CrossRef]
- Li, Z.; Xu, Z. The problems and progress in the experimental study of Mico/Nano-scale flow. J. Exp. Fluid Mech. 2014, 28, 1–11. [Google Scholar] [CrossRef]
- Majumder, M.; Chopra, N.; Andrews, R.; Hinds, B. Enhanced flow in carbon nanotubes. Nature 2005, 438, 44. [Google Scholar] [CrossRef] [PubMed]
- Holt, J.; Park, H.; Wang, Y.; Stadermann, M.; Artyukhin, A.; Grigoropoulos, C.; Aleksandr, N.; Bakajin, O. Fast mass transport through sub-2-nanometer carbon nanotubes. Science 2006, 312, 1034–1037. [Google Scholar] [CrossRef] [PubMed]
- Qin, X.; Yuan, Q.; Zhao, Y.; Xie, S.; Liu, Z. Measurement of the rate of water translocation through carbon nanotubes. Nano Lett. 2011, 11, 2173–2177. [Google Scholar] [CrossRef] [PubMed]
- Whitby, M.; Cagnon, L.; Thanou, M.; Quirke, N. Enhanced fluid flow through nanoscale carbon pipes. Nano Lett. 2008, 8, 2632–2637. [Google Scholar] [CrossRef] [PubMed]
- Secchi, E.; Marbach, S.; Nigues, A.; Stein, D.; Siria, A.; Bocquet, L. Massive radius-dependent flow slippage in carbon nanotubes. Nature 2016, 537, 210–213. [Google Scholar] [CrossRef] [PubMed]
- Chen, M.; Li, M.; Zhao, J.; Kuang, Y. Irreducible water distribution from nuclear magnetic resonance and constant-rate mercury injection methods in tight oil reservoirs. Int. J. Oil Gas Coal Technol. 2018, 17, 443–457. [Google Scholar] [CrossRef]
- Su, Y.; Fu, J.; Li, L.; Wang, W.; Zafar, A.; Zhang, M.; Ouyang, W. A new model for predicting irreducible water saturation in tight gas reservoirs. Petrol. Sci. 2020, 17, 1087–1100. [Google Scholar] [CrossRef] [Green Version]
- Xia, Y.; Wei, W.; Liu, Y.; Cai, Z.; Zhang, Q.; Cai, J. A fractal-based approach to evaluate the effect of microstructure on the permeability of two-dimensional porous media. Appl. Geochem. 2021, 131, 105013. [Google Scholar] [CrossRef]
- Zhang, Y.; Zeng, J.; Cai, J.; Feng, S.; Feng, X.; Qiao, J. A Mathematical Model for Determining Oil Migration Characteristics in Low-Permeability Porous Media Based on Fractal Theory. Transp. Porous Med. 2019, 129, 633–652. [Google Scholar] [CrossRef]
- Vinogradov, J.; Hill, R.; Jougnot, D. Influence of pore size distribution on the electrokinetic coupling coefficient in two-phase flow conditions. Water 2021, 13, 2316. [Google Scholar] [CrossRef]
- Soldi, M.; Guarracino, L.; Jougnot, D. A simple hysteretic constitutive model for unsaturated flow. Transp. Porous Med. 2017, 120, 271–285. [Google Scholar] [CrossRef] [Green Version]
- Guarracino, L. A fractal constitutive model for unsaturated flow in fractured hard rocks. J. Hydrol. 2006, 324, 154–162. [Google Scholar] [CrossRef]
- Guarracino, L.; Rötting, T.; Carrera, J. A fractal model to describe the evolution of multiphase flow properties during mineral dissolution. Adv. Water Resour. 2014, 67, 78–86. [Google Scholar] [CrossRef]
- Nguyen, V.; Damien, J.; Luong, D.; Phan, V.; Tran, T.; Dang, T.; Nguyen, M. Predicting water flow in fully and partially saturated porous media: A new fractal-based permeability model. Hydrogeol. J. 2021, 29, 2017–2031. [Google Scholar]
- Chen, H.; Chen, K.; Yang, M.; Xu, P. A fractal capillary model for multiphase flow in porous media with hysteresis effect. Int. J. Multiph. Flow 2020, 125, 103208. [Google Scholar] [CrossRef]
- Makhnenko, R.Y.; Labuz, J.F. Elastic and inelastic deformation of fluid-saturated rock. Philos. Trans. R. Soc. A 2016, 374, 20150422. [Google Scholar] [CrossRef] [Green Version]
- Pride, S.R.; Berryman, J.G.; Commer, M.; Nakagawa, S.; Newman, G.A.; Vasco, D.W. Changes in geophysical properties caused by fluid injection into porous rocks: Analytical models. Geophys. Prospect. 2017, 65, 766–790. [Google Scholar] [CrossRef] [Green Version]
- Tan, X.; Li, X.; Liu, J.; Zhang, L.; Cai, J. Fractal analysis of stress sensitivity of permeability in porous media. Fractals 2014, 23, 1550001. [Google Scholar] [CrossRef]
- Tan, X.; Li, X.; Liu, J.; Zhang, L.; Fan, Z. Study of the effects of stress sensitivity on the permeability and porosity of fractal porous media. Phys. Lett. A 2015, 397, 2458–2465. [Google Scholar] [CrossRef]
- Lei, G.; Dong, P.; Wu, Z.; Mo, S.; Gai, S.; Zhao, C.; Liu, Z. A fractal model for the stress-dependent permeability and relative permeability in tight sandstones. J. Can. Pet. Technol. 2015, 54, 36–48. [Google Scholar] [CrossRef]
- Lei, G.; Dong, Z.; Li, W.; Wen, Q.; Wang, C. Theoretical study on stress sensitivity of fractal porous media with irreducible water. Fractal 2018, 26, 1850004. [Google Scholar] [CrossRef]
- Wang, F.; Liu, Z.; Jiao, L.; Wang, C.; Guo, H. A fractal permeability model coupling boundary-lager effect for tight oil reservoir. Fractal 2017, 25, 1750042. [Google Scholar] [CrossRef]
- Huang, S.; Yao, Y.; Zhang, S.; Ji, J.; Ma, R. A fractal model for oil transport in tight porous media. Transp. Porous Med. 2018, 121, 725–739. [Google Scholar] [CrossRef]
- Wang, F.; Cheng, H. Effect of tortuosity on the stress-dependent permeability of tight sandstones: Analytical modelling and experimentation. Mar. Petrol. Geol. 2020, 120, 104524. [Google Scholar] [CrossRef]
- Dong, S.; Xu, L.; Dai, Z.; Xu, B.; Yu, Q.; Yin, S.; Zhang, X.; Zhang, C.; Zang, X.; Zhou, X.; et al. A novel fractal model for estimating permeability in low-permeable sandstone reservoirs. Fractals 2020, 28, 2040005. [Google Scholar] [CrossRef]
- Yu, B.; Cheng, P. A fractal permeability model for bi-dispersed porous media. Int. J. Heat Mass Tran. 2002, 45, 2983–2993. [Google Scholar] [CrossRef]
- Yu, B.; Li, J. Some fractal characters of porous media. Fractals 2001, 9, 365–372. [Google Scholar] [CrossRef]
- Wu, Z.; Cui, C.; Hao, Y.; Sun, Y.; Lv, G.; Sun, D.; Zhang, Z. Relative permeability model taking the roughness and actual fluid distributions into consideration for water flooding reservoirs. Arab. J. Sci. Eng. 2019, 44, 10513–10523. [Google Scholar] [CrossRef]
- Bonnet, E.; Bour, O.; Odling, N.; Davy, P.; Main, I.; Cowie, P.; Berkowitz, B. Scaling of fracture systems in geological media. Rev. Geophys. 2001, 39, 347–383. [Google Scholar] [CrossRef] [Green Version]
- Zheng, Q.; Yu, B.; Duan, Y.; Fang, Q. A fractal model for gas slippage factor in porous media in the slip flow regime. Chem. Eng. Sci. 2016, 87, 209–215. [Google Scholar] [CrossRef]
- Xu, P.; Yu, B. Developing a new form of permeability and Kozeny–Carman constant for homogeneous porous media by means of fractal geometry. Adv. Water Resour. 2008, 31, 74–81. [Google Scholar] [CrossRef]
- Yu, B.; Li, J. A Geometry Model for Tortuosity of Flow Path in Porous Media. Chin. Phys. Lett. 2004, 21, 1569–1571. [Google Scholar]
- Li, L.; Su, Y.; Wang, H.; Sheng, G.; Wang, W. A new slip length model for enhanced water flow coupling molecular interaction, pore dimension, wall roughness, and temperature. Adv. Polym. Technol. 2019, 6424012. [Google Scholar] [CrossRef] [Green Version]
- Wu, K.; Chen, Z.; Li, J.; Li, X.; Xu, J.; Dong, X. Wettability effect on nanoconfined water flow. Proc. Natl. Acad. Sci. USA 2019, 116, 3358–3363. [Google Scholar] [CrossRef] [Green Version]
- Mattia, D.; Calabro, F. Explaining high flow rate of water in carbon nanotubes via solid–liquid molecular interactions. Microfluid. Nanofluidics 2012, 13, 125–130. [Google Scholar] [CrossRef] [Green Version]
- Ma, C.; Chen, Y.; Sun, G.; Li, Q.; Gao, W.; Jiang, Q. Understanding water slippage through carbon nanotubes. R. Soc. Chem. 2021, 23, 14737. [Google Scholar] [CrossRef]
- Liu, G.; Yin, H.; Lan, Y.; Fei, S.; Yang, D. Experimental determination of dynamic pore-throat structure characteristics in a tight gas sandstone formation with consideration of effective stress. Mar. Petrol. Geol. 2020, 113, 104170. [Google Scholar] [CrossRef]
- Zhong, X.; Zhu, Y.; Liu, L.; Yang, H.; Li, Y.; Xie, Y.; Liu, L. The characteristics and influencing factors of permeability stress sensitivity of tight sandstone reservoirs. J. Petrol. Sci. Eng. 2020, 191, 107221. [Google Scholar] [CrossRef]
| Sources | Core’s No. | Porosity,% | Permeability, 10−3 μm2 | Core’s Length, cm | Core’s Diameter, cm | The Maximum Pore Diameter, μm | The Minimum Pore Diameter, μm |
|---|---|---|---|---|---|---|---|
| Liu et al. [48] | S161-1 | 13.95 | 1.00 | 3 | 2.5 | 32.6482 | 0.0123 |
| S148-2 | 10.54 | 0.55 | 3 | 2.5 | 0.6701 | 0.0021 | |
| Z41-9 | 6.16 | 0.20 | 3 | 2.5 | 4.9643 | 0.0001 | |
| Zhong et al. [49] | M132-1 | 15.01 | 1.99 | 3.11 | 2.51 | 12.9105 | 0.0067 |
| M217-1 | 6.21 | 0.95 | 3.12 | 2.51 | 7.2083 | 0.0068 | |
| M23-1 | 3.06 | 0.22 | 2.97 | 2.52 | 2.3986 | 0.0068 |
| Sources | Core’s No. | The Pore Fractal Dimension | The Tortuosity Fractal Dimension |
|---|---|---|---|
| Liu et al. [48] | S161-1 | 1.8916 | 1.1374 |
| S148-2 | 1.8300 | 1.2100 | |
| Z41-9 | 1.8851 | 1.1632 | |
| Zhong et al. [49] | M132-1 | 1.8912 | 1.1358 |
| M217-1 | 1.8267 | 1.2298 | |
| M23-1 | 1.7418 | 1.3408 |
| The Effective Stress, MPa | Core’s Number: M132-1 | Core’s Number: M217-1 | Core’s Number: M23-1 | ||||||
|---|---|---|---|---|---|---|---|---|---|
| Experimental Results | Calculated Results | Relative Errors | Experimental Results | Calculated Results | Relative Errors | Experimental Results | Calculated Results | Relative Errors | |
| 0 | 1.000 | 1.000 | 0.000% | 1.0000 | 1.0000 | 0.000% | 1.000 | 1.000 | 0.000% |
| 5 | 0.731 | 0.759 | 3.818% | 0.6906 | 0.6629 | 4.014% | 0.629 | 0.640 | 1.741% |
| 15 | 0.596 | 0.591 | 0.802% | 0.4487 | 0.4710 | 4.984% | 0.430 | 0.445 | 3.484% |
| 25 | 0.502 | 0.489 | 2.622% | 0.3651 | 0.3668 | 0.469% | 0.357 | 0.340 | 4.801% |
| 35 | 0.435 | 0.414 | 4.846% | 0.3284 | 0.2949 | 10.208% | 0.298 | 0.269 | 9.806% |
| 40 | 0.410 | 0.383 | 6.443% | 0.3160 | 0.2665 | 15.651% | 0.263 | 0.242 | 8.230% |
| The Effective Stress, MPa | Dimensionless Permeability | ||||||||
|---|---|---|---|---|---|---|---|---|---|
| Core’s Number: S161-1 | Core’s Number: S148-2 | Core’s Number: Z41-9 | |||||||
| Experimental Results | Calculated Results | Relative Errors | Experimental Results | Calculated Results | Relative Errors | Experimental Results | Calculated Results | Relative Errors | |
| 0 | 1.000 | 1 | 0.000% | 1.000 | 1.000 | 0.00% | 1.000 | 1.000 | 0.000% |
| 10 | 0.709 | 0.674 | 4.937% | 0.585 | 0.558 | 4.62% | 0.531 | 0.515 | 3.107% |
| 20 | 0.462 | 0.508 | 10.043% | 0.264 | 0.314 | 18.75% | 0.170 | 0.239 | 40.588% |
| 29 | 0.415 | 0.450 | 8.386% | 0.219 | 0.265 | 21.05% | 0.110 | 0.162 | 47.364% |
| Parameters | Case 1 | Case 2 | Case 3 | Case 4 | Case 5 | Case 6 |
|---|---|---|---|---|---|---|
| The pore fractal dimension | 1.5–1.7 | 1.8912 | 1.8912 | 1.8912 | 1.8912 | 1.8912 |
| The tortuosity fractal dimension | 1.1358 | 1.1–1.5 | 1.1358 | 1.1358 | 1.1358 | 1.1358 |
| Irreducible water | 0.45 | 0.45 | 0.35–0.55 | 0.45 | 0.45 | 0.45 |
| The length of slipage, nm | 23 | 23 | 23 | 1–200 | 23 | 23 |
| Poisson’s ratio | 0.15 | 0.15 | 0.15 | 0.15 | 0.15–0.35 | 0.15 |
| The rock elastic modulus, GPa | 1.8 | 1.8 | 1.8 | 1.8 | 1.8 | 1–6 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wu, Z.; Cui, C.; Yang, Y.; Zhang, C.; Wang, J.; Cai, X. A Fractal Permeability Model of Tight Oil Reservoirs Considering the Effects of Multiple Factors. Fractal Fract. 2022, 6, 153. https://doi.org/10.3390/fractalfract6030153
Wu Z, Cui C, Yang Y, Zhang C, Wang J, Cai X. A Fractal Permeability Model of Tight Oil Reservoirs Considering the Effects of Multiple Factors. Fractal and Fractional. 2022; 6(3):153. https://doi.org/10.3390/fractalfract6030153
Chicago/Turabian StyleWu, Zhongwei, Chuanzhi Cui, Yong Yang, Chuanbao Zhang, Jian Wang, and Xin Cai. 2022. "A Fractal Permeability Model of Tight Oil Reservoirs Considering the Effects of Multiple Factors" Fractal and Fractional 6, no. 3: 153. https://doi.org/10.3390/fractalfract6030153
APA StyleWu, Z., Cui, C., Yang, Y., Zhang, C., Wang, J., & Cai, X. (2022). A Fractal Permeability Model of Tight Oil Reservoirs Considering the Effects of Multiple Factors. Fractal and Fractional, 6(3), 153. https://doi.org/10.3390/fractalfract6030153





