Mixed Convection Flow over an Elastic, Porous Surface with Viscous Dissipation: A Robust Spectral Computational Approach
Abstract
:1. Introduction
2. Problem Description and Modeling
Similarity Analysis
3. Implementation of Numerical Method
3.1. Basic Steps to Apply Spectral Local Linearization Method
3.2. Implementation of the Spectral Local Linearization Method
3.3. Convergence Analysis
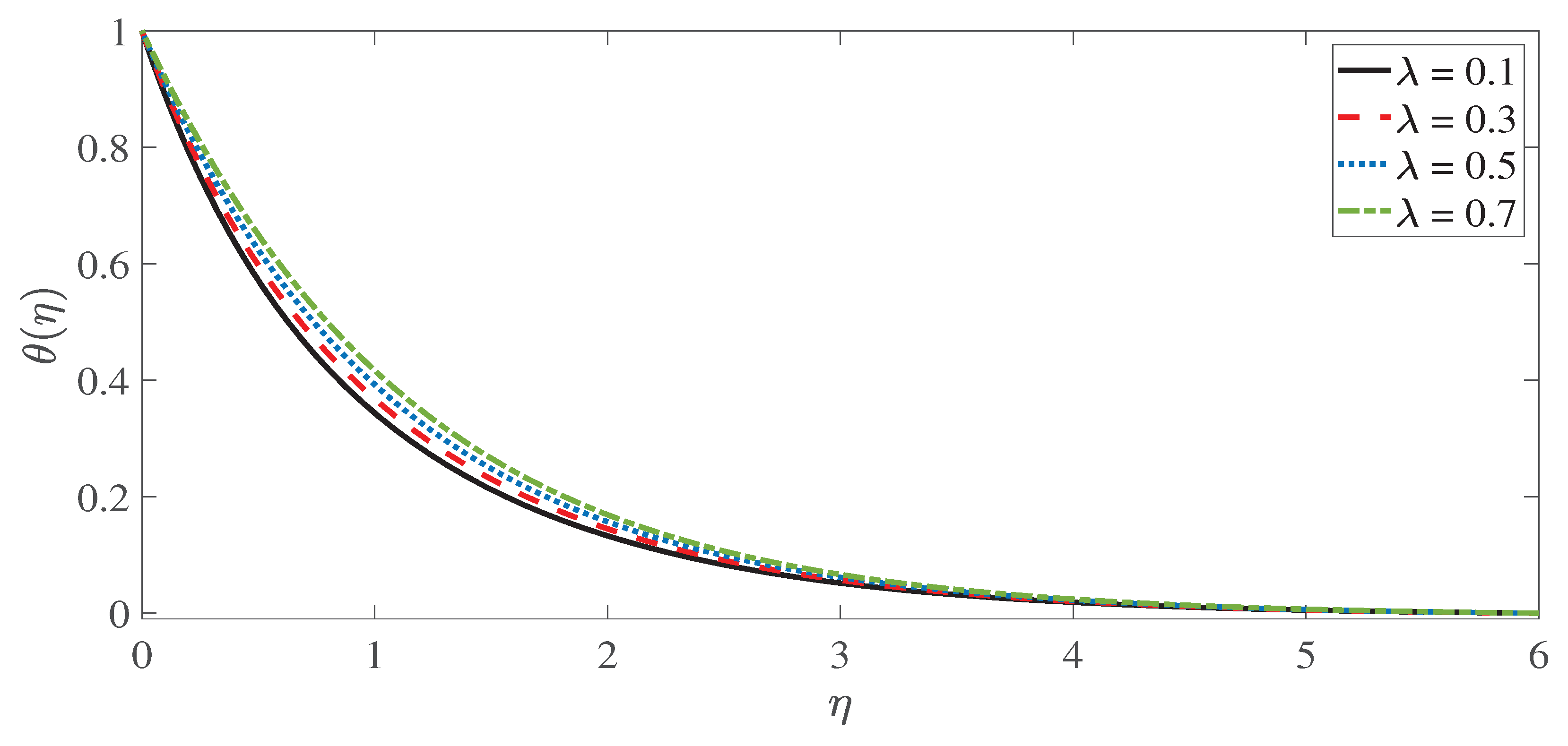
4. Numerical Results and Discussion
5. Summary and Conclusions
- (i)
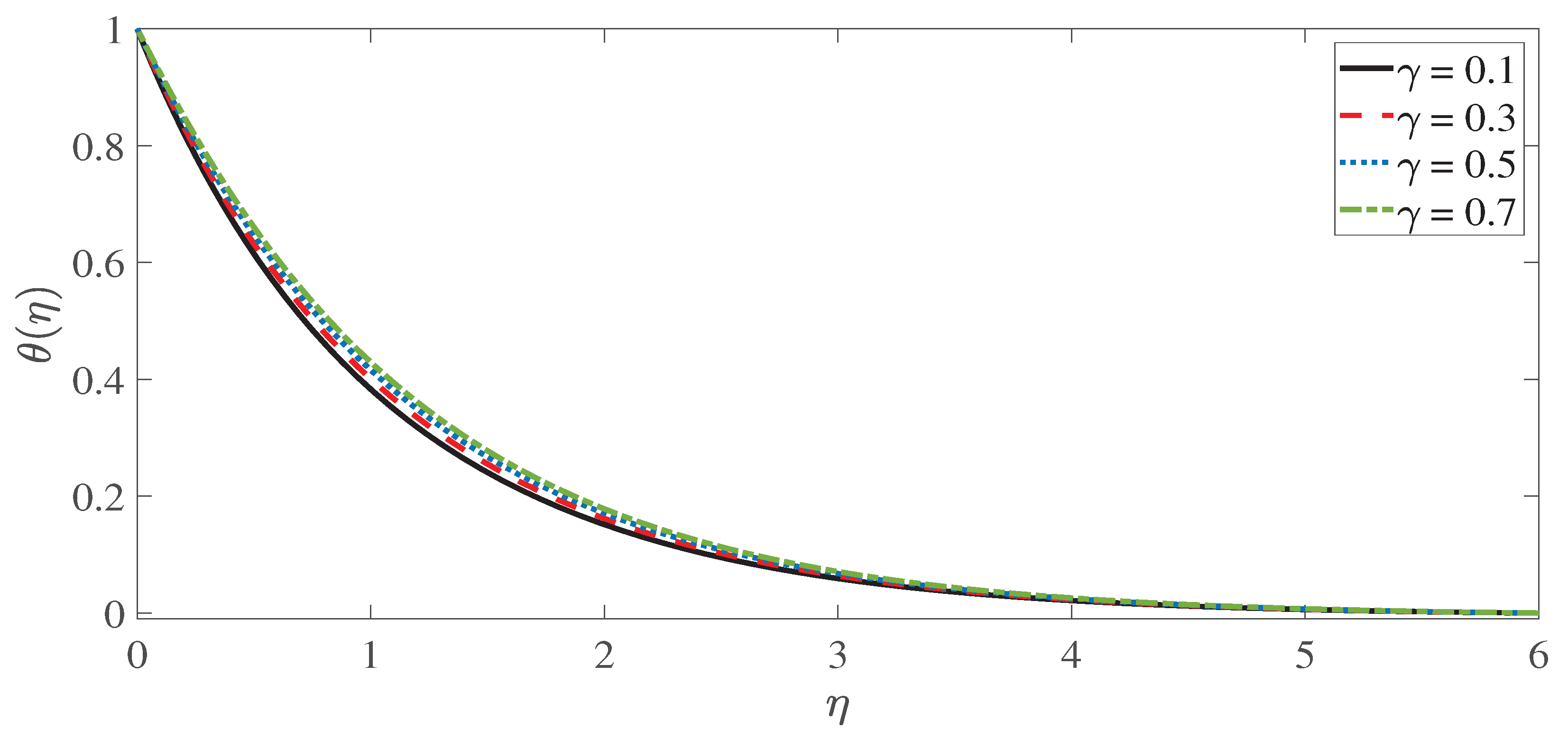
- The magnetic and permeability parameters augment the temperature profile, while decreasing the velocity profile.
- (ii)
- The mixed convection parameter increases the velocity profile, while reducing the temperature profile.
- (iii)
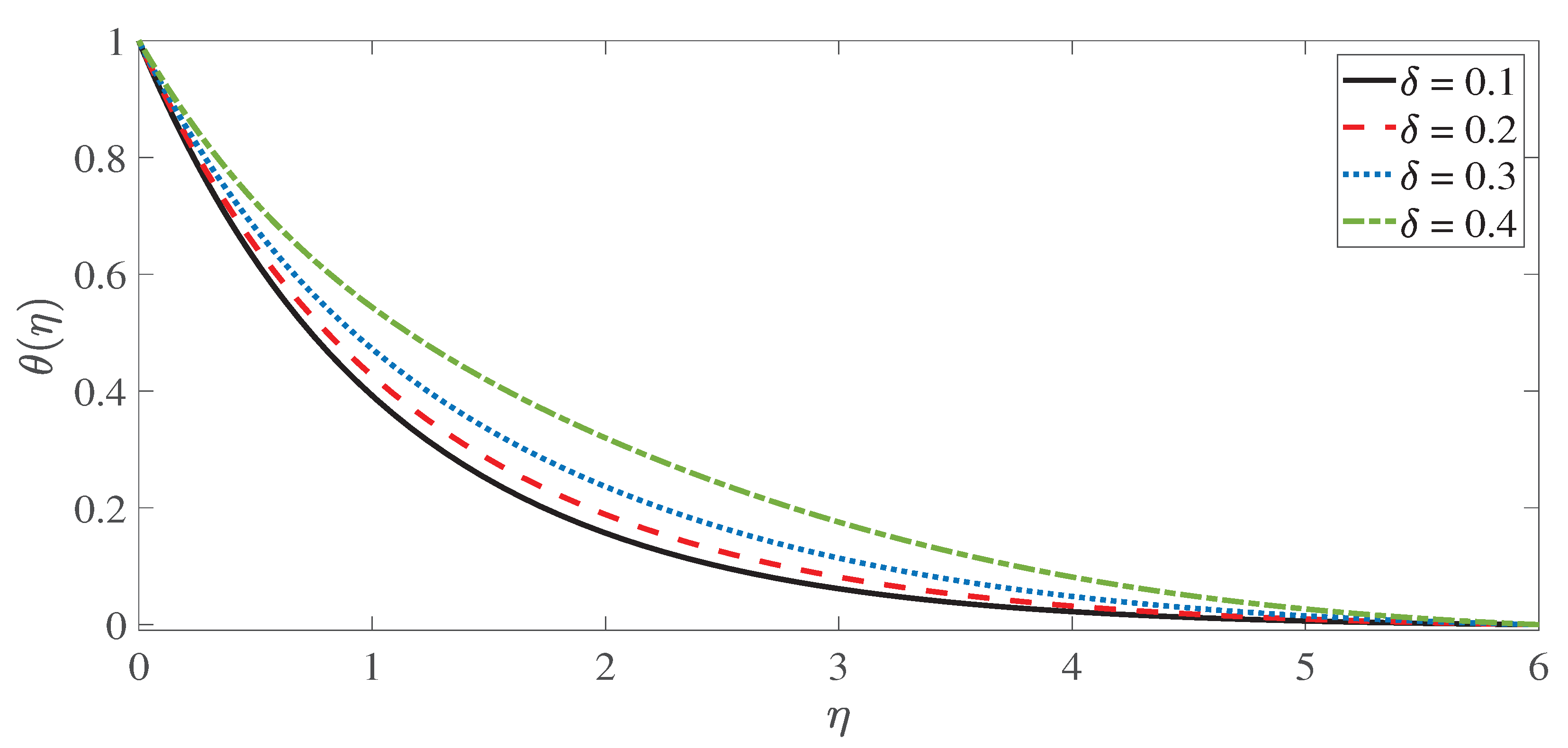
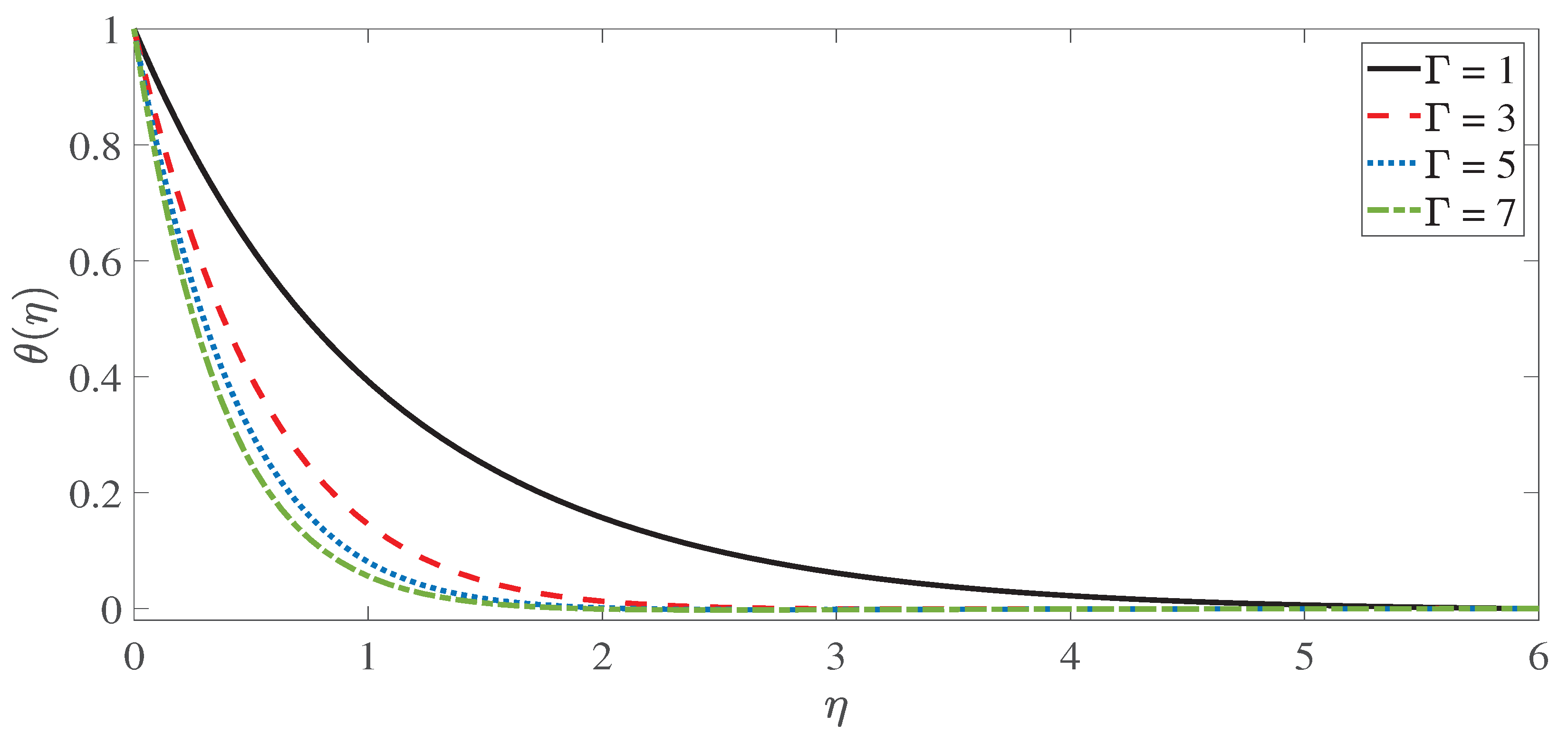
- The Eckert number and the heat generation parameter have a significant effect to increase the temperature profile and the thickness of the thermal boundary layer.
- (iv)
- Increasing the Prandtl number reduces the temperature profile, because the momentum diffusivity is more dominant and the increased flow dampens the development of the temperature profile.
- (v)
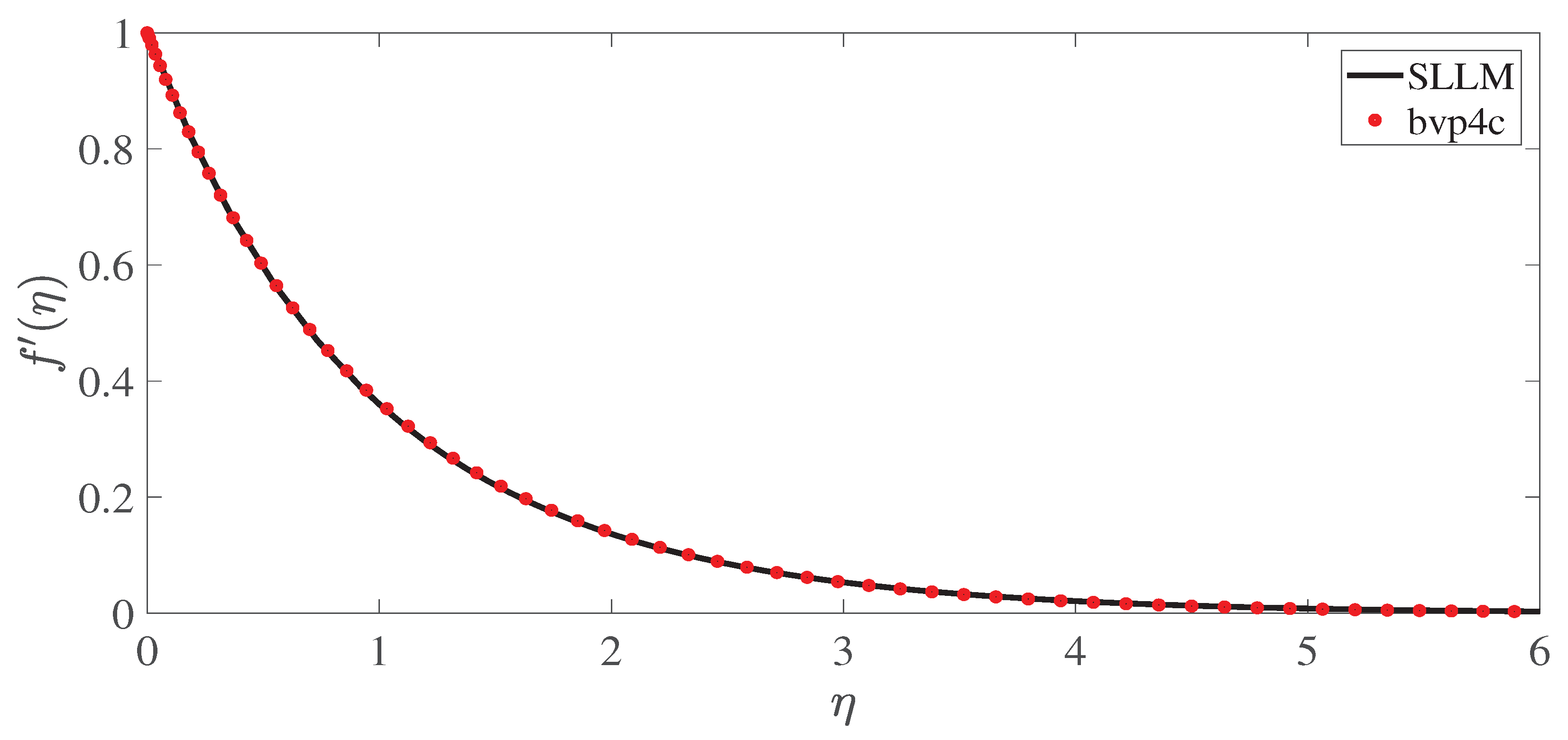
- The numerical results obtained with the Spectral local linearization method are consistent with the results obtained with other related methodologies such as bvp4c.
- (vi)
- When the skin friction profile is compared to previously published data, it is found that the current numerical results show a good agreement and this validates the proposed method.
- (vii)
- The SLLM does not lose accuracy as the number of collocation points increases.
- (viii)
- For all of the model parameters investigated in this work, the method has been found to rapidly converge to the respective solutions.
- (ix)
- When compared to other approaches, the suggested methodology is computationally more efficient and shows better performance with fewer collocation points and four iterations. Because this method is more reliable, simple, and efficient, the SLLM methodology is considered more suitable for the solution of nonlinear boundary value problems.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Janna, W.S. Engineering Heat Transfer; CRC Press: Boca Raton, FL, USA, 2018. [Google Scholar]
- Özisik, M.N.; Orlande, H.R. Inverse Heat Transfer: Fundamentals and Applications; CRC Press: Boca Raton, FL, USA, 2021. [Google Scholar]
- Kay, J.M.; Nedderman, R.M. An Introduction to Fluid Mechanics and Heat Transfer: With Applications in Chemical and Mechanical Process Engineering; Cambridge University Press: Cambridge, UK, 1975. [Google Scholar]
- McDonough, J. A perspective on the current and future roles of additive manufacturing in process engineering, with an emphasis on heat transfer. Therm. Sci. Eng. Prog. 2020, 19, 100594. [Google Scholar] [CrossRef]
- Rahmati, A.R.; Akbari, O.A.; Marzban, A.; Toghraie, D.; Karimi, R.; Pourfattah, F. Simultaneous investigations the effects of non-Newtonian nanofluid flow in different volume fractions of solid nanoparticles with slip and no-slip boundary conditions. Therm. Sci. Eng. Prog. 2018, 5, 263–277. [Google Scholar] [CrossRef]
- Sene, N. Second-grade fluid with Newtonian heating under Caputo fractional derivative: Analytical investigations via Laplace transforms. Math. Model. Numer. Simul. Appl. 2022, 2, 13–25. [Google Scholar] [CrossRef]
- Stangle, G.C.; Aksay, I.A. Simultaneous momentum, heat and mass transfer with chemical reaction in a disordered porous medium: Application to binder removal from a ceramic green body. Chem. Eng. Sci. 1990, 45, 1719–1731. [Google Scholar] [CrossRef] [Green Version]
- Polyanin, A.D.; Kutepov, A.M.; Kazenin, D.; Vyazmin, A. Hydrodynamics, Mass and Heat Transfer in Chemical Engineering; CRC Press: Boca Raton, FL, USA, 2001. [Google Scholar]
- Dogonchi, A.; Nayak, M.; Karimi, N.; Chamkha, A.J.; Ganji, D.D. Numerical simulation of hydrothermal features of Cu–H2O nanofluid natural convection within a porous annulus considering diverse configurations of heater. J. Therm. Anal. Calorim. 2020, 141, 2109–2125. [Google Scholar] [CrossRef]
- Cai, J.; Hajibeygi, H.; Yao, J.; Hassanizadeh, M. Advances in porous media science and engineering from InterPore2020 perspective. Adv.-Geo-Energy Res. 2020, 4, 352–355. [Google Scholar] [CrossRef]
- Nield, D.A.; Bejan, A. Convection in Porous Media; Springer: New York, NY, USA, 2006; Volume 3. [Google Scholar]
- Golparvar, A.; Zhou, Y.; Wu, K.; Ma, J.; Yu, Z. A comprehensive review of pore scale modeling methodologies for multiphase flow in porous media. Adv.-Geo-Energy Res. 2018, 2, 418–440. [Google Scholar] [CrossRef] [Green Version]
- Michaelides, E. Exergy Analysis for Energy Conversion Systems; Cambridge University Press: Cambridge, UK, 2021. [Google Scholar]
- Sakiadis, B.C. Boundary-layer behavior on continuous solid surfaces: I. Boundary-layer equations for two-dimensional and axisymmetric flow. AIChE J. 1961, 7, 26–28. [Google Scholar] [CrossRef]
- Crane, L.J. Flow past a stretching plate. Zeitschrift für angewandte Mathematik und Physik ZAMP 1970, 21, 645–647. [Google Scholar] [CrossRef]
- Roşca, A.V.; Pop, I. Flow and heat transfer over a vertical permeable stretching/shrinking sheet with a second order slip. Int. J. Heat Mass Transf. 2013, 60, 355–364. [Google Scholar] [CrossRef]
- Swain, I.; Mishra, S.; Pattanayak, H. Flow over exponentially stretching sheet through porous medium with heat source/sink. J. Eng. 2015, 2015, 452592. [Google Scholar] [CrossRef] [Green Version]
- Othman, N.A.; Yacob, N.A.; Bachok, N.; Ishak, A.; Pop, I. Mixed convection boundary-layer stagnation point flow past a vertical stretching/shrinking surface in a nanofluid. Appl. Therm. Eng. 2017, 115, 1412–1417. [Google Scholar] [CrossRef]
- Kumar, K.G.; Krishnamurthy, M.; Rudraswamy, N. Boundary layer flow and melting heat transfer of Prandtl fluid over a stretching surface by considering Joule heating effect. Multidiscip. Model. Mater. Struct. 2019, 15, 337–352. [Google Scholar] [CrossRef]
- Gangadhar, K.; Edukondala Nayak, R.; Venkata Subba Rao, M. Buoyancy effect on mixed convection boundary layer flow of Casson fluid over a non linear stretched sheet using the spectral relaxation method. Int. J. Ambient. Energy 2020, 1–9. [Google Scholar] [CrossRef]
- Prabha, G.S.S.; Bharathi, M.; Kudenatti, R.B. Heat transfer through mixed convection boundary layer in a porous medium: LTNE analysis. Appl. Therm. Eng. 2020, 179, 115705. [Google Scholar] [CrossRef]
- Badruddin, I.A.; Khan, T.Y.; Baig, M.A.A. Heat transfer in porous media: A mini review. Mater. Today Proc. 2020, 24, 1318–1321. [Google Scholar] [CrossRef]
- Ali, A.; Marwat, D.N.K.; Ali, A. Analysis of flow and heat transfer over stretching/shrinking and porous surfaces. J. Plast. Film Sheeting 2021, 38, 21–45. [Google Scholar] [CrossRef]
- Ilya, A.; Ashraf, M.; Ali, A.; Shah, Z.; Kumam, P.; Thounthong, P. Heat source and sink effects on periodic mixed convection flow along the electrically conducting cone inserted in porous medium. PLoS ONE 2021, 16, e0260845. [Google Scholar] [CrossRef]
- Adeniyan, A.; Mabood, F.; Okoya, S. Effect of heat radiating and generating second-grade mixed convection flow over a vertical slender cylinder with variable physical properties. Int. Commun. Heat Mass Transf. 2021, 121, 105110. [Google Scholar] [CrossRef]
- Winter, H. Viscous dissipation term in energy equations. Calc. Meas. Tech. Momentum Energy Mass Transf. 1987, 7, 27–34. [Google Scholar]
- Barletta, A.; Celli, M.; Rees, D.A. The onset of convection in a porous layer induced by viscous dissipation: A linear stability analysis. Int. J. Heat Mass Transf. 2009, 52, 337–344. [Google Scholar] [CrossRef]
- Jha, B.K.; Ajibade, A.O. Effect of viscous dissipation on natural convection flow between vertical parallel plates with time-periodic boundary conditions. Commun. Nonlinear Sci. Numer. Simul. 2012, 17, 1576–1587. [Google Scholar] [CrossRef]
- Ashraf, M.; Fatima, A.; Gorla, R. Periodic momentum and thermal boundary layer mixed convection flow around the surface of a sphere in the presence of viscous dissipation. Can. J. Phys. 2017, 95, 976–986. [Google Scholar] [CrossRef]
- Jafar, K.; Nazar, R.; Ishak, A.; Pop, I. MHD flow and heat transfer over stretching/shrinking sheets with external magnetic field, viscous dissipation and Joule effects. Can. J. Chem. Eng. 2012, 90, 1336–1346. [Google Scholar] [CrossRef]
- Dessie, H.; Kishan, N. MHD effects on heat transfer over stretching sheet embedded in porous medium with variable viscosity, viscous dissipation and heat source/sink. Ain Shams Eng. J. 2014, 5, 967–977. [Google Scholar] [CrossRef] [Green Version]
- Bibi, M.; Malik, M.; Tahir, M. Numerical study of unsteady Williamson fluid flow and heat transfer in the presence of MHD through a permeable stretching surface. Eur. Phys. J. Plus 2018, 133, 154. [Google Scholar] [CrossRef]
- Alarifi, I.M.; Abokhalil, A.G.; Osman, M.; Lund, L.A.; Ayed, M.B.; Belmabrouk, H.; Tlili, I. MHD flow and heat transfer over vertical stretching sheet with heat sink or source effect. Symmetry 2019, 11, 297. [Google Scholar] [CrossRef] [Green Version]
- Swain, B.; Parida, B.; Kar, S.; Senapati, N. Viscous dissipation and joule heating effect on MHD flow and heat transfer past a stretching sheet embedded in a porous medium. Heliyon 2020, 6, e05338. [Google Scholar] [CrossRef]
- Megahed, A.M.; Reddy, M.G.; Abbas, W. Modeling of MHD fluid flow over an unsteady stretching sheet with thermal radiation, variable fluid properties and heat flux. Math. Comput. Simul. 2021, 185, 583–593. [Google Scholar] [CrossRef]
- Sarada, K.; Gowda, R.J.P.; Sarris, I.E.; Kumar, R.N.; Prasannakumara, B.C. Effect of magnetohydrodynamics on heat transfer behaviour of a non-Newtonian fluid flow over a stretching sheet under local thermal non-equilibrium condition. Fluids 2021, 6, 264. [Google Scholar] [CrossRef]
- Zhou, J.C.; Abidi, A.; Shi, Q.H.; Khan, M.R.; Rehman, A.; Issakhov, A.; Galal, A.M. Unsteady radiative slip flow of MHD Casson fluid over a permeable stretched surface subject to a non-uniform heat source. Case Stud. Therm. Eng. 2021, 26, 101141. [Google Scholar] [CrossRef]
- Ullah, H.; Khan, I.; Fiza, M.; Hamadneh, N.N.; Fayz-Al-Asad, M.; Islam, S.; Khan, I.; Raja, M.A.Z.; Shoaib, M. MHD boundary layer flow over a stretching sheet: A new stochastic method. Math. Probl. Eng. 2021, 2021, 9924593. [Google Scholar] [CrossRef]
- Bhatti, M.M.; Jun, S.; Khalique, C.M.; Shahid, A.; Fasheng, L.; Mohamed, M.S. Lie group analysis and robust computational approach to examine mass transport process using Jeffrey fluid model. Appl. Math. Comput. 2022, 421, 126936. [Google Scholar] [CrossRef]
- Keskin, A.Ü. Solution of BVPs using bvp4c and bvp5c of MATLAB. In Boundary Value Problems for Engineers; Springer: Berlin/Heidelberg, Germany, 2019; pp. 417–510. [Google Scholar]
- Tabbakh, Z.; Ellaia, R.; Ouazar, D. Application of a local meshless modified characteristic method to incompressible fluid flows with heat transport problem. Eng. Anal. Bound. Elem. 2022, 134, 612–624. [Google Scholar] [CrossRef]
- Incropera, F.P.; Dewitt, D.P.; Bergman, T.L.; Lavine, A.S. Fundamentals of Heat and Mass Transfer; John Wiley & Sons Inc.: Hoboken, NJ, USA, 2002; 981p. [Google Scholar]
- Feng, Z.G.; Michaelides, E.E. Inclusion of heat transfer computations for particle laden flows. Phys. Fluids 2008, 20, 040604. [Google Scholar] [CrossRef]
- Shen, J.; Tang, T.; Wang, L.L. Spectral Methods: Algorithms, Analysis and Applications; Springer Science & Business Media: Berlin/Heidelberg, Germany, 2011; Volume 41. [Google Scholar]
- Fang, T.; Zhang, J.; Zhong, Y. Boundary layer flow over a stretching sheet with variable thickness. Appl. Math. Comput. 2012, 218, 7241–7252. [Google Scholar] [CrossRef]
- Prakash, D.; Muthtamilselvan, M.; Doh, D.H. Unsteady MHD non-Darcian flow over a vertical stretching plate embedded in a porous medium with non-uniform heat generation. Appl. Math. Comput. 2014, 236, 480–492. [Google Scholar]






| Ceramic engineering [7] | Simultaneous mass and heat transfer in disordered media occurs during the burnout/drying of the binder system from green compacts during the colloidal process of ceramics. |
| Chemical engineering [8] | During the interim eventual and storage of nuclear waste, as well as in packet bed reactors. |
| Ground water hyrology [9] | The investigation of seepage water through river beds and underground water resources. |
| Industrial engineering [10] | The primary goal of filtration analysis is to examine the movement of fluid through a porous medium, leaving behind unwanted material. As a result of the mass deposition, the porous medium is constantly changing and altering the system’s pressure drop properties. |
| Mechanical engineering [11] | To achieve effective insulation, solid conduction must be minimized, porosity must be maximized to reduce effective thermal conductivity, and free convection must be suppressed. The same concept is useful when producing high-performance insulators for cryogenic containers. |
| Petroleum engineering [12] | For oil recovery mechanisms. |
| Geophysics [13] | In the analysis of geo-pressurized reservoirs, and extraction of geothermal energy. |
| Function Name | Calls | Total Time (s) | Self Time (s) |
|---|---|---|---|
| SLLM code | 1 | 0.284 | 0.202 |
| Newplot | 2 | 0.033 | 0.013 |
| xlabel | 2 | 0.029 | 0.023 |
| newplot > ObserveAxesNextPlot | 2 | 0.017 | 0.004 |
| cla | 2 | 0.013 | 0.007 |
| hold | 2 | 0.011 | 0.009 |
| ylabel | 2 | 0.010 | 0.008 |
| convertStringToCharArgs | 4 | 0.007 | 0.005 |
| graphics/private/clo | 2 | 0.005 | 0.005 |
| gobjects | 4 | 0.003 | 0.003 |
| convertStringsToChars | 4 | 0.002 | 0.001 |
| markfigure | 2 | 0.001 | 0.001 |
| graphics/private/claNotify | 2 | 0.001 | 0.001 |
| graph2d/private/labelcheck | 4 | 0.001 | 0.001 |
| convertStringsToChars > convertStrings | 16 | 0.001 | 0.001 |
| axescheck | 2 | 0.000 | 0.000 |
| newplot > ObserveFigureNextPlo | 2 | 0.000 | 0.000 |
| Iterations | N | Skin Friction Coefficient | Nusselt Number |
|---|---|---|---|
| 4 | 5 | ||
| 4 | 10 | ||
| 4 | 100 | ||
| − | bvp4c |
| SLLM | bvp4c | ||||||||
|---|---|---|---|---|---|---|---|---|---|
| 0.2 | 0.2 | 0.5 | 1 | 0.1 | 0.2 | 0 | 1 | ||
| 1 | |||||||||
| 1.5 | |||||||||
| 0.5 | |||||||||
| 0.8 | |||||||||
| 1.2 | |||||||||
| 0.4 | |||||||||
| 1.0 | |||||||||
| 1.5 | |||||||||
| 0.71 | |||||||||
| 2 | |||||||||
| 3 | |||||||||
| 0 | |||||||||
| 0.12 | |||||||||
| 0.3 | |||||||||
| 0.4 | |||||||||
| 0.5 | |||||||||
| 0 | |||||||||
| 0.5 | |||||||||
| 0 | |||||||||
| 0.6 |
| SLLM | bvp4c | ||||||
|---|---|---|---|---|---|---|---|
| 0.2 | 0.2 | 0.5 | 1 | 0.1 | 0.2 | ||
| 1 | |||||||
| 1.5 | |||||||
| 0.5 | |||||||
| 0.8 | |||||||
| 1.2 | |||||||
| 0.4 | |||||||
| 1 | |||||||
| 1.5 | |||||||
| 0.71 | |||||||
| 2 | |||||||
| 3 | |||||||
| 0 | |||||||
| 0.12 | |||||||
| 0.3 | |||||||
| 0.4 | |||||||
| 0.5 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, L.; Tariq, N.; Bhatti, M.M.; Michaelides, E.E. Mixed Convection Flow over an Elastic, Porous Surface with Viscous Dissipation: A Robust Spectral Computational Approach. Fractal Fract. 2022, 6, 263. https://doi.org/10.3390/fractalfract6050263
Zhang L, Tariq N, Bhatti MM, Michaelides EE. Mixed Convection Flow over an Elastic, Porous Surface with Viscous Dissipation: A Robust Spectral Computational Approach. Fractal and Fractional. 2022; 6(5):263. https://doi.org/10.3390/fractalfract6050263
Chicago/Turabian StyleZhang, Lijun, Nafisa Tariq, Muhammad Mubashir Bhatti, and Efstathios E. Michaelides. 2022. "Mixed Convection Flow over an Elastic, Porous Surface with Viscous Dissipation: A Robust Spectral Computational Approach" Fractal and Fractional 6, no. 5: 263. https://doi.org/10.3390/fractalfract6050263
APA StyleZhang, L., Tariq, N., Bhatti, M. M., & Michaelides, E. E. (2022). Mixed Convection Flow over an Elastic, Porous Surface with Viscous Dissipation: A Robust Spectral Computational Approach. Fractal and Fractional, 6(5), 263. https://doi.org/10.3390/fractalfract6050263








