Applications of Prabhakar-like Fractional Derivative for the Solution of Viscous Type Fluid with Newtonian Heating Effect
Abstract
:1. Introduction
2. Problem Description
- When , the Prabhakar derivative will transform into the Caputo derivative .
- When , then the relation between Prabhakar and CF derivative will become .
- When , then the connection between the AB derivative and Prabhakar derivative will develop as .
- When , the Prabhakar derivative will be with its kernel .
- When , the Prabhakar derivative with its kernel . As the LT of Prabhakar, fractional operator is, consequently,
3. Solution of the Problem
3.1. Solution of the Energy Profile
Classical Solution of the Energy Field
3.2. Solution of the Concentration Profile
Classical Solution of the Concentration Profile
3.3. Solution of Momentum Field
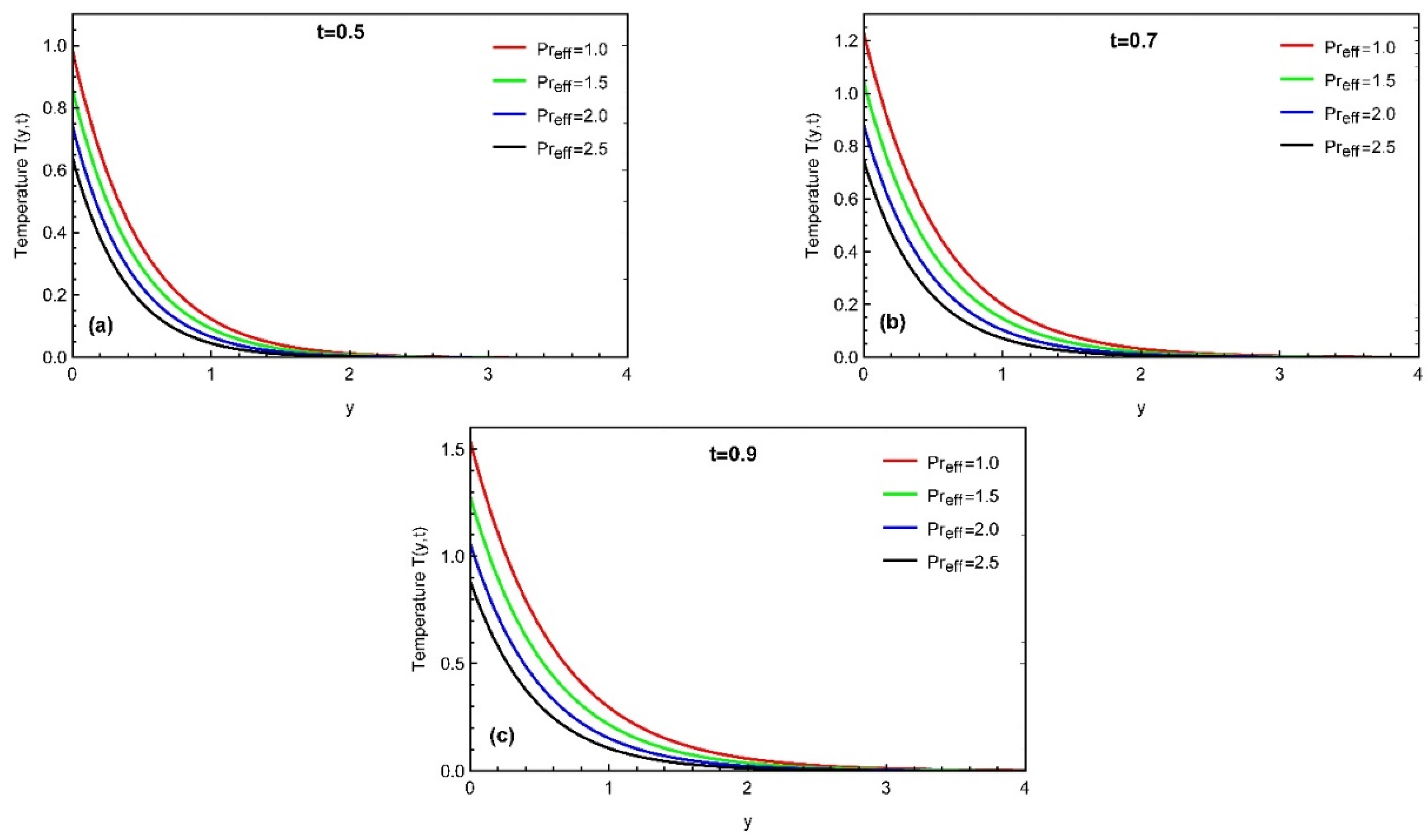
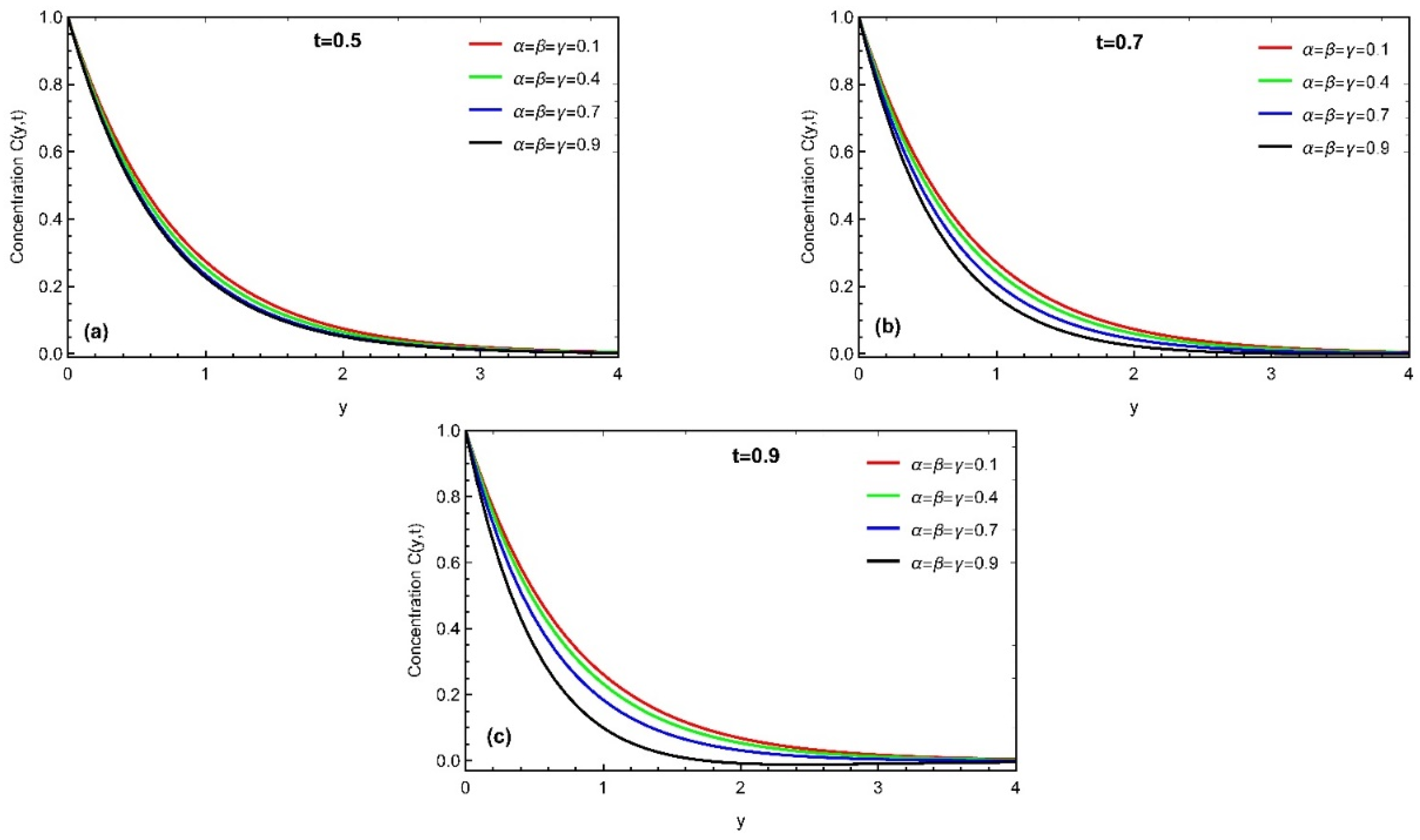
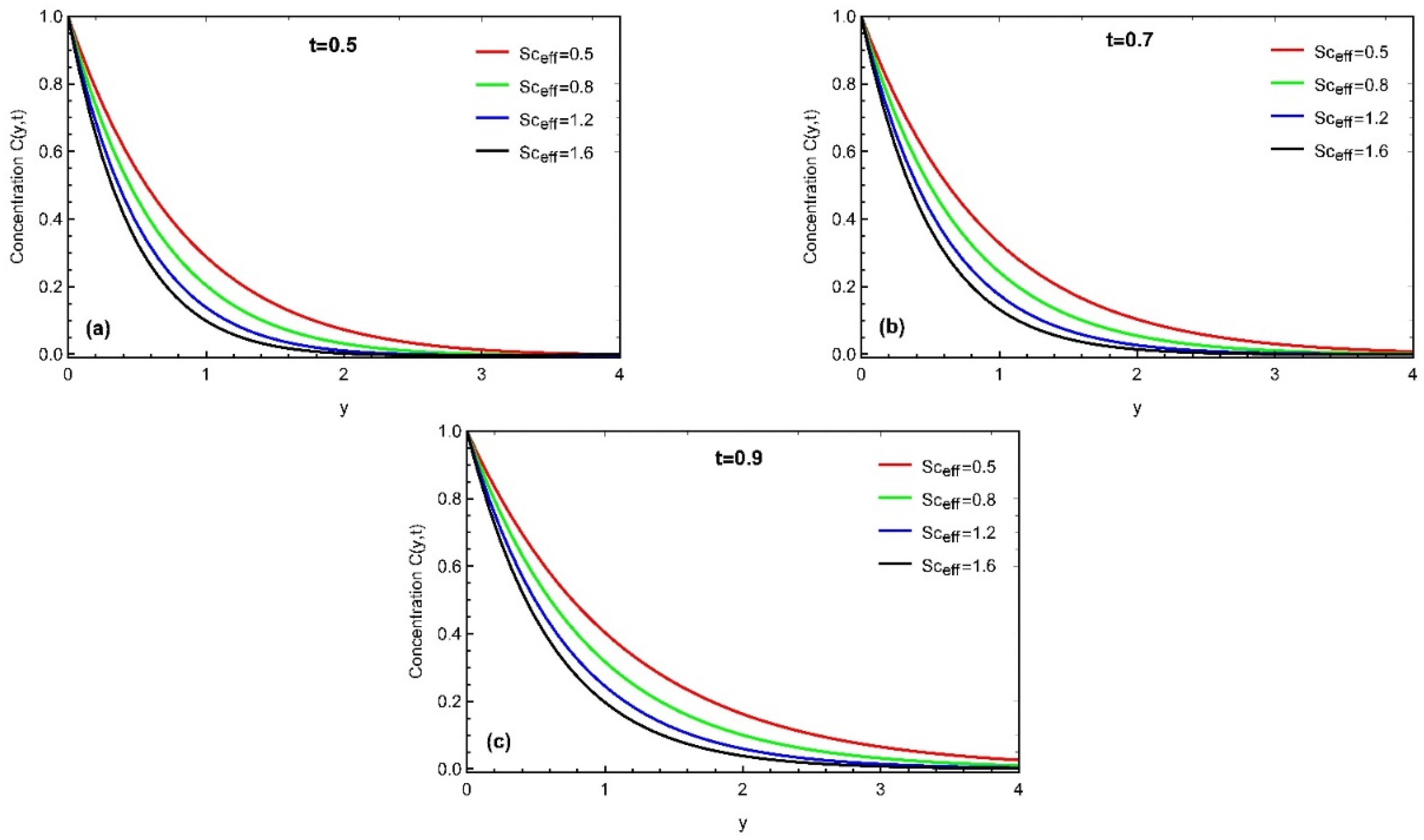
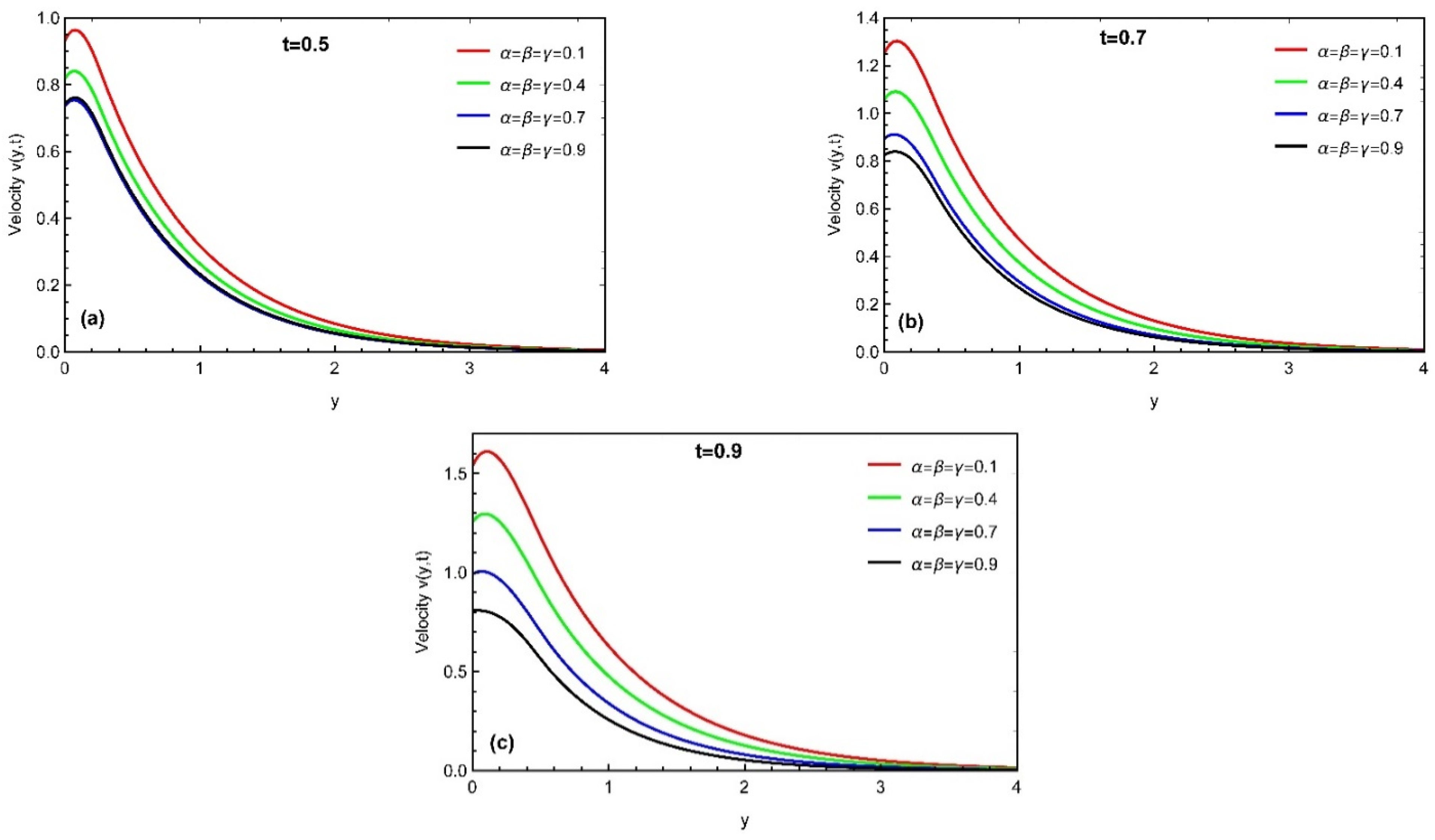
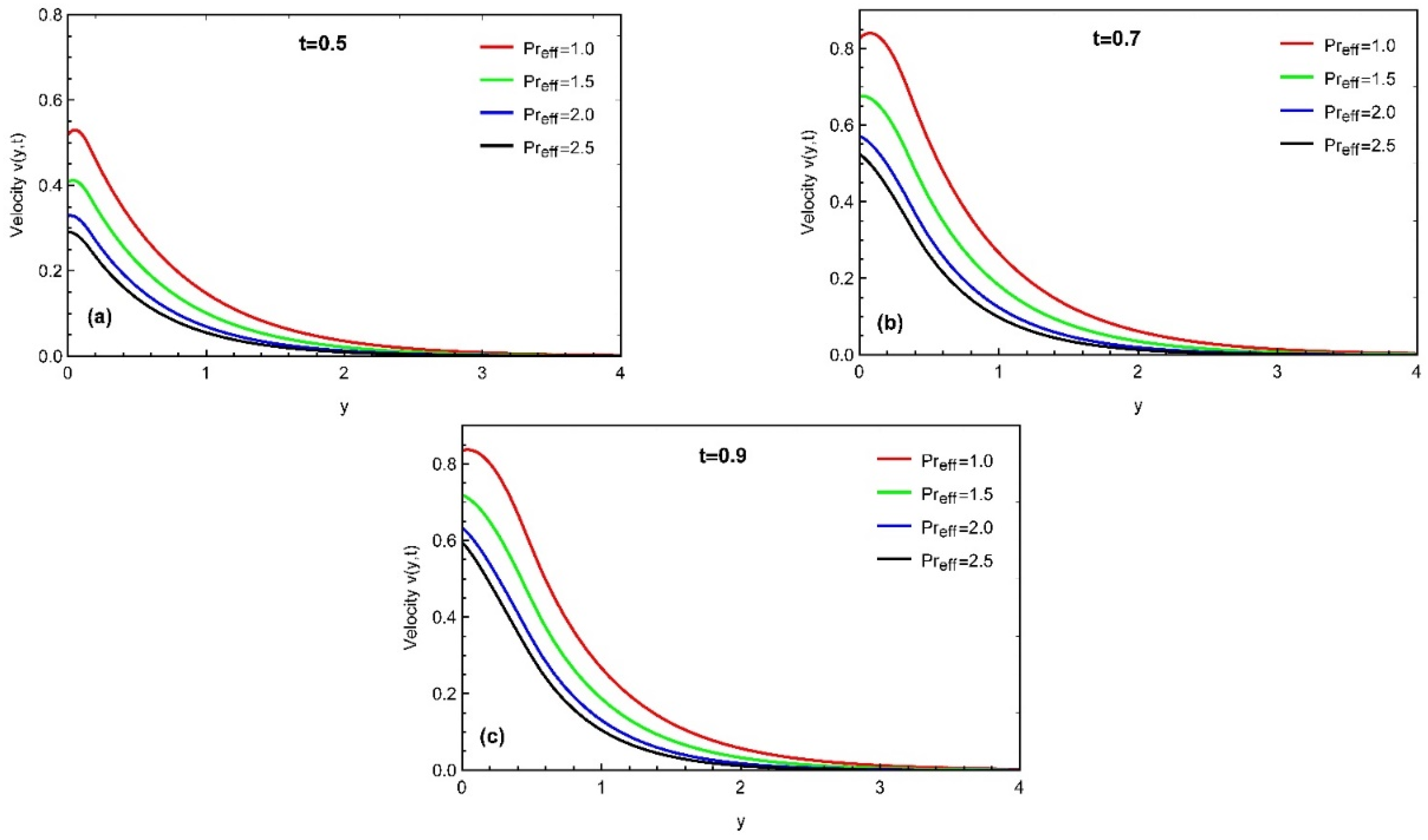
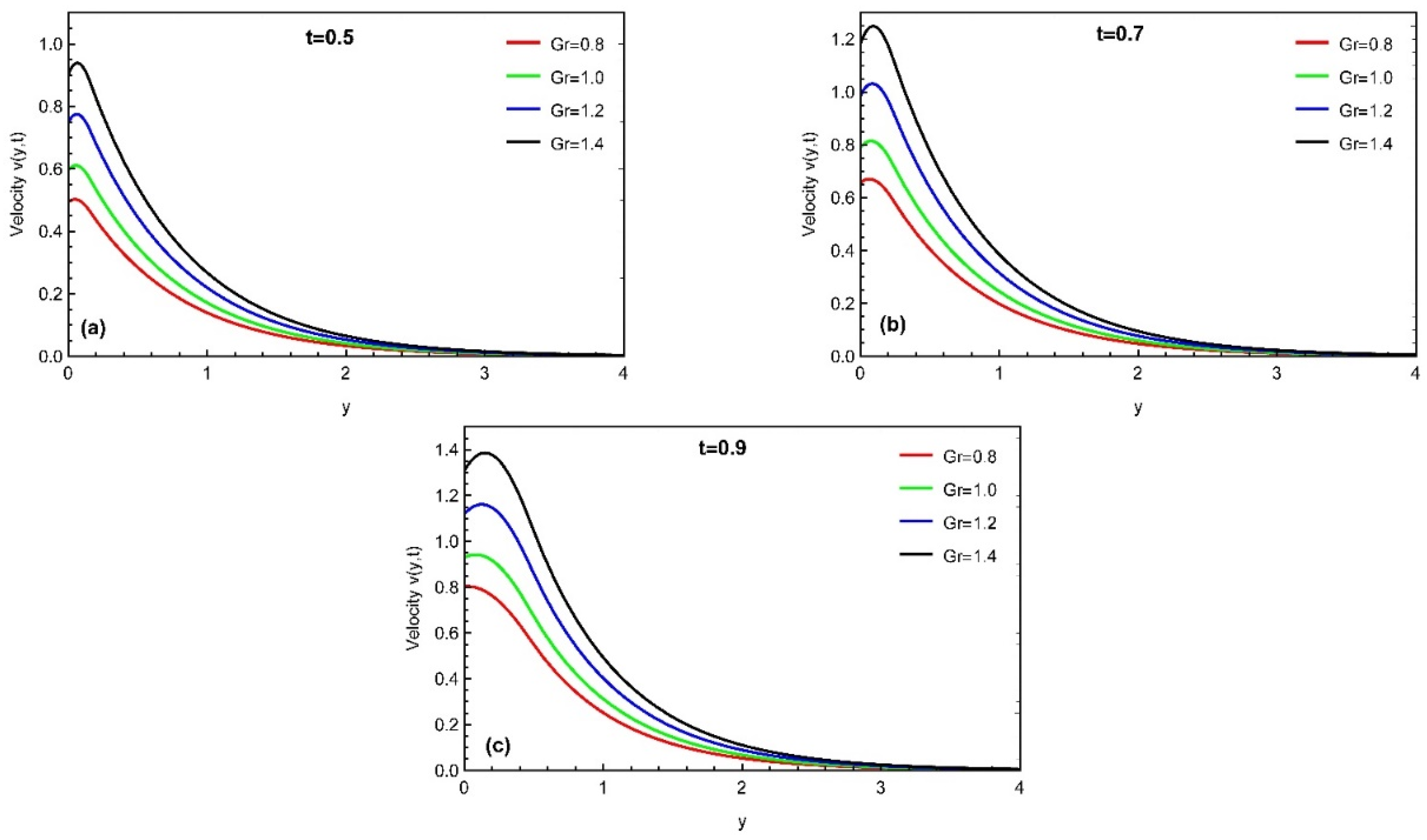
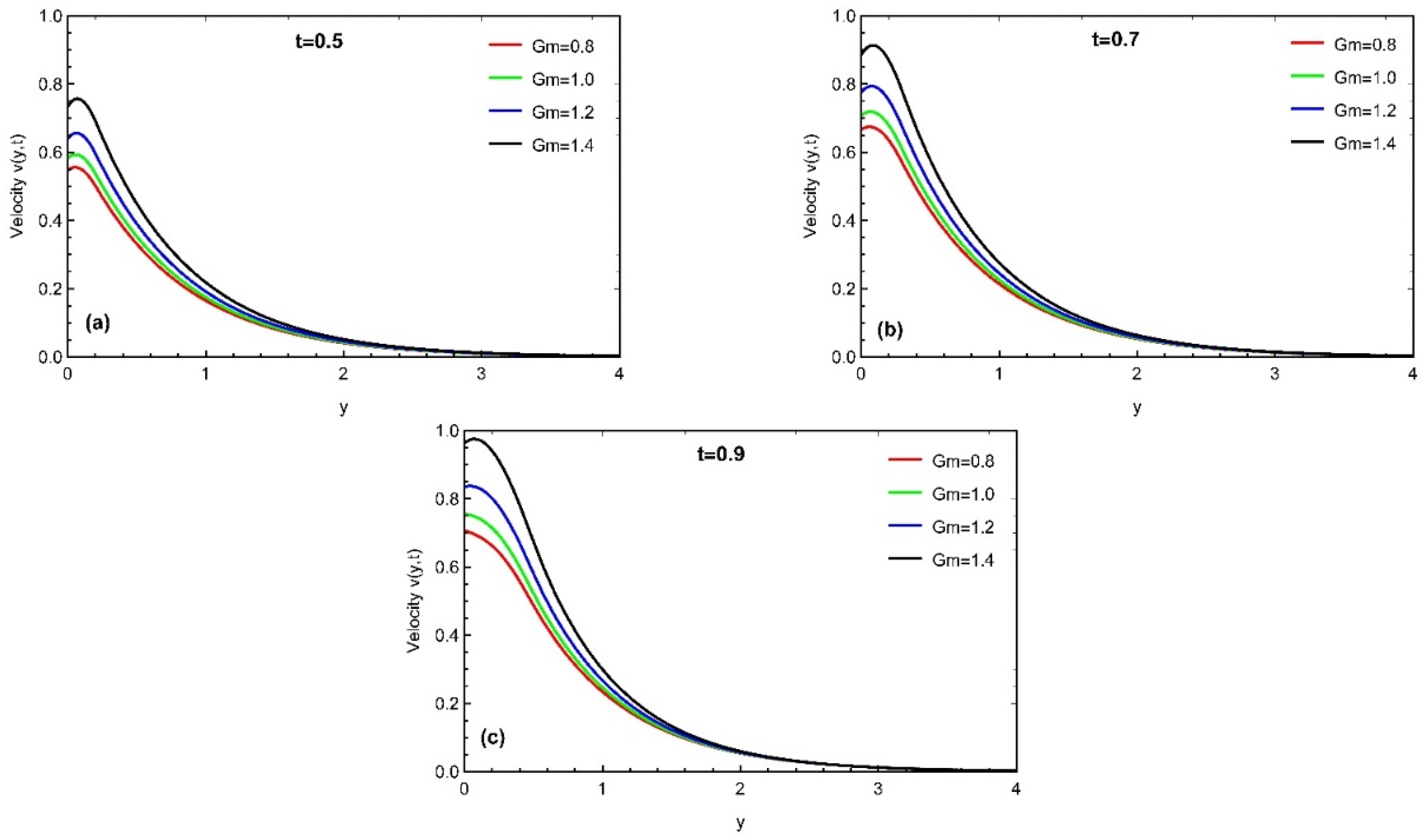
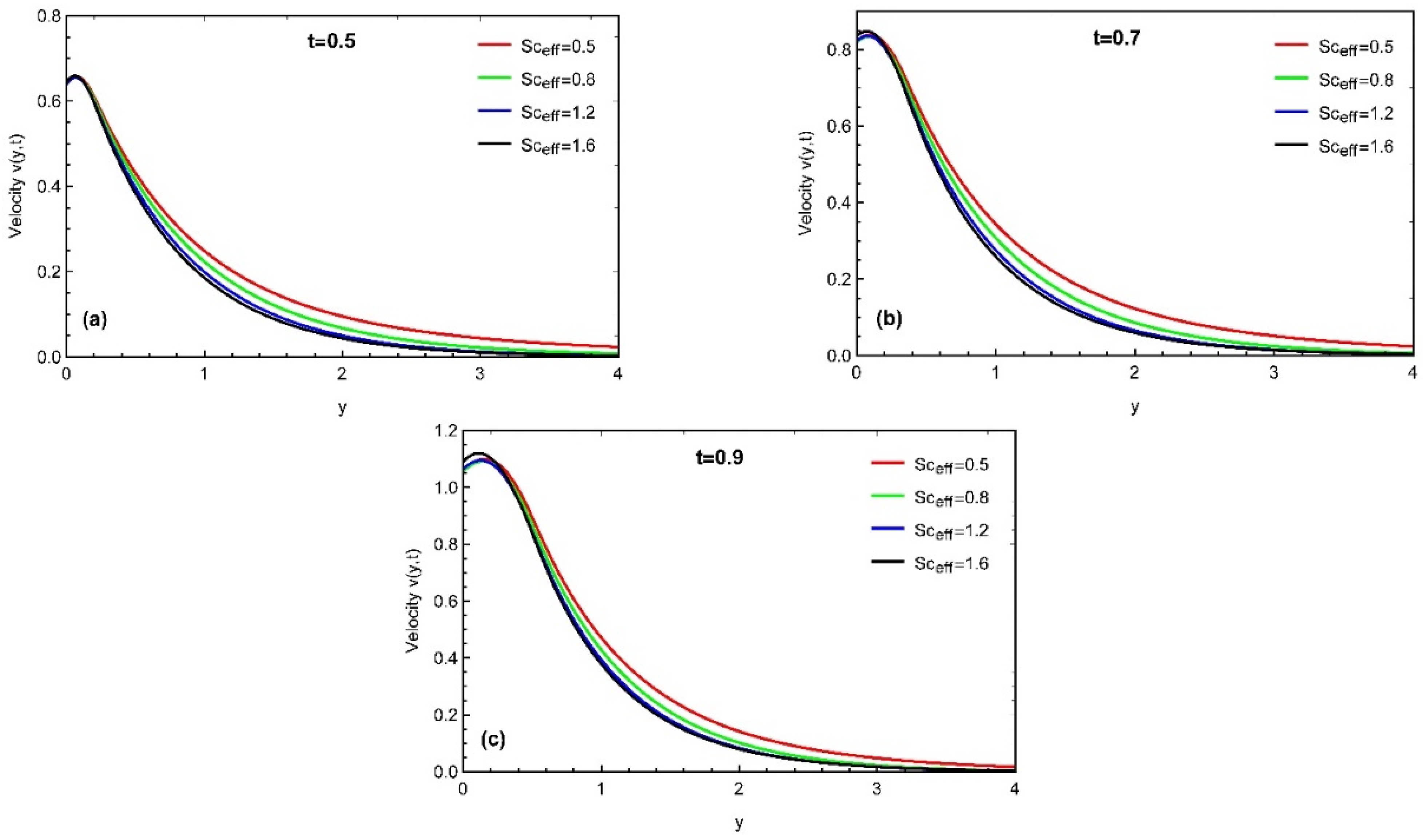
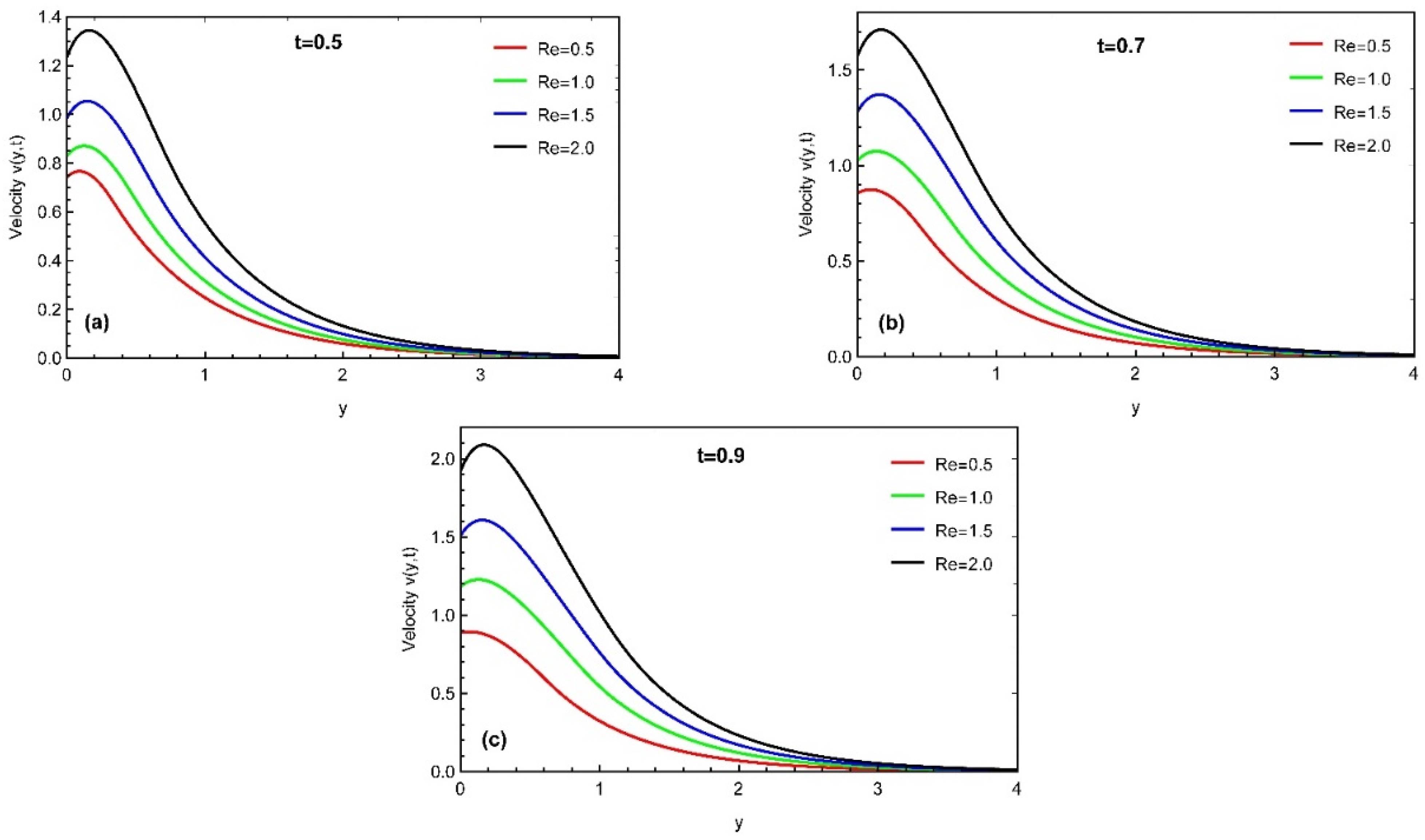
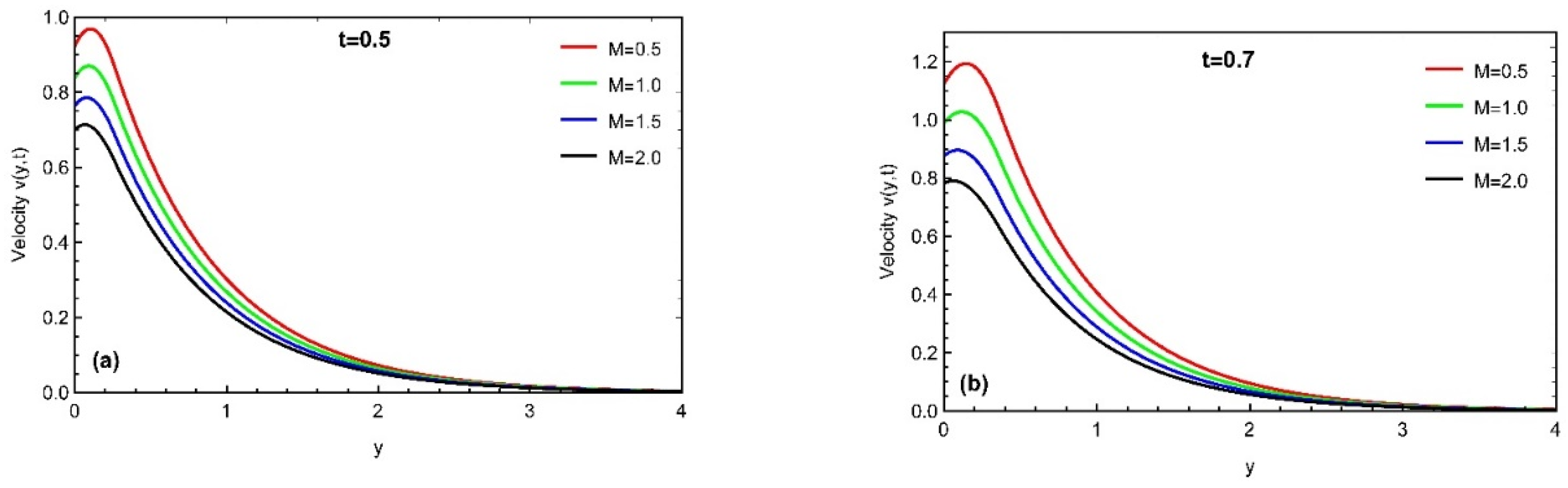
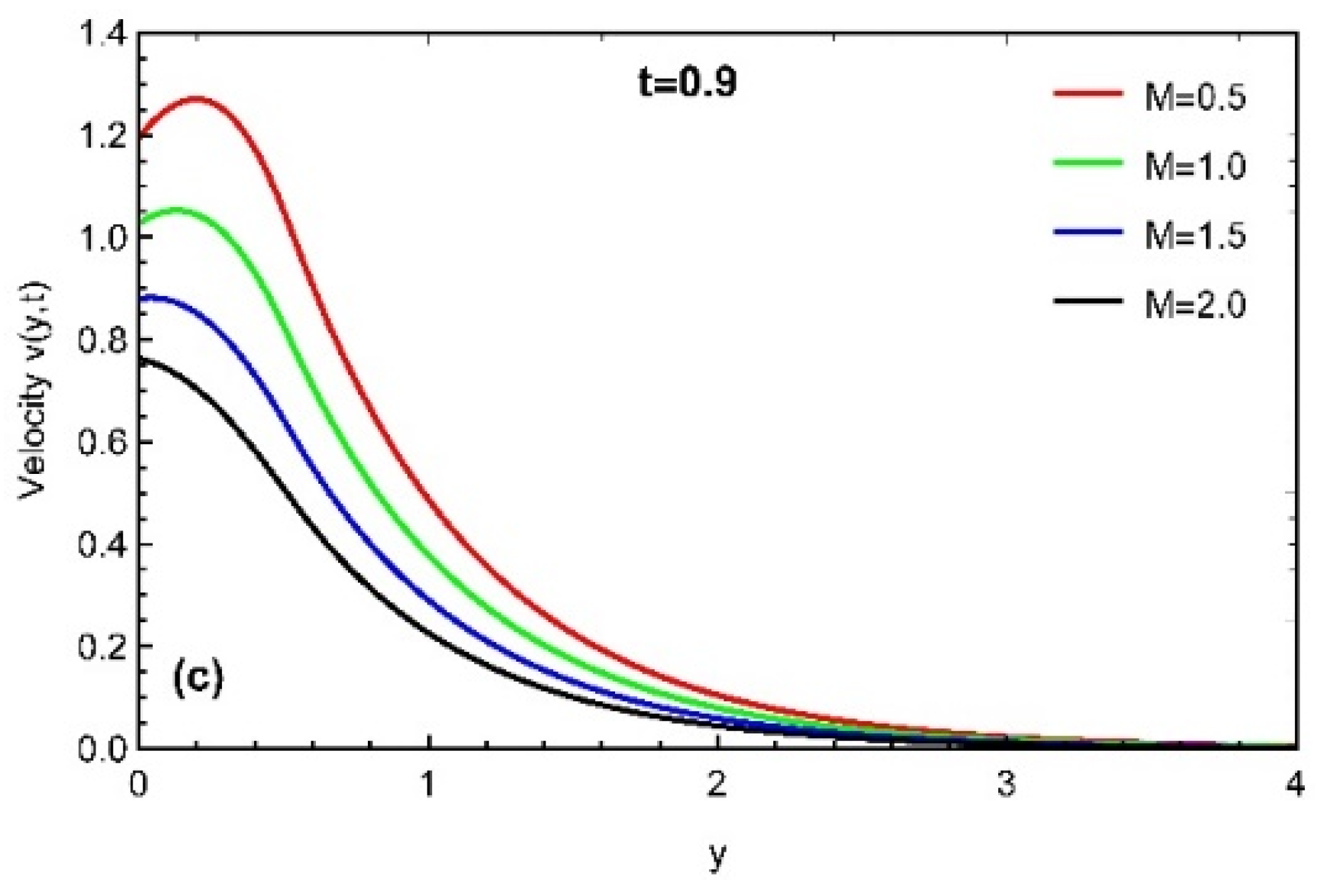
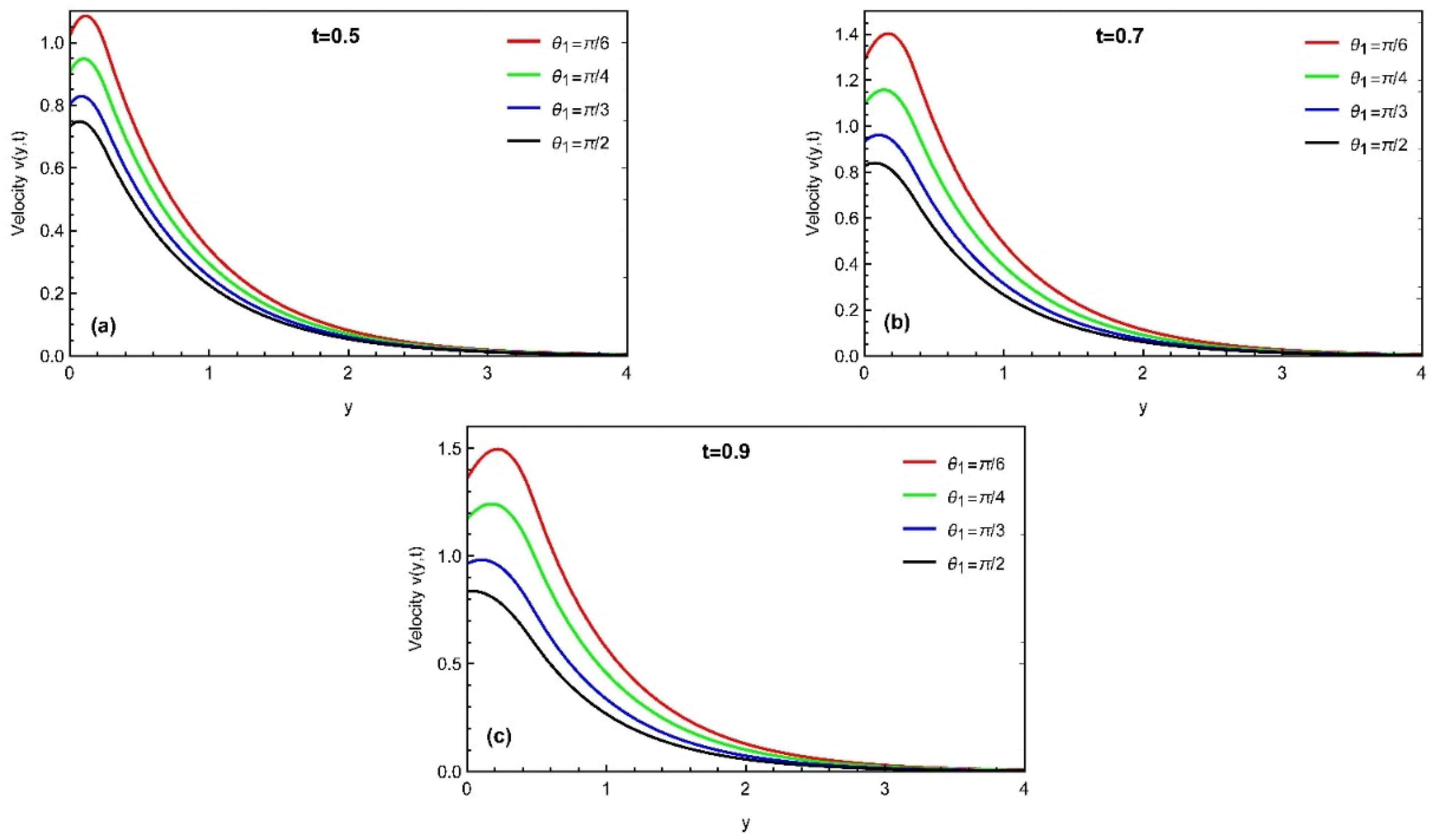
4. Results and Discussion
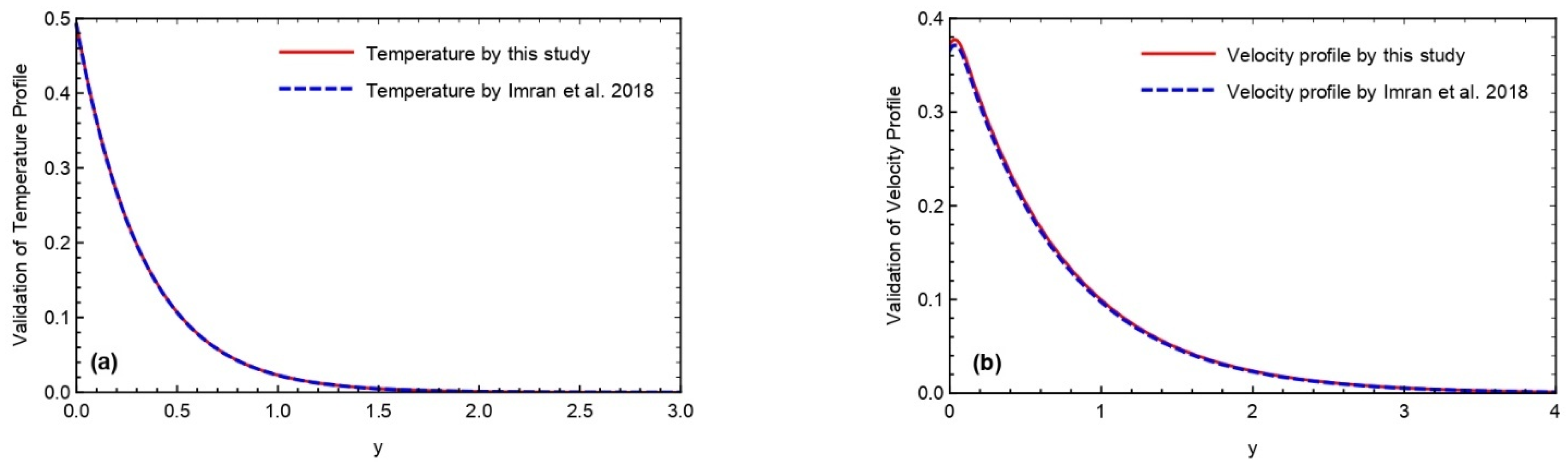
5. Validation of Attained Results
6. Conclusions
- The impact of larger values of fractional parameter and an adequate Prandtl number declines the profiles of temperature distributions.
- The boundary layer concentration also decays with the enhancement in fractional parameter and Schmidt number.
- The momentum profile is an increasing function for ,while it decreases with the variation in and Prabhakar fractional parameters.
- Thermal profile, concentration, and momentum profiles asymptotically increase with time.
- The overlapping of both numerical schemes validates the attained solution of all governed equations.
- The momentum profile is maximal near the plate. It approaches its distinctive peak values in the stream region and then decreases away along the y-axis.
- The rate of heat transfer, mass transfer, and skin friction varies with the increment in time values.
- In the comparison of numerical techniques and with the attained results of Imran et al. [54], the overlapping of both curves validates the attained results of this study.
- As the Prabhakar fractional derivative is the more recent definition of the fractional derivatives technique, it has more efficient and accurate results as compared to other fractional operators as depicted in the comparison of Imran et al. [54].
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Nomenclature
| Symbol | Quantity | Unit |
| Prabhakar fractional constraints | ||
| Dynamic Viscosity | ||
| Kinematic viscosity coefficient | ||
| Gravitational acceleration | ||
| Thermal expansion | ||
| Density | ||
| Specific heat at constant pressure | ||
| Laplace-transformed parameter | ||
| Electrical conductivity | ||
| Thermal conductivity | ||
| Dimensionless temperature profile | ||
| Dimensionless momentum field | ||
| Dimensionless concentration profile | ||
| Heat Grashof number | ||
| Mass Grashof number | ||
| Effective Prandtl number | ||
| Schmidt number | ||
| Magnetic field strength | ||
| Magnetic field | ||
| Laplace transformation | ||
| Nusselt number | ||
| Skin friction |
References
- Georgantopoulos, G.; Douskos, C.; Kafousias, N.; Goudas, C. Hydromagnetic free convection effects on the Stokes problem for an infinite vertical plate. Lett. Heat Mass Transf. 1979, 6, 397–404. [Google Scholar] [CrossRef]
- Raptis, A.; Singh, A. MHD free convection flow past an accelerated vertical plate. Int. Commun. Heat Mass Transf. 1983, 10, 313–321. [Google Scholar] [CrossRef]
- Singh, A.; Kumar, N. Free-convection flow past an exponentially accelerated vertical plate. Astrophys. Space Sci. 1984, 98, 245–248. [Google Scholar] [CrossRef]
- Soundalgekar, V. Free convection effects on the oscillatory flow past an infinite, vertical, porous plate with constant suction. I. Proc. R. Soc. London A. Math. Phys. Sci. 1973, 333, 25–36. [Google Scholar] [CrossRef]
- Mansour, M. Radiative and free-convection effects on the oscillatory flow past a vertical plate. Astrophys. Space Sci. 1990, 166, 269–275. [Google Scholar] [CrossRef]
- Ishak, A. Mixed convection boundary layer flow over a horizontal plate with thermal radiation. Heat Mass Transf. 2009, 46, 147–151. [Google Scholar] [CrossRef]
- Ishak, A. Thermal boundary layer flow over a stretching sheet in a micropolar fluid with radiation effect. Meccanica 2010, 45, 367–373. [Google Scholar] [CrossRef]
- Samiulhaq, F.C.; Khan, I.; Ali, F.; Shafie, S. Radiation and porosity effects on the magnetohydrodynamic flow past an oscillating vertical plate with uniform heat flux. Z. Nat. 2012, 67, 572–580. [Google Scholar]
- Domnich, A.; Baranovskii, E.; Artemov, M. A nonlinear model of the non-isothermal slip flow between two parallel plates. J. Phys. Conf. Ser. 2020, 1479, 012005. [Google Scholar] [CrossRef]
- Baranovskii, E.; Domnich, A. Model of a nonuniformly heated viscous flow through a bounded domain. Differ. Equ. 2020, 56, 304–314. [Google Scholar] [CrossRef]
- Hussanan, A.; Anwar, M.I.; Ali, F.; Khan, I.; Shafie, S. Natural convection flow past an oscillating plate with Newtonian heating. Heat Transf. Res. 2014, 45, 119–135. [Google Scholar] [CrossRef]
- Jaturonglumlert, S.; Kiatsiriroat, T. Heat and mass transfer in combined convective and far-infrared drying of fruit leather. J. Food Eng. 2010, 100, 254–260. [Google Scholar] [CrossRef]
- Javaid, M.; Imran, M.; Imran, M.; Khan, I.; Nisar, K. Natural convection flow of a second grade fluid in an infinite vertical cylinder. Sci. Rep. 2020, 10, 8327. [Google Scholar] [CrossRef] [PubMed]
- Wang, X.; Qi, H.; Xu, H. Transient electro-osmotic flow of generalized second-grade fluids under slip boundary conditions. Can. J. Phys. 2017, 95, 1313–1320. [Google Scholar] [CrossRef]
- Nisa, Z.U.; Shah, N.A.; Tlili, I.; Ullah, S.; Nazar, M. Natural convection flow of second grade fluid with thermal radiation and damped thermal flux between vertical channels. Alex. Eng. J. 2019, 58, 1119–1125. [Google Scholar] [CrossRef]
- Jie, Z.; Khan, M.I.; Al-Khaled, K.; El-Zahar, E.R.; Acharya, N.; Raza, A.; Khan, S.U.; Xia, W.F.; Tao, N.X. Thermal transport model for Brinkman type nanofluid containing carbon nanotubes with sinusoidal oscillations conditions: A fractional derivative concept. Waves Random Complex Media 2022, 1–20. [Google Scholar] [CrossRef]
- Wang, Y.; Mansir, I.B.; Al-Khaled, K.; Raza, A.; Khan, S.U.; Khan, M.I.; El-Sayed Ahmed, A. Thermal outcomes for blood-based carbon nanotubes (SWCNT and MWCNTs) with Newtonian heating by using new Prabhakar fractional derivative simulations. Case Stud. Therm. Eng. 2022, 32, 101904. [Google Scholar] [CrossRef]
- Raza, A.; Khan, S.U.; Al-Khaled, K.; Khan, M.I.; Haq, A.U.; Alotaibi, F.; Mousa, A.A.A.; Qayyum, S. A fractional model for the kerosene oil and water-based Casson nanofluid with inclined magnetic force. Chem. Phys. Lett. 2022, 787, 139277. [Google Scholar] [CrossRef]
- Raza, A.; Khan, S.U.; Khan, M.I.; El-Zahar, E.R. Heat Transfer Analysis for Oscillating Flow of Magnetized Fluid by Using the Modified Prabhakar-Like Fractional Derivatives. Res. Sq. 2021. [Google Scholar] [CrossRef]
- Raza, A.; Ghaffari, A.; Khan, S.U.; Haq, A.U.; Khan, M.I.; Khan, M.R. Non-singular fractional computations for the radiative heat and mass transfer phenomenon subject to mixed convection and slip boundary effects. Chaos Solitons Fractals 2022, 155, 111708. [Google Scholar] [CrossRef]
- Raza, A.; Khan, S.U.; Farid, S.; Ijaz khan, M.; Khan, M.R.; Haq, A.U.; Alsallami, S.A.M. Transport properties of mixed convective nano-material flow considering the generalized Fourier law and a vertical surface: Concept of Caputo-Time Fractional Derivative. Proc. Inst. Mech. Eng. Part A J. Power Energy 2022, 09576509221075110. [Google Scholar] [CrossRef]
- Raza, A.; Al-Khaled, K.; Khan, M.; Khan, S.; Khan, S.U.; Shah, S.I.; Ali, R. Investigation of dynamics of SWCNTs and MWCNTs nanoparticles in blood flow using the Atangana–Baleanu time fractional derivative with ramped temperature. Proc. Inst. Mech. Eng. Part E J. Process Mech. Eng. 2021. [Google Scholar] [CrossRef]
- Ali, F.; Saqib, M.; Khan, I.; Sheikh, N.A. Application of Caputo-Fabrizio derivatives to MHD free convection flow of generalized Walters’-B fluid model. Eur. Phys. J. Plus 2016, 131, 377. [Google Scholar] [CrossRef]
- Ali, F.; Sheikh, N.A.; Khan, I.; Saqib, M. Magnetic field effect on blood flow of Casson fluid in axisymmetric cylindrical tube: A fractional model. J. Magn. Magn. Mater. 2017, 423, 327–336. [Google Scholar] [CrossRef]
- Shah, N.A.; Khan, I. Heat transfer analysis in a second grade fluid over and oscillating vertical plate using fractional Caputo–Fabrizio derivatives. Eur. Phys. J. C 2016, 76, 362. [Google Scholar] [CrossRef] [Green Version]
- Zafar, A.; Fetecau, C. Flow over an infinite plate of a viscous fluid with non-integer order derivative without singular kernel. Alex. Eng. J. 2016, 55, 2789–2796. [Google Scholar] [CrossRef] [Green Version]
- Imran, M.; Riaz, M.; Shah, N.; Zafar, A. Boundary layer flow of MHD generalized Maxwell fluid over an exponentially accelerated infinite vertical surface with slip and Newtonian heating at the boundary. Results Phys. 2018, 8, 1061–1067. [Google Scholar] [CrossRef]
- Sheikh, N.A.; Ali, F.; Saqib, M.; Khan, I.; Jan, S.A.A.; Alshomrani, A.S.; Alghamdi, M.S. Comparison and analysis of the Atangana–Baleanu and Caputo–Fabrizio fractional derivatives for generalized Casson fluid model with heat generation and chemical reaction. Results Phys. 2017, 7, 789–800. [Google Scholar] [CrossRef]
- Raza, A.; Al-Khaled, K.; Khan, M.I.; Khan, S.U.; Farid, S.; Haq, A.U.; Muhammad, T. Natural convection flow of radiative maxwell fluid with Newtonian heating and slip effects: Fractional derivatives simulations. Case Stud. Therm. Eng. 2021, 28, 101501. [Google Scholar] [CrossRef]
- Raza, A.; Khan, A.U.; Khan, M.I.; Farid, S.; Muhammad, T.; Khan, M.I.; Galal, A.M. Fractional order simulations for the thermal determination of graphene oxide (GO) and molybdenum disulphide (MoS2) nanoparticles with slip effects. Case Stud. Therm. Eng. 2021, 28, 101453. [Google Scholar] [CrossRef]
- Raza, A.; Khan, I.; Farid, S.; My, C.A.; Khan, A.; Alotaibi, H. Non-singular fractional approach for natural convection nanofluid with Damped thermal analysis and radiation. Case Stud. Therm. Eng. 2021, 28, 101373. [Google Scholar] [CrossRef]
- Song, Y.-Q.; Raza, A.; Al-Khaled, K.; Farid, S.; Khan, M.I.; Khan, S.U.; Shi, Q.-H.; Malik, M.Y.; Khan, M.I. Significances of exponential heating and Darcy’s law for second grade fluid flow over oscillating plate by using Atangana-Baleanu fractional derivatives. Case Stud. Therm. Eng. 2021, 27, 101266. [Google Scholar] [CrossRef]
- Raza, A.; Khan, S.U.; Farid, S.; Khan, M.I.; Sun, T.C.; Abbasi, A.; Khan, M.I.; Malik, M.Y. Thermal activity of conventional Casson nanoparticles with ramped temperature due to an infinite vertical plate via fractional derivative approach. Case Stud. Therm. Eng. 2021, 27, 101191. [Google Scholar] [CrossRef]
- Ali, Q.; Riaz, S.; Awan, A.U.; Abro, K.A. A mathematical model for thermography on viscous fluid based on damped thermal flux. Z. Für Nat. A 2021, 76, 285–294. [Google Scholar] [CrossRef]
- Yavuz, M. European option pricing models described by fractional operators with classical and generalized Mittag-Leffler kernels. Numer. Methods Partial. Differ. Equ. 2020, 38, 434–456. [Google Scholar]
- Sulaiman, T.A.; Yavuz, M.; Bulut, H.; Baskonus, H.M. Investigation of the fractional coupled viscous Burgers’ equation involving Mittag-Leffler kernel. Phys. A Stat. Mech. Its Appl. 2019, 527, 121126. [Google Scholar] [CrossRef]
- Yavuz, M.; Özdemir, N. Comparing the new fractional derivative operators involving exponential and Mittag-Leffler kernel. Discret. Contin. Dyn. Syst.-S 2020, 13, 995. [Google Scholar] [CrossRef] [Green Version]
- Singh, Y.; Kumar, D.; Modi, K.; Gill, V. A new approach to solve Cattaneo-Hristov diffusion model and fractional diffusion equations with Hilfer-Prabhakar derivative. AIMS Math. 2020, 5, 843–855. [Google Scholar]
- Samraiz, M.; Perveen, Z.; Rahman, G.; Nisar, K.S.; Kumar, D. On the (k, s)-Hilfer-Prabhakar fractional derivative with applications to mathematical physics. Front. Phys. 2020, 8, 309. [Google Scholar] [CrossRef]
- Basit, A.; Asjad, M.I.; Akgül, A. Convective flow of a fractional second grade fluid containing different nanoparticles with Prabhakar fractional derivative subject to non-uniform velocity at the boundary. Math. Methods Appl. Sci. 2021. [Google Scholar] [CrossRef]
- Rehman, A.U.; Jarad, F.; Riaz, M.B.; Shah, Z.H. Generalized Mittag-Leffler Kernel Form Solutions of Free Convection Heat and Mass Transfer Flow of Maxwell Fluid with Newtonian Heating: Prabhakar Fractional Derivative Approach. Fractal Fract. 2022, 6, 98. [Google Scholar] [CrossRef]
- Tanveer, M.; Ullah, S.; Shah, N.A. Thermal analysis of free convection flows of viscous carbon nanotubes nanofluids with generalized thermal transport: A Prabhakar fractional model. J. Therm. Anal. Calorim. 2021, 144, 2327–2336. [Google Scholar] [CrossRef]
- Shah, N.A.; Elnaqeeb, T.; Animasaun, I.; Mahsud, Y. Insight into the natural convection flow through a vertical cylinder using caputo time-fractional derivatives. Int. J. Appl. Comput. Math. 2018, 4, 80. [Google Scholar] [CrossRef]
- Mittag-Leffler, G.M. Sur la nouvelle fonction Eα (x). CR Acad. Sci. Paris 1903, 137, 554–558. [Google Scholar]
- Wiman, A. Uber den fundamental Satz in der Theories der Funktionen Eα (z). Acta Math 1905, 29, 191–201. [Google Scholar] [CrossRef]
- Garra, R.; Garrappa, R. The Prabhakar or three parameter Mittag–Leffler function: Theory and application. Commun. Nonlinear Sci. Numer. Simul. 2018, 56, 314–329. [Google Scholar] [CrossRef] [Green Version]
- Giusti Colombaro, I.A. Prabhakar-like fractional viscoelasticity. Commun. Nonlinear Sci. Numer. Simul. 2018, 56, 138. [Google Scholar] [CrossRef] [Green Version]
- Polito, F.; Tomovski, Z. Some properties of Prabhakar-type fractional calculus operators. arXiv 2015, arXiv:1508.03224. [Google Scholar] [CrossRef]
- Tiwana, M.H.; Mann, A.B.; Rizwan, M.; Maqbool, K.; Javeed, S.; Raza, S.; Khan, M.S. Unsteady magnetohydrodynamic convective fluid flow of Oldroyd-B model considering ramped wall temperature and ramped wall velocity. Mathematics 2019, 7, 676. [Google Scholar] [CrossRef] [Green Version]
- Aleem, M.; Asjad, M.I.; Shaheen, A.; Khan, I. MHD Influence on different water based nanofluids (TiO2, Al2O3, CuO) in porous medium with chemical reaction and newtonian heating. Chaos Solitons Fractals 2020, 130, 109437. [Google Scholar] [CrossRef]
- Chu, Y.-M.; Ali, R.; Asjad, M.I.; Ahmadian, A.; Senu, N. Heat transfer flow of Maxwell hybrid nanofluids due to pressure gradient into rectangular region. Sci. Rep. 2020, 10, 16643. [Google Scholar] [CrossRef] [PubMed]
- Asjad, M.I.; Shah, N.A.; Aleem, M.; Khan, I. Heat transfer analysis of fractional second-grade fluid subject to Newtonian heating with Caputo and Caputo-Fabrizio fractional derivatives: A comparison. Eur. Phys. J. Plus 2017, 132, 340. [Google Scholar] [CrossRef]
- Stehfest, H. Algorithm 368: Numerical inversion of Laplace transforms [D5]. Commun. ACM 1970, 13, 47–49. [Google Scholar] [CrossRef]
- Imran, M.; Sarwar, S.; Abdullah, M.; Khan, I. An analysis of the semi-analytic solutions of a viscous fluid with old and new definitions of fractional derivatives. Chin. J. Phys. 2018, 56, 1853–1871. [Google Scholar] [CrossRef]



| y | T(y,t) by Stehfest | T(y,t) by Tzou’s | C(y,t) by Stehfest | C(y,t) by Tzou’s | v(y,t) by Stehfest | v(y,t) by Tzou’s |
|---|---|---|---|---|---|---|
| 0.1 | 0.6524 | 0.6396 | 0.8453 | 0.8460 | 0.8039 | 0.7981 |
| 0.3 | 0.4169 | 0.4068 | 0.6029 | 0.6046 | 0.7247 | 0.7209 |
| 0.5 | 0.2658 | 0.2579 | 0.4291 | 0.4311 | 0.5643 | 0.5615 |
| 0.7 | 0.1690 | 0.1630 | 0.3046 | 0.3067 | 0.4118 | 0.4095 |
| 0.9 | 0.1071 | 0.1026 | 0.2156 | 0.2176 | 0.3007 | 0.2988 |
| 1.1 | 0.0677 | 0.0644 | 0.1521 | 0.1539 | 0.2196 | 0.2181 |
| 1.3 | 0.0426 | 0.0402 | 0.1069 | 0.1085 | 0.1605 | 0.1593 |
| 1.5 | 0.0267 | 0.0249 | 0.0749 | 0.0763 | 0.1173 | 0.1163 |
| 1.7 | 0.0167 | 0.0154 | 0.0522 | 0.0534 | 0.0858 | 0.0850 |
| 1.9 | 0.0104 | 0.0094 | 0.0362 | 0.0372 | 0.0628 | 0.0621 |
| α | Nu at t = 0.5 | Nu at t = 0.7 | Sh at t = 0.5 | Sh at t = 0.7 | Cf at t = 0.5 | Cf at t = 0.7 |
|---|---|---|---|---|---|---|
| 0.1 | 2.4196 | 2.5332 | 1.2886 | 1.3048 | 0.9056 | 1.2143 |
| 0.2 | 2.3024 | 2.3874 | 1.3457 | 1.3687 | 0.7385 | 0.9344 |
| 0.3 | 2.2067 | 2.2599 | 1.4021 | 1.4384 | 0.6290 | 0.7390 |
| 0.4 | 2.1308 | 2.1502 | 1.4546 | 1.5088 | 0.5583 | 0.5994 |
| 0.5 | 2.0734 | 2.0518 | 1.4973 | 1.5739 | 0.5158 | 0.4996 |
| 0.6 | 2.0330 | 1.9831 | 1.5286 | 1.6290 | 0.4952 | 0.4305 |
| 0.7 | 2.0080 | 1.9250 | 1.5481 | 1.6711 | 0.4918 | 0.3867 |
| 0.8 | 1.9966 | 1.8831 | 1.5569 | 1.6996 | 0.5027 | 0.3648 |
| 0.9 | 1.9971 | 1.8564 | 1.5568 | 1.7154 | 0.5249 | 0.3623 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Raza, A.; Khan, U.; Zaib, A.; Mahmoud, E.E.; Weera, W.; Yahia, I.S.; Galal, A.M. Applications of Prabhakar-like Fractional Derivative for the Solution of Viscous Type Fluid with Newtonian Heating Effect. Fractal Fract. 2022, 6, 265. https://doi.org/10.3390/fractalfract6050265
Raza A, Khan U, Zaib A, Mahmoud EE, Weera W, Yahia IS, Galal AM. Applications of Prabhakar-like Fractional Derivative for the Solution of Viscous Type Fluid with Newtonian Heating Effect. Fractal and Fractional. 2022; 6(5):265. https://doi.org/10.3390/fractalfract6050265
Chicago/Turabian StyleRaza, Ali, Umair Khan, Aurang Zaib, Emad E. Mahmoud, Wajaree Weera, Ibrahim S. Yahia, and Ahmed M. Galal. 2022. "Applications of Prabhakar-like Fractional Derivative for the Solution of Viscous Type Fluid with Newtonian Heating Effect" Fractal and Fractional 6, no. 5: 265. https://doi.org/10.3390/fractalfract6050265
APA StyleRaza, A., Khan, U., Zaib, A., Mahmoud, E. E., Weera, W., Yahia, I. S., & Galal, A. M. (2022). Applications of Prabhakar-like Fractional Derivative for the Solution of Viscous Type Fluid with Newtonian Heating Effect. Fractal and Fractional, 6(5), 265. https://doi.org/10.3390/fractalfract6050265








