On the Linear–Quadratic–Gaussian Control Strategy for Fractional-Order Systems
Abstract
1. Introduction
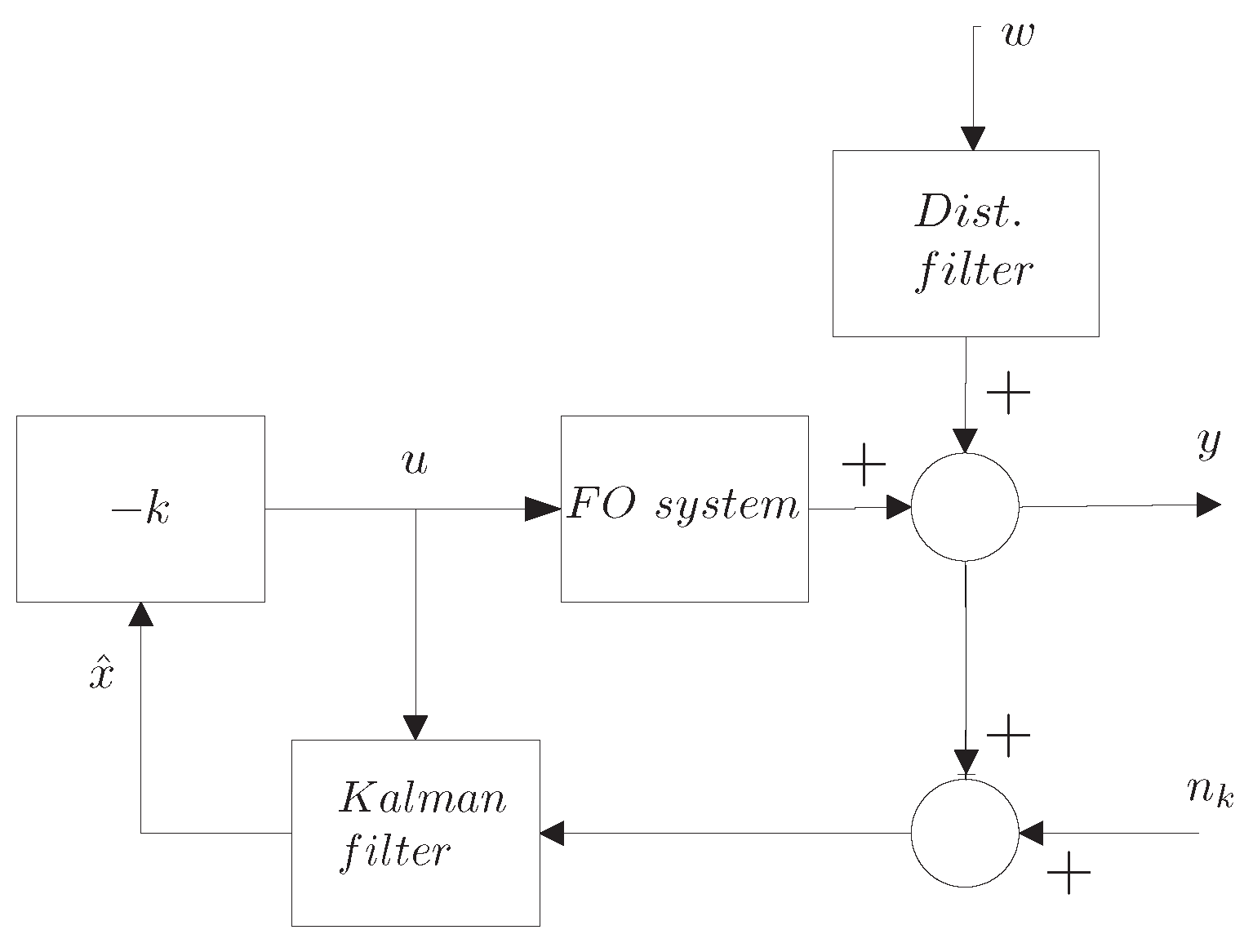
2. Problem Statement
3. Controller Design
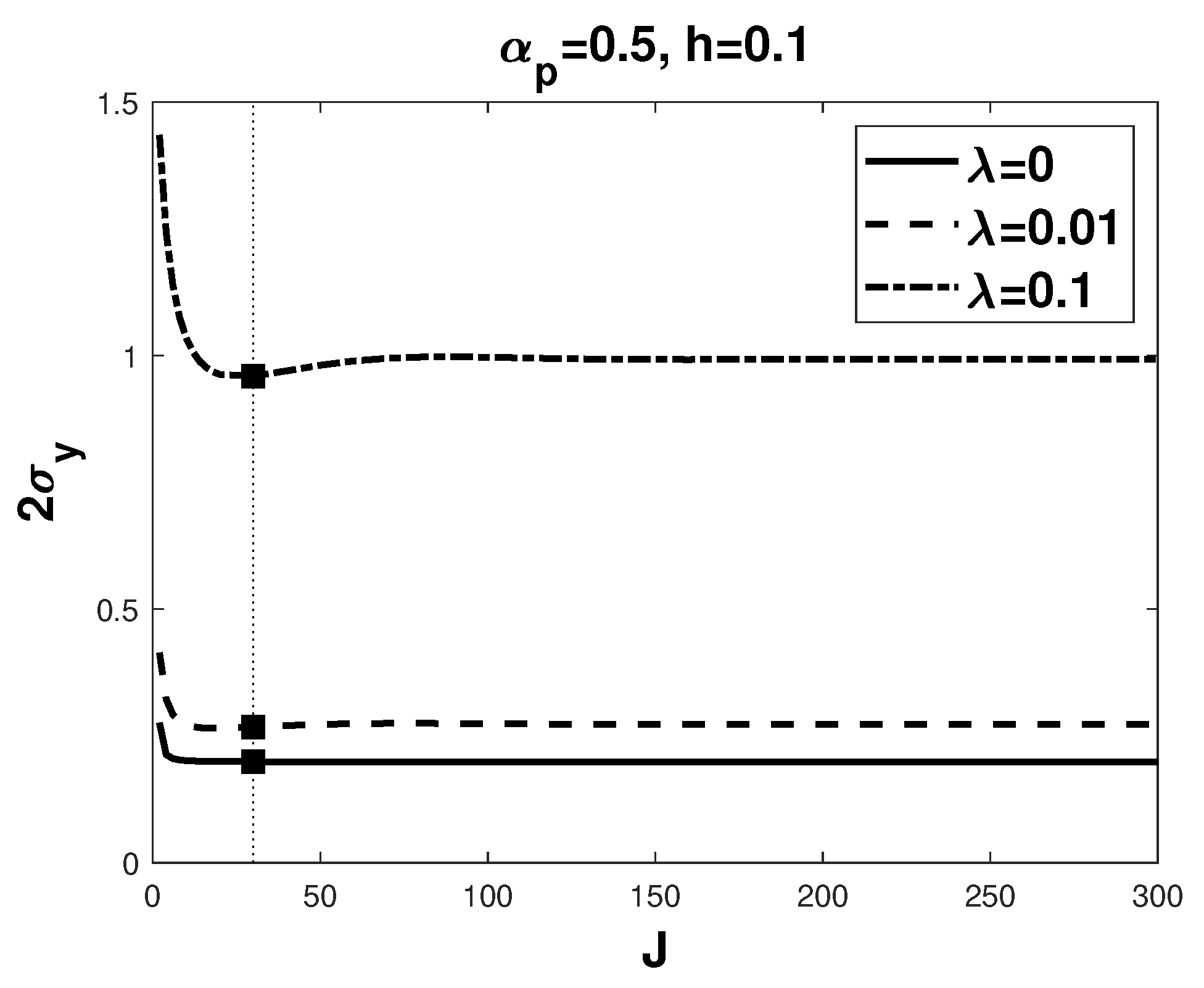
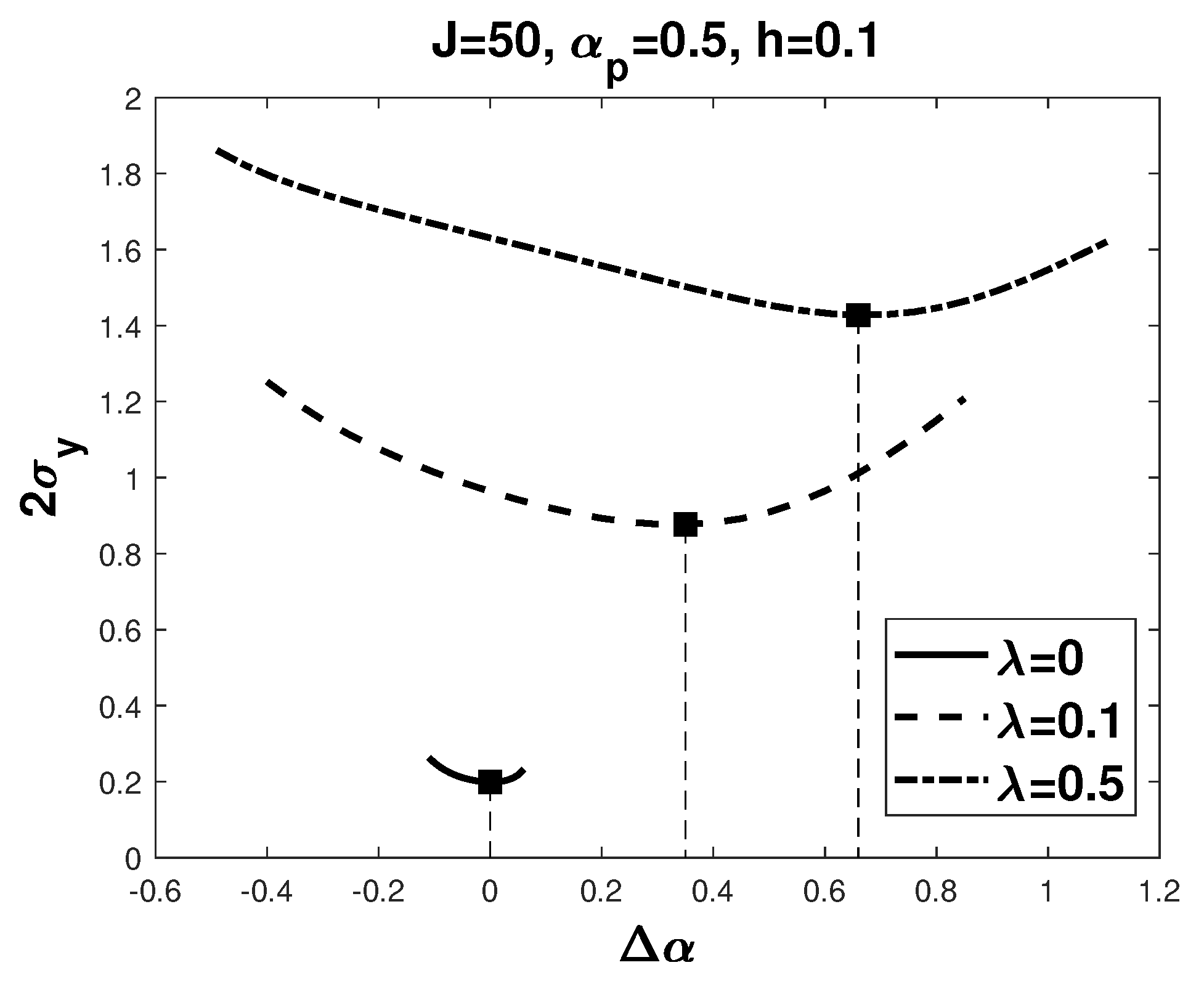
4. Output Variance
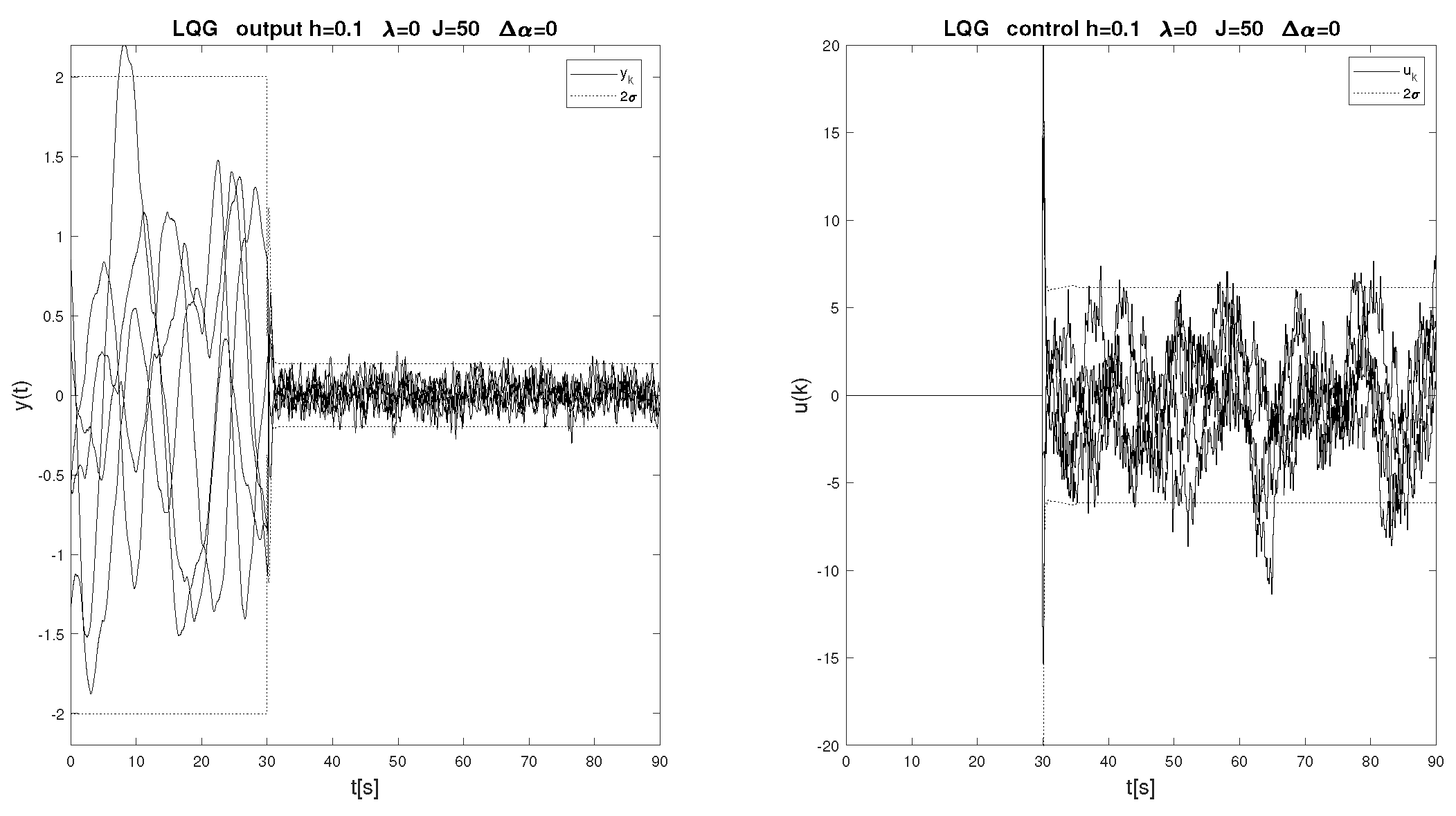
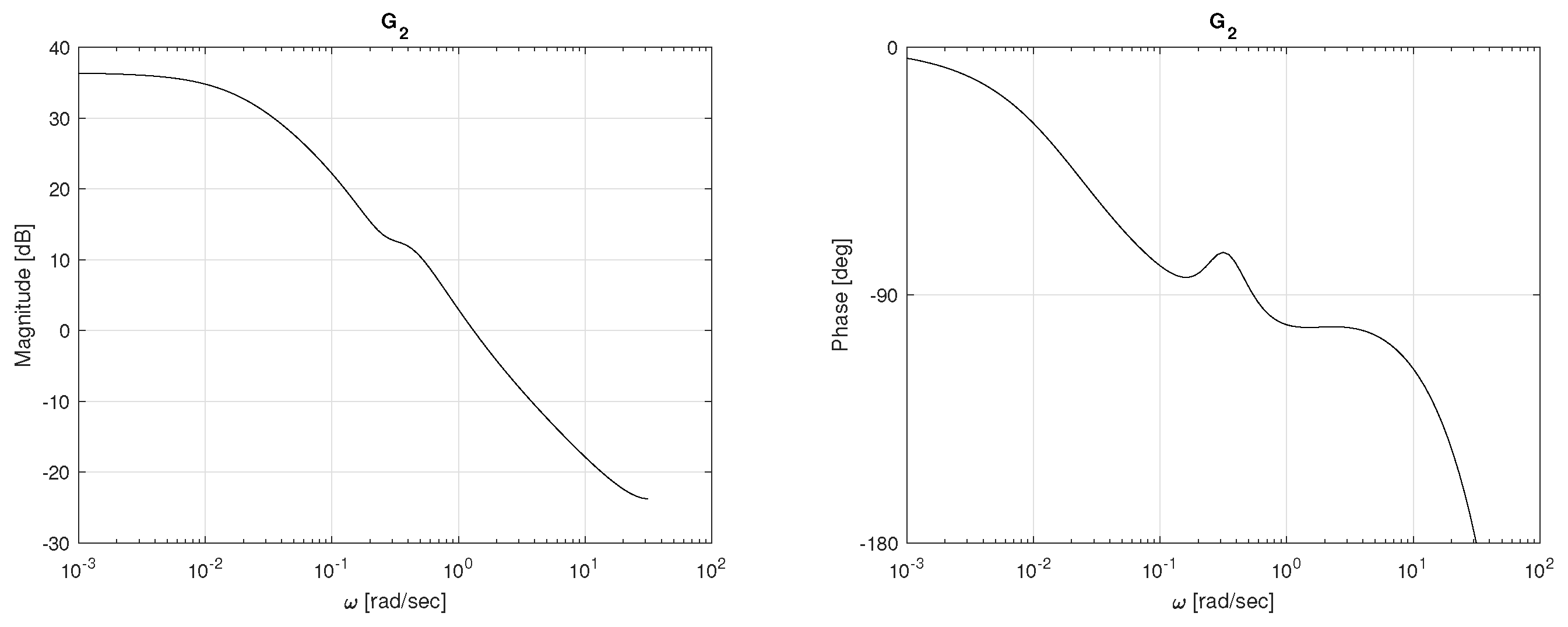
5. Simulation Results
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Ali, M.S.; Narayanan, G.; Nahavandi, S.; Wang, J.; Cao, J. Global dissipativity analysis and stability analysis for fractional-order quaternion-valued neural networks with time delays. IEEE Trans. Syst. Man Cybern. Syst. 2021, 1–11. [Google Scholar] [CrossRef]
- Ali, M.S.; Narayanan, G.; Sevgen, S.; Shekher, V.; Arik, S. Global stability analysis of fractional-order fuzzy bam neural networks with time delay and impulsive effects. Commun. Nonlinear Sci. Numer. Simul. 2019, 78, 104853. [Google Scholar]
- Hymavathi, M.; Muhiuddin, G.; Ali, M.S.; Al-Amri, J.F.; Gunasekaran, N.; Vadivel, R. Global exponential stability of fractional order complex-valued neural networks with leakage delay and mixed time varying delays. Fractal Fract. 2022, 6, 140. [Google Scholar] [CrossRef]
- Bettou, K.; Charef, A. Control quality enhancement using fractional PIλDμ controller. Int. J. Syst. Sci. 2009, 40, 875–888. [Google Scholar] [CrossRef]
- Dumlu, A.; Erenturk, K. Trajectory tracking control for a 3-DOF parallel manipulator using fractional-order PIλDμ control. IEEE Trans. Ind. Electron. 2014, 61, 3417–3426. [Google Scholar] [CrossRef]
- Meng, F.; Liu, S.; Pang, A.; Liu, K. Fractional order pid parameter tuning for solar collector system based on frequency domain analysis. IEEE Access 2020, 8, 148980–148988. [Google Scholar] [CrossRef]
- Seo, S.-W.; Choi, H.-H. Digital implementation of fractional order pid-type controller for boost dc–dc converter. IEEE Access 2019, 7, 142652–142662. [Google Scholar] [CrossRef]
- Shah, P.; Agashe, S. Review of fractional PID controller. Mechatronics 2016, 38, 29–41. [Google Scholar] [CrossRef]
- Stanisławski, R.; Rydel, M.; Li, Z. A new reduced-order implementation of discrete-time fractional-order pid controller. IEEE Access 2022, 10, 17417–17429. [Google Scholar] [CrossRef]
- Yaghi, M.; Önder Efe, M. H2/H∞-neural-based FOPID controller applied for radar-guided missile. IEEE Trans. Ind. Electron. 2020, 67, 4806–4814. [Google Scholar] [CrossRef]
- Ravari, M.A.; Yaghoobi, M. Optimum design of fractional order pid controller using chaotic firefly algorithms for a control cstr system. Asian J. Control 2019, 21, 2245–2255. [Google Scholar] [CrossRef]
- Momani, S.; El-Khazali, R.; Batiha, I.M. Tuning pid and piλdδ controllers using particle swarm optimization algorithm via el-khazali’s approach. AIP Conf. Proc. 2019, 2172, 050003. [Google Scholar]
- Pan, I.; Das, S.; Gupta, A. Handling packet dropouts and random delays for unstable delayed processes in NCS by optimal tuning of PIλDμ controllers with evolutionary algorithms. ISA Trans. 2011, 50, 557–572. [Google Scholar] [CrossRef] [PubMed]
- Ramezanian, H.; Balochian, S. Optimal design a fractional- order PID controller using particle swarm optimization algorithm. Int. J. Control Autom. 2013, 6, 55–67. [Google Scholar]
- Verma, S.K.; Yadav, S.; Nagar, S.K. Optimization of fractional order pid controller using grey wolf optimizer. J. Control Autom. Electr. Syst. 2017, 28, 314–322. [Google Scholar] [CrossRef]
- Bazanella, A.S.; Pereira, L.F.A.; Parraga, A. A new method for PID tuning including plants without ultimate frequency. IEEE Trans. Control Syst. Technol. 2017, 25, 637–644. [Google Scholar] [CrossRef]
- Chevalier, A.; Francis, C.; Copot, C.; Ionescu, C.M.; De Keyser, R. Fractional-order pid design: Towards transition from state-of-art to state-of-use. ISA Trans. 2019, 84, 178–186. [Google Scholar] [CrossRef]
- Sierociuk, D.; Macias, M. Comparison of variable fractional order pid controller for different types of variable order derivatives. In Proceedings of the 14th International Carpathian Control Conference (ICCC), Rytro, Poland, 26–29 May 2013; pp. 334–339. [Google Scholar]
- Sierociuk, D.; Wiraszka, M.S. A new variable fractional-order pi algorithm—This work was supported by the polish national science center with the decision number umo-2014/15/b/st7/00480. IFAC-PapersOnLine 2018, 51, 745–750. [Google Scholar] [CrossRef]
- Sierociuk, D.; Wiraszka, M.S. Variable-order pi control algorithm with order scheduled according to the control error and anti-windup strategy. In Proceedings of the 2019 20th International Carpathian Control Conference (ICCC), Wieliczka, Poland, 26–29 May 2019; pp. 1–5. [Google Scholar]
- Domek, S. Fuzzy predictive control of fractional-order nonlinear discrete-time systems. Acta Mech. Autom. 2011, 5, 23–26. [Google Scholar]
- Stanisławski, R.; Latawiec, K.J.; Łukaniszyn, M.; Gałek, M. Linear finite fractional difference predictors for model predictive control. In Proceedings of the IEEE Multiconference on Systems and Control (MSC), Sydney, Australia, 21–23 September 2015; pp. 341–346. [Google Scholar]
- Ski, A.D.; Czyronis, P.M. Fixed final time and free final state optimal control problem for fractional dynamic systems—Linear quadratic discrete-time case. Bull. Pol. Acad. Sci. Tech. Sci. 2013, 61, 681–690. [Google Scholar]
- Ski, A.D.; Czyronis, P.M. Optimal control problem for fractional dynamic systems—Linear quadratic discrete-time case. In Advances in the Theory and Applications of Non-Integer Order Systems; Lecture Notes in Electrical Engineering; Springer: Berlin/Heidelberg, Germany, 2013; Volume 257, pp. 87–97. [Google Scholar]
- Sierociuk, D.; Vinagre, B.M. Infinite horizon state-feedback LQR controller for fractional systems. In Proceedings of the 49th IEEE Conference on Decision and Control (CDC), Atlanta, GA, USA, 15–17 December 2010; pp. 10824–10829. [Google Scholar]
- Okuya, A.; Kaneko, O. On the data-driven update of the free parameter in the generalized internal model controller by using frit. Trans. Soc. Instrum. Control Eng. 2016, 52, 581–588. [Google Scholar] [CrossRef][Green Version]
- Dabri, A.; Nazari, M.; Butcher, E.A. Adaptive neural-fuzzy inference system to control dynamical systems with fractional order dampers. In Proceedings of the American Control Conference (ACC), Seattle, WA, USA, 24–26 May 2017; pp. 1972–1977. [Google Scholar]
- Mehandiratta, V.; Mehra, M.; Leugering, G. Fractional optimal control problems on a star graph: Optimality system and numerical solution. Math. Control Relat. Fields 2021, 11, 189. [Google Scholar] [CrossRef]
- Yang, Y.; Tan, J.; Yue, D.; Xie, X.; Yue, W. Observer-based containment control for a class of nonlinear multiagent systems with uncertainties. IEEE Trans. Syst. Man Cybern. Syst. 2021, 51, 588–600. [Google Scholar] [CrossRef]
- Domek, S. Switched fractional state-space predictive control methods for non-linear fractional systems. In Proceedings of the Conference on Non-Integer Order Calculus and Its Applications, Bialystok, Poland, 20–21 September 2018; Lecture Notes in Electrical Engineering. Springer: Cham, Switzerland, 2019; Volume 559, pp. 113–127. [Google Scholar]
- Domek, S. Switched state model predictive control of fractional-order nonlinear discrete-time systems. Asian J. Control. 2013, 15, 658–668. [Google Scholar] [CrossRef]
- Li, Y.; Chen, Y.Q. Fractional order linear quadratic regulator. In Proceedings of the 2008 IEEE/ASME International Conference on Mechtronic and Embedded Systems and Applications, Beijing, China, 12–15 October 2008; pp. 363–368. [Google Scholar]
- Tejado, I.; Vinagre, D.; Sierociuk, D. State space methods for fractional controllers design. In Handbook of Fractional Calculus with Applications; De Gruyter: Berlin, Germany, 2019; Volume 2, pp. 175–200. [Google Scholar]
- Sierociuk, D. Fractional Order Discrete State-Space System Simulink Toolkit User Guide. 2005. Available online: http://www.ee.pw.edu.pl/~dsieroci/fsst/fsst.pdf (accessed on 27 February 2022).
- Li, H.; Li, R.; Wu, F. A new control performance evaluation based on lqg benchmark for the heating furnace temperature control system. Processes 2020, 8, 1428. [Google Scholar] [CrossRef]
- Li, R.; Wu, F.; Hou, P.; Zou, H. Performance assessment of fo-pid temperature control system using a fractional order lqg benchmark. IEEE Access 2020, 8, 116653–116662. [Google Scholar] [CrossRef]
- Duncan, T.E.; Pasik-Duncan, B. Linear-quadratic fractional gaussian control. SIAM J. Control Optim. 2013, 51, 4504–4519. [Google Scholar] [CrossRef]
- Blachuta, M.J.; Bialic, G. On the impact of plant model and controller sophistication on performance of disturbance attenuation and system robustness. In Proceedings of the 45th IEEE Conference on Decision and Control, San Diego, CA, USA, 13–15 December 2006; pp. 3248–3253. [Google Scholar]
- Blachuta, M.J.; Bialic, G. On control performance assessment based on lag-delay models. In Proceedings of the 2005, American Control Conference, Portland, OR, USA, 8–10 June 2005; Volume 1, pp. 374–379. [Google Scholar]
- Li, S.; Zhao, J.; Zhang, Z. Investigation on linear quadratic gaussian control of semi-active suspension for three-axle vehicle. J. Low Freq. Noise Vib. Act. Control 2021, 40, 1633–1648. [Google Scholar] [CrossRef]
- Stanisławski, R.; Rydel, M.; Latawiec, K.J. Modeling of discrete-time fractional-order state space systems using the balanced truncation method. J. Frankl. Inst. 2017, 354, 3008–3020. [Google Scholar] [CrossRef]


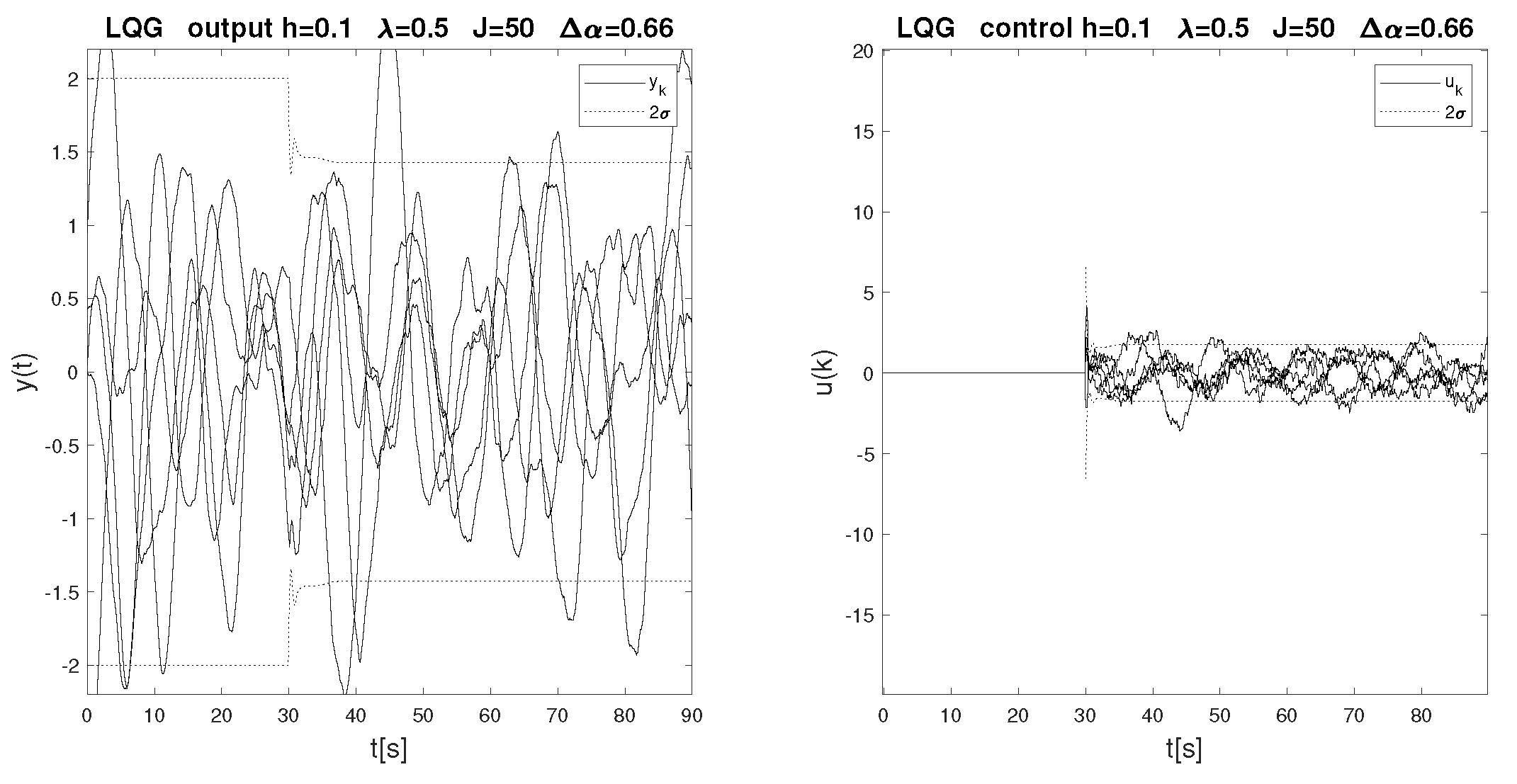
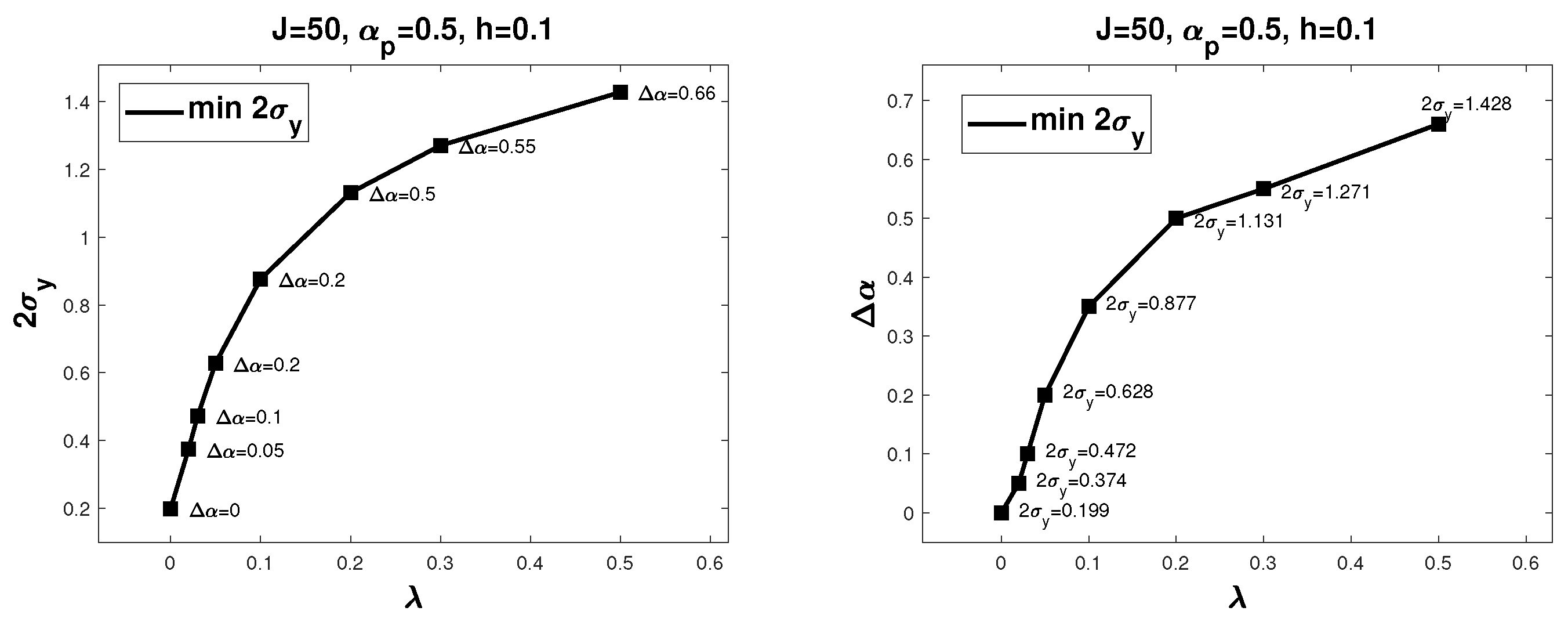
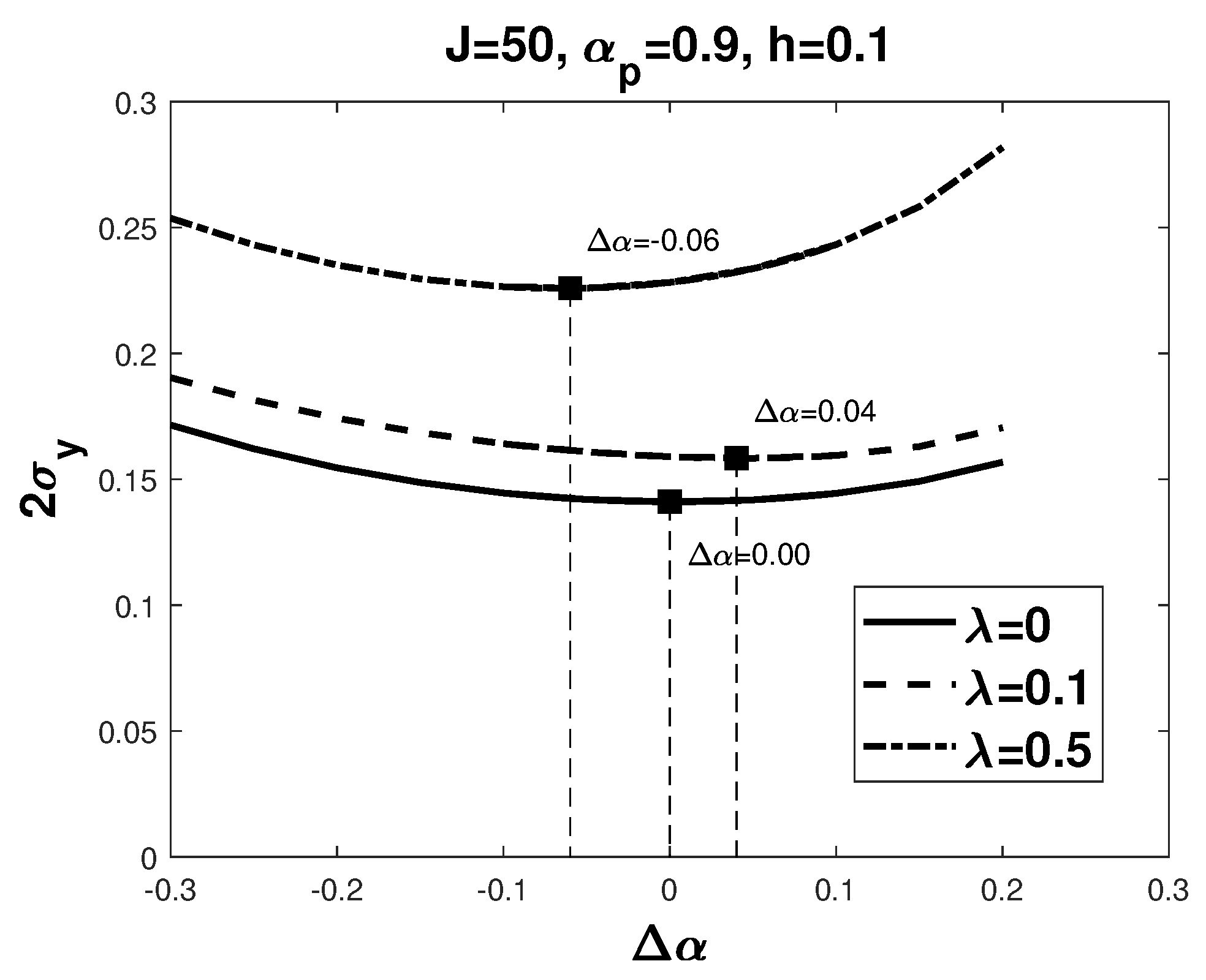
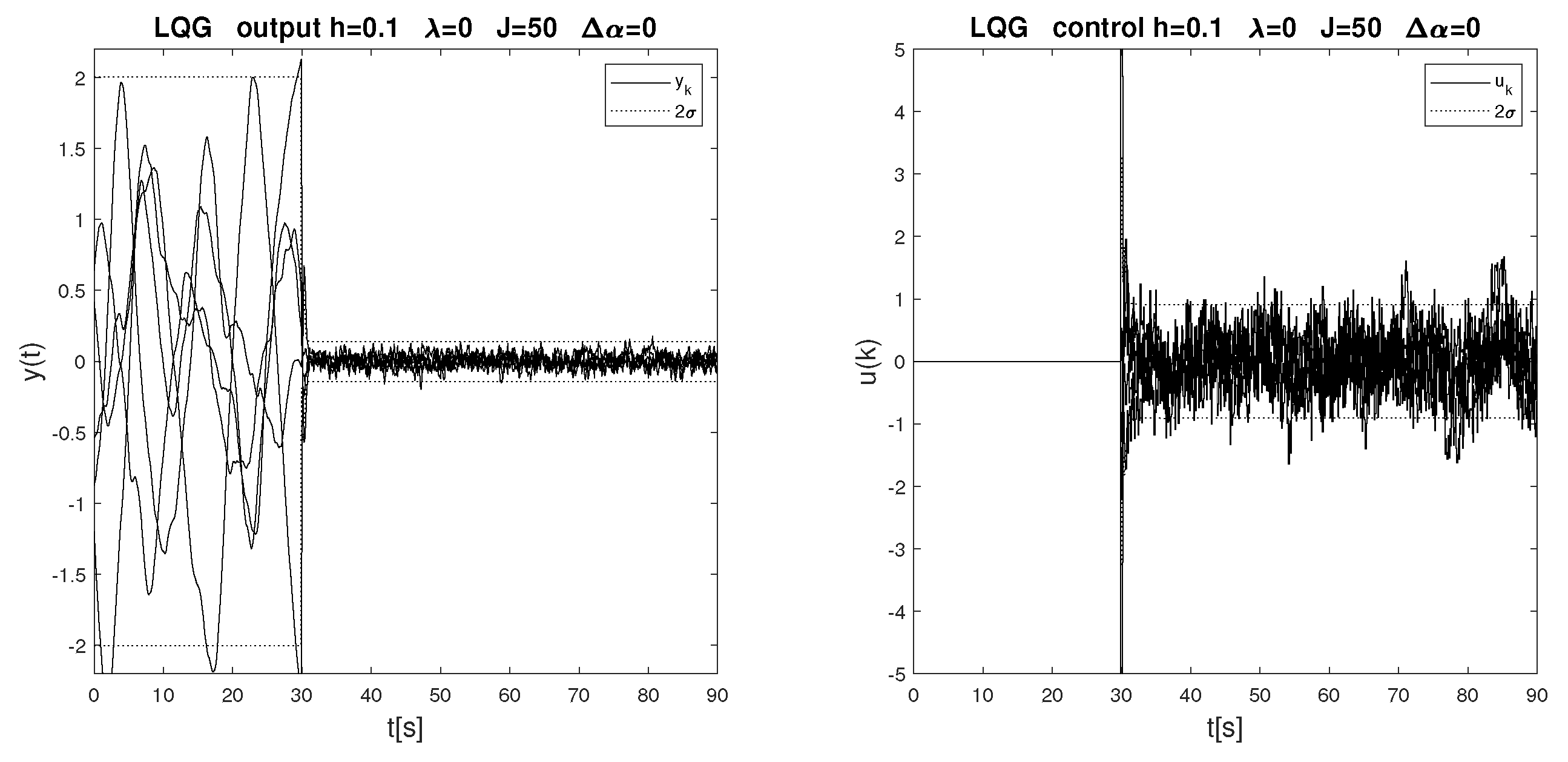


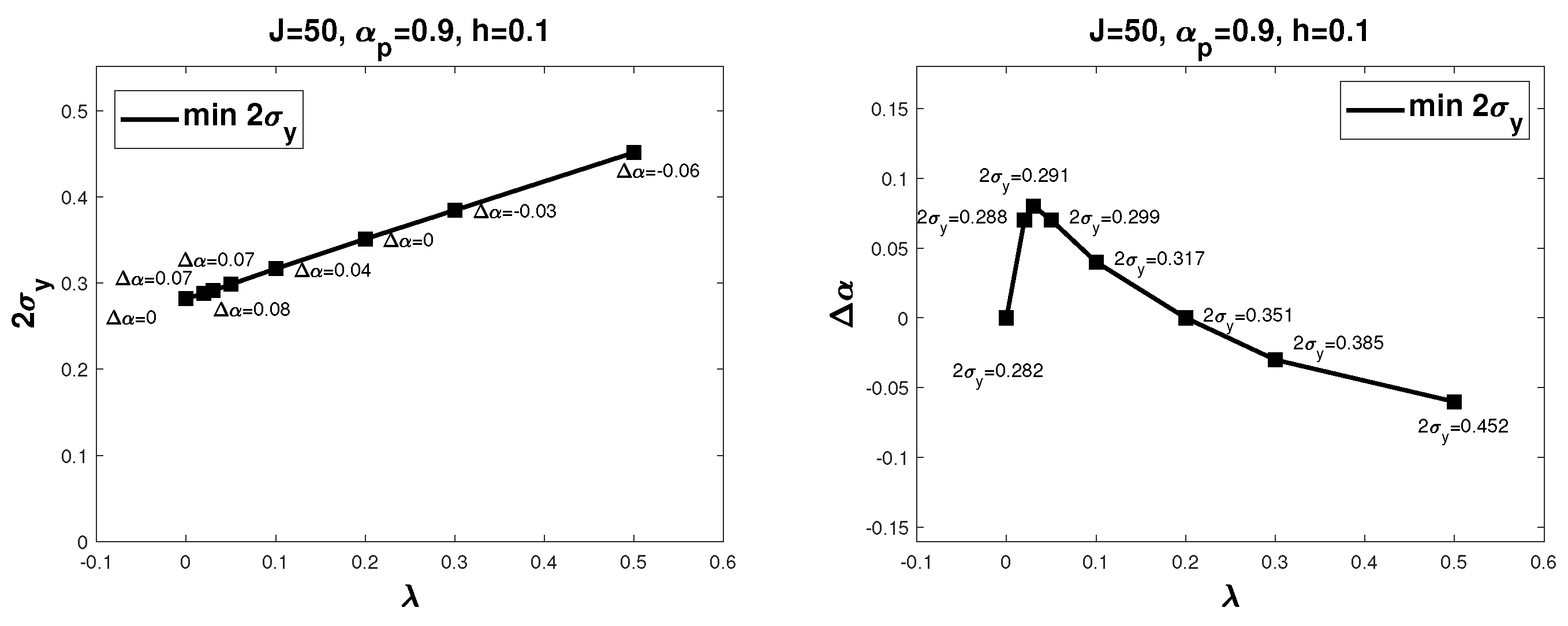
| 0 | 0 | 0.199 |
| 0.01 | 0.05 | 0.374 |
| 0.02 | 0.10 | 0.472 |
| 0.05 | 0.20 | 0.628 |
| 0.1 | 0.33 | 0.877 |
| 0.2 | 0.50 | 1.131 |
| 0.3 | 0.55 | 1.271 |
| 0.5 | 0.66 | 1.428 |
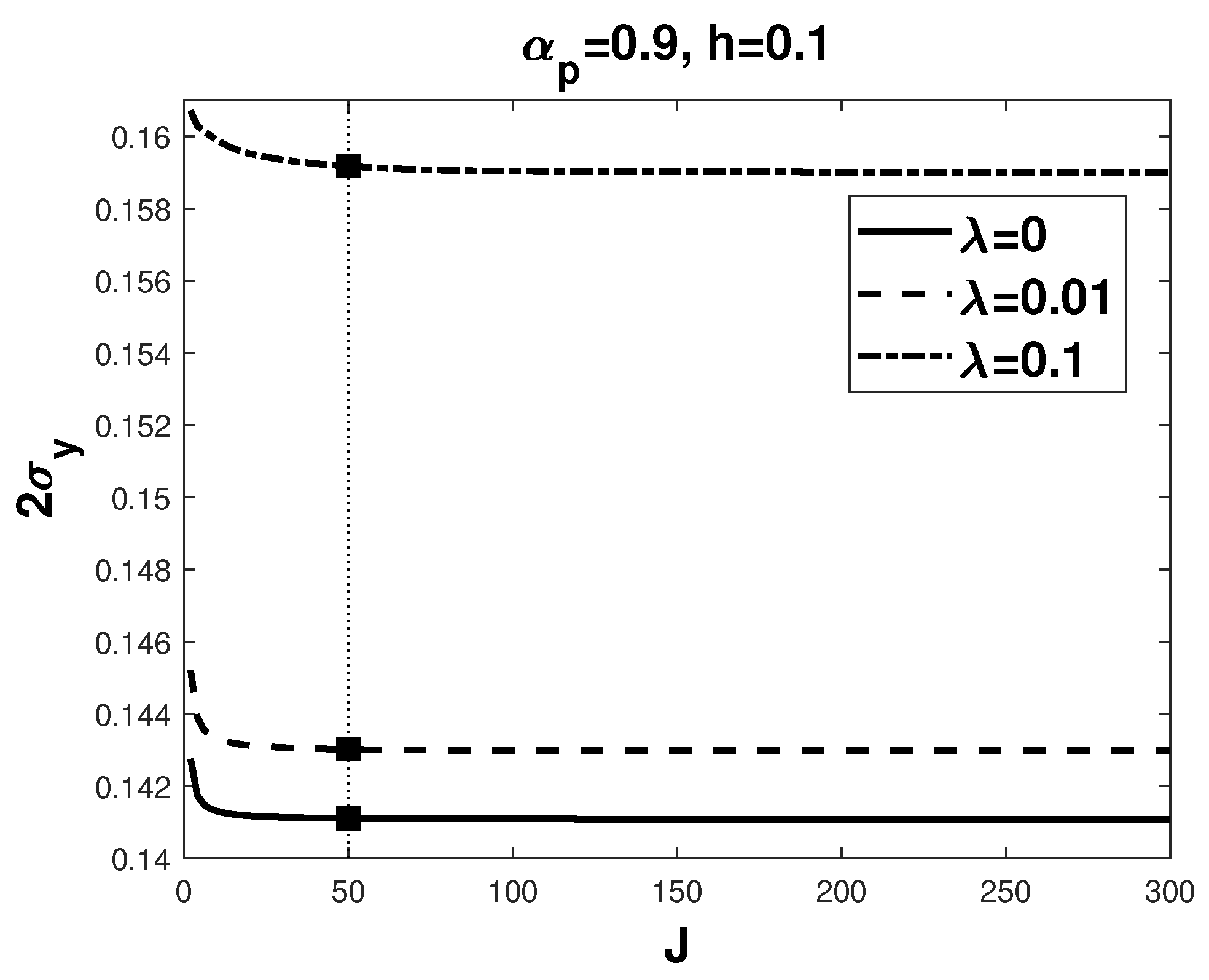
| 0 | 0 | 0.282 |
| 0.01 | 0.07 | 0.288 |
| 0.02 | 0.08 | 0.291 |
| 0.05 | 0.07 | 0.299 |
| 0.1 | 0.04 | 0.317 |
| 0.2 | 0 | 0.351 |
| 0.3 | −0.03 | 0.385 |
| 0.5 | −0.06 | 0.452 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Bialic, G.; Stanisławski, R. On the Linear–Quadratic–Gaussian Control Strategy for Fractional-Order Systems. Fractal Fract. 2022, 6, 248. https://doi.org/10.3390/fractalfract6050248
Bialic G, Stanisławski R. On the Linear–Quadratic–Gaussian Control Strategy for Fractional-Order Systems. Fractal and Fractional. 2022; 6(5):248. https://doi.org/10.3390/fractalfract6050248
Chicago/Turabian StyleBialic, Grzegorz, and Rafał Stanisławski. 2022. "On the Linear–Quadratic–Gaussian Control Strategy for Fractional-Order Systems" Fractal and Fractional 6, no. 5: 248. https://doi.org/10.3390/fractalfract6050248
APA StyleBialic, G., & Stanisławski, R. (2022). On the Linear–Quadratic–Gaussian Control Strategy for Fractional-Order Systems. Fractal and Fractional, 6(5), 248. https://doi.org/10.3390/fractalfract6050248






