Abstract
Fast and strong interacting systems are hard to control from both performance and control effort points of view. Moreover, multiple objective functions or objectives with various identifiers of varying weights can hold unfeasible solutions at times. A novel cost objective function is proposed here to overcome both feasibility set limitations and computational burdens. An application example is used to illustrate its added value, which is a fast and strong interacting multivariable system: a landscape office lighting regulatory problem. New lighting technology and an intelligent control system have been produced to improve control accuracy and reduce power consumption. While optimizing the hardware of the lighting system, the energy consumption can be further reduced by applying advanced control strategy in the lighting system. This paper designed a fractional order distributed model predictive control (FOMPC) scheme to realize the reference tracking and stability control of multiple illuminations at the same time. In order to test the efficiency of the control strategy, an experiment was carried out on the lighting setup based on the dSPACE control system. The FOMPC scheme was analyzed through simulation and lighting experiments based on the dSPACE control system. Through a comparison with the mode predictive control (MPC) scheme, the superiority of the FOMPC scheme for the dynamic behavior and control performance of multiple lighting systems was verified. The research results provide a basis for multiple lighting control and its application.
1. Introduction
With the development of communication technology and the intelligent manufacturing industry, the structure of control systems is becoming more and more complex, and the control objectives involved are also increasing. Various multi-objective systems are widely used in science and engineering fields, such as smart grids, satellite communication, navigation, intelligent robots, biological networks, sensor networks, driverless vehicles, and smart homes [1,2,3]. Each agent in the multi-objective system has its own model and its characteristics or skills when performing specific operations [4]. All agents in a multi-objective system should be located in a similar environment, and they can communicate with each other by designing interaction protocols [5]. Therefore, a multi-objective system can be used to model many existing complex systems, and its corresponding research can bring us new methods to deal with problems that cannot be solved by any single agent. In addition, the multi-objective control scheme can appropriately describe the group behavior, which is the research direction of natural and artificial system swarm intelligence [6]. In particular, all agents of swarm intelligence can evolve into multiple groups through simple rules and local communication between agents, finally realizing the global deployment of multi-target areas. Multi-objective control technology has excellent characteristics such as reliability, flexibility, robustness, scalability, and maintainability [7]. On the basis of the multi-objective control and its caveats, this paper proposes a solution and validates it on a fast and strong interacting lighting control system in a mimicked landscape office scaled to a laboratory setup.
With the increasing impact of lighting systems on human life, lighting is consuming more and more electric energy. New lighting technology and intelligent control systems have been produced to improve control accuracy and system efficiency [8]. Reducing energy consumption by improving the lighting system has a significant impact on the energy goal [9]. While optimizing the hardware of the lighting system, the energy consumption can be further reduced by using intelligent lamps to implement the control strategy in the lighting system. In recent years, the field of multiple lighting control systems has been widely studied. One study designed the controller, enabled it to use the past behavior mode as a reference, and controlled the light on this basis [10]. While ensuring lighting comfort, artificial lighting is controlled to achieve the important purpose of reducing energy consumption and reduce the operation cost of the building. The method of establishing a multi-lighting control system is to realize stable cooperative control of artificial lighting and adapt to the change of sunlight [11]. The control system works by minimizing the number of data transmission to improve the control efficiency. The performance of multiple lighting control largely depends on the computational efficiency and speed. In multiple lighting control, there are multiple agents, and the controller needs to interact with the information between each agent, which must be considered by the controller [12]. The controller solves the control problem according to the information of each agent and shares the information with other agents to improve the overall performance. In addition, with the expansion of system scale in multiple lighting control, the data scale of captured real-time data and required real-time calculation will increase sharply [13]. There are many challenges in data acquisition, storage, visualization, sharing, transmission, and analysis, as well as the allocation and coordination of computing tasks [14].
Model predictive control (MPC) is an advanced control algorithm developed in the 1970s, which can ensure good control performance and index requirements. After decades of development and the continuous deepening and expansion of predictive control theory, the predictive control algorithm is becoming more and more widely used in many industrial process control fields, such as the chemical, electric power, and transportation industries [15]. MPC theory was further developed in the analysis of algorithm stability and control performance in the 1990s. At the same time, its application scope was also extended to nonlinear systems and more complex hybrid systems [16]. At this stage, the research of MPC takes the optimal control as the main theoretical basis, uses the Lyapunov stability analysis method to ensure the closed-loop stability of the system, and then analyzes the performance of the system on the basis of the characteristics of the rolling time domain, thus forming a relatively perfect theoretical system of MPC stability analysis [17]. Thus, the stability and robustness of MPC have been widely concerned and deeply studied. Using model predictive control, the coordination strategy research of distributed predictive control, the stability theory of distributed predictive control, the distributed control for different systems, and their application in various fields have been gradually enriched [18]. Distributed model predictive control allows communication and information sharing among agents to achieve the global optimality of multi-agent systems. Therefore, distributed model predictive control reduces the complexity of optimization problems and improves work efficiency. In recent years, distributed model predictive control has been used in vehicle and ship control, energy systems, smart grids, machine learning, networked control, etc. [19,20,21,22]. With the development of theory and the rise in actual industrial demand, the application of fractional calculus theory in predictive control has attracted the attention of more and more scholars producing in-depth research [23,24].
Fractional calculus theory can better describe the dynamic process and system characteristics of some complex systems [25,26]. In fractional calculus, the order of differentiation and integration can be arbitrary, which extends the well-known integer calculus [27]. Moreover, with the increasing complexity of the actual industrial system and the increasing requirements for control accuracy and energy saving, control technology based on integer order theory sometimes struggles to obtain satisfactory performance [28,29]. Fractional calculus provides a feasible and effective method to solve the problems in a practical industrial process [30]. Compared with the control method based on integer order, the fractional order system model and control design can ensure that the system has good stability and can better adapt to the changes of the system in complex actual situations [31].
The innovation of this paper is that the time-varying weighting factor in the fractional order distributed MPC (FOMPC) is used to replace the constant weighting factor in classical MPC. As such, this creates a significant broadening of the feasibility set of achievable solutions when multi-objective cost optimization is performed. The weight factor in classical MPC has elements. These two parameters are used for tracking error and control performance, where is the horizon of prediction, and is the horizon of control. The optimal problem for the weighting factors will be difficult. Therefore, most of the weight factors remain unchanged in MPC, which reduces the overall control performance of the system. By contrast, in FOMPC, the weighting factor is obtained by fractional order, in which different weighting factors can be adjusted by two fractional orders, one for tracking error and the other for control performance [32]. Therefore, FOMPC can produce better system performance than MPC method [33]. In this work, FOMPC is innovatively applied to a multi-light control system based on dSPACE. Next, the integer order cost function is replaced by the fractional order cost function in MPC. In order to obtain a relatively good value set of the eight subloops in our system, each subloop gives a different fractional order to obtain the optimal control performance. Finally, by building the dSPACE multiple lighting control experimental platform, the application practice of the control scheme is realized. Through trajectory tracking experiments, it is verified that the fractional order model predictive controller is superior to the conventional controller in robustness, disturbance rejection, steady-state error minimization etc. The structure of the paper is as follows: in the Section 2, the multiple lighting control system based on dSPACE is introduced. The Section 3 briefly introduces the research problems and control strategies, as well as designs the fractional cost function. The Section 4 gives the comparison results between FOMPC and classical MPC. Section 5 summarizes the results of the paper.
2. Description of Multiple Lighting Control Systems
2.1. Multiple Lighting Control System Based on dSPACE
The multiple lighting control system based on dSPACE is shown in Figure 1. It mainly includes a light box feedback device, Matlab server, and dSPACE controller. The box contains eight incandescent lamps, Mini Bayonet/BA9S, at the top and eight photo light-dependent resistors (LDR), N5AC501085, at the bottom. The lower part of each lamp corresponds to a sensor to form one zone. The box has a total of eight zones; in order to simulate the office environment, the eight zones are separated from each other by walls, and the existence of walls largely blocks the transmission of light between different zones. However, because the walls in the experimental equipment are not completely separated, there is still a certain coupling between the zones.

Figure 1.
Multiple lighting control system based on dSPACE: (a) system block diagram; (b) real system (picture).
The control programs were designed in MATLAB and Simulink. The files were then compiled into the controller dSPACE DS1104 for execution. With the real-time interface (RTI), dSPACE controller can implement the Simulink models on the real-time hardware. This reduces the time significantly. Furthermore, the RTI can cooperate with Controldesk for real-time data monitoring and processing. In this control system, each lamp belongs to a control subloop. The lamp and sensor are divided into eight control zones by delimiter panels, which weakens the coupling between each zone. The control input is transmitted to the lamp by the electronic equipment responsible for signal conditioning and power management based on a current amplifier construed with bipolar NPN transistors (electronics block). The brightness of the lamps can be manipulated by the input signals, and the output signal is transmitted to the controller through the corresponding light sensor.
2.2. System Characterization and Calibration
Before the control design of the system, it is beneficial to know the static characteristics of the system to check linearity zones. The static characteristics of the control zone 1 can be obtained by several staircase experiments. In the experiment, the lamp input voltage of the zone 1 was varied linearly from 0 to 10 V while recording the output value according to the sensor. The measurement result is shown in Figure 2. It can be seen from the experimental results that, when the input voltage between 0 and 5 V, the output voltage is almost zero. There are two main reasons for this phenomenon. One is that the sensor is not sensitive to weak light response, and the other is that the lamp does not emit brightness when the voltage is small. When the input voltage is 5–10 V, the output increases almost linearly. A linear system is more conducive to the realization of the control method in the research. Consequently, we chose to operate in the interval from 5 to 10 V. In this region, the output rises almost linearly with the input voltage. Next, a staircase experiment was carried out in zone 1 to verify the dynamics of the system. The input was altered from 0 to 10 V, increasing by 2 V each step. Between the two jumps, the input value remained unchanged such that the system could reach its steady-state value. In order to compare the dynamics of each step, the data of each step were standardized, as shown in Figure 2.
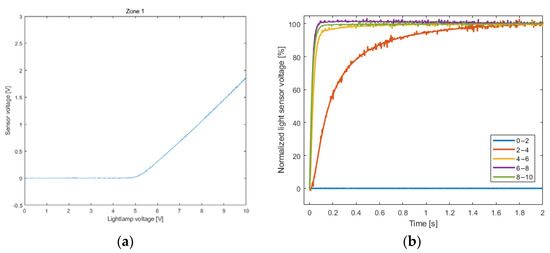
Figure 2.
System characteristics before calibration: (a) static characteristics of zone 1; (b) normalized staircase experiment of zone 1.
For steps from 0 to 2 V, the system did not respond as expected by the static characteristics. The jump from 2 to 4 V first encountered a dead zone before responding slowly, and a large amount of noise was measured. For higher steps, the response of the system was closely linked. Moreover, when working at high voltage, the dead time was eliminated. It can also be seen that a higher input voltage resulted in a faster system response speed. As the voltage approached 10 V, the rise times converged. The staircase experiment again showed that the valuable research part of the system input is between 5 and 10 V. Since each area uses the same lamps and sensors, and the sensors are calibrated, the characteristics of each area are roughly the same. The characteristics of other zones can be verified by repeating the above experiments. By calibrating the sensor, when the input voltage of all lamps was 5 V, the reading of the sensor was 0 V, and when the input voltage of all lamps was 10 V, the output voltage of the sensor was 5 V. In this way, the controller could change the input between 0 and 5 to send a voltage between 5 V and 10 V to the lamp. Through calculation, a coefficient was added such that the input of each system was between 0 and 5 and the corresponding output was also between 0 and 5. The input and output voltages no longer represent the real voltage value in the system; thus, they can be expressed in numbers or percentages. After calibration, the static characteristics and normalized staircase tests were carried out again. The input value was changed between 0 and 5, and the staircase experiment was increased by 1 V each step; the calibrated experimental results are shown in Figure 3.
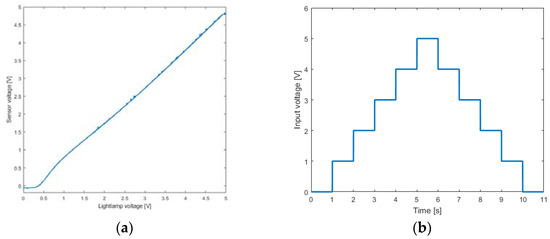
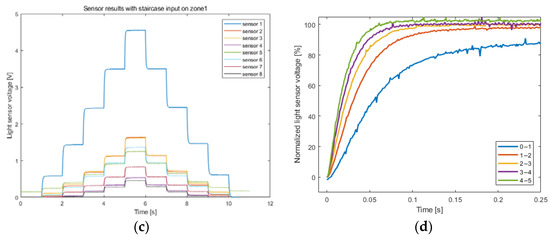
Figure 3.
System characteristics after calibration: (a) static characteristic of zone 1 after calibration; (b) staircase experiment input signal; (c) staircase experiment data for each zone with the input is given in zone 1; (d) normalized staircase of zone 1 after calibration.
The static characteristic after calibration was a positive correlation line, which was slightly nonlinear. The standardized staircase in Figure 3b depicts five very similar steps. Although the rise time was different, the difference was within an acceptable range. The other seven agents had similar results. Hence, the basic tests of the experimental platform were completed and could be further used for identification purposes.
2.3. System Identication
When designing advanced model-based controllers, a better quality of the model and its accuracy will generate better performance in terms of the response of the controller. On the other hand, the model can also be used to simulate the system characteristics to avoid damaging the equipment in the process of optimizing the control method. The model is based on experiments and standard recognition methods. The multiple lighting control system can be regarded as a Hammerstein system. The model of the system is composed of a linear transfer function and polynomial nonlinear static gain. The polynomial is calculated by fitting the static characteristics, and the nonlinear polynomial is fitted using the static characteristics in Figure 3a. The polynomial with the least error is a quartic polynomial with the following function:
By using the built-in MATLAB function tfest, set the transfer function on the second stair step in Figure 3b can be used to approximate the dynamics of this zone. Then, the transfer function can be normalized so that its static gain is equal to 1. The resulting transfer function becomes
where and are the Laplace transformations of and , respectively.
Using a polynomial in simulation can minimize the simulation reality error, but the use of a nonlinear polynomial will complicate the design of control structure; therefore, static gain was used to replace it in the design of controller. Because there is a certain coupling between various zones of the multiple lighting control system, the polynomial and transfer functions are multiplied by a constant to simulate each interaction according to the intensity of the interaction. The interaction constant is equal to
The complete transfer matrix is composed of the coupling matrix, transfer function, and nonlinear polynomial. This transfer matrix is called .
3. Design of Control Scheme Based on Fractional Order Distributed MPC
3.1. Problem Formulation
In practical engineering, there are many complex systems that cannot be accurately described by integer order differential equations; on the other hand, fractional order differential equations can more accurately describe the characteristics of the system. As a kind of advanced control method, MPC is good at dealing with multi-input and multi-output systems and nonlinear situations with complex constraints. It has been successfully applied in the field of practical process control [34,35]. In addition, for some complex fractional order systems, the traditional MPC and integer order predictive function control method often have less versatility, poor robustness, and unsatisfactory control performance. It is necessary to study the controller with good control performance to control actual objects described by the fractional order model. If the integer order predictive function control method is extended to the fractional order predictive function control method, it is expected to effectively compensate for the deficiency of the former by improving the outcome and promoting the application of the predictive function control method in the fractional order system.
In this paper, an FOMPC method was designed for a class of multiple-input multiple-output (MIMO) systems. The proposed method required that the fractional order term was approximated to the integer order system, which was achieved using the RDK approximation method [36]. The predictive output model was established on the basis of the RDK approximation model, and the fractional integral was introduced into the objective function to further calculate the optimal control quantity. Finally, the fractional order controller was simulated and tested, and then compared against MPC based on the integer order model.
3.2. Fractional Order Distributed MPC
There are many forms of fractional calculus. In this paper, the definitions of Grünwald–Letnikov (GL) and Riemann–Liouville (RL) were used.
Grünwald–Letnikov (GL) fractional differential definition:
where α is the initial state time, h is the sampling step, and [χ] is the greatest integer smaller than χ. is a polynomial coefficient,
Riemann–Liouville (RL) fractional differential definition:
where , is the Euler gamma function, and .
In this formulation, is the original function of , and the Laplace transform defined by fractional calculus of Riemann-Liouville is
Under the zero initial condition, the Laplace transform result of RL is
From Equation (9), the transfer function of the ĸ-order fractional calculus operator can be expressed as
According to [36], for any given nonrational continuous-time transfer function with real parameters, one can find a rational discrete-time transfer function of specified order N, , which adequately approximates the frequency response of the nonrational continuous-time transfer function in a specified frequency range. Using the RDK method, a rational discrete-time transfer function can be determined, which produces a similar impulse response to that obtained from the inverse fast Fourier transform. To determine the rational discrete-time transfer function the signal modeling techniques through the Matlab built-in function tfest is used. The coefficients of the rational discrete time transfer function,
are determined on the basis of the desired order N of the resulted approximation. The order N is a tuning parameter.
According to the characteristics of predictive function control, combined with the established model and input control quantity, the predictive output value of the process object at the future time is predicted.
where is generated by the basic future control input , and is obtained with optimized future control action . The future input can be obtained as follows:
According to the discretization of the input, the optimal expression of the output can be obtained.
where and are the impulse response and step response coefficients of the system obtained after discrete approximation, is the control horizon corresponding to the input order, and is the prediction horizon corresponding to the output order. The system output can be rewritten as
and ,
where is the time delay of the system.
For an integer order controller, considering the rolling optimization problem in the finite time domain, the following MPC objective functions are generally selected:
where is the reference trajectory, and and are nonnegative weighting factors, which are kept as constants.
Rewriting Equation (12) in matrix form, the following expression can be obtained:
where and .
When there are constraints in the optimization problem, it can be solved by quadratic programming. Without constraints, the optimal input sequence of is as follows:
For a fractional order controller, the objective function of integer order predictive control is designed using the content introduced in Section 2. The objective function of an FOMPC can be selected as follows:
Using the discrete form of Grünwald–Letnikov fractional calculus, the above objective function can be discretized at the sampling time to obtain the discrete form of the objective function,
The with fractional order α gives
where n is the number of .
Using Equation (21) to Equation (24), the weight matrix can be calculated by the fractional order term in the objective function and . The weight factors in FOMPC are time-varying in the prediction horizon and control horizon. If there are constraints, quadratic programming can be used to solve the optimization problem. Without constraints, the optimal input sequence of in the FOMPC can be obtained as follows:
Compared with the traditional MPC method, this FOMPC scheme improves the tracking performance and disturbance rejection performance to a certain extent, as well as reduces the computing load for real-time control applications.
4. Results and Discussion
For the designed fractional order predictive function controller, the effectiveness of the controller was verified by MATLAB numerical simulation and experiments based on a multi-light control system. By comparing the effects of FOMPC and MPC in the reference tracking experiment, the improved performance of FOMPC in reference tracking and energy control can be validated.
4.1. Numerical Simulation
In order to evaluate the control performance of FOMPC proposed in this paper, we compared the classical MPC control method with the proposed FOMPC control method. Taking the eight zone models of the multiple lighting control system as the object, the simulation experiment was carried out. Through the reference tracking experiment, the step signal was introduced into the system at different times. The simulation time was 40 s, and the sampling time was 0.01 s. The set values of the eight zones are shown in Table 1. In addition, in order to test the disturbance rejection performance of the controller, a random disturbance signal less than 0.5 was added through the Simulink repeating sequence module when the simulation time was 20 s to 40 s.

Table 1.
Set points for different zones in the experiments.
As expected from the literature [30], within a certain range, a larger fractional order leads to a faster response time and smaller overshoot. Through the test, the fractional orders of the eight zones were set to 2.2, 2.2, 2.2, 1.62, 1.62, 1.82, 1.82, and 1.82. As tuning parameters for MPC, the control horizon was one sample and the prediction horizon was 18 samples. The simulation results of reference tracking performance are shown in Figure 4 and Figure 5.
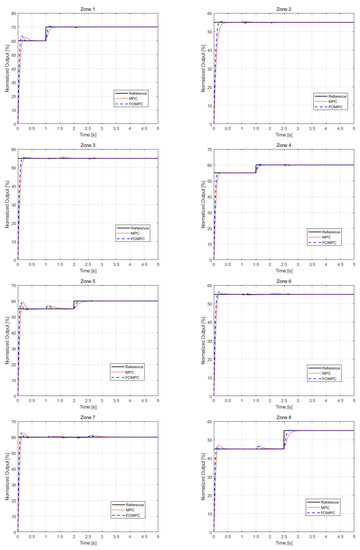
Figure 4.
Output of multiple lighting control with MPC and FOMPC in reference tracking simulation.
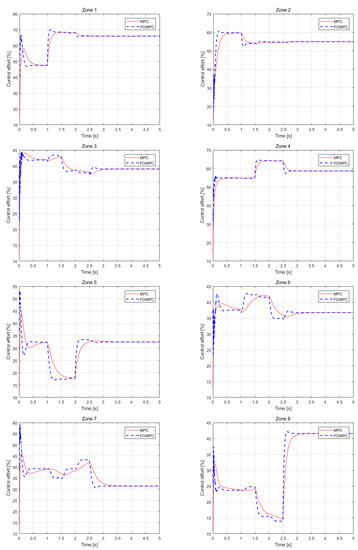
Figure 5.
Control effort of multiple lighting controls with MPC and FOMPC in reference tracking simulation.
By observing the response time and overshoot of the tracking experimental results, it can be clearly seen that the control effect of the FOMPC was better than that of MPC. The performance of the FOMPC and MPC can be more clearly evaluated by calculating the integrated absolute relative error (IARE) and ratio of integrated absolute relative error (RIARE), and correspond to the FOMPC and MPC controllers, respectively.
The reference tracking performance indicators of the FOMPC and MPC are illustrated in Table 2 and Table 3.

Table 2.
Indices for IARE in reference tracking simulation.

Table 3.
Indices for RIARE in reference tracking simulation.
Next, in order to verify the effect of disturbance rejection performance control, the experimental waveforms for the normalized output with disturbance are depicted in Figure 6.
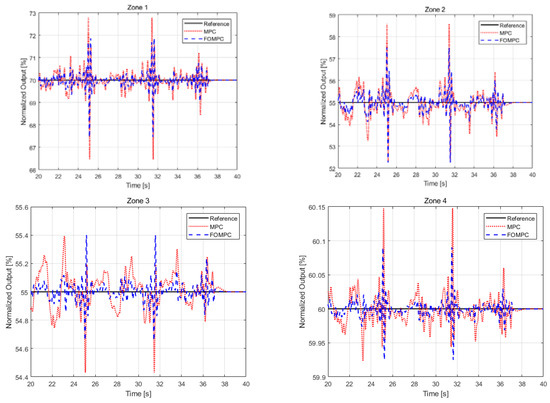
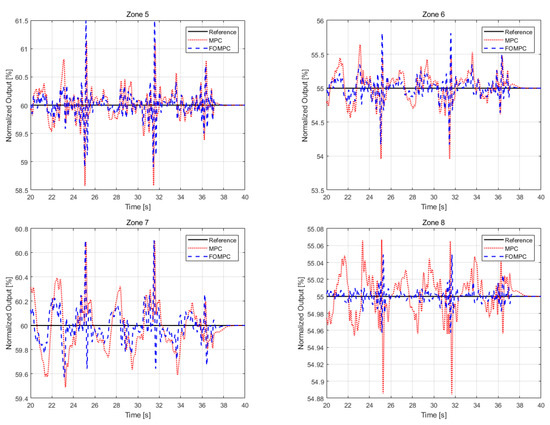
Figure 6.
Comparison of disturbance rejection performance between MPC and FOMPC.
According to the comparison in Figure 6, the FOMPC controller outperformed the MPC controller and had better disturbance suppression ability. As observed from the simulation results and performance indices, the controller proposed in this paper had better tracking performance and smaller overshoot, while the MPC controller exhibited strong oscillations and long settling times. In conclusion, compared with the MPC controller, the proposed approach to the FOMPC controller produced less overshoot and oscillation, had better tracking performance and disturbance rejection performance, and could obtain better control performance.
4.2. Experiment Based on Multiple Lighting Control System
Taking the multiple lighting control system based on dSPACE as the experimental object, a physical experiment was carried out using the same parameter configuration in the simulation experiment. The experiment results of the reference tracking performance are given in Figure 7.
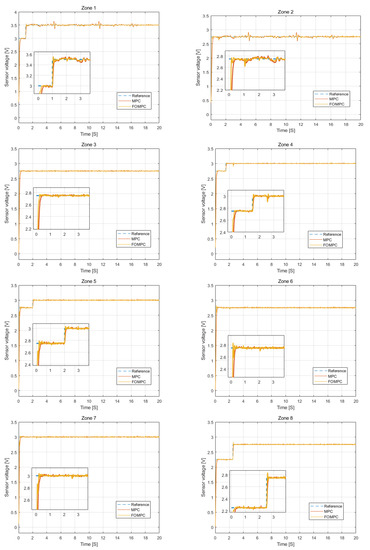
Figure 7.
Output of multiple lighting control with MPC and FOMPC in reference tracking experiment.
The reference tracking performance indicators of FOMPC and MPC are summarized in Table 4 and Table 5.

Table 4.
Indices for IARE in the reference tracking experiment based on multiple lighting control.

Table 5.
Indices for RIARE in the reference tracking experiment based on multiple lighting control.
In order to verify the advantages of the FOMPC in reducing energy consumption and output error in the control process, Figure 8 illustrates the real-time control input.
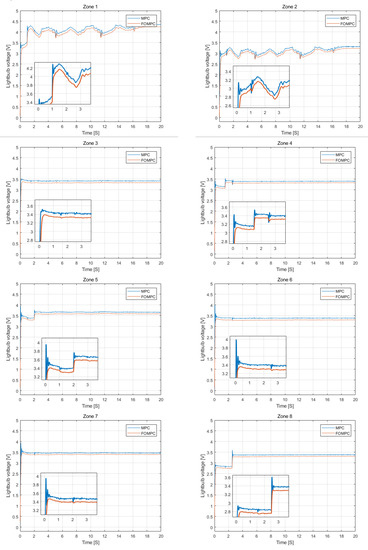
Figure 8.
Control input of multiple lighting control with MPC and FOMPC in reference tracking experiment.
It can be concluded from the experimental comparison in Figure 8 that, compared with the traditional MPC, the FOMPC could not only quickly realize the tracking response and reduce the output error, but also reduce the control input and achieve the effect of reducing energy consumption. Thus, it is proven again that the FOMPC has better control performance than MPC.
5. Conclusions
For a class of MIMO systems, a design method of an FOMPC controller was proposed. By replacing the integer cost function with the fractional cost function, the FOMPC was applied to the MIMO system with multiple lighting control. Through simulation and multiple lighting control experiments based on dSPACE, the designed FOMPC and traditional MPC controller were compared. Simulation and experimental results show that, by adjusting reasonable control parameters, the response speed of the FOMPC controller was faster, the overshoot and oscillation were smaller, and the control effect was better. At the same time, the FOMPC was applied to different zones of a multiple lighting control system to prove the effectiveness of this method in the MIMO system. However, in the actual MIMO system, there exist many challenges, such as network delays, uncertainty, interferences, and nonlinearities. In order to solve these challenging problems, the fractional order distributed model predictive control scheme proposed for multi-agent systems needs further research.
Author Contributions
Methodology, R.C., S.Z., C.-M.I. and C.C.; software, C.C., R.C. and S.Z.; formal analysis, C.C.; writing—original draft preparation, C.C.; writing—review and editing, C.C., R.C., G.-P.L. and C.-M.I.; supervision, C.-M.I. and G.-P.L.; funding acquisition, C.C. and C.-M.I. All authors have read and agreed to the published version of the manuscript.
Funding
Clara-Mihaela Ionescu gratefully acknowledges the financial support for this work from Ghent University research fund BOF STG MIMOPREC 2018. Chuanguo Chi gratefully acknowledges the financial support from Chinese Scholarship Council (CSC) under grant 202106120085. Ricardo Cajo gratefully acknowledges the financial support for this work from ESPOL University through the research project nr. FIEC-730-2021 and Shiquan Zhao gratefully acknowledges the financial support from the Fundamental Research Funds for the Central Universities (no. 3072021CFJ0408).
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Cho, J.-H.; Wang, Y.; Chen, I.-R.; Chan, K.S.; Swami, A. A Survey on modeling and optimizing multi-objective systems. IEEE Commun. Surv. Tutorials 2017, 19, 1867–1901. [Google Scholar] [CrossRef]
- Fazlollahi, S.; Becker, G.; Ashouri, A.; Maréchal, F. Multi-objective, multi-period optimization of district energy systems: IV–A case study. Energy 2015, 84, 365–381. [Google Scholar] [CrossRef]
- Khezri, R.; Amin, M. Review on the state-of-the-art multi-objective optimisation of hybrid standalone/grid-connected energy systems. IET Gener. Trans. Distrib. 2020, 14, 4285–4300. [Google Scholar] [CrossRef]
- Lokeshgupta, B.; Sivasubramani, S. Multi-objective home energy management with battery energy storage systems. Sustain. Cities Soc. 2019, 47, 101458. [Google Scholar] [CrossRef]
- Gangwar, P.; Singh, S.N.; Chakrabarti, S. Multi-objective planning model for multi-phase distribution system under uncertainty considering reconfiguration. IET Renew. Power Gener. 2019, 13, 2070–2083. [Google Scholar] [CrossRef]
- Miao, Z.; Yu, J.; Ji, J.; Zhou, J. Multi-objective region reaching control for a swarm of robots. Automatica 2019, 103, 81–87. [Google Scholar] [CrossRef]
- Tan, H.; Wang, Y.; Zhong, H.; Wu, M.; Jiang, Y. Coordination of low-power nonlinear multi-agent systems using cloud computing and a data-driven hybrid predictive control method. Control Eng. Pr. 2021, 108, 104722. [Google Scholar] [CrossRef]
- Pandharipande, A.; Newsham, G. Lighting controls: Evolution and revolution. Light. Res. Technol. 2018, 50, 115–128. [Google Scholar] [CrossRef]
- Wagiman, K.R.; Abdullah, M.N.; Hassan, M.Y.; Radzi, N.H.M. A new optimal light sensor placement method of an indoor lighting control system for improving energy performance and visual comfort. J. Build. Eng. 2020, 30, 101295. [Google Scholar] [CrossRef]
- Pandharipande, A.; Caicedo, D. Smart indoor lighting systems with luminaire-based sensing: A review of lighting control approaches. Energy Build. 2015, 104, 369–377. [Google Scholar] [CrossRef]
- Cimini, G.; Freddi, A.; Ippoliti, G.; Monteriù, A.; Pirro, M. A smart lighting system for visual comfort and energy savings in industrial and domestic use. Electr. Power Components Syst. 2015, 43, 1696–1706. [Google Scholar] [CrossRef]
- Ghita, M.; Diaz, R.A.C.; Birs, I.R.; Copot, D.; Ionescu, C.M. Ergonomic and economic office light level control. Energies 2022, 15, 734. [Google Scholar] [CrossRef]
- Juntunen, E.; Sarjanoja, E.-M.; Eskeli, J.; Pihlajaniemi, H.; Österlund, T. Smart and dynamic route lighting control based on movement tracking. Build. Environ. 2018, 142, 472–483. [Google Scholar] [CrossRef]
- Byun, W.-J.; Jin, Y.-S.; Kim, Y.-W.; Lim, J.-H. Design of Lighting Control System Considering Lighting Uniformity and Discomfort Glare for Indoor Space. In Proceedings of the 2018 International Conference on Platform Technology and Service (PlatCon), Sydney, NSW, Australia, 21–23 November 2018; pp. 1–6. [Google Scholar]
- Liu, G.-P. Coordinated control of networked multiagent systems with communication constraints using a proportional integral predictive control strategy. IEEE Trans. Cybern. 2020, 50, 4735–4743. [Google Scholar] [CrossRef]
- Manzano, J.M.; Limon, D.; de la Peña, D.M.; Calliess, J.-P. Robust learning-based MPC for nonlinear constrained systems. Automatica 2020, 117, 108948. [Google Scholar] [CrossRef]
- Peng, H.; Wang, W.; An, Q.; Xiang, C.; Li, L. Path tracking and direct yaw moment coordinated control based on robust MPC with the finite time horizon for autonomous independent-drive vehicles. IEEE Trans. Veh. Technol. 2020, 69, 6053–6066. [Google Scholar] [CrossRef]
- Christofides, P.D.; Scattolini, R.; de la Peña, D.M.; Liu, J. Distributed model predictive control: A tutorial review and future research directions. Comput. Chem. Eng. 2013, 51, 21–41. [Google Scholar] [CrossRef]
- Halvgaard, R.; Vandenberghe, L.; Poulsen, N.K.; Madsen, H.; Jørgensen, J.B. Distributed model predictive control for smart energy systems. IEEE Trans. Smart Grid 2016, 7, 1675–1682. [Google Scholar] [CrossRef]
- Spudić, V.; Conte, C.; Baotić, M.; Morari, M. Cooperative distributed model predictive control for wind farms. Optim. Control Appl. Methods 2015, 36, 333–352. [Google Scholar] [CrossRef]
- Chen, L.; Hopman, H.; Negenborn, R.R. Distributed model predictive control for vessel train formations of cooperative multi-vessel systems. Transp. Res. Part C Emerg. Technol. 2018, 92, 101–118. [Google Scholar] [CrossRef]
- Wu, Z.; Rincon, D.; Christofides, P.D. Real-time adaptive machine-learning-based predictive control of nonlinear processes. Ind. Eng. Chem. Res. 2020, 59, 2275–2290. [Google Scholar] [CrossRef]
- Domek, S. Fractional-Order Differential Calculus in Model Predictive Control; West Pomeranian University of Technology Academic Press: Szczecin, Poland, 2013. [Google Scholar]
- Nigmatullin, R.; Baleanu, D.; Fernandez, A. Balance equations with generalised memory and the emerging fractional kernels. Nonlinear Dyn. 2021, 104, 4149–4161. [Google Scholar] [CrossRef]
- Domek, S. Mixed logical dynamical modeling of discrete-time hybrid fractional systems. In Fractional Dynamical Systems: Methods, Algorithms and Applications; Springer: Berlin/Heidelberg, Germany, 2022; pp. 77–105. [Google Scholar]
- Zheng, W.; Huang, R.; Luo, Y.; Chen, Y.; Wang, X.; Chen, Y. A look-up table based fractional order composite controller synthesis method for the pmsm speed servo system. Fractal Fract. 2022, 6, 47. [Google Scholar] [CrossRef]
- Zhao, S.; Cajo, R.; De De Keyser, R.; Ionescu, C.-M. The potential of fractional order distributed MPC applied to steam/water loop in large scale ships. Processes 2020, 8, 451. [Google Scholar] [CrossRef] [Green Version]
- Cajo, R.; Zhao, S.; Plaza, D.; Keyser, R.D.; Ionescu, C. A fractional order predictive control for trajectory tracking of the AR. drone quadrotor. In Portuguese Conference on Automatic Control; Springer: Berlin/Heidelberg, Germany, 2020; pp. 528–537. [Google Scholar]
- Juchem, J.; Muresan, C.; De Keyser, R.; Ionescu, C.-M. Robust fractional-order auto-tuning for highly-coupled MIMO systems. Heliyon 2019, 5, e02154. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Domek, S. Switched fractional state-space predictive control methods for non-linear fractional systems. In Conference on Non-Integer Order Calculus and Its Applications; Springer: Berlin/Heidelberg, Germany, 2018; pp. 113–127. [Google Scholar]
- Si, X.; Wang, Z.; Song, Z.; Zhang, Z. Asymptotic stabilization of delayed linear fractional-order systems subject to state and control constraints. Fractal Fract. 2022, 6, 67. [Google Scholar] [CrossRef]
- Ionescu, C.M.; Dulf, E.H.; Ghita, M.; Muresan, C.I. Robust controller design: Recent emerging concepts for control of mechatronic systems. J. Frankl. Inst. 2020, 357, 7818–7844. [Google Scholar] [CrossRef]
- Cajo, R.; Mac, T.T.; Plaza, D.; Copot, C.; De Keyser, R.; Ionescu, C. A survey on fractional order control techniques for unmanned aerial and ground vehicles. IEEE Access 2019, 7, 66864–66878. [Google Scholar] [CrossRef]
- Vilanova, R.; Antonio, V. PID Control in the Third Millennium; Springer: Berlin/Heidelberg, Germany, 2012. [Google Scholar]
- Padula, F.; Visioli, A. Advances in Robust Fractional Control; Springer: Berlin/Heidelberg, Germany, 2015. [Google Scholar]
- De Keyser, R.; Muresan, C.I.; Ionescu, C.M. An efficient algorithm for low-order direct discrete-time implementation of fractional order transfer functions. ISA Trans. 2018, 74, 229–238. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).