Tool Embodiment Is Reflected in Movement Multifractal Nonlinearity

Abstract

Recent advances in neuroscience have linked dynamical systems theory to cognition. The main contention is that extended cognition relies on a unitary brain-body-tool system showing the expected signatures of interaction-dominance reflected in a multifractal behavior. This might be particularly relevant when it comes to understanding how the brain is able to embody a tool to perform a task. Here we applied the multifractal formalism to the dynamics of hand movement while one was performing a computer task (the herding task) using a mouse or its own hand as a tool to move an object on the screen. We applied a focus-based multifractal detrended fluctuation analysis to acceleration time series. Then, multifractal nonlinearity was assessed by comparing original series to a finite set of surrogates obtained after Iterated Amplitude Adjusted Fourier transformation, a method that removes nonlinear multiscale dependencies while preserving the linear structure of the time series. Both hand and mouse task execution demonstrated multifractal nonlinearity, a typical form of across-scales interactivity in cognitive control. In addition, a wider multifractal spectrum was observed in mouse condition, which might highlight a richer set of interactions when the cognitive system is extended to the embodied mouse. We conclude that the emergence of multifractal nonlinearity from a brain-body-tool system pleads for recent theories of radical tool embodiment. Multifractal nonlinearity may be a promising metric to appreciate how physical objects—but also virtual tools and potentially prosthetics—are efficiently embodied by the brain.

1. Introduction

In order to adapt to an ever-changing environment, the brain is able to dynamically organize a variety of networked architectures involved in maintaining a given function or a stable performance during a task. This successful organization can form a cognitive system that ensures an adequate behavior, and reflects the way the system is adapting to the task. From this perspective, it has been theorized that the emergent behavior contains relevant information about the dynamic organization of cognition [1]. In line with this intuition, it has been shown that the adaptive capacity of the cognitive system can be grasped quite equivalently from fractal characteristics of brain functional networks organization, or from fractal-like dynamics that emerge in movement time series [2]. Increasingly, over several years, fractal and multifractal approaches have helped researchers to show the great relevance of analyzing the temporal structure of the movement system to infer the adaptive capacity of the system linking the brain, the body, and the task at hand [3,4,5,6,7,8,9].

Performing a task requires the recruitment of a huge number of components to form a functional system. Although it is obvious that a cognitive system has a lot to do with brain functions, mapping cognitive systems based on the activity of specific brain structures has not provided convincing evidence. As a first explanation, cognitive tasks activate overlapped brain areas through dynamically interacting networks [10,11], so that one can hardly associate a given function to a given cerebral structure [12]. More intriguingly, it is suggested that critical interactions can take place beyond the confines of the brain, e.g., at the frontier between the body and the environment [13]. Recent theorizations used the term extended cognition to describe the capacity of the brain to embody manipulated objects or tools into a unitary cognitive system [14].

How the brain can extend a coordinated cognitive architecture toward body and environmental interactions when using a tool has received significant attention in recent years [7,14,15,16]. Fractal-like temporal structures in movement time series have been used to distinguish when a tool appears as ready-to-hand (embodied) or only present-at-hand (disembodied) [7,15,16]. Readiness-to-hand is originally a philosophical concept in Heidegger’s phenomenology that refers to the fact that a tool can become part of one’s body. When it happens, rather than thinking about the instructions to give to the tool to complete a task, the user shifts its attention directly to the task, the tool being incorporated in an extended cognitive system. To admit that brain, body and tool become a unitary system is to suppose that this system must exhibit the expected signature of interaction dominance [14], a property reflected in nonlinear characteristics of the emergent behavior [4,5,17,18,19]. Interaction-dominance in cognitive sciences posits that interdependencies between the activity of the multiple components of the system matter more than the component activities themselves [1]. A unitary system is not additively decomposable as a result of tightly interwoved interactions. Therefore, it is futile to distinguish any independent subpart. Interactions unfold across several time scales at once, which gives rise to a specific nonlinear multifractal pattern in the emergent movement dynamics [17].

A recent experiment using a computer mouse as a tool to perform a computer task showed that perturbing the mouse functioning was concomitant to a degradation in fractal characteristics of the acceleration time series of the hand. Degraded (multi)fractal properties were interpreted as a disembodiment of the tool, let say the transition from ready-to-hand to unready-to-hand [7,15,16]. Here we used the herding task as an experimental attempt to show that tool embodiment may be inferred from nonlinear characteristics of acceleration time series. For that, we compared task performance when using the hand, an obvious and naturally embodied ‘tool’, to task performance when using the computer mouse. We expected nonlinear processes to infer extended cognition and tool embodiment, which makes it necessary to disentangle the ambiguity between across-scales vs. scale-dependent interactions, giving rise to movement multifractality. The presence of scale-dependent interactivity would not be a sufficient argument to conclude that a tool has been embodied, because such behavior may emerge from coordination among distinct, insular subparts of a cognitive system. Multifractal nonlinearity is mandatory to conclude unambiguously that the mouse has been embodied. Nonlinearity in multifractal processes can be tested by generating phase-randomized surrogates of the original series, in which linear processes are preserved while the interactions between multiple scales are eliminated [17]. More clearly, multifractal nonlinearity is the term used to indicate how the multifractality of the original series departs from the multifractality attributable to the linear structure of phase-randomized surrogates [6,20]. This has been used as an elegant way to infer across-scales interactivity in a cognitive system [19,20].

In the present study, we developed our own version of the sheep herding task, a computer task during which participants could move a cursor on the screen with their own hand (thanks to motion capture) or with a computer mouse as a tool. Hand and mouse acceleration during displacements was collected to serve as experimental time series in which we evaluated multifractal nonlinearity.

The main hypothesis was that multifractal nonlinearity is the expected signature of a unitary cognitive system, leading to the view that the tool is embodied. This way, greater multifractality was also expected in the mouse condition, reflecting more interactions emerging from an extended cognitive system.

2. Materials and Methods

2.1. Participants

Seventy-four undergraduate students (43 males, 31 females; 21 ± 2 years old) gave their informed consent to participate in the experiment approved by an Institutional Review Board (Faculte des STAPS Institutional Review Board). All the procedures respected ethical recommendations and followed the declaration of Helsinki. The participants had normal or corrected to normal vision. They completed a questionnaire about their video game and computer mouse use habits (

Table 1. Characteristics of participant.

Group		Hand	Mouse
Gender	Male	22	21
	Female	14	17
Video Games	Player	16	18
	Non player	20	20
Mouse usage	Never	6	9
	Less than once a month	7	6
	Less than once a week	9	8
	Almost once a day	3	9
	Daily	11	6

).

They were randomly assigned to one of the two experimental groups (Table 1). About half of them performed the task by using their own hand as a tool (n = 36), and the other used the computer mouse (n = 38). None of them was familiar with the computer task. Repetition 1 served as familiarization (see below).

Table 1 shows even distribution of gender and habits in the experimental groups.

2.2. The Sheep Herding Task

The task used here is an adaptation of the sheep herding task [7,15], and is largely inspired by the experimental design in a previous work by Bennett et al. [21]. We created our own version of the task using Unity software (Unity Technologies, San Francisco, CA, USA). The participant needs to move a “dog” object (the cursor) to keep three moving “sheep” objects as close as possible to the center of the screen (for scoring), thereby preventing the sheep from going outside the circular pen (Figure 1).

Each sheep moved permanently according to three forces: (1) Repulsion force: the sheep is repelled by the dog. The closer the dog is to the sheep, the faster the sheep moves in the opposite direction; (2) Pack force: the sheep moves towards the barycenter of the sheep positions; and (3) Random force: a Perlin noise was used to move the sheep randomly over time. The coefficients applied to each force depended on the task’s difficulty level. Every six seconds if the sheep were successfully kept inside the pen, the difficulty level increased, making the noise and repulsion forces more prominent while reducing the strength of the pack force. When the sheep remained outside the pen for too long, the difficulty level dropped. If one animal went outside the boundaries of the screen, all the sheep reappeared in the center of the pen and the difficulty level dropped as well. Importantly, this dynamic difficulty has been implemented to maintain the user’s attention over time. The participant was informed that a scoring system was operating, with more points being credited the closer the sheep are to the center of the screen over time. The higher the difficulty level reached by the player, the faster the score increased; for this reason, the score of the first repetition—during which the difficulty level increased progressively—was systematically lower than the following repetitions (see Section 3.1). The overall difficulty perceived by each participant is expected to be maintained during successive repetitions, which is addressed a posteriori by comparing scores.

2.3. Procedure

During the experiment, the participants remained seated with their forearms lying on a large table, facing a 27 inch screen. They performed five 70-s repetitions of the same task, with 5 s rest between them. Participants were told that seven repetitions were needed, which avoids potential bias in the last effective repetition (repetition 5).

2.4. Hand as a Tool

In hand condition, the dog on the screen was moved in perfect synchronization with the hand displacement on the table. For that, three markers were fixed on the back of the hand (wearing a glove) and tracked by an Optitrack motion capture system (V120: Trio, OptiTrack; NaturalPoint, Inc., Corvallis, OR, USA), consisting of three infrared cameras following reflective markers. The position of the rigid body was streamed at 90 Hz to the Sheep Herding task in the Unity software to act as a guide for the dog’s movements. No latency was perceptible by the participant. The gain between hand and cursor displacement was adjusted to offer a sensitivity similar to that of the computer mouse in mouse condition.

2.5. Collected Time Series

Here, to infer tool embodiment from a cognitive organization that emerges in movement, we collected the acceleration time series of the hand or the mouse when participants were performing several repetitions (70 s each) of the herding task. For that, a Series 4 Apple Watch (Apple, Cupertino, CA, USA) was firmly fixed either inside the mouse or on the back of the hand to collect acceleration signals along three axes at 100 Hz. The watch was plugged in a specifically designed and 3D-printed receptacle, that was inserted into the mouse (mouse condition) or on the top of the hand (hand condition) using a glove on which the motion capture markers were already positioned.

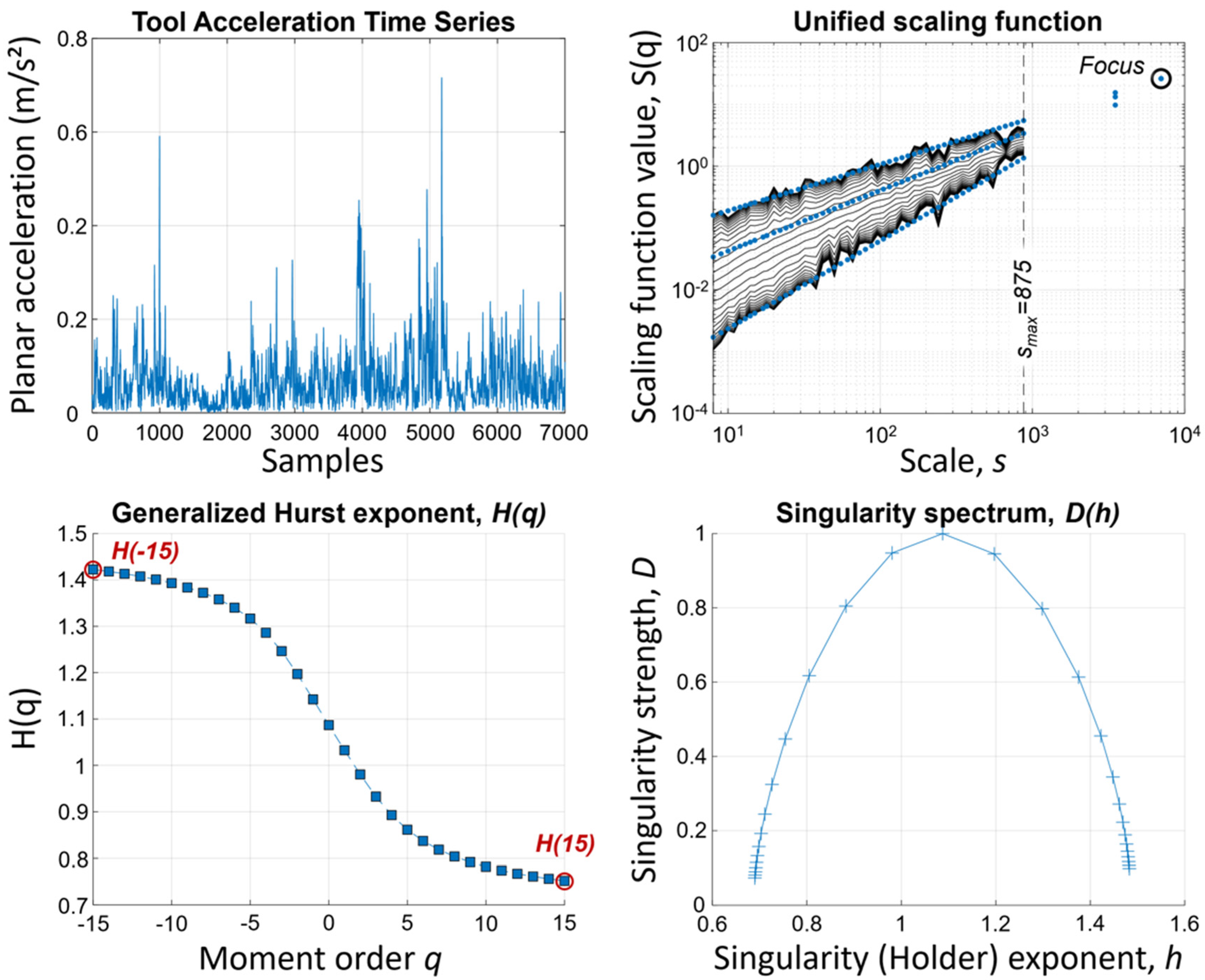
The planar acceleration was computed from acceleration values collected along x-axis (x) and y-axis (y) of the watch accelerometer, as the square root of x² + y². This variable constitutes the acceleration time series that served as experimental signals analyzed by using a multifractal analysis. A typical experimental signal obtained during one repetition of the herding task (70 s at 100 Hz provided 7000 samples) is illustrated in the top left of Figure 2, together with the subsequent multifractal analysis (Section 2.6) of this signal (other panels).

2.6. Multifractal Assessments

Multifractal characteristics in original acceleration time series and in their phase-randomized surrogates (see Section 2.7) were obtained by using a method based on multifractal detrended fluctuation analysis [22]. The successive steps of calculations were as follows:

Given an initial acceleration time series x of size L (here, L = 7000 due to 70 s at 100 Hz):

(1)

We computed the cumulated sum from which the mean is subtracted:

$$y\left(i\right)={\displaystyle \sum }_{k=1}^i\left[xk-\langle x\rangle \right], i=1,\dots ,L$$

(1)

(2)

y(i) was then divided into N_s = floor (L/s) nonoverlapping ‘boxes’ of length s, where s represents consequently a time scale at which the signal is observed. The time scales we effectively used in our calculations were constructed equidistantly on a logarithmic scale. For each box ν, a local linear trend y_ν was calculated by least-square approximation. Then, the trend was subtracted (detrending).

(3)

The variance $F^2\left(\nu ,s\right)$ of the detrended time series was then calculated for each box ν and for each scale s:

$$F^2\left(\nu ,s\right)=\frac{1}{s}{{\displaystyle \int }}_{i=1}^s{\left\{y\left[\left(\nu -1\right)s+i\right]-y_{\nu }\left(i\right)\right\}}^2$$

(2)

(4)

The next step consisted in calculating the qth order fluctuation function by averaging the variance $F^2\left(\nu ,s\right)$ over all the N_s boxes.

$$F_q\left(s\right)={\left\{\frac{1}{N_s}{{\displaystyle \int }}_{v=1}^{N_s}[F^2{\left(\nu ,s\right)]}^{\frac{q}{2}}\right\}}^{\frac{1}{q}} for q\ne 0$$

(3)

$$F_q\left(s\right)=exp\left\{\frac{1}{2N_s}{{\displaystyle \int }}_{v=1}^{N_s}ln\left[F^2\left(\nu ,s\right)\right]\right\} for q=0$$

(4)

(5)

Finally, the fluctuation functions $F_q\left(s\right)$ were logarithmically plotted against the scales s for each q moment within the range q = −15 to +15 (Figure 2, top right). If the original signal x shows fractal scaling properties, the fluctuation function follows a power law for increasing scales s, that can be fitted to a linear approximation using a log-log representation (Figure 2 top right):

$$F_q\left(s\right)\propto s^{H\left(q\right)}$$

(5)

The value taken by the generalized Hurst exponent H(q) when q varies from −15 to +15 was used here to obtain the multifractal signature of the acceleration time series (Figure 2, bottom left). To avoid a corrupted assessment of multifractality in our time series, we employed a focus-based method.

2.6.1. Focus-Based Multifractal Formalism

In order to calculate H(q) with a more robust and unbiased method, we use a reference point (focus) during the regression of scaling functions as developed in [22]. Briefly, the method is based on the fact that, for a signal with finite length, all qth order scaling functions converge towards an identical point when the signal length L is used as the scale s (Figure 2, top right). Most importantly, it prevents the multifractal analysis of empirical time series from being corrupted by enforcing a family of scaling functions with the ideal fan-like geometry when fitting for H(q).

To resume, multifractality in each acceleration times series was evaluated here with a metric called ∆H15, quantified as the difference between values taken by the generalized Hurst exponent H(q) at q moment −15 and +15 (Figure 2, bottom left):

∆H15 = H(−15)–H(15)

(6)

2.6.2. Assessment of Multifractal Nonlinearity

Testing for multifractal nonlinearity in acceleration time series is a central topic in the present study. This crucial step consisted in appreciating the part of nonlinear processes present in each acceleration time series, by comparing each of them with a finite set of linearized surrogates. For that, each original acceleration time series was phase-randomized using the IAAFT method (Iterated Amplitude Adjusted Fourier Transform) to obtain 40 linearized surrogates. This procedure developed by Schreiber and Schmitz [23] to test for nonlinearity [23] has been recommended by Ihlen and Vereijken [17,18] and by Kelty-Stephen [5,6,19,20]. By preserving the amplitude spectrum but shuffling the phase spectrum, IAAFT provides a linearly equivalent time series. The presence of multifractal nonlinearity in our acceleration time series was unveiled by a one-sample t-test that compared ∆H15 in the original series to multifractality of the 40 IAAFT surrogates with matching linear structure. This t-statistics called t_MF grows larger the more the original series departs from the multifractality attributable to the linear structure of IAAFT surrogates. When t-test reaches significance (here p < 0.05) it is reasonable to admit that multifractality reflected in ∆H15 encodes processes that a linear contingency cannot. Multifractal nonlinearity is the metric we want to promote here to show the emergence of across-scales interactions as roots of tool embodiment.

2.7. Statistical Analysis

The statistical analysis was performed using Matlab (Matlab 2021b, Matworks, Natick, MA, USA). Outliers were identified by using the matlab ‘isoutlier’ function, which is based on three scaled median absolute deviations (MAD) away from the median. Each set of computed variables was tested for normality with the Shapiro-Wilk test using significant level p = 0.05. A large majority of samples showed normal distribution. When this was not the case, log-transformed data were used for further statistical analyses. A two-way ANOVA with tool (mouse, hand) and repetition (1–5) as independent variables was used to detect possible interactions. When no interaction effect was found, a subsequent one-way ANOVA with repeated measures was performed.

3. Results

3.1. Scores Achieved during the Herding Task

Participants reached similar scores when using their own hand or the computer mouse; a two-way ANOVA on scores from repetitions 2 to 5 showed no tool effect (F(1, 295) = 0.9, p = 0.34), no repetition effect (F(3, 295) = 1.98, p = 0.12) and no interaction effect (F(3, 295) = 0.79, p = 0.50). Repetition 1 was not included in the statistical analysis because it serves as a familiarization step to the task as explained in methods (Section 2.1).

Finding similar scores in both conditions is not trivial; it proves similar task difficulty whatever the condition (hand or mouse), as well as the absence of fatigue.

3.2. Multifractal Nonlinearity

Based on the t-statistics (t_MF) that compared original series with their 40 linearized surrogates, nonlinearity was demonstrated (p < 0.05) in 174 out of 180 series (97%) in hand conditions and in 187 out of 190 (98%) in mouse condition. Reasonably enough, multifractality evaluated by ∆H15 (Equation (6)) in our conditions reflected nonlinear rather than linear processes. The values of t_MF obtained in each repetition of the task are indicated in

Table 2. Values obtained with t_MF as a marker to distinguish nonlinear from linear processes in multifractality of time series. Here, the level of significance (p < 0.05) corresponded to t_MF > 2.02, which means that t_MF in each condition was highly significant.

Repetition	1	2	3	4	5
tMF mouse	44.2	52.8	56.1	49.2	47.4
tMF hand	16.6	16.3	21.1	25.0	31.7

.

Figure 3 illustrates the greater multifractality (larger ∆H15) observed in mouse condition when compared to hand (F(1, 369) = 50.21, p = 7 × 10⁻¹²). There was no repetition effect (F(4, 369) = 1.3, p = 0.27) and no interaction effects (F(4, 369) = 1.25, p = 0.29).

4. Discussion

The main finding of the present study was that when participants performed a computer task using their own hand or a computer mouse as a tool, the hand and the mouse displacements—formally acceleration time series—exhibited multifractal nonlinearity (Table 2). It should be stressed that nonlinearity was evidenced in more than 97% of the experimental series, exhibiting greater multifractality than their linearized surrogates. The presence of multifractal nonlinearity in mouse condition is particularly relevant because it may be interpreted as a direct evidence of tool embodiment.

The scientific understanding of tool use has challenged researchers in many different academic disciplines, such as anthropology, philosophy, psychology, neuroscience and movement science. Recent conceptions of tool embodiment as they emerge from these different disciplines have been reviewed [14,24]. This shows globally that the viewpoint of radical tool embodiment is specific in that it does not suppose any form of body representation in the cognitive user-tool system [14]. Although the brain carries information about the body’s boundaries, radical embodiment conceives porous and fuzzy boundaries, fluidly spilling over contextual constraints and supported by nonlinear body-tool interdependencies [24]. This way, the successful embodiment of a tool in a given context is a state where the mutual contingency between the body and the tool emerges from interactions unfolding across multiple time scales at once. The multifractal nonlinearity observed here during the herding task performed with a mouse perfectly matches with such a behavior and likely signs cognitive processes embedded in a unitary user-tool system. In other words, what a multifractal approach combined with the radical embodiment perspective could provide is a quantitative metric that accounts for non-conscious engagements with a tool that can be labeled as embodied.

This line of reasoning is grounded in recent theorization of multifractal dynamics in the emergence of cognitive structure [4] and the prominence of across-scale interactivity in a unitary architecture [5,19]. Both conceptions have yielded significant advances. As an example, by confronting people to a sudden shortage of sensory feedbacks, Torre et al. [3] demonstrated a correlation between multifractality in movement series and the capacity to maintain task equivalence despite sensory input deprivation [3]. The degree of multifractality of the movement series increased in correlation with the number of neural networks identified by brain functional connectivity [2]. In another study using a card sorting task, the dynamics of the hand movements show greater multifractality when the sorting rule had to be inferred from experimenter feedbacks [5,25]. By analyzing linearized surrogate, multifractal nonlinearity in original series was confirmed and led the authors to conclude that cognitive control arose from the interactions across multiple time scales at once rather than from a central executive. In the same vein, multifractal nonlinearity observed in hand dynamics supported stabilization and more accurate aiming behavior during the speed/accuracy trade-off of the Fitts task [6]. Although the above studies did not directly address the question of tool embodiment, they demonstrate how multifractal properties in movement dynamics provide reliable information on a specific cognitive architecture when tasking under various constraints. Inferring the rules during card sorting or overcoming the lack of sensory information during a sensorimotor task pushes the cognitive system to a richer interactivity reflected in a larger multifractal spectrum in emergent movement time series. This interpretation is in line with the higher ∆H15 values we obtained in mouse condition (Figure 3), while participants maintained scoring equivalence during the herding task (Section 3.1). The greater multifractality in mouse condition may arise from a larger set of interactions as hypothesized in an equivalent work realized by the group of Dotov [16]. In their study, the malfunctioning of the mouse induced a transition from ready-to-hand to unready-to-hand, a narrower multifractal spectrum which suggested that the perturbation impaired the richness of interactions which causes the tool to be experienced as disembodied. Here we used a different approach to explore the same phenomenon by comparing the naturally embodied hand with mouse use. Dotov et al. first used a monofractal based approach to study tool embodiment, then a multifractal one to confirm that the system was interaction-dominant [7,16]. Interestingly, the multifractal approach unveils a persistence in the perturbation that was blind to the monofractal one, which indicates that a finer analysis could be obtained by using multifractality. 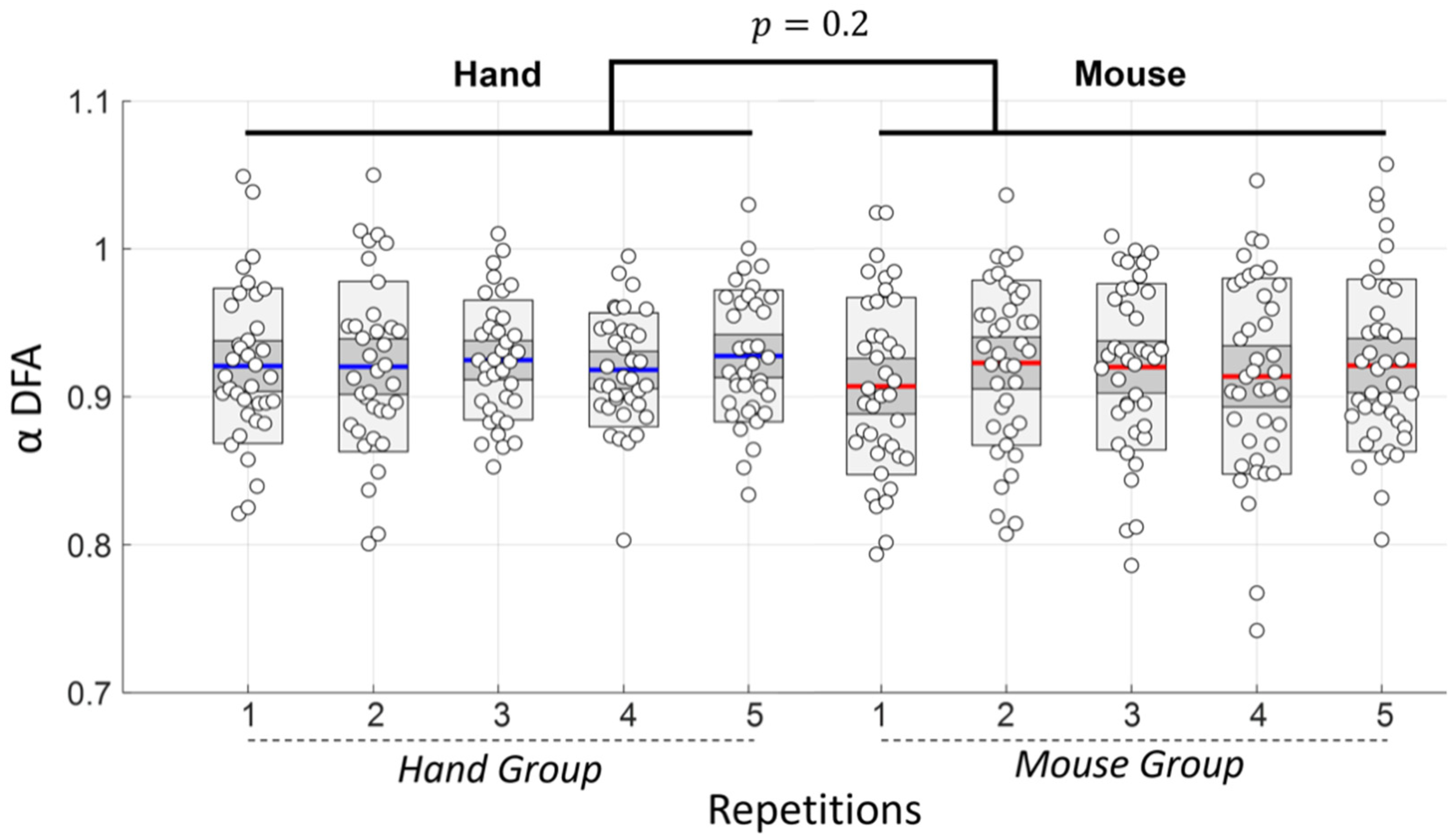In the same vein, in our conditions, we note that the use of a classical DFA (monofractal approach) did not reveal any differences between hand and mouse conditions (Figure 4). This is an interesting observation which shows that although monofractal dynamics are the same, multifractal dynamics are not.

Here, by showing greater multifractal nonlinearity we confirm that mouse use corresponds to an extended cognitive system wherein a richer network of interactions is fluidly assembled. Tool embodiment can effectively be viewed as a source of new interdependencies not present in hand condition. High values of t_MF in mouse condition (Table 2) indicated that the extended system did not depart from nonlinearity. Typically, in recent research, nonlinearity has been linked to across-scales interactivity, which strengthens the interpretation of successful embodiment of the tool. So, a large multifractal index ∆H15 and high values of t_MF in collected movement dynamics may promote multifractal nonlinearity as a reliable index for inferring successful tool embodiment. Going beyond the present experiment, it is possible that ∆H15 and t_MF may have additional virtue in providing more than an all-or-nothing proof of embodiment. They may vary depending on geometries of the interactions that give rise to individual abilities of tasking through a more or less ‘transparent’ tool use. An appreciation of the degree of embodiment would be an asset for designing tools that allow a better focus on the task, and perhaps a better performance.

In conclusion, our results provide new evidence in the field of cognitive neuroscience that tool embodiment can be achieved through a specific type of nonlinear interactivity. Multifractal nonlinearity might be relevant to grasp the essential properties that emerge from this interaction-dominant coupling. Although at this stage the relationship between multifractal metrics and tool embodiment is hardly testable other than by default reasoning, such markers may nevertheless be promising to appreciate cognitive embodiment of physical objects, and by extension virtual tools or prosthetics. In addition, indicators derived from tool displacements provide ecological way to measure tool embodiment, using, e.g., a single accelerometer. The methodology used in the present work could be applied to evaluate and design new user interfaces and new means of seamless interactions between man and machine.