Abstract
Quantization for a probability distribution refers to the idea of estimating a given probability by a discrete probability supported by a finite set. In this article, we consider a probability distribution generated by an infinite system of affine transformations on with associated probabilities such that for all and . For such a probability measure P, the optimal sets of n-means and the nth quantization error are calculated for every natural number n. It is shown that the distribution of such a probability measure is the same as that of the direct product of the Cantor distribution. In addition, it is proved that the quantization dimension exists and is finite; whereas, the -dimensional quantization coefficient does not exist, and the -dimensional lower and the upper quantization coefficients lie in the closed interval .
Keywords:
affine transformations; affine set; affine measure; optimal quantizers; quantization error MSC:
60Exx; 28A80; 94A34
1. Introduction
The quantization problem for probability measures is concerned with approximating a given measure by discrete measures of finite support in -metrics. This problem has roots in information theory and engineering technology, in particular in signal processing and pattern recognition [1,2]. For a Borel probability measure P on a quantizer is a function q mapping d-dimensional vectors in the domain into a finite set of vectors . In this case, the error where is the Euclidean norm is often referred to as the variance, cost, or distortion error for with respect to the measure P, and is denoted by . The value is called the nth quantization error for the P, and is denoted by . A set on which this infimum is attained and contains no more than n points is called an optimal set of n-means. The elements of an optimal set are called optimal quantizers. It is known that for a Borel probability measure P if its support contains infinitely many elements and is finite, then an optimal set of n-means always has exactly n-elements [3,4,5,6]. The number if exists, is called the quantization dimension of the measure P, and is denoted by ; likewise, for any , the number , if it exists, is called the s-dimensional quantization coefficient for P.
For a finite set the Voronoi region generated by denoted by is the set of all points in which are closer to than to all other elements in For a probability distribution P on the centroids of the regions are given by A Voronoi tessellation is called a centroidal Voronoi tessellation (CVT) if , i.e., if the generators are also the centroids of their own Voronoi regions. For a Borel probability measure P on , an optimal set of n-means forms a CVT; however, the converse is not true in general [7,8]. The following fact is known [6,9]:
Proposition 1.
Let α be an optimal set of n-means and . Then,
- (i)
- and ,
- (ii)
- , where X is a random variable with distribution
- (iii)
- P-almost surely the set forms a Voronoi partition of .
Let and consider the probability distribution where and for all . Because its support is the standard Cantor set generated by and , is called the Cantor distribution. S. Graf and H. Luschgy determined the optimal sets of n-means and the nth quantization errors for the Cantor distribution, for all completing its quantization program [10]. This result has been extended to the setting of a nonuniform Cantor distribution by L. Roychowdhury [11]. Analogously, the Cantor dust is generated by the contractive mappings on where , , , and . If P is a Borel probability measure on such that , then P has support the Cantor dust. For this measure, D. Çömez and M.K. Roychowdhury determined the optimal sets of n-means and the nth quantization errors [12]. Let P be a probability measure on generated by an infinite collection of similitudes where for all and P is given by . For this measure, M.K. Roychowdhury determined the optimal sets of n-means and the nth quantization errors [13], which is an infinite extension of the result of S. Graf and H. Luschgy in [10]. The quantization dimension for probability distributions generated by an infinite collection of similitudes was determined by E. Mihailescu and M.K. Roychowdhury in [14], which is an infinite extension of the result of S. Graf and H. Luschgy in [15]. In this article, we study extension of the result of D. Çömez and M.K. Roychowdhury in [12] to the setting of countably infinite affine maps on , which will also complete the program initiated in [14].
Let be a collection of countably infinite affine transformations on , where , where Clearly, these affine transformations are all contractive but are not similarity mappings. Associate the mappings with the probabilities such that for all , where . Then, there exists a unique Borel probability measure P on ([16,17,18], etc.) such that
The support of such a probability measure lies in the unit square We call such a measure an affine measure on or more specifically, an infinitely generated affine measure on . This article deals with the quantization of this measure P. The arrangement of the paper is as follows: in Section 2, we discuss the basic definitions and lemmas about the optimal sets of n-means and the nth quantization errors. The arguments in this section point out that determining optimal sets of n-means and the nth quantization errors for all and for arbitrary require very intricate and complicated analysis; hence, for clarity purposes, in the remaining sections the focus will be on the case Section 3 is devoted to determining the optimal sets of n-means for and . In Section 4, we first define a mapping F which enables us to convert the infinitely generated affine measure P to a finitely generated product measure , each is the Cantor distribution. Having this connection between P and together with the optimal sets of n-means for in Section 5 we will utilize the dynamics of the affine maps to obtain the main results of the paper: closed formulas to determine the optimal sets of n-means and the corresponding quantization errors for all . For clarity of the exposition, we also provide some examples and figures to illustrate the constructions. Lastly, having closed form for the quantization errors for each we prove the existence of the quantization dimension and show that the -dimensional quantization coefficient for P does not exist (but are finite) and the -dimensional lower and the upper quantization coefficients lie in the closed interval .
The results and the arguments in this article are not straightforward generalizations of those in [13]; in particular, this is the case for optimal sets. By the nature of the affine transformations considered in this paper, the optimal sets of order are the same as the cross product of optimal sets of order k obtained in [13]; however, the same cannot be said for other Clearly, for n a prime number, optimal sets of n-means cannot be obtained this way. Furthermore, as will be seen from the main theorem, even for optimal sets of n-means are not the same as the cross product of optimal sets of k- and l-means in [13]. For example, optimal sets of 2- and 3-means in [13] are and (or respectively; hence, the cross product of these sets produce some of the optimal sets of 6-means. On the other hand, one of the optimal sets of 6-means is , which cannot be obtained as the cross product of optimal sets of 2- and 3-means in [13].
2. Preliminaries
Let P be the affine measure on generated by the affine maps defined above. Consider the alphabet . By a "string" or a "word" over , it is meant a finite sequence of symbols from the alphabet, , where k is called the length of the word . A word of length zero is called the "empty word", and is denoted by ∅. By we denote the set of all words over the alphabet of some finite length including the empty word ∅. By , we denote the length of a word . For any two words and in , by we mean the word obtained from the concatenation of and . For and we define . Note that is the empty word if the length of is one. Analogously, by we denote the set of all words over the alphabet , and for any , , etc. are defined similarly. Let , , be such that , then and will denote the “coordinate words"; i.e., and . Thus, and . These lead us to define the following notations: For , by it is meant the set of all words obtained by concatenating the word with the word for , i.e.,
Similarly, and represent the sets
respectively. Analogously, for any , by it is meant the set , and represents the set . Thus, if , then we write and ; if , then we write and ; and if , then we write and . For , let us write
In particular, the identity mapping on and . Then, the probability measure P supports the closure of the limit set , where . The limit set is called the affine set or infinitely generated affine set. For and , the rectangles , into which is split up at the th level are called the children or the basic rectangles of (see Figure 1). For , we write
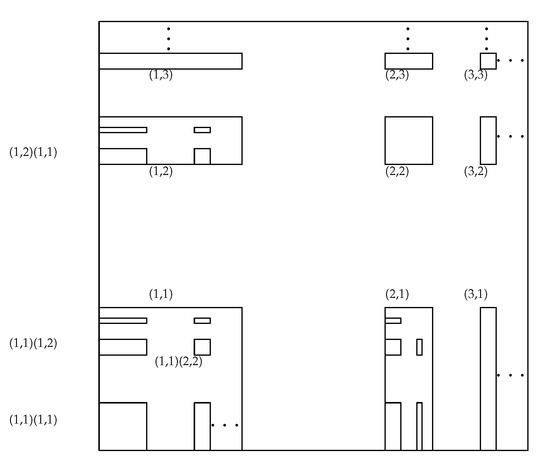
Figure 1.
Basic rectangles of the infinite affine transformations.
Notice that for any , ; and similarly,
Because , then, by induction, for any . Hence, we have the following statement:
Lemma 1.
Let be Borel measurable and . Then,
Let and be the horizontal and vertical components of the transformations Then, for all we have and hence, and are similarity mappings on with similarity ratios and respectively. Similarly, for , , let and represent the horizontal and vertical components of the transformation on . Then, and are similarity mappings on with similarity ratios and respectively, such that and . Thus, it follows that
Moreover, we have . Let be a bivariate random variable with distribution P. Let be the marginal distributions of P, i.e., for all , and for all , where are projections given by and for all . Here is the Borel -algebra on . Then, has distribution and has distribution . Let and denote respectively the inverse images of the horizontal and vertical components of the transformations for all . Then, the following lemma is known [16,17,18]:
Lemma 2.
Let and be the marginal distributions of the probability measure P. Then,
Remark 1.
Since and are similarity mappings, from Lemma 2, one can see that both the marginal distributions and are self-similar measures on generated by an infinite collection of similarities associated with the probability vector .
Lemma 3.
Let and denote the expectation and the variance of the random variable X. Then,
Proof.
By Lemma 2, , where is a unique Borel probability measure on such that
Hence, , and by ([11], Lemma 2.2), and which implies that □
Remark 2.
By using the standard rule of probability, for any , we have , which yields that the optimal set of one-mean consists of the expected value and the corresponding quantization error is the variance V of the random variable X.
Lemma 4.
Let . Then,
and
Proof.
First prove . Because and
Notice that
Because
and similarly
Hence, we have that
where and Therefore,
Proofs of (ii) and (iii) are similar. □
Note 1.
For words in , by we denote the conditional expectation of the random variable X giveni.e.,
Then, for ,
Thus, by Lemma 4, if , then , , , and . In addition,
Moreover, for , , it is easy to see that
where for . The expressions (2) and (4) are useful to obtain the optimal sets and the corresponding quantization errors with respect to the probability distribution P.
For the rest of the article is assumed, which is the most important case due to its intimate connection with the standard Cantor system.
3. Optimal Sets of n-Means for n = 2, 3
In the this section, we determine the optimal sets of two- and three-means, and their quantization errors.
Lemma 5.
Let P be the affine measure on and let . Then,
Proof.
Let us first prove . By Lemma 4, we have
Note that and
. Moreover, we have
Now break the above expression by using the square formula and note the fact that
Thus, it follows that
Therefore, (5) implies that
Other equalities of the statement are proved similarly. □
Lemma 6.
Let P be the affine measure on , and let be a set of two points lying on the line for which the distortion error is smallest. Then, , , and the distortion error is
Proof.
Let . Because the points for which the distortion error is smallest are the centroids of their own Voronoi regions, by the properties of centroids, we have
which implies , i.e, . Thus, the boundary of the Voronoi regions is the line . Now, using the definition of conditional expectation,
which implies yielding . Similarly, . Then, the distortion error is
This completes the proof the lemma. □
The following lemma provides us information on where to look for points of an optimal set of two-means.
Lemma 7.
Let P be the affine measure on . The points in an optimal set of two-means can not lie on an oblique line of the affine set.
Proof.
In the affine set, among all the oblique lines that pass through the point , the line has the maximum symmetry, i.e., with respect to the line the affine set is geometrically symmetrical. Also, observe that, if two basic rectangles of similar geometrical shape lie in the opposite sides of the line , and are equidistant from the line , then they have the same probability (see Figure 1); hence, they are symmetrical with respect to the probability distribution P. Due to this, among all the pairs of two points which have the boundaries of the Voronoi regions oblique lines passing through the point , the two points which have the boundary of the Voronoi regions the line will give the smallest distortion error. Again, we know the two points which give the smallest distortion error are the centroids of their own Voronoi regions. Let and be the centroids of the left half and the right half of the affine set with respect to the line respectively. Then, from the definition of conditional expectation, we have
and
Let . Then, due to symmetry,
Write
Because A is a proper subset of , we have Now using (4), and then upon simplification, it follows that
which is larger than the distortion error obtained in Lemma 6. Hence, the points in an optimal set of two-means can not lie on a oblique line of the affine set. Thus, the assertion of the lemma follows. □
Proposition 2.
Let P be the affine measure on . Then, the sets and form two different optimal sets of two-means with quantization error
Proof.
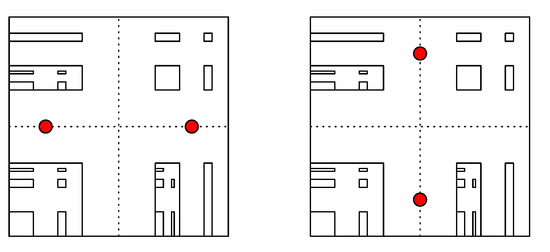
By Lemma 7, it is known that the points in an optimal set of two-means cannot lie on an oblique line of the affine set. Thus, by Lemma 6, we see that forms an optimal set of two-means with quantization error . Due to symmetry, forms another optimal set of two-means (see Figure 2); thus, the assertion follows. □

Figure 2.
Optimal sets of two-means.
Proposition 3.
Let P be the affine measure on . Then, the set forms an optimal set of three-means with quantization error .
Proof.
Let us first consider a three-point set given by . Then, by using Lemma 5 and Equation (4), we have
Because is the quantization error for an optimal set of three-means, we have . Let be an optimal set of three-means. Because the optimal points are the centroids of their own Voronoi regions, we have . Let , , , and . Note that the centroids of , , and with respect to the probability distribution P are respectively , , and . Suppose that does not contain any point from . Then, we can assume that all the points of are on the line , i.e., with . If quantization error can be strictly reduced by moving the point to . So, we can assume that . Similarly, we can show that . Now, if , then . Moreover, for any , we have and so by (4) and Lemma 5, we obtain
which is a contradiction, and so must be true. If , similarly we can show that a contradiction arises. So, . Next, suppose that . Then, we have which implies , for otherwise quantization error can be strictly reduced by moving to , contradicting the fact that is an optimal set. Then, and So, for any , . If and then
which is a contradiction. Similarly, if we assume , a contradiction will arise. Therefore, all the points in can not lie on the line . Let and lie on the line , and is above or below the horizontal line . If is above the horizontal line, then the quantization error can be strictly reduced by moving to and to contradicting the fact that is an optimal set. Similarly, if is below the horizontal line, a contradiction will arise. All these contradictions arise due to our assumption that does not contain any point from . Hence, contains at least one point from . In order to complete the proof of the Proposition, first we will prove the following claim:
Claim 1.
.
For the sake of contradiction, assume that . Then, without any loss of generality we assume that and for . Due to symmetry of the affine set with respect to the diagonal , we can assume that lies on the diagonal ; and are equidistant from the diagonal and are in opposite sides of the diagonal . Now, consider the following cases:
Case 1. Assume that both and are below the diagonal , but not in . Let be above the diagonal and be below the diagonal . In that case, the quantization error can be strictly reduced by moving to and to which contradicts the optimality of .
Case 2. Assume that both and are above the diagonal . Let lie above the diagonal and lie below the diagonal . Then, due to symmetry we can assume that which is the centroid of , which is the midpoint of the line segment joining the centroids of and , which is the midpoint of the line segment joining the centroids of and . Then,
which is a contradiction. Thus, cannot hold.
Next, for the sake of contradiction, assume that . Then, without any loss of generality we assume that , and . Let and be the regions of which are respectively above and below the diagonal of passing through . Due to symmetry, we must have and . Notice that implies
and by using (1), we have
which shows that the point falls below the line , which is a contradiction, as we assumed that . This contradiction arises due to our assumption that . Hence, we conclude that , which proves the claim.
By the claim, we assume that and . Notice that are geometrically symmetric as well as their corresponding centroids are symmetrically distributed over the square . Without any loss of generality, we can assume that the optimal point is the centroid of , i.e., . Then, due to symmetry with respect to the line , it follows that , and lies on but above the line . Now, notice that
which occurs when . Moreover, the three points , and are the centroids of their own Voronoi regions. Thus, forms an optimal set of three-means with quantization error Hence, the proposition follows. □
Remark 3.
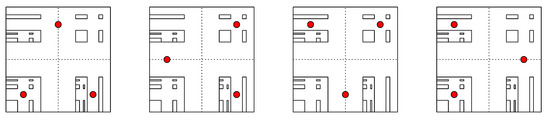
Due to symmetry, in addition to the optimal set given in Proposition 3, there are three more optimal sets of three-means with quantization error (see Figure 3).

Figure 3.
Optimal sets of three-means.
4. Affine Measures
In this section, we show that the affine measure P under consideration is the direct product of the Cantor distribution .
For the rest of the article, by a word of length k over the alphabet , it is meant , . By a word of length zero it is meant the empty word ∅. represents the set of all words over the alphabet including the empty word ∅. Length of a word is denoted by . If , we write . represents the identity mapping on . By we represent the similarity ratio of . If is the random variable with distribution , then and [10]. For , write . Notice that for , we have , , the contractive factor of and for the empty word ∅, . For define . For any positive integer n, by it is meant the concatenation of the symbol 2 with itself n-times successively, i.e., , with the convention that is the empty word. For any positive integer k, by it is meant the direct product of the set with itself. By it is meant the set . Also, recall the notations defined in Section 2. Let us now introduce the map such that
where is such that
The function f is one-to-one and onto, and consequently, F is also one-to-one and onto. For any , write and .
The map F is instrumental in converting the infinitely generated affine measure P to a finitely generated affine measure . Furthermore, to improve the clarity of the arguments, we will write for , and for , where for all form an infinite collection of similarity mappings on such that for all . Thus, if , then and for all . Again, is the identity mapping on .
Lemma 8.
Let for be the infinite collection of similitudes defined above, and and be the similitudes generating the Cantor set. Then, for any and , we have
Proof.
If , then for any Assume that the lemma is true if for some positive integer k, i.e., . Then,
Thus, by the Principle of Mathematical Induction, for all . Again, for any , by (6), it follows that . Hence, for any , , we have
which completes the proof. □
Lemma 9.
Let , and F be the function as defined in (6). Then for , we have , and .
Proof.
By Lemma 8, we have
Without any loss of generality, we can assume for . Then,
Because, we have
Similarly, . □
Remark 4.
By Lemmas 4 and 9, for any , we have
The following example illustrates the outcome of the lemma above.
Example 1.
,
,
,
,
,
,
, and
, etc.
Lemma 10.
Let . Then, for any , we have , where .
Proof.
Without any loss of generality, let for any . See that , and thus Consequently,
which proves the lemma. □
Proposition 4.
Let P be the affine measure. Then, , where is the Cantor distribution.
Proof.
Borel -algebra on the affine set is generated by all sets of the form for , where . Notice that
Again, the sets of the form , where , generate the Borel -algebra on the Cantor set C. Thus, we see that the Borel -algebra of the affine set is the same as the product of the Borel -algebras on the Cantor set. Moreover, for any , by Remark 1 and Lemma 10, we have
Hence, the proposition follows. □
Remark 5.
By Proposition 4, it follows that the optimal sets of n-means for P are the same as the optimal sets n-means for the product measure on the affine set. Moreover, for we can write
where for , .
5. Optimal Sets of n-Means for all
In this section, we will derive closed formulas to determine the optimal sets of n-means and the nth quantization error for all . For , write and .
Lemma 11.
Let α be an optimal set of n-means with . Then, for all .
Proof.
Let be an optimal set of n-means for . As the optimal points are the centroids of their own Voronoi regions we have .
Consider the four-point set given by . Then,
Because is the quantization error of four-means, we have .
Assume that does not contain any point from . We know that
If all the points of are below the line , i.e., if then by (7), we see that , which is a contradiction. Similarly, it follows that if all the points of are above the line , or left of the line , or right of the line , a contradiction will arise.
Next, suppose that all the points of are on the line . We will consider two cases: and When let with for . Due to symmetry, we can assume that the boundary of the Voronoi regions of the points , , , and are respectively , , and yielding , and then writing , by symmetry we have
which is a contradiction. We consider the case . Because for any , , we have
which implies , a contradiction. Thus, we see that all the points of can not lie on . Similarly, all the points of can not lie on .
Notice that the lines and partition the square into four quadrants with center . If for some positive integer k, due to symmetry, we can assume that each quadrant contains k-points from the set . But then, any of the k points in the quadrant containing a basic rectangle can be moved to which strictly reduce the quantization error, and it gives a contradiction as we assumed that the set is an optimal set of n-means and does not contain any point from for .
If , or , then, again due to symmetry, each quadrant gets at least k points. Then, as in the case here also, one can strictly reduce the quantization error by moving a point in the quadrant containing a basic rectangle to for , which is a contradiction.
Thus, we have proved that for all . □
Lemma 12.
Let α be an optimal set of n-means with . Then, .
Proof.
By Lemma 11, we know that for all . Now, we will prove the statement by considering four distinct cases:
Case 1: for some integer .
In this case, due to symmetry, we can assume that contains k points from each of , otherwise, quantization error can be reduced by redistributing the points of equally among for , and so .
Case 2: for some integer .
In this case, again due to symmetry, we can assume that contains k points from each of and if possible, one point, say , from . By symmetry, one can assume that is the midpoint of the line segment joining any two centroids of the basic rectangles for . Let us first take which is the center of the affine set. For simplicity, we first assume , i.e., . Then, contains only one point from each of . Let be the point that takes from . As lies on the diagonal , due to symmetry we can also assume that lies on the diagonal . By Proposition 1, we have . This yields that which implies and . Then, we see that
where , which is a contradiction. Similarly, if we take as the midpoint of a line segments joining the centroids of any two adjacent basic rectangles for , contradiction arises. Proceeding in the similar way, by taking , we see that contradiction arises at each value k takes. Therefore, .
Case 3: for some integer .
In this case, due to symmetry, we can assume that contains k points from each of , and if possible, two points, say and , from . Then, by symmetry, we can assume that lies on the midpoint of the line segment joining the centroids of , ; and lies on the midpoint of the line segment joining the centroids of and . As in Case 2, this leads to a contradiction. Thus, .
Case 4: for some integer . Due to symmetry, in this case, we can assume that each of and gets points; each of and gets k points. The remaining one point lies on the midpoint of the line segment joining the centroids of and . But, in that case, proceeding as in Case 2, we can show that a contradiction arises. Thus, .
We have shown that in all possible cases ; hence, the lemma follows. □
Corollary 1.
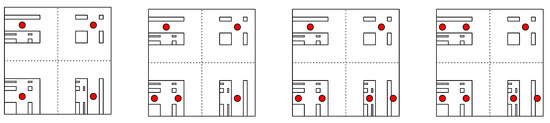
The set is a unique optimal set of four-means of the affine measure P with quantization error (see Figure 4).

Figure 4.
Optimal sets of n-means for . Optimal set of 4-means is unique; on the other hand, optimal sets of n-means for are not unique.
Remark 6.
Let α be an optimal set of n-means, and where for . Then, for .
Lemma 13.
Let and α be an optimal set of n-means for the product measure . For , set , and let . Then, is an optimal set of -means, and .
Proof.
For , by Lemma 11, we have , , and so
If is not an optimal set of -means for , then there exists a set with such that . But then, is a set of cardinality n and it satisfies contradicting the fact that is an optimal set of n-means for . Similarly, it can be proved that , , and are optimal sets of -, -, and -means respectively. Thus,
which gives the lemma. □
Proposition 5.
Let be such that for some positive integer . Then, the set
forms a unique optimal set of n-means for the affine measure P with quantization error
Proof.
We will prove the statement by induction. By Corollary 1, it is true if . Let us assume that it is true for for some positive integer k. We now show that it is also true if . Let be an optimal set of -means. Set for . Then, by Lemmas 11 and 13, is an optimal set of -means, and so which implies . Thus, is an optimal set of -means. Because is the centroid of for each , the set is unique. Now, by Lemma 13, we have the quantization error as
Thus, by induction, the proof of the proposition is complete. □
Definition 1.
For with let be the unique natural number with . For with card let be the set defined as follows:
Remark 7.
In Definition 1, instead of choosing the set , one can choose , i.e., the set associated with each can be chosen in two different ways. Moreover, the subset I can be chosen from in ways. Hence, the number of the sets is .
The following example illustrates Definition 1.
Example 2.
Let . Then, , with , and so
or,
Similarly, one can get six more sets by taking , , or , i.e., the number of the sets in this case is .
Proposition 6.
Let and be the set as defined in Definition 1. Then, forms an optimal set of n-means with quantization error
Proof.
We have where . Set with for . Let us prove it by induction. We first assume . By Lemmas 11 and 13, we can assume that each of for and , are optimal sets of -means and is an optimal set of -means. Thus, for and , we can write
for some , where is an optimal set of two-means. Thus,
for some , where is an optimal set of two-means. Notice that instead of choosing as an optimal set of -means, one can choose any one from for , , as an optimal set of -means. Hence, for , one can write
where for some as an optimal set of n-means. Thus, we see that the proposition is true if . Similarly, one can prove that the proposition is true for any . Then, the quantization error is
Because , , , upon simplification, we have . Thus, the proof of the proposition is complete. □
Definition 2.
For with let be the unique natural number with . For with card let be the set defined as follows:
Remark 8.
In Definition 2, instead of choosing the set , one can choose . Instead of choosing the set
, one can choose either the set
, or
, or
, i.e., the set corresponding to each can be chosen in two different ways, and the set corresponding to each can be chosen in four different ways. Because and the subset I can be chosen from in ways, the number of the sets is .
We now give an example illustrating Definition 2.
Example 3.
Let . Then, , with . Take . Then,
Note that each of , , , can be chosen in 32 ways, i.e., the numbers of the sets in this case is . Moreover, by using the formula in Remark 8, we have
Proposition 7.
Let and be the set as defined in Definition 2. Then, forms an optimal set of n-means with quantization error
Proof.
We have where . Set with for . Let us prove it by induction. We first assume . By Lemmas 11 and 13, we can assume that each of for and , are optimal sets of -means and is an optimal set of -means. Thus, for and , we can write
for some , where is an optimal set of three-means. Thus
for some , where is an optimal set of three-means. Notice that instead of choosing as an optimal set of -means, one can choose any one from for , , as an optimal set of -means. Hence, for , one can write
where for some as an optimal set of n-means. Thus, we see that the proposition is true if . Similarly, one can prove that the proposition is true for any . Thus, writing , and , we have, in general,
where with for some . Then, we obtain the quantization error as
Because , , , upon simplification, we have . Thus, the proof of the proposition is complete. □
6. Quantization Dimension and Quantization Coefficient for P
The techniques employed in the previous sections also provide closed formulas for the quantization errors involved at each step. Such closed formulas are amenable for direct calculation of the quantization dimension and the quantization coefficient for the probability distribution involved. Hence, in this section we will calculate the quantization dimension of the probability distribution P, and the accumulation points for the -dimensional quantization coefficients. By Propositions 5–7, the nth quantization error is given by
Proposition 8.
The quantization dimension of the probability distribution P exists and equals
Proof.
By (8), for it follows that , i.e.,
and so
Thus, we deduce that
Similarly, for , we also obtain the same limit. Hence,
Thus, the proof of the proposition is complete. □
Proposition 9.
Let be the quantization dimension of P. Then, the β-dimensional quantization coefficient forP does not exist, and the accumulation points of lie in the closed interval .
Proof.
Recall the sequence of quantization errors given by (8). Again, notice that . Along the sequence , we have Similarly, along the sequence we have Consequently, does not exist. Now, we calculate the range for the accumulation points of . The following two cases can arise:
Case 1. .
In this case, we have implying Because
it follows that along such subsequences, we have
Case 2. .
In this case, we have , implying
Because
it follows that
By Case 1 and Case 2, for , we see that
which yields the fact that the accumulation points of lie in the closed interval . Thus, the proof of the proposition is complete. □
7. Discussion and Concluding Remarks
Motivation. As it has been mentioned in Introduction, the main motivation for this article is completion of the programme initiated in [14]. In the meantime, we extend the results in [12] to the setting of infinite affine transformations. Analogously to [10], this completes the programme of providing complete quantization for affine measures on
Observations and Remarks. Quantization of continuous random signals (or random variables and processes) is an important part of digital representation of analog signals for various coding techniques (e.g., source coding, data compression, archiving, restoration). The oldest example of quantization in statistics is rounding off. Sheppard (see [19]) was the first who analyzed rounding off for estimating densities by histograms. Any real number x can be rounded off (or quantized) to the nearest integer, say , with a resulting quantization error Hence, the restored signal may differ from the original one and some information can be lost. Thus, in quantization of a continuous set of values there is always a distortion (also known as noise or error) between the original set of values and the quantized set of values. The main goal in quantization theory is finding a set of quantizers with minimum distortion, which has been extensively investigated by numerous authors [2,20,21,22,23,24]. A different approach for uniform scalar quantization is developed in [25], where the correlation properties of a Gaussian process are exploited to evaluate the asymptotic behavior of the random quantization rate for uniform quantizers. General quantization problems for Gaussian processes in infinite-dimensional functional spaces are considered in [26]. In estimating weighted integrals of time series with no quadratic mean derivatives, by means of samples at discrete times, it is known that the rate of convergence of mean-square error is reduced from to when the samples are quantized (see [27]). For smoother time series, with quadratic mean derivatives, the rate of convergence is reduced from to when the samples are quantized, which is a very significant reduction (see [28]). The interplay between sampling and quantization is also studied in [28], which asymptotically leads to optimal allocation between the number of samples and the number of levels of quantization. Quantization also seems to be a promising tool in recent development in numerical probability (see, e.g., [29]).
By Proposition 1 the points in an optimal set are the centroids of their own Voronoi regions. Consequently, the points in an optimal set are an evenly spaced distribution of sites in the domain with minimum distortion error with respect to a given probability measure and is therefore very useful in many fields, such as clustering, data compression, optimal mesh generation, cellular biology, optimal quadrature, coverage control and geographical optimization; for more details one can see [7,30]. In addition, it has applications in energy-efficient distribution of base stations in a cellular network [31,32,33]. In both geographical and cellular applications the distribution of users is highly complex and often modeled by a fractal [34,35].
Future Directions.k-means clustering is a method of vector quantization, originally from signal processing, that aims to partition n observations, or the underlying data set into k clusters in which each observation belongs to the cluster with the nearest mean, also known as cluster center or cluster centroid. For a given k and a given probability distribution in a dataset there can be two or more different sets of k-means clusters: for example, with respect to a uniform distribution the unit square has four different sets of two-means clusters with cluster centers , , , and . Among these only , and form two different optimal sets of two-means. In other words, we can say that for a given k, among the multiple sets of k-means clusters, the centers of a set with the smallest distortion error form an optimal set of k-means. Thus, it is much more difficult to calculate an optimal set of k-means than to calculate a set of k-means clusters. There are several work done in the direction of k-means clustering. On the other hand, there is not much work in the direction of finding optimal sets of k-means clusters, and the work in this paper is an addition in this direction.
The probability measure P considered in this study has identical marginal distributions, which is instrumental in determining optimal sets of 2-, 3-, and 4-means accurately. Besides, it enables us to bridge infinitely generated affine measures with finitely generated ones, and consequently, connect optimal sets of n-means for P and It would be interesting to investigate if similar results can be achieved when P is induced by different infinite probability vectors than considered in this article.
Author Contributions
The work in this paper is completely new. Both the authors equally contributed in writing the draft of this work. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
Not applicable.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Bucklew, J.A.; Wise, G.L. Multidimensional asymptotic quantization with rth power distortion measures. IEEE Trans. Inf. Theory 1982, 28, 239–247. [Google Scholar] [CrossRef]
- Gray, R.; Neuhoff, D. Quantization. IEEE Trans. Inform. Theory 1998, 44, 2325–2383. [Google Scholar] [CrossRef]
- Abaya, E.F.; Wise, G.L. Some remarks on the existence of optimal quantizers. Stat. Probab. Lett. 1984, 2, 349–351. [Google Scholar] [CrossRef]
- Gray, R.M.; Kieffer, J.C.; Linde, Y. Locally optimal block quantizer design. Inf. Control. 1980, 45, 178–198. [Google Scholar] [CrossRef]
- György, A.; Linder, T. On the structure of optimal entropy-constrained scalar quantizers. IEEE Trans. Inf. Theory 2002, 48, 416–427. [Google Scholar] [CrossRef]
- Graf, S.; Luschgy, H. Foundations of Quantization for Probability Distributions; Lecture Notes in Mathematics; Springer: Berlin/Heidelberg, Germany, 2000; Volume 1730. [Google Scholar]
- Du, Q.; Faber, V.; Gunzburger, M. Centroidal Voronoi Tessellations: Applications and Algorithms. Siam Rev. 1999, 41, 637–676. [Google Scholar] [CrossRef]
- Roychowdhury, M.K. Quantization and centroidal Voronoi tessellations for probability measures on dyadic Cantor sets. J. Fractal Geom. 2017, 4, 127–146. [Google Scholar] [CrossRef]
- Gersho, A.; Gray, R.M. Vector Quantization and Signal Compression; Kluwer Academy Publishers: Boston, MA, USA, 1992. [Google Scholar]
- Graf, S.; Luschgy, H. The Quantization of the Cantor Distribution. Math. Nachr. 1997, 183, 113–133. [Google Scholar] [CrossRef]
- Roychowdhury, L. Optimal quantization for nonuniform Cantor distributions. J. Interdiscip. Math. 2019, 22, 1325–1348. [Google Scholar] [CrossRef]
- Çömez, D.; Roychowdhury, M.K. Quantization for uniform distributions of Cantor dusts on R2. Topol. Proc. 2020, 56, 195–218. [Google Scholar]
- Roychowdhury, M.K. Optimal quantization for the Cantor distribution generated by infinite similitudes. Isr. J. Math. 2019, 231, 437–466. [Google Scholar] [CrossRef]
- Mihailescu, E.; Roychowdhury, M.K. Quantization coefficients in infinite systems. Kyoto J. Math. 2015, 55, 857–873. [Google Scholar] [CrossRef][Green Version]
- Graf, S.; Luschgy, H. The quantization dimension of self-similar probabilities. Math. Nachr. 2002, 241, 103–109. [Google Scholar] [CrossRef]
- Hutchinson, J. Fractals and self-similarity. Indiana Univ. J. 1981, 30, 713–747. [Google Scholar] [CrossRef]
- Moran, M. Hausdorff measure of infinitely generated self-similar sets. Monatsh. Math. 1996, 122, 387–399. [Google Scholar] [CrossRef]
- Mauldin, D.; Urbański, M. Dimensions and measures in infinite iterated function systems. Proc. Lond. Math. Soc. 1996, 73, 105–154. [Google Scholar] [CrossRef]
- Sheppard, W.F. On the calculation of the most probable values of frequency constants for data arranged according to equidistant divisions of a scale. Proc. Lond. Math. Soc. 1897, 1, 353–380. [Google Scholar] [CrossRef]
- Cambanis, S.; Gerr, N. A simple class of asymptotically optimal quantizers. IEEE Trans. Inform. Theory 1983, 29, 664–676. [Google Scholar] [CrossRef]
- Gray, R.M.; Linder, T. Mismatch in high rate entropy constrained vector quantization. IEEE Trans. Inform. Theory 2003, 49, 1204–1217. [Google Scholar] [CrossRef]
- Li, J.; Chaddha, N.; Gray, R.M. Asymptotic performance of vector quantizers with a perceptual distortion measure. IEEE Trans. Inform. Theory 1999, 45, 1082–1091. [Google Scholar]
- Shykula, M.; Seleznjev, O. Stochastic structure of asymptotic quantization errors. Stat. Prob. Lett. 2006, 76, 453–464. [Google Scholar] [CrossRef]
- Zador, P.L. Asymptotic quantization error of continuous signals and the quantization dimensions. IEEE Trans. Inform. Theory 1982, 28, 139–148. [Google Scholar] [CrossRef]
- Shykula, M.; Seleznjev, O. Uniform Quantization of Random Processes; Univ. Umeȧ Research Report; Umeå University: Umeå, Sweden, 2004; pp. 1–16. [Google Scholar]
- Luschgy, H.; Pagès, G. Functional quantization of Gaussian processes. J. Funct. Anal. 2002, 196, 486–531. [Google Scholar] [CrossRef]
- Bucklew, J.A.; Cambanis, S. Estimating random integrals from noisy observations: Sampling designs and their performance. IEEE Trans. Inform. Theory 1988, 34, 111–127. [Google Scholar] [CrossRef]
- Benhenni, K.; Cambanis, S. The effect of quantization on the performance of sampling designs. IEEE Trans. Inform. Theory 1998, 44, 1981–1992. [Google Scholar] [CrossRef]
- Pagès, G.; Pham, H.; Printemps, J. Optimal quantization methods and applications to numerical problems in finance. In Handbook of Computational and Numerical Methods in Finance; Rachev, S., Ed.; Birkhäuser Boston: Boston, MA, USA, 2004; pp. 253–297. [Google Scholar]
- Okabe, A.; Boots, B.; Sugihara, K.; Chiu, S.N. Spatial Tessellations: Concepts and Applications of Voronoi Diagrams, 2nd ed.; Wiley: Hoboken, NJ, USA, 2000. [Google Scholar]
- Hao, Y.; Chen, M.; Hu, L.; Song, J.; Volk, M.; Humar, I. Wireless Fractal Ultra-Dense Cellular Networks. Sensors 2017, 17, 841. [Google Scholar] [CrossRef]
- Kaza, K.R.; Kshirsagar, K.; Rajan, K.S. A bi-objective algorithm for dynamic reconfiguration of mobile networks. In Proceedings of the IEEE International Conference on Communications (ICC), Ottawa, ON, Canada, 10–15 June 2012; pp. 5741–5745. [Google Scholar]
- Song, Y. Cost-Effective Algorithms for Deployment and Sensing in Mobile Sensor Networks. Ph.D. Thesis, University of Conneticut, Storrs, CT, USA, 2014. [Google Scholar]
- Abundo, C.; Bodnar, T.; Driscoll, J.; Hatton, I.; Wright, J. City population dynamics and fractal transport networks. In Proceedings of the Santa Fe Institute’s CSSS2013; Santa Fe Institute: Santa Fe, NM, USA, 2013. [Google Scholar]
- Lu, Z.; Zhang, H.; Southworth, F.; Crittenden, J. Fractal dimensions of metropolitan area road networks and the impacts on the urban built environment. Ecol. Indic. 2016, 70, 285–296. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).