Mitochondrial DNA Profiling by Fractal Lacunarity to Characterize the Senescent Phenotype as Normal Aging or Pathological Aging
Abstract
1. Introduction
2. Materials and Methods
2.1. Subjects and mtDNA Resequencing
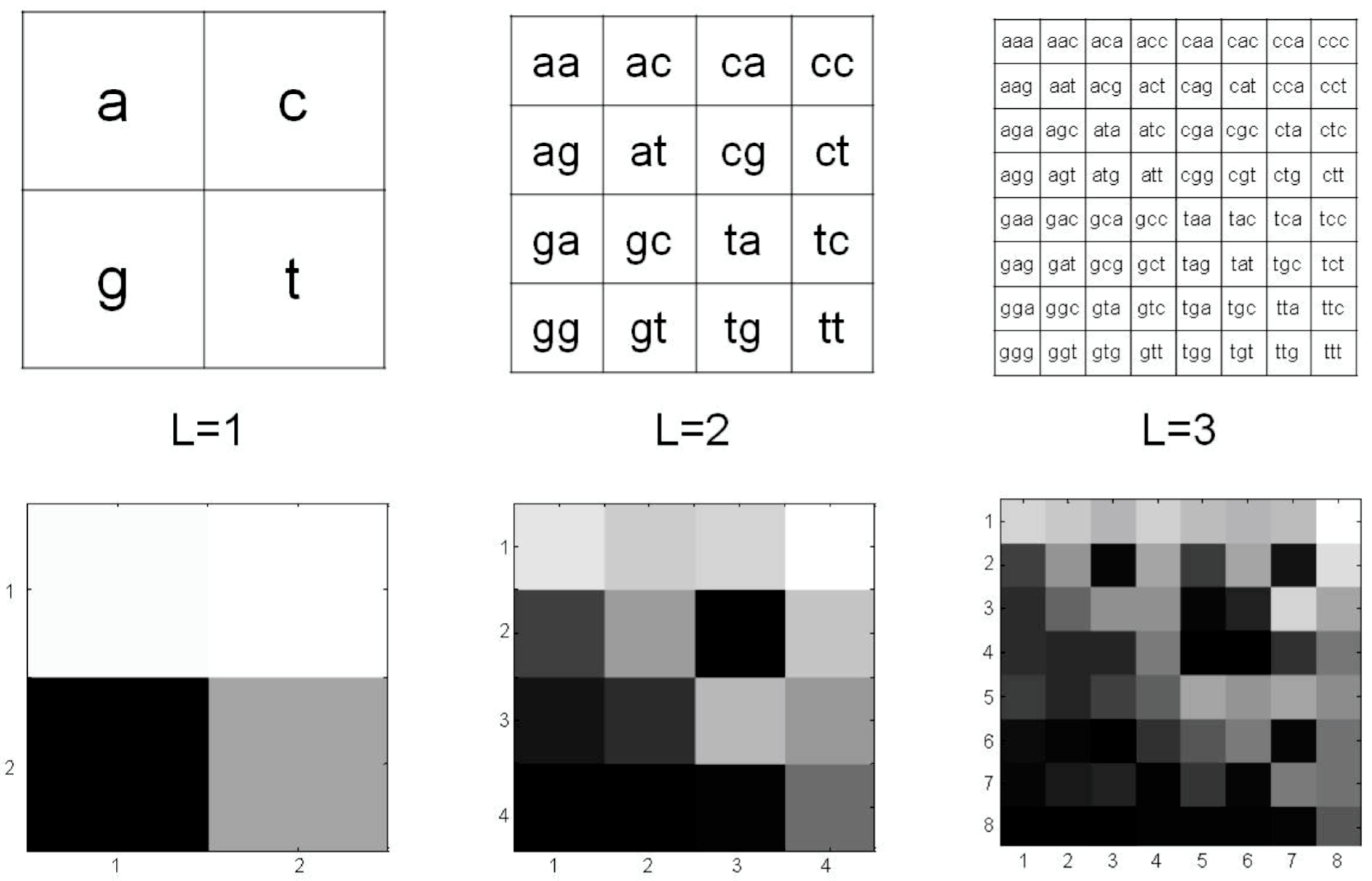
2.2. The Modified Chaos Game Representation of mtDNA
- (a)
- L = 5, s = ‘tacgm’, where ‘m’ means ‘a’ or ‘c’. This string is substituted by s1 = ‘tacga’, s2 = ‘tacgc’; the weight is w = 1/2.
- (b)
- L = 6, s = ‘vtacgm’, where ‘v’ means ‘a’, ‘c’, or ‘g’, and ‘m’ means ‘a’ or ‘c’. This string is substituted by s1 = ‘atacga’, s2 = ‘ctacga’, s3 = ‘gtacga’, s4 = ‘atacgc’, s5 = ‘ctacgc’, s6 = ‘gtacgc’; the weight is w = 1/6.
2.3. Estimate of Lacunarity
3. Results
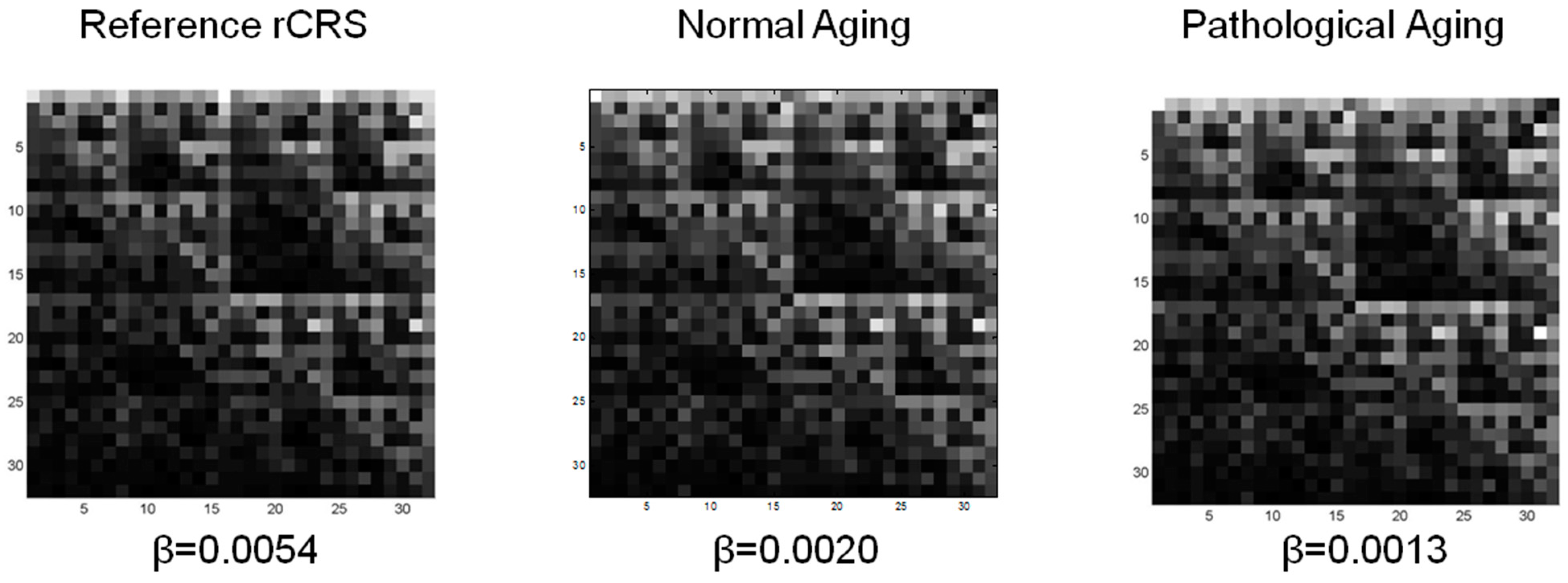
3.1. CGR of Human mtDNA
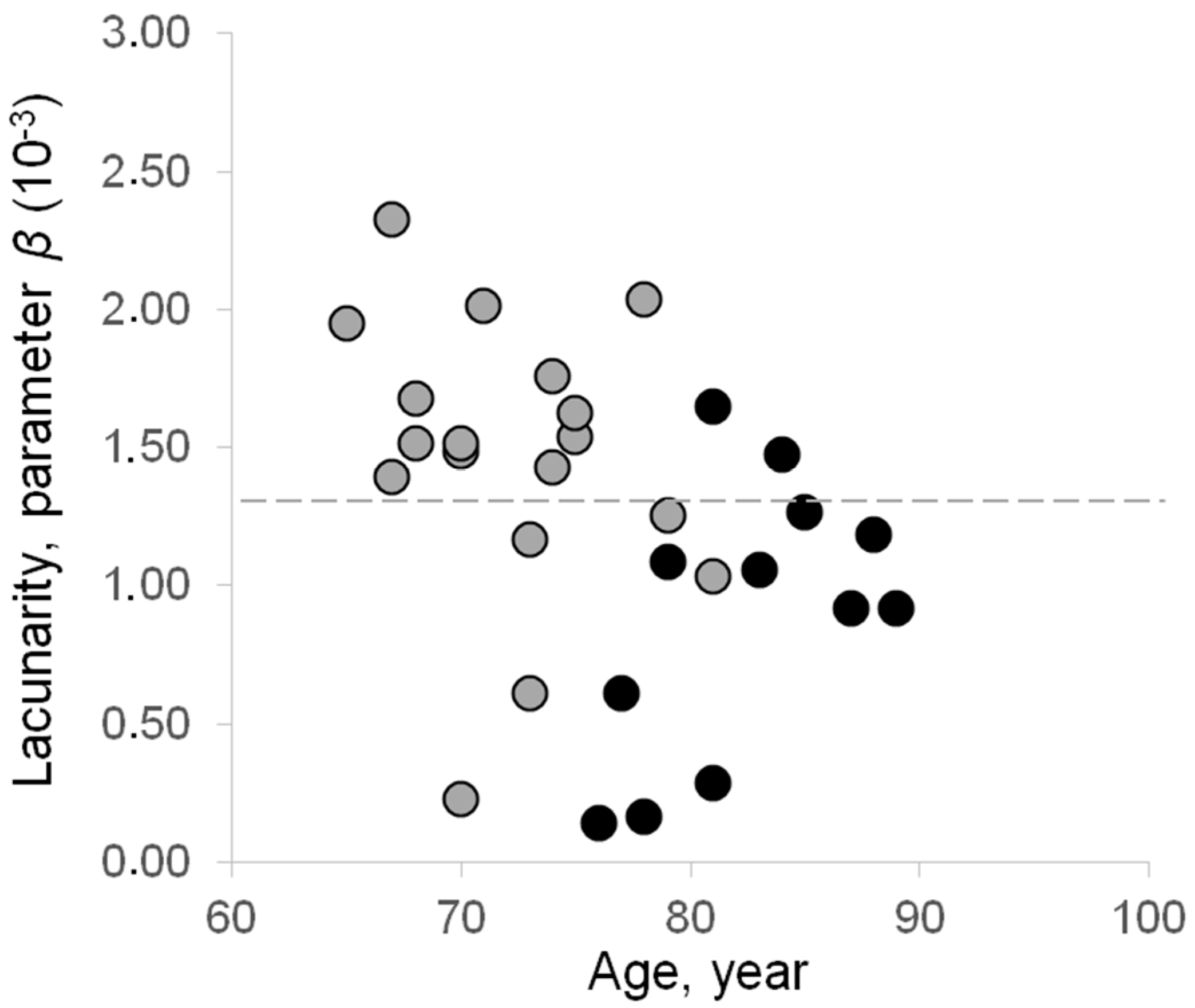
3.2. Lacunarity of mtDNA in Normal Aging and Pathological Aging
4. Discussion
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Piantanelli, L.; Rossolini, G.; Basso, A.; Piantanelli, A.; Malavolta, M.; Zaia, A. Use of mathematical models of survivorship in the study of biomarkers of aging: The role of heterogeneity. Mech. Ageing Dev. 2001, 122, 1461–1475. [Google Scholar] [CrossRef]
- Zaia, A. Osteoporosis and fracture risk: New perspectives for early diagnosis and treatment assessment. In Osteoporosis: Etiology, Diagnosis and Treatment; Mattingly, B.E., Pillare, A.C., Eds.; Nova Science Publishers: Hauppauge, NY, USA, 2009; pp. 267–290. [Google Scholar]
- Pettersson, M. Complexity and Evolution; Cambridge University Press: Cambridge, UK, 1996. [Google Scholar]
- Grassberger, A.; Procaccia, I. Measuring the strangeness of strange attractors. Phys. D 1983, 9, 189–208. [Google Scholar] [CrossRef]
- Goldberger, A.L.; Rigney, D.R.; West, B.J. Chaos and fractals in human physiology. Sci. Am. 1990, 262, 42–49. [Google Scholar] [CrossRef]
- Goldberger, A.L. Non-linear dynamics for clinicians: Chaos theory, fractals, and complexity at the bedside. Lancet 1996, 347, 1312–1314. [Google Scholar] [CrossRef]
- Nonnenmacher, T.F.; Baumann, G.; Losa, G.A. Self-organization and fractal scaling patterns in biological systems. In Trends in Biological Cybernetics; Menon, J., Ed.; Publication Manager, Research Trends, Council of Scientific Research Integration: Trivandrum, India, 1990; pp. 65–73. [Google Scholar]
- Weibel, E.R. Fractal geometry: A design principle for living organisms. Am. J. Physiol. 1991, 261, L361–L369. [Google Scholar] [CrossRef] [PubMed]
- Trifunovic, A.; Larsson, N.G. Mitochondrial dysfunction as a cause of ageing. J. Int. Med. 2008, 263, 167–178. [Google Scholar] [CrossRef]
- Fleming, J.E.; Miquel, J.; Cottrell, S.F.; Yengoyan, L.S.; Economos, A.C. Is cell aging caused by respiration-dependent injury to the mitochondrial genome? Gerontology 1982, 28, 44–53. [Google Scholar] [CrossRef]
- Harman, D. Aging: A theory based on free radical and radiation chemistry. J. Gerontol. 1956, 11, 298–300. [Google Scholar] [CrossRef]
- Bratic, A.; Larsson, N.G. The role of mitochondria in aging. J. Clin. Investig. 2013, 123, 951–957. [Google Scholar] [CrossRef]
- Gomez-Cabrera, M.C.; Sanchis-Gomar, F.; Garcia-Valles, R.; Pareja-Galeano, H.; Gambini, J.; Borras, C.; Vina, J. Mitochondria as sources and targets of damage in cellular aging. Clin. Chem. Lab. Med. 2012, 50, 1287–1295. [Google Scholar] [CrossRef]
- Kennedy, S.R.; Loeb, L.A.; Herr, A.J. Somatic mutations in aging, cancer and neurodegeneration. Mech. Ageing Dev. 2012, 133, 118–126. [Google Scholar] [CrossRef] [PubMed]
- Wei, Y.H.; Lee, H.C. Oxidative stress, mitochondrial DNA mutation, and impairment of antioxidant enzymes in aging. Exp. Biol. Med. 2002, 227, 671–682. [Google Scholar] [CrossRef]
- Cortopassi, G.A.; Arnheim, N. Detection of a specific mitochondrial DNA deletion in tissues of older humans. Nucleic Acids Res. 1990, 18, 6927–6933. [Google Scholar] [CrossRef] [PubMed]
- Soong, N.W.; Hinton, D.R.; Cortopassi, G.; Arnheim, N. Mosaicism for a specific somatic mitochondrial DNA mutation in adult human brain. Nat. Genet. 1992, 2, 318–323. [Google Scholar] [CrossRef] [PubMed]
- Munscher, C.; Rieger, T.; Muller-Hocker, J.; Kadenbach, B. The point mutation of mitochondrial DNA characteristic for MERRF disease is found also in healthy people of different ages. FEBS Lett. 1993, 317, 27–30. [Google Scholar] [CrossRef]
- Schwarze, S.R.; Lee, C.M.; Chung, S.S.; Roecker, E.B.; Weindruch, R.; Aiken, J.M. High levels of mitochondrial DNA deletions in skeletal muscle of old rhesus monkeys. Mech. Ageing Dev. 1995, 83, 91–101. [Google Scholar] [CrossRef]
- Khaidakov, M.; Heflich, R.H.; Manjanatha, M.G.; Myers, M.B.; Aidoo, A. Accumulation of point mutations in mitochondrial DNA of aging mice. Mutat. Res. 2003, 526, 1–7. [Google Scholar] [CrossRef]
- Hebert, S.L.; Lanza, I.R.; Nair, K.S. Mitochondrial DNA alterations and reduced mitochondrial function in aging. Mech. Ageing Dev. 2010, 131, 451–462. [Google Scholar] [CrossRef]
- Payne, B.A.; Wilson, I.J.; Yu-Wai-Man, P.; Coxhead, J.; Deehan, D.; Horvath, R.; Taylor, R.W.; Samuels, D.C.; Santibanez-Koref, M.; Chinnery, P.F. Universal heteroplasmy of human mitochondrial DNA. Hum. Mol. Genet. 2012, 22, 384–390. [Google Scholar] [CrossRef]
- Dhillon, V.S.; Fenech, M. Mutations that affect mitochondrial functions and their association with neurodegenerative diseases. Mutat. Res. Rev. Mutat. Res. 2014, 759, 1–13. [Google Scholar] [CrossRef]
- Rossignol, R.; Malgat, M.; Mazat, J.P.; Letellier, T. Threshold effect and tissue specificity. Implication for mitochondrial cytopathies. J. Biol. Chem. 1999, 274, 33426–33432. [Google Scholar] [CrossRef] [PubMed]
- Wallace, D.C. Mitochondrial DNA mutations in disease and aging. Environ. Mol. Mutagen. 2010, 51, 440–450. [Google Scholar] [CrossRef] [PubMed]
- Kujoth, G.C.; Bradshaw, P.C.; Haroon, S.; Prolla, T.A. The role of mitochondrial DNA mutations in mammalian aging. PLoS Genet. 2007, 3, e24. [Google Scholar] [CrossRef] [PubMed]
- Shuster, R.C.; Rubenstein, A.J.; Wallace, D.C. Mitochondrial DNA in anucleate human blood cells. Biochem. Biophys. Res. Commun. 1988, 155, 1360–1365. [Google Scholar] [CrossRef]
- Zaia, A.; Maponi, P.; Di Stefano, G.; Casoli, T. Biocomplexity and fractality in the search of biomarkers of aging and pathology: Focus on mitochondrial DNA and Alzheimer’s disease. Aging Dis. 2017, 8, 44–56. [Google Scholar] [CrossRef] [PubMed][Green Version]
- Zaia, A.; Maponi, P.; Zannotti, M.; Casoli, T. Biocomplexity and Fractality in the Search of Biomarkers of Aging and Pathology: Mitochondrial DNA Profiling of Parkinson’s Disease. Int. J. Mol. Sci. 2020, 21, 1758. [Google Scholar] [CrossRef]
- Mandelbrot, B.B. The Fractal Geometry of Nature; WH Freeman: New York, NY, USA, 1982. [Google Scholar]
- Lipsitz, L.A.; Goldberger, A.L. Loss of ‘complexity’ and aging: Potential applications of fractals and chaos theory to senescence. JAMA 1992, 267, 1806–1809. [Google Scholar] [CrossRef]
- Losa, G.A.; Nonnenmacher, T.F. Self-similarity and fractal irregularity in pathologic tissues. Mod. Pathol. 1996, 9, 174–182. [Google Scholar]
- Cross, S.S. Fractals in pathology. J. Pathol. 1997, 182, 1–8. [Google Scholar] [CrossRef]
- Oiwa, N.N.; Glazier, J.A. Self-similar mitochondrial DNA. Cell Biochem. Biophys. 2004, 41, 41–62. [Google Scholar] [CrossRef]
- Goldberger, L.A.; Peng, C.K.; Lipsitz, L.A. What is physiologic complexity and how does it change with aging and disease? Neurobiol. Aging 2002, 23, 23–26. [Google Scholar] [CrossRef]
- Piantanelli, A.; Serresi, S.; Ricotti, G.; Rossolini, G.; Zaia, A.; Basso, A.; Piantanelli, L. Color-based method for fractal dimension estimation of pigmented skin lesion contour. In Fractals in Biology and Medicine; Losa, G.A., Ed.; Birkhauser Press: Basel, Switzerland, 2002; pp. 127–136. [Google Scholar]
- Vaillancourt, D.E.; Newell, K.M. Changing complexity in human behaviour and physiology through aging and disease. Neurobiol. Aging 2002, 23, 1–11. [Google Scholar] [CrossRef]
- Lipsitz, L.A. Physiological complexity, aging, and the path to frailty. Sci. Aging Knowl. Environ. 2004, 16, pe16. [Google Scholar] [CrossRef] [PubMed]
- Doubal, F.N.; MacGillivray, T.J.; Patton, N.; Dhillon, B.; Dennis, M.S.; Wardlaw, J.M. Fractal analysis of retinal vessels suggests that a distinct vasculopathy causes lacunar stroke. Neurology 2010, 74, 1102–1107. [Google Scholar] [CrossRef]
- Fiz, J.A.; Monte-Moreno, E.; Andreo, F.; Auteri, S.J.; Sanz-Santos, J.; Serra, P.; Bonet, G.; Castellà, E.; Manzano, J.R. Fractal dimension analysis of malignant and benign endobronchial ultrasound nodes. BMC Med. Imaging 2014, 14, 22. [Google Scholar] [CrossRef]
- Captur, G.; Karperien, A.L.; Li, C.; Zemrak, F.; Tobon-Gomez, C.; Gao, X.; Bluemke, D.A.; Elliott, P.M.; Petersen, S.E.; Moon, J.C. Fractal frontiers in cardiovascular magnetic resonance: Towards clinical implementation. J. Cardiovasc. Magn. Reson. 2015, 17, 80. [Google Scholar] [CrossRef]
- Hao, B.L. Fractals from genomes—Exact solutions of a biology-inspired problem. Phys. A 2000, 282, 225–246. [Google Scholar] [CrossRef]
- Kirilyuk, A.P. Complex-dynamical extension of the fractal paradigm and its applications in life sciences. In Fractals in Biology and Medicine; Losa, G.A., Merlini, D., Nonnenmacher, T.F., Weibel, E., Eds.; Birkhauser Press: Basel, Switzerland, 2004; pp. 233–244. [Google Scholar]
- Zhou, L.Q.; Yu, Z.G.; Deng, J.Q.; Anh, V.; Long, S.C. A fractal method to distinguish coding and non-coding sequences in a complete genome based on a number sequence representation. J. Theor. Biol. 2005, 232, 559–567. [Google Scholar] [CrossRef]
- Aldrich, P.R.; Horsley, R.K.; Turcic, S.M. Symmetry in the language of gene expression: A survey of gene promoter networks in multiple bacterial species and non-σ regulons. Symmetry 2011, 3, 750–766. [Google Scholar] [CrossRef]
- Cattani, C.; Pierro, G. On the fractal geometry of DNA by the binary image analysis. Bull. Math. Biol. 2013, 75, 1544–1570. [Google Scholar] [CrossRef]
- Mandelbrot, B.B. A Fractal’s Lacunarity, and how it can be Tuned and Measured. In Fractals in Biology and Medicine; Nonnenmacher, T.F., Losa, G.A., Weibel, E.R., Eds.; Birkhauser Press: Basel, Switzerland, 1993; pp. 8–21. [Google Scholar]
- Plotnick, R.E.; Gardner, R.H.; Hargrove, W.W.; Prestegard, K.; Perlmutter, M. Lacunarity analysis: A general technique for the analysis of spatial patterns. Phys. Rev. E 1996, 53, 5461–5468. [Google Scholar] [CrossRef] [PubMed]
- Allain, C.; Cloitre, M. Characterizing the lacunarity of random and deterministic fractal sets. Phys. Rev. A 1991, 44, 3552–3558. [Google Scholar] [CrossRef] [PubMed]
- Jeffrey, H.J. Chaos game representation of gene structure. Nucleic Acids Res. 1990, 18, 2163–2170. [Google Scholar] [CrossRef] [PubMed]
- Deschavanne, P.J.; Giron, A.; Vilain, J.; Fagot, G.; Fertil, B. Genomic signature: Characterization and classification of species assessed by chaos game representation of sequences. Mol. Biol. Evol. 1999, 16, 1391–1399. [Google Scholar] [CrossRef]
- Fu, W.; Wang, Y.; Lu, D. Multifractal analysis of genomic sequences CGR images. In Proceedings of the 2005 IEEE Engineering in Medicine and Biology 27th Annual Conference, Shanghai, China, 17–18 January 2006; Volume 5, pp. 4783–4786. [Google Scholar] [CrossRef]
- Stan, C.; Cristescu, C.P.; Scarlat, E.I. Similarity analysis for DNA sequences based on chaos game representation. Case study: The albumin. J. Theor. Biol. 2010, 267, 513–518. [Google Scholar] [CrossRef]
- Zaia, A.; Eleonori, R.; Maponi, P.; Rossi, R.; Murri, R. Medical imaging and osteoporosis: Fractal’s lacunarity analysis of trabecular bone in MR images. Proceedings of Eighteenth IEEE Symposium on Computer-Based Medical Systems (CBMS 2005), Dublin, Ireland, 23–24 June 2005; IEEE: Piscataway, NJ, USA, 2005; pp. 3–8. [Google Scholar] [CrossRef]
- Zaia, A.; Eleonori, R.; Maponi, P.; Rossi, R.; Murri, R. MR imaging and osteoporosis: Fractal lacunarity analysis of trabecular Bone. IEEE Trans. Inf. Technol. Biomed. 2006, 10, 484–489. [Google Scholar] [CrossRef]
- Zaia, A.; Rossi, R.; Egidi, N.; Maponi, P. Fractal’s lacunarity analysis of trabecular bone in MR images. In Computational Vision and Medical Image Processing; Tavares, J., Jorge, N., Eds.; CRC Press: Boca Raton, FL, USA, 2010; pp. 421–426. [Google Scholar]
- Zaia, A. Fractal lacunarity of trabecular bone and magnetic resonance imaging: New perspectives for osteoporotic fracture risk assessment. World J. Orthop. 2015, 6, 221–235. [Google Scholar] [CrossRef]
- Edgar, R.; Domrachev, M.; Lash, A.E. Gene expression omnibus: NCBI gene expression and hybridization array data repository. Nucleic Acids Res. 2002, 30, 207–210. [Google Scholar] [CrossRef]
- Casoli, T.; Di Stefano, G.; Spazzafumo, L.; Balietti, M.; Giorgetti, B.; Giuli, C.; Postacchini, D.; Fattoretti, P.; Conti, F. Contribution of non-reference alleles in mtDNA of Alzheimer’s disease patients. Ann. Clin. Transl. Neurol. 2014, 1, 284–289. [Google Scholar] [CrossRef]
- Vinga, S.; Carvalho, A.M.; Francisco, A.P.; Russo, L.M.; Almeida, J.S. Pattern matching through chaos game representation: Bridging numerical and discrete data structures for biological sequence analysis. Algorithms Mol. Biol. 2012, 7, 10. [Google Scholar] [CrossRef]
- Wang, Y.; Hill, K.; Singh, S.; Kari, L. The spectrum of genomic signatures: From dinucleotides to chaos game representation. Gene 2005, 346, 173–185. [Google Scholar] [CrossRef] [PubMed]
- Trifunovic, A. Mitochondrial DNA and ageing. Biochem. Biophys. Acta 2006, 1757, 611–617. [Google Scholar] [CrossRef] [PubMed]
- Federico, A.; Cardaioli, E.; Da Pozzo, P.; Formichi, P.; Gallus, G.N.; Radi, E. Mitochondria, oxidative stress and neurodegeneration. J. Neurol. Sci. 2012, 322, 254–262. [Google Scholar] [CrossRef] [PubMed]
- Jang, J.Y.; Blum, A.; Liu, J.; FinkelJ, T. The role of mitochondria in aging. J. Clin. Investig. 2018, 128, 3662–3670. [Google Scholar] [CrossRef] [PubMed]
- Linnane, A.W.; Marzuki, S.; Ozawa, T.; Tanaka, M. Mitochondrial DNA mutations as an important contributor to ageing and degenerative diseases. Lancet 1989, 1, 642–645. [Google Scholar] [CrossRef]
- Gellerich, F.N.; Deschauer, M.; Chen, Y.; Muller, T.; Neudecker, S.; Zierz, S. Mitochondrial respiratory rates and activities of respiratory chain complexes correlate linearly with heteroplasmy of deleted mtDNA without threshold and independently of deletion size. Biochem. Biophys. Acta 2002, 1556, 41–52. [Google Scholar] [CrossRef]
- Taylor, R.W.; Turnbull, D.M. Mitochondrial DNA mutations in human disease. Nat. Rev. Genet. 2005, 6, 389–402. [Google Scholar] [CrossRef] [PubMed]
- Lagouge, M.; Larsson, N.G. The role of mitochondrial DNA mutations and free radicals in disease and ageing. J. Intern. Med. 2013, 273, 529–543. [Google Scholar] [CrossRef]
- Kazachkova, N.; Ramos, A.; Santos, C.; Lima, M. Mitochondrial DNA Damage Patterns and Aging: Revising the Evidences for Humans and Mice. Aging Dis. 2013, 4, 337–350. [Google Scholar] [CrossRef] [PubMed]
- Zapico, S.C.; Ubelaker, D.H. mtDNA Mutations and Their Role in Aging, Diseases and Forensic Sciences. Aging Dis. 2013, 4, 364–380. [Google Scholar] [CrossRef]
- Itsara, L.S.; Kennedy, S.R.; Fox, E.J.; Yu, S.; Hewitt, J.J.; Sanchez-Contreras, M.; Cardozo-Pelaez, F.; Pallanck, L.J. Oxidative stress is not a major contributor to somatic mitochondrial DNA mutations. PLoS Genet. 2014, 10, e1003974. [Google Scholar] [CrossRef] [PubMed]
- Ziada, A.S.; Smith, M.S.R.; Côté, H.C.F. Updating the Free Radical Theory of Aging. Front. Cell Dev. Biol. 2020, 8, 575–645. [Google Scholar] [CrossRef] [PubMed]
- Collerton, J.; Ashok, D.; Martin-Ruiz, C.; Pyle, A.; Hudson, G.; Yadegarfar, M.; Davies, K.; Jagger, C.; von Zglinicki, T.; Kirkwood, T.B.; et al. Frailty and mortality are not influenced by mitochondrial DNA haplotypes in the very old. Neurobiol. Aging 2013, 34, 2889.e1–2889.e4. [Google Scholar] [CrossRef] [PubMed]
- Courtenay, M.D.; Gilbert, J.R.; Jiang, L.; Cummings, A.C.; Gallins, P.J.; Caywood, L.; Reinhart-Mercer, L.; Fuzzell, D.; Knebusch, C.; Laux, R.; et al. Mitochondrial haplogroup X is associated with successful aging in the Amish. Hum. Genet. 2012, 131, 201–208. [Google Scholar] [CrossRef]
- De Benedictis, G.; Rose, G.; Carrieri, G.; De Luca, M.; Falcone, E.; Passarino, G.; Bonafe, M.; Monti, D.; Baggio, G.; Bertolini, S.; et al. Mitochondrial DNA inherited variants are associated with successful aging and longevity in humans. Faseb J. 1999, 13, 1532–1536. [Google Scholar] [CrossRef]
- Feng, J.; Zhang, J.; Liu, M.; Wan, G.; Qi, K.; Zheng, C.; Lv, Z.; Hu, C.; Zeng, Y.; Gregory, S.G.; et al. Association of mtDNA haplogroup F with healthy longevity in the female Chuang population, China. Exp. Gerontol. 2011, 46, 987–993. [Google Scholar] [CrossRef]
- Ross, O.A.; McCormack, R.; Curran, M.D.; Duguid, R.A.; Barnett, Y.A.; Rea, I.M.; Middleton, D. Mitochondrial DNA polymorphism: Its role in longevity of the Irish population. Exp. Gerontol. 2001, 36, 1161–1178. [Google Scholar] [CrossRef]
- Tanaka, M.; Gong, J.-S.; Zhang, J.; Yoneda, M.; Yagi, K. Mitochondrial genotype associated with longevity. Lancet 1998, 351, 185–186. [Google Scholar] [CrossRef]
- Tanaka, M.; Gong, J.-S.; Zhang, J.; Yamada, Y.; Borgeld, H.; Yagi, K. Mitochondrial genotype associated with longevity and its inhibitory effect on mutagenesis. Mech. Ageing Dev. 2000, 116, 65–76. [Google Scholar] [CrossRef]
- Niemi, A.K.; Hervonen, A.; Hurme, M.; Karhunen, P.J.; Jylha, M.; Majamaa, K. Mitochondrial DNA polymorphisms associated with longevity in a Finnish population. Hum. Genet. 2003, 112, 29–33. [Google Scholar] [CrossRef]
- Niemi, A.K.; Moilanen, J.S.; Tanaka, M.; Hervonen, A.; Hurme, M.; Lehtimaki, T.; Arai, Y.; Hirose, N.; Majamaa, K. A combination of three common inherited mitochondrial DNA polymorphisms promotes longevity in Finnish and Japanese subjects. Eur. J. Hum. Genet. 2005, 13, 166–170. [Google Scholar] [CrossRef] [PubMed]
- Yang, X.; Wang, X.; Yao, H.; Deng, J.; Jiang, Q.; Guo, Y.; Lan, G.; Liao, D.J.; Jiang, H. Mitochondrial DNA polymorphisms are associated with the longevity in the Guangxi Bama population of China. Mol. Biol. Rep. 2012, 39, 9123–9131. [Google Scholar] [CrossRef] [PubMed]
- Elson, J.L.; Herrnstadt, C.; Preston, G.; Thal, L.; Morris, C.M.; Edwardson, J.A.; Beal, M.F.; Turnbull, D.M.; Howell, N. Does the mitochondrial genome play a role in the etiology of Alzheimer’s disease? Hum. Genet. 2006, 119, 241–254. [Google Scholar] [CrossRef] [PubMed]
- Corral-Debrinski, M.; Horton, T.; Lott, M.T.; Shoffner, J.M.; Beal, M.F.; Wallace, D.C. Mitochondrial DNA deletions in human brain: Regional variability and increase with advanced age. Nat. Genet. 1992, 2, 324–329. [Google Scholar] [CrossRef] [PubMed]
- Fayet, G.; Jansson, M.; Sternberg, D.; Moslemi, A.R.; Blondy, P.; Lombes, A.; Fardeau, M.; Oldfors, A. Ageing muscle: Clonal expansions of mitochondrial DNA point mutations and deletions cause focal impairment of mitochondrial function. Neuromuscul. Disord. 2002, 12, 484–493. [Google Scholar] [CrossRef]
- Corral-Debrinski, M.; Shoffner, J.M.; Lott, M.T.; Wallace, D.C. Association of mitochondrial DNA damage with aging and coronary atherosclerotic heart disease. Mutat. Res. 1992, 275, 169–180. [Google Scholar] [CrossRef]
- Franceschi, C.; Garagnani, P.; Morsiani, C.; Conte, M.; Santoro, A.; Grignolio, A.; Monti, D.; Capri, M.; Salvioli, S. The Continuum of Aging and Age-Related Diseases: Common Mechanisms but Different Rates. Front. Med. 2018, 5, 61. [Google Scholar] [CrossRef]
- Gopakumar, G.; Nair, A.S. Lacunarity Analysis of Genomic Sequences: A Potential Bio-sequence Analysis Method. In Proceedings of the 5th International Conference on of Bioinformatics and Biomedical Engineering (iCBBE), Wuhan, China, 10–12 May 2011; IEEE: Piscataway, NJ, USA, 2011; pp. 1–4. [Google Scholar] [CrossRef]
- Zaia, A.; Rossi, R.; Galeazzi, R.; Sallei, M.; Maponi, P.; Scendoni, P. Fractal lacunarity of trabecular bone in vertebral MRI to predict osteoporotic fracture risk in over-fifties women. The LOTO study. BMC Musculoskelet. Disord. 2021, 22, 108. [Google Scholar] [CrossRef]


| Overall | nA | pA | |
|---|---|---|---|
| Number (Female/Male) | 33 (23/10) | 18 (14/4) | 15 (9/6) |
| Age (year) | 76.1 ± 6.4 | 72.1 ± 4.4 | 80.9 ± 5.1 |
| ADL (hierarchy scale) | 0.0 (0.0–0.0) | 0.0 (0.0–0.0) | 0.0 (4.5–0.0) |
| MMSE (scale 30–0) | - | 28.2 (28.4–27.4) | - |
| CPS (hierarchy scale) | - | - | 1.0 (2.0–0.0) |
| Number | rCRS | nA | pA | p Value |
|---|---|---|---|---|
| Subjects | - | 18 | 15 | |
| Adenine | 5117 | 5172 ± 11 | 4912 ± 111 | <0.001 |
| Cytosine | 5175 | 4946 ± 18 | 4618 ± 168 | <0.001 |
| Guanine | 2163 | 2270 ± 23 | 2108 ± 49 | <0.001 |
| Thymine | 4089 | 4157 ± 7 | 3916 ± 101 | <0.001 |
| No-call | - | 488 ± 145 | 980 ± 390 | <0.001 |
| Homoplasmy | - | 18 ± 9 | 21 ± 8 | 0.170 |
| Heteroplasmy | - | 5 ± 4 | 10 ± 6 | 0.006 |
| mtDNA | bmin = 3 | bmin = 5 | |||
|---|---|---|---|---|---|
| α (100) | β (*) | α (100) | β (*) | ||
| CGR matrix L = 5 | rCRS | 1.6425 | 5.3650 | 2.0978 | 10.8327 |
| nA | 1.6543 ± 0.0005 | 1.4772 ± 0.5060 | 2.1725 ± 0.0016 | 3.6416 ± 1.3046 | |
| pA | 1.6403 ± 0.0007 | 0.8988 ± 0.4990 | 2.0364 ± 0.0013 | 1.7004 ± 1.0239 | |
| p Value | <0.0001 | 0.0023 | <0.0001 | 0.0001 | |
| CGR matrix L = 6 | rCRS | 1.0099 | 1.2013 | 1.0369 | 1.1125 |
| nA | 1.0521 ± 0.0233 | 1.1225 ± 0.0367 | 1.1328 ± 0.1954 | 1.3821 ± 0.6591 | |
| pA | 0.9955 ± 0.0590 | 0.8828 ± 0.2060 | 0.9982 ± 0.0637 | 0.9305 ± 0.1791 | |
| p Value | 0.0004 | <0.0001 | 0.0079 | 0.0076 | |
| mtDNA | Overall | Age-Matched | ||
|---|---|---|---|---|
| α (100) | β (10−3) | α (100) | β (10−3) | |
| rCRS | 1.6425 | 5.3650 | 1.6425 | 5.3650 |
| nA | 1.6543 ± 0.0005 | 1.4772 ± 0.5060 | 1.6544 ± 0.0005 | 1.3850 ± 0.4227 |
| pA | 1.6403 ± 0.0007 | 0.8988 ± 0.4990 | 1.6399 ± 0.0009 | 0.6596 ± 0.6026 |
| p Value | <0.0001 | 0.0023 | <0.0001 | 0.0082 |
| Number | rCRS | nA (n.9) | pA (n.9) | p Value |
|---|---|---|---|---|
| Age | - | 75.8 ± 2.9 | 77.4 ± 3.0 | 0.1245 |
| Adenine | 5117 | 5173 ± 6 | 4873 ± 122 | <0.0001 |
| Cytosine | 5175 | 4945 ± 19 | 4551 ± 189 | <0.0001 |
| Guanine | 2163 | 2268 ± 18 | 2090 ± 56 | <0.0001 |
| Thymine | 4089 | 4158 ± 8 | 3875 ± 110 | <0.0001 |
| No-call | - | 481 ± 135 | 1142 ± 427 | 0.0002 |
| Homoplasmy | - | 17 ± 9 | 20 ± 8 | 0.2056 |
| Heteroplasmy | - | 6 ± 4 | 13 ± 7 | 0.0074 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zaia, A.; Maponi, P. Mitochondrial DNA Profiling by Fractal Lacunarity to Characterize the Senescent Phenotype as Normal Aging or Pathological Aging. Fractal Fract. 2022, 6, 219. https://doi.org/10.3390/fractalfract6040219
Zaia A, Maponi P. Mitochondrial DNA Profiling by Fractal Lacunarity to Characterize the Senescent Phenotype as Normal Aging or Pathological Aging. Fractal and Fractional. 2022; 6(4):219. https://doi.org/10.3390/fractalfract6040219
Chicago/Turabian StyleZaia, Annamaria, and Pierluigi Maponi. 2022. "Mitochondrial DNA Profiling by Fractal Lacunarity to Characterize the Senescent Phenotype as Normal Aging or Pathological Aging" Fractal and Fractional 6, no. 4: 219. https://doi.org/10.3390/fractalfract6040219
APA StyleZaia, A., & Maponi, P. (2022). Mitochondrial DNA Profiling by Fractal Lacunarity to Characterize the Senescent Phenotype as Normal Aging or Pathological Aging. Fractal and Fractional, 6(4), 219. https://doi.org/10.3390/fractalfract6040219







