Design and High-Order Precision Numerical Implementation of Fractional-Order PI Controller for PMSM Speed System Based on FPGA
Abstract
:1. Introduction
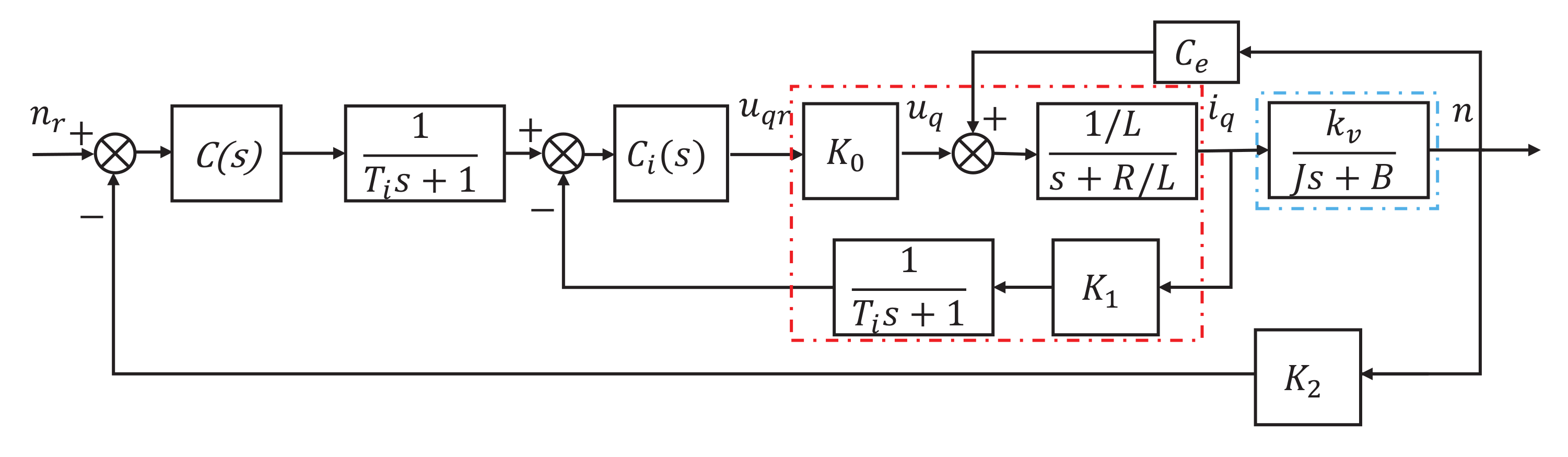
2. The Plant Model and Controller Design
2.1. The Plant Model of PMSM Servo System
2.2. The Controller Design
2.2.1. Fractional Order PI Controller Design
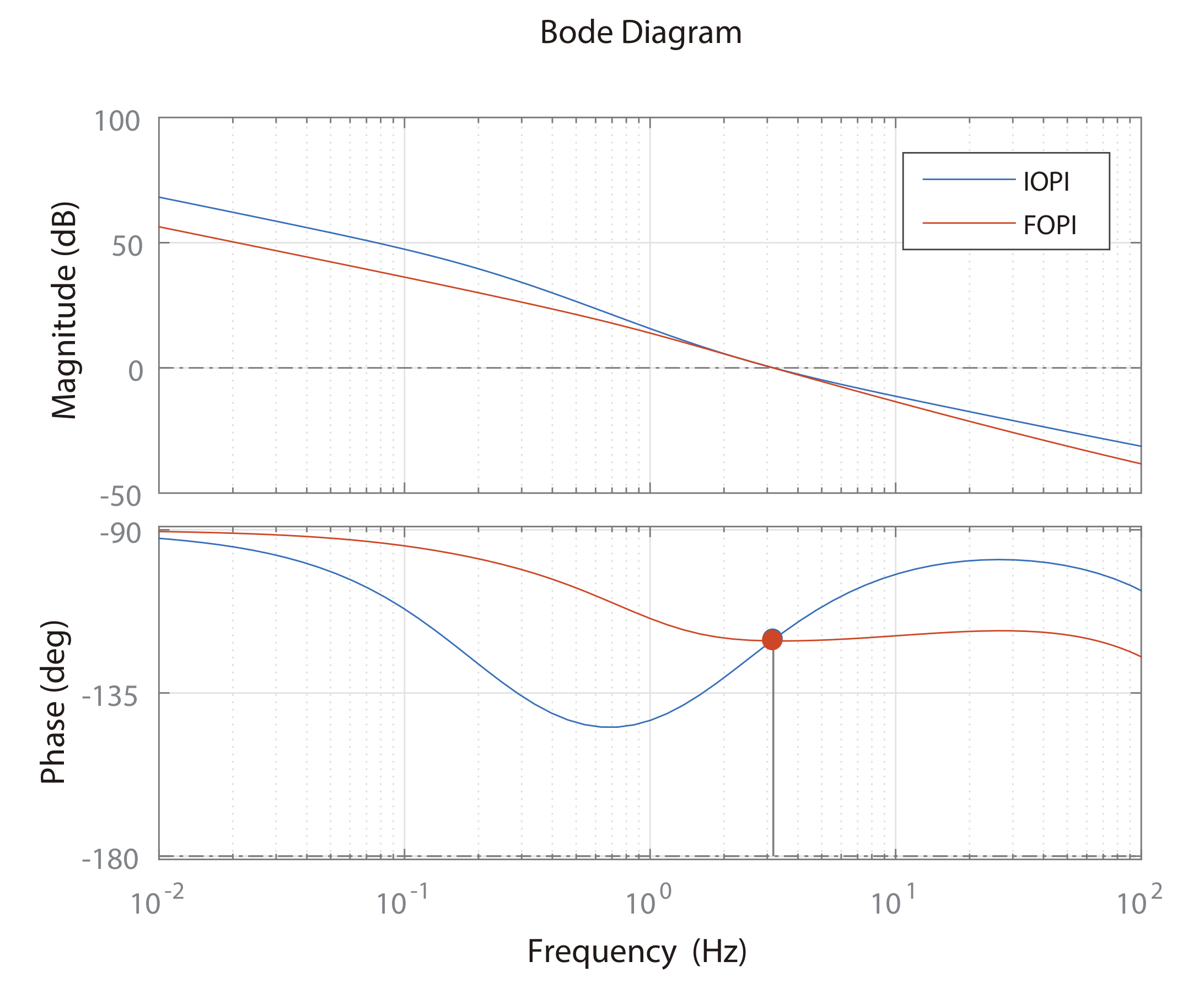
2.2.2. Integer-Order PI Controller Design
3. Numerical Implementation of Fractional Order Operators
3.1. Impulse Response Invariance Method
3.2. Oustaloup Method
3.3. GL Method
4. Simulation Analysis
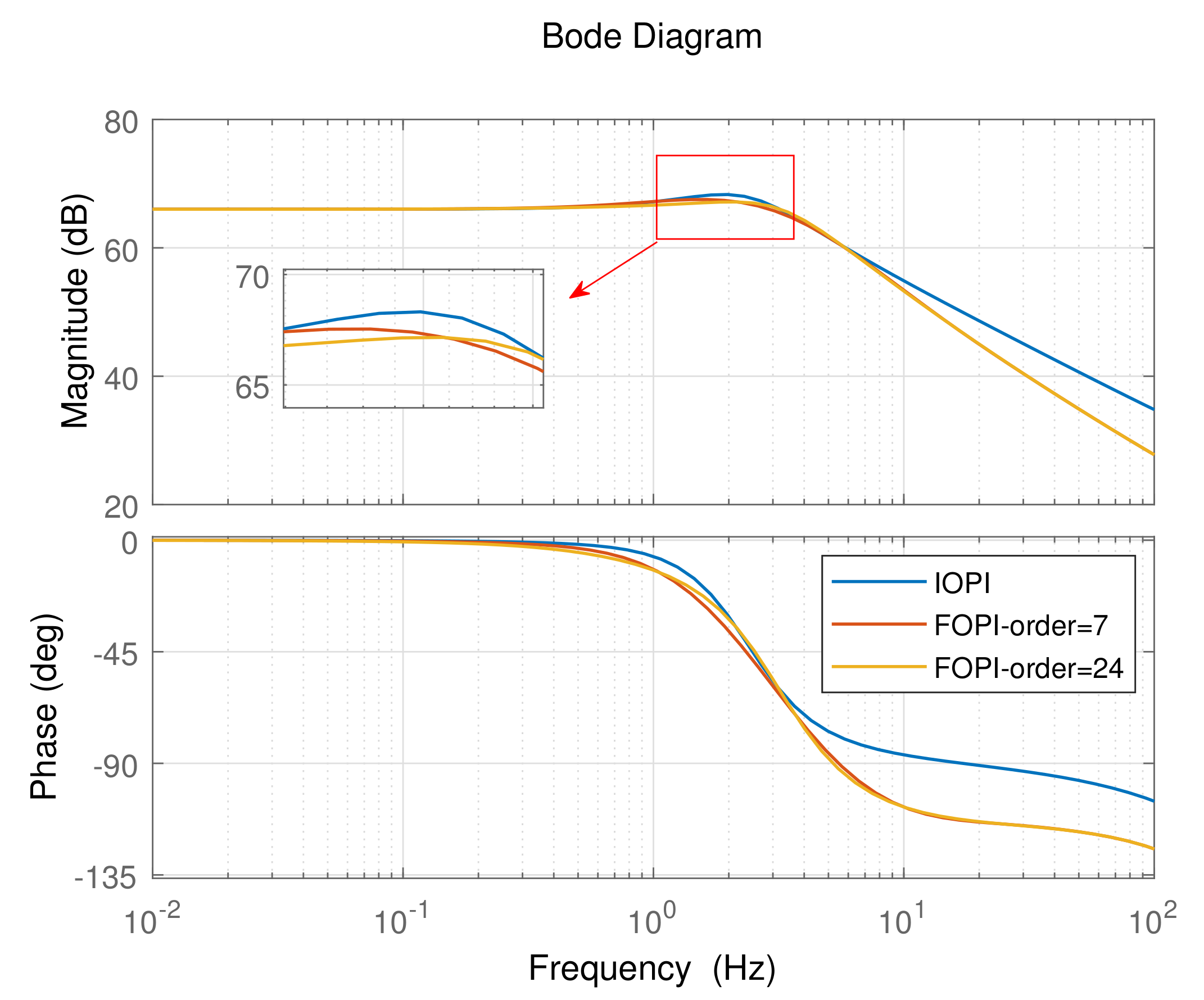
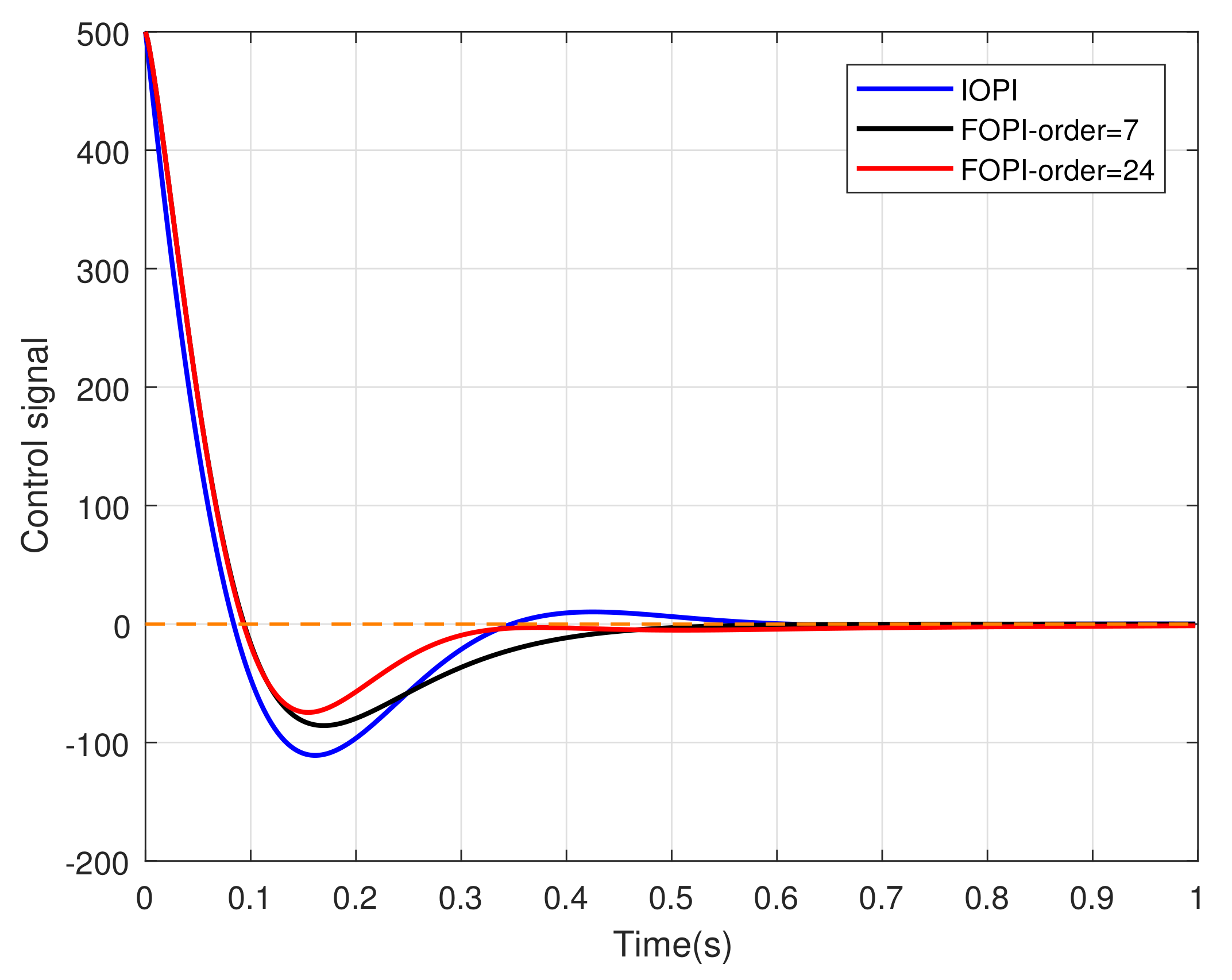
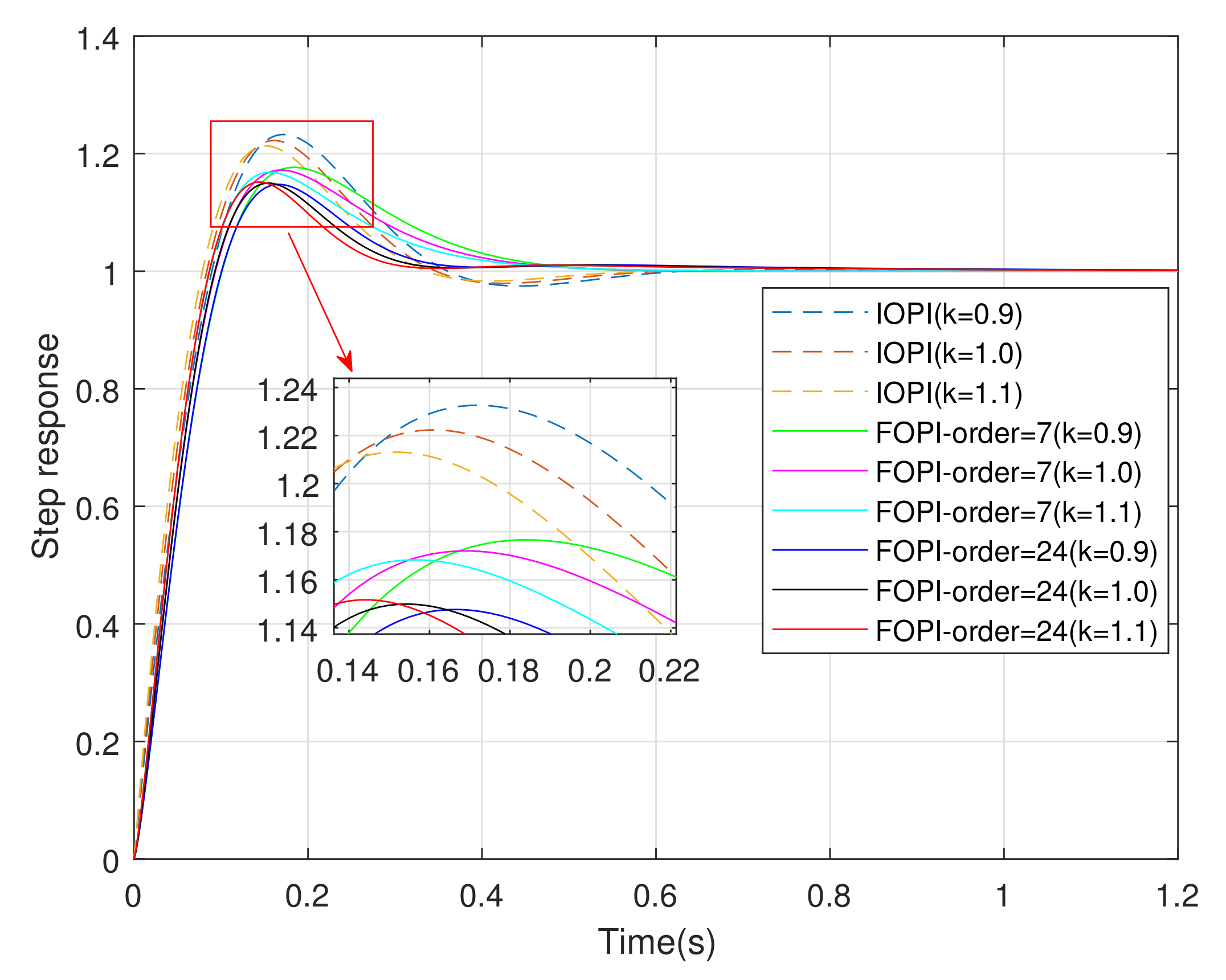
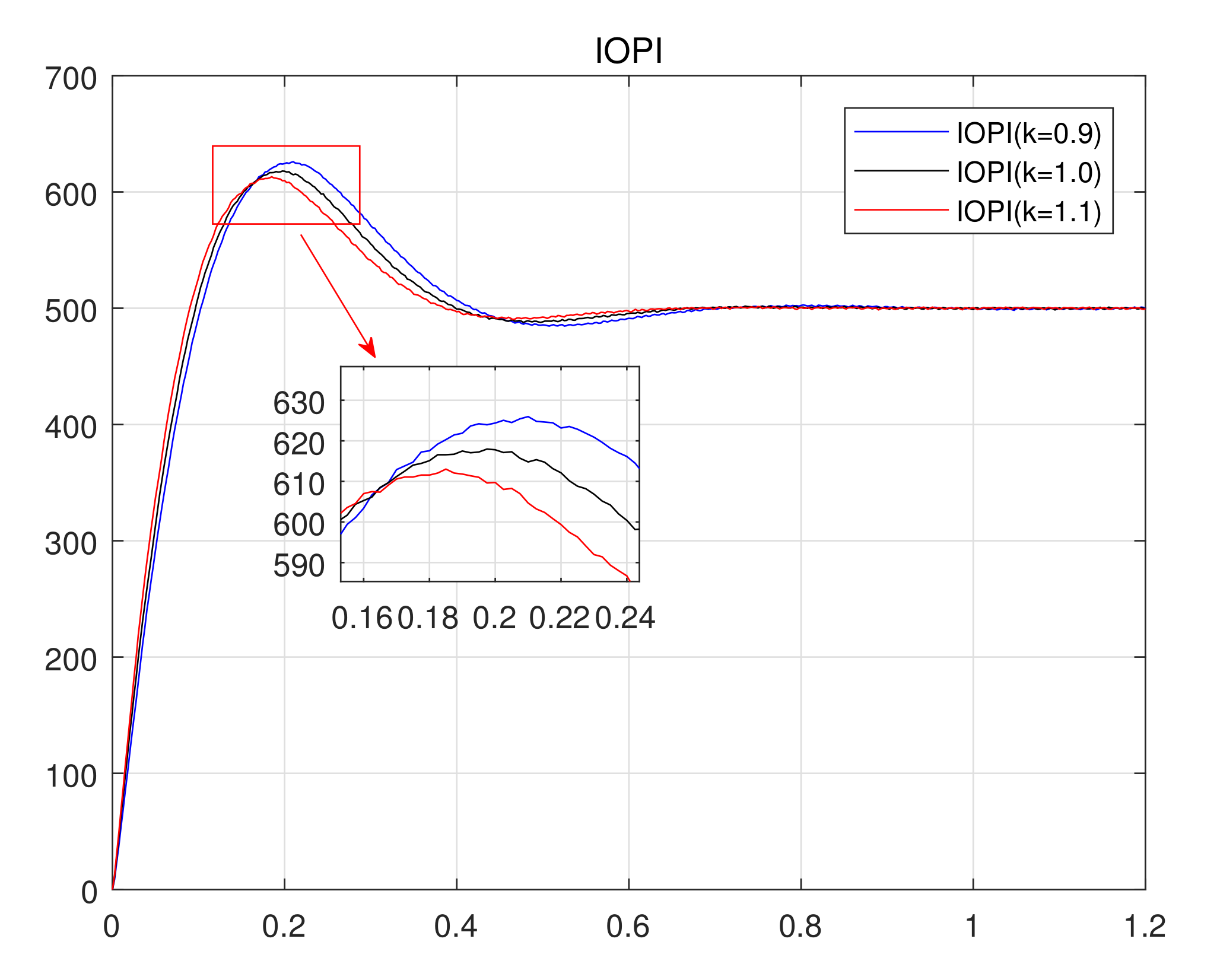
4.1. Comparison of Three Discretization Methods
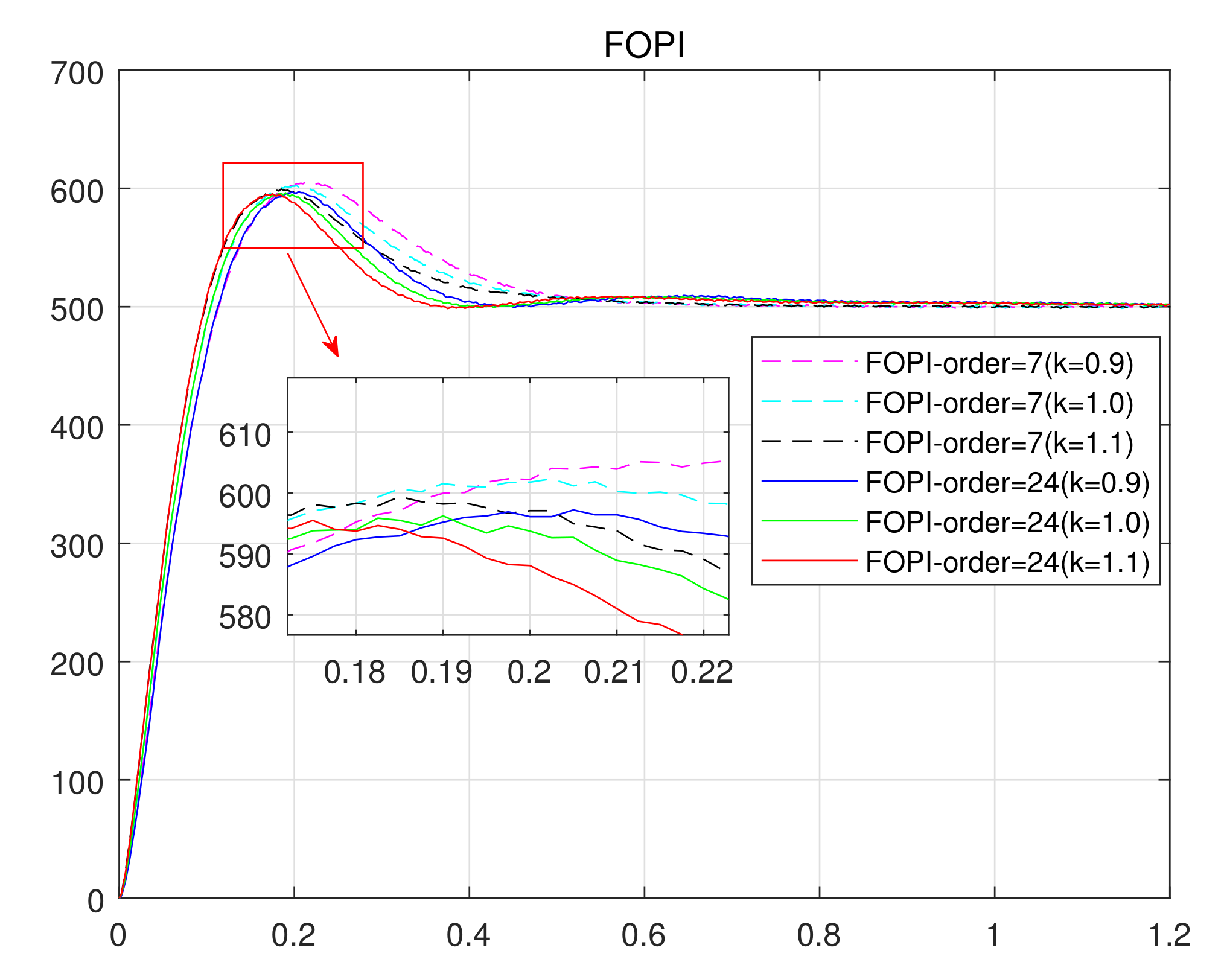
4.2. The Influence of Discretization Order of Impulse Response Invariant Method
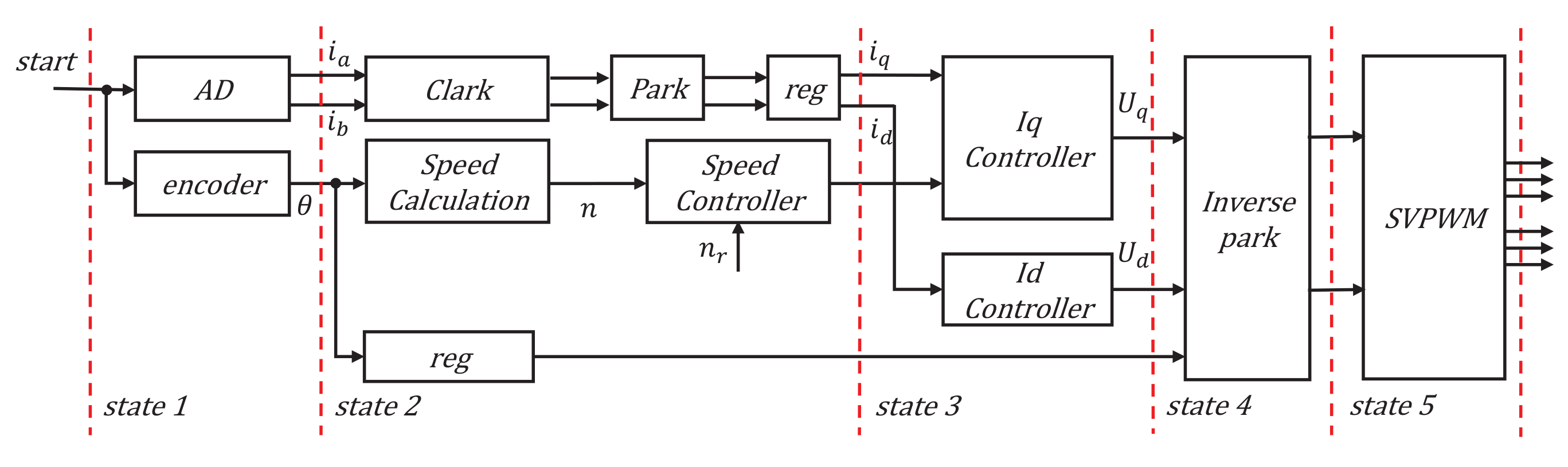
5. FPGA Design Experimental Verification
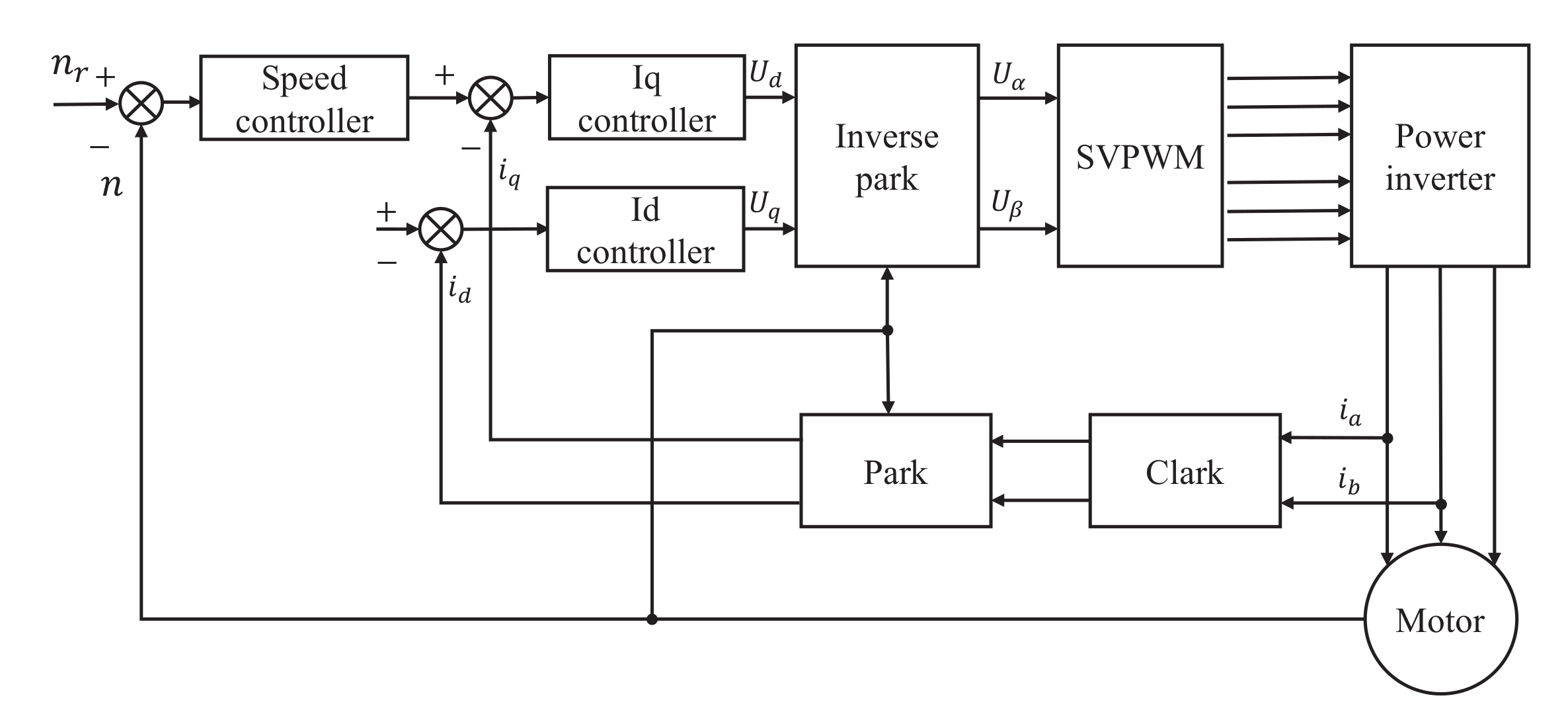
5.1. FOC Algorithm Implementation Based on FPGA
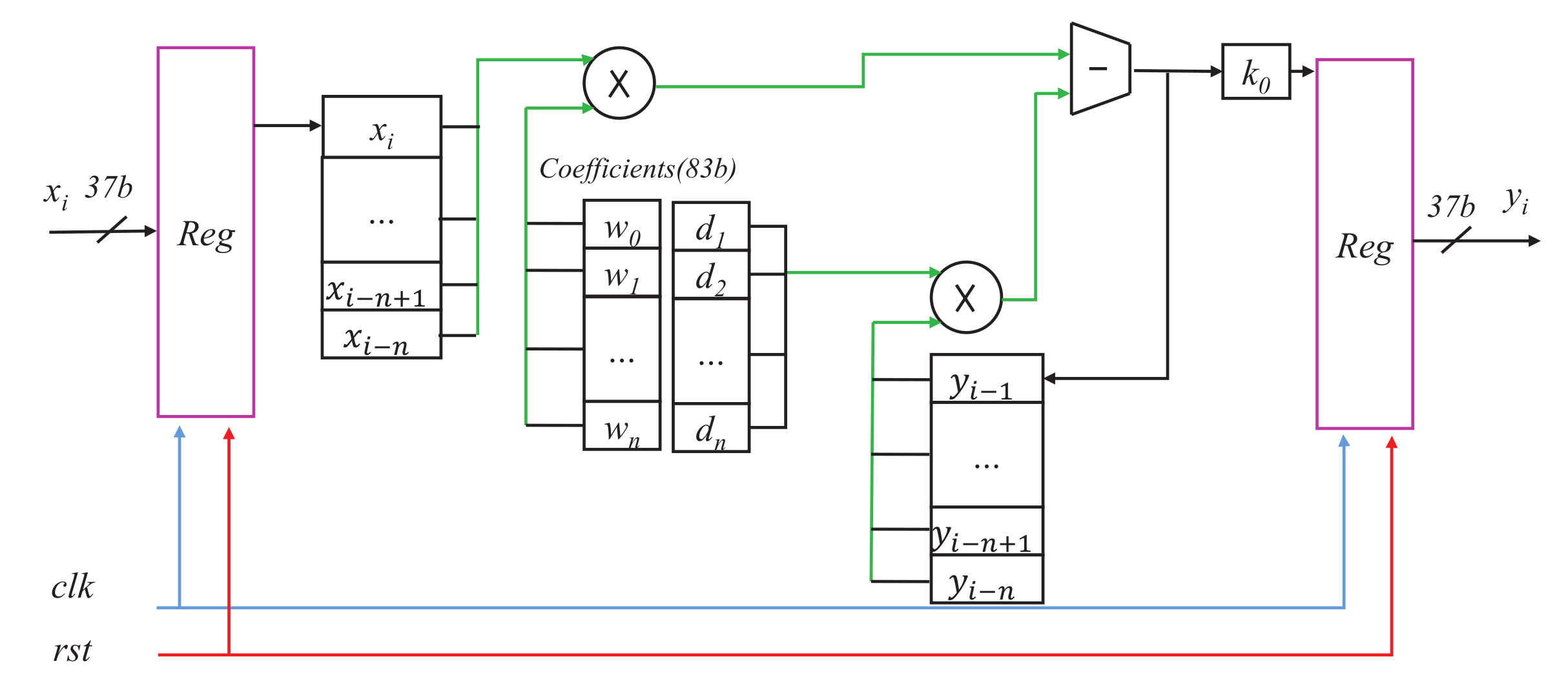
5.2. FPGA Implementation of Fractional-Order Operator
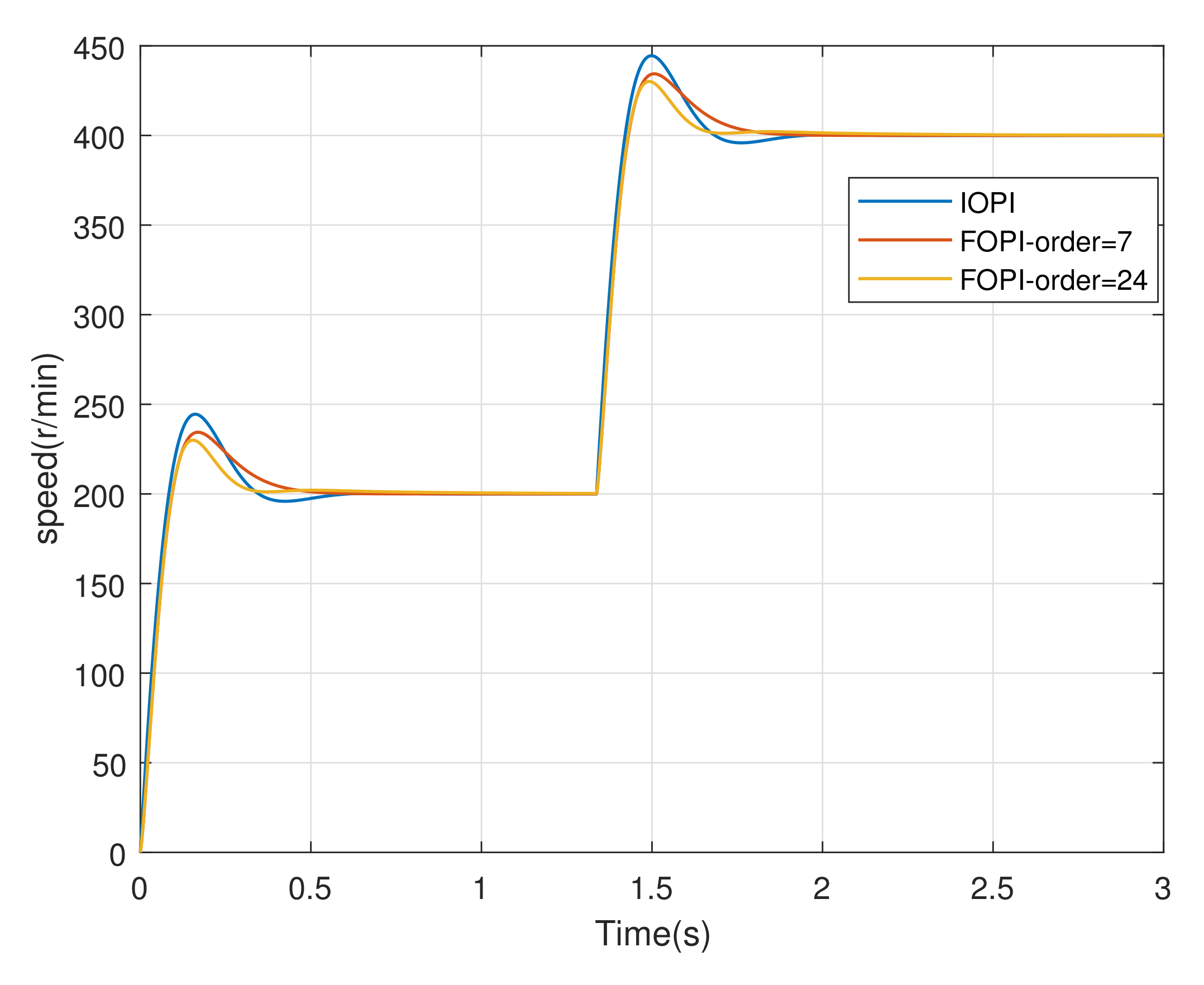
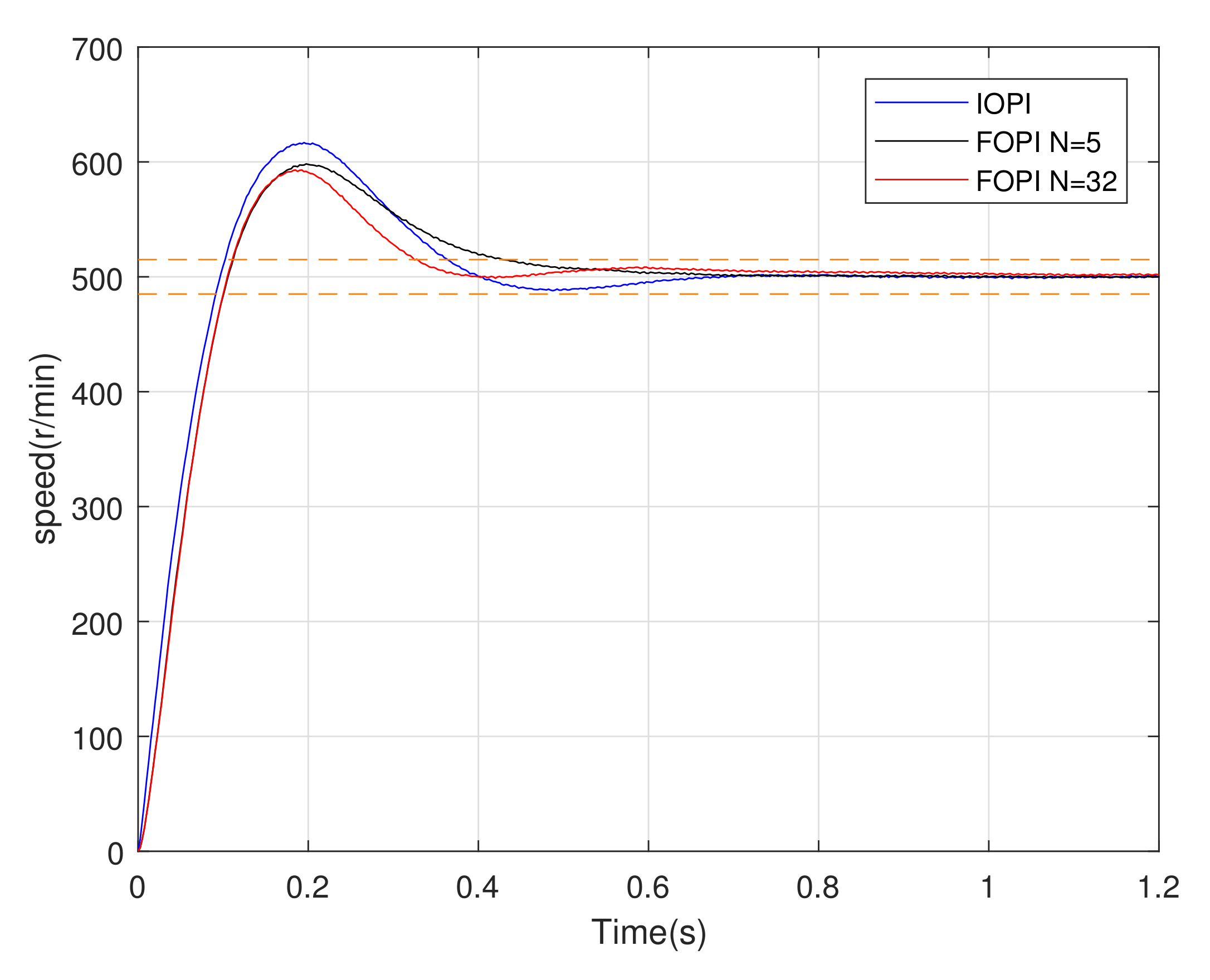
5.3. Experimental Verification
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Machado, J. Analysis and design of fractional-order digital control systems. Syst. Anal. Model. Simul. 1997, 27, 107–122. [Google Scholar]
- Vinagre, B.M.; Petras, I.; Merchan, P.; Dorcak, L. Two digital realization of fractional controllers: Application to temperature control of a solid. In Proceedings of the 2001 European Control Conference (ECC), Porto, Portugal, 4–7 September 2001; pp. 1764–1767. [Google Scholar]
- Luo, Y.; Wang, C.Y.; Chen, Y. Tuning fractional order proportional integral controllers for fractional order systems. J. Process. Control 2010, 20, 823–831. [Google Scholar] [CrossRef]
- Wang, X.; He, Y. Projective synchronization of fractional order chaotic system based on linear separation. Acta Phys. Sin. 2007, 372, 435–441. [Google Scholar] [CrossRef]
- Abdelaty, A.M.; Roshdy, M.; Said, L.A.; Radwan, A.G. Numerical Simulations and FPGA Implementations of Fractional-Order Systems Based on Product Integration Rules. IEEE Access 2020, 8, 102093–102105. [Google Scholar] [CrossRef]
- Engheta, N. Fractional calculus and fractional paradigm in electromagnetic theory. In Proceedings of the MMET Conference Proceedings, 1998 International Conference on Mathematical Methods in Electromagnetic Theory, MMET 98 (Cat. No.98EX114), Kharkov, Ukraine, 2–5 June 1998; pp. 879–880. [Google Scholar]
- Fogang, C.; Pelap, F.; Tanekou, G.B.; Kengne, R.; Fidèle, K. Earthquake dynamic induced by the magma up flow with fractional power law and fractional-order friction. Ann. Geophys. 2021, 64, SE101. [Google Scholar] [CrossRef]
- Li, H.S.; Luo, Y.; Chen, Y.Q. A fractional order proportional and derivative (FOPD) motion controller: Tuning rule and experiments. IEEE Trans. Control Syst. Technol. 2010, 18, 516–520. [Google Scholar] [CrossRef]
- Shi, L.; Gao, S.; Xi, H.; Yuan, H.; Zhou, T. FPGA realization of a speech encryption system based on a generalized modified chaotic transition map and bit permutation. Multimed. Tools Appl. 2019, 78, 16097–16127. [Google Scholar]
- Sabatini, V.; Benedetto, M.D.; Lidozzi, A. Synchronous Adaptive Resolver-to-Digital Converter for FPGA-Based High-Performance Control Loops. IEEE Trans. Instrum. Meas. 2019, 68, 3972–3982. [Google Scholar] [CrossRef]
- Romero-Troncoso, R.J.; Saucedo-Gallaga, R.; Cabal-Yepez, E.; Garcia-Perez, A.; Osornio-Rios, R.A.; Alvarez-Salas, R.; Mir a-Vidales, H.; Huber, N. FPGA-based online detection of multiple combined faults in induction motors through information entropy and fuzzy inference. IEEE Trans. Ind. Electron. 2011, 58, 5263–5270. [Google Scholar] [CrossRef]
- Gulbudak, O.; Santi, E. FPGA-Based Model Predictive Controller for Direct Matrix Converter. IEEE Trans. Ind. Electron. 2016, 63, 4560–4570. [Google Scholar] [CrossRef]
- Kung, Y.; Tseng, K.; Tai, T. FPGA-based Servo Control IC for X-Y Table. In Proceedings of the 2006 IEEE International Conference on Industrial Technology, Mumbai, India, 15–17 December 2006; pp. 2913–2918. [Google Scholar]
- Cho, J.U.; Le, Q.N.; Jeon, J.W. An FPGA-based multiple-axis motion control chip. IEEE Trans. Ind. Electron. 2009, 56, 856–870. [Google Scholar]
- Rovere, L.; Formentini, A.; Zanchetta, P. FPGA Implementation of a Novel Oversampling Deadbeat Controller for PMSM Drives. IEEE Trans. Ind. Electron. 2019, 66, 3731–3741. [Google Scholar] [CrossRef]
- Chen, Z.; Zhang, H.; Tu, W.; Tan, B.; Luo, G. FPGA Implementation of an Arbitrary Injection based Sensorless Control for PMSM. In Proceedings of the 2018 IEEE Energy Conversion Congress and Exposition (ECCE), Portland, OR, USA, 23–27 September 2018; pp. 1741–1747. [Google Scholar]
- Xu, Y.; Shuang, K.; Jiang, S.; Wu, X. FPGA implementation of a best-precision fixed-point digital PID controller. In Proceedings of the 2009 International Conference on Measuring Technology and Mechatronics Automation, Zhangjiajie, China, 11–12 April 2009; pp. 384–387. [Google Scholar]
- Jatoth, R.K.; Rajasekhar, A. Adaptive bacterial foraging optimization based tuning of optimal PI speed controller for PMSM drive. Int. Conf. Contemp. Comput. 2010, 94, 588–599. [Google Scholar]
- Chen, P.C.; Luo, Y.; Zheng, W.J.; Gao, Z.; Chen, Y.Q. Fractional order active disturbance rejection control with the idea of cascaded fractional order integrator equivalence. ISA Trans. 2020, 114, 1879–2022. [Google Scholar] [CrossRef]
- Zheng, W.J.; Luo, Y.; Wang, X.H.; Pi, Y.G.; Chen, Y.Q. Fractional order PID controller design for satisfying time and frequency domain specifications simultaneously. ISA Trans. 2017, 68, 212–222. [Google Scholar] [CrossRef]
- Zaihidee, F.M.; Mekhilef, S.; Mubin, M. Fractional order PID sliding mode control for speed regulation of permanent magnet synchronous motor. Nonlinear Dyn. 2021, 9, 209–218. [Google Scholar] [CrossRef]
- Chen, P.; Luo, Y.; Peng, Y.; Chen, Y. Optimal Fractional-Order Active Disturbance Rejection Controller Design for PMSM Speed Servo System. Entropy 2021, 23, 262. [Google Scholar] [CrossRef]
- Chopade, A.S.; Khubalkar, S.W.; Junghare, A.S.; Aware, M.V.; Das, S. Design and implementation of digital fractional order pid controller using optimal pole-zero approximation method for magnetic levitation system. IEEE/CAA J. Autom. Sin. 2018, 5, 977–989. [Google Scholar] [CrossRef]
- Tolba, M.F.; Said, L.A.; Madian, A.H.; Radwan, A.G. FPGA implementation of fractional-order integrator and differentiator based on Grünwald Letnikov’s definition. In Proceedings of the 2017 29th International Conference on Microelectronics (ICM), Beirut, Lebanon, 10–13 December 2017; Volume 78, pp. 1–4. [Google Scholar]
- Tolba, M.F.; AboAlNaga, B.M.; Said, L.A.; Madian, A.H.; Radwan, A.G. Fractional order integrator/differentiator: FPGA implementation and FOPID controller application. AEU-Int. J. Electron. Commun. 2019, 98, 220–229. [Google Scholar] [CrossRef]
- Tolba, M.F.; Saleh, H.; Mohammad, B. Enhanced FPGA realization of the fractional-order derivative and application to a variable-order chaotic system. Nonlinear Dyn. 2020, 99, 3143–3154. [Google Scholar] [CrossRef]
- Poinot, T.; Trigeassou, J.C. Identification of fractional systems using an output-error technique. Nonlinear Dyn. 2004, 38, 133–154. [Google Scholar] [CrossRef]
- Luo, Y.; Chen, Y.Q. Fractional Order Motion Controls; John Wiley Sons Ltd.: Hoboken, NJ, USA, 2013; pp. 1–24. [Google Scholar]
- Tolba, M.F.; AbdelAty, A.M.; Said, L.A.; Ahmed, S.; Elwakil, A.T.A.; Madian, A.H.; Ounnas, A.; Radwan, A.G. FPGA realization of Caputo and Grünwald-Letnikov operators. In Proceedings of the 2017 6th International Conference on Modern Circuits and Systems Technologies (MOCAST), Thessaloniki, Greece, 4–6 May 2017; pp. 1–4. [Google Scholar]
- Podlubny, I. Fractional Differential Equations: An Introduction to Fractional Derivatives, Fractional Differential Equations, to Methods of Their Solution and Some of Their Applications; Elsevier: Amsterdam, The Netherlands, 1999; pp. 41–119. [Google Scholar]
- Tolba, M.F.; Said, L.A.; Madian, A.H.; Radwan, A.G. FPGA Implementation of the Fractional Order Integrator/Differentiator: Two Approaches and Applications. IEEE Trans. Circuits Syst. I Regul. Pap. 2019, 66, 1484–1495. [Google Scholar] [CrossRef]
- Ferdi, Y. Computation of fractional order derivative and integral via power series expansion and signal modelling. Nonlinear Dyn. 2006, 46, 1–15. [Google Scholar] [CrossRef]
- Chen, Y.; Vinagre, B.M.; Podlubny, I. Continued fraction expansion approaches to discretizing fractional order derivatives—An expository review. Nonlinear Dyn. 2004, 38, 155–170. [Google Scholar] [CrossRef]
- Oustaloup, A.; Levron, F.; Mathieu, B.; Nanot, F.M. Frequency-band complex noninteger differentiator: Characterization and synthesis. IEEE Trans. Circuits Syst. I Fundam Theory Appl. 2000, 47, 25–39. [Google Scholar] [CrossRef]
- Carlson, G.; Halijak, C. Approximation of fractional capacitors by a regular Newton process. IEEE Trans. Circuit Theory 1964, CT-11, 210–213. [Google Scholar] [CrossRef]
- Impulse Response Invariant Discretization of Fractional Order Integrators/Dierentiators. Available online: http://www.mathworks.com/matlabcentral/fileexchange/21342-impulse-response-invariant-discretization-of-fractional-order-integrators-dierentiators (accessed on 1 September 2020).


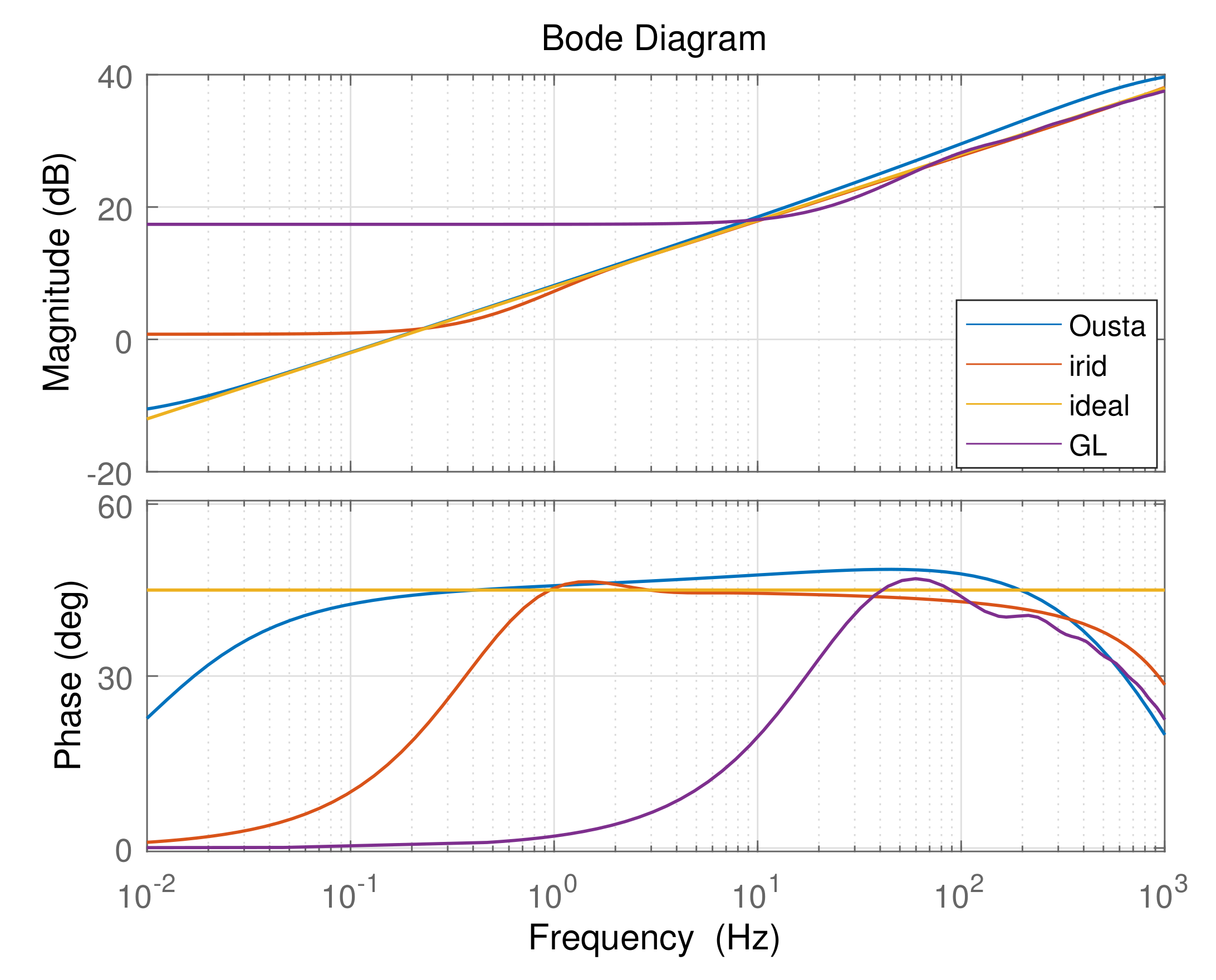
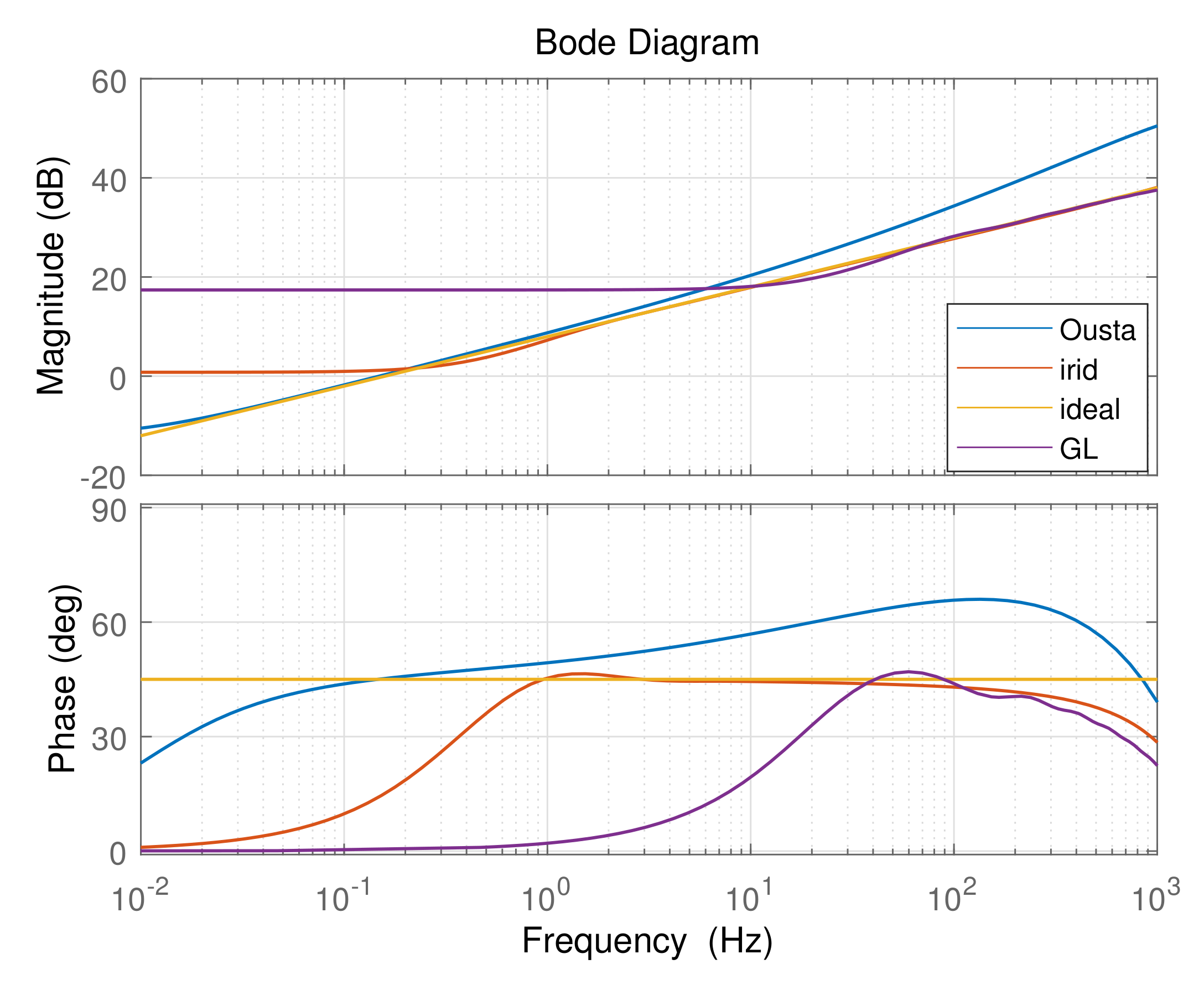
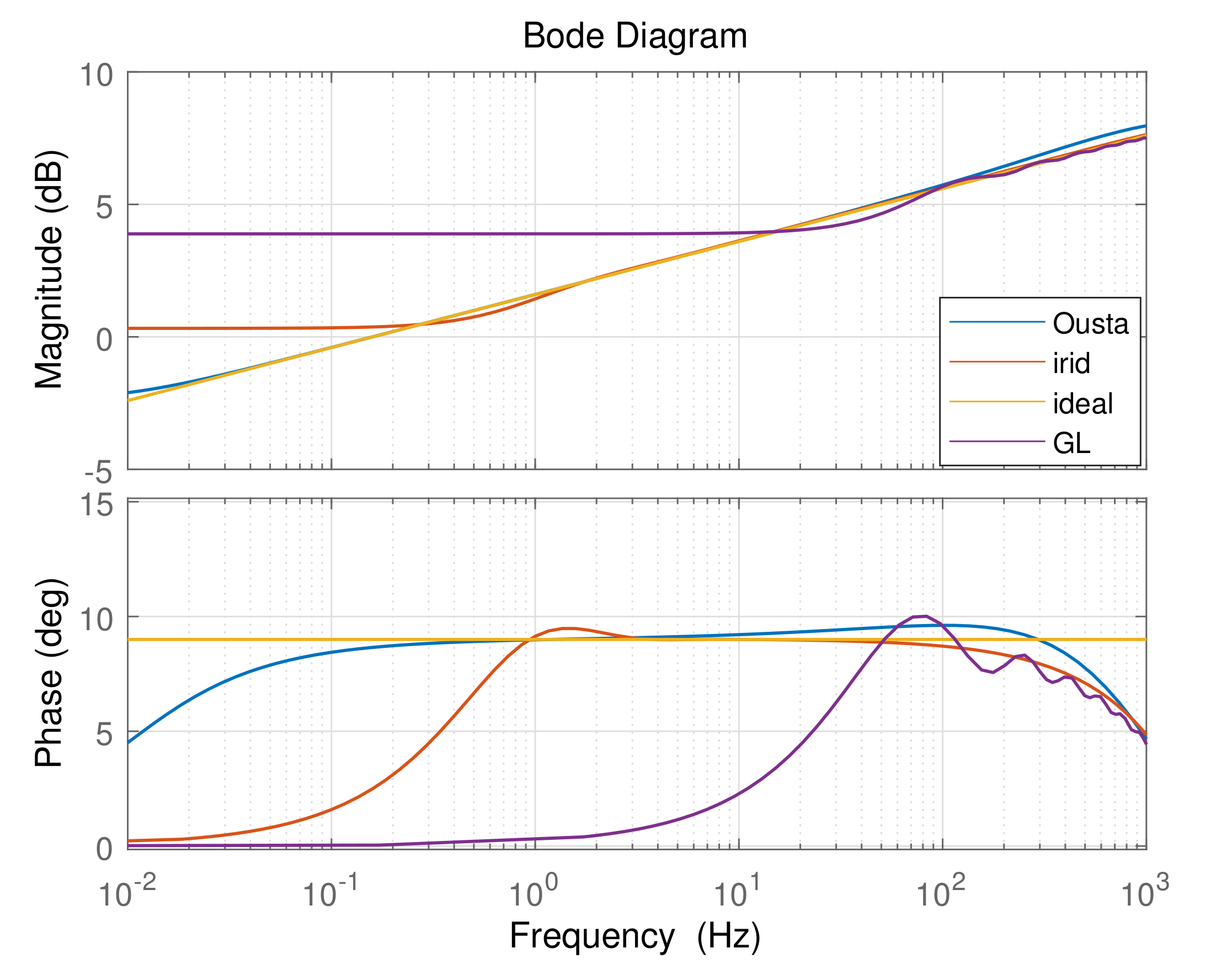
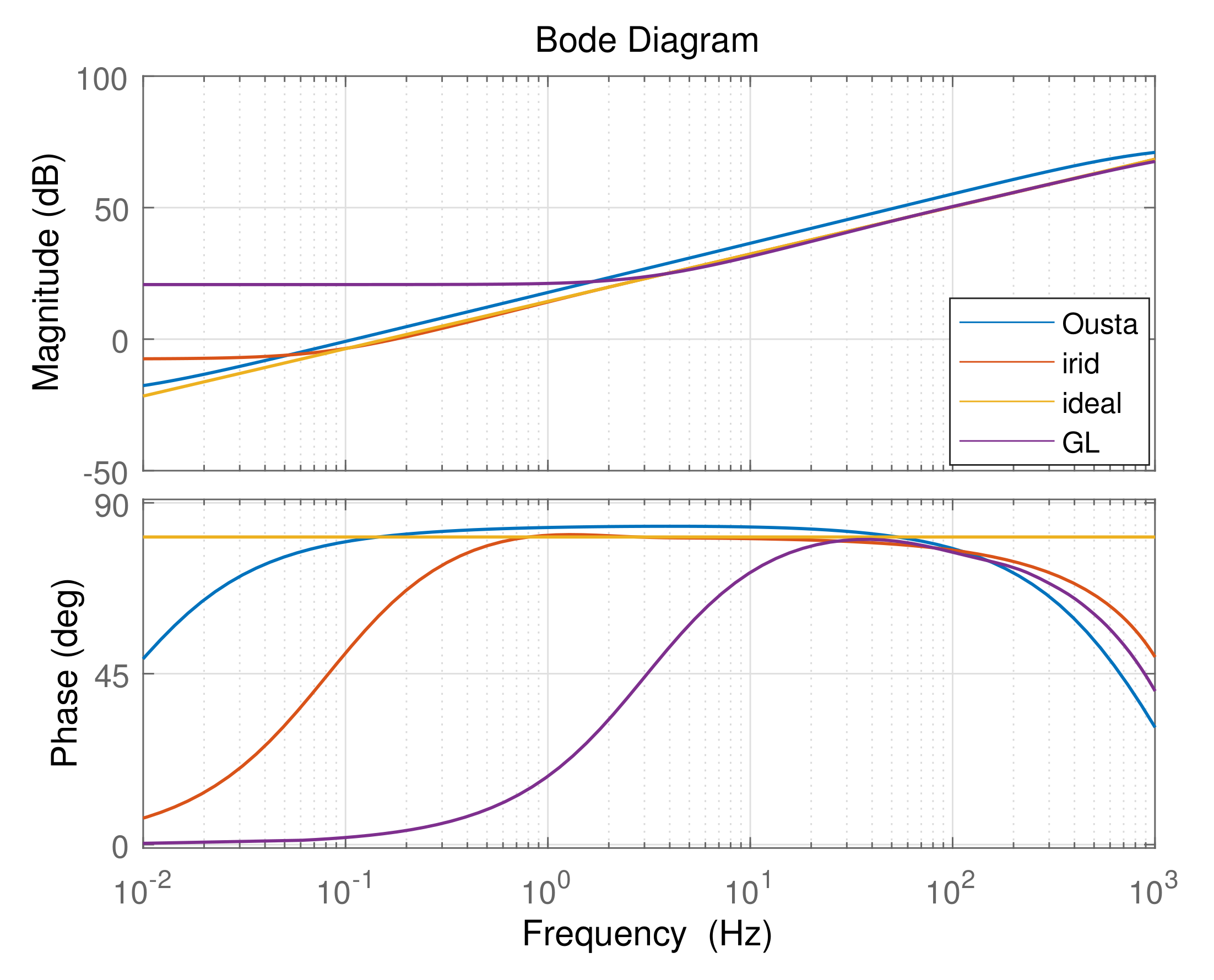
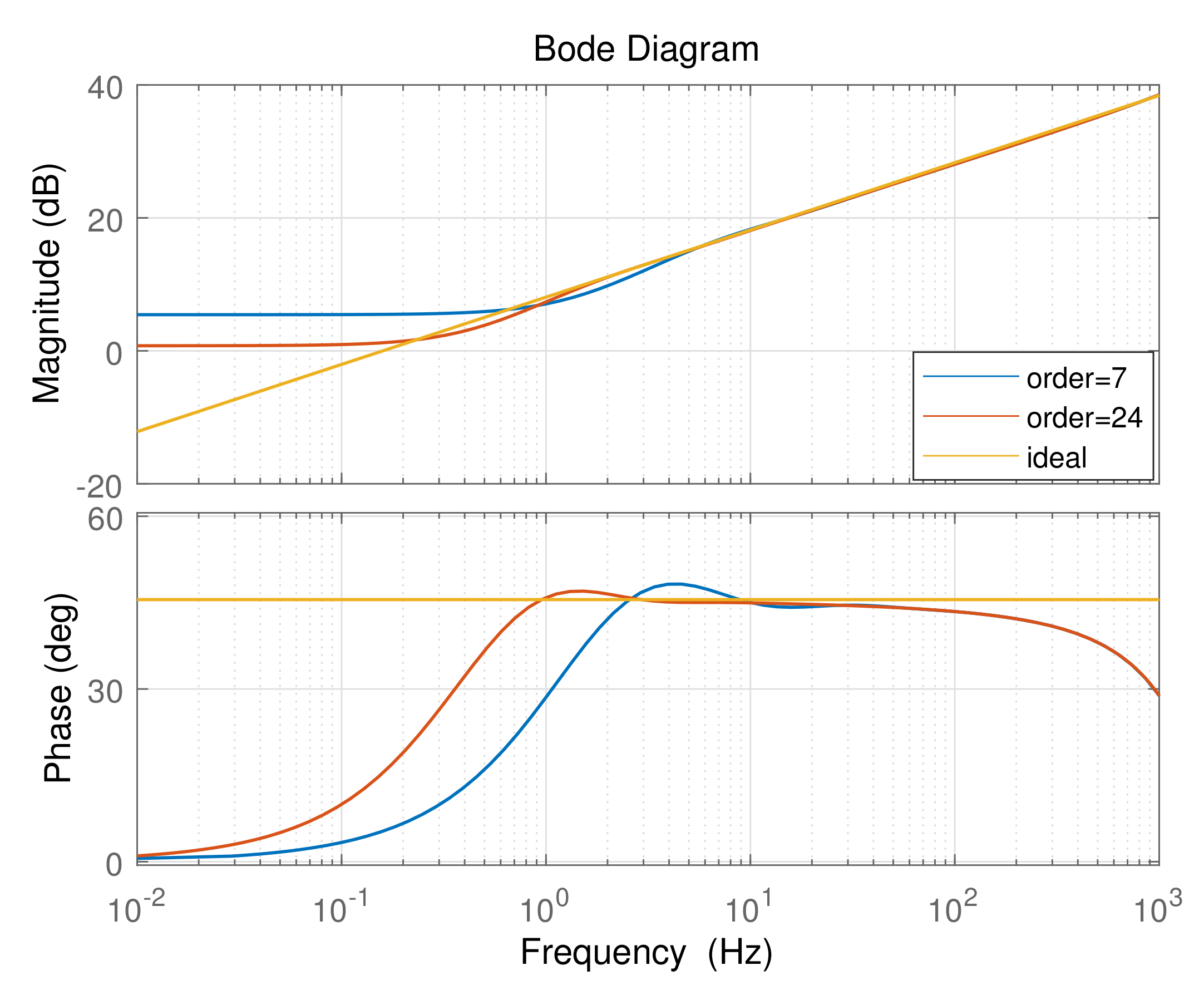
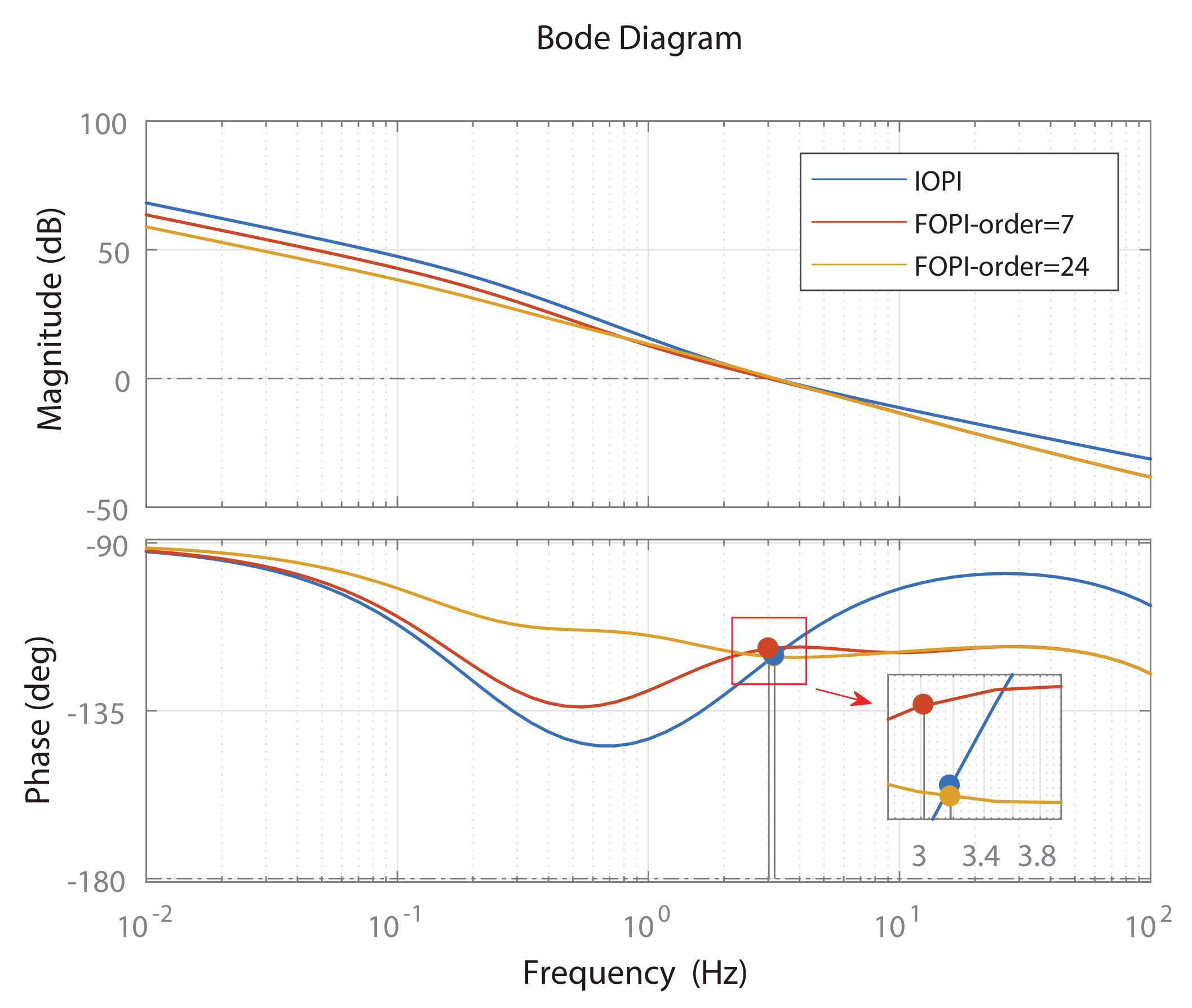




| Operator | Considered Frequency | The Discretization | |
|---|---|---|---|
| Band (Hz) | Order N | ||
| Case 1 | [0.01,1000] | 7 | |
| Case 2 | [0.01,1000] | 24 | |
| Case 3 | [0.01,10,000] | 24 | |
| Case 4 | [0.01,1000] | 24 | |
| Case 5 | [0.01,1000] | 24 |
| Motor Parameters | Value | Unit |
|---|---|---|
| Rated power | 2.0 | kW |
| Rated speed | 2000 | r/min |
| Rated voltage | 220 | V |
| Rated current | 9.1 | A |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, B.; Wang, S.; Peng, Y.; Pi, Y.; Luo, Y. Design and High-Order Precision Numerical Implementation of Fractional-Order PI Controller for PMSM Speed System Based on FPGA. Fractal Fract. 2022, 6, 218. https://doi.org/10.3390/fractalfract6040218
Wang B, Wang S, Peng Y, Pi Y, Luo Y. Design and High-Order Precision Numerical Implementation of Fractional-Order PI Controller for PMSM Speed System Based on FPGA. Fractal and Fractional. 2022; 6(4):218. https://doi.org/10.3390/fractalfract6040218
Chicago/Turabian StyleWang, Baokun, Shaohua Wang, Yibing Peng, Youguo Pi, and Ying Luo. 2022. "Design and High-Order Precision Numerical Implementation of Fractional-Order PI Controller for PMSM Speed System Based on FPGA" Fractal and Fractional 6, no. 4: 218. https://doi.org/10.3390/fractalfract6040218
APA StyleWang, B., Wang, S., Peng, Y., Pi, Y., & Luo, Y. (2022). Design and High-Order Precision Numerical Implementation of Fractional-Order PI Controller for PMSM Speed System Based on FPGA. Fractal and Fractional, 6(4), 218. https://doi.org/10.3390/fractalfract6040218







