Numerical Investigations of the Fractional-Order Mathematical Model Underlying Immune-Chemotherapeutic Treatment for Breast Cancer Using the Neural Networks
Abstract
:1. Introduction
2. Mathematical Model
3. Innovative Topographies Including an Overview of Stochastic Solvers
- Relying upon that NTIE impacts, a novel design of the fractional-order derivatives of the breast cancer mathematical model is presented.
- Stochastic solvers based measurements/assessments have never been used to solve the fractional order derivatives of a breast cancer mathematical model relying on NTIE impacts
- The numerical studies employing stochastic paradigms are shown effectiveness of using the fractional-order derivatives terms in the breast cancer mathematical model considering on the NTIE effects.
- Artificial intelligence (AI) knacks based LMBNNs is introduced to solve the nonlinear fractional order derivatives of the breast cancer mathematical model relying upon that NTIE impacts.
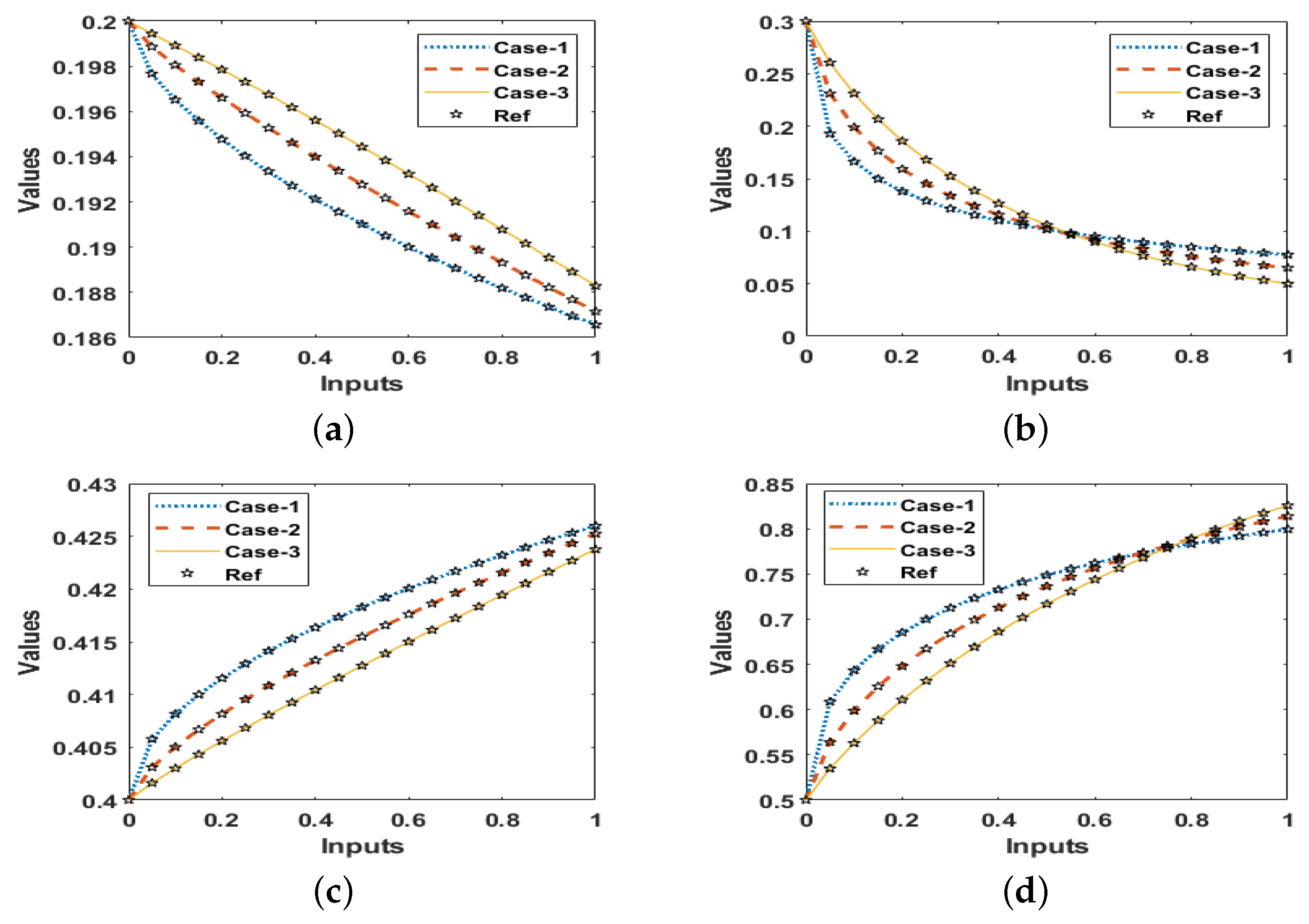
- Three appropriate fractional-order variants depending upon that breast cancer mathematical model have been numerically solved to validate the reliability of proposed LMBNNs.
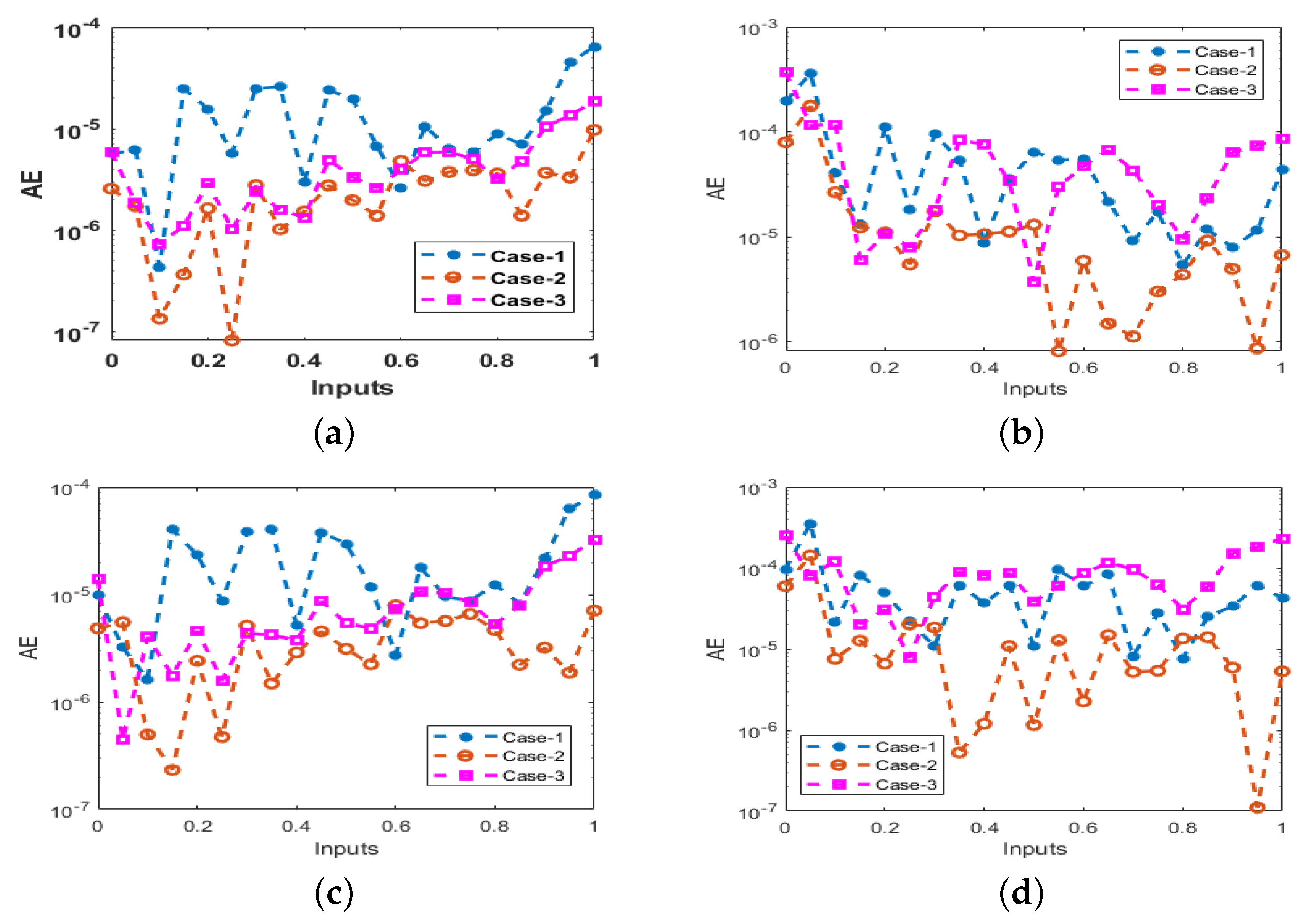
- The correctness/brilliance of stochastic computing solver-based of LMBNNs is demonstrated by comparing the outcomes of produced and reference solutions Adams–Bashforth–Moulton method in good agreement.
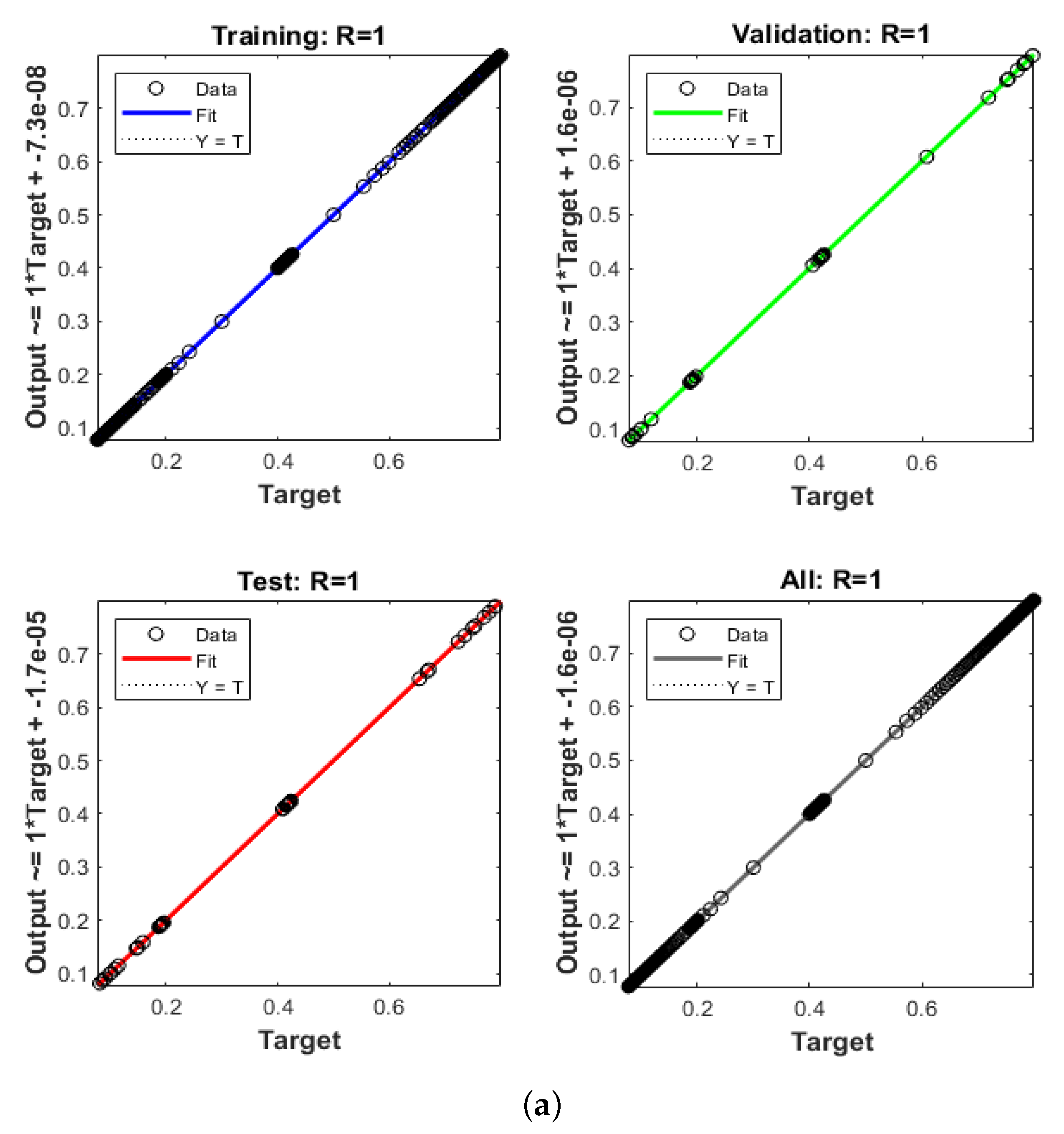
- The regression, STs, MSE, EHs, and correlation performances validate the developed LMBNNs’ dependability and consistency in solving the fractional order breast cancer mathematical model.
4. Suggested Methodology: LMBNNs
5. Results Obtained Employing the Planned Method
- Case 1:
- Case 2:
- Case 3:
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Oke, S.I.; Matadi, M.B.; Xulu, S.S. Optimal control analysis of a mathematical model for breast cancer. Math. Comput. Appl. 2018, 23, 21. [Google Scholar]
- Olufemi, A.S. Mathematical modelling of breast cancer thermo-therapy treatment: Ultrasound-based approach. Math. Model. 2016, 2, 1158–1164. [Google Scholar]
- Patel, M.; Nagl, S. The Role of Model Integration in Complex Systems Modelling: An Example from Cancer Biology; Springer: Berlin/Heidelberg, Germany, 2010. [Google Scholar]
- Sethi, M.; Chakravarti, S.K. Hyperthermia techniques for cancer treatment: A review. Int. J. PharmTech Res. 2015, 8, 292–299. [Google Scholar]
- Wei, H.C. Mathematical modeling of ER-positive breast cancer treatment with AZD9496 and palbociclib. AIMS Math. 2020, 5, 3446–3455. [Google Scholar] [CrossRef]
- Valentim, C.A., Jr.; Oliveira, N.A.; Rabi, J.A.; David, S.A. Can fractional calculus help improve tumor growth models? J. Comput. Appl. Math. 2020, 379, 112964. [Google Scholar] [CrossRef]
- Sweilam, N.H.; Al-Mekhlafi, S.M.; Assiri, T.; Atangana, A. Optimal control for cancer treatment mathematical model using Atangana-Baleanu-Caputo fractional derivative. Adv. Differ. Equ. 2020, 2020, 334. [Google Scholar] [CrossRef]
- Huang, C.; Cao, J.; Xiao, M.; Alsaedi, A.; Hayat, T. Bifurcations in a delayed fractional complex-valued neural network. Appl. Math. Comput. 2017, 292, 210–227. [Google Scholar] [CrossRef]
- Huang, C.; Cao, J.; Xiao, M.; Alsaedi, A.; Alsaadi, F.E. Controlling bifurcation in a delayed fractional predator-prey system with incommensurate orders. Appl. Math. Comput. 2017, 293, 293–310. [Google Scholar] [CrossRef]
- Huang, C.; Cao, J.; Xiao, M.; Alsaedi, A.; Hayat, T. Effects of time delays on stability and Hopf bifurcation in a fractional ring-structured network with arbitrary neurons. Commun. Nonlinear Sci. Numer. Simul. 2018, 57, 1–13. [Google Scholar] [CrossRef]
- Patnaik, S.; Jokar, M.; Semperlotti, F. Variable-order approach to nonlocal elasticity: Theoretical formulation, order identification via deep learning, and applications. Comput. Mech. 2021, 69, 267–298. [Google Scholar] [CrossRef]
- Patnaik, S.; Semperlotti, F. A generalized fractional-order elastodynamic theory for non-local attenuating media. Proc. R. Soc. A 2020, 476, 20200200. [Google Scholar] [CrossRef] [PubMed]
- Patnaik, S.; Sidhardh, S.; Semperlotti, F. A Ritz-based finite element method for a fractional-order boundary value problem of nonlocal elasticity. Int. J. Solids Struct. 2020, 202, 398–417. [Google Scholar] [CrossRef]
- Patnaik, S.; Sidhardh, S.; Semperlotti, F. Towards a unified approach to nonlocal elasticity via fractional-order mechanics. Int. J. Mech. Sci. 2021, 189, 105992. [Google Scholar] [CrossRef]
- Fellah, Z.E.A.; Chapelon, J.Y.; Berger, S.; Lauriks, W.; Depollier, C. Ultrasonic wave propagation in human cancellous bone: Application of Biot theory. J. Acoust. Soc. Am. 2004, 116, 61–73. [Google Scholar] [CrossRef]
- Patnaik, S.; Semperlotti, F. Application of variable-and distributed-order fractional operators to the dynamic analysis of nonlinear oscillators. Nonlinear Dyn. 2020, 100, 561–580. [Google Scholar] [CrossRef]
- Patnaik, S.; Semperlotti, F. Modeling contacts and hysteretic behavior in discrete systems via variable-order fractional operators. J. Comput. Nonlinear Dyn. 2020, 15, 091008. [Google Scholar] [CrossRef]
- Patnaik, S.; Semperlotti, F. Variable-order particle dynamics: Formulation and application to the simulation of edge dislocations. Philos. Trans. R. Soc. A 2020, 378, 20190290. [Google Scholar] [CrossRef]
- Solis-Perez, J.E.; Gomez-Aguilar, J.F. Variable-order fractal-fractional time delay equations with power, exponential and Mittag-Leffler laws and their numerical solutions. Eng. Comput. 2020, 38, 555–577. [Google Scholar] [CrossRef]
- Atangana, A.; Gómez-Aguilar, J.F. Numerical approximation of Riemann-Liouville definition of fractional derivative: From Riemann-Liouville to Atangana-Baleanu. Numer. Methods Partial Differ. Equ. 2018, 34, 1502–1523. [Google Scholar] [CrossRef]
- Yousef, A.; Yousef, F.B. Bifurcation and stability analysis of a system of fractional-order differential equations for a plant–herbivore model with Allee effect. Mathematics 2019, 7, 454. [Google Scholar] [CrossRef] [Green Version]
- Al-Khaled, K.; Alquran, M. An approximate solution for a fractional model of generalized Harry Dym equation. Math. Sci. 2014, 8, 125–130. [Google Scholar] [CrossRef] [Green Version]
- Magin, R.L. Fractional calculus models of complex dynamics in biological tissues. Comput. Math. Appl. 2010, 59, 1586–1593. [Google Scholar] [CrossRef] [Green Version]
- Nikan, O.; Avazzadeh, Z.; Machado, J.T. Numerical study of the nonlinear anomalous reaction–subdiffusion process arising in the electroanalytical chemistry. J. Comput. Sci. 2021, 53, 101394. [Google Scholar] [CrossRef]
- Özköse, F.; Yılmaz, S.; Yavuz, M.; Öztürk, İ.; Şenel, M.T.; Bağcı, B.Ş.; Doğan, M.; Önal, Ö. A Fractional Modeling of Tumor–Immune System Interaction Related to Lung Cancer with Real Data. Eur. Phys. J. Plus 2022, 137, 1–28. [Google Scholar] [CrossRef]
- d’Onofrio, A.; Ledzewicz, U.; Maurer, H.; Schättler, H. On optimal delivery of combination therapy for tumors. Math. Biosci. 2009, 222, 13–26. [Google Scholar] [CrossRef] [PubMed]
- Kermark, M.; Mckendrick, A. Contributions to the mathematical theory of epidemics. Part I Proc. R. Soc. A 1927, 115, 700–721. [Google Scholar]
- Kermack, W.O.; McKendrick, A.G. Contributions to the mathematical theory of epidemics: V. Analysis of experimental epidemics of mouse-typhoid; a bacterial disease conferring incomplete immunity. Epidemiol. Infect. 1939, 39, 271–288. [Google Scholar] [CrossRef] [Green Version]
- Sweilam, N.H.; Al-Mekhlafi, S.M.; Albalawi, A.O.; Machado, J.T. Optimal control of variable-order fractional model for delay cancer treatments. Appl. Math. Model. 2021, 89, 1557–1574. [Google Scholar] [CrossRef]
- Sowndarrajan, P.T.; Manimaran, J.; Debbouche, A.; Shangerganesh, L. Distributed optimal control of a tumor growth treatment model with cross-diffusion effect. Eur. Phys. J. Plus 2019, 134, 463. [Google Scholar] [CrossRef]
- Özdemir, N.; Uçar, E. Investigating of an immune system-cancer mathematical model with Mittag-Leffler kernel. AIMS Math. 2020, 5, 1519–1531. [Google Scholar] [CrossRef]
- de Pillis, L.G.; Radunskaya, A.E.; Wiseman, C.L. A validated mathematical model of cell-mediated immune response to tumor growth. Cancer Res. 2005, 65, 7950–7958. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Mufudza, C.; Sorofa, W.; Chiyaka, E.T. Assessing the effects of estrogen on the dynamics of breast cancer. Comput. Math. Methods Med. 2012, 2012, 473572. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Abernathy, K.; Abernathy, Z.; Baxter, A.; Stevens, M. Global dynamics of a breast cancer competition model. Differ. Equ. Dyn. Syst. 2017, 28, 791–805. [Google Scholar] [CrossRef] [PubMed]
- Jarrett, A.M.; Shah, A.; Bloom, M.J.; McKenna, M.T.; Hormuth, D.A.; Yankeelov, T.E.; Sorace, A.G. Experimentally-driven mathematical modeling to improve combination targeted and cytotoxic therapy for HER2+ breast cancer. Sci. Rep. 2019, 9, 12830. [Google Scholar] [CrossRef] [Green Version]
- Li, L.; Liu, J.G. A generalized definition of Caputo derivatives and its application to fractional ODEs. SIAM J. Math. Anal. 2018, 50, 2867–2900. [Google Scholar] [CrossRef] [Green Version]
- Sabir, Z.; Wahab, H.A.; Javeed, S.; Baskonus, H.M. An Efficient Stochastic Numerical Computing Framework for the Nonlinear Higher Order Singular Models. Fractal Fract. 2021, 5, 176. [Google Scholar] [CrossRef]
- Sabir, Z.; Nisar, K.; Raja, M.A.Z.; Ibrahim, A.A.B.A.; Rodrigues, J.J.; Al-Basyouni, K.S.; Mahmoud, S.R.; Rawat, D.B. Design of Morlet wavelet neural network for solving the higher order singular nonlinear differential equations. Alex. Eng. J. 2021, 60, 5935–5947. [Google Scholar] [CrossRef]
- Sabir, Z.; Raja, M.A.Z.; Guirao, J.L.; Saeed, T. Meyer wavelet neural networks to solve a novel design of fractional order pantograph Lane-Emden differential model. Chaos Solitons Fractals 2021, 152, 111404. [Google Scholar] [CrossRef]
- Sabir, Z.; Raja, M.A.Z.; Guirao, J.L.; Shoaib, M. A novel design of fractional Meyer wavelet neural networks with application to the nonlinear singular fractional Lane-Emden systems. Alex. Eng. J. 2021, 60, 2641–2659. [Google Scholar] [CrossRef]
- Guirao, J.L.; Sabir, Z.; Saeed, T. Design and numerical solutions of a novel third-order nonlinear Emden–Fowler delay differential model. Math. Probl. Eng. 2020, 2020, 7359242. [Google Scholar] [CrossRef]
- Sabir, Z.; Guirao, J.L.; Saeed, T. Solving a novel designed second order nonlinear Lane–Emden delay differential model using the heuristic techniques. Appl. Soft Comput. 2021, 102, 107105. [Google Scholar] [CrossRef]
- Sabir, Z.; Raja, M.A.Z.; Guirao, J.L.; Shoaib, M. A neuro-swarming intelligence-based computing for second order singular periodic non-linear boundary value problems. Front. Phys. 2020, 8, 224. [Google Scholar] [CrossRef]
- Ghanbari, B.; Djilali, S. Mathematical analysis of a fractional-order predator-prey model with prey social behavior and infection developed in predator population. Chaos Solitons Fractals 2020, 138, 109960. [Google Scholar] [CrossRef]
- Ghanbari, B.; Djilali, S. Mathematical and numerical analysis of a three-species predator-prey model with herd behavior and time fractional-order derivative. Math. Methods Appl. Sci. 2020, 43, 1736–1752. [Google Scholar] [CrossRef]
- Vajravelu, K.; Sreenadh, S.; Saravana, R. Influence of velocity slip and temperature jump conditions on the peristaltic flow of a Jeffrey fluid in contact with a Newtonian fluid. Appl. Math. Nonlinear Sci. 2017, 2, 429–442. [Google Scholar] [CrossRef]
- Selvi, M.S.M.; Rajendran, L. Application of modified wavelet and homotopy perturbation methods to nonlinear oscillation problems. Appl. Math. Nonlinear Sci. 2019, 4, 351–364. [Google Scholar] [CrossRef] [Green Version]
- İlhan, E.; Kıymaz, İ.O. A generalization of truncated M-fractional derivative and applications to fractional differential equations. Appl. Math. Nonlinear Sci. 2020, 5, 171–188. [Google Scholar] [CrossRef] [Green Version]
- Durur, H.; Tasbozan, O.; Kurt, A. New analytical solutions of conformable time fractional bad and good modified Boussinesq equations. Appl. Math. Nonlinear Sci. 2020, 5, 447–454. [Google Scholar] [CrossRef]
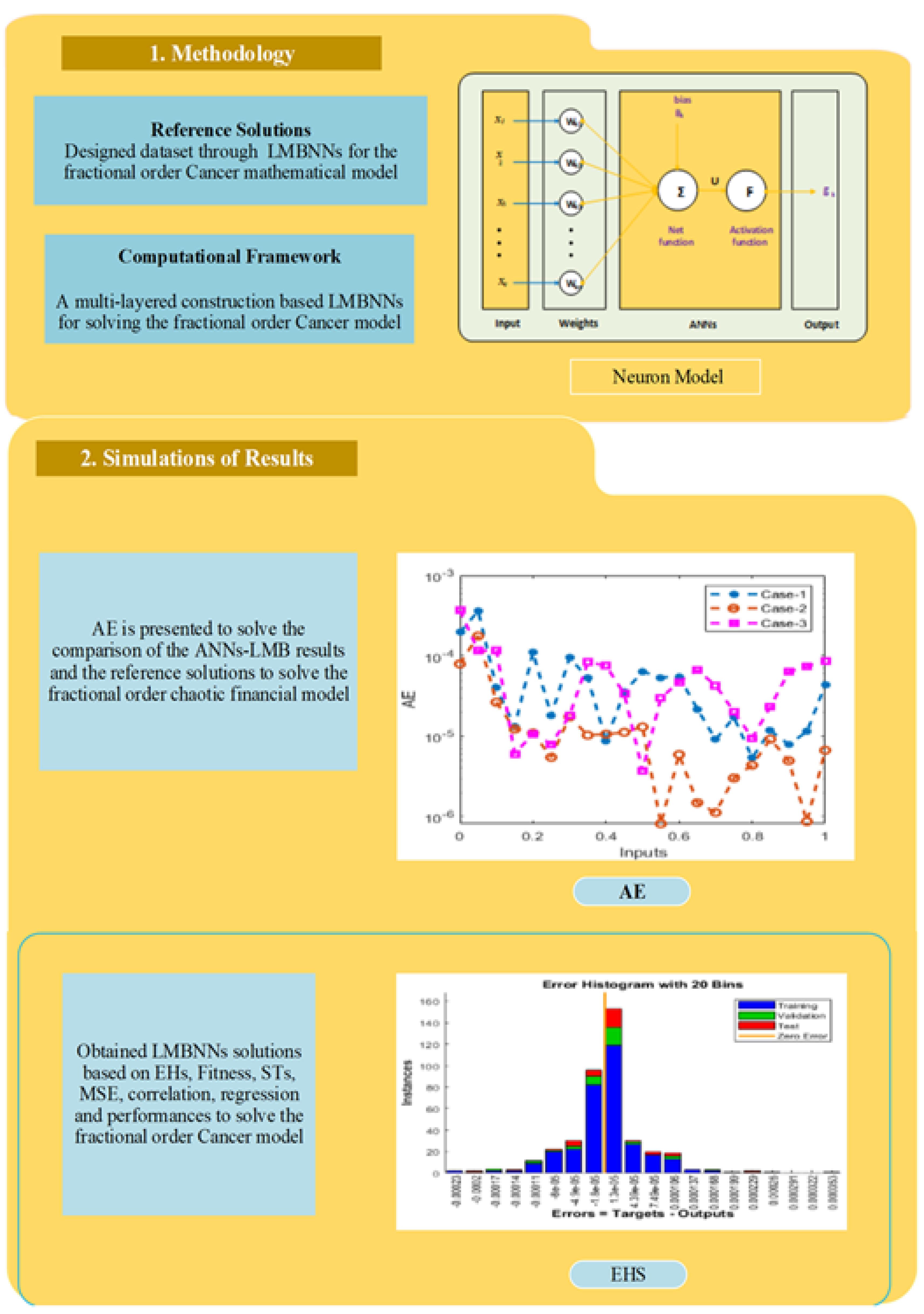
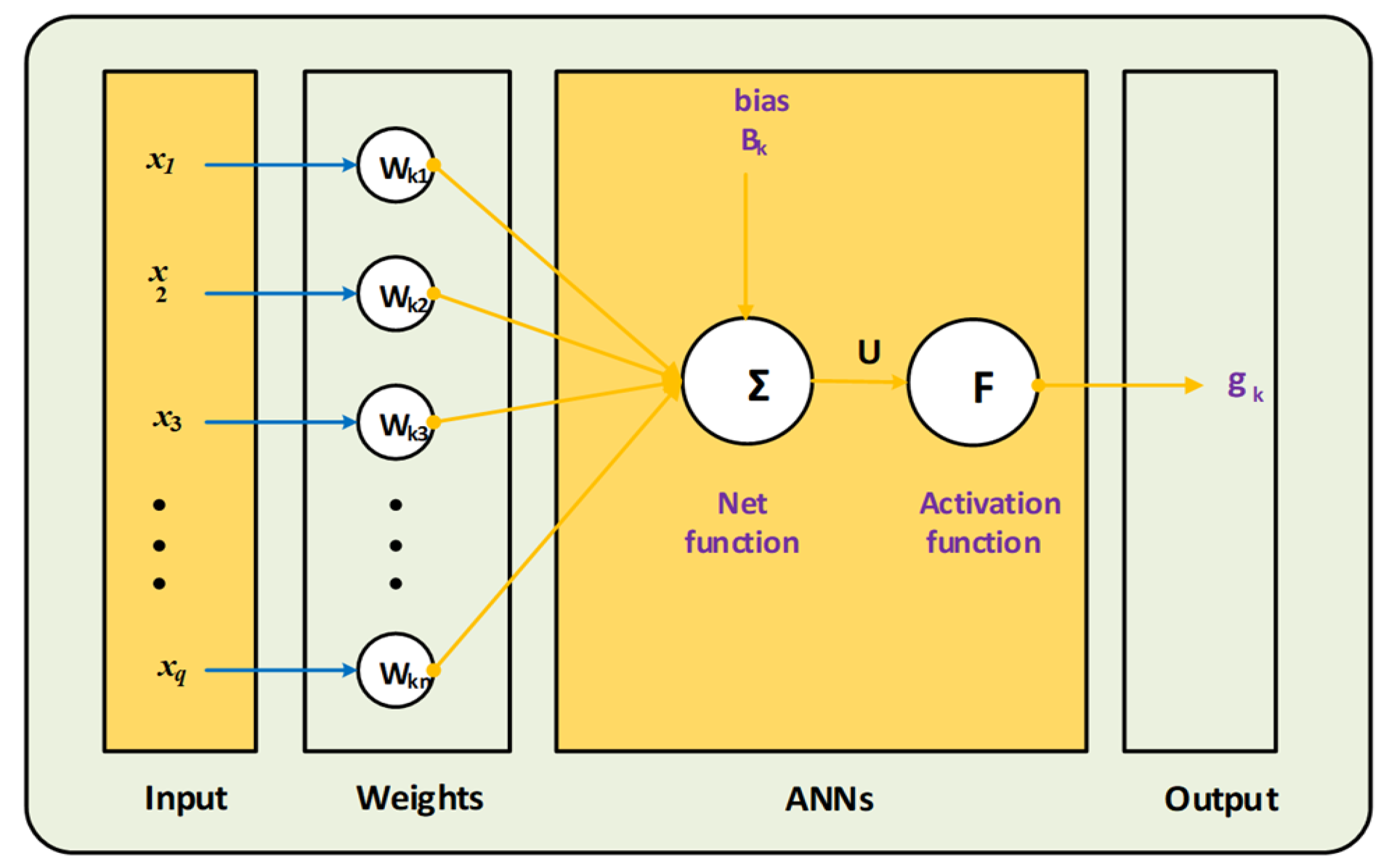
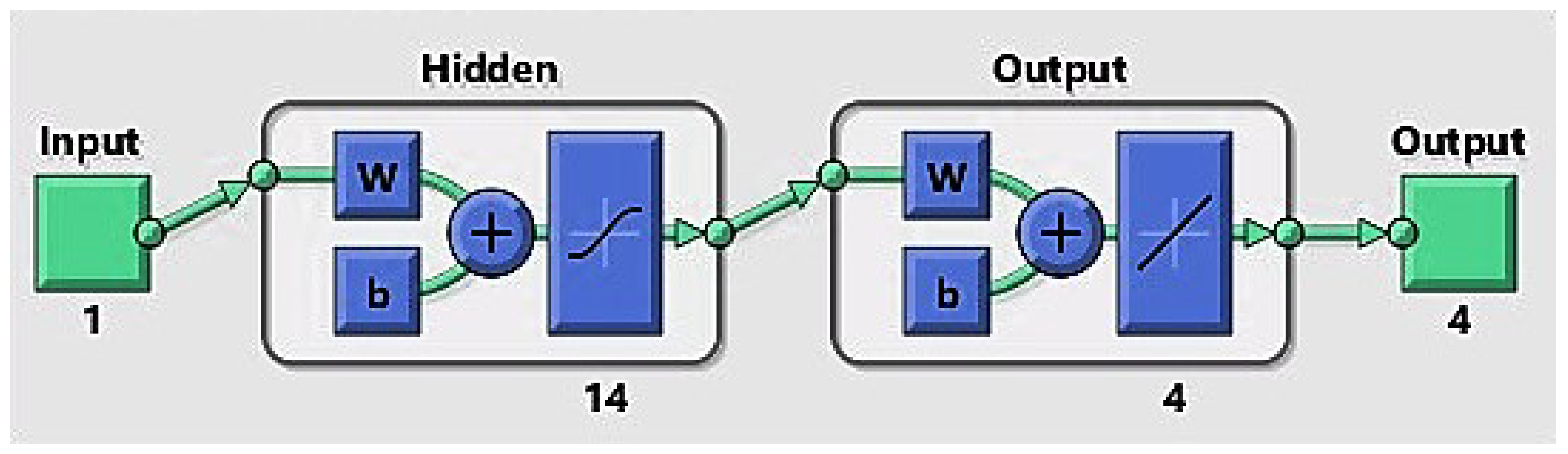

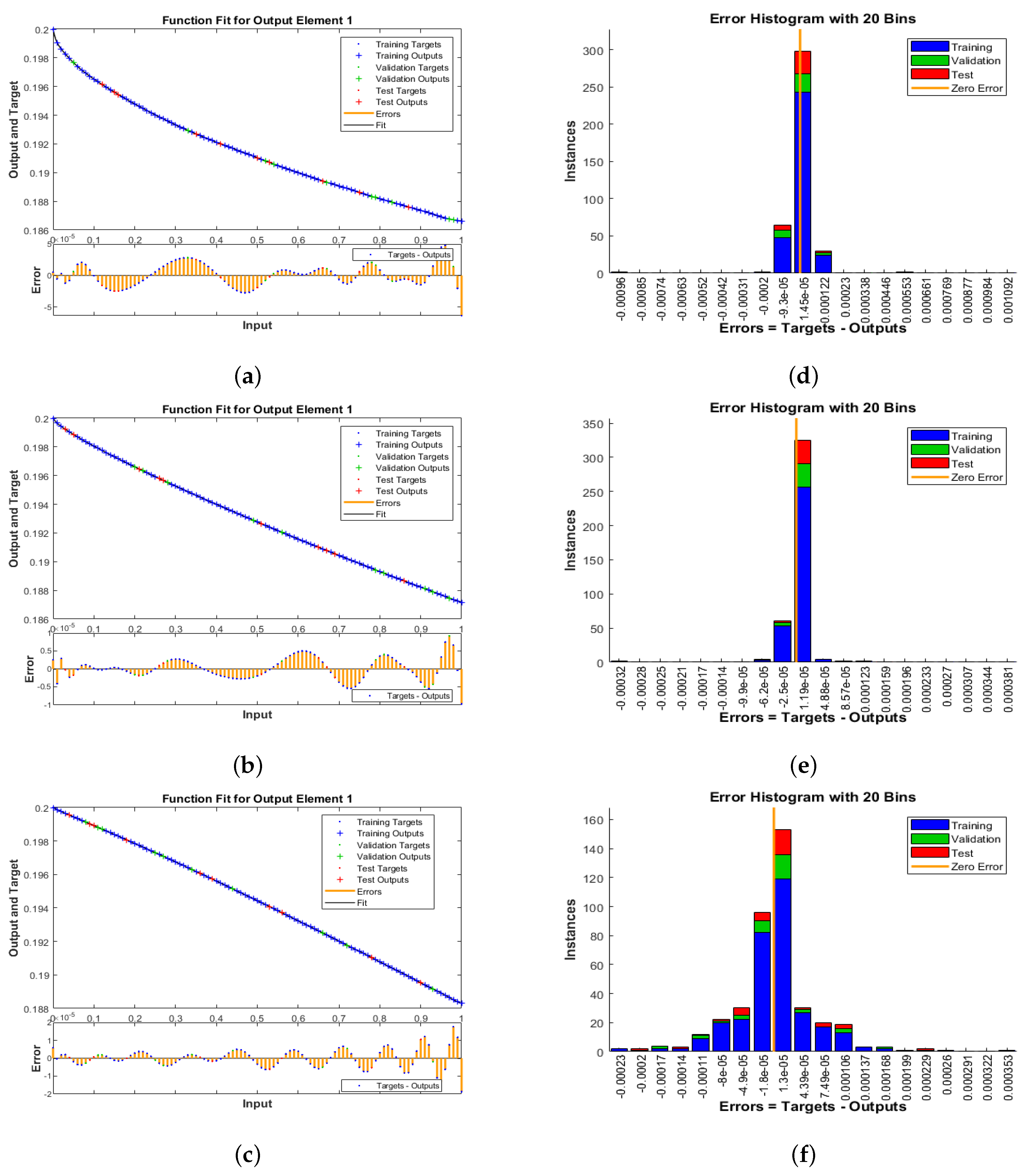

| Parameter | Symbol | Value |
|---|---|---|
| NC’s logistic rate | [0.05–0.2] | |
| TC’s logistic rate | [0.5–0.95] | |
| IC’s logistic rate | [0.05–0.2] | |
| NC’s rate of growth | 0.3 | |
| The rate of TC growth | 0.4 | |
| The ketogenic diet’s constant rate | d | 0.5 |
| The rate of NC inhibition | ||
| TC mortality rate as a result of immune reaction | ||
| Rate of interaction coefficient with immune reaction | 1 × 10 | |
| Estrogen’s natural death rate | 0.97 | |
| Estrogen source rate | [0.6–3] | |
| Immune boosting supplement | 0.01 | |
| The ketogenic diet’s effect on TC mortality | 2 | |
| The rate of tumor formation as | ||
| a response of estrogen-induced DNA damage | 0.2 | |
| Excess oestrogen causes immune suppression | 0.002 | |
| The anti-cancer drug’s efficacy | 0–1 | |
| IC source rate | ||
| NC’s carrying capacity | 1.232 | |
| TC’s carrying capacity | 1.75 | |
| IC’s carrying capacity | [0.11, 1.17] |
| MSE | ||||||||
|---|---|---|---|---|---|---|---|---|
| Case | Training | Verification | Testing | Performance | Gradient | Mu | Epoch | Time |
| 1 | 96 | 2 | ||||||
| 2 | 115 | 2 | ||||||
| 3 | 24 | 1 | ||||||
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Sabir, Z.; Munawar, M.; Abdelkawy, M.A.; Raja, M.A.Z.; Ünlü, C.; Jeelani, M.B.; Alnahdi, A.S. Numerical Investigations of the Fractional-Order Mathematical Model Underlying Immune-Chemotherapeutic Treatment for Breast Cancer Using the Neural Networks. Fractal Fract. 2022, 6, 184. https://doi.org/10.3390/fractalfract6040184
Sabir Z, Munawar M, Abdelkawy MA, Raja MAZ, Ünlü C, Jeelani MB, Alnahdi AS. Numerical Investigations of the Fractional-Order Mathematical Model Underlying Immune-Chemotherapeutic Treatment for Breast Cancer Using the Neural Networks. Fractal and Fractional. 2022; 6(4):184. https://doi.org/10.3390/fractalfract6040184
Chicago/Turabian StyleSabir, Zulqurnain, Maham Munawar, Mohamed A. Abdelkawy, Muhammad Asif Zahoor Raja, Canan Ünlü, Mdi Begum Jeelani, and Abeer S. Alnahdi. 2022. "Numerical Investigations of the Fractional-Order Mathematical Model Underlying Immune-Chemotherapeutic Treatment for Breast Cancer Using the Neural Networks" Fractal and Fractional 6, no. 4: 184. https://doi.org/10.3390/fractalfract6040184
APA StyleSabir, Z., Munawar, M., Abdelkawy, M. A., Raja, M. A. Z., Ünlü, C., Jeelani, M. B., & Alnahdi, A. S. (2022). Numerical Investigations of the Fractional-Order Mathematical Model Underlying Immune-Chemotherapeutic Treatment for Breast Cancer Using the Neural Networks. Fractal and Fractional, 6(4), 184. https://doi.org/10.3390/fractalfract6040184






