The Mixed Boundary Value Problems and Chebyshev Collocation Method for Caputo-Type Fractional Ordinary Differential Equations
Abstract
:1. Introduction
2. The Shifted Chebyshev Polynomials of the First Kind
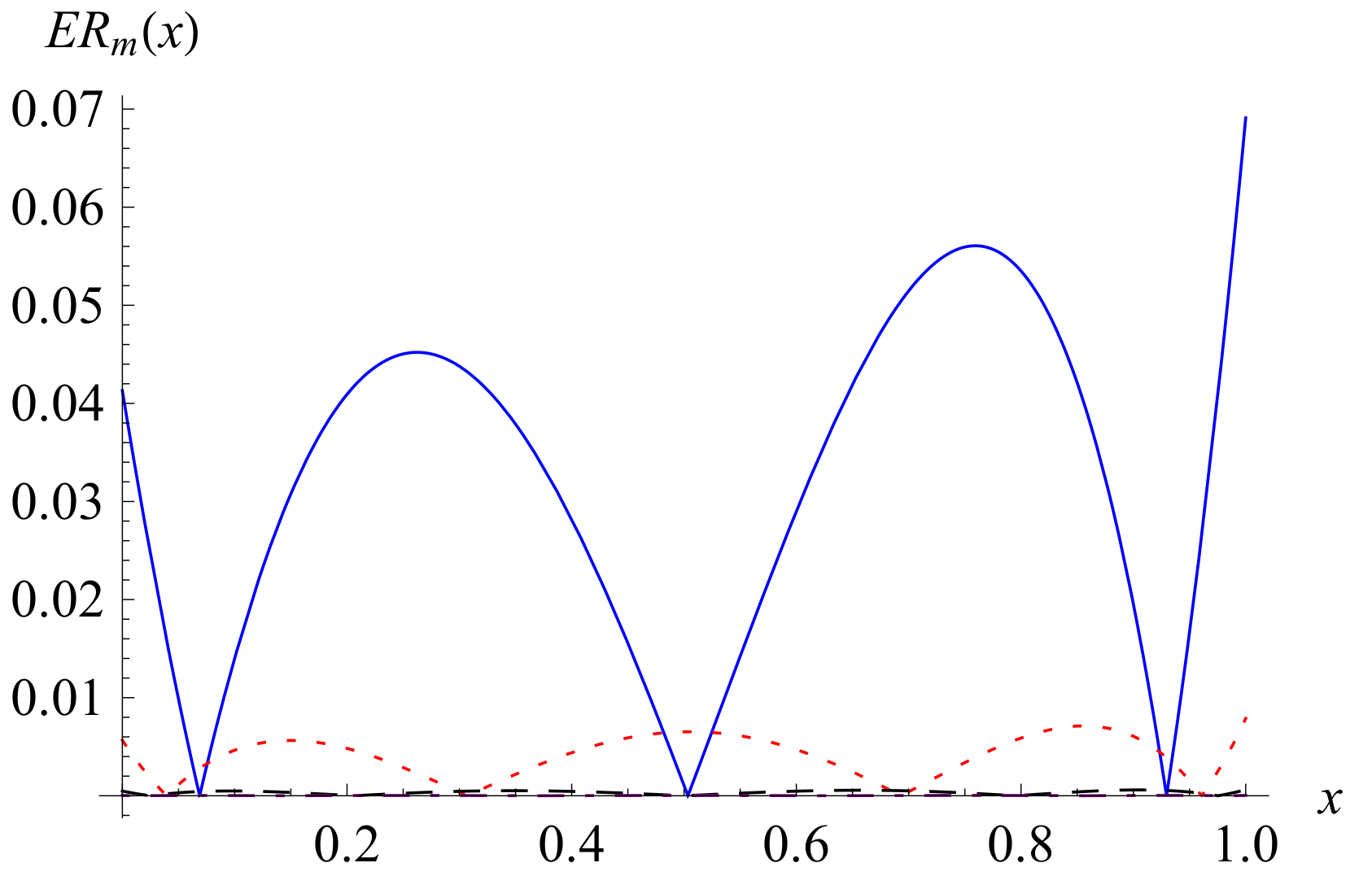
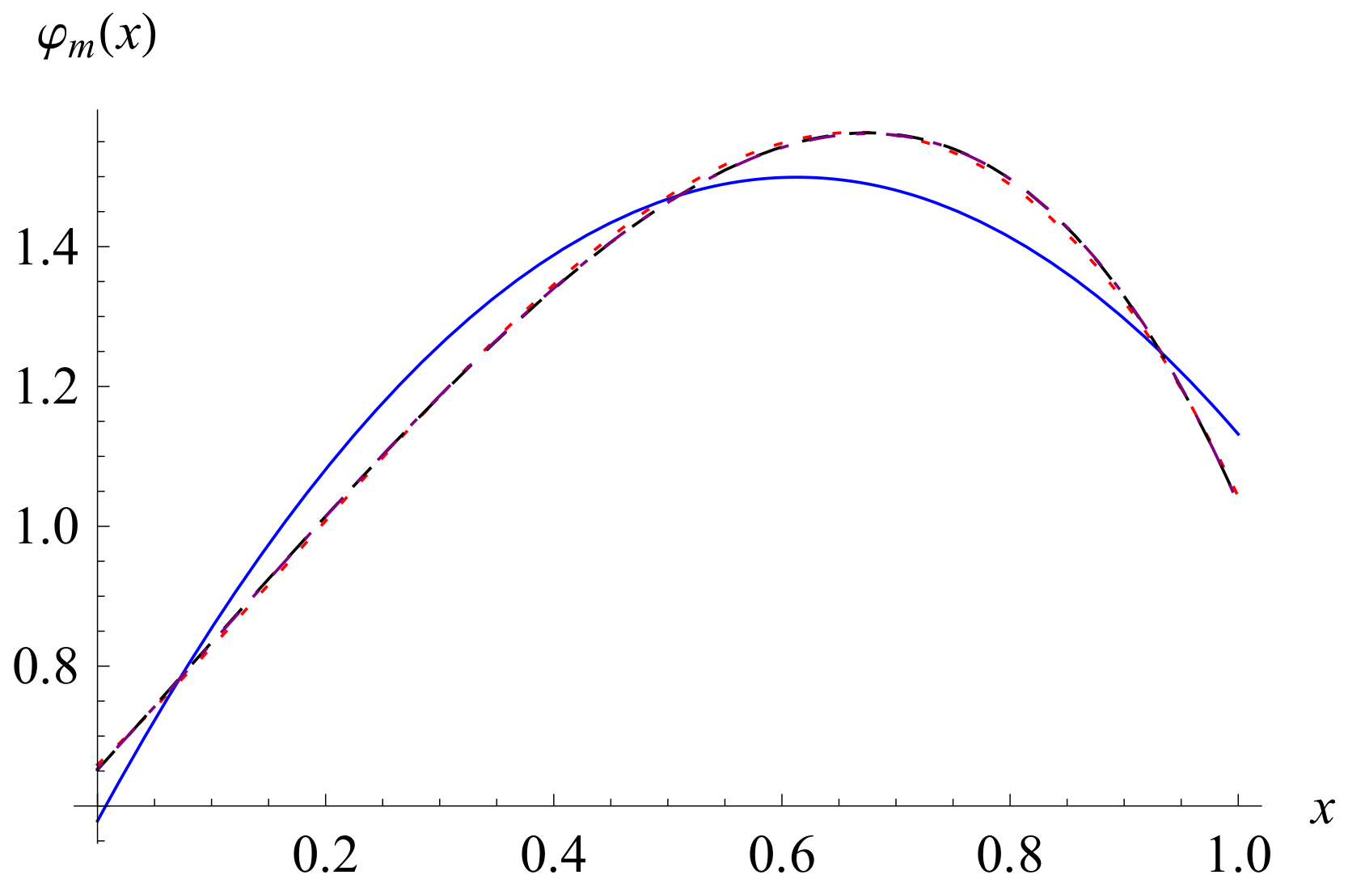
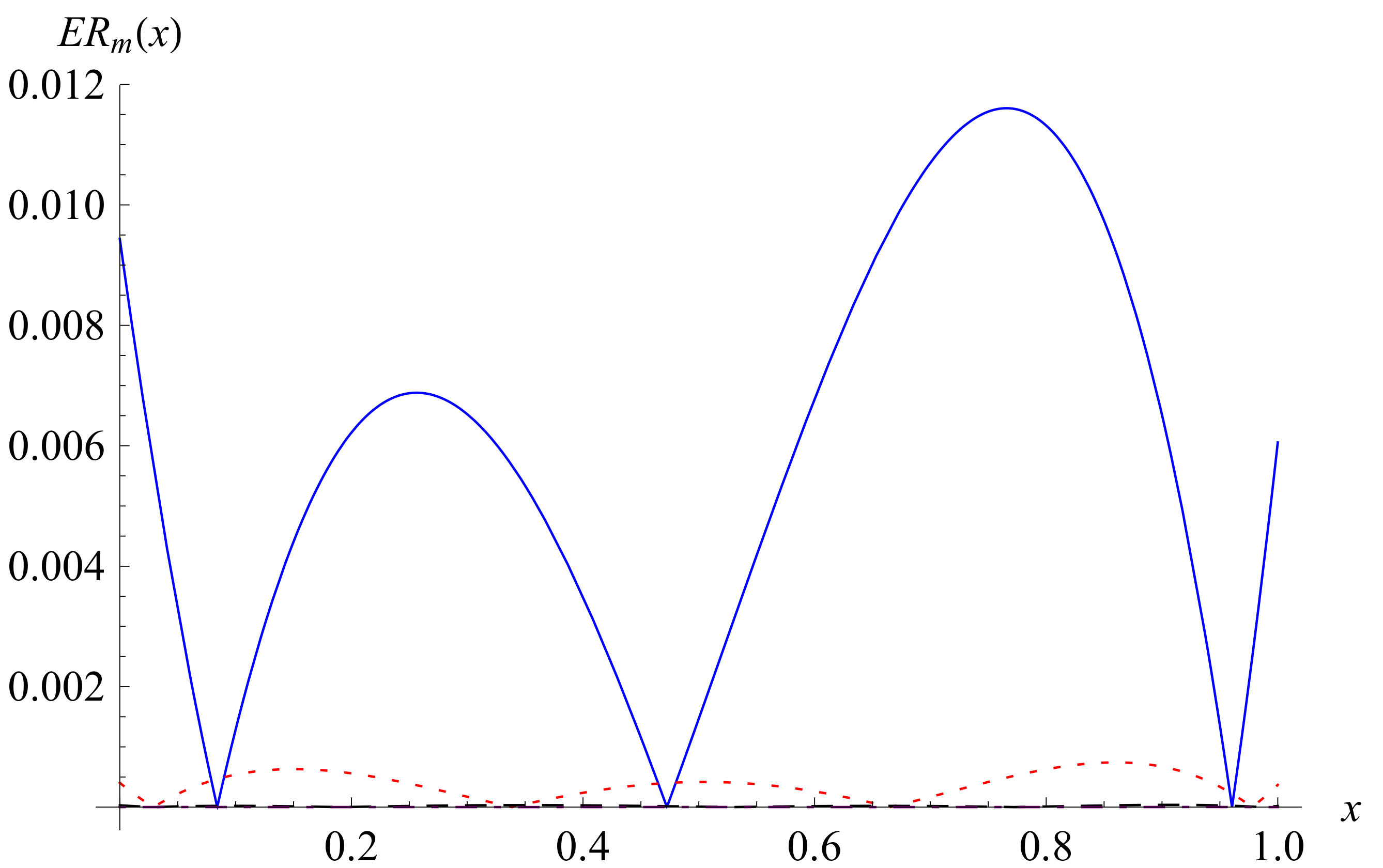
3. The Equivalent Fractional Differential-Integral Equation and Chebyshev Collocation Method
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Oldham, K.B.; Spanier, J. The Fractional Calculus; Academic: New York, NY, USA, 1974. [Google Scholar]
- Miller, K.S.; Ross, B. An Introduction to the Fractional Calculus and Fractional Differential Equations; Wiley: New York, NY, USA, 1993. [Google Scholar]
- Podlubny, I. Fractional Differential Equations; Academic: San Diego, CA, USA, 1999. [Google Scholar]
- Kilbas, A.A.; Srivastava, H.M.; Trujillo, J.J. Theory and Applications of Fractional Differential Equations; Elsevier: Amsterdam, The Netherlands, 2006. [Google Scholar]
- Băleanu, D.; Diethelm, K.; Scalas, E.; Trujillo, J.J. Fractional Calculus Models and Numerical Methods. Series on Complexity, Nonlinearity and Chaos; World Scientific: Boston, MA, USA, 2012. [Google Scholar]
- Mainardi, F. Fractional Calculus and Waves in Linear Viscoelasticity; Imperial College: London, UK, 2010. [Google Scholar]
- Li, M. Theory of Fractional Engineering Vibrations; De Gruyter: Berlin, Germany, 2021. [Google Scholar]
- Bagley, R.L.; Torvik, P.J. On the fractional calculus model of viscoelastic behavior. J. Rheol. 1986, 30, 133–155. [Google Scholar] [CrossRef]
- Li, M. Three classes of fractional oscillators. Symmetry 2018, 10, 40. [Google Scholar] [CrossRef] [Green Version]
- Ferras, L.L.; Ford, N.J.; Morgado, M.L.; Rebelo, M.; McKinley, G.H.; Nobrega, J.M. Theoretical and numerical analysis of unsteady fractional viscoelastic flows in simple geometries. Comput. Fluids 2018, 174, 14–33. [Google Scholar] [CrossRef] [Green Version]
- Duan, J.S.; Hu, D.C.; Chen, Y.Q. Simultaneous characterization of relaxation, creep, dissipation, and hysteresis by fractional-order constitutive models. Fractal Fract. 2021, 5, 36. [Google Scholar] [CrossRef]
- Jiang, X.; Xu, M.; Qi, H. The fractional diffusion model with an absorption term and modified Fick’s law for non-local transport processes. Nonlinear Anal. Real World Appl. 2010, 11, 262–269. [Google Scholar] [CrossRef]
- Morgado, M.L.; Rebelo, M.; Ferras, L.L.; Ford, N.J. Numerical solution for diffusion equations with distributed order in time using a Chebyshev collocation method. Appl. Numer. Math. 2017, 114, 108–123. [Google Scholar] [CrossRef]
- Atangana, A. Fractional Operators with Constant and Variable Order with Application to Geo-Hydrology; Elsevier: London, UK, 2018. [Google Scholar]
- Jiao, Z.; Chen, Y.; Podlubny, I. Distributed-Order Dynamic Systems—Stability, Simulation, Applications and Perspectives; Springer: London, UK, 2012. [Google Scholar]
- Li, Y.; Duan, J.S. The periodic response of a fractional oscillator with a spring-pot and an inerter-pot. J. Mech. 2021, 37, 108–117. [Google Scholar] [CrossRef]
- Duan, J.S.; Hu, D.C. Vibration systems with fractional-order and distributed-order derivatives characterizing viscoinertia. Fractal Fract. 2021, 5, 67. [Google Scholar] [CrossRef]
- Diethelm, K. The Analysis of Fractional Differential Equations; Springer: Berlin/Heidelberg, Germany, 2010. [Google Scholar]
- Duan, J.S.; Wang, Z.; Liu, Y.L.; Qiu, X. Eigenvalue problems for fractional ordinary differential equations. Chaos Solitons Fractals 2013, 46, 46–53. [Google Scholar] [CrossRef]
- Băleanu, D.; Mustafa, O.G.; Agarwal, R.P. An existence result for a superlinear fractional differential equation. Appl. Math. Lett. 2010, 23, 1129–1132. [Google Scholar] [CrossRef] [Green Version]
- Diethelm, K.; Ford, N.J.; Freed, A.D. Detailed error analysis for a fractional Adams method. Numer. Algorithms 2004, 36, 31–52. [Google Scholar] [CrossRef] [Green Version]
- Liu, F.; Zhuang, P.; Anh, V.; Turner, I.; Burrage, K. Stability and convergence of the difference methods for the space-time fractional advection-diffusion equation. Appl. Math. Comput. 2007, 191, 12–20. [Google Scholar] [CrossRef]
- Wu, G.C. A fractional characteristic method for solving fractional partial differential equations. Appl. Math. Lett. 2011, 24, 1046–1050. [Google Scholar] [CrossRef] [Green Version]
- Atabakzadeh, M.H.; Akrami, M.H.; Erjaee, G.H. Chebyshev operational matrix method for solving multi-order fractional ordinary differential equations. Appl. Math. Model. 2013, 37, 8903–8911. [Google Scholar] [CrossRef]
- Duan, J.S.; Hu, D.C.; Li, M. Comparison of two different analytical forms of response for fractional oscillation equation. Fractal Fract. 2021, 5, 188. [Google Scholar] [CrossRef]
- Jafari, H.; Daftardar-Gejji, V. Positive solutions of nonlinear fractional boundary value problems using Adomian decomposition method. Appl. Math. Comput. 2006, 180, 700–706. [Google Scholar] [CrossRef]
- Rehman, M.U.; Khan, R.A. A numerical method for solving boundary value problems for fractional differential equations. Appl. Math. Model. 2012, 36, 894–907. [Google Scholar] [CrossRef]
- Al-Refai, M.; Hajji, M.A. Monotone iterative sequences for nonlinear boundary value problems of fractional order. Nonlinear Anal. 2011, 74, 3531–3539. [Google Scholar] [CrossRef]
- Doha, E.H.; Bhrawy, A.H.; Ezz-Eldien, S.S. A Chebyshev spectral method based on operational matrix for initial and boundary value problems of fractional order. Comput. Math. Appl 2011, 62, 2364–2373. [Google Scholar] [CrossRef] [Green Version]
- Mason, J.C.; Handscomb, D.C. Chebyshev Polynomials; Chapman & Hall/CRC: London, UK, 2003. [Google Scholar]


Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Duan, J.-S.; Jing, L.-X.; Li, M. The Mixed Boundary Value Problems and Chebyshev Collocation Method for Caputo-Type Fractional Ordinary Differential Equations. Fractal Fract. 2022, 6, 148. https://doi.org/10.3390/fractalfract6030148
Duan J-S, Jing L-X, Li M. The Mixed Boundary Value Problems and Chebyshev Collocation Method for Caputo-Type Fractional Ordinary Differential Equations. Fractal and Fractional. 2022; 6(3):148. https://doi.org/10.3390/fractalfract6030148
Chicago/Turabian StyleDuan, Jun-Sheng, Li-Xia Jing, and Ming Li. 2022. "The Mixed Boundary Value Problems and Chebyshev Collocation Method for Caputo-Type Fractional Ordinary Differential Equations" Fractal and Fractional 6, no. 3: 148. https://doi.org/10.3390/fractalfract6030148
APA StyleDuan, J.-S., Jing, L.-X., & Li, M. (2022). The Mixed Boundary Value Problems and Chebyshev Collocation Method for Caputo-Type Fractional Ordinary Differential Equations. Fractal and Fractional, 6(3), 148. https://doi.org/10.3390/fractalfract6030148







