Complexity-Based Analysis of the Effect of Forming Parameters on the Surface Finish of Workpiece in Single Point Incremental Forming (SPIF)

Abstract

Nowadays, the manufacturing industry is focused on newer modern manufacturing methods, such as single point incremental forming (SPIF). The popularity of the SPIF process in the manufacturing industry is increasing due to its capability for rapid prototyping, forming complex geometry with simple steps, and customizing products for customers. This study investigates the effect of forming parameters (feed rate and step size) on the surface structure of the aluminum AA6061 sheet. We employ fractal theory to investigate the complexity of deformed surfaces. Accordingly, we study the relationship between the complexity and roughness of the deformed surface. The results show that the complexity and roughness of the deformed surface vary due to the changes in forming parameters. Fractal analysis can be further employed in other manufacturing processes to investigate the relation between the complexity and roughness of processed surfaces.

1. Introduction

In recent years, the application of SPIF has extended for rapid prototyping because unlike conventional forming, it does not require component-specific tools, such as die. The process of SPIF can be done just by modifying available CNC machines that make it suitable for small-scale productions with lower cost and energy consumption, compared to conventional forming, which is only sensible for mass production [1]. Since the demand for using SPIF is increasing, it is helpful to evaluate the effects of the forming parameters to improve product quality.

In this process, the CNC machine, rounded tip tool, and metal sheet holder, which consist of a clamping plate and support plate, are required. A conical tool with a rounded tip tool can be mounted to the machine spindle to perform a small series of incremental deformation processes on the clamped metal sheet until the desired shape is achieved. Unlike conventional forming methods, such as hammering, spinning, and stamping, the forming in SPIF happens by the localized deformation caused by a forming tool and the incremental deformation.

Besides several reported research works on different areas, such as modeling [2], analysis [3], and prediction [4] of forming forces, investigating the effects of process parameters on residual stresses [5], proposing processing strategies using the CAD approach [6], evaluating the effect of process parameters on forming forces [7], and analysis of deformation mechanism [8], a significant number of research studies have been devoted to the analysis of the quality of the deformed surface. In one group, the influence of forming parameters on the quality of the deformed surface was evaluated [9,10,11,12]. In these research works, the surface roughness was analyzed as the indicator of the quality of the surface. In another group of studies, researchers worked on the modeling and optimization of forming parameters to reach high surface quality [13,14,15].

Martins et al. [16] proposed an equation to predict the maximum angle of forming, while Wei et al. [17] reported that the forming angle influences the metal sheet springback and dimensional accuracy of the deformed part. The effect of forming tool paths on the deformed surface quality was investigated in several studies [18,19]. The inefficiency of the zig-zag tool path was reported due to entry and exit marks, while the spiral transition and step circle can generate a better surface quality. The effect of tool size on formability was also studied by Arshad [20], and it was concluded that formability and surface finish are enhanced by the use of a smaller tool radius, due to higher strain and concentrated force. Oraon et al. [21] stated the interaction effect of rotational speed and the feed rate in a study where they believed that the higher tool wear at a higher rotational speed and low feed rate is responsible for poor surface finish. Chatter was also reported as the main reason for the rough surface finish at a high feed rate [22]. However, the effect of step size on the formability is argued to be significant, though it has a great impact on the forming duration [23].

Besides all conducted studies on the analysis of the variations of the deformed surface due to the variations of forming parameters, the relationship between the complexity and roughness of the deformed surface has not been investigated. To do this job, for this research, we benefit from the fractal theory. The fractal theory is a useful tool to analyze the complexity of objects (time series and patterns). A greater fractal dimension stands for a higher complexity in an object [24]. There are various papers in the literature that applied fractal theory to analyze the variations of the complexity of time series and patterns in manufacturing engineering [25,26,27,28].

As was mentioned before, there are a few parameters, such as material thickness, forming angle, forming tool path, spindle speed, and forming shape, that are generally studied by many researchers. However, the feed rate and step size are the two parameters that are debatable, due to conflicting results presented by different researchers [29,30]. Therefore, in this research, the step size and feed rate are selected as input variables. We utilize fractal theory to evaluate how the complexity of the deformed surface varies with the variations of step size and feed rate, and how this alteration is accordingly related to the variation of roughness.

In the following, the method of analysis is firstly discussed in detail. After that, we describe the data collection procedure followed by data analysis. Then, the results are provided. The discussion is given in the last section.

2. Method

We would like to analyze how the changes in deforming parameters affect the complexity of the deformed surface and also investigate the relationship between complexity and roughness of the surface.

Since the surface of the deformed sheet (Figure 1) has a complex structure, we benefit from fractal analysis. Scientists have developed various techniques to calculate the fractal dimension. In this study, the box-counting method is employed in which the object (the deformed surface) is covered with $N$ same-size boxes in each step, where the size of the boxes ($\in$) varies between various steps. The fractal dimension is computed using (1) as follows:

$$D_F=\underset{\in \to 0}{\lim } \frac{{\log }_{}N (\in )}{{\log }_{ }1/\in }$$

(1)

Six experiments were designed based on the variations of feed rate and step size. The forming parameters were selected in the range of published articles for having a reasonable forming time [31,32]. The forming parameters of the experiments are shown in

Table 1. Experiment plan with different feed rates and step sizes.

Exp. No.	Feed Rate (mm/min)	Step Size (mm)
1	1000	0.2
2	1000	0.6
3	1000	1.0
4	1500	0.2
5	1500	0.6
6	1500	1.0

. This table indicates that the experiments were performed at different feed rates (1000 mm/min and 1500 mm/min) and step sizes (0.2 mm, 0.5 mm, and 1 mm). The minimum forming time of 4 min was achieved at the lowest feed and step size of 1.0 mm.

Therefore, we changed the feed rate and step size between different experiments and accordingly analyzed how these variations affect the complexity and roughness of the formed surface.

3. Data Collection and Analysis

In this research, aluminum alloy 6061 (AA6061) was selected as the forming sheet. The material properties of AA6061 can be reinforced via the addition of selected reinforcements, which helps to obtain specific strength and stiffness at room temperature. This is one of the factors why the demand for AA6061 is increasing in the aircraft and automotive fields [33]. The material properties of AA6061 are shown in

Table 2. The properties of forming sheet material (AA6061) [34].

Property	Value
Young Modulus (GPa)	69
Ultimate Tensile strength (Mpa)	310
Elongate at break (1.6 m)	12%
Modulus of elasticity (Gpa)	68.9
Yield strength (Mpa)	155
Shear Modulus (GPa)	26

.

SKD 61 steel was selected for the fabrication of incremental forming tools. The selection of this material was due to its good machinability, hardenability, and wear resistance. The tip radius of forming tool was 4 mm with a shank diameter of 20 mm that was mounted into the machine spindle (Figure 2).

The geometry of the SPIF fixture was designed and fabricated, as shown in Figure 3. As can be seen in this figure, it was made up of four pieces of 260 mm × 50 mm × 12 mm and another four pieces of 160 mm × 50 mm × 12 mm mild steel bar. The holes were drilled and threaded according to the dimension of the detail drawing. The assembly of the fixture is shown in Figure 3. M8 bolts were used to fix the position of the forming sheet between the top and bottom plates to reduce the vibration and offset of the forming sheet during the forming process.

In this research, Autodesk Inventor software was selected to create the truncated cone shape CAD model, and Autodesk Inventor HSM software was used to generate G-code for SPIF. Six G-codes were required for running the CNC machine as the result of two different feed rates and three different step sizes (as independent variables). The forming angle, forming depth, and spindle speed were kept fixed at 65°, 28 mm, and 300 rpm, respectively. We selected spiral transition for the forming tool path to obtain lower surface roughness, less tool entry, and exit mark [18,35]. Six pieces of AA6061 sheet with a size of 200 mm × 200 mm × 1.6 mm were prepared as the workpiece for the SPIF process.

Figure 4 shows the setup of the fixture, forming tool, and sheet metal on the Deckelmaho Computerized Numerical Control (CNC) machine worktable. We used Castrol 20 W engine oil as the lubricant for all experiments.

As was mentioned before (Table 1), in this research, two forming parameters, which are the feed rate and step size, were set as the manipulated variables. The forming processes were performed with a constant spindle speed of 300 rev/min. Six pieces of AA6061 aluminum sheet were formed in six different experiments. Figure 5 shows the result of the formed truncated cone on the AA6061 sheet by using a CNC machine. Microscopic images of the deformed surfaces in experiments 1, 2, and 3 are displayed in Figure 6a–c, respectively.

The surface roughness of the deformed sheet was tested with a Mahr Marsurf XCR 20 surface roughness tester. The deformed cones were placed and oriented in a way that the internal cone surface was parallel to the traveling direction of the machine stylus. The travel distance of 5.60 mm was set to measure the surface roughness. The measurement was repeated at different regions of the deformed surface to obtain the average value of the surface roughness.

To calculate the fractal dimension of formed surfaces, the box-counting algorithm was used. The taken images using a microscope were processed, using the box-counting code in MATLAB (MathWorks, U.S.A.), and a single value of the fractal dimension was obtained for each image.

4. Results

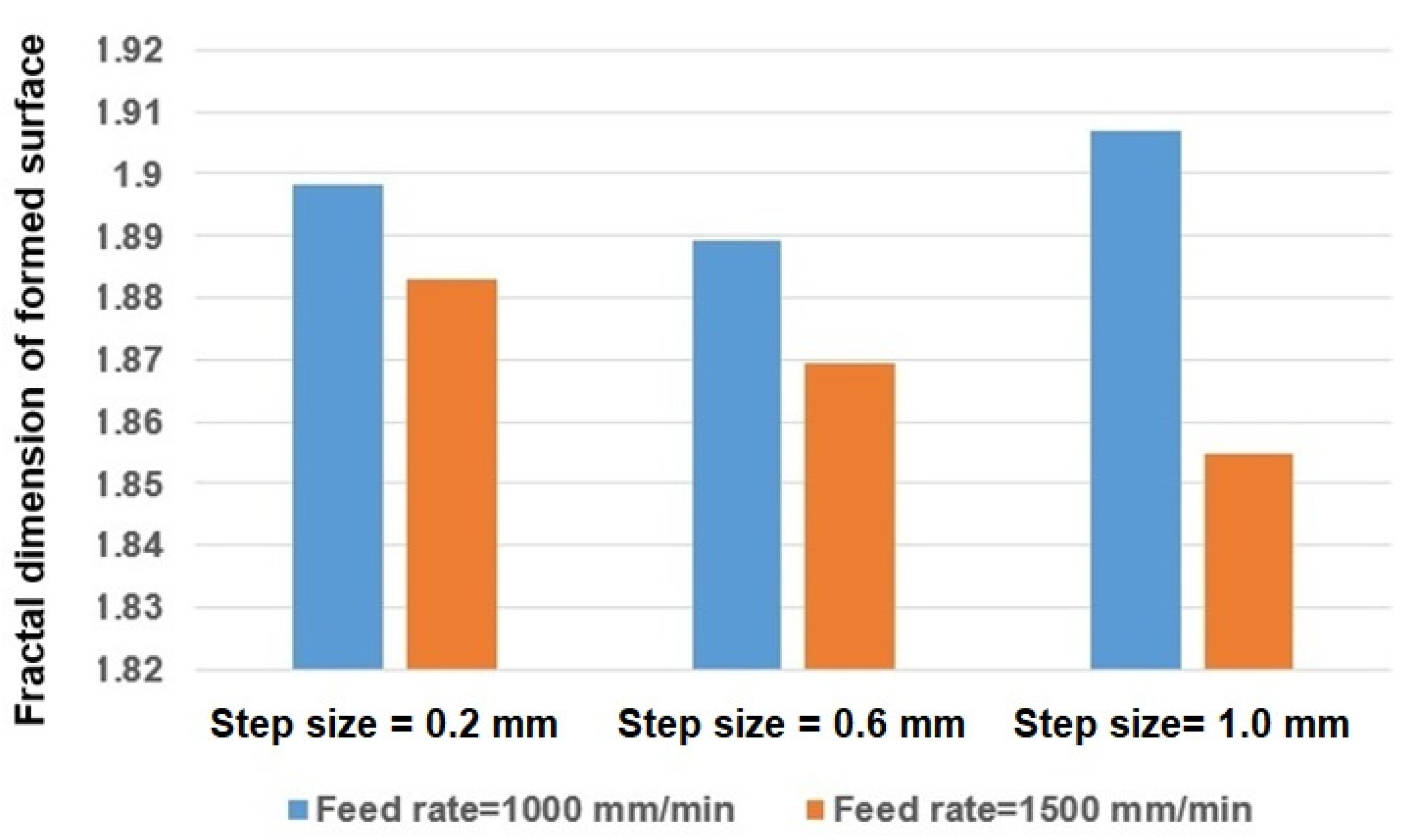
Figure 7 presents the fractal dimension of the formed surfaces as the result of the different step sizes and feed rates.

According to the result for the feed rate of 1000 mm/min, the fractal dimension of the deformed surface had the lowest value for the step size of 0.6 mm. The value of the fractal dimension increased as we chose the step size of 0.2 mm and 1.0 mm. It can be stated that the formed surface had the lowest complexity by choosing a step size of 0.6 mm and that it increased when the step size changed to 0.2 mm and 1.0 mm.

The results in the case of the feed rate of 1500 mm/min indicate that the formed surface had the highest complexity in the case of a step size of 0.2 mm, which decreased with the increment in step size from 0.6 mm to 1.0 mm. In other words, increasing the step size caused lower complexity on the formed surfaces.

A comparison of the obtained results for the feed rates of 1500 mm/min with the obtained results for the feed rate of 1000 mm/min demonstrates that forming the surface using a greater feed rate caused lower complexity in it.

To compare the alterations of the complexity and average roughness (Ra) of deformed surfaces for different step sizes and feed rates, Figure 8 is presented.

The results for the feed rate of 1500 mm/min show that the surface had the lowest value of surface roughness in the case of a step size of 1.0 mm. The value of the surface roughness increased as the step size of 0.2 mm and 0.6 mm were chosen. Since the higher value of Ra stands for the poorer quality of the surface, the deformed surface had the worst and best quality in the cases of a step size of 0.2 mm and 1.0 mm, respectively.

The results for the feed rate of 1500 mm/min showed that the surface had the highest value of surface roughness for the step size of 0.2 mm, which decreased with the increment in step size from 0.6 mm to 1.0 mm. In other words, increasing the step size caused lower roughness on the formed surfaces.

A comparison of the obtained results for the feed rates of 1500 mm/min with the obtained results for the feed rate of 1000 mm/min states that, except for the step size of 1.0 mm, forming the surface using a higher feed rate caused higher roughness on the surface.

Comparing the obtained results for surface roughness with the results in the case of fractal dimension of surface in Figure 7 indicates that for the feed rate of 1500 mm/min, the complexity and roughness of the surface demonstrated the similar trend of alterations, where in both cases, increasing the step size caused lower fractal dimension and roughness. However, in the case of the feed rate of 1000 mm/min, the complexity and roughness of the formed surface showed the opposite trends of alterations.

5. Discussion

The analysis of the effect of forming parameters on the alterations of the complexity of the surface in forming operation was conducted in this research work. We also investigated how the complexity of the deformed surface changes with its roughness. For this purpose, we designed six experiments in which the feed rate and step size changed. Accordingly, we calculated the fractal dimension and roughness of the formed surface for each experiment.

The results indicated that the complexity and roughness of formed surfaces varied with the variations in the forming parameters. In the case of the feed rate of 1000 mm/min, the changes in complexity were the reverse of the variations in roughness. However, in the case of the feed rate of 1500 mm/min, both the complexity and roughness showed a similar trend of variations, whereby increasing the step size decreased the complexity and roughness. This can be explained by the fact that the step size increment can have two opposite effects on the surface. Firstly, a bigger step size results in the formation of step marks on the surface with a bigger pitch distance. Although it might lead to bigger peaks on the surface, it lowers the surface roughness and complexity in total because they form less often. Secondly, the increase in step size can cause chatter due to a higher strain rate, which increases the complexity of the surface texture, while the first effect is still dominating on the average surface roughness. However, the higher feed rate generates the higher temperature, and hence, it enhances the sheet metal deformability. Consequently, surface fractal dimension decreases with step size at a feed rate of 1500 mm/min since the chattering effect is no longer dominating.

The feed rate has also a similar effect on the fractal dimension. A higher feed rate results in bigger pitch distances of feed marks on the deformed surface. Fewer occurrences of feed marks in the feed direction lead to less complexity of the deformed surface. On other hand, a higher feed rate causes feed marks with greater heights but that are moderated at the highest combination feed rate and step size, which generate higher forming temperature and enhance the deformability.

The obtained results in this study are in accordance with the obtained results in other studies which indicated that the surface roughness of the formed surface increases with the increment of the feed rate [32,36] and decrement of step size [11]. However, as was mentioned previously, no study has been conducted on the analysis of the fractal structure of the formed surface.

Therefore, it was successfully evaluated the changes in complexity and roughness of formed surfaces due to the changes in forming parameters. This study is novel since, based on our investigation, although several studies have analyzed the fractal dimension of machined surfaces in different manufacturing processes [37,38], this is the first time that fractal theory was employed to investigate the complexity of the deformed surface. Furthermore, although many works have focused on the analysis of the surface roughness of formed surfaces [9,10,11,12], for the first time, we simultaneously analyzed the complexity and surface roughness of the formed surfaces in this research.

In this study, we analyzed the relationship between the complexity and roughness of the formed surface. In further studies, we can extend our investigation to analyze the relation between other complex features (such as vibration signal and force signal) with the variations of the formed surface. We can also perform a similar analysis in the case of other operations (e.g., turning operation) to study how the complexity and roughness of a surface are related. All these efforts will enable researchers to investigate the relationship among various features of machining operations that are mainly beneficial to reach higher quality on the machined surface.