Fractal Analysis on Surface Topography of Thin Films: A Review
Abstract
1. Introduction
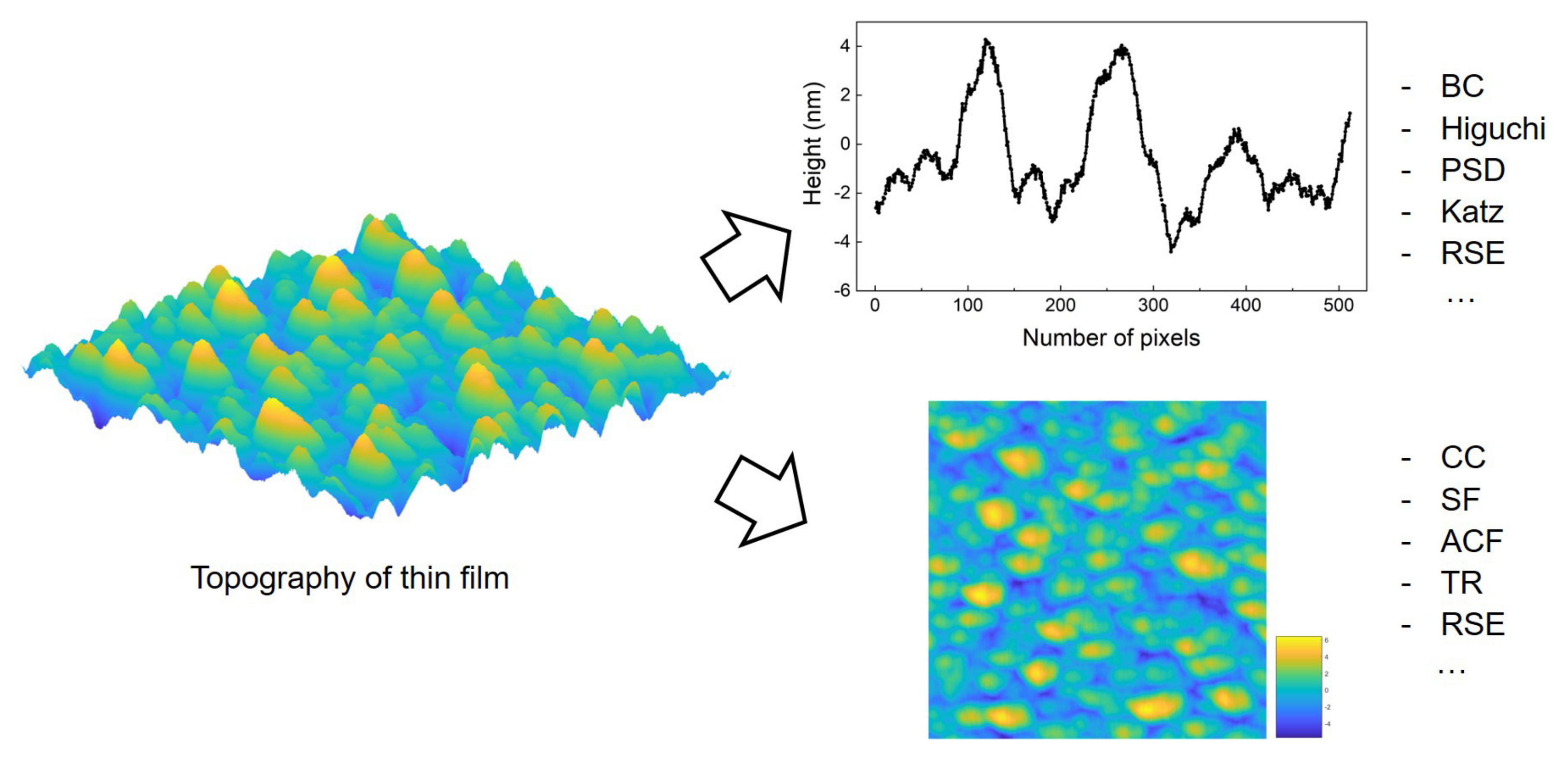
2. Methods of Fractal Analysis
2.1. Simulation Methods for Fractal Features
2.1.1. Artificial Profile Generated by W-M Function
2.1.2. Artificial Surface Generated by W-M Function
2.1.3. Other Function
- (1)
- Takagi function
- (2)
- Fractal Brownian motion function
2.2. Surface Characterization Methods
2.3. Calculation Methods for FD
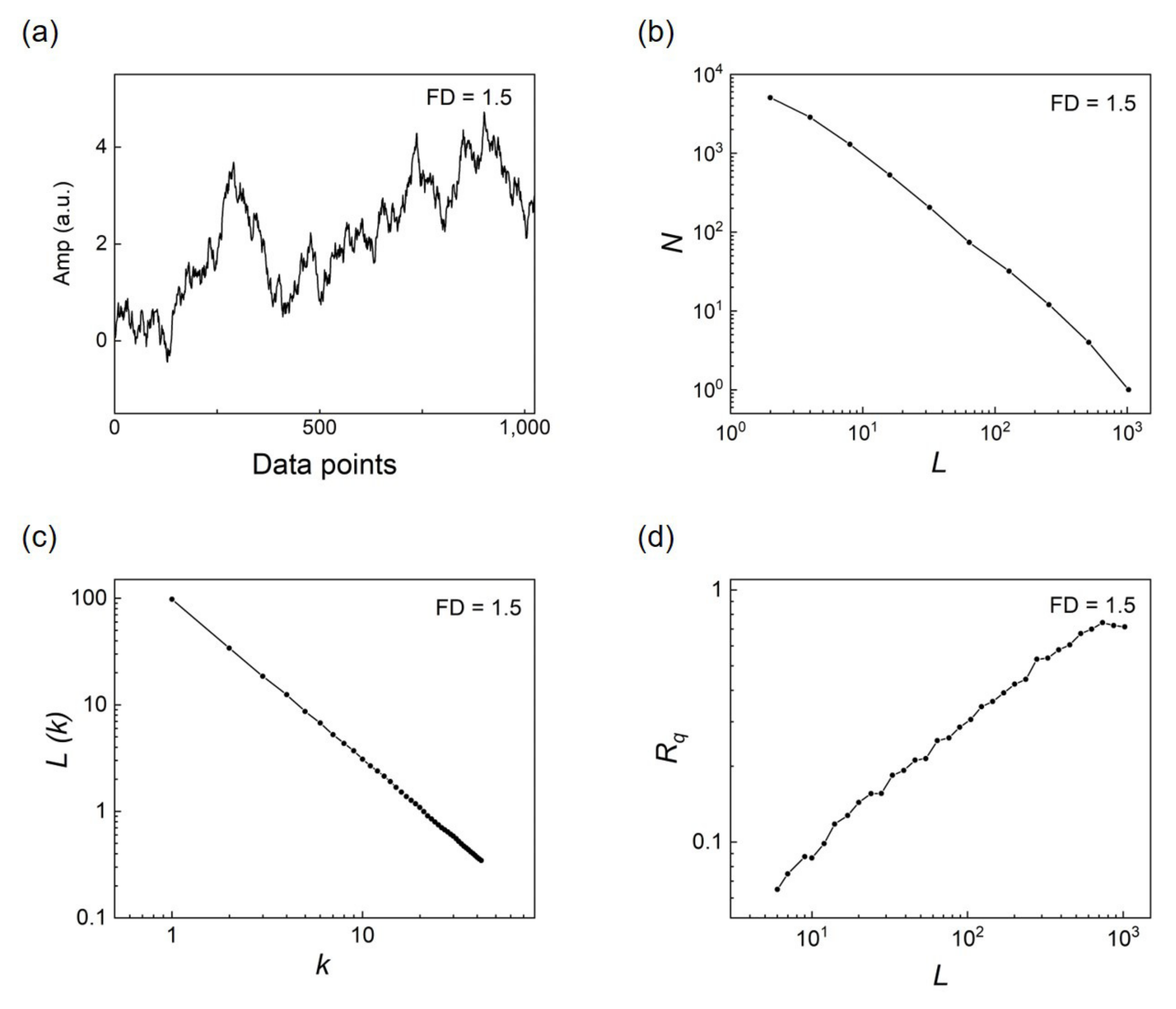
2.3.1. Scanline-Based Methods
- (1)
- Box counting method
- (2)
- Higuchi method
- (3)
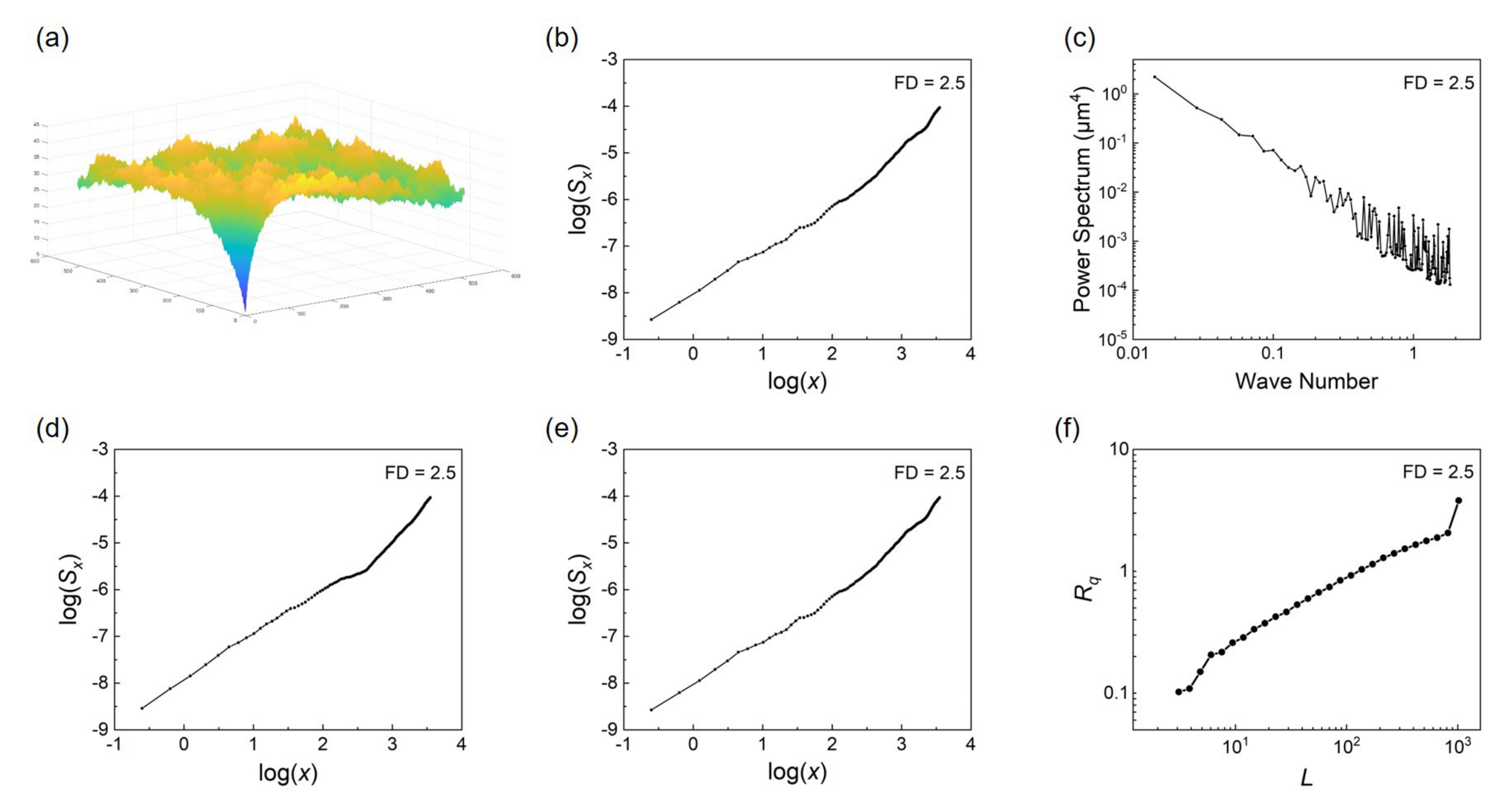
- Power spectral density method
- (4)
- Katz Method
2.3.2. Single-Image-Based Methods
- (1)
- The Cube counting method
- (2)
- Structure function method
- (3)
- Autocorrelation function method
- (4)
- Height-height correlation function
2.3.3. Multi-Image-Based Method
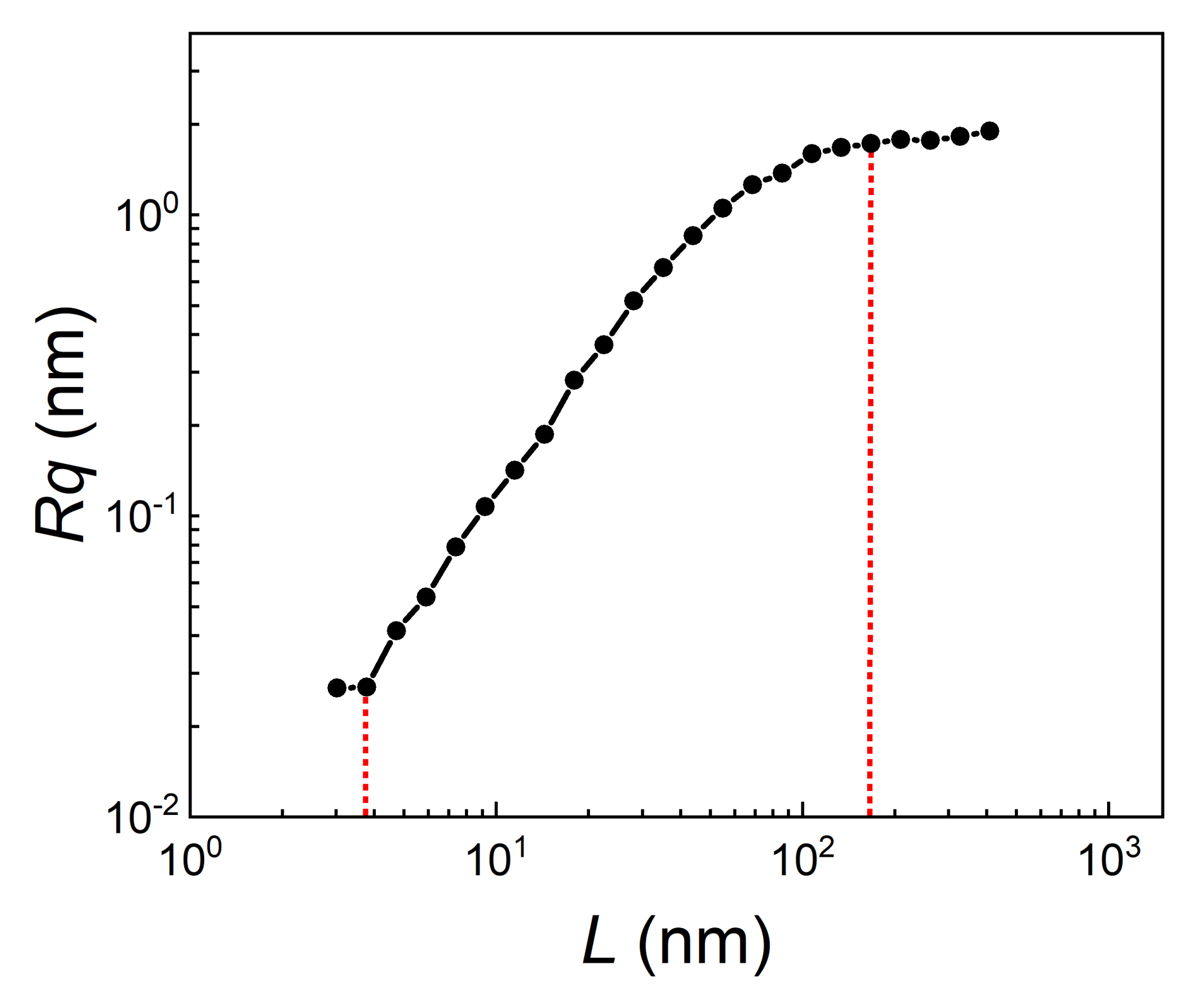
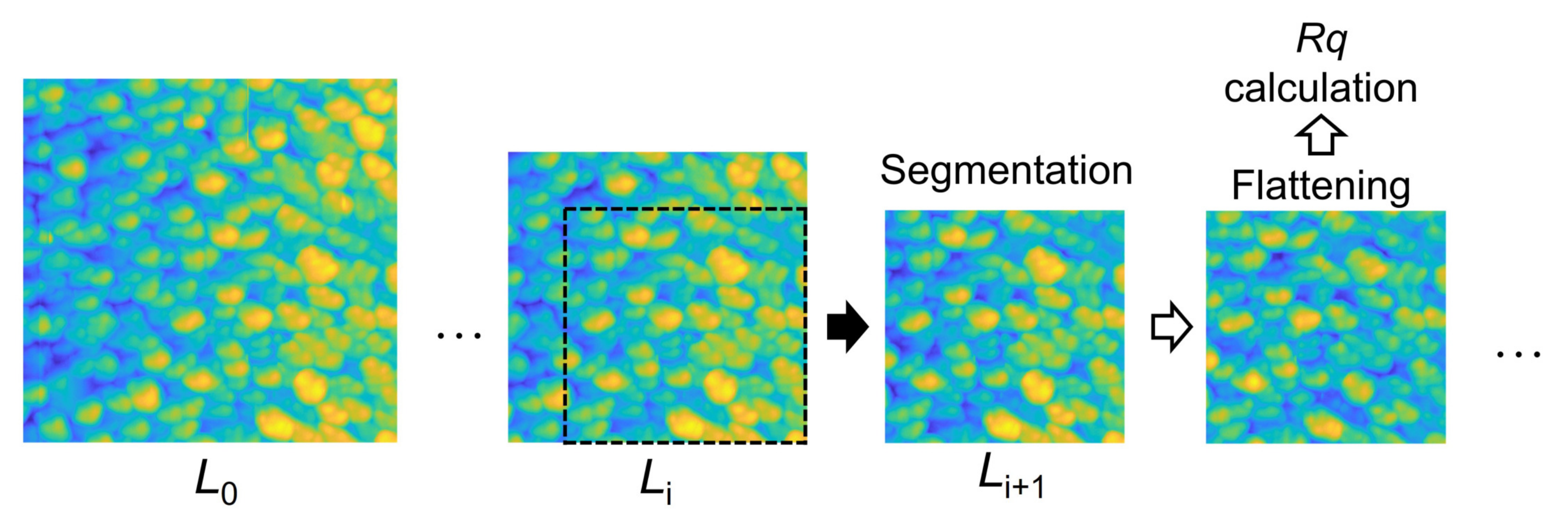
2.3.4. Roughness Scaling Extraction Method
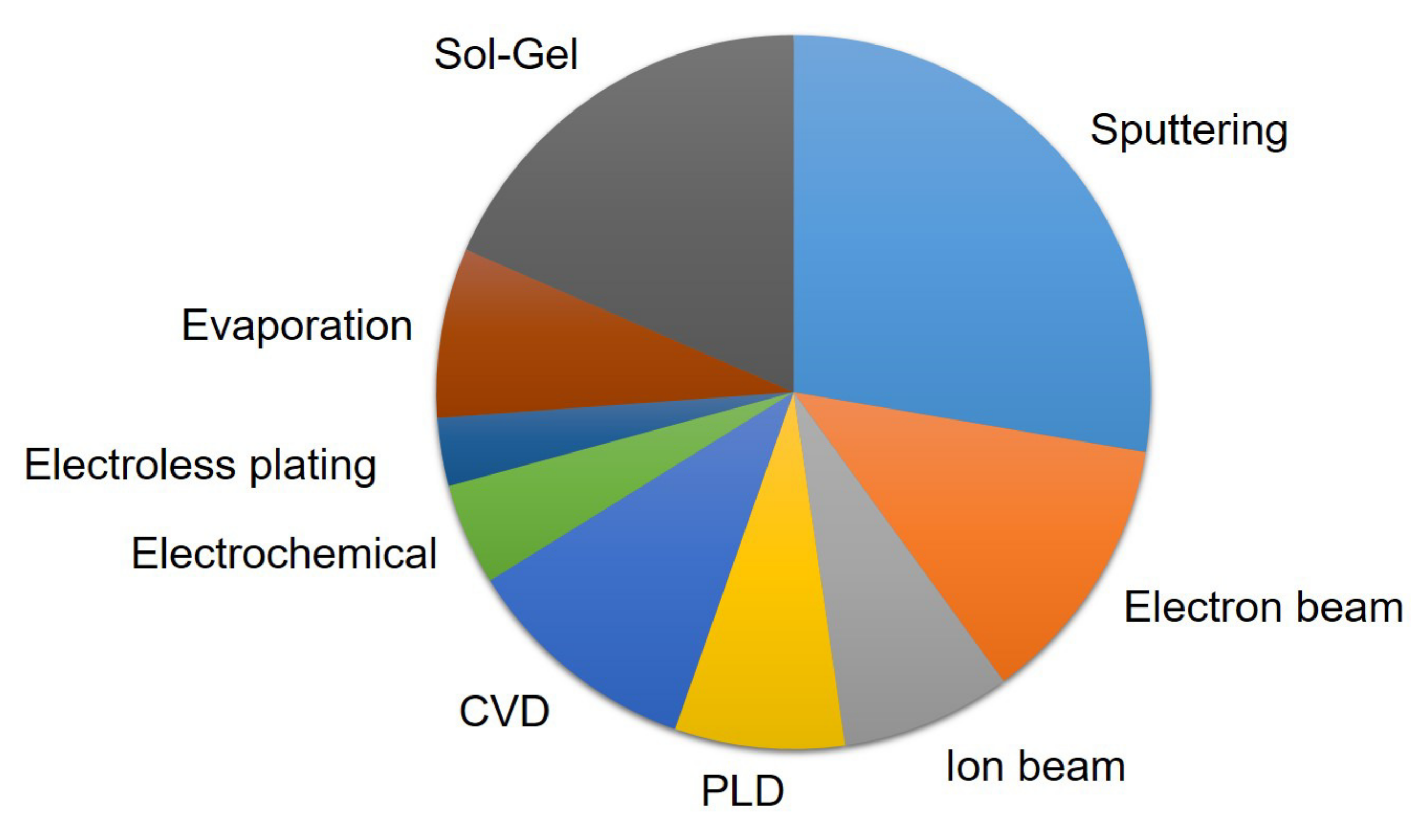
3. Mechanism and Techniques of Thin Films
3.1. Surface Growth and Factors
3.2. Physical Vapor Deposition
3.2.1. Electron Beam Evaporation
3.2.2. Pulsed Laser Deposition
3.2.3. Magnetron Sputtering Deposition
3.3. Chemical Vapor Deposition
3.4. Non-Vacuum Methods
3.4.1. Electroplating Method
3.4.2. Sol–Gel Method
3.5. Parameters Related to FD
4. Factors and Effects of Fractal Properties
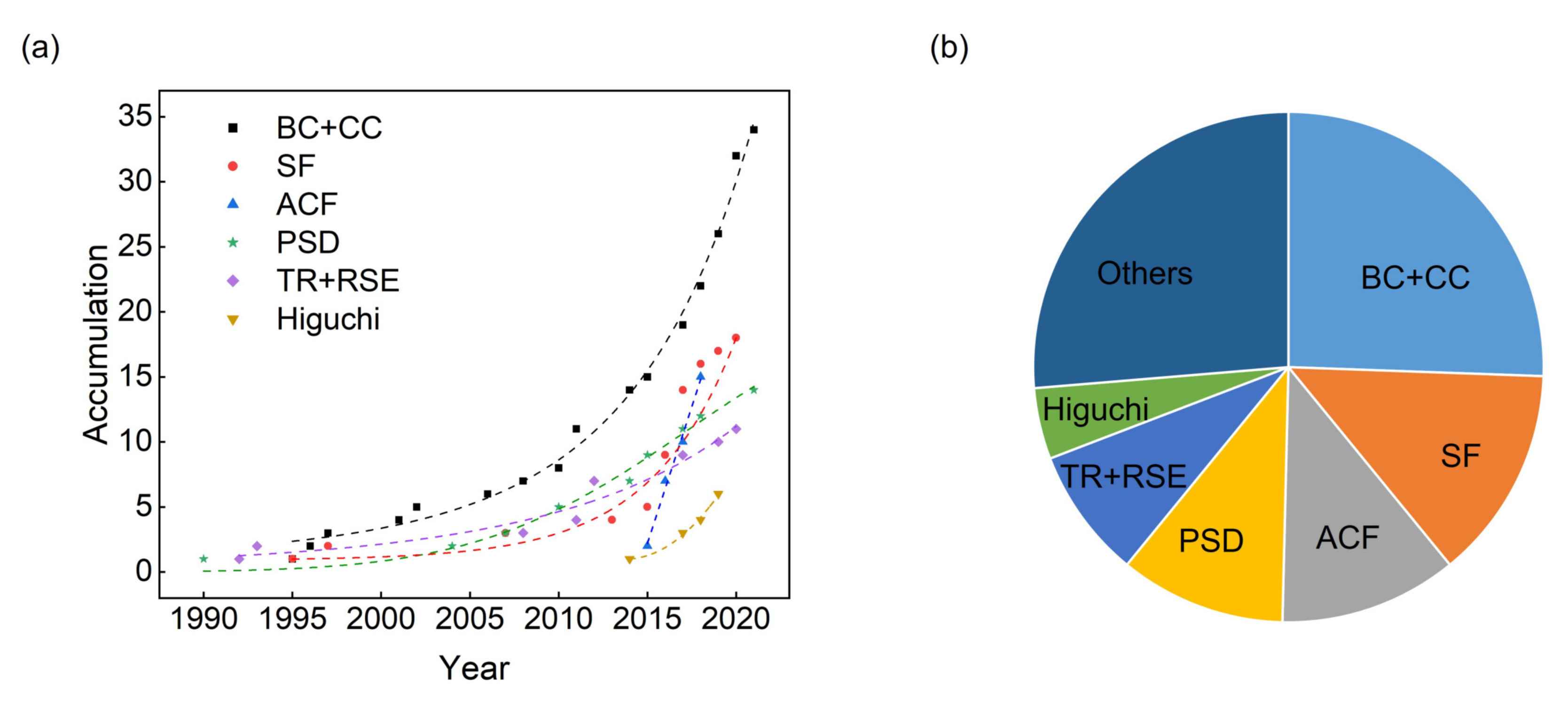
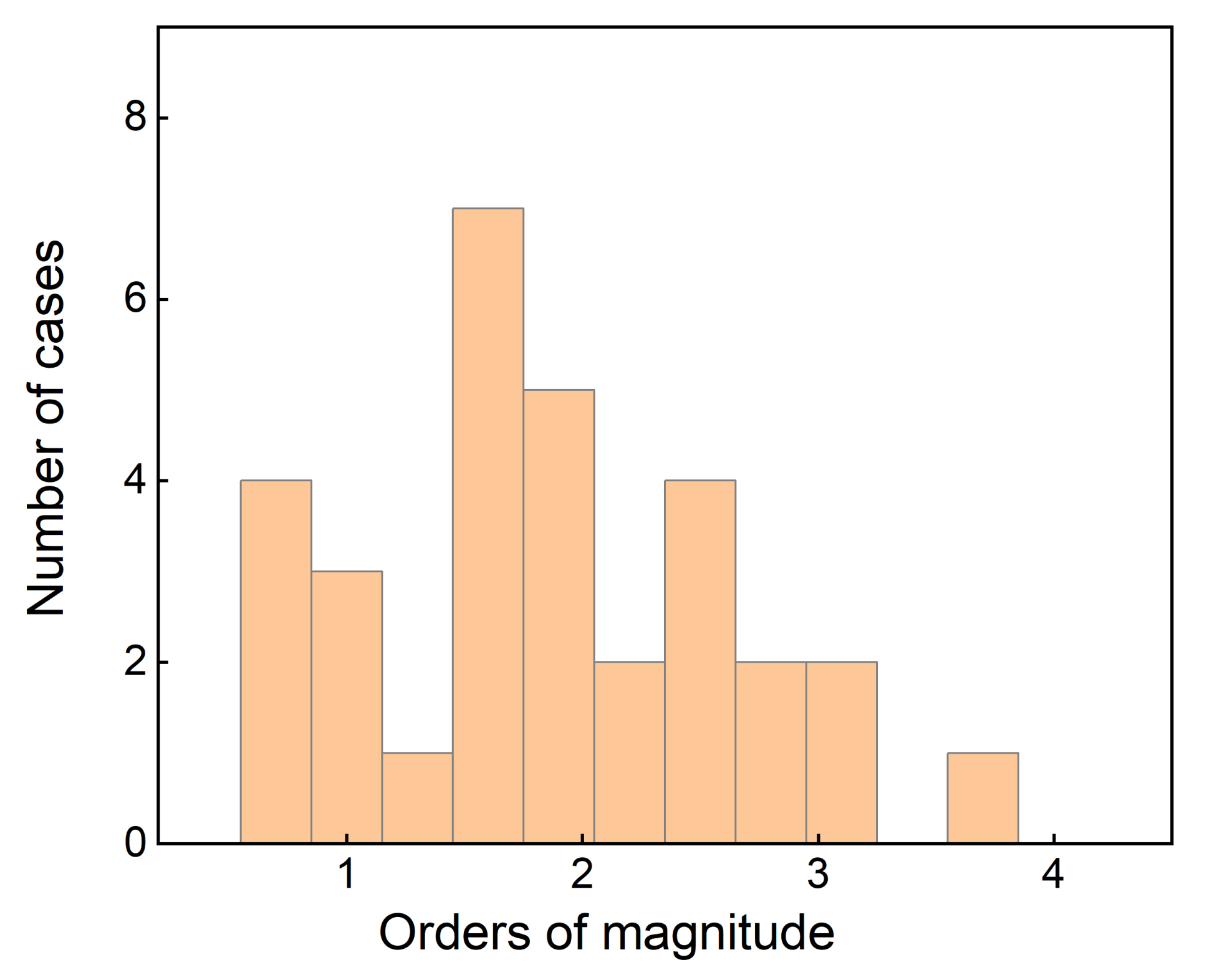
4.1. Fractal Study of Various Thin Films
4.2. Application of Fractal Calculating Methods
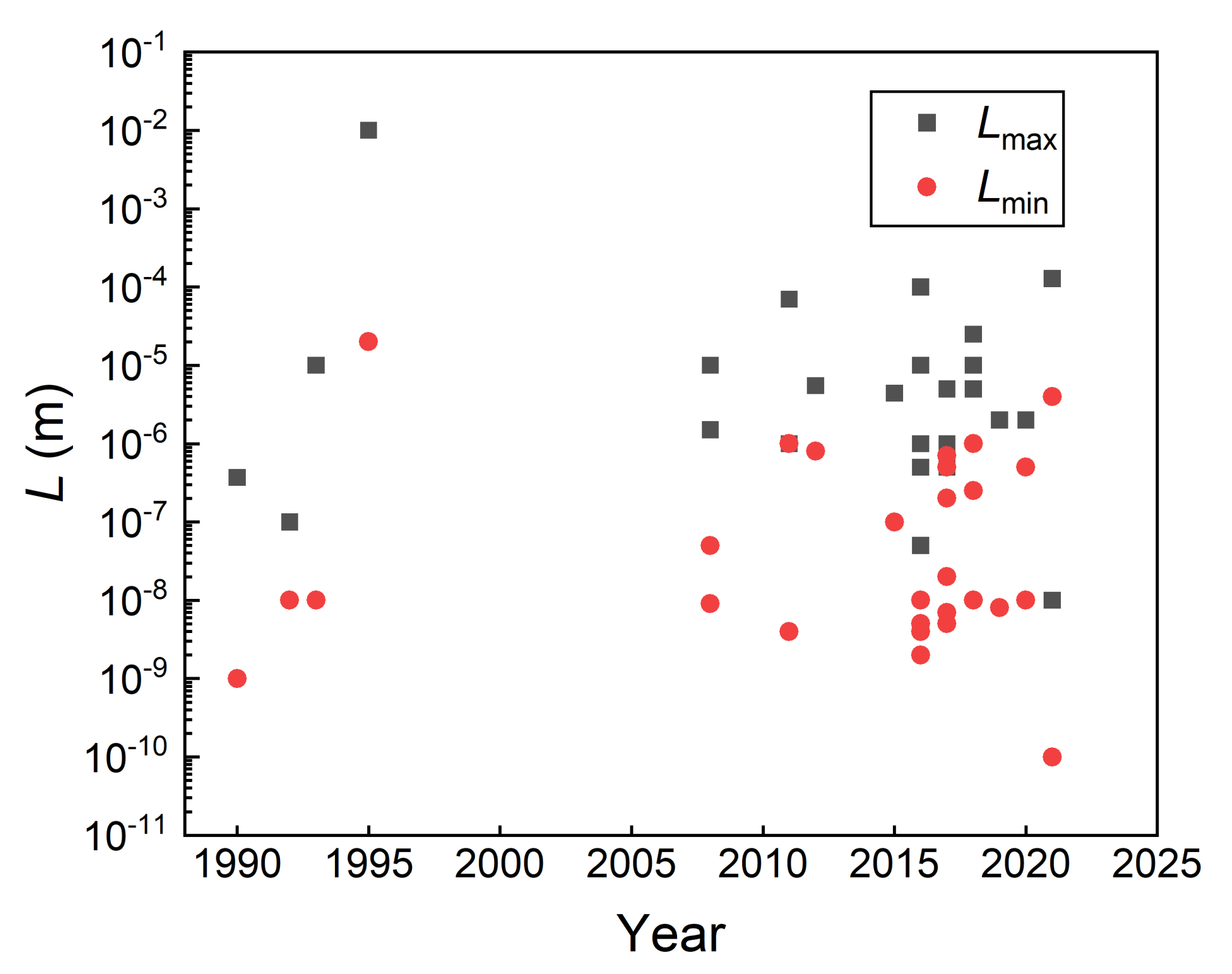
4.3. Reality Issue for Fractal Analysis
5. Prospective Developing Trends
5.1. Multifractal Analysis for Thin Films
5.2. Fractal for Surface Mechanism and Properties
6. Summary
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| ACF | Auto-correlation function |
| AFM | Atomic force microscopy |
| BC | Box counting |
| CC | Cube counting |
| CVD | Chemical vapor deposition |
| EBE | Electron beam evaporation |
| EEG | Electroencephalogram |
| EPSAD | Energetic partical self-assisted deposition |
| FD | Fractal dimension |
| OM | Optical microscope |
| PLD | Pulsed laser deposition |
| PSD | Power spectrum density |
| PVD | Physical vapor deposition |
| RSE | Roughness scaling extraction |
| SCM | Scanning confocal microscope |
| SEM | Scanning electron microscope |
| SF | Structure function |
| SRT | Surface roughness tester |
| STEM | Scanning transmission electron microscopy |
| STM | Scanning tunneling microscope |
| TEM | Transmission electron microscope |
| TR | Traditional roughness |
| W-M | Weierstrass-Mandelbrot |
Appendix A
Appendix A.1
| Authors | Year | Calculation | FD Range | Lmax | Lmin |
|---|---|---|---|---|---|
| Mitchell M. W. al. [119] | 1990 | PSD | 1.06–1.63 | 370 nm | 1 nm |
| Herrasti P. al. [120] | 1992 | TR | 2.5 ± 0.1 (Au) 2.7 ± 0.1 (Vapour) | 100 nm | 10 nm |
| Krim J. al. [14] | 1993 | TR | 2.47–2.98 | 10 m | 10 nm |
| Ba L. al. [121] | 1995 | BC | 1.67–1.83 | - | - |
| Strizhak P. E. [122] | 1995 | other | 1.49–2 | 10 mm | 0.02 mm |
| Ba L. et al. [123] | 1996 | BC | 1.67–1.78 | - | - |
| Chen Z. W. et al. [124] | 2001 | BC | 1.52–1.75 | - | - |
| Sun X. et al. [125] | 2002 | BC | 1.18–2.0 | 3 m | - |
| Fang T. H. et al. [75] | 2003 | SF | 2.03–2.07 | 1 m | - |
| Wang Y. et al. [37] | 2004 | PSD | 2.0–2.7 | 2 m | |
| Catalan G. et al. [126] | 2008 | other | 1.29–1.52 | 300 nm | 8 nm |
| Raoufi D. [127] | 2010 | PSD | 2.67–2.91 | 1 m | - |
| Raoufi D. [88] | 2010 | PSD | 2.1 | - | - |
| Chen Z. W. et al. [128] | 2010 | BC | 1.82–1.90 | - | - |
| Miyata S. et al. [129] | 2011 | TR | 2.2–2.4 | 1 m | 4 nm |
| Gao H. J. et al. [130] | 2011 | BC | 1.69 ± 0.07 | - | - |
| Chen Z. W. et al. [61] | 2011 | BC | 1.65–1.86 | - | - |
| Feng F. et al. [5] | 2012 | TR | 2.01–2.16 | 70 m | 1 m |
| Ponomareva A. A. et al. [131] | 2014 | PSD | 2–2.73; 1.85–2 | 5.5 m | 0.8 m |
| Zheng G. M. et al. [50] | 2014 | Higuchi | 1.33–1.94 | - | - |
| Hou L. et al. [132] | 2014 | BC | 1.77 | - | - |
| Haniam P. et al. [79] | 2014 | BC | 1.87 | - | - |
| Kong Y. L. et al. [133] | 2014 | PSD | 2.33–2.45 | 100 nm | - |
| Park K. et al. [134] | 2014 | log–log plot | 1.22–1.53 | - | - |
| Arman A. et al. [135] | 2015 | PSD | 2.31–2.50 | 4.4 m | 0.1 m |
| Yadav R. P. et al. [20] | 2015 | PSD | 2.82–2.90 | 1 m | - |
| Yadav R. P. et al. [136] | 2015 | ACF&H-H | 2.07–2.40 | 20 m | - |
| Talu S. et al. [137] | 2015 | ACCF | 2.28-2.55 | - | - |
| Talu S. et al. [138] | 2015 | morphological envelopes | 2.33–2.66 | 1 m | - |
| Talu S. et al. [74] | 2016 | ACF/SF | 2.43–2.66 | 500 nm | 5 nm |
| Talu S. et al. [78] | 2016 | AACF/SF | 2.31–2.33 | 1 m | 4 nm |
| Talu S. et al. [139] | 2016 | SF | 2.33–2.36 (AFM) 2.64–2.93 (SEM) | 10 m | 2 nm |
| Talu S. et al. [140] | 2016 | SF | 2.42–2.84 | 10 m | 2 m |
| Talu S. et al. [77] | 2016 | AACF | 2.20–2.38 | - | - |
| Talu S. et al. [141] | 2016 | AACF | 2.27–2.49 | 50 nm | 2 nm |
| Talu S. et al. [32] | 2016 | AACF | 2.45–2.80 | 1 m | 2 nm |
| Feng F. et al. [76] | 2017 | RSE | 2.65–2.98 | 5 m | 0.5 m |
| Nasehnejad M. et al. [81] | 2017 | BC | 2.57–2.64 | 5 m | 0.7 m |
| Soumya S. et al. [43] | 2017 | BC/PSD | 1.63–1.99 | 1 m | - |
| Yadav R. P. et al. [91] | 2017 | Higuchi | 1.54–1.62 | 5 m | - |
| Talu S. et al. [73] | 2017 | Higuchi | 1.26–1.51 | 1 m | 0.2 m |
| Talu S. et al. [142] | 2017 | SF | 2.3–2.7 | 500 nm | 5 nm |
| Talu S. et al. [143] | 2017 | ACF/SF | 2.20–2.69 | - | - |
| Talu S. et al. [144] | 2017 | SF | 2.2–2.8 | 1 m | 7 nm |
| Sani Z. K. et al. [145] | 2017 | BC/triangulation method | 2.24–2.48 | 1 m | 200 nm |
| Nasehnejad M. et al. [146] | 2017 | height–height correlation | 2.33–2.45 | 1 m | 20 nm |
| Pan A. et al. [147] | 2017 | BC | 1.38–1.41 | - | - |
| Pandey R. K. et al. [87] | 2018 | PSD | 2.03–2.11 | 10 m | 0.25 m |
| Singh G. et al. [69] | 2018 | Higuchi | 1.68–1.89 | 25 m | - |
| Naseri N. et al. [82] | 2018 | ACF | 2.27–2.50 | - | - |
| Talu S. et al. [148] | 2018 | ACF | 2.24–2.66 | - | - |
| Talu S. et al. [149] | 2018 | ACF | 2.4–2.7 | - | - |
| Talu S. et al. [150] | 2018 | AACF | 2.30–2.42 | - | - |
| Talu S. et al. [151] | 2018 | ACF | 2.26–2.49 | - | - |
| Nabiyouni G. et al. [83] | 2018 | BC | 1.2–2 | 5 m | 1 m |
| Kim S. et al. [152] | 2018 | R-based algorithm | 1.04–1.65 | - | - |
| Kavyashree et al. [68] | 2019 | Higuchi | 1.31–1.67 | 2 m | - |
| Ren L. et al. [153] | 2019 | SF | 1.21–1.36 | - | - |
| Li B. et al. [154] | 2019 | BC | 1.94–2.14 | - | - |
| Zhu W. et al. [155] | 2019 | perimeter–area relationship | 1.2–1.9 | - | - |
| Ghosh K. et al. [86] | 2019 | Higuchi | 1.16–1.5 | 2 m | 8 nm |
| Mwema F. M. et al. [156] | 2019 | PSD | 2.12–2.40 | - | - |
| Pedro, G.d.C. et al. [157] | 2019 | BC | 1.54–1.66 | - | - |
| Talu S. et al. [63] | 2020 | BC | 2.78–2.32 | 1 m | - |
| Jafari A. et al. [158] | 2020 | BC | 2.06 | 1 m | - |
| Yildiz K. et al. [159] | 2020 | BC | 1.9 | - | - |
| Aminirastabi H. et al. [160] | 2020 | BC | 2.1–2.75 | - | - |
| Yang L. et al. [161] | 2021 | SF/BC/Diviers method | 1.6 | - | - |
| Dorgham A. et al. [162] | 2021 | BC/Triangulation | 2.14–2.30 | 10 m | - |
| Jiang Y. et al. [163] | 2021 | BC | 1.52–1.95 (monolayer) 1.98–1.83 (multilayer) | 128 m | 4 m |
| Jiang H. et al. [15] | 2021 | BC | 1.63 ± 0.01 | 10 nm | 0.1 nm |
| Romaguera Y. et al. [164] | 2021 | PSD | 2.21–2.28 | - | - |
Appendix A.2
| Authors | Year | Material | Fabrication | Characterization |
|---|---|---|---|---|
| Mitchell M. W. et al. [119] | 1990 | Gold, polycrystalline copper | sputter deposition | STM |
| Herrasti P. et al. [120] | 1992 | Au | electrochemically | STM |
| Krim J. et al. [14] | 1993 | iron | ion-beam erosion | STM |
| Ba L. et al. [121] | 1995 | Ge-22% Au | deposited & annealed | TEM |
| Strizhak P. E. [122] | 1995 | CuS | chemical synthesis | OM |
| Ba L. et al. [123] | 1996 | Ge-5% Au | deposited & annealed | TEM |
| Chen Z. W. et al. [124] | 2001 | Au/Ge | evaporation& annealed | TEM |
| Sun X. et al. [125] | 2002 | ZnO | reactive sputtering | AFM |
| Fang T. H. et al. [75] | 2003 | ZnO | magnetron sputtering | AFM |
| Wang Y. et al. [37] | 2004 | Cu-W | magnetron sputtering | AFM |
| Catalan G. et al. [126] | 2008 | multiferroic BiFeO3 | PLD | PFM |
| Raoufi D. [127] | 2010 | ITO | EBE | AFM |
| Raoufi D. [88] | 2010 | SiO2-SiO2 | polymeric sol-gel | AFM |
| Chen Z. W. et al. [128] | 2010 | SiO2 | PLD | SEM |
| Miyata S. et al. [129] | 2011 | MgO | Ion beam assisted deposition | AFM |
| Gao H. J. et al. [130] | 2011 | C60-polymer | ionized-cluster-beam | TEM |
| Chen Z. W. et al. [61] | 2011 | Pd/Ge | evaporation & annealing | TEM |
| Feng F. et al. [5] | 2012 | alumina/Hastelloy C276 | Ion beam assisted deposition | AFM |
| Ponomareva A. A. et al. [131] | 2014 | Oxide | sol-gel deposited | AFM |
| Hou L. et al. [132] | 2014 | Pd/Ge | thermal evaporation | TEM |
| Haniam P. et al. [79] | 2014 | cobalt oxides | laser CVD | SEM |
| Kong Y. L. et al. [133] | 2014 | TsNiPc | spin-coating & annealed | AFM |
| Park K. et al. [134] | 2014 | ferroelectric copolymer | spin-coating | PFM |
| Arman A. et al. [135] | 2015 | copper | magnetron sputtering | AFM |
| Yadav R. P. et al. [20] | 2015 | BaF2 | EBE | AFM |
| Yadav R. P. et al. [136] | 2015 | silicon | ion beam irradiation | AFM |
| Talu S. et al. [137] | 2015 | (FeNPs@a-C:H) | RE-PECVD | AFM |
| Talu S. et al. [138] | 2015 | TiN | magnetron sputtering | AFM |
| Talu S. et al. [74] | 2016 | carbon–nickel (C–Ni) | magnetron sputtering | AFM |
| Talu S. et al. [78] | 2016 | Cu/Co | magnetron sputtering | AFM |
| Talu S. et al. [139] | 2016 | silver | resistive evaporation | AFM |
| Talu S. et al. [140] | 2016 | resin-based composites | polymerised & polished | AFM |
| Talu S. et al. [77] | 2016 | Zinc Oxide | magnetron sputtering | AFM |
| Talu S. et al. [141] | 2016 | gold (NPs) | CVD | AFM |
| Talu S. et al. [32] | 2016 | Co/CP/X | Electrochemistry | SEM |
| Feng F. et al. [76] | 2017 | MgO | EPSAD | AFM |
| Nasehnejad M. et al. [81] | 2017 | silver | electrodeposition sputtering | AFM |
| Soumya S. et al. [43] | 2017 | ZnS | PLD | AFM |
| Yadav R. P. et al. [91] | 2017 | ZnO | atom beam sputtering | AFM |
| Talu S. et al. [73] | 2017 | Ag–Cu | magnetron sputtering | AFM |
| Talu S. et al. [142] | 2017 | carbon-nickel | magnetron sputtering | AFM |
| Talu S. et al. [165] | 2017 | contact lenses | polished | AFM |
| Talu S. et al. [143] | 2017 | filler nanoparticles | spin-coating | AFM |
| Talu S. et al. [144] | 2017 | Ni NPs@a-C | CVD | AFM |
| Sani Z. K. et al. [145] | 2017 | undoped & Cu-doped CeO2 | sol-gel | AFM |
| Nasehnejad M. et al. [146] | 2017 | silver | electrodeposition | AFM |
| Pan A. et al. [147] | 2017 | titanium oxide | inverse PLD | SCM |
| Nabiyouni G. et al. [83] | 2018 | silver | electrodeposited sputtering | AFM |
| Pandey R. K. et al. [87] | 2018 | Al: ZnO | spin-coating | AFM |
| Singh G. et al. [69] | 2018 | Multiferroic BiFeO3 | PLD | AFM |
| Naseri N. et al. [82] | 2018 | TiO2 | electrodeposition | SEM |
| Talu S. et al. [148] | 2018 | 2,6-diphenyl anthracene | evaporated in vacuum | AFM |
| Talu S. et al. [149] | 2018 | nanocomposite | sputtering & CVD | AFM |
| Talu S. et al. [150] | 2018 | ITO | magnetron sputtering | AFM |
| Talu S. et al. [151] | 2018 | CdTe after oxidation | Everson etch | AFM |
| Kim S. et al. [152] | 2018 | ferroelectric copolymer | spin-coating | AFM |
| Kavyashree et al. [68] | 2019 | BaF2 | EBE | AFM |
| Ren L. et al. [153] | 2019 | Ni–W–P | electroless plating | SEM |
| Li B. et al. [154] | 2019 | beta-SiC | laser CVD | SEM |
| Zhu W. et al. [155] | 2019 | C8-BTBT | meniscus-guided coating | OM |
| Ghosh K. et al. [86] | 2019 | ZnO | sol-gel spin-coating | AFM |
| Mwema F. M. et al. [156] | 2019 | Al | magnetron sputtering | AFM |
| Pedro, G.d.C. et al. [157] | 2019 | chlorophyll (Chl) | casting & drying | OM |
| Talu S. et al. [63] | 2020 | Ag–Cu | magnetron sputtering | AFM |
| Jafari A. et al. [158] | 2020 | copper oxide | magnetron sputtering | AFM |
| Yildiz K. et al. [159] | 2020 | montmorillonite | cast | OM |
| Aminirastabi H. et al. [160] | 2020 | BaTiO3 | sol-gel | - |
| Yang L. et al. [161] | 2021 | Pt | electroless plating | SEM |
| Jiang Y. et al. [163] | 2021 | MoS2 | CVD | OM |
| Jiang H. et al. [15] | 2021 | metallic glass | ion beam deposition | STEM |
| Romaguera Y. et al. [164] | 2021 | GdMnO3 | spin-coating | AFM |
References
- Freund, L.; Suresh, S. Thin Film Materials: Stress, Defect Formation, and Surface Evolution; Cambridge University Press: New York, NY, USA, 2004. [Google Scholar]
- Sayles, R.S.; Thomas, T.R. The spatial representation of surface roughness by means of the structure function: A practical alternative to correlation. Wear 1977, 42, 263–276. [Google Scholar] [CrossRef]
- Mandelbrot, B. Self-affinity and fractal dimension. Phys. Scr. 1985, 32, 257–260. [Google Scholar] [CrossRef]
- Koyuncu, I.; Brant, J.; Lüttge, A.; Wiesner, M.R. A comparison of vertical scanning interferometry (VSI) and atomic force microscopy (AFM) for characterizing membrane surface topography. J. Membr. Sci. 2006, 278, 410–417. [Google Scholar] [CrossRef]
- Feng, F.; Shi, K.; Xiao, S.Z.; Zhang, Y.Y.; Zhao, Z.J.; Wang, Z.; Wei, J.J.; Han, Z. Fractal analysis and atomic force microscopy measurements of surface roughness for Hastelloy C276 substrates and amorphous alumina buffer layers in coated conductors. Appl. Surf. Sci. 2012, 258, 3502–3508. [Google Scholar] [CrossRef]
- Boussu, K.; Van der Bruggen, B.; Volodin, A.; Snauwaert, J.; Van Haesendonck, C.; Vandecasteele, C. Roughness and hydrophobicity studies of nanofiltration membranes using different modes of AFM. J. Colloid Interface Sci. 2005, 286, 632–638. [Google Scholar] [CrossRef]
- Qiao, Y.; Chen, Y.; Xiong, X.; Kim, S.; Matias, V.; Sheehan, C.; Zhang, Y.; Selvamanickam, V. Scale Up of Coated Conductor Substrate Process by Reel-to-Reel Planarization of Amorphous Oxide Layers. IEEE Trans. Appl. Supercond. 2011, 21, 3055–3058. [Google Scholar] [CrossRef]
- Mandelbrot, B. How long is the coast of britain? Statistical self-similarity and fractional dimension. Science 1967, 156, 636–638. [Google Scholar] [CrossRef]
- Campbell, P.; Abhyankar, S. Fractals, form, chance and dimension. Math. Intell. 1978, 1, 35–37. [Google Scholar] [CrossRef]
- Mandelbrot, B.B.; Wheeler, J.A. The Fractal Geometry of Nature. Am. J. Phys. 1983, 51, 286–287. [Google Scholar] [CrossRef]
- Yehoda, J.E.; Messier, R. Are thin-film physical structures fractals. Appl. Surf. Sci. 1985, 22–23, 590–595. [Google Scholar] [CrossRef]
- Messier, R.; Yehoda, J.E. Geometry of thin-film morphology. J. Appl. Phys. 1985, 58, 3739–3746. [Google Scholar] [CrossRef]
- Barabasi, A.L.; Stanley, H.E.; Sander, L.M. Fractal Concepts in Surface Growth. Phys. Today 1995, 48, 68–69. [Google Scholar] [CrossRef]
- Krim, J.; Heyvaert, I.I.; Van Haesendonck, C.; Bruynseraede, Y. Scanning tunneling microscopy observation of self-affine fractal roughness in ion-bombarded film surfaces. Phys. Rev. Lett. 1993, 70, 57–60. [Google Scholar] [CrossRef]
- Jiang, H.; Xu, J.; Zhang, Q.; Yu, Q.; Shen, L.; Liu, M.; Sun, Y.; Cao, C.; Su, D.; Bai, H.; et al. Direct observation of atomic-level fractal structure in a metallic glass membrane. Sci. Bull. 2021, 66, 1312–1318. [Google Scholar] [CrossRef]
- Habenicht, S.; Bolse, W.; Lieb, K.P.; Reimann, K.; Geyer, U. Nanometer ripple formation and self-affine roughening of ion-beam-eroded graphite surfaces. Phys. Rev. B 1999, 60, R2200–R2203. [Google Scholar] [CrossRef]
- Eklund, E.A.; Bruinsma, R.; Rudnick, J.; Williams, R.S. Submicron-scale surface roughening induced by ion bombardment. Phys. Rev. Lett. 1991, 67, 1759–1762. [Google Scholar] [CrossRef]
- Stanley, H.E.; Meakin, P. Multifractal phenomena in physics and chemistry. Nature 1988, 335, 405–409. [Google Scholar] [CrossRef]
- Sreenivasan, K.R. Fractals and Multifractals in Fluid Turbulence. Annu. Rev. Fluid Mech. 1991, 23, 539. [Google Scholar] [CrossRef]
- Yadav, R.P.; Kumar, M.; Mittal, A.K.; Pandey, A.C. Fractal and multifractal characteristics of swift heavy ion induced self-affine nanostructured BaF2 thin film surfaces. Chaos 2015, 25, 83115. [Google Scholar] [CrossRef]
- Smith, T.G.; Lange, G.D.; Marks, W.B. Fractal methods and results in cellular morphology—Dimensions, lacunarity and multifractals. J. Neurosci. Methods 1996, 69, 123–136. [Google Scholar] [CrossRef]
- Berry, M.V.; Lewis, Z.V. On the Weierstrass-Mandelbrot fractal function. Proc. R. Soc. Lond. Ser.-Math. Phys. Sci. 1980, 370, 459–484. [Google Scholar] [CrossRef]
- Wang, S.; Zhang, J.; Feng, F.; Qian, X.; Jiang, L.; Huang, J.; Liu, B.; Li, J.; Xia, Y.; Feng, P. Fractal analysis on artificial profiles and electroencephalography signals by roughness scaling extraction algorithm. IEEE Access 2019, 7, 89265–89277. [Google Scholar] [CrossRef]
- Feng, F.; Liu, B.; Zhang, X.; Qian, X.; Li, X.; Huang, J.; Qu, T.; Feng, P. Roughness scaling extraction method for fractal dimension evaluation based on a single morphological image. Appl. Surf. Sci. 2018, 458, 489–494. [Google Scholar] [CrossRef]
- Majumdar, A.; Tien, C.L. Fractal characterization and simulation of rough surfaces. Wear 1990, 136, 313–327. [Google Scholar] [CrossRef]
- Gou, X.; Schwartz, J. Fractal analysis of the role of the rough interface between Bi2Sr2CaCu2Oxfilaments and the Ag matrix in the mechanical behavior of composite round wires. Supercond. Sci. Technol. 2013, 26, 55016. [Google Scholar] [CrossRef]
- Feng, F.; Huang, J.L.; Li, X.H.; Qu, T.M.; Liu, B.B.; Zhou, W.M.; Qian, X.; Feng, P.F. Influences of planarization modification and morphological filtering by AFM probe-tip on the evaluation accuracy of fractal dimension. Surf. Coat. Technol. 2019, 363, 436–441. [Google Scholar] [CrossRef]
- Takagi, T. A simple example of the continuous function without derivative. Collect. Pap. Teiji Takagi 1973, 5–6. [Google Scholar] [CrossRef]
- Raghavendra, B.S.; Narayana Dutt, D. A note on fractal dimensions of biomedical waveforms. Comput. Biol. Med. 2009, 39, 1006–1012. [Google Scholar] [CrossRef]
- Hata, M.; Yamaguti, M. The Takagi function and its generalization. Jpn. J. Appl. Math. 1984, 1, 183–199. [Google Scholar] [CrossRef]
- Falconer, K.J. Fractal geometry-mathematical foundations and applications. Biometrics 1990, 46, 499. [Google Scholar] [CrossRef]
- Talu, S.; Solaymani, S.; Bramowicz, M.; Naseri, N.; Kulesza, S.; Ghaderi, A. Surface micromorphology and fractal geometry of Co/CP/X (X = Cu, Ti, SM and Ni) nanoflake electrocatalysts. RSC Adv. 2016, 6, 27228–27234. [Google Scholar] [CrossRef]
- Risović, D.; Poljaček, S.M.; Furić, K.; Gojo, M. Inferring fractal dimension of rough/porous surfaces—A comparison of SEM image analysis and electrochemical impedance spectroscopy methods. Appl. Surf. Sci. 2008, 255, 3063–3070. [Google Scholar] [CrossRef]
- Kizu, R.; Misumi, I.; Hirai, A.; Gonda, S. Direct comparison of line edge roughness measurements by SEM and a metrological tilting-atomic force microscopy for reference metrology. J. Micro-Nanolithogr. Mems Moems 2020, 19, 44001. [Google Scholar] [CrossRef]
- Liebovitch, L.S.; Toth, T. A fast algorithm to determine fractal dimensions by box counting. Phys. Lett. A 1989, 141, 386–390. [Google Scholar] [CrossRef]
- Higuchi, T. Approach to an irregular time-series on the basis of the farctal theory. Phys. D-Nonlinear Phenom. 1988, 31, 277–283. [Google Scholar] [CrossRef]
- Wang, Y.; Xu, K.W. Characterization of surface morphology of copper tungsten thin film by surface fractal geometry and resistivity. Thin Solid Film 2004, 468, 310–315. [Google Scholar] [CrossRef]
- Katz, M.J. Fractals and the analysis of waveforms. Comput. Biol. Med. 1988, 18, 145–156. [Google Scholar] [CrossRef]
- Meakin, P.; Vicsek, T.; Family, F. Dynamic cluster-size distribution in cluster-cluster aggregation: Effects of cluster diffusivity. Phys. Rev. B 1985, 31, 564–569. [Google Scholar] [CrossRef]
- Li, J.M.; Li, L.; Lai, M.O.; Ralph, B. Image-Based Fractal Description of Microstructures; Springer: Berlin/Heidelberg, Germany, 2003. [Google Scholar]
- Yadav, R.P.; Kumar, M.; Mittal, A.K.; Dwivedi, S.; Pandey, A.C. On the scaling law analysis of nanodimensional LiF thin film surfaces. Mater. Lett. 2014, 126, 123–125. [Google Scholar] [CrossRef]
- Mwema, F.M.; Akinlabi, E.T.; Oladijo, O.P. Fractal Analysis of Thin Films Surfaces: A Brief Overview. In Advances in Material Sciences and Engineering; Springer: Berlin/Heidelberg, Germany, 2020; pp. 251–263. [Google Scholar] [CrossRef]
- Soumya, S.; Swapna, M.S.; Raj, V.; Pillai, V.P.M.; Sankararaman, S. Fractal analysis as a potential tool for surface morphology of thin films. Eur. Phys. J. Plus 2017, 132, 551. [Google Scholar] [CrossRef]
- Kulesza, S.; Bramowicz, M. A comparative study of correlation methods for determination of fractal parameters in surface characterization. Appl. Surf. Sci. 2014, 293, 196–201. [Google Scholar] [CrossRef]
- Zhou, W.M.; Li, X.H.; Feng, F.; Qu, T.M.; Huang, J.L.; Qian, X.; Zha, H.T.; Feng, P.F. Robustness of surface roughness against low number of picture elements and its benefit for scaling analysis. Coatings 2020, 10, 776. [Google Scholar] [CrossRef]
- Qadri, M.O.; Namazi, H. Fractal-based analysis of the relation between surface finish and machine vibration in milling operation. Fluct. Noise Lett. 2019, 19, 2050006. [Google Scholar] [CrossRef]
- Melbouci, B.; Yezli, S. Influence of the Fractal Dimension on the Mechanical Properties of Granular Materials. Key Eng. Mater. 2013, 550, 99–106. [Google Scholar] [CrossRef]
- Zhao, H.; Wu, Q.L. Application study of fractal theory in mechanical transmission. Chin. J. Mech. Eng. 2016, 29, 871–879. [Google Scholar] [CrossRef]
- Tian, F.; Jiang, A.; Yang, T.; Qian, J.; Liu, R.; Jiang, M. Application of fractal geometry in gas sensor: A review. IEEE Sens. J. 2021, 21, 14587–14600. [Google Scholar] [CrossRef]
- Zheng, G.M.; Zhao, J.; Li, Z.Y.; Cheng, X.; Li, L. Fractal characterization of the friction forces of a graded ceramic tool material. Int. J. Adv. Manuf. Technol. 2014, 74, 707–714. [Google Scholar] [CrossRef]
- Kang, M.C.; Kim, J.S.; Kim, K.H. Fractal dimension analysis of machined surface depending on coated tool wear. Surf. Coat. Technol. 2005, 193, 259–265. [Google Scholar] [CrossRef]
- Edwards, S.F.; Wilkinson, D. The surface statistics of a granular aggregate. Proc. R. Soc. Lond. A Math. Phys. Sci. 1982, 381, 17–31. [Google Scholar]
- Kardar, M.; Parisi, G.; Zhang, Y.C. Dynamic scaling of growing interfaces. Phys. Rev. Lett. 1986, 56, 889. [Google Scholar] [CrossRef]
- Lai, Z.W.; Sarma, S.D. Kinetic growth with surface relaxation: Continuum versus atomistic models. Phys. Rev. Lett. 1991, 66, 2348. [Google Scholar] [CrossRef]
- Kuramoto, Y. Diffusion-induced chaos in reaction systems. Prog. Theor. Phys. Suppl. 1978, 64, 346–367. [Google Scholar] [CrossRef]
- Ghosh, K.; Pandey, R. Fractal assessment of thin films deposited by random and ballistic deposition models. AIP Conf. Proc. 2020, 2265, 30316. [Google Scholar]
- Qi, H.J.; Shao, J.D.; Zhang, D.P.; Yi, K.; Fan, Z.X. Simulation of growth process of thin film on non-planar substrate. Appl. Surf. Sci. 2005, 249, 85–90. [Google Scholar] [CrossRef]
- Pelliccione, M.; Karabacak, T.; Gaire, C.; Wang, G.C.; Lu, T.M. Mound formation in surface growth under shadowing. Phys. Rev. B 2006, 74, 125420. [Google Scholar] [CrossRef]
- Paritosh; Srolovitz, D.J. Shadowing effects on the microstructure of obliquely deposited films. J. Appl. Phys. 2002, 91, 1963–1972. [Google Scholar] [CrossRef]
- Bourlier, C.; Berginc, G.; Saillard, J. One- and two-dimensional shadowing functions for any height and slope stationary uncorrelated surface in the monostatic and bistatic configurations. IEEE Trans. Antennas Propag. 2002, 50, 312–324. [Google Scholar] [CrossRef]
- Chen, Z.; Li, Q.; Wang, J.; Pan, D.; Jiao, Z.; Wu, M.; Shek, C.H.; Wu, C.M.; Lai, J.K. Probing into interesting effects of fractal Ge nanoclusters induced by Pd nanoparticles. Inorg. Chem. 2011, 50, 6756–6761. [Google Scholar] [CrossRef]
- Das, A.; Chawla, V.; Matos, R.S.; da Fonseca Filho, H.D.; Yadav, R.P.; Talu, S.; Kumar, S. Surface microtexture and wettability analysis of Quasi Two-Dimensional (Ti, Al)N thin films using Fractal Geometry. Surf. Coat. Technol. 2021, 421, 127420. [Google Scholar] [CrossRef]
- Talu, S.; Matos, R.S.; Pinto, E.P.; Rezaee, S.; Mardani, M. Stereometric and fractal analysis of sputtered Ag-Cu thin films. Surfaces Interfaces 2020, 21, 100650. [Google Scholar] [CrossRef]
- Matos, R.S.; Lopes, G.A.C.; Ferreira, N.S.; Pinto, E.P.; Carvalho, J.C.T.; Figueiredo, S.S.; Oliveira, A.F.; Zamora, R.R.M. Superficial Characterization of Kefir Biofilms Associated with Açaí and Cupuaçu Extracts. Arab. J. Sci. Eng. 2017, 43, 3371–3379. [Google Scholar] [CrossRef]
- De Melo, R.H.C.; Conci, A. Succolarity: Defining a method to calculate this fractal measure. In Proceedings of the Iwssip 2008, 15th International Conference on Systems, Signals and Image Processing, Bratislava, Slovakia, 25–28 June 2008; pp. 291–294. [Google Scholar] [CrossRef]
- Matos, R.S.; Ramos, G.Q.; da Fonseca Filho, H.D.; Talu, S. Advanced micromorphology study of microbial films grown on Kefir loaded with Acai extract. Micron 2020, 137, 102912. [Google Scholar] [CrossRef]
- Mandelbrot, B.B. A Fractal’s Lacunarity, and how it can be Tuned and Measured. In Fractals in Biology and Medicine; Springer: Basel, Switzerland, 1994; pp. 8–21. [Google Scholar] [CrossRef]
- Pandey, R.K.; Yadav, R.P.; Kumar, M.; Bhasker, H.P.; Mittal, A.K.; Pandey, A.C.; Pandey, S.N. Substrate effect on the evolution of surface morphology of BaF2thin films: A study based on fractal concepts. Appl. Surf. Sci. 2019, 466, 780–786. [Google Scholar] [CrossRef]
- Singh, G.; Yadav, R.P.; Bhasker, H.P.; Kumar, M.; Rajput, P.; Rao, P.N.; Rai, S.K.; Singh, M.K. Investigation of fractal feature of multiferroic BiFeO3 thin films deposited on different substrates. Mater. Res. Express 2018, 5, 126405. [Google Scholar] [CrossRef]
- Fetisov, I.K.; Filippov, A.A.; Khodachenko, G.V.; Mozgrin, D.V.; Pisarev, A.A. Impulse irradiation plasma technology for film deposition. Vacuum 1999, 53, 133–136. [Google Scholar] [CrossRef]
- Alami, J.; Eklund, P.; Emmerlich, J.; Wilhelmsson, O.; Jansson, U.; Högberg, H.; Hultman, L.; Helmersson, U. High-power impulse magnetron sputtering of Ti–Si–C thin films from a Ti3SiC2 compound target. Thin Solid Film 2006, 515, 1731–1736. [Google Scholar] [CrossRef]
- Gaedike, B.; Guth, S.; Kern, F.; Killinger, A.; Gadow, R. Deposition of 3YSZ-TiC PVD Coatings with High-Power Impulse Magnetron Sputtering (HiPIMS). Appl. Sci. 2021, 11, 2753. [Google Scholar] [CrossRef]
- Talu, S.; Yadav, R.P.; Mittal, A.K.; Achour, A.; Luna, C.; Mardani, M.; Solaymani, S.; Arman, A.; Hafezi, F.; Ahmadpourian, A. Application of Mie theory and fractal models to determine the optical and surface roughness of Ag–Cu thin films. Opt. Quantum Electron. 2017, 49, 256. [Google Scholar] [CrossRef]
- Talu, S.; Bramowicz, M.; Kulesza, S.; Dalouji, V.; Solaymani, S.; Valedbagi, S. Fractal features of carbon-nickel composite thin films. Microsc. Res. Tech. 2016, 79, 1208–1213. [Google Scholar] [CrossRef]
- Fang, T.H.; Jian, S.R.; Chuu, D.S. Nanotribology and fractal analysis of ZnO thin films using scanning probe microscopy. J. Phys. D-Appl. Phys. 2003, 36, 878–883. [Google Scholar] [CrossRef]
- Feng, F.; Zhang, X.S.; Qu, T.M.; Liu, B.B.; Huang, J.L.; Li, J.; Xiao, S.Z.; Han, Z.H.; Feng, P.F. Surface scaling analysis of textured MgO thin films fabricated by energetic particle self-assisted deposition. Appl. Surf. Sci. 2017, 437, 287–293. [Google Scholar] [CrossRef]
- Talu, S.; Bramowicz, M.; Kulesza, S.; Solaymani, S.; Ghaderi, A.; Dejam, L.; Elahi, S.M.; Boochani, A. Microstructure and micromorphology of ZnO thin films: Case study on Al doping and annealing effects. Superlattices Microstruct. 2016, 93, 109–121. [Google Scholar] [CrossRef]
- Talu, S.; Bramowicz, M.; Kulesza, S.; Ghaderi, A.; Dalouji, V.; Solaymani, S.; Khalaj, Z. Microstructure and micromorphology of Cu/Co nanoparticles: Surface texture analysis. Electron. Mater. Lett. 2016, 12, 580–588. [Google Scholar] [CrossRef]
- Haniam, P.; Kunsombat, C.; Chiangga, S.; Songsasen, A. Synthesis of cobalt oxides thin films fractal structures by laser chemical vapor deposition. Sci. World J. 2014, 2014, 685270. [Google Scholar] [CrossRef] [PubMed]
- Li, J.; Chen, M.; Zhang, C.; Dong, H.; Lin, W.; Zhuang, P.; Wen, Y.; Tian, B.; Cai, W.; Zhang, X. Fractal-Theory-Based Control of the Shape and Quality of CVD-Grown 2D Materials. Adv. Mater. 2019, 31, e1902431. [Google Scholar] [CrossRef] [PubMed]
- Nasehnejad, M.; Nabiyouni, G.; Shahraki, M.G. Fractal analysis of nanostructured silver film surface. Chin. J. Phys. 2017, 55, 2484–2490. [Google Scholar] [CrossRef]
- Naseri, N.; Talu, S.; Kulesza, S.; Qarechalloo, S.; Achour, A.; Bramowicz, M.; Ghaderi, A.; Solaymani, S. How morphological surface parameters are correlated with electrocatalytic performance of cobalt-based nanostructures. J. Ind. Eng. Chem. 2018, 57, 97–103. [Google Scholar] [CrossRef]
- Nabiyouni, G.; Nasehnejad, M. Conventional and fractal analyses and nanoscale behavior studies of electrodeposited silver films. Phys. B Condens. Matter 2018, 548, 46–52. [Google Scholar] [CrossRef]
- Roy, J.; Das, S.; Maitra, S. Solgel-processed mullite coating-a review. Int. J. Appl. Ceram. Technol. 2015, 12, E71–E77. [Google Scholar] [CrossRef]
- Brinker, C.J.; Brinker, C.J.; Scherer, G.W. Sol-Gel Science: The Physics and Chemistry of Sol-Gel Processing; Gulf Professional Publishing: Houston, TX, USA, 1990. [Google Scholar]
- Ghosh, K.; Pandey, R.K. Fractal assessment of ZnO thin films using Higuchi’s algorithm. Aip Conf. Proc. 2019, 2115, 30280. [Google Scholar] [CrossRef]
- Pandey, R.K.; Ghosh, K.; Mishra, S.; Bange, J.P.; Bajpai, P.K.; Gautam, D.K. Effect of film thickness on structural and optical properties of sol-gel spin coated aluminum doped zinc oxide (Al:ZnO) thin films. Mater. Res. Express 2018, 5, 86408. [Google Scholar] [CrossRef]
- Raoufi, D. Fractal analyses of ITO thin films: A study based on power spectral density. Phys. B-Condens. Matter 2010, 405, 451–455. [Google Scholar] [CrossRef]
- Solaymani, S.; Kulesza, S.; Talu, S.; Bramowicz, M.; Nezafat, N.B.; Dalouji, V.; Rezaee, S.; Karami, H.; Malekzadeh, M.; Dorbidi, E.S. The effect of different laser irradiation on rugometric and microtopographic features in zirconia ceramics: Study of surface statistical metrics. J. Alloy Compd. 2018, 765, 180–185. [Google Scholar] [CrossRef]
- Kiew, C.L.; Brahmananda, A.; Islam, K.T.; Lee, H.N.; Venier, S.A.; Saraar, A.; Namazi, H. Analysis of the relation between fractal structures of machined surface and machine vibration signal in turning operation. Fractals 2020, 28, 2050019. [Google Scholar] [CrossRef]
- Yadav, R.P.; Agarwal, D.C.; Kumar, M.; Rajput, P.; Tomar, D.S.; Pandey, S.N.; Priya, P.K.; Mittal, A.K. Effect of angle of deposition on the Fractal properties of ZnO thin film surface. Appl. Surf. Sci. 2017, 416, 51–58. [Google Scholar] [CrossRef]
- Gneiting, T.; Schlather, M. Stochastic models that separate fractal dimension and the Hurst effect. Siam Rev. 2004, 46, 269–282. [Google Scholar] [CrossRef]
- Avnir, D.; Biham, O.; Lidar, D.; Malcai, O. Is the geometry of nature fractal? Science 1998, 279, 39–40. [Google Scholar] [CrossRef]
- Ji, C.; Zhu, H.; Jiang, W. A novel method to identify the scaling region for chaotic time series correlation dimension calculation. Chin. Sci. Bull. 2011, 56, 925–932. [Google Scholar] [CrossRef]
- Yokoya, N.; Yamamoto, K.; Funakubo, N. Fractal-based analysis and interpolation of 3D natural surface shapes and their application to terrain modeling. Comput. Vis. Graph. Image Process. 1989, 45, 284–302. [Google Scholar] [CrossRef]
- Fei, B.; Jiang, Z.; Wang, H. Genetic algorithm for determining scale independent fractals associated with grinding surface. J. Xi’An Jiaotong Univ. 1998, 32, 74–77. [Google Scholar]
- Zuo, X.; Tang, X.; Zhou, Y. Influence of sampling length on estimated fractal dimension of surface profile. Chaos Solitons Fractals 2020, 135, 109755. [Google Scholar] [CrossRef]
- Li, Z.; Li, J.; Xia, Y.; Feng, P.; Feng, F. Variation trends of fractal dimension in epileptic EEG signals. Algorithms 2021, 14, 316. [Google Scholar] [CrossRef]
- Yang, F.; Ning, Z.; Liu, H. Fractal characteristics of shales from a shale gas reservoir in the Sichuan Basin, China. Fuel 2014, 115, 378–384. [Google Scholar] [CrossRef]
- Zhang, X.; Zhou, Q.; Yuan, M.; Liao, B.; Wu, X.; Ying, M. Etching-controlled preparation of large-area fractal graphene by low-pressure CVD on polycrystalline Cu substrate. Mater. Today Commun. 2020, 24, 101093. [Google Scholar] [CrossRef]
- Modabberasl, A.; Sharifi, M.; Shahbazi, F.; Kameli, P. Multifractal analysis of DLC thin films deposited by pulsed laser deposition. Appl. Surf. Sci. 2019, 479, 639–645. [Google Scholar] [CrossRef]
- Singh, U.B.; Yadav, R.P.; Pandey, R.K.; Agarwal, D.C.; Pannu, C.; Mittal, A.K. Insight mechanisms of surface structuring and wettability of ion-treated Ag thin films. J. Phys. Chem. C 2016, 120, 5755–5763. [Google Scholar] [CrossRef]
- Zuo, R.; Wang, J. Fractal/multifractal modeling of geochemical data: A review. J. Geochem. Explor. 2016, 164, 33–41. [Google Scholar] [CrossRef]
- Nasehnejad, M.; Gholipour Shahraki, M.; Nabiyouni, G. Atomic force microscopy study, kinetic roughening and multifractal analysis of electrodeposited silver films. Appl. Surf. Sci. 2016, 389, 735–741. [Google Scholar] [CrossRef]
- Dallaeva, D.; Talu, S.; Stach, S.; Skarvada, P.; Tomanek, P.; Grmela, L. AFM imaging and fractal analysis of surface roughness of AlN epilayers on sapphire substrates. Appl. Surf. Sci. 2014, 312, 81–86. [Google Scholar] [CrossRef]
- Kantelhardt, J.W.; Zschiegner, S.A.; Koscielny-Bunde, E.; Havlin, S.; Bunde, A.; Stanley, H.E. Multifractal detrended fluctuation analysis of nonstationary time series. Phys. A Stat. Mech. Its Appl. 2002, 316, 87–114. [Google Scholar] [CrossRef]
- Zhang, X.; Zhang, G.; Qiu, L.; Zhang, B.; Sun, Y.; Gui, Z.; Zhang, Q. A Modified Multifractal Detrended Fluctuation Analysis (MFDFA) Approach for Multifractal Analysis of Precipitation in Dongting Lake Basin, China. Water 2019, 11, 891. [Google Scholar] [CrossRef]
- Zhou, G.U.O.; Wang, X.; Feng, F.; Feng, P.; Zhang, M.I.N. Calculation of fractal dimension based on artificial neural network and its application for machined surfaces. Fractals 2021, 29, 2150129-1936. [Google Scholar] [CrossRef]
- Xie, S.; Zhou, W.; Zhu, Y. Formation Mechanism of Mg2SiO4 Fishbone-like Fractal Nanostructures. J. Phys. Chem. B 2004, 108, 11561–11566. [Google Scholar] [CrossRef]
- Azpeitia, E.; Tichtinsky, G.; Le Masson, M.; Serrano-Mislata, A.; Lucas, J.; Gregis, V.; Gimenez, C.; Prunet, N.; Farcot, E.; Kater, M.M.; et al. Cauliflower fractal forms arise from perturbations of floral gene networks. Science 2021, 373, 192–197. [Google Scholar] [CrossRef]
- Yu, S.; Lakshminarayanan, V. Fractal dimension and retinal pathology: A meta-analysis. Appl. Sci. 2021, 11, 2376. [Google Scholar] [CrossRef]
- Liu, Y.; Chang, L.; Hu, Y.; Niu, Q.; Yu, L.; Wang, Y.; Lu, P.; Wu, Y. Rough interface in IPMC: Modeling and its influence analysis. Smart Mater. Struct. 2018, 27, 75055. [Google Scholar] [CrossRef]
- Zou, M.Q.; Yu, B.M.; Feng, Y.J.; Xu, P. A Monte Carlo method for simulating fractal surfaces. Phys. A-Stat. Mech. Its Appl. 2007, 386, 176–186. [Google Scholar] [CrossRef]
- Warren, T.L.; Krajcinovic, D. Fractal models of elastic-perfectly plastic contact of rough surfaces based on the Cantor set. Int. J. Solids Struct. 1995, 32, 2907–2922. [Google Scholar] [CrossRef]
- Warren, T.L.; Krajcinovic, D. Random Cantor set models for the elastic-perfectly plastic contact of rough surfaces. Wear 1996, 196, 1–15. [Google Scholar] [CrossRef]
- Wang, M.; Sun, H.; Cheng, L. Investigation of convective heat transfer performance in nanochannels with fractal Cantor structures. Int. J. Heat Mass Transf. 2021, 171, 121086. [Google Scholar] [CrossRef]
- Wu, S.; Cheng, Q.; Peng, Q.; Shen, C. Molecular Dynamics Study on Liquid Film Evaporation on the Fractal Rough Surfaces. Fractals 2019, 27, 1950081. [Google Scholar] [CrossRef]
- Singh, U.B.; Yadav, R.P.; Kumar, R.; Ojha, S.; Mittal, A.K.; Ghosh, S.; Singh, F. Nanostructuring and wettability of ion treated Au thin films. J. Appl. Phys. 2017, 122, 185303. [Google Scholar] [CrossRef]
- Mitchell, M.W.; Bonnell, D.A. Quantitative topographic analysis of fractal surfaces by scanning tunneling microscopy. J. Mater. Res. 1990, 5, 2244–2254. [Google Scholar] [CrossRef]
- Herrasti, P.; Ocon, P.; Salvarezza, R.C.; Vara, J.M.; Vazquez, L.; Arvia, A.J. A comparative-study of electrodeposited and vapor-deposited Gold-Films-fractal surface characterization through scanning tunneling microscopy. Electrochim. Acta 1992, 37, 2209–2214. [Google Scholar] [CrossRef]
- Ba, L.; Zen, J.L.; Zhang, S.Y.; Wu, Z.Q. Fractals in annealed Ge-Au Au bilayer films. J. Appl. Phys. 1995, 77, 587–590. [Google Scholar] [CrossRef]
- Strizhak, P.E. New approach to synthesis of fractal materials with a given fractal dimension. synthesis and some properties of amorphous fractal films of copper sulfide. Berichte Bunsenges. Phys. Chem. 1995, 99, 1226–1229. [Google Scholar] [CrossRef]
- Ba, L.; Zeng, J.L.; Zhang, S.Y.; Wu, Z.Q. Microstructure and fractal formation of annealed Ge-Au film and Ge-Au/Au bilayer films. Acta Phys. Sin.-Overseas Ed. 1996, 5, 530–537. [Google Scholar]
- Chen, Z.W.; Wang, X.P.; Tan, S.; Zhang, S.Y.; Hou, J.G.; Wu, Z.Q. Multifractal behavior of crystallization on Au/Ge bilayer films. Phys. Rev. B 2001, 63, 5. [Google Scholar] [CrossRef]
- Sun, X.; Fu, Z.X.; Wu, Z.Q. Fractal processing of AFM images of rough ZnO films. Mater. Charact. 2002, 48, 169–175. [Google Scholar] [CrossRef]
- Catalan, G.; Béa, H.; Fusil, S.; Bibes, M.; Paruch, P.; Barthélémy, A.; Scott, J.F. Fractal dimension and size scaling of domains in thin films of multiferroic BiFeO3. Phys. Rev. Lett. 2008, 100, 27602. [Google Scholar] [CrossRef]
- Raoufi, D.; Fallah, H.R.; Kiasatpour, A.; Rozatian, A.S.H. Multifractal analysis of ITO thin films prepared by electron beam deposition method. Appl. Surf. Sci. 2008, 254, 2168–2173. [Google Scholar] [CrossRef]
- Chen, Z.; Pan, D.; Zhao, B.; Ding, G.; Jiao, Z.; Wu, M.; Shek, C.H.; Wu, L.C.; Lai, J.K. Insight on fractal assessment strategies for tin dioxide thin films. ACS Nano 2010, 4, 1202–1208. [Google Scholar] [CrossRef]
- Miyata, S.; Ibi, A.; Izumi, T.; Shiohara, Y. Surface roughness of MgO thin film and its critical thickness for optimal biaxial texturing by ion-beam-assisted deposition. J. Appl. Phys. 2011, 109, 219. [Google Scholar] [CrossRef]
- Gao, H.J.; Xue, Z.Q.; Wu, Q.D.; Pang, S. Observation of fractal patterns in C60-polymer thin films. J. Mater. Res. 2011, 9, 2216–2218. [Google Scholar] [CrossRef]
- Ponomareva, A.A.; Moshnikov, V.A.; Suchaneck, G. Evaluation of the fractal dimension of sol-gel deposited oxide films by means of the power spectral density. Glass Phys. Chem. 2014, 40, 203–207. [Google Scholar] [CrossRef]
- Hou, L.; Liu, P.; Chen, Z.; Wang, W.; Shek, C.H.; Lawrence Wu, C.M.; Lai, J.K.L. Annealing-dependent growth and nonlinear electrical properties of fractal Ge nanojoints based on Pd matrix. Mater. Lett. 2014, 115, 29–33. [Google Scholar] [CrossRef]
- Kong, Y.L.; Muniandy, S.V.; Fakir, M.S.; Sulaiman, K. Morphological image interpretation of organic nickel(II) phthalocyanine-tetrasulfonic acid tetrasodium film using fractal analysis. Appl. Surf. Sci. 2014, 301, 363–368. [Google Scholar] [CrossRef]
- Park, K.W.; Seo, H.; Kim, J.; Seol, D.; Hong, J.; Kim, Y. Humidity effect of domain wall roughening behavior in ferroelectric copolymer thin films. Nanotechnology 2014, 25, 355703. [Google Scholar] [CrossRef]
- Arman, A.; Talu, S.; Luna, C.; Ahmadpourian, A.; Naseri, M.; Molamohammadi, M. Micromorphology characterization of copper thin films by AFM and fractal analysis. J. Mater. Sci.-Mater. Electron. 2015, 26, 9630–9639. [Google Scholar] [CrossRef]
- Yadav, R.P.; Kumar, T.; Mittal, A.K.; Dwivedi, S.; Kanjilal, D. Fractal characterization of the silicon surfaces produced by ion beam irradiation of varying fluences. Appl. Surf. Sci. 2015, 347, 706–712. [Google Scholar] [CrossRef]
- Talu, S.; Bramowicz, M.; Kulesza, S.; Shafiekhani, A.; Ghaderi, A.; Mashayekhi, F.; Solaymani, S. Microstructure and tribological properties of FeNPs@a-C:H films by micromorphology analysis and fractal geometry. Ind. Eng. Chem. Res. 2015, 54, 8212–8218. [Google Scholar] [CrossRef]
- Ţalu, S.; Stach, S.; Valedbagi, S.; Elahi, S.M.; Bavadi, R. Surface morphology of titanium nitride thin films synthesized by DC reactive magnetron sputtering. Mater. Sci.-Pol. 2015, 33, 137–143. [Google Scholar] [CrossRef][Green Version]
- Talu, S.; Bramowicz, M.; Kulesza, S.; Ghaderi, A.; Solaymani, S.; Savaloni, H.; Babaei, R. Micromorphology analysis of specific 3-D surface texture of silver chiral nanoflower sculptured structures. J. Ind. Eng. Chem. 2016, 43, 164–169. [Google Scholar] [CrossRef]
- Talu, S.; Bramowicz, M.; Kulesza, S.; Lainovic, T.; Vilotic, M.; Blazic, L. Influence of the artificial saliva storage on 3-D surface texture characteristics of contemporary dental nanocomposites. J. Microsc. 2016, 264, 198–206. [Google Scholar] [CrossRef] [PubMed]
- Talu, S.; Bramowicz, M.; Kulesza, S.; Solaymani, S.; Shafikhani, A.; Ghaderi, A.; Ahmadirad, M. Gold nanoparticles embedded in carbon film: Micromorphology analysis. J. Ind. Eng. Chem. 2016, 35, 158–166. [Google Scholar] [CrossRef]
- Talu, S.; Bramowicz, M.; Kulesza, S.; Dalouji, V.; Ilkhani, M.; Ghaderi, A.; Solaymani, S. Influence of annealing process on surface micromorphology of carbon-nickel composite thin films. Opt. Quantum Electron. 2017, 49, 9. [Google Scholar] [CrossRef]
- Talu, S.; Bramowicz, M.; Kulesza, S.; Pignatelli, F.; Salerno, M. Surface morphology analysis of composite thin films based on Titanium-Dioxide nanoparticles. Acta Phys. Pol. A 2017, 131, 1529–1533. [Google Scholar] [CrossRef]
- Talu, S.; Bramowicz, M.; Kulesza, S.; Shafiekhani, A.; Rahmati, M.; Ghaderi, A.; Ahmadirad, M.; Solaymani, S. Microstructure of nickel nanoparticles embedded in carbon films: Case study on annealing effect by micromorphology analysis. Surf. Interface Anal. 2017, 49, 153–160. [Google Scholar] [CrossRef]
- Sani, Z.K.; Ghodsi, F.E.; Mazloom, J. Surface morphology effects on Li ion diffusion toward CeO2:Cu nanostructured thin films incorporated in PEG matrix. J. Sol-Gel Sci. Technol. 2017, 82, 643–653. [Google Scholar] [CrossRef]
- Nasehnejad, M.; Nabiyouni, G.; Shahraki, M.G. Morphological characterisation and microstructure of silver films prepared by electrodeposition method. Surf. Eng. 2017, 33, 389–394. [Google Scholar] [CrossRef]
- Pan, A.; Wang, W.; Mei, X.; Lin, Q.; Cui, J.; Wang, K.; Zhai, Z. Fractal titanium oxide under inverse 10-ns laser deposition in air and water. Appl. Phys. A 2017, 123, 253. [Google Scholar] [CrossRef]
- Talu, S.; Bramowicz, M.; Kulesza, S.; Solaymani, S. Topographic characterization of thin film field-effect transistors of 2,6-diphenyl anthracene (DPA) by fractal and AFM analysis. Mater. Sci. Semicond. Process. 2018, 79, 144–152. [Google Scholar] [CrossRef]
- Talu, S.; Kulesza, S.; Bramowicz, M.; Arman, A.; Luna, C.; Achour, A.; Ahmadpourian, A. Fractal Nature of Nanocomposite Thin Films with Co NPs in a-C:H Matrix. Silicon 2018, 10, 675–680. [Google Scholar] [CrossRef]
- Talu, S.; Kulesza, S.; Bramowicz, M.; Pringle, A.M.; Pearce, J.M.; Murugesan, M.; Venkatachalapathy, V.; Mayandi, J. Micromorphology analysis of sputtered indium tin oxide fabricated with variable ambient combinations. Mater. Lett. 2018, 220, 169–171. [Google Scholar] [CrossRef]
- Talu, S.; Yadav, R.P.; Sik, O.; Sobola, D.; Dallaev, R.; Solaymani, S.; Man, O. How topographical surface parameters are correlated with CdTe monocrystal surface oxidation. Mater. Sci. Semicond. Process. 2018, 85, 15–23. [Google Scholar] [CrossRef]
- Kim, S.; Park, K.W.; Woo, H.y.; Hong, J. Time-resolved fractal dimension analysis in ferroelectric copolymer thin films using R-based image processing. Mater. Lett. 2018, 230, 195–198. [Google Scholar] [CrossRef]
- Ren, L.; Cheng, Y.; Han, Z.; Meng, X.; Yang, J. Investigation on the mechanical performance of the electroless Ni–W–P coating based on fractal theory. Surf. Topogr. Metrol. Prop. 2019, 7, 25017. [Google Scholar] [CrossRef]
- Li, B.; Chen, Z.; Ren, E. A fractal analysis for the microstructures of beta-SiC films. Int. J. Mater. Res. 2019, 110, 746–756. [Google Scholar] [CrossRef]
- Zhu, W.; Mohammadi, E.; Diao, Y. Quantitative image analysis of fractal-like thin film of organic semiconductors. J. Polym. Sci. Part B Polym. Phys. 2019, 57, 1622–1634. [Google Scholar] [CrossRef]
- Mwema, F.M.; Akinlabi, E.T.; Oladijo, O.P. Effect of substrate type on the fractal characteristics of AFM images of sputtered aluminium thin films. Mater. Sci. 2019, 26, 49–57. [Google Scholar] [CrossRef]
- Pedro, G.d.C.; Gorza, F.D.S.; da Silva, R.J.; de Souza, N.C.; Silva, J.R. Effects of electric field and temperature on the shape of chlorophyll aggregates in casting films. Thin Solid Film 2019, 692, 137608. [Google Scholar] [CrossRef]
- Jafari, A.; Tahani, K.; Dastan, D.; Asgary, S.; Shi, Z.; Yin, X.T.; Zhou, W.D.; Garmestani, H.; Talu, S. Ion implantation of copper oxide thin films; statistical and experimental results. Surf. Interfaces 2020, 18, 100463. [Google Scholar] [CrossRef]
- Yildiz, K.; Yildiz, Z. Evaluation of nano-filler dispersion quality in polymeric films with binary feature characteristics and fractal analysis. IET Image Process. 2020, 14, 2006–2012. [Google Scholar] [CrossRef]
- Aminirastabi, H.; Xue, H.; Mitić, V.V.; Lazović, G.; Ji, G.; Peng, D. Novel fractal analysis of nanograin growth in BaTiO3 thin film. Mater. Chem. Phys. 2020, 239, 122261. [Google Scholar] [CrossRef]
- Yang, L.; Zhang, D.; Zhang, X.; Tian, A. Surface profile topography of ionic polymer metal composite based on fractal theory. Surf. Interfaces 2021, 22, 100834. [Google Scholar] [CrossRef]
- Dorgham, A.; Azam, A.; Parsaeian, P.; Wang, C.; Morina, A.; Neville, A. An assessment of the effect of relative humidity on the decomposition of the ZDDP antiwear additive. Tribol. Lett. 2021, 69, 12. [Google Scholar] [CrossRef]
- Jiang, Y.; Baben, M.T.; Lin, Y.; Littler, C.L.; Syllaios, A.J.; Neogi, A.; Philipose, U. Analyzing growth kinematics and fractal dimensions of molybdenum disulfide films. Nanotechnology 2021, 32, 245602. [Google Scholar] [CrossRef] [PubMed]
- Romaguera-Barcelay, Y.; Talu, S.; Matos, R.S.; Oliveira, R.M.P.B.; Moreira, J.A.; de Cruz, J.P.; da Fonseca Filho, H.D. Fractal-stereometric correlation of nanoscale spatial patterns of GdMnO3 thin films deposited by spin coating. Appl. Sci. 2021, 11, 3886. [Google Scholar] [CrossRef]
- Talu, S.; Bramowicz, M.; Kulesza, S.; Fiorillo, I.; Giovanzana, S. Fractal features and Surface micromorphology of unworn surfaces of rigid gas permeable contact lenses. Curr. Eye Res. 2017, 42, 1118–1123. [Google Scholar] [CrossRef] [PubMed]


Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhou, W.; Cao, Y.; Zhao, H.; Li, Z.; Feng, P.; Feng, F. Fractal Analysis on Surface Topography of Thin Films: A Review. Fractal Fract. 2022, 6, 135. https://doi.org/10.3390/fractalfract6030135
Zhou W, Cao Y, Zhao H, Li Z, Feng P, Feng F. Fractal Analysis on Surface Topography of Thin Films: A Review. Fractal and Fractional. 2022; 6(3):135. https://doi.org/10.3390/fractalfract6030135
Chicago/Turabian StyleZhou, Wenmeng, Yating Cao, Haolin Zhao, Zhiwei Li, Pingfa Feng, and Feng Feng. 2022. "Fractal Analysis on Surface Topography of Thin Films: A Review" Fractal and Fractional 6, no. 3: 135. https://doi.org/10.3390/fractalfract6030135
APA StyleZhou, W., Cao, Y., Zhao, H., Li, Z., Feng, P., & Feng, F. (2022). Fractal Analysis on Surface Topography of Thin Films: A Review. Fractal and Fractional, 6(3), 135. https://doi.org/10.3390/fractalfract6030135







