On Variable-Order Fractional Discrete Neural Networks: Solvability and Stability
Abstract
:1. Introduction
2. Background on Fractional Discrete Calculus
- Discrete Leibniz integral law:
- Fractional Caputo difference of a constant c:
- Delta difference of the h–falling factorial function:
- (i)
- S is a contraction;
- (ii)
- For any ;
- (iii)
- T is continuous, and is relatively compact.
3. Variable-Order Fractional Discrete Neural Network
4. Existence of the Solution
- For all represents a continuous function with respect to x, and there exists a constant such that:
- There exists a constant such that , where:and:
- We show that S maps into . For any , we have:This implies ;
- We need to prove that S is continuous. Let be a sequence of satisfying as . Then, we can obtain:Then, we can conclude that when which implies that S is continuous;
- We show that S is relatively compact. We choose , and . Then, we have:This implies that is a bounded and uniformly Cauchy subset and together with Arzela–Ascoli’s lemma 2, we obtain that is relatively compact;
- We choose a fixed and for all . Then, we have:Therefore, . Finally, we prove that the operator T is the contraction mapping. For taking the norm of yields:According to , it can be concluded that the operator T is a contraction mapping. From Lemma (3), has a fixed point in , which is a solution of (1).
5. Ulam–Hyers Stability of a Variable-Order Fractional Discrete Neural Network
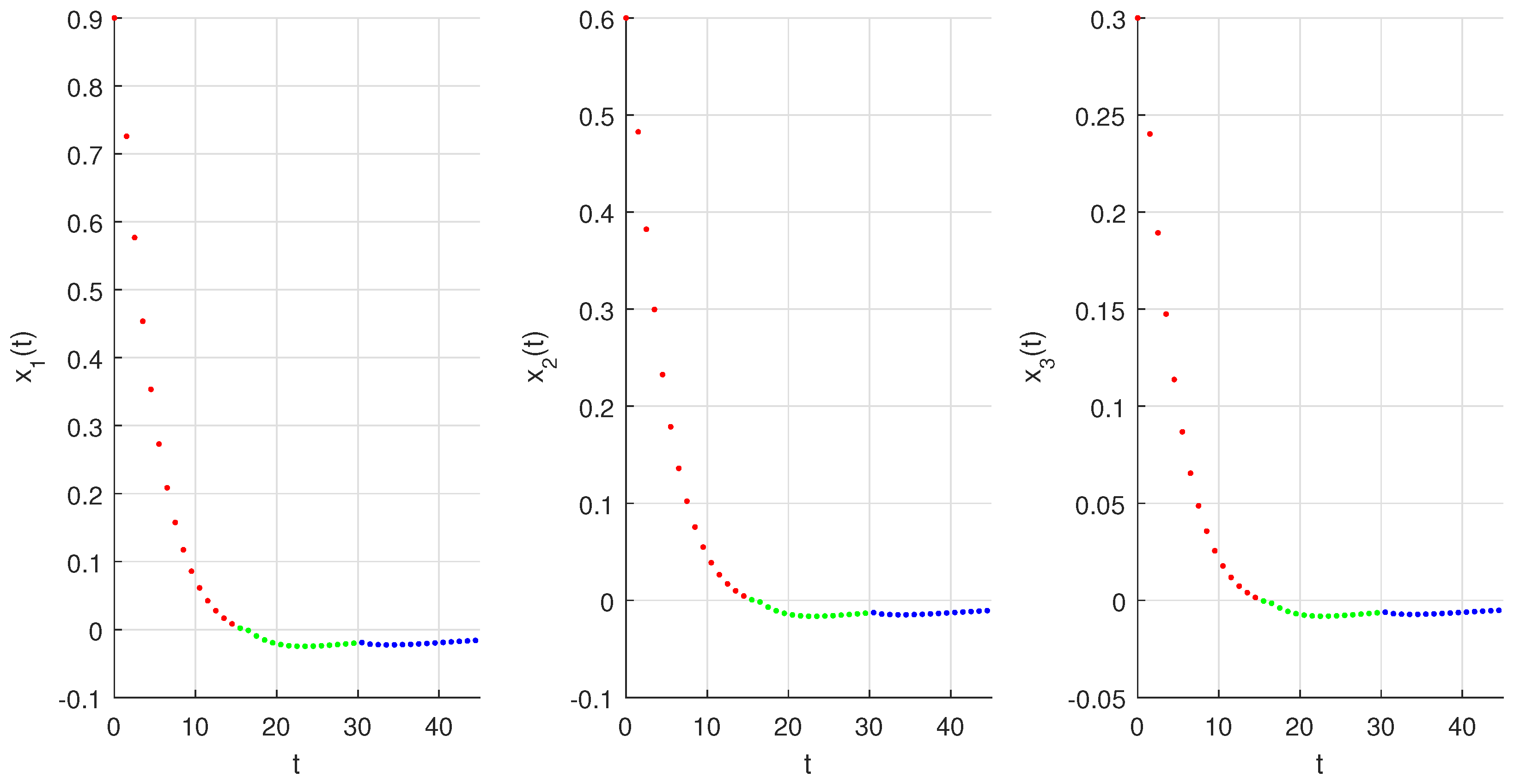
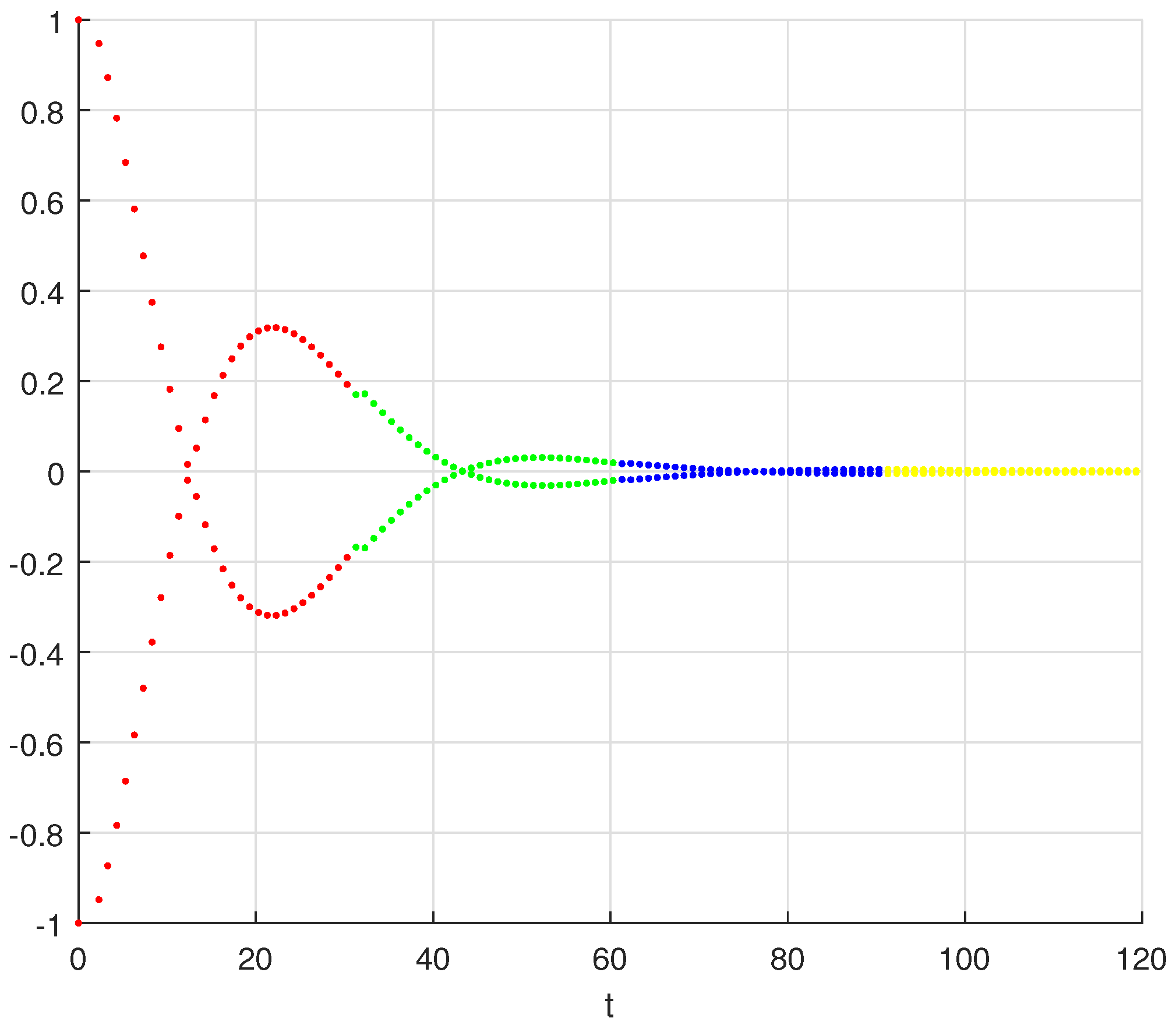
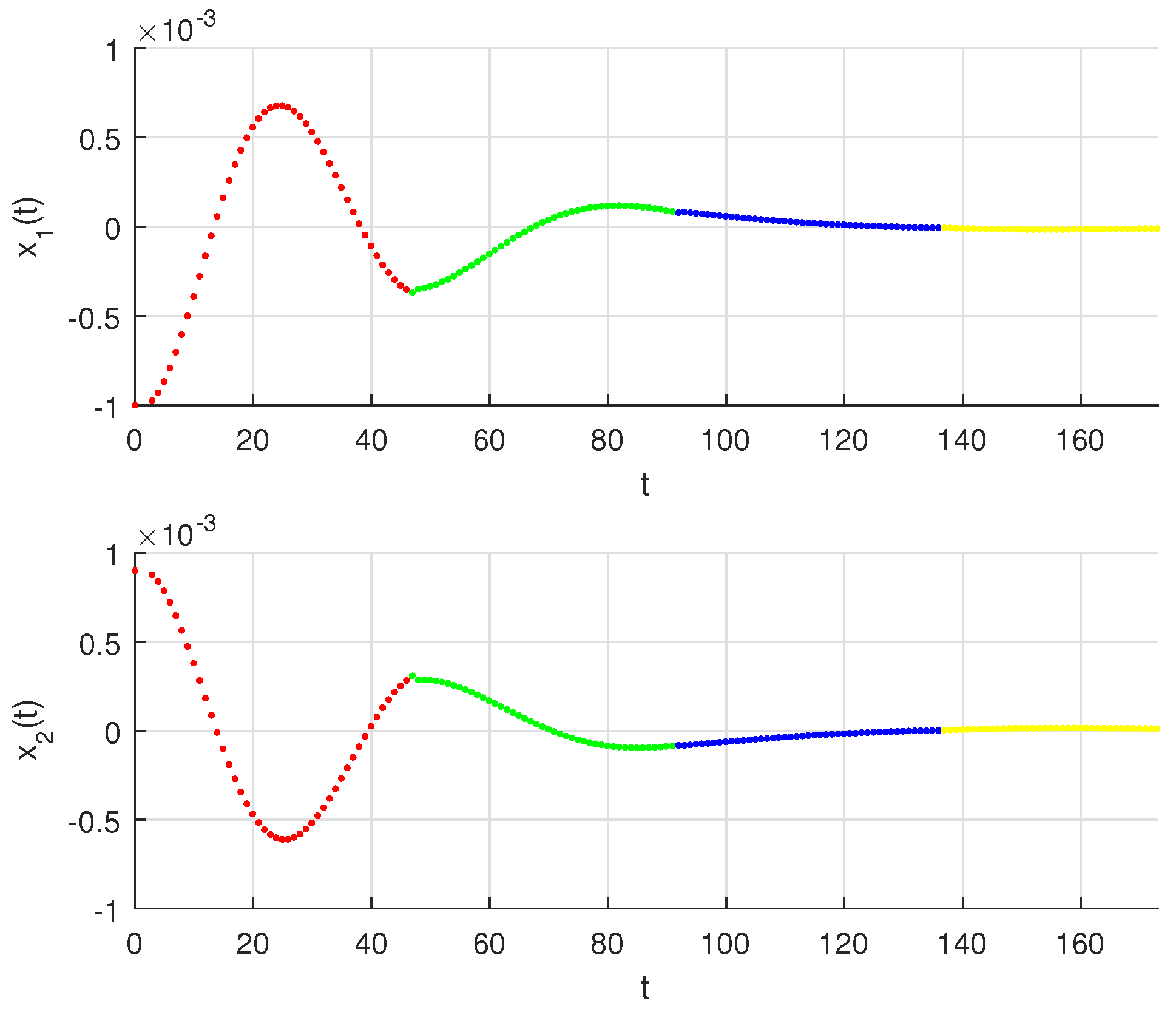
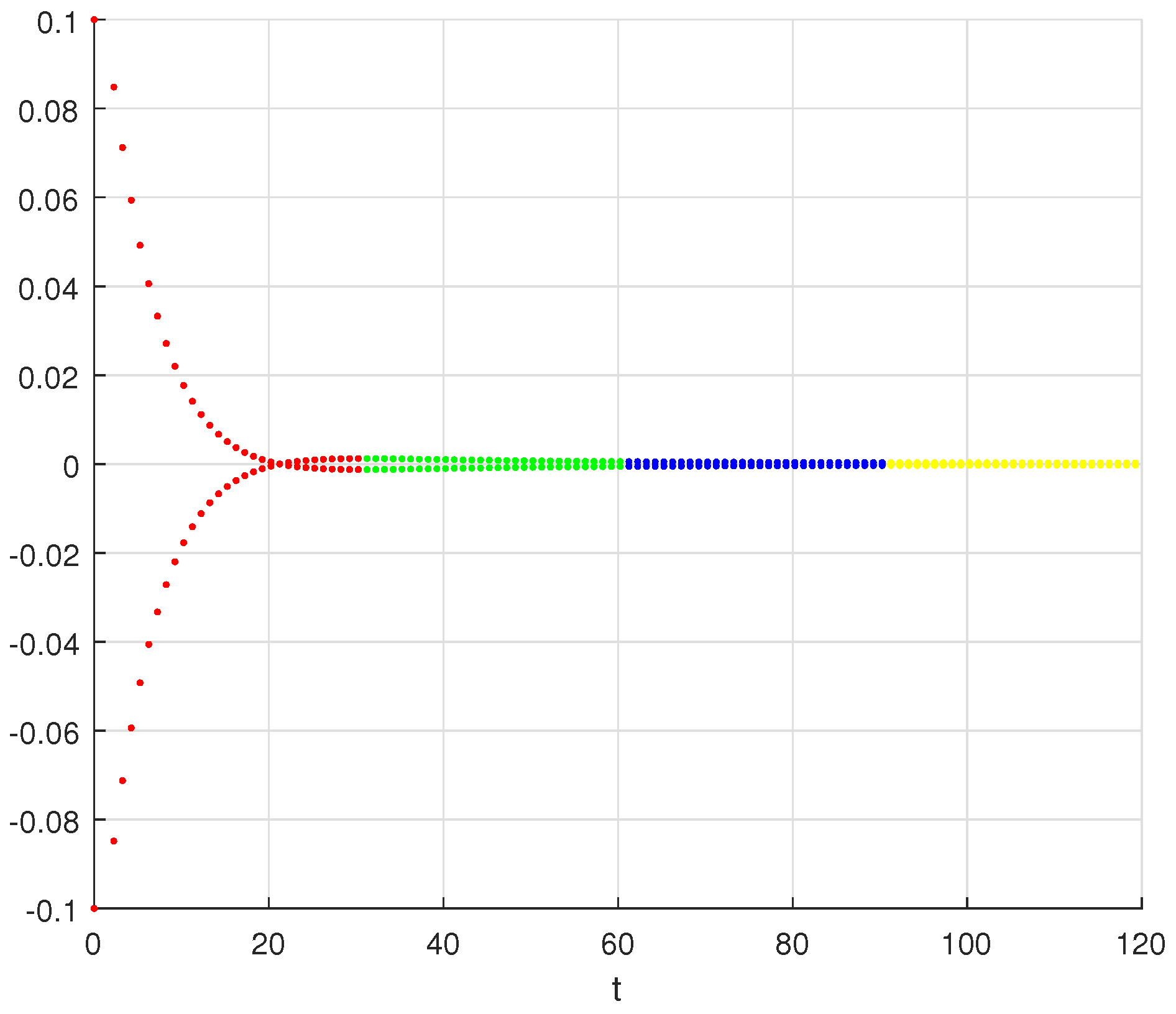
6. Numerical Simulations
- Let and:Here, from the given data, we obtain and . Clearly, the assumptions () and () hold with . Thus, all the conditions of Theorem 1 and Theorem 2 are satisfied. Therefore, the system (7) has at least one solution that is Ulam–Hyers stable for and ;
- We admit that and:As observed, () and are valid for , and . With , Theorem 1 is valid, which implies the existence of the solution. We can easily confirm that the neural network (7) is Ulam–Hyers stable, as there is a constant where , and hence, Theorem 2 accurately holds.
7. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Hilfer, R. Applications of Fractional Calculus in Physics; World Scientific: Singapore, 2000. [Google Scholar]
- Goodrich, C.; Peterson, A.C. Discrete Fractional Calculus; Springer: Berlin/Heidelberg, Germany, 2015. [Google Scholar]
- Stanisławski, R.; Latawiec, K.J. A modified Mikhailov stability criterion for a class of discrete-time noncommensurate fractional-order systems. Commun. Nonlinear Sci. Numer. Simul. 2021, 96, 105697. [Google Scholar] [CrossRef]
- Wei, Y.; Wei, Y.; Chen, Y.; Wang, Y. Mittag–Leffler stability of nabla discrete fractional-order dynamic systems. Nonlinear Dyn. 2020, 101, 407–417. [Google Scholar] [CrossRef]
- Khennaoui, A.-A.; Ouannas, A.; Bendoukha, S.; Grassi, G.; Wang, X.; Pham, V.-T.; Alsaadi, F.E. Chaos, control, and synchronization in some fractional-order difference equations. Adv. Differ. Equ. 2019, 2019, 412. [Google Scholar] [CrossRef] [Green Version]
- Humphries, U.; Rajchakit, G.; Kaewmesri, P.; Chanthorn, P.; Sriraman, R.; Samidurai, R.; Lim, C.P. Global Stability Analysis of Fractional-Order Quaternion-Valued Bidirectional Associative Memory Neural Networks. Mathematics 2020, 8, 801. [Google Scholar] [CrossRef]
- Ratchagit, K. Asymptotic stability of delay-difference system of Hopfield neural networks via matrix inequalities and application. Int. J. Neural Syst. 2007, 17, 425–430. [Google Scholar] [CrossRef]
- Pratap, A.; Raja, R.; Alzabut, J.; Cao, J.; Rajchakit, G.; Huang, C. Mittag–Leffler stability and adaptive impulsive synchronization of fractional order neural networks in quaternion field. Math. Methods Appl. Sci. 2020, 43, 6223–6253. [Google Scholar] [CrossRef]
- Du, F.; Jia, B. Finite time stability of fractional delay difference systems: A discrete delayed Mittag–Leffler matrix function approach. Chaos Solitons Fractals 2020, 141, 110430. [Google Scholar] [CrossRef]
- Chen, C.; Bohner, M.; Jia, B. Ulam–Hyers stability of Caputo fractional difference equations. Math. Methods Appl. Sci. 2019, 42, 7461–7470. [Google Scholar] [CrossRef]
- Jonnalagadda, J.M. Hyers-Ulam stability of fractional nabla difference equations. Int. J. Anal. 2016, 2016, 1–5. [Google Scholar] [CrossRef] [Green Version]
- Selvam, A.G.M.; Baleanu, D.; Alzabut, J.; Vignesh, D.; Abbas, S. On Hyers–Ulam Mittag–Leffler stability of discrete fractional Duffing equation with application on inverted pendulum. Adv. Differ. Equ. 2020, 2020, 456. [Google Scholar] [CrossRef]
- Sun, H.; Zhang, Y.; Baleanu, D.; Chen, W.; Chen, Y. A new collection of real world applications of fractional calculus in science and engineering. Commun. Nonlinear Sci. Numer. Simul. 2018, 64, 213–231. [Google Scholar] [CrossRef]
- Pratap, A.; Raja, R.; Cao, J.; Huang, C.; Niezabitowski, M.; Bagdasar, O. Stability of discrete-time fractional-order time-delayed neural networks in complex field. Math. Methods Appl. Sci. 2021, 44, 419–440. [Google Scholar] [CrossRef]
- Li, R.; Cao, J.; Xue, C.; Manivannan, R. Quasi-stability and quasi-synchronization control of quaternion-valued fractional-order discrete-time memristive neural networks. Appl. Math. Comput. 2021, 395, 125851. [Google Scholar] [CrossRef]
- You, X.; Song, Q.; Zhao, Z. Global Mittag–Leffler stability and synchronization of discrete-time fractional-order complex-valued neural networks with time delay. Neural Netw. 2020, 122, 382–394. [Google Scholar] [CrossRef] [PubMed]
- Gu, Y.; Wang, H.; Yu, Y. Synchronization for fractional-order discrete-time neural networks with time delays. Appl. Math. Comput. 2020, 372, 124995. [Google Scholar] [CrossRef]
- Wu, G.-C.; Abdeljawad, T.; Liu, J.; Baleanu, D.; Wu, K.-T. Mittag–Leffler Stability Analysis of Fractional Discrete-Time Neural Networks via Fixed Point Technique; Institute of Mathematics and Informatics: Sofia, Bulgaria, 2019. [Google Scholar]
- You, X.; Dian, S.; Guo, R.; Li, S. Exponential stability analysis for discrete-time quaternion-valued neural networks with leakage delay and discrete time-varying delays. Neurocomputing 2021, 430, 71–81. [Google Scholar] [CrossRef]
- You, X.; Song, Q.; Zhao, Z. Existence and finite-time stability of discrete fractional-order complex-valued neural networks with time delays. Neural Netw. 2020, 123, 248–260. [Google Scholar] [CrossRef] [PubMed]
- Huang, L.-L.; Park, J.H.; Wu, G.-C.; Mo, Z.-W. Variable-order fractional discrete-time recurrent neural networks. J. Comput. Appl. Math. 2020, 370, 112633. [Google Scholar] [CrossRef]
- Baleanu, D.; Wu, G.-C.; Bai, Y.-R.; Chen, F.-L. Stability analysis of Caputo–like discrete fractional systems. Commun. Nonlinear Sci. Numer. Simul. 2017, 48, 520–530. [Google Scholar] [CrossRef]
- Burton, T.A.; Furumochi, T. Krasnoselskii’s fixed point theorem and stability. Nonlinear Anal. Theory Methods Appl. 2002, 49, 445–454. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Hioual, A.; Ouannas, A.; Oussaeif, T.-E.; Grassi, G.; Batiha, I.M.; Momani, S. On Variable-Order Fractional Discrete Neural Networks: Solvability and Stability. Fractal Fract. 2022, 6, 119. https://doi.org/10.3390/fractalfract6020119
Hioual A, Ouannas A, Oussaeif T-E, Grassi G, Batiha IM, Momani S. On Variable-Order Fractional Discrete Neural Networks: Solvability and Stability. Fractal and Fractional. 2022; 6(2):119. https://doi.org/10.3390/fractalfract6020119
Chicago/Turabian StyleHioual, Amel, Adel Ouannas, Taki-Eddine Oussaeif, Giuseppe Grassi, Iqbal M. Batiha, and Shaher Momani. 2022. "On Variable-Order Fractional Discrete Neural Networks: Solvability and Stability" Fractal and Fractional 6, no. 2: 119. https://doi.org/10.3390/fractalfract6020119
APA StyleHioual, A., Ouannas, A., Oussaeif, T.-E., Grassi, G., Batiha, I. M., & Momani, S. (2022). On Variable-Order Fractional Discrete Neural Networks: Solvability and Stability. Fractal and Fractional, 6(2), 119. https://doi.org/10.3390/fractalfract6020119





