Starlike Functions of Complex Order with Respect to Symmetric Points Defined Using Higher Order Derivatives

Abstract

In this paper, we introduce and study a new subclass of multivalent functions with respect to symmetric points involving higher order derivatives. In order to unify and extend various well-known results, we have defined the class subordinate to a conic region impacted by Janowski functions. We focused on conic regions when it pertained to applications of our main results. Inclusion results, subordination property and coefficient inequality of the defined class are the main results of this paper. The applications of our results which are extensions of those given in earlier works are presented here as corollaries.

1. Introduction and Definitions

Throughout this paper, we let $\mathbb{C},{\mathbb{Z}}^{-}$ and $\mathbb{N}$ to denote the sets of complex numbers, negative integers and natural numbers, respectively. Let $\mathcal{H}(a,n)$ be the class comprising of all analytic functions defined in unit disc $\mathbb{E}=\left\{z\in \mathbb{C}:\left|z\right|<1\right\}$ and having a power series representation of the form $h\left(z\right)=a+a_n{z}^n+a_{n+1}{z}^{n+1}+\cdots$. Furthermore, let $\mathcal{A}(p,n)$ denote the class of functions h analytic in $\mathbb{E}$ and having a power series representation of the form

$$h\left(z\right)=z^p+\sum _{k=p+n}^{\infty }{a}_k{z}^k,(p,n\in \mathbb{N})$$

(1)

and let $\mathcal{A}(1,1)=\mathcal{A}$. Two prominent subclasses of $\mathcal{A}$ are the so-called families of starlike functions and convex functions which have the analytic characterization of the form

$$Re\left(\frac{z{h}^{\prime }\left(z\right)}{h\left(z\right)}\right)>0\mathrm{and}Re\left(1+\frac{z{h}^{″}\left(z\right)}{h^{\prime }\left(z\right)}\right)>0,$$

respectively. Here we let ${\mathcal{S}}^{\ast }$ and $\mathcal{C}$ to denote the class of starlike functions and convex functions, respectively. The two preceding descriptions reveal an interesting close analytic characterization between starlike and convex functions. This says that $h\left(z\right)\in \mathcal{C}$ if and only if $z{h}^{\prime }\left(z\right)\in {\mathcal{S}}^{\ast }$. For detailed study and developments pertaining to various subclasses of $\mathcal{A}(p,n)$, refer to [1,2]. We let the collection $\mathcal{P}$ of functions $\psi \left(z\right)$ that are analytic in the unit disc $\mathbb{E}$ with $\psi \left(0\right)=1$ and $Re\psi \left(z\right)>0$. Hereafter, we let $\psi \in \mathcal{P}$ and $\psi$, has a power series expansion of the form

$$\psi \left(z\right)=1+L_{1}z+L_2{z}^2+L_3{z}^3+\cdots ,z\in \mathbb{E},L_1>0.$$

(2)

Subordination, quasi-subordination and Hadamard product (or convolution) are the three main tools that are predominantly used in the study of univalent functions theory. We let ≺, ${\prec }_{\kappa }$ and ∗ to denote the subordination, quasi-subordination and Hadamard product, respectively. For detailed discussion and formal definition of the quasi-subordination and Hadamard product, refer to [3,4].

Using the principal of subordination, Ma and Minda [5] defined the classes ${\mathcal{S}}^{\ast }\left(\psi \right)$ and $\mathcal{C}\left(\psi \right)$ as follows:

$${\mathcal{S}}^{\ast }\left(\psi \right)=\left\{h\in \mathcal{A}:\frac{z{h}^{\prime }\left(z\right)}{h\left(z\right)}\prec \psi \left(z\right)\right\}\mathrm{and}\mathcal{C}\left(\psi \right)=\left\{h\in \mathcal{A}:1+\frac{z{h}^{″}\left(z\right)}{h^{\prime }\left(z\right)}\prec \psi \left(z\right)\right\},$$

where $\psi \left(z\right)$ is defined as in (2). They assumed the superordinate function $\psi$ maps the open unit disc $\mathbb{E}$ onto a starlike region with respect to 1 and symmetric with respect to the real axis. The classes ${\mathcal{S}}^{\ast }\left(\psi \right)$ and $\mathcal{C}\left(\psi \right)$ consolidated the study of several generalizations of starlike and convex functions. By restricting the $\psi$ to a specific conic region for example to parabola, cardioid and Bernoulli lemniscate, several authors studied the properties of starlike functions with respect to conic regions. Most popular among the study of starlike functions associated with conic regions are the classes ${\mathcal{S}}^{\ast }\left(\sqrt{1+z}\right)$ defined by Sokół [6] and followed by ${\mathcal{S}}^{\ast }(z+\sqrt{1+z^2})$ defined by Raina and Sokół [7]. For studies related to conic region, refer to [8,9,10,11,12,13,14,15] and references provided therein.

The famous Janowski starlike functions and Janowski convex functions (see [16]), are denoted by the special case of ${\mathcal{S}}^{\ast }\left(\psi \right)$ and $\mathcal{C}\left(\psi \right)$, although they are still in spotlight due to their versatility. We denote by ${\mathcal{S}}^{\ast }(F,G)$ and $\mathcal{C}(F,G)$ the class of Janowski starlike functions and Janowski convex functions, defined by

$${\mathcal{S}}^{\ast }(F,G):=\left\{h\in \mathcal{A}:\frac{z{h}^{\prime }\left(z\right)}{h\left(z\right)}\prec {\displaystyle \frac{1+Fz}{1+Gz}},-1\le G<F\le 1\right\},$$

and

$$\mathcal{C}(F,G):=\left\{h\in \mathcal{A}:1+\frac{z{h}^{″}\left(z\right)}{h^{\prime }\left(z\right)}\prec {\displaystyle \frac{1+Fz}{1+Gz}},-1\le G<F\le 1\right\},$$

respectively. It should be noted that all the classes mentioned above were extended for $h\left(z\right)$, which belongs to $\mathcal{A}(p,1)$. Extending the well-known Janowski class of functions [16], Aouf [17] (Equation (1.4)) defined the class $\ell \left(z\right)\in \mathcal{P}(F,G,p,\alpha )$ if and only if

$$\ell \left(z\right)=\frac{p+\left[pG+(F-G)(p-\alpha )\right]w\left(z\right)}{\left[1+Gw\left(z\right)\right]},(-1\le G<F\le 1,0\le \alpha <1)$$

(3)

for all $z\in \mathbb{E}=\left\{z:\left|z\right|<1\right\}$ where $w\left(z\right)$ is the Schwartz function. Recently, Breaz et al. [18] (Equation (4)) used the following expression to study a new class of multivalent function

$$\aleph (p;F,G;\alpha ;\psi ;z)=\frac{\left[(1+F)p+\alpha (G-F)\right]\psi \left(z\right)+\left[(1-F)p-\alpha (G-F)\right]}{\left[(G+1)\psi \left(z\right)+(1-G)\right]},$$

(4)

where $\psi \left(z\right)$ is defined as in (2). $\aleph (p;F,G;\alpha ;\psi ;z)$ is an extension of the class $\mathcal{P}(F,G,p,\alpha )$. Refer to [18,19], for an explanation of the purpose and motivation in order to define a class of functions superordinate to $\aleph (p;F,G;\alpha ;\psi ;z)$.

Recently, Aouf, Bulboacă and Seoudy in [20] (Definition 1) introduced a class so-called multivalent non-Bazilevič functions as follows: A function $h\in \mathcal{A}(p,n)$ is said to be in ${\mathcal{N}}_p^n(\lambda ,\beta ,m;F,G)$ if it satisfies

$$(1+\lambda ){\left(\frac{\delta (p,m)z^{p-m}}{h^{\left(m\right)}\left(z\right)}\right)}^{\beta }-\lambda \frac{z{h}^{(1+m)}\left(z\right)}{(p-m)h^{\left(m\right)}\left(z\right)}{\left(\frac{\delta (p,m)z^{p-m}}{h^{\left(m\right)}\left(z\right)}\right)}^{\beta }\prec \frac{1+Fz}{1+Gz}$$

$$(\lambda \in \mathbb{C},0<\beta <1,p,n\in \mathbb{N},m\in {\mathbb{N}}_0=\mathbb{N}\cup \left\{0\right\},p>m\mathrm{and}-1\le G<F\le 1),$$

where ≺ denotes usual subordination of analytic functions and $\delta (p,m)=\frac{p!}{(p-m)!}$.

Using Hadamard product (or convolution), Karthikeyan et al. [21] (Definition 1.1) defined a class ${\mathcal{PS}}_{\delta }^{\lambda }(\beta ,\theta ;b;\psi ;h;F,G)$ of $\mathcal{A}(1,1)$ subject to satisfying the condition

$$1+\frac{(1+itan\theta )}{b}\left[\frac{z^{1-\lambda }{\left[{\mathcal{R}}^{\prime }\left(z\right)\right]}^{\delta }}{{\left[(1-\beta )\mathcal{R}\left(z\right)+\beta z\right]}^{1-\lambda }}-1\right]\prec \aleph (1;F,G;0;\psi ;z),$$

where $\mathcal{R}=h\ast g$, $-\frac{\pi }{2}<\theta <\frac{\pi }{2},\delta \ge 1,0\le \beta \le 1,\lambda \ge 0,b\in \mathbb{C}\backslash \left\{0\right\}$ and $\aleph (p;F,G;\alpha ;\psi ;z)$ is defined as in (4).

1.1. Motivation, Novelty and Discussion

Motivated by the classes ${\mathcal{N}}_p^n(\lambda ,\beta ,m;F,G)$ and ${\mathcal{PS}}_{\delta }^{\lambda }(\beta ,\theta ;b;\psi ;h;F,G)$, we aim to define and study an interesting subclass of multivalent functions with respect to symmetric points subordinate to $\aleph (p;F,G;\alpha ;\psi ;z)$. However, the present study is not a direct generalization or unification of ${\mathcal{N}}_p^n(\lambda ,\beta ,m;F,G)$ and ${\mathcal{PS}}_{\delta }^{\lambda }(\beta ,\theta ;b;\psi ;h;F,G)$, but is closely related to the above defined function classes.

This paper is structured as follows. In this section, we will begin by illustrating that impact of $\aleph (p;F,G;\alpha ;\psi ;z)$ is not same on all conic regions and it varies from region to region. Subsequently, we define a class of multivalent functions using higher order derivatives superordinated by $\aleph (p;F,G;\alpha ;\psi ;z)$. In the Section 2, we discuss some elementary and known results which would be used to obtain our main results. Section 3 and Section 4 are devoted to provide our main results namely solution to the Fekete-Szegö problem and interesting subordination conditions. Finally attempting the discretization of our results, we study the same defined function class by replacing the ordinary derivative with q-difference operator.

In [18], the geometrical interpretation and the impact of $\aleph (p;F,G;\alpha ;\psi ;z)$ on various conic region was not discussed in detail. Here we will consider few conic regions and we will illustrate the impact of $\aleph (p;F,G;\alpha ;\psi ;z)$ on $\psi \left(z\right)$. For uniformity, the colour of graphs have been based on the parameter values, which are as follows: Red colour is used when $\aleph (1;1,-1;0;\psi ;z)$; Blue colour is used if $\aleph (1;0,-0.3;0.9;\psi ;z)$; Green colour is used if $\aleph (1;0.9,0.0;0.5;\psi ;z)$; and Yellow colour is used if $\aleph (1;0.9,0.8;0.8;\psi ;z)$.

1.2. Comparison on The Impact of $\aleph (p;F,G;\alpha ;\psi ;z)$ on Two Different Conic Regions

The behaviour or impact of $\aleph (p;F,G;\alpha ;\psi ;z)$ is not same on all conic region $\psi$. To illustrate this fact, we consider two functions which maps unit disc on to a conic region of same shape namely

• Cardioid region with cusp on the right hand side, ($\psi \left(z\right)=\frac{3+2z-z^2}{2}$).
• Cardioid region with cusp on left hand side, $\left(\psi \left(z\right)=1+\frac{z}{k}\left(\frac{k+z}{k-z}\right),k=1+\sqrt{2}\right)$.

We begin the illustration with the following.

• It is well-known that $\psi \left(z\right)=\frac{3+2z-z^2}{2}$ is univalent in $\mathbb{E}$ and maps the unit disc onto the interior of the cardioid with cusp on the right hand side in the right half plane (see Figure 1a). Note that while $Re\left[\psi \left(z\right)\right]=Re\left[\frac{3+2z-z^2}{2}\right]>0$, it does not have the usual normalization $\psi \left(0\right)=1$. The impact of $\aleph (p;F,G;\alpha ;\psi ;z)$ on $\psi \left(z\right)=\frac{3+2z-z^2}{2}$ is that the map is circular if F and G are chosen remotely (far off), while the curves are polygonal (see Figure 1d) if F and G are chosen close enough. The presence of $\alpha$ is helpful in translation.
  

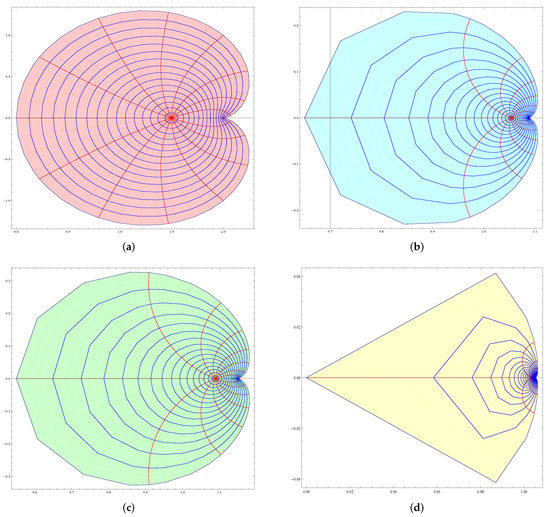  Figure 1. Impact of $\aleph (p;F,G;\alpha ;\psi ;z)$ on the conic region $\psi \left(z\right)=\frac{3}{2}+z-\frac{z^2}{2}$. (a) Mapping of $\mathbb{E}$ under the transformation $\psi \left(z\right)=\frac{3}{2}+z-\frac{z^2}{2}$. (b) Mapping of $\mathbb{E}$ under the transformation $\aleph (1;0,-0.3;0.9;\psi ;z)$ if $\psi \left(z\right)=\frac{3}{2}+z-\frac{z^2}{2}$. (c) Mapping of $\mathbb{E}$ under the transformation $\aleph (1;0.9,0.0;0.5;\psi ;z)$ if $\psi \left(z\right)=\frac{3}{2}+z-\frac{z^2}{2}$. (d) Mapping of $\mathbb{E}$ under the transformation $\aleph (1;0.9,0.8;0.8;\psi ;z)$ if $\psi \left(z\right)=\frac{3}{2}+z-\frac{z^2}{2}$.
• Now, if we choose

  $$\begin{array}{cc}\hfill \psi \left(z\right)& =1+\frac{z}{k}\left(\frac{k+z}{k-z}\right),(k=1+\sqrt{2}),\hfill \\ & =1+\frac{z}{1+\sqrt{2}}+\frac{2z^2}{{\left(1+\sqrt{2}\right)}^2}+\cdots +\frac{2z^n}{{\left(1+\sqrt{2}\right)}^n}+O{\left[z\right]}^{n+1}.\hfill \end{array}$$
  We can easily see that the function has a normalization $\psi \left(0\right)=1$, $Re\left[\psi \left(z\right)\right]>0$ and maps unit disc on to the cardioid with cusp on the left hand side (see Ahuja et al. [22]). From Figure 2a–d, we find that there is no major changes to the conic.
  

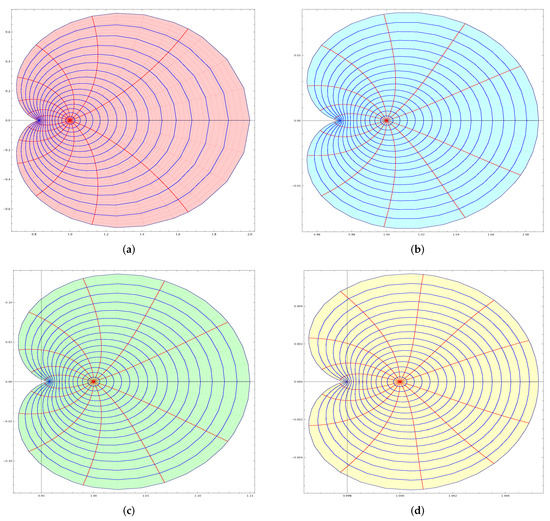  Figure 2. Impact of $\aleph (p;F,G;\alpha ;\psi ;z)$ on the conic region $\psi \left(z\right)=1+\frac{z}{k}\left(\frac{k+z}{k-z}\right)$. (a) Mapping of $\mathbb{E}$ under the transformation $\psi \left(z\right)=1+\frac{z}{k}\left(\frac{k+z}{k-z}\right)$. (b) Mapping of $\mathbb{E}$ under the transformation $\aleph (1;0,-0.3;0.9;\psi ;z)$ if $\psi \left(z\right)=1+\frac{z}{k}\left(\frac{k+z}{k-z}\right)$. (c) Mapping of $\mathbb{E}$ under the transformation $\aleph (1;0.9,0.0;0.5;\psi ;z)$ if $\psi \left(z\right)=1+\frac{z}{k}\left(\frac{k+z}{k-z}\right)$. (d) Mapping of $\mathbb{E}$ under the transformation $\aleph (1;0.9,0.8;0.8;\psi ;z)$ if $\psi \left(z\right)=1+\frac{z}{k}\left(\frac{k+z}{k-z}\right)$.

Notice that Figure 1 and Figure 2 have been assigned same set parameter values, the only difference being different $\psi \left(z\right)$. Comparing Figure 1 and Figure 2, we see that the behaviour of $\aleph (p;F,G;\alpha ;\psi ;z)$ on various conic regions are not same (also see Noor and Malik [19]).

If $\psi \in \mathcal{P}$, then $\aleph (p;F,G;\alpha ;\psi ;0) = p$ and $Re\left(\aleph (p;F,G;\alpha ;\psi ;z)\right)>0$. We say that $\aleph (p;F,G;\alpha ;\psi ;z)\in \mathcal{P}(F,G,p,\alpha )$ if and only if it satisfies (3). We denote by ${\mathcal{S}}_p^{\ast }(F,G;\alpha ;\psi )$ and ${\mathcal{C}}_p(F,G;\alpha ;\psi )$, the classes of functions satisfying the condition $\frac{z{h}^{\prime }\left(z\right)}{h\left(z\right)}\prec \aleph (p;F,G;\alpha ;\psi ;z)$ and $1+\frac{z{h}^{″}\left(z\right)}{h^{\prime }\left(z\right)}\prec \aleph (p;F,G;\alpha ;\psi ;z),$ respectively. Additionally, ${\mathcal{S}}_1^{\ast }(1,-1;0;\psi ):={\mathcal{S}}^{\ast }\left(\psi \right)$ and ${\mathcal{C}}_1(1,-1;0;\psi ):=\mathcal{C}\left(\psi \right)$.

The function $p_{\nu ,\sigma }\left(\zeta \right)$, that plays the role of an extremal function related to the conic domain, is given by

$${\widehat{p}}_{\nu ,\sigma }\left(z\right)=\left\{\begin{array}{cc}\frac{1+(1-2\sigma )z}{1-z},\hfill & \mathrm{if} \nu =0\hfill \\ 1+\frac{2(1-\sigma )}{{\pi }^2}{\left(log\frac{1+\sqrt{z}}{1-\sqrt{z}}\right)}^2,\hfill & \mathrm{if} \nu =1\hfill \\ 1+\frac{2(1-\sigma )}{1-{\nu }^2}{sinh}^2\left[\left(\frac{2}{\pi }arccos\nu \right)arctanh\sqrt{z}\right],\hfill & \mathrm{if} 0<\nu <1\hfill \\ 1+\frac{2(1-\sigma )}{1-{\nu }^2}sin\left(\frac{\pi }{2R\left(t\right)}{\int }_0^{\frac{u\left(z\right)}{t}}\frac{1}{\sqrt{1-x^2}\sqrt{1-{\left(tx\right)}^2}}dx\right)+\frac{1}{{\nu }^2-1},\hfill & \mathrm{if} \nu >1,\hfill \end{array}\right.$$

(5)

where $u\left(z\right)=\frac{z-\sqrt{t}}{1-\sqrt{tz}},t\in (0,1)$ and t is chosen such that $\nu =cosh\left(\frac{\pi R^{\prime }\left(t\right)}{4R\left(t\right)}\right)$, $R\left(t\right)$ is Legendre’s complete elliptic integral of the first kind and $R^{\prime }\left(t\right)$ is the complementary integral of $R\left(t\right)$. Clearly, ${\widehat{p}}_{\nu ,\sigma }\left(z\right)$ is in $\mathcal{P}$ with the expansion of the form

$${\widehat{p}}_{\nu ,\sigma }\left(z\right)=1+{\tau }_{1}z+{\tau }_2{z}^2+\cdots ,({\tau }_j=p_j(\nu ,\sigma ),j=1,2,3,\dots ),$$

(6)

we obtain

$${\tau }_1=\left\{\begin{array}{cc}\frac{8(1-\sigma ){(arccos\nu )}^2}{{\pi }^2(1-{\nu }^2)},\hfill & \mathrm{if} 0\le \nu <1,\hfill \\ \frac{8(1-\sigma )}{{\pi }^2},\hfill & \mathrm{if} \nu =1\hfill \\ \frac{{\pi }^2(1-\sigma )}{4\sqrt{t}({\nu }^2-1)R^2\left(t\right)(1+t)},\hfill & \mathrm{if} \nu >1.\hfill \end{array}\right.$$

(7)

To avoid repetition, we let once for all throughout this paper

$$-1\le G<F\le 1,0\le \alpha <1,-\frac{\pi }{2}<\theta <\frac{\pi }{2},p,n\in \mathbb{N},m\in {\mathbb{N}}_0.$$

Additionally, let

$$\chi \left(z\right)=d_0+d_{1}z+d_2{z}^2+\cdots (d_0\ne 0)\mathrm{and}\left|d_0\right|\le 1.$$

(8)

Motivated by the study of Tang, Karthikeyan and Murugusundaramoorthy [23] and definition of ${\mathcal{N}}_p^n(\lambda ,\beta ,m;F,G)$, we now introduce the following class of functions:

Definition 1.

For $t\in \mathbb{C}$, with $\left|t\right|\le 1$, $t\ne 1$, $\lambda \ge 0$, and $\chi \left(z\right)$ is defined as in (8), we say that the function $h\in \mathcal{A}(p,1)$ belongs to the class ${\mathfrak{S}}_p^m(b;\psi ;\alpha ;\lambda ;F;G;\theta )$ if it satisfies the subordination condition

$$\frac{1+itan\theta }{b}\left[\frac{{{\rm Y}}_{\lambda }^p(m;t)z^{1-\lambda (p-m)}{h}^{(m+1)}\left(z\right)}{{\left[h^{\left(m\right)}\left(z\right)-h^{\left(m\right)}\left(tz\right)\right]}^{1-\lambda }}-p+m\right]{\prec }_{\kappa }\aleph (p;F,G;\alpha ;\psi ;z)-p$$

(9)

where p is an odd integer, ${{\rm Y}}_{\lambda }^p(m;t)={\left(1-t^p\right)}^{(1-\lambda )}{\left[\delta (p,m)\right]}^{-\lambda }$ and $\aleph (p;F,G;\alpha ;\psi ;z)$ defined as in (4).

Remark 1.

Now we will present some special cases of our class.

(i) 

Let $p=b=1$, $\alpha =m=\theta =\lambda =0$, $\chi \left(z\right)=1$ and $\psi ={\widehat{p}}_{\nu ,\sigma }\left(z\right)$ (see (5)) in Definition 1, then the class ${\mathfrak{S}}_p^m(b;\psi ;\alpha ;\lambda ;F;G;\theta )$ reduces to class $k-\mathcal{US}(F,G,\sigma ,t)$ defined by Arif et al. [24] (Definition 1.3) (also see [25]).

(ii) 

If we replace $p=b=1$, $\alpha =t=\theta =\lambda =0$, $\chi \left(z\right)=1$ and $\psi \left(z\right)={\widehat{p}}_{\nu ,0}\left(z\right)$ in ${\mathfrak{S}}_p^m(b;\psi ;\alpha ;\lambda ;F;G;\theta ),$ where ${\widehat{p}}_{\nu ,0}\left(z\right)$ is defined as in (5), we can obtain $\eta -\mathcal{ST}[F,G]$ and $\eta -\mathcal{UC}[F,G]$ classes defined by Noor and Malik in [19] (Definition 1.3 and Definition 1.4) by choosing $m=0$ and $m=1$, respectively.

(iii) 

If we let $\alpha =\lambda =m=\theta =0$, $b=1$, $p=1$, $F=1$ and $G=-1$, then ${\mathfrak{S}}_p^m(b;\psi ;\alpha ;\lambda ;F;G;\theta )$ reduces to the classes ${\mathcal{S}}_{\ast }^s\left(\psi \right)$ defined by Shanmugam, Ramachandran and Ravichandran [26] (Definition 1.3).

(iv) 

If we let $t=\theta =m=\alpha =0$, $p=b=1$, $F=1$, $G=-1$ and $\psi \left(z\right)=1+z/1-z$, then the class ${\mathfrak{S}}_p^m(b;\psi ;\alpha ;\lambda ;F;G;\theta )$ reduces to well-known class Bazilevič function defined by

$$\mathcal{B}\left(\lambda \right)=\left\{h\in \mathcal{A}(1,1);Re\frac{z^{1-\lambda }{h}^{\prime }\left(z\right)}{{\left[h\left(z\right)\right]}^{1-\lambda }}>0\right\}.$$

Apart from the above classes of functions, several classes of functions which were defined in earlier works are closer to the class of functions defined in Definition 1, for example see [21,27,28,29,30,31,32,33].

2. Preliminaries

In this section, we will state some results, which we will be using to establish our main results namely subordination properties and coefficient inequalities.

Lemma 1.

Ref. [34] If $\vartheta \left(z\right)=1+{\displaystyle \sum _{k=1}^{\infty }}{\vartheta }_k{z}^k\in \mathcal{P}$, then $\left|{\vartheta }_k\right|\le 2$ for all $k\ge 1$, and the inequality is sharp for ${\displaystyle {\vartheta }_{\mu }\left(z\right)=\frac{1+\mu z}{1-\mu z},\left|\mu \right|\le 1}$.

Lemma 2.

Ref. [5] Let $\vartheta \left(z\right)=1+{\displaystyle \sum _{k=1}^{\infty }}{\vartheta }_k{z}^k\in \mathcal{P}$ and also let v be a complex number, then

$$|{\vartheta }_2-v{\vartheta }_1^2|\le 2max\left\{1,|2v-1|\right\},$$

the result is sharp for functions given by

$$\vartheta \left(z\right)=\frac{1+z^2}{1-z^2},\vartheta \left(z\right)=\frac{1+z}{1-z}.$$

Lemma 3.

Ref. [35] Let r be convex in $\mathbb{E}$, with $r\left(0\right)=a$, $\delta \ne 0$ and $Re\delta \ge 0$. If $k\in \mathcal{H}(a,n)$ and

$$k\left(z\right)+\frac{z{k}^{\prime }\left(z\right)}{\delta }\prec r\left(z\right),$$

then

$$k\left(z\right)\prec q\left(z\right)\prec r\left(z\right),$$

where

$$q\left(z\right)=\frac{\delta }{n{z}^{\delta /n}}{\int }_0^{z}r\left(t\right)t^{(\delta /n)-1}dt.$$

The function q is convex and is the best $(a,n)$-dominant.

Throughout this paper, we let

$$\begin{array}{c}\aleph (p;F,G;\alpha ;\psi ;z)=\frac{\left[(1+F)p+\alpha (G-F)\right]\psi \left(z\right)+\left[(1-F)p-\alpha (G-F)\right]}{\left[(G+1)\psi \left(z\right)+(1-G)\right]}\end{array}$$

(10)

From [18] (Theorem 2), with

$$w\left(z\right)=\frac{1}{2}{\vartheta }_{1}z+\frac{1}{2}\left({\vartheta }_2-\frac{1}{2}{\vartheta }_1^2\right)z^2+\frac{1}{2}\left({\vartheta }_3-{\vartheta }_1{\vartheta }_2+\frac{1}{4}{\vartheta }_1^3\right)z^3+\cdots ,z\in \mathbb{E},$$

we can obtain

$$\begin{array}{c}\frac{b\chi \left(z\right)}{1+itan\theta }\left\{\aleph (p;F,G;\alpha ;\psi ;w(z\left)\right)-p\right\}=\frac{b{d}_0{L}_1{\vartheta }_1(F-G)(p-\alpha )}{4(1+itan\theta )}z+\\ \frac{b(F-G)(p-\alpha )d_0{L}_1}{4(1+itan\theta )}\left[{\vartheta }_2-{\vartheta }_1^2\left(\frac{(G+1)L_1+2\left(1-\frac{L_2}{L_1}\right)}{4}\right)+\frac{d_1{\vartheta }_1}{d_0}\right]z^2+\cdots .\end{array}$$

(11)

3. Fekete-Szegö Inequalities for the Class ${\mathfrak{S}}_{\mathit{p}}^{\mathit{m}}(\mathit{b};\mathit{\psi };\mathit{\alpha };\mathit{\lambda };\mathit{F};\mathit{G};\mathit{\theta })$

Obtaining the solution to the Fekete-Szegö problem has been a main focus of researchers in this field, as it plays an very important role in obtaining the algebraic properties of a function. It continues to remain in spotlight to date, refer [36,37,38] where authors have obtained the Fekete-Szegö inequality for classes of functions with respect to symmetric points.

In this section, we obtain the solution to the Fekete-Szegö problem for functions belonging to the class ${\mathfrak{S}}_p^m(b;\psi ;\alpha ;\lambda ;F;G;\theta )$.

Theorem 1.

If $h\left(z\right)=z^p+\sum _{j=p+1}^{\infty }{a}_j{z}^j$, $p\in N=\left\{1,2,3,\dots \right\}$ and $h\left(z\right)\in {\mathfrak{S}}_p^m(b;\psi ;\alpha ;\lambda ;F;G;\theta )$, then for odd values of $p+m$ we have

$$\left|a_{p+1}\right|\le \frac{L_1\left|b\right|(F-G)(p-\alpha )\left|{\Gamma }_1\right|}{2(p+1)sec\theta },$$

(12)

and

$$\begin{array}{c}\left|a_{p+2}\right|\le \frac{L_1\left|b\right|(F-G)(p-\alpha )\left|{\Gamma }_2\right|}{2sec\theta }\left[\left|\frac{d_1}{d_0}\right|+max\left\{1;\left|\frac{(G+1)L_1}{2}\right.\right.\right.\\ \left.\left.\left.-\frac{L_2}{L_1}-\frac{b{d}_0(F-G)(p-\alpha )L_1{\Gamma }_1^2{\Gamma }_3}{4(1+itan\theta )}\right|\right\}\right],\end{array}$$

(13)

where ${\Gamma }_1$, ${\Gamma }_2$ and ${\Gamma }_3$ are given by

$$\begin{array}{cc}\hfill {\Gamma }_1& =\frac{(p-m+1)(1-t^p)}{(p-m+1)(1-t^p)+(p-m)(\lambda -1)(1-t^{p+1})}\hfill \\ \hfill {\Gamma }_2& =\frac{(p-m+1)(p-m+2)(1-t^p)}{(p+1)(p+2)[(p-m+2)(1-t^p)+(p-m)(\lambda -1)(1-t^{p+2})]}\hfill \\ \hfill {\Gamma }_3& =\frac{(1-t^{p+1})[2(p-m+1)(1-t^p)(\lambda -1)+(p-m)(\lambda -1)(\lambda -2)(1-t^{p+1})]}{{(p-m+1)}^2{(1-t^p)}^2}.\hfill \end{array}$$

In addition, for all $\mu \in \mathbb{C}$ we have

$$\left|a_{p+2}-\mu a_{p+1}^2\right|\le \frac{L_1\mid b\mid (F-G)(p-\alpha )\mid {\Gamma }_2\mid }{2sec\theta }\left[\left|\frac{d_1}{d_0}\right|+max\left\{1,\left|2{\mathcal{H}}_1-1\right|\right\}\right],$$

where ${\mathcal{H}}_1$ is given by

$$\begin{array}{c}\hfill {\mathcal{H}}_1=\frac{1}{4}\left\{(G+1)L_1+2\left(1-\frac{L_2}{L_1}\right)-\frac{b{d}_0(F-G)(p-\alpha )L_1{\Gamma }_1^2{\Gamma }_3}{2(1+itan\theta )}\right.\\ \hfill \left.+\frac{\mu b{d}_0(F-G)(p-\alpha )L_1{\Gamma }_1^2}{{(p+1)}^2(1+itan\theta ){\Gamma }_2}\right\}.\end{array}$$

The inequality is sharp for each $\mu \in \mathbb{C}$.

Proof. 

By Definition 1, $h\left(z\right)\in {\mathfrak{S}}_p^m(b;\psi ;\alpha ;\lambda ;F;G;\theta )$ implies

$$\frac{1+itan\theta }{b}\left[\frac{{\Gamma }_{\lambda }^p(m;t)z^{1-\lambda (p-m)}{h}^{(m+1)}\left(z\right)}{{\left[h^{\left(m\right)}\left(z\right)-h^{\left(m\right)}\left(tz\right)\right]}^{1-\lambda }}-p+m\right]=\chi \left(z\right)\left[\aleph (p;F,G;\alpha ;\psi ;w(z\left)\right)-p\right],$$

(14)

where $\aleph (p;F,G;\alpha ;\psi ;w(z\left)\right)$ is defined as in (10). For odd values of p, the left hand side of (14) is given by

$$\begin{array}{c}\frac{{\Gamma }_{\lambda }^p(m;t)z^{1-\lambda (p-m)}{h}^{(m+1)}\left(z\right)}{{\left[h^{\left(m\right)}\left(z\right)-h^{\left(m\right)}\left(tz\right)\right]}^{1-\lambda }}\\ =(p-m)\{1+\left[\frac{(\lambda -1)(p+1)}{1!(p-m+1)}\left(\frac{1-t^{p+1}}{1-t^p}\right)+\frac{p+1}{p-m}\right]a_{p+1}z\\ +[\left(\frac{(\lambda -1)(p+1)(p+2)}{1!(p-m+1)(p-m+2)}\left(\frac{1-t^{p+2}}{1-t^p}\right)+\frac{(p+1)(p+2)}{(p-m+1)(p-m)}\right)a_{p+2}\\ +(\frac{(\lambda -1)(\lambda -2){(p+1)}^2}{2!{(p-m+1)}^2}{\left(\frac{1-t^{p+1}}{1-t^p}\right)}^2+\\ \frac{(\lambda -1){(p+1)}^2}{1!(p-m)(p-m+1)}\left(\frac{1-t^{p+1}}{1-t^p}\right)\left)a_{p+1}^2\right]z^2+\cdots \}.\end{array}$$

(15)

From (15) and (11), the coefficients of z and $z^2$ are given by

$$\begin{array}{cc}\hfill a_{p+1}& =\frac{b{d}_0(F-G)(p-\alpha )L_1{\vartheta }_1{\Gamma }_1}{4(p+1)(1+itan\theta )}\hfill \end{array}$$

(16)

and

$$a_{p+2}=\frac{b{d}_0(F-G)(p-\alpha )L_1{\Gamma }_2}{4(1+itan\theta )}\left[{\vartheta }_2-\frac{{\vartheta }_1^2}{4}\left(L_1(G+1)+2\left(1-\frac{L_2}{L_1}\right)-\frac{b{d}_0(F-G)(p-\alpha )L_1{\Gamma }_1^2{\Gamma }_3}{2(1+itan\theta )}\right)+\frac{d_1{\vartheta }_1}{d_0}\right].$$

(17)

Applying Lemma 1 on (16), we can obtain (12). Using (17) together with Lemma 1, we have

$$\begin{array}{cc}\hfill \left|a_{p+2}\right|& =\frac{\mid b\mid |d_0\left|(F-G)(p-\alpha )\right|L_1|{\Gamma }_2}{4sec\theta }|{\vartheta }_2-\frac{{\vartheta }_1^2}{4}((G+1)L_1+2\left(1-\frac{L_2}{L_1}\right)\hfill \\ & -\frac{b{d}_0(F-G)(p-\alpha )L_1{\Gamma }_1^2{\Gamma }_3}{2(1+itan\theta )})+\frac{d_1{\vartheta }_1}{d_0}|\hfill \\ & \le \frac{\left|b\right|(F-G)(p-\alpha )\left|L_1\right|{\Gamma }_2}{2sec\theta }[\left|\frac{d_1}{d_0}\right|+max\left\{1;\left|\frac{(G+1)L_1}{2}-\frac{L_2}{L_1}\right.\right.\hfill \\ & \left.\left.-\frac{b{d}_0(F-G)(p-\alpha )L_1{\Gamma }_1^2{\Gamma }_3}{4(1+itan\theta )}\right|\right\}].\hfill \end{array}$$

Hence the proof of (13).

Now to prove the Fekete-Szegö inequality for the class ${\mathfrak{S}}_p^m(b;\psi ;\alpha ;\lambda ;F;G;\theta )$, we consider

$$\begin{array}{c}\left|a_{p+2}-\mu a_{p+1}^2\right|=\left|\frac{b{d}_0(F-G)(p-\alpha )L_1{\Gamma }_2}{4(1+itan\theta )}\left[{\vartheta }_2-\frac{{\vartheta }_1^2}{4}\left((G+1)L_1+2\left(1-\frac{L_2}{L_1}\right)\right.\right.\right.\\ \left.-\frac{b{d}_0(F-G)(p-\alpha )L_1{\Gamma }_1^2{\Gamma }_3}{2(1+itan\theta )}\right)+\frac{d_1{\vartheta }_1}{d_0}]-\frac{\mu d_0^2{b}^2{(F-G)}^2{(p-\alpha )}^2{L}_1^2{\vartheta }_1^2{\Gamma }_1^2}{16{(p+1)}^2{(1+itan\theta )}^2}|\\ =\left|\frac{b{d}_0(F-G)(p-\alpha )L_1{\Gamma }_2}{4(1+itan\theta )}\right[{\vartheta }_2-\frac{{\vartheta }_1^2}{2}+\frac{{\vartheta }_1^2}{4}(\frac{2L_2}{L_1}-(G+1)L_1\\ +\frac{b{d}_0(F-G)(p-\alpha )L_1{\Gamma }_1^2{\Gamma }_3}{2(1+itan\theta )}-\frac{\mu b(F-G)(p-\alpha )L_1{\Gamma }_1^2}{{(p+1)}^2(1+itan\theta ){\Gamma }_2})+\frac{d_1{\vartheta }_1}{d_0}]|\\ \le \frac{\mid b\mid (F-G)(p-\alpha )\mid L_1\mid {\Gamma }_2}{4sec\theta }[2+\frac{\mid {\vartheta }_1{\mid }^2}{4}(|\frac{2L_2}{L_1}-(G+1)L_1\\ +\frac{b{d}_0(F-G)(p-\alpha )L_1{\Gamma }_1^2{\Gamma }_3}{2(1+itan\theta )}-\frac{\mu b{d}_0(F-G)(p-\alpha )L_1{\Gamma }_1^2}{{(p+1)}^2(1+itan\theta ){\Gamma }_2}|-2)+2\left|\frac{d_1}{d_0}\right|].\end{array}$$

(18)

Denoting

$$\begin{array}{c}H:=\left|\frac{2L_2}{L_1}-(G+1)L_1+\frac{b{d}_0(F-G)(p-\alpha )L_1{\Gamma }_1^2{\Gamma }_3}{2(1+itan\theta )}-\frac{\mu b{d}_0(F-G)(p-\alpha )L_1{\Gamma }_1^2}{{(p+1)}^2(1+itan\theta ){\Gamma }_2}\right|.\end{array}$$

If $H\le 2$, from (18) we obtain

$$\left|a_{p+2}-\mu a_{p+1}^2\right|\le \frac{\mid b\mid (F-G)(p-\alpha )\mid L_1\mid {\Gamma }_2}{2sec\theta }\left|\frac{d_1}{d_0}\right|.$$

(19)

Further, if $H\ge 2$ from (18) we deduce

$$\begin{array}{c}\left|a_{p+2}-\mu a_{p+1}^2\right|\le \frac{\mid b\mid (F-G)(p-\alpha )\mid L_1\mid {\Gamma }_2}{2sec\theta }\left(\right|\frac{2L_2}{L_1}-(G+1)L_1\\ +\frac{b{d}_0(F-G)(p-\alpha )L_1{\Gamma }_1^2{\Gamma }_3}{2(1+itan\theta )}-\frac{\mu b{d}_0(F-G)(p-\alpha )L_1{\Gamma }_1^2}{{(p+1)}^2(1+itan\theta ){\Gamma }_2}|+\left|\frac{d_1}{d_0}\right|).\end{array}$$

(20)

Equality of (19) will be attained if ${\vartheta }_1=0$, ${\vartheta }_2=2$ and $d_0=1$. Equivalently, by Lemma 2 we have $\psi \left(z^2\right)={\psi }_2\left(z\right)={\displaystyle \frac{1+z^2}{1-z^2}}$. Therefore, the extremal function of the class ${\mathfrak{S}}_p^m(b;\psi ;\alpha ;\lambda ;F;G;\theta )$ is given by

$$\begin{array}{c}\frac{1+itan\theta }{b}\left[\frac{{\Gamma }_{\lambda }^p(m;t)z^{1-\lambda (p-m)}{h}^{(m+1)}\left(z\right)}{{\left[h^{\left(m\right)}\left(z\right)-h^{\left(m\right)}\left(tz\right)\right]}^{1-\lambda }}-p+m\right]\\ =\frac{\left[(1+F)p+\alpha (G-F)\right]\psi \left(z^2\right)+\left[(1-F)p-\alpha (G-F)\right]}{\left[(G+1)\psi \left(z^2\right)+(1-G)\right]}-p.\end{array}$$

Similarly, equality of (20) will be attained if ${\vartheta }_2=2$. Equivalently, by Lemma 2 we have $\psi \left(z\right)={\psi }_1\left(z\right)={\displaystyle \frac{1+z}{1-z}}$ and ${\chi }_1\left(z\right)=1+z+z^2+\cdots$. Therefore, the extremal function in ${\mathfrak{S}}_p^m(b;\psi ;\alpha ;\lambda ;F;G;\theta )$ is given by

$$\begin{array}{c}1+\frac{1+itan\alpha }{\gamma }\left[\frac{z^{1-t}{\left[H^{\prime }\left(z\right)\right]}^{\lambda }}{{\left[(1-\beta )H\left(z\right)+\beta z\right]}^{1-t}}-1\right]\\ ={\chi }_1\left(z\right)\left[\frac{\left[(1+F)p+\alpha (G-F)\right]{\psi }_1\left(z\right)+\left[(1-F)p-\alpha (G-F)\right]}{\left[(G+1){\psi }_1\left(z\right)+(1-G)\right]}-p\right],\end{array}$$

and the proof of the theorem is complete. □

If we let $p=b=1$, $\alpha =\theta =\lambda =0$, $\chi \left(z\right)=1$ and $\psi ={\widehat{p}}_{\nu ,\sigma }\left(z\right)$ and $m=0$ in Theorem 1, we obtain the following result.

Corollary 1.

Ref. [24] (Theorem 2.3) If $h\left(z\right)\in k-\mathcal{US}(F,G,\sigma ,t)$ (see Remark 1 (i)), then we have

$$\left|a_2\right|\le \frac{(F-G)\left|{\tau }_1\right|}{2|1-t|},$$

and

$$\left|a_3\right|\le \frac{(F-G)\left|{\tau }_1\right|}{2\left|2-t-t^2\right|}max\left\{1;\left|\frac{(G+1){\tau }_1}{2}-\frac{{\tau }_2}{{\tau }_1}+\frac{(F-G){\tau }_1(1+t)}{2(1-t)}\right|\right\},$$

In addition, for all $\mu \in \mathbb{C}$ we have

$$\left|a_3-\mu a_2^2\right|\le \frac{(F-G)\mid {\tau }_1\mid }{2\left|1-t-t^2\right|}max\left\{1,\left|2{\mathcal{H}}_1-1\right|\right\}$$

where ${\mathcal{H}}_1$ is given by

$${\mathcal{H}}_1=\frac{1}{4}\left\{(G+1){\tau }_1+2\left(1-\frac{{\tau }_2}{{\tau }_1}\right)+\frac{(F-G){\tau }_1(1+t)}{2(1-t)}+\frac{\mu (F-G){\tau }_1[2-t-t^2]}{{(1-t)}^2}\right\}.$$

The inequality is sharp for each $\mu \in \mathbb{C}$.

If we let $p=b=1$, $\alpha =\theta =\lambda =0$, $\chi \left(z\right)=1$, $F=1$, $G=-1$ and $m=0$ in Theorem 1, we obtain the following result which was obtained by Shanmugam et al. [26] for real valued $\mu$.

Corollary 2.

Ref. [26] (Theorem 2.1)

If $h\left(z\right)\in {\mathcal{S}}_{\ast }^s\left(\psi \right)$ (see Remark 1 (iii)), then we have

$$\left|a_2\right|\le L_1,$$

and

$$\left|a_3\right|\le \frac{L_1}{2}max\left\{1;\left|\frac{L_2}{L_1}-4L_1\right|\right\},$$

In addition, for all $\mu \in \mathbb{C}$ we have

$$\left|a_3-\mu a_2^2\right|\le \frac{L_1}{2}max\left\{1,\left|\frac{L_2}{L_1}-2L_1(1+\mu )\right|\right\}.$$

The inequality is sharp for each $\mu \in \mathbb{C}$.

Some Applications Involving Bernoulli Lemniscate and Shell Shaped Region

Raina and Sokół [7] (also see [39]) defined the class ${\mathcal{S}}^{\ast }(z+\sqrt{1+z^2})$. The function $\psi \left(z\right)=z+\sqrt{1+z^2}$ maps the unit disc onto the interior of lune-shaped (shell-shaped) starlike region (see Figure 3a). The impact of $\aleph (p;F,G;\alpha ;\psi ;z)$ on the shell-shaped region is illustrated in Figure 3. It could be seen that if the distance between F and G are increased, then the mapping of unit disc becomes convex. If they are closer to each other, then the mapping is starlike. Furthermore, notice that in Figure 3, we have shown by the varying parameters involved that a shell-shaped region with corner $-2i$ is rotated to $\pi$ radians in a counterclockwise direction and corner $+2i$ is rotated to $\pi$ radians in clockwise direction.

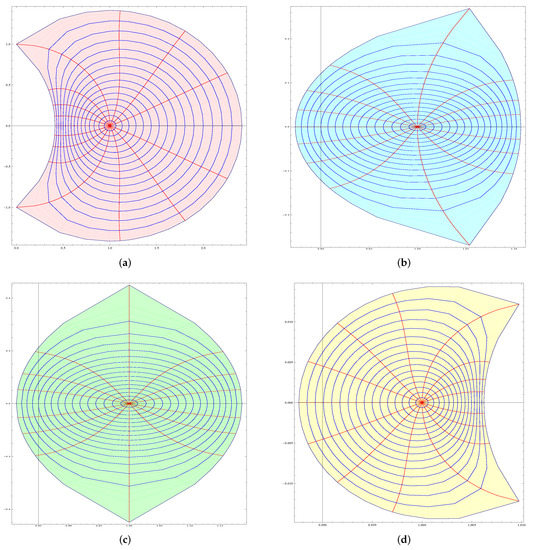
Figure 3. Impact of $\aleph (p;F,G;\alpha ;\psi ;z)$ on the conic region $\psi \left(z\right)=z+\sqrt{1+z^2}$. (a) Mapping of $\mathbb{E}$ under the transformation $\psi \left(z\right)=z+\sqrt{1+z^2}$. (b) Mapping of $\mathbb{E}$ under the transformation $\aleph (1;0,-0.3;0.9;\psi ;z)$ if $\psi \left(z\right)=z+\sqrt{1+z^2}$. (c) Mapping of $\mathbb{E}$ under the transformation $\aleph (1;0.9,0.0;0.5;\psi ;z)$ if $\psi \left(z\right)=z+\sqrt{1+z^2}$. (d) Mapping of $\mathbb{E}$ under the transformation $\aleph (1;0.9,0.8;0.8;\psi ;z)$ if $\psi \left(z\right)=z+\sqrt{1+z^2}$.

Corollary 3.

Ref. [32] If $h\in {\mathcal{S}}^{\ast }(z+\sqrt{1+z^2})$, then $|a_2|\le 1$, $|a_3|\le \frac{3}{4}$ and $|a_3-\mu a_2^2|\le max\left\{\frac{1}{2},|\mu -\frac{3}{4}|\right\}$.

Proof. 

The function $\psi \left(z\right)=z+\sqrt{1+z^2}$ has a Maclaurin series expansion of the form

$$\psi \left(z\right)=1+z+\frac{z^2}{2}-\frac{z^4}{8}+\frac{z^6}{16}-\frac{5z^8}{128}+\frac{7z^{10}}{256}-\frac{21z^{12}}{1024}+O{\left[z\right]}^{13}.$$

Now if we let $t=\alpha =\theta =\lambda =0$, $p=F=1$, $G=-1$, $L_1=1$ and $L_2=\frac{1}{2}$ in Theorem 1, we obtain the assertion of the Corollary. □

The function $\psi \left(z\right)=\sqrt{1+z}$ maps $\mathbb{E}$ onto a set bounded by Bernoulli lemniscate (see [6]). Subigures in Figure 4 describes the impact of $\aleph (p;F,G;\alpha ;\psi ;z)$ on Bernoulli lemniscate.

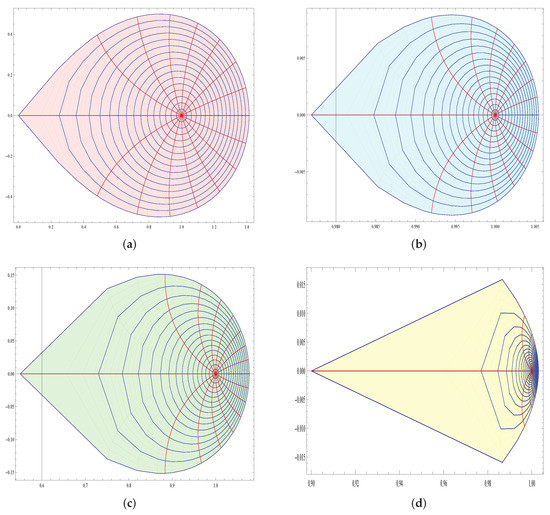
Figure 4. Impact of $\aleph (p;F,G;\alpha ;\psi ;z)$ on the conic region $\psi \left(z\right)=\sqrt{1+z}$. (a) Mapping of $\mathbb{E}$ under the transformation $\psi \left(z\right)=\sqrt{1+z}$. (b) Mapping of $\mathbb{E}$ under the transformation $\aleph (1;0,-0.3;0.9;\psi ;z)$ if $\psi \left(z\right)=\sqrt{1+z}$. (c) Mapping of $\mathbb{E}$ under the transformation $\aleph (1;0.9,0.0;0.5;\psi ;z)$ if $\psi \left(z\right)=\sqrt{1+z}$. (d) Mapping of $\mathbb{E}$ under the transformation $\aleph (1;0.9,0.8;0.8;\psi ;z)$ if $\psi \left(z\right)=\sqrt{1+z}$.

Corollary 4.

Ref. [6] (Theorem 2) If $h\in {\mathcal{S}}^{\ast }\left(\sqrt{1+z}\right)$, then $|a_2|\le \frac{1}{2}$, $|a_3|\le \frac{1}{4}$ and $|a_3-\mu a_2^2|\le max\left\{\frac{1}{4},|\mu -\frac{7}{4}|\right\}$.

Proof. 

The function $\psi \left(z\right)=\sqrt{1+z}$ has a Maclaurin series expansion of the form

$$\psi \left(z\right)=1+\frac{z}{2}-\frac{z^2}{8}+\frac{z^3}{16}-\frac{5z^4}{128}+\frac{7z^5}{256}-\frac{21z^6}{1024}+\frac{33z^7}{2048}-\frac{429z^8}{32768}+O{\left[z\right]}^9.$$

Now if we let $t=\alpha =\theta =\lambda =0$, $p=F=1$, $G=-1$, $L_1=\frac{1}{2}$ and $L_2=-\frac{1}{8}$ in Theorem 1, we obtain the assertion of the Corollary. □

Remark 2.

By specializing the parameters involved, we can easily obtain the coefficient inequalities of starlike functions with respect to symmetric points associated with Bernoulli lemniscate and Shell-shaped region.

4. Subordination Results for Functions with Respect to Symmetric Points

Researchers have investigated and obtained several interesting subordination conditions, see for example [20,21,40,41]. In this section we follow the steps detailed in Goyal and Goswami [42], to obtain some sufficient conditions for functions to be in our defined function class. We let

$${\omega }_{\theta }=(1+itan\theta )\mathrm{and}{G}^m(z,t)=\left[h^{\left(m\right)}\left(z\right)-h^{\left(m\right)}\left(tz\right)\right].$$

We begin with the following

Theorem 2.

Let $h\in \mathcal{A}(p,1)$ with $h^{\left(m\right)}\left(z\right)$, $h^{(m+1)}\left(z\right)$ and $G^m(z,t)\ne 0$ for all $z\in \mathbb{E}\backslash \left\{0\right\}$. Moreover, let $\aleph (p;F,G;\alpha ;\psi ;z)$ be convex univalent in $\mathbb{E}$ with $\aleph (p;F,G;\alpha ;0)=p$ and $Re\aleph (p;F,G;\alpha ;\psi ;z)>0$. Further suppose that

$$\begin{array}{c}{\left(p+\frac{{\omega }_{\theta }}{b\chi \left(z\right)}\left[\frac{{{\rm Y}}_{\lambda }^p(m;t)z^{1-\lambda (p-m)}{h}^{(m+1)}\left(z\right)}{{\left[G^m(z,t)\right]}^{1-\lambda }}-p+m\right]\right)}^2[1+2\{\frac{(\lambda -1)z{G}^{m+1}(z,t)}{G^m(z,t)}\\ +\frac{(1-\lambda )z{G}^{m+1}(z,t)\left[pb\chi \left(z\right)-(p-m){\omega }_{\theta }\right]{\left[G^m(z,t)\right]}^{-\lambda }+pbz{\chi }^{\prime }\left(z\right){\left[G^m(z,t)\right]}^{1-\lambda }}{\left[pb\chi \left(z\right)-(p-m){\omega }_{\theta }\right]{\left[G^m(z,t)\right]}^{1-\lambda }+{\omega }_{\theta }{{\rm Y}}_{\lambda }^p(m;t)z^{1-\lambda (p-m)}{h}^{(m+1)}\left(z\right)}\\ +\frac{{\omega }_{\theta }{{\rm Y}}_{\lambda }^p(m;t)z^{1-\lambda (p-m)}\left[(1-\lambda (p-m))h^{(m+1)}\left(z\right)+z{h}^{(m+2)}\left(z\right)\right]}{\left[pb\chi \left(z\right)-(p-m){\omega }_{\theta }\right]{\left[G^m(z,t)\right]}^{1-\lambda }+{\omega }_{\theta }{{\rm Y}}_{\lambda }^p(m;t)z^{1-\lambda (p-m)}{h}^{(m+1)}\left(z\right)}\end{array}$$

(21)

$$-\frac{z{\chi }^{\prime }\left(z\right)}{\chi \left(z\right)}\left\}\right]\prec \aleph (p;F,G;\alpha ;\psi ;z).$$

(22)

Then

$$\frac{1+itan\theta }{b}\left[\frac{{{\rm Y}}_{\lambda }^p(m;t)z^{1-\lambda (p-m)}{h}^{(m+1)}\left(z\right)}{{\left[h^{\left(m\right)}\left(z\right)-h^{\left(m\right)}\left(tz\right)\right]}^{1-\lambda }}-p+m\right]{\prec }_{\kappa }\varphi \left(z\right)=\sqrt{Q\left(z\right)}-p$$

(23)

where

$$Q\left(z\right)=\frac{1}{z}{\int }_0^z\aleph (p;F,G;\alpha ;\psi ;t)dt$$

and ϕ is convex and is the best dominant.

Proof. 

Let

$$k\left(z\right)=p+\frac{1+itan\theta }{b\chi \left(z\right)}\left[\frac{{{\rm Y}}_{\lambda }^p(m;t)z^{1-\lambda (p-m)}{h}^{(m+1)}\left(z\right)}{{\left[h^{\left(m\right)}\left(z\right)-h^{\left(m\right)}\left(tz\right)\right]}^{1-\lambda }}-p+m\right](z\in \mathbb{E}),$$

then $k\left(z\right)\in \mathcal{H}(p,1)$ with $k\left(z\right)\ne 0$.

Since $\aleph (p;F,G;\alpha ;\psi ;z)$ is convex, it can be easily seen that Q is convex and univalent in $\mathbb{E}$. If we make the change of the variables $K\left(z\right)=k^2\left(z\right)$, then $K\left(z\right)\in \mathcal{H}(p,1)$ with $K\left(z\right)\ne 0$ in $\mathbb{E}$.

By a straight forward computation, we have

$$\begin{array}{c}\frac{z{K}^{\prime }\left(z\right)}{K\left(z\right)}=2\left[\frac{{\omega }_{\theta }{{\rm Y}}_{\lambda }^p(m;t)z^{1-\lambda (p-m)}\left[(1-\lambda (p-m))h^{(m+1)}\left(z\right)+z{h}^{(m+1)}\left(z\right)\right]}{\left[pb\chi \left(z\right)-(p-m){\omega }_{\theta }\right]{\left[G^m(z,t)\right]}^{1-\lambda }+{\omega }_{\theta }{{\rm Y}}_{\lambda }^p(m;t)z^{1-\lambda (p-m)}{h}^{(m+1)}\left(z\right)}\right.\\ +\frac{(1-\lambda )z{G}^{m+1}(z,t)\left[pb\chi \left(z\right)-(p-m){\omega }_{\theta }\right]{\left[G^m(z,t)\right]}^{-\lambda }+pbz{\chi }^{\prime }\left(z\right){\left[G^m(z,t)\right]}^{1-\lambda }}{\left[pb\chi \left(z\right)-(p-m){\omega }_{\theta }\right]{\left[G^m(z,t)\right]}^{1-\lambda }+{\omega }_{\theta }{{\rm Y}}_{\lambda }^p(m;t)z^{1-\lambda (p-m)}{h}^{(m+1)}\left(z\right)}\\ \left.-\frac{z{\chi }^{\prime }\left(z\right)}{\chi \left(z\right)}+\frac{(\lambda -1)z{G}^{m+1}(z,t)}{G^m(z,t)}\right].\end{array}$$

Thus, by (22), we have

$$K\left(z\right)+z{K}^{\prime }\left(z\right)\prec r\left(z\right)(z\in \mathbb{E}).$$

(24)

Now by Lemma 3, we deduce that

$$K\left(z\right)\prec Q\left(z\right)\prec r\left(z\right).$$

Since $Rer\left(z\right)>0$ and $Q\left(z\right)\prec r\left(z\right)$ we also have $ReQ\left(z\right)>0$. Hence the univalence of Q implies the univalence of $\sqrt{Q\left(z\right)}$ and $k^2\left(z\right)\prec Q\left(z\right)$ implies that $k\left(z\right)\prec \sqrt{Q\left(z\right)}.$ Since subordination is invariant under translation and using the fact that $g/\chi \prec r$ implies $g{\prec }_{\kappa }r$, we have

$$\frac{1+itan\theta }{b}\left[\frac{{{\rm Y}}_{\lambda }^p(m;t)z^{1-\lambda (p-m)}{h}^{(m+1)}\left(z\right)}{{\left[h^{\left(m\right)}\left(z\right)-h^{\left(m\right)}\left(tz\right)\right]}^{1-\lambda }}-p+m\right]{\prec }_{\kappa }\sqrt{Q\left(z\right)}-p,$$

and the proof is complete. □

If we let $p=b=1,\lambda =m=\theta =0$ in Theorem 2, we have

Corollary 5.

Let $h\in \mathcal{A}$ with $h\left(z\right)$, $h^{\prime }\left(z\right)$ and $\left[h\left(z\right)-h\left(tz\right)\right]\ne 0$ for all $z\in \mathbb{E}\backslash \left\{0\right\}$. Furthermore, let $\aleph (p;F,G;\alpha ;\psi ;z)$ is convex in $\mathbb{E}$ with $\aleph (p;F,G;\alpha ;\psi ;0)=p$ and $Re\aleph (p;F,G;\alpha ;\psi ;z)>0$. Further suppose that

$$\begin{array}{c}{\left(1+\frac{1}{\chi \left(z\right)}\left[\frac{z{h}^{\prime }\left(z\right)}{\left[h\left(z\right)-h\left(tz\right)\right]}-1\right]\right)}^2[1+2\{\frac{z{h}^{\prime }\left(z\right)+z^2{h}^{\prime \prime }\left(z\right)}{\left[\chi \left(z\right)-1\right]\left[h\left(z\right)-h\left(tz\right)\right]+z{h}^{\prime }\left(z\right)}\\ +\frac{z{\left[h\left(z\right)-h\left(tz\right)\right]}^{\prime }\left[\chi \left(z\right)-1\right]+z{\chi }^{\prime }\left(z\right)\left[h\left(z\right)-h\left(tz\right)\right]}{\left[\chi \left(z\right)-1\right]\left[h\left(z\right)-h\left(tz\right)\right]+z{h}^{\prime }\left(z\right)}\\ -\frac{z{\left[h\left(z\right)-h\left(tz\right)\right]}^{\prime }}{\left[h\left(z\right)-h\left(tz\right)\right]}-\frac{z{\chi }^{\prime }\left(z\right)}{\chi \left(z\right)}\left\}\right]\prec \aleph (p;F,G;\alpha ;\psi ;z).\end{array}$$

Then

$$\frac{z{h}^{\prime }\left(z\right)}{\left[h\left(z\right)-h\left(tz\right)\right]}-1{\prec }_{\kappa }\varphi \left(z\right)=\sqrt{Q\left(z\right)}-1$$

where

$$Q\left(z\right)=\frac{1}{z}{\int }_0^z\aleph (p;F,G;\alpha ;\psi ;t)dt$$

and ϕ is convex and is the best dominant.

From the Corollary 5, we deduce that on letting $p=b=1$, $m=\alpha =\theta =\lambda =0$, $\chi \left(z\right)=1$ and $\psi ={\widehat{p}}_{\nu ,\sigma }\left(z\right)$ (see (5)) in Theorem 1, then we can obtain the sufficient conditions for functions to be in $k-\mathcal{US}(F,G,\sigma ,t)$ (see Remark 1 (i)).

Corollary 6.

Let $h\in \mathcal{A}$ with $h^{\prime }\left(z\right)$ and $\left[h\left(z\right)-h(-z)\right]\ne 0$ for all $z\in \mathbb{E}\backslash \left\{0\right\}$. If

$$Re\left\{{\left(\frac{z{h}^{\prime }\left(z\right)}{\left[h\left(z\right)-h(-z)\right]}\right)}^2\left[3+\frac{2z{h}^{″}\left(z\right)}{h^{\prime }\left(z\right)}-\frac{2z{\left[h\left(z\right)-h(-z)\right]}^{\prime }}{\left[h\left(z\right)-h(-z)\right]}\right]\right\}>\alpha ,$$

then

$$Re\frac{z{h}^{\prime }\left(z\right)}{\left[h\left(z\right)-h(-z)\right]}>\eta \left(\alpha \right),$$

where $\eta \left(\alpha \right)={\left[2(1-\alpha )·log2+(2\alpha -1)\right]}^{\frac{1}{2}}$. This result is sharp

Proof. 

Letting $p=1,F=1$, $G=-1$ and $\psi \left(z\right)=\frac{1-z}{1+z}$ in (4), we obtain

$$\aleph (1;1,-1;\alpha ;z)=\frac{1+(2\alpha -1)z}{1+z},(0\le \alpha <1).$$

Additionally, if we let $\chi \left(z\right)=1,p=b=1,\theta =m=\lambda =0$, in Theorem 2, we have

$$Q\left(z\right)=\frac{1}{z}{\int }_0^z\frac{1+(2\alpha -1)t}{1+t}dt$$

which is convex in $\mathbb{E}$ along with $ReQ\left(z\right)>0$. Therefore

$$\underset{\left|z\right|\le 1}{min}Re\sqrt{Q\left(z\right)}=\sqrt{Q\left(1\right)}={\left[2(1-\alpha )·log2+(2\alpha -1)\right]}^{\frac{1}{2}}.$$

Hence the proof of the Corollary. □

5. Classes of Multivalent Functions Using Quantum Calculus

Now, we give a very brief introduction of the q-calculus. We let

$${\left[n\right]}_q=\sum _{k=1}^n{q}^{k-1},{\left[0\right]}_q=0,(q\in \mathbb{C}).$$

Srivastava in [43] initiated the study of geometric function theory in dual with quantum calculus in 1988. However, this dulaity theory was brought into the spotlight by Ismail et al. [44] who introduced and studied the so-called class of q-starlike functions. For detailed study of the developments and applications of this duality theory, refer to the recent survey-cum-expository article of Srivastava [45] and references provided therein.

The q-difference operator for a function $h\in \mathcal{A}(p,1)$ is defined by

$${\mathfrak{D}}_{q}h\left(z\right):=\left\{\begin{array}{cc}{h}^{\prime }\left(0\right),\hfill & \mathrm{if}z=0,\hfill \\ {\displaystyle \frac{h\left(z\right)-h\left(qz\right)}{(1-q)z}},\hfill & \mathrm{if}z\ne 0.\hfill \end{array}\right.$$

(25)

From (25), if $h\in \mathcal{A}(p,1)$ we can easily see that ${\mathfrak{D}}_{q}h\left(z\right)=p{z}^{p-1}+{\displaystyle \sum _{k=p+n}^{\infty }}{\left[k\right]}_q{a}_k{z}^{k-1}$, for $z\ne 0$ and note that $\underset{q\to 1^{-}}{lim}{\mathfrak{D}}_{q}h\left(z\right)=h^{\prime }\left(z\right)$. The q-Jackson integral is defined by (see [46])

$$I_q\left[h\left(z\right)\right]:={\int }_0^{z}h\left(t\right)d_{q}t=z(1-q)\sum _{n=0}^{\infty }{q}^{n}h\left(z{q}^n\right)$$

(26)

provided the q-series converges. Further observe that

$${\mathfrak{D}}_q{I}_{q}h\left(z\right)=h\left(z\right)\mathrm{and}{I}_q{\mathfrak{D}}_{q}h\left(z\right)=h\left(z\right)-h\left(0\right),$$

where the second equality holds if h is continuous at $z=0$. Ismail et al. in [44] defined the class ${\mathcal{S}}_q^{\ast }$ as class of functions which satisfies the condition

$$\left|\frac{z{\mathfrak{D}}_{q}h\left(z\right)}{h\left(z\right)}-\frac{1}{1-q}\right|\le \frac{1}{1-q},(h\in \mathcal{S}).$$

The class ${\mathcal{S}}_q^{\ast }$ is the so-called class of q-starlike functions. Equivalently, a function $h\in {\mathcal{S}}_q^{\ast }$, if and only if the subordination condition (see ([47], Definition 7))

$$\frac{z{\mathfrak{D}}_{q}h\left(z\right)}{h\left(z\right)}\prec \frac{1+z}{1-qz},$$

holds.

Let us define the q-analogue of $\aleph (p;F,G;\alpha ;\psi ;z)$ (see (4)) as

$${\aleph }_q(p;F,G;\alpha ;\psi ;z)=\frac{[(F+1){\left[p\right]}_q+\alpha (G-F)]\psi \left(z\right)+\left[(1-F){\left[p\right]}_q-\alpha (G-F)\right]}{\left[(G+1)\psi \left(z\right)+(1-G)\right]}$$

(27)

Srivastava et al. [47,48,49,50,51,52,53,54] introduced function classes of q-starlike functions related with conic region and also studied the impact of Janowski functions on those conic regions. For recent advances pertaining to quantum calculus, refer to Aldawish and Ibrahim [55] and Zhou et al. [56]. Motivated by aforementioned works on q-calculus, we define the following class by replacing ordinary derivative with q-derivative in function class ${\mathfrak{S}}_p^m(b;\psi ;\alpha ;\lambda ;F;G;\theta )$ (see Definition 1).

Definition 2.

Let ${\mathfrak{D}}_q^{m}h={\mathfrak{D}}_q^{m-1}\left({\mathfrak{D}}_q^{1}h\left(z\right)\right)$. For $t\in \mathbb{C}$, with $\left|t\right|\le 1$, $\lambda \ge 0$, $p,n\in \mathbb{N},m\in {\mathbb{N}}_0$ and ${\aleph }_q(p;F,G;\alpha ;\psi ;z)$ defined as in (27), we say that the function $h\in \mathcal{A}(p,1)$ belongs to the class ${\mathcal{QS}}_p^m(b;\psi ;\alpha ;\lambda ;\delta ;F;G;\theta )$ if it satisfies the subordination condition

$$\begin{array}{c}\frac{1+itan\theta }{b}\left(\frac{{\Gamma }_{\lambda }^p(m;t)z^{1-\lambda (p-m)}{\mathfrak{D}}_q^{m+1}h\left(z\right)}{{\left[{\mathfrak{D}}_q^{m}h\left(z\right)-{\mathfrak{D}}_q^{m}h\left(tz\right)\right]}^{1-\lambda }}-{[p-m]}_q\right){\prec }_{\kappa }{\aleph }_q(p;F,G;\alpha ;\psi ;z)-{\left[p\right]}_q\end{array}$$

(28)

where ${\Gamma }_{\lambda }^p(m;t)={\left(1-t^p\right)}^{(1-\lambda )}{\left[{\Delta }_q(p,m-1)\right]}^{-\lambda }$, $\psi \in \mathcal{P}$ is defined as in (2).

Suppose ${\prec }_{\kappa }$ is replaced with ≺ and let $\psi =\frac{1+z}{1-qz},q\in (0,1)$ in ${\mathcal{QS}}_p^m(b;\psi ;\alpha ;\lambda ;\delta ;F;G;\theta )$, then by definition of subordination of analytic function, a function $h\in \mathcal{A}(p,1)$ is said to be in ${\mathcal{QS}}_p^m(b;\psi ;\alpha ;\lambda ;\delta ;F;G;\theta )$ if and only if $\left(q\in (0,1),z\in \mathbb{E}\right),$

$$\begin{array}{c}{\left[p\right]}_q+\frac{1+itan\theta }{b}\left(\frac{{\Gamma }_{\lambda }^p(m;t)z^{1-\lambda (p-m)}{\mathfrak{D}}_q^{m+1}h\left(z\right)}{{\left[{\mathfrak{D}}_q^{m}h\left(z\right)-{\mathfrak{D}}_q^{m}h\left(tz\right)\right]}^{1-\lambda }}-{[p-m]}_q\right)\\ =\frac{\left\{(F+1){\left[p\right]}_q+\alpha (G-F)\right\}w\left(z\right)+2{\left[p\right]}_q+\left\{\alpha (G-F)-(1-F){\left[p\right]}_q\right\}qw\left(z\right)}{(G+1)w\left(z\right)+2+(G-1)qw\left(z\right)},\end{array}$$

where $w\left(z\right)$ is analytic in $\mathbb{E}$ and $w\left(0\right)=0$, $\left|w\right(z\left)\right|<1$.

Remark 3.

If we let $m=\alpha =\lambda =\theta =0$, $b=1$, $p=1$, $F=1$ and $G=-1$, then ${\mathcal{QS}}_p^m(b;\psi ;\alpha ;\lambda ;\delta ;F;G;\theta )$ reduces to the classes ${\mathcal{S}}_{q,s}^{\ast }\left(\psi \right)$ defined by Ramachandran et al. [57] (Definition 1).

Main Results Involving Quantum Calculus

We just state q-analogue result of Theorems 1 and 2. Here we have omitted the proof, as it could be obtained by retracing the steps of Theorems 1 and 2.

Theorem 3.

If $h\left(z\right)=z^p+{\displaystyle \sum _{j=p+1}^{\infty }}{a}_j{z}^j$, $p\in N=\left\{1,2,3,\dots \right\}$ and $h\left(z\right)\in \mathcal{Q}{\mathcal{S}}_p^m(b;\psi ;\alpha ;\lambda ;\delta ;$$F;G;\theta )$, then for odd values of p we have

$$\left|a_{p+1}\right|\le \frac{\left|b\right|(F-G)(p-\alpha )\left|L_1{{\rm Y}}_1\right|}{2{[p+1]}_{q}sec\theta },$$

(29)

and

$$\begin{array}{c}\left|a_{p+2}\right|\le \frac{\left|b\right|(F-G)(p-\alpha )\left|L_1{{\rm Y}}_2\right|}{2sec\theta }\left[\left|\frac{d_1}{d_0}\right|+max\left\{1;\left|\frac{(G+1)L_1}{2}-\frac{L_2}{L_1}\right.\right.\right.\\ \left.\left.\left.-\frac{b{d}_0(F-G)(p-\alpha )L_1{{\rm Y}}_1^2{{\rm Y}}_3}{4(1+itan\theta )}\right|\right\}\right],\end{array}$$

where ${{\rm Y}}_1$, ${{\rm Y}}_2$ and ${{\rm Y}}_3$ are given by

$$\begin{array}{cc}\hfill {{\rm Y}}_1& =\frac{{[p-m+1]}_q(1-t^p)}{{[p-m+1]}_q(1-t^p)+{[p-m]}_q(\lambda -1)(1-t^{p+1})}\hfill \\ \hfill {{\rm Y}}_2& =\frac{{[p-m+1]}_q{[p-m+2]}_q(1-t^p)}{{[p+1]}_q{[p+2]}_q\left[{[p-m+2]}_q(1-t^p)+{[p-m]}_q(\lambda -1)(1-t^{p+2})\right]}\hfill \\ \hfill {{\rm Y}}_3& =\frac{(1-t^{p+1})\left[2{[p-m+1]}_q(1-t^p)(\lambda -1)+{[p-m]}_q(\lambda -1)(\lambda -2)(1-t^{p+1})\right]}{{[p-m+1]}_q^2{(1-t^p)}^2}.\hfill \end{array}$$

Furthermore, for all $\mu \in \mathbb{C}$ we have

$$\left|a_{p+2}-\mu a_{p+1}^2\right|\le \frac{\mid b\mid (F-G)(p-\alpha )\mid L_1{{\rm Y}}_2\mid }{2sec\theta }\left[\left|\frac{d_1}{d_0}\right|+max\left\{1,\left|2{\mathcal{Q}}_1-1\right|\right\}\right],$$

where ${\mathcal{Q}}_1$ is given by

$$\begin{array}{c}\hfill {\mathcal{Q}}_1=\frac{1}{4}\left\{(G+1)L_1+2\left(1-\frac{L_2}{L_1}\right)-\frac{b{d}_0(F-G)(p-\alpha )L_1{{\rm Y}}_1^2{{\rm Y}}_3}{2(1+itan\theta )}\right.\\ \hfill \left.+\frac{\mu b{d}_0(F-G)(p-\alpha )L_1{{\rm Y}}_1^2}{{(p+1)}^2(1+itan\theta ){{\rm Y}}_2}\right\}.\end{array}$$

The inequality is sharp for each $\mu \in \mathbb{C}$.

Remark 4.

If we let $q\to 1^{-}$ in Theorem 3, then we obtain the solution to the Fekete-Szegö problem of the class ${\mathfrak{S}}_p^m(b;\psi ;\alpha ;\lambda ;F;G;\theta )$.

q-analogue of the Lemma 3 (ordinary derivative replaced with a quantum derivative) need not be true for all $q\in (0,1)$. It is true only if we could choose a sequence $q_n$ that tends to $1^{-}$. Thus, we will use same lemma with ordinary derivative to establish the sufficient conditions for functions in ${\mathcal{QS}}_p^m(b;\psi ;\alpha ;\lambda ;\delta ;F;G;\theta )$.

Theorem 4.

Let $h\in \mathcal{A}(p,1)$ with ${\mathfrak{D}}_q^{m}h\left(z\right)$, ${\mathfrak{D}}_q^{m+1}h\left(z\right)$ and $\left[{\mathfrak{D}}_q^{m}h\left(z\right)-{\mathfrak{D}}_q^{m}h\left(tz\right)\right]\ne 0$ for all $z\in \mathbb{E}\backslash \left\{0\right\}$. Furthermore, let ${\aleph }_q(p;F,G;\alpha ;\psi ;z)$ is convex in $\mathbb{E}$ with ${\aleph }_q(p;F,G;\alpha ;0)={\left[p\right]}_q$ and $Re{\aleph }_q(p;F,G;\alpha ;\psi ;z)>0$. Let ${\mathcal{G}}_q^m(t;z)={\mathfrak{D}}_q^{m}h\left(z\right)-{\mathfrak{D}}_q^{m}h\left(tz\right)$, ${\omega }_{\theta }=1+itan\theta$ and $L(p;b;\chi ;\theta )=\left({\left[p\right]}_{q}b\chi \left(z\right)-{[p-m]}_q{\omega }_{\theta }\right)$. Further suppose that

$$\begin{array}{c}{\left[{\left[p\right]}_q+\frac{{\omega }_{\theta }}{b}\left(\frac{{\Gamma }_{\lambda }^p(m;t)z^{1-\lambda (p-m)}{\mathfrak{D}}_q^{m+1}h\left(z\right)}{{\left[{\mathcal{G}}_q^m(t;z)\right]}^{1-\lambda }}-{[p-m]}_q\right)\right]}^2[1+2\{\frac{(\lambda -1)z{\left[{\mathcal{G}}_q^m(t;z)\right]}^{\prime }}{\left[{\mathcal{G}}_q^m(t;z)\right]}\\ +\frac{(1-\lambda )z{\left[{\mathcal{G}}_q^m(t;z)\right]}^{\prime }L(p;b;\chi ;\theta ){\left[{\mathcal{G}}_q^m(t;z)\right]}^{-\lambda }+{\left[p\right]}_{q}bz{\chi }^{\prime }\left(z\right){\left[{\mathcal{G}}_q^m(t;z)\right]}^{1-\lambda }}{L(p;b;\chi ;\theta ){\left[{\mathcal{G}}_q^m(t;z)\right]}^{1-\lambda }+{\omega }_{\theta }{\Gamma }_{\lambda }^p(m;t)z^{1-\lambda (p-m)}{\left({\mathfrak{D}}_q^{m+1}h\left(z\right)\right)}^{\prime }}\\ +\frac{{\omega }_{\theta }{{\rm Y}}_{\lambda }^p(m;t)z^{1-\lambda (p-m)}\left({[1-\lambda (p-m)]}_q{\mathfrak{D}}_q^{m+1}h\left(z\right)+z{\left({\mathfrak{D}}_q^{m+1}h\left(z\right)\right)}^{\prime }\right)}{L(p;b;\chi ;\theta ){\left[{\mathcal{G}}_q^m(t;z)\right]}^{1-\lambda }+{\omega }_{\theta }{\Gamma }_{\lambda }^p(m;t)z^{1-\lambda (p-m)}{\left({\mathfrak{D}}_q^{m+1}h\left(z\right)\right)}^{\prime }}\\ -\frac{z{\chi }^{\prime }\left(z\right)}{\chi \left(z\right)}\left\}\right]\prec {\aleph }_q(p;F,G;\alpha ;\psi ;z).\end{array}$$

Then

$$\frac{{\omega }_{\theta }}{b}\left(\frac{{\Gamma }_{\lambda }^p(m;t)z^{1-\lambda (p-m)}{\mathfrak{D}}_q^{m+1}h\left(z\right)}{{\left[{\mathcal{G}}_q^m(t;z)\right]}^{1-\lambda }}-{[p-m]}_q\right){\prec }_{\kappa }\varphi \left(z\right)=\sqrt{R\left(z\right)}-{\left[p\right]}_q$$

where

$$R\left(z\right)=\frac{1}{z}{\int }_0^z{\aleph )}_q(p;F,G;\alpha ;\psi ;t)dt$$

and ϕ is convex and is the best dominant.

Remark 5.

As $q\to 1^{-}$, the Theorem 4 reduces to Theorem 2.

6. Conclusions

The study of geometrical implications is an integral part of research in geometric function theory. Here we have shown that a function $\aleph (p;F,G;\alpha ;z)$ which was defined analytically in [18] indeed has beautiful geometric implications.

Extension and unification of various well-known classes of functions were the main objective of this paper. We defined a new family of multivalent functions of complex order using higher order derivatives. Inclusion relations, Fekete-Szegö inequalities and subordination conditions for starlikeness of the defined function class have been established. Attempting discretization of the results, we extend the defined function class using q-derivative. All the results involving quantum calculus were just stated, as the method of proof though cumbersome but is similar to our main results.