1. Introduction
Fractional differential equations (FDEs) have gained mathematical significance in recent decades due to the growing interest in dynamics of anomalous diffusion processes in amorphous materials. They have governed significant models in many fields of applied sciences and engineering, such as viscoelastic materials, image processing, option pricing models, control theory, etc. Surveys or collections of applications can be found in [
1,
2,
3,
4,
5].
This paper is concerned with approximating the solution
to the fractional initial-value problem
where
, and
denotes the Caputo fractional derivative of order
(
). Throughout this paper, we assume without loss of generality that
.
A number of numerical methods have been proposed for solving FDEs [
6,
7,
8,
9,
10,
11]. Two common approaches have been considered by many authors. The first approach is based on a direct discretization of the fractional derivative operators in the considered FDEs [
6,
7,
12]. The second approach to solving FDEs is based on discretizing the integral in the equivalent forms [
13,
14,
15,
16]. There are also several numerical methods for FDEs, for example see [
17,
18,
19,
20].
Low-order approaches are the most frequently employed methods for FDEs, and it has been proven to be difficult to construct high-order and adaptive schemes [
13,
15,
21,
22]. In this paper, we present high-order computational schemes for solving nonlinear FDEs. The proposed schemes deal with integral forms of the FDEs and then split the fractional integral into a history term and a local term. We employ a sum of exponentials scheme (SOE) for the approximation of the history term and low-order quadrature approximations of the fractional integral. We further modify a spectral deferred correction (SDC) scheme to increase the order of the local approximation. In contrast to the methods inspired by [
13], here we use an accurate sum of exponentials method as a kernel compression scheme and a completely different deferred correction scheme as a high-order adaptive method for FDEs.
The remainder of the paper is organized as follows. In
Section 2, we provide an overview of the proposed methods.
Section 3 discusses the sum of exponentials method.
Section 4 introduces high-order time-stepping techniques for solving FDEs and discuses the relevant error analysis. Some numerical results are presented in
Section 5 before the conclusion is given in
Section 6.
2. Overview
We discuss a numerical method for the fractional initial value problem
where
may be an arbitrary real number, and where
. In (
1),
denotes the Caputo differential operator, defined by
where
is the smallest integer
. Here,
is the usual differential operator of (integer) order
n, and for
,
is the integral operator of order
in the sense of Riemann–Liouville, defined by
We assume the function
f to be such that a unique solution to (
1) exists on some interval
. The initial-value problem (
1) is known to be equivalent to the Volterra integral equation
Consider the fractional integral
Fix
and
, and let
. It is clear that
Owing to (
2) and (
3), we obtain
where
and
We call H and L the history and local parts, respectively.
We can observe that Equation (
4) can be written as a Volterra integral equation (VIE),
where
,
and
.
3. Approximation of the History Term
In this section, we describe a kernel compression scheme for the approximation of the history term. This will reduce the cost of evaluating the history term.
It is proved in [
6] that for any specified error
, we are able to find positive real numbers
and
,
, such that
where
Roughly, for fixed , the number of exponentials needed is of order if or if , where is the number of time-steps.
Approximating the kernel
in
by the sum of exponentials (SOE), we can write the history term (
5) as
where
and
Observe that each
is the solution to the IVP
To simplify the notation, we consider
to be components of a vector
; similarly,
,
, and
. Thus we recover
A stable Runge-Kutta (RK) methods may be used for approximating (
9).
4. Approximation of the History Term
Let
N be a positive integer and
T be the given time. We divide the interval
into
with step sizes
,
. Let
be the approximate solution of
,
…
.
At
, we consider (
7),
in
, where
is given. Divide the interval
into
, and let
V be the numerical approximation to
Y. Suppose that we know the approximate solutions
at
, for each
, and let
. We compute
by solving
for
, where
, and
are the weights characterizing the scheme.
4.1. Quadrature Rules on Non-Uniform Meshes
To obtain
we need to approximate the fractional integral
To do so, we use the following approach
where
,
…
is an approximation of
, where
. Notice that different choices of
lead to different schemes.
(i) By choosing
as
the fractional rectangle method is derived as
where
(ii) If
is selected as
then the fractional trapezoid method is given by
in which
and
It is proved in [
8] that for
, we have that
and for
,
4.2. The Spectral Deferred Correction Framework
Let
denote the desired time-step size. Then, (
4) can be written as
where
is given. Let
be a set of distinct points in the closed interval
, where
.
Replacing the integral in (
12) by a quadrature from
Section 4.1 yields the collocation approximation
This can be written as
where
,
and
substitutes for
. At
, the values
are defined explicitly by the formula
or implicitly through the nonlinear system
To obtain higher-order schemes, we can apply a spectral deferred correction (SDC) scheme [
23,
24,
25].
While the time is stepping from
to
, an SDC method subdivides the interval
into
p substeps
At each substep
, the method computes a provisional solution using a low-order method with initial condition
. We will refer to the provisional solution as
To improve the accuracy of the provisional solution, we perform a process of iterated corrections of the form
where
Consider again the integral formulation of the solution,
Let
be an approximate solution to (
15). Then, plugging
into (
15) yields the integral equation
Consequently, the error function can be written as
where
To compute the error
we replace
with the Lagrange interpolating polynomial
,
To approximate the error, we first use a quadrature formula with nodes at
to approximate the integral appearing in the residual term
, and then we use a fractional implicit or explicit Euler approximation to approximate the remaining integral term in (
16). This process leads to the implicit (
) or the explicit (
) time-stepping method
where
and
During the iteration process, we always use the initial conditions,
From now on, we will refer to the implicit method as IM-SDC and the explicit method as EX-SDC.
Practically, we start by using the fractional Euler’s method of order
to compute the provisional solution and then repeat the iteration (
17) followed by (
14) a total of
m times to obtain solutions with an increasingly high order of accuracy
The scheme can be rewritten under a more compact form
where
.
4.3. Order of Convergence
Suppose that the integrator used to construct the provisional solution has order
, the integrator used to compute the correction approximation at level
k has order
, and
m correction steps are taken. If we have
p groups of
N uniformly distributed nodes, then the SDC methods can attain order [
26,
27]
where
.
The convergence rate of our fully discrete time-stepping SDC method is given in the following theorem.
Theorem 1. For any sufficiently smooth function , the SDC method outlined in the previous section using distinct quadrature nodes and m correction steps converges to the exact solution with order of accuracy 5. Adaptive Implementation
Adaptive marching and accuracy control play a significant role in practical applications involving numerical schemes for solving differential equations. The schemes proposed in this paper are essentially one-step methods, making adaptive implementation relatively simple. Additionally, the schemes have a high order of convergence, which makes accuracy control much easier.
In what follows in this section, we describe details of an adaptive implementation of the SDC schemes and illustrate a number of numerical applications we have performed.
5.1. Accuracy Control
Given a fractional IVP (
1) on the interval
, an approximate solution
,
and a positive
, we would like to determine whether
The structure of the proposed SDC method provides us with a number of completely reliable conditions which can be used as stopping criteria:
We verify that
, where the vector
(see (
17)),
is obtained during the last correction.
Once has been computed; the value of the approximate solution at an arbitrary time can be obtained by the Lagrange interpolant. We apply the interpolation process to both and and demand that the difference be less than . This indicates that both the correction process and the discretization have converged to precision.
We can also control the step-size
h. We start with an arbitrary step-size
h and attempt to apply the SDC scheme. The step-size is halved and the procedure is repeated if the obtained precision is insufficient (per criteria (
18) and (
19)). However, the step-size is unchanged if the precision is acceptable and doubled if the precision is acceptable two steps in a row.
5.2. Computational Details and Numerical Tests
In what follows, we present some numerical results of our numerical method applied to nonlinear fractional differential equations.
We solve all test problems using the proposed SDC methods: implicit SDC (IM-SDC) or explicit SDC (EX-SDC). While using the implicit scheme, we use Newton’s method to solve the resulting system of nonlinear equations. Moreover, if the exact solution to the given problem is not known, we use reference solutions computed by the IM-SDC with error tolerance instead.
As a first example, we study the nonlinear fractional differential equation
The exact solution is .
We apply the IM-SDC method to (
20) with
,
,
,
, and initial step-size
. When
, the local order of the method is
. When we perform correction iterations, i.e.,
, we measure a high order of convergence. For example, with
, we obtain order three which is in agreement with the expected theoretical results. We present our numerical results in
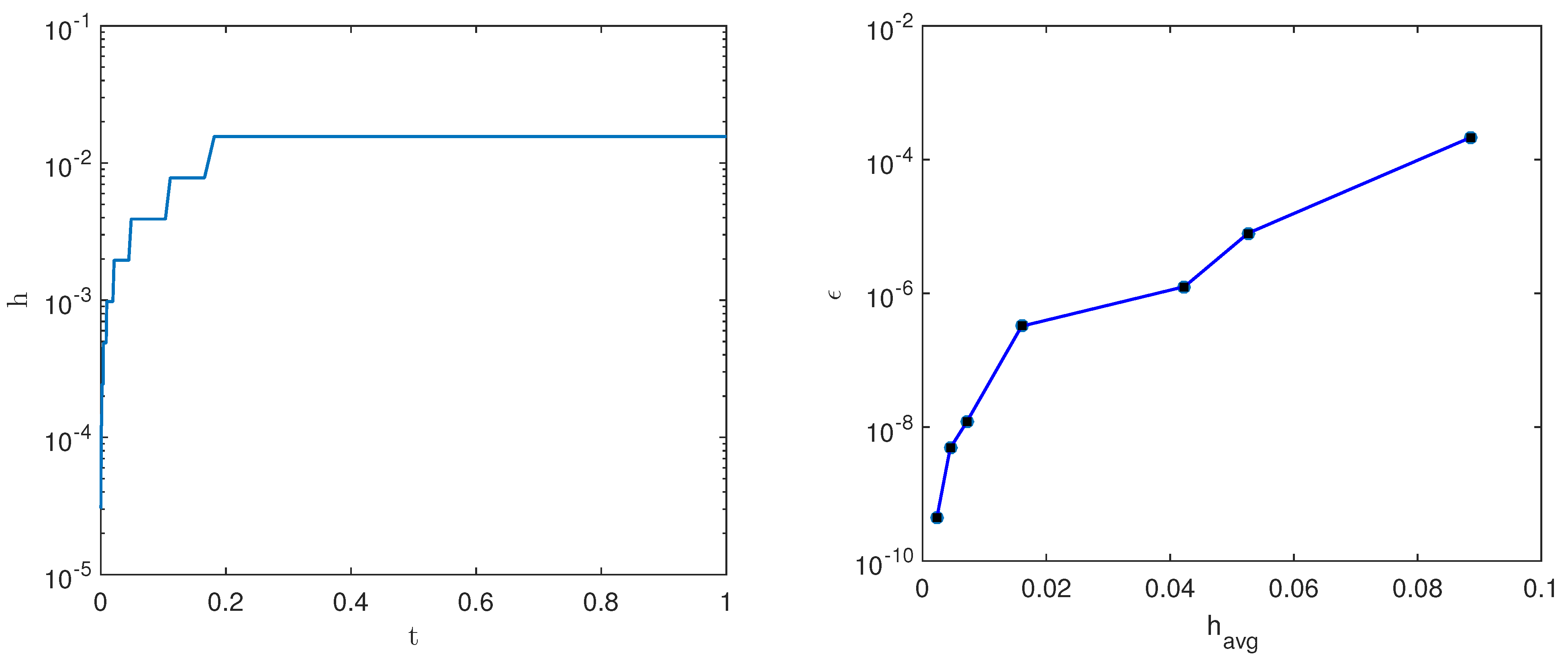
Figure 1. The results show that high accuracy can be obtained using few correction iterations after applying high-order SDC methods.
We also studied the fractional-order Chua’s circuit system [
28]
where
and
are constant parameters, and
is given by
In this test,
,
,
,
,
,
,
, and
. The approximations
are compared with a reference solution
obtained with
.
Figure 2 shows the reference solutions
and the curve
in the
plane.
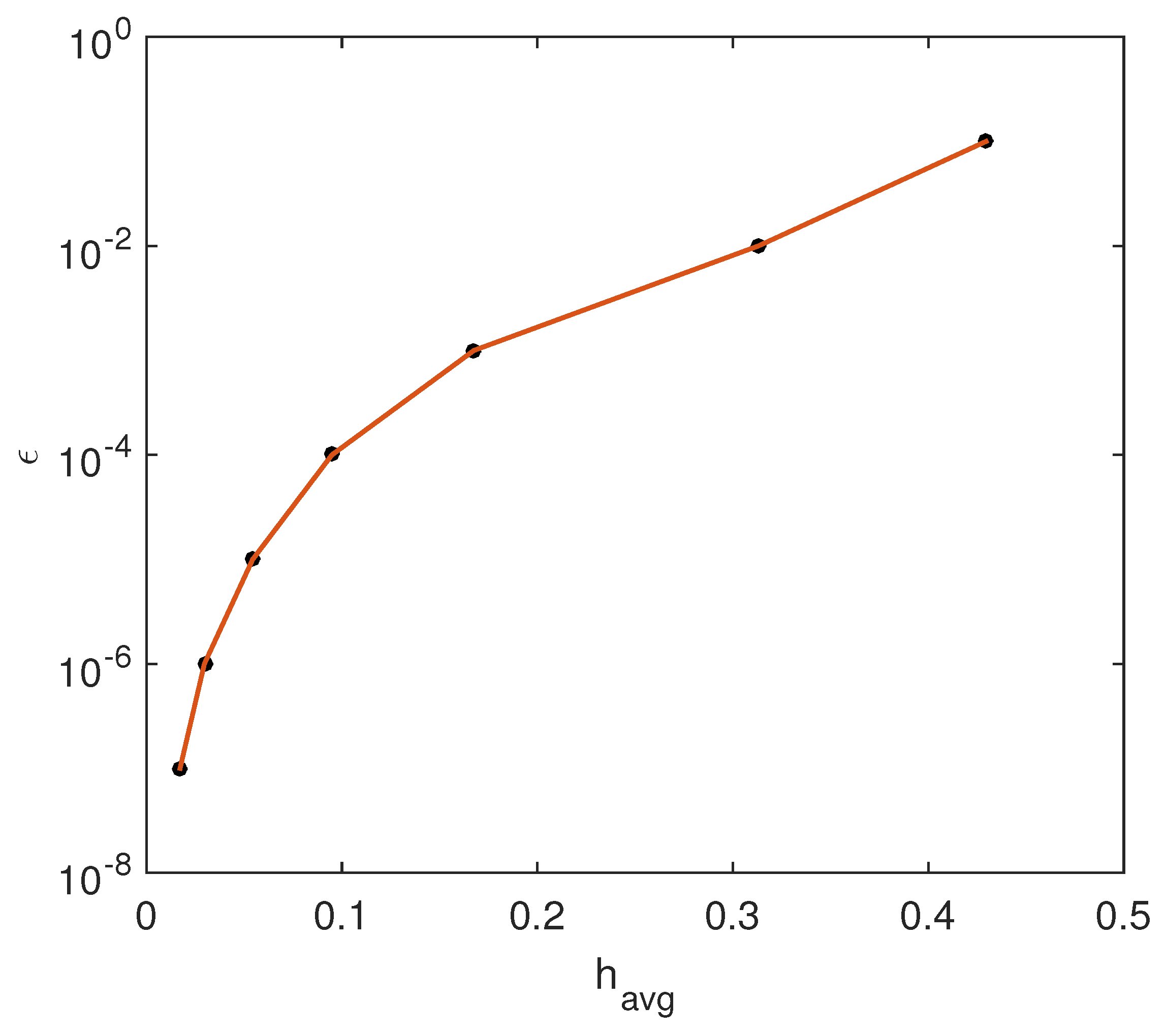
In
Figure 3, the accuracy is plotted as a function of the average time-step
.
6. Conclusions
We proposed high-order adaptive time-stepping schemes for nonlinear FDEs by using suitable kernel compression and SDC methods. We discussed the accuracy and local convergence of the proposed schemes. We also discussed the extension of these schemes to construct other higher-order methods for nonlinear fractional initial-value problems.
We provided numerical examples to verify the efficiency of the proposed schemes, which shows that applying suitable correction iterations can increase the accuracy in a significant way.
In future work, we will focus on proposing high-order schemes for the numerical solutions of fractional boundary value problems and time-fractional diffusion equations.
Author Contributions
Conceptualization, O.A. and F.A.; methodology, F.A., S.A.-S. and E.R.; software, F.A.; validation, S.A.-S., O.A. and E.R.; formal analysis, F.A.; investigation, S.A.-S. and O.A.; resources, E.R.; data curation, E.R.; writing—original draft preparation, F.A., O.A., E.R. and S.A.-S.; writing—review and editing, S.A.-S. and O.A.; supervision, E.R.; project administration, F.A.; funding acquisition, F.A. All authors have read and agreed to the published version of the manuscript.
Funding
Fadi Awawdeh work was supported by The Hashemite University through project 12/2021.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
Not applicable.
Acknowledgments
The authors are very grateful to the anonymous referees for their careful reading and valuable suggestions.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Dastgerdi, M.; Bastani, A. Solving Parametric Fractional Differential Equations Arising from the Rough Heston Model Using Quasi-Linearization and Spectral Collocation. SIAM J. Financ. Math. 2020, 11, 1063–1097. [Google Scholar] [CrossRef]
- Li, C.; Zeng, F. Numerical Methods for Fractional Calculus. In Chapman & Hall/CRC Numerical Analysis and Scientific Computing; CRC Press: Boca Raton, FL, USA, 2015. [Google Scholar]
- Metzler, R.; Klafter, J. The restaurant at the end of the random walk: Recent developments in the description of anomalous transport by fractional dynamics. J. Phys. A 2004, 37, 161–208. [Google Scholar] [CrossRef]
- Perdikaris, P.; Karniadakis, G.E. Fractional-order viscoelasticity in one-dimensional blood flow models. Ann. Biomed. Eng. 2014, 42, 1012–1023. [Google Scholar] [CrossRef]
- Wang, W.; Chen, X.; Ding, D.; Lei, S.L. Circulant preconditioning technique for barrier options pricing under fractional diffusion models. Int. J. Comput. Math. 2015, 92, 2596–2614. [Google Scholar] [CrossRef]
- Gao, G.H.; Sun, Z.Z.; Zhang, H.W. A new fractional numerical differentiation formula to approximate the Caputo fractional derivative and its applications. J. Comput. Phys. 2014, 259, 33–50. [Google Scholar] [CrossRef]
- Jiang, S.; Zhang, J.; Zhang, Q.; Zhang, Z. Fast evaluation of the Caputo fractional derivative and its applications to fractional diffusion equations. Commun. Comput. Phys. 2017, 21, 650–678. [Google Scholar] [CrossRef]
- Li, C.; Yi, Q.; Chen, A. Finite difference methods with non-uniform meshes for nonlinear fractional differential equations. J. Comput. Phys. 2016, 316, 614–631. [Google Scholar] [CrossRef]
- Lv, C.W.; Xu, C.J. Error analysis of a high order method for time-fractional diffusion equations. SIAM J. Sci. Comput. 2016, 38, A2699–A2724. [Google Scholar] [CrossRef]
- Zayernouri, M.; Karniadakis, G.E. Exponentially accurate spectral and spectral element methods for fractional ODEs. J. Comput. Phys. 2014, 257, 460–480. [Google Scholar] [CrossRef]
- Zeng, F.; Turner, I.; Burrage, K. A Stable Fast Time-Stepping Method for Fractional Integral and Derivative Operators. J. Sci. Comput. 2018, 77, 283–307. [Google Scholar] [CrossRef]
- Yan, Y.G.; Sun, Z.Z.; Zhang, J.W. Fast evaluation of the Caputo fractional derivative and its applications to fractional diffusion equations: A second-order scheme. Commun. Comput. Phys. 2017, 22, 1028–1048. [Google Scholar] [CrossRef]
- Baffet, D.; Hesthaven, J.S. High-order accurate adaptive kernel compression time-stepping schemes for fractional differential equations. J. Sci. Comput. 2019, 72, 1169–1195. [Google Scholar] [CrossRef]
- Baffet, D.; Hesthaven, J.S. A kernel compression scheme for fractional differential equations. SIAM J. Numer. Anal. 2017, 55, 496–520. [Google Scholar] [CrossRef]
- Cao, W.; Zhang, Z.; Karniadakis, G.E. Time-splitting schemes for fractional differential equations I: Smooth solutions. SIAM J. Sci. Comput. 2015, 37, A1752–A1776. [Google Scholar] [CrossRef]
- Li, J.R. A fast time stepping method for evaluating fractional integrals. SIAM J. Sci. Comput. 2010, 31, 4696–4714. [Google Scholar] [CrossRef]
- Jin, B.; Lazarov, R.; Pasciak, J.; Zhou, Z. Error analysis of a finite element method for the space-fractional parabolic equation. SIAM J. Numer. Anal. 2014, 52, 2272–2294. [Google Scholar] [CrossRef]
- Tian, W.Y.; Deng, W.; Wu, Y. Polynomial spectral collocation method for space fractional advection-diffusion equation. Numer. Methods Partial. Differ. Equ. 2014, 30, 514–535. [Google Scholar] [CrossRef]
- Podlubny, I.; Chechkin, A.; Skovranek, T.; Chen, Y.; Vinagre Jara, B.M. Matrix approach to discrete fractional calculus. II. Partial fractional differential equations. J. Comput. Phys. 2009, 228, 3137–3153. [Google Scholar] [CrossRef]
- Stynes, M.; O’Riordan, E.; Gracia, J. Error analysis of a finite difference method on graded meshes for a time-fractional diffusion equation. SIAM J. Numer. Anal. 2017, 55, 1057–1079. [Google Scholar] [CrossRef]
- Rauh, A.; Jaulin, L. Novel Techniques for a Verified Simulation of Fractional-Order Differential Equations. Fractal Fract. 2021, 5, 17. [Google Scholar] [CrossRef]
- Jin, S.; Xie, J.; Qu, J.; Chen, Y. A Numerical Method for Simulating Viscoelastic Plates Based on Fractional Order Model. Fractal Fract. 2022, 6, 150. [Google Scholar] [CrossRef]
- Bohmer, K.; Stetter, H.J. Defect Correction Methods Theory and Applications; Springer: New York, NY, USA, 1984. [Google Scholar]
- Buvoli, T. A Class of Exponential Integrators Based on Spectral Deferred Correction. SIAM J. Sci. Comput. 2020, 42, A1–A27. [Google Scholar] [CrossRef]
- Dutt, A.; Greengard, L.; Rokhlin, V. Spectral deferred correction methods for ordinary differential equations. BIT 2000, 40, 241–266. [Google Scholar] [CrossRef]
- Causley, M.F.; Seal, D.C. On the convergence of spectral deferred correction methods. Commun. Appl. Math. Comput. Sci. 2019, 14, 33–64. [Google Scholar] [CrossRef]
- Ong, B.W.; Spiteri, R.J. Deferred Correction Methods for Ordinary Differential Equations. J. Sci. Comput. 2020, 38, 60–83. [Google Scholar] [CrossRef]
- Cafagna, D.; Grassi, G. Fractional-Oder Chua’s Circuit: Time-Domain Analysis, Bifurcation, Chaotic Behavior and Test for Chaos. Int. J. Bifurcat Chaos 2008, 18, 615–639. [Google Scholar] [CrossRef]
| Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).