Theoretical and Experimental Designs of the Planetary Boundary Layer Dynamics through a Multifractal Theory of Motion
Abstract
1. General Considerations: From Differentiability to Non-Differentiability in Atmospheric Process Dynamics
2. Theoretical Design: Non-Differentiability Calibrated on PBL Dynamics in the Form of the Multifractal Hydrodynamic Model
- I.
- The existence of a multifractal specific force implies that all PBL structure units must be considered through a multifractal medium;
- II.
- This medium can be considered a multifractal fluid whose dynamics are characterized by the hydrodynamic model presented previously;
- III.
- Since the velocity field, , is absent from the multifractal states density conservation laws, it induces the possibility of non-manifest PBL dynamics, meaning that it facilitates the transmission of multifractal specific momentum and multifractal energy;
- IV.
- All potential issues regarding reversibility and existence of the eigenstates are solved by the conservation of multifractal energy and multifractal momentum;
- V.
- When using the tensor:
3. PBL Dynamics Mimed as a Multifractal Atmospheric Tunnel Effect
- I.
- The PBL, as a complex system both in a structural and functional perspective, can be assimilated with a mathematical object of multifractal type;
- II.
- PBL dynamics can be described through the scale relativity theory in the form of multifractal hydrodynamic equations;
- III.
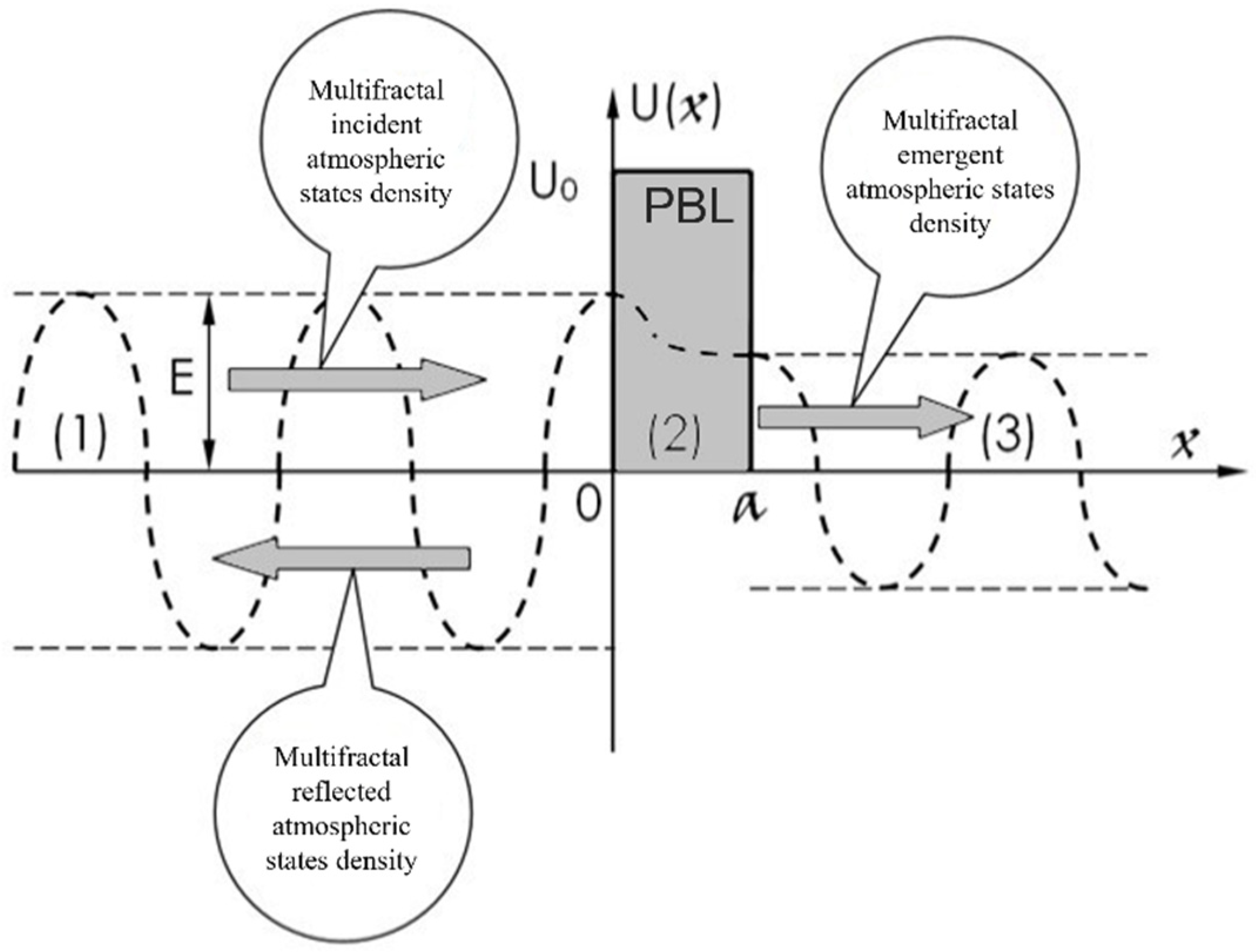
- The PBL works as a multifractal atmospheric tunnel effect described through the external scalar potential (see Figure 1):
- (1).
- the multifractal atmospheric incidence zone;
- (2).
- the multifractal atmospheric barrier;
- (3).
- the multifractal atmospheric emergence zone.
- I.
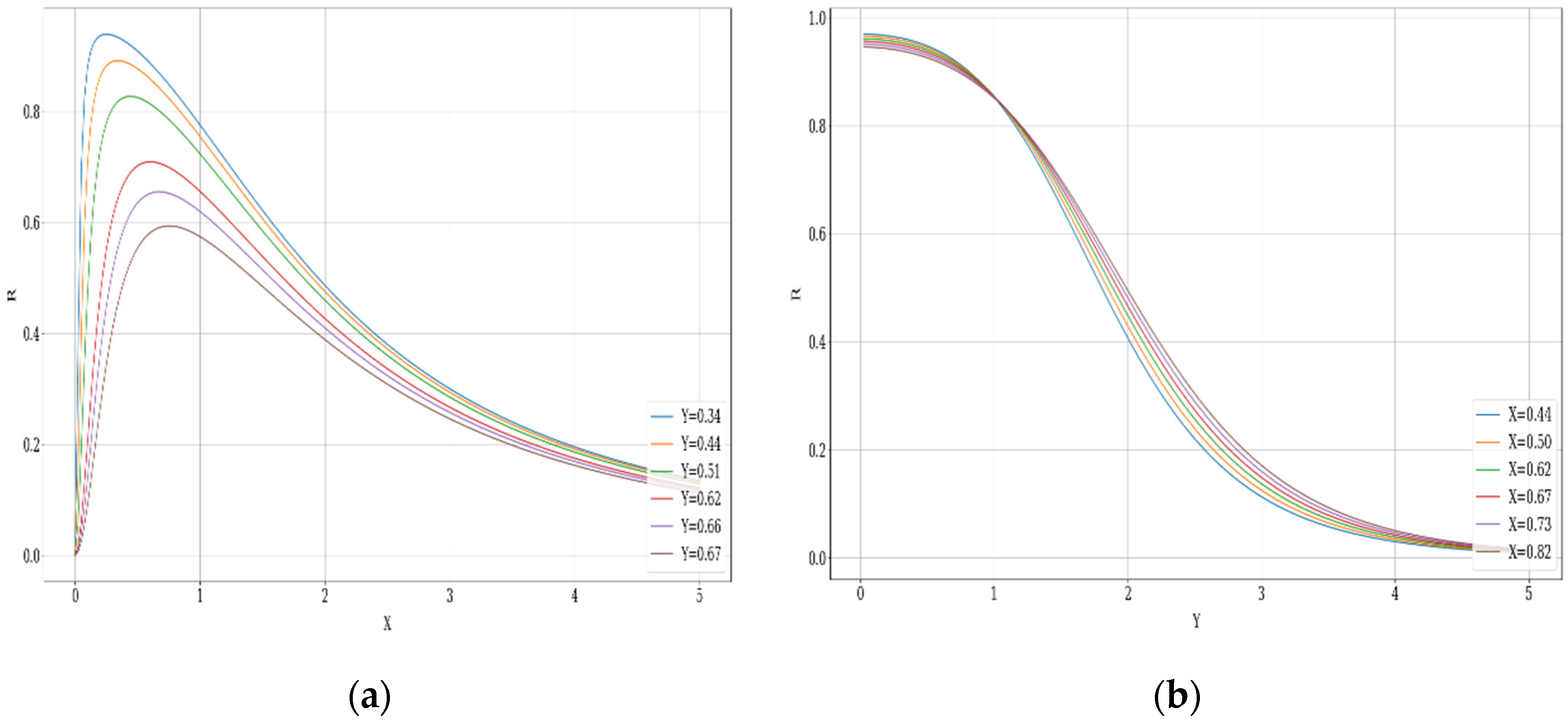
- corresponds to the multifractal incident atmospheric states density (from ) in the multifractal zone (1) and to the multifractal emergent atmospheric states density (to ) in the multifractal zone (3);
- II.
- corresponds to the multifractal reflected atmospheric states density, which exists only in the multifractal zone (1), passing from to since in the multifractal zone (3), the external scalar potential is uniformly null.
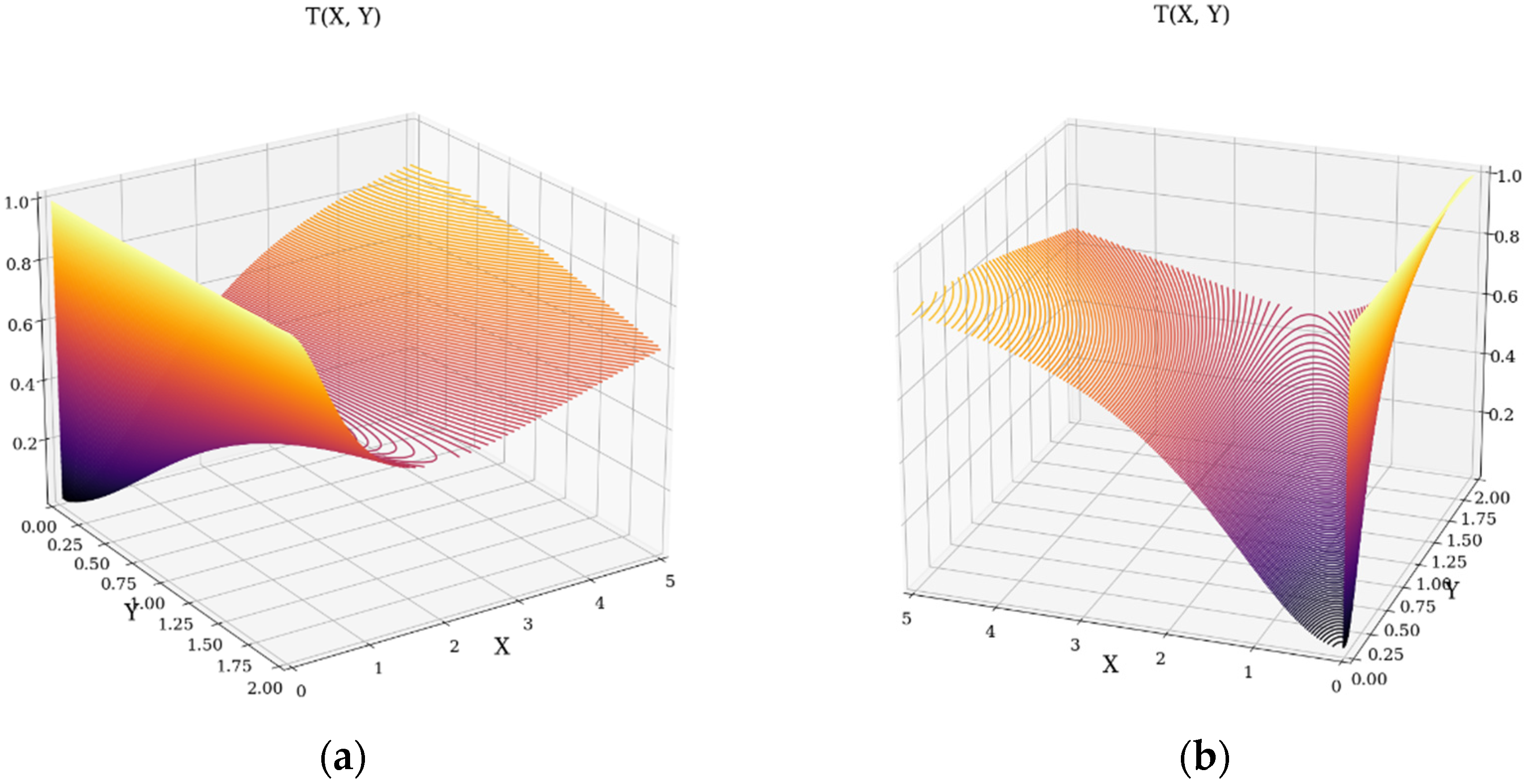
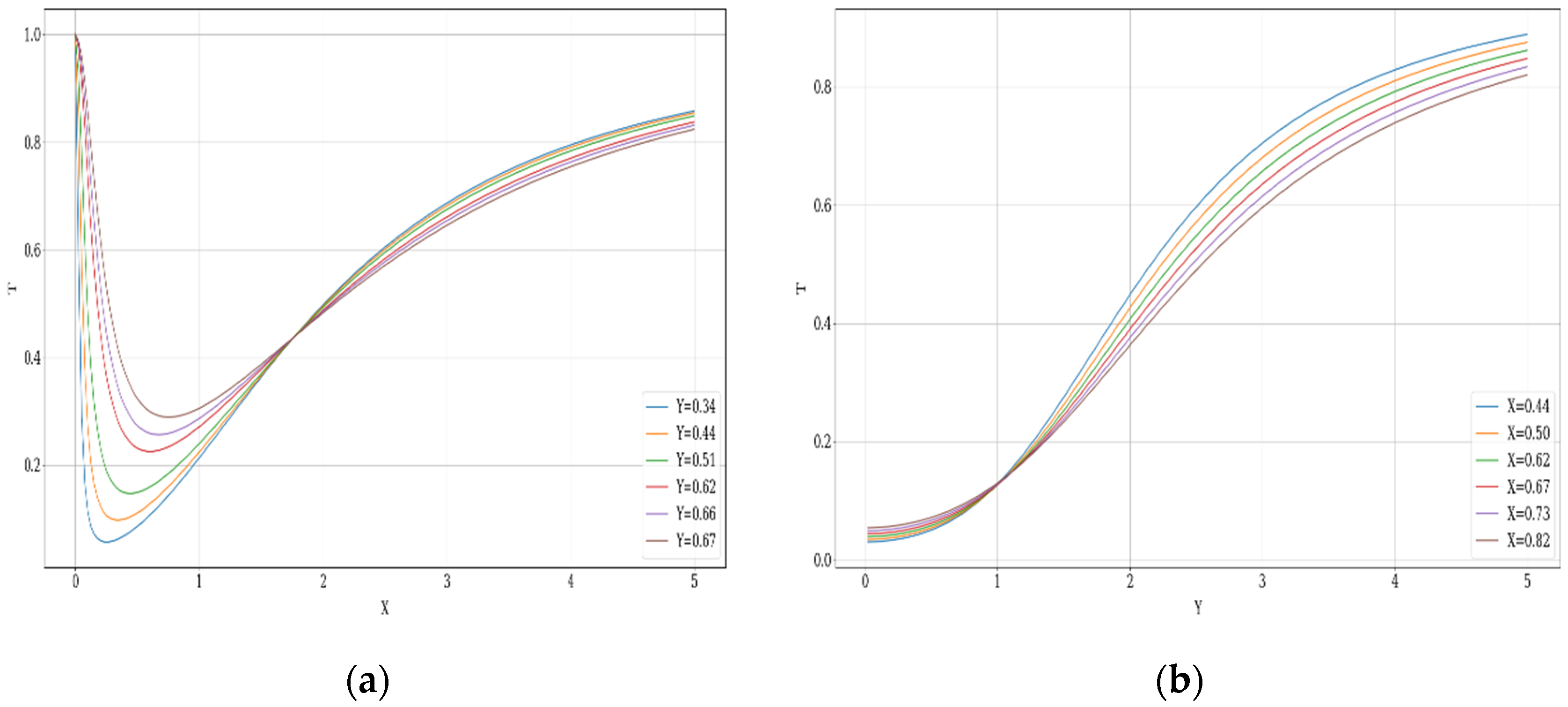
- The multifractal atmospheric current density of the multifractal atmospheric incident states density in zone (1):
- The multifractal atmospheric current density of the multifractal atmospheric emergent states density in zone (3):
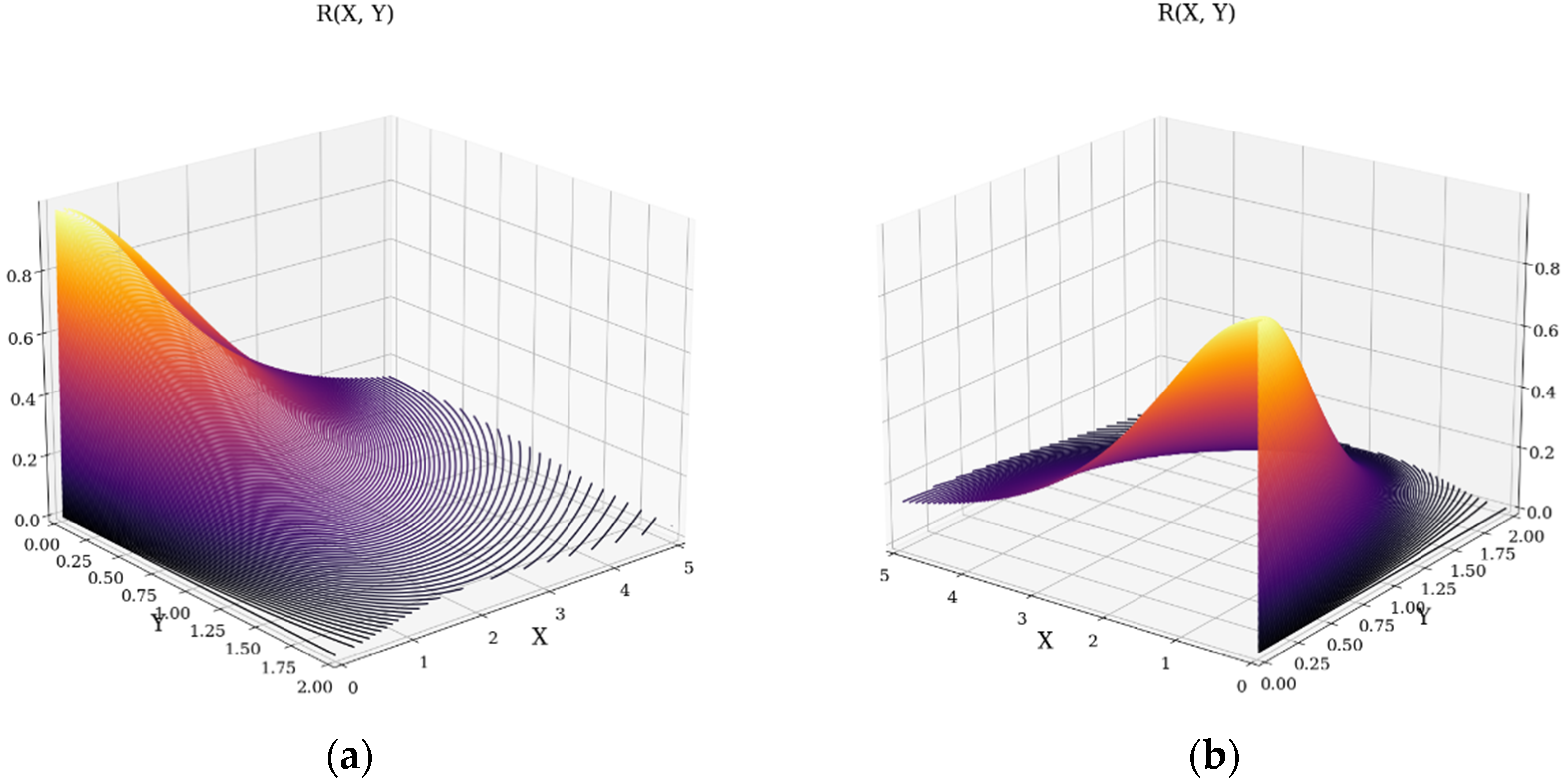
- The multifractal atmospheric current density of the multifractal reflected atmospheric states density:
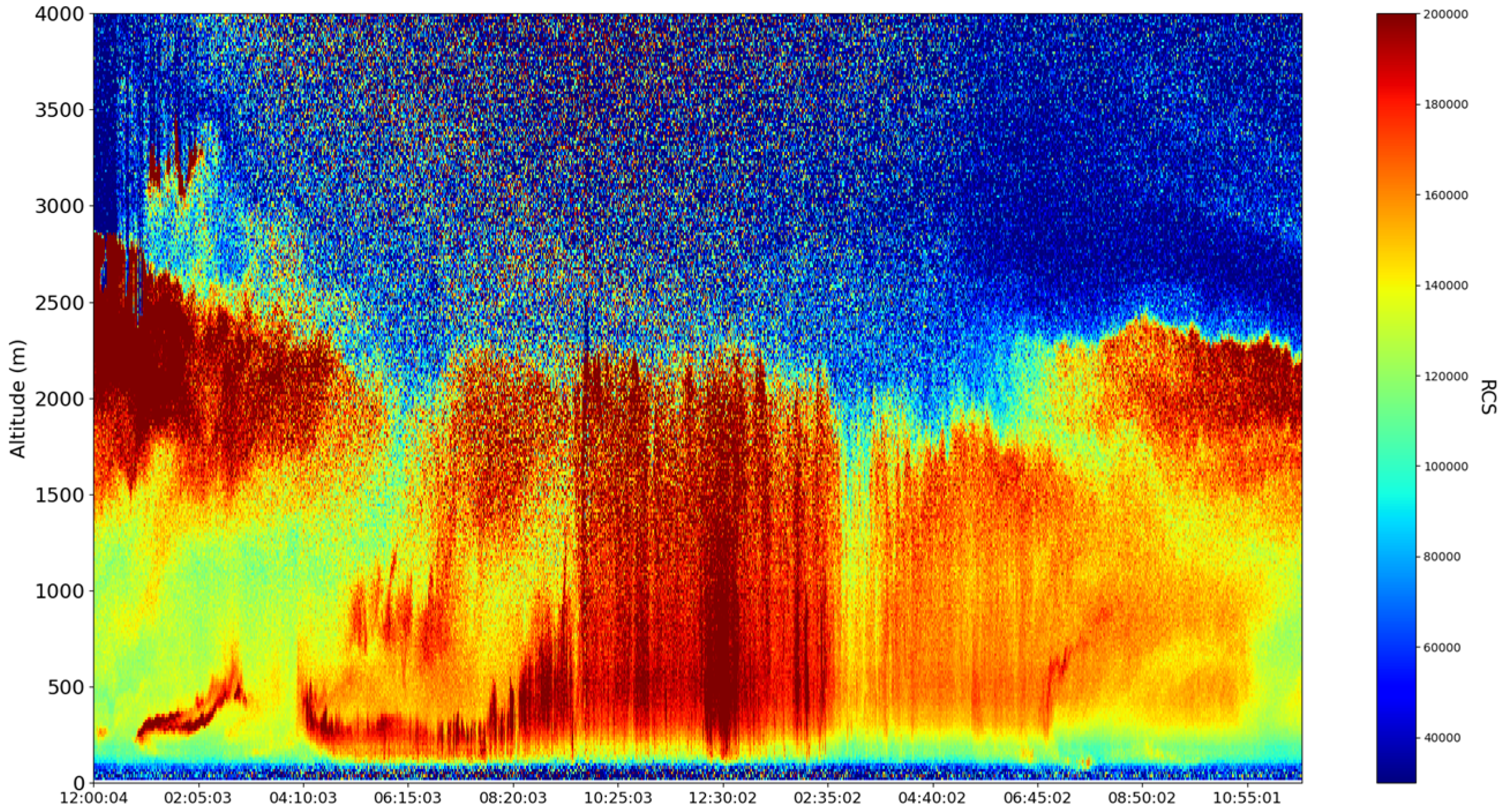
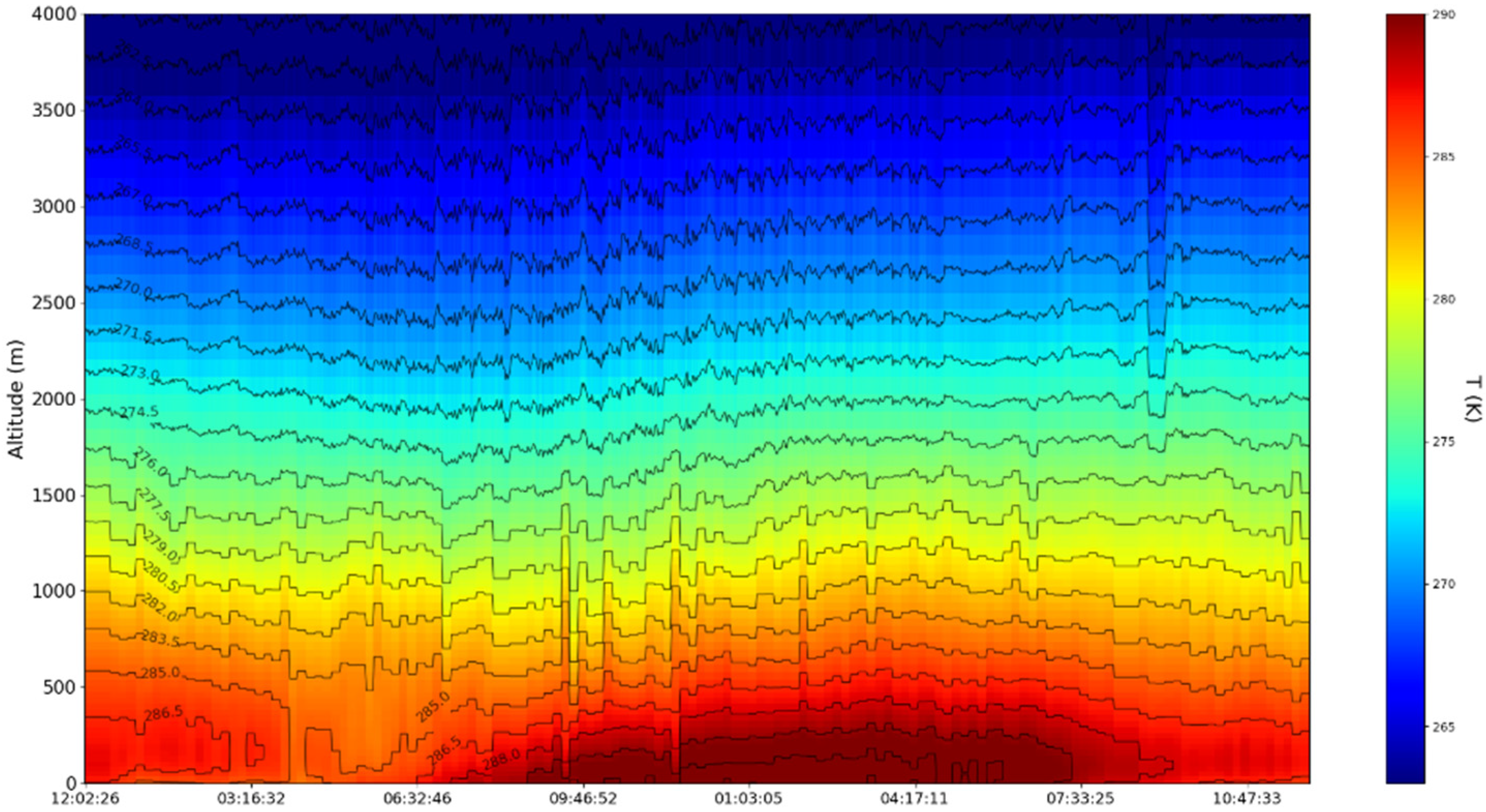
4. Experimental Design
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Roland, S. Practical Meteorology: An Algebra-Based Survey of Atmospheric Science; The University of British Columbia: Vancouver, BC, Canada, 2015. [Google Scholar]
- Badii, R.; Politi, A. Complexity: Hierarchical Structures and Scaling in Physics; Cambridge University Press: Cambridge, UK, 1997. [Google Scholar]
- Mitchell, M. Complexity: A Guided Tour; Oxford University Press: Oxford, UK, 2009. [Google Scholar]
- Notalle, L. Fractal Space-Time and Microphysics; World Scientific Publisher: Singapore, 1993. [Google Scholar]
- Merches, I.; Agop, M. Differentiability and Fractality in Dynamics of Physical Systems; World Scientific Publisher: Singapore, 2015. [Google Scholar]
- Nottale, L. Scale Relativity and Fractal Space-Time: A New Approach to Unifying Relativity and Quantum Mechanics; Imperial College Press: London, UK, 2011. [Google Scholar]
- Agop, M.; Buzea, C.; Vasincu, D.; Timofte, D. Dynamics of Biostructures on a Fractal/Multifractal Space-Time Manifold. In Progress in Relativity; IntechOpen: London, UK, 2019; p. 117. [Google Scholar]
- Liu, L.; Hu, F.; Huang, S. A Multifractal Random-Walk Description of Atmospheric Turbulence: Small-Scale Multiscaling, Long-Tail Distribution, and Intermittency. Bound. Layer Meteorol. 2019, 172, 351–370. [Google Scholar] [CrossRef]
- Kalamaras, N.; Tzanis, C.G.; Deligiorgi, D.; Philippopoulos, K.; Koutsogiannis, I. Distribution of Air Temperature Multifractal Characteristics Over Greece. Atmosphere 2019, 10, 45. [Google Scholar] [CrossRef]
- Plocoste, T.; Carmona-Cabezas, R.; Jiménez-Hornero, F.J.; de Ravé, E.G. Background PM10 atmosphere: In the seek of a multifractal characterization using complex networks. J. Aerosol Sci. 2021, 155, 105777. [Google Scholar] [CrossRef]
- Ruelle, D.; Takens, F. On the nature of turbulence. Les Rencontres Phys. Mathématiciens Strasbg. RCP25 1971, 12, 1–44. [Google Scholar]
- Takens, F. Detecting Strange Attractors in Turbulence. In Dynamical Systems and Turbulence. Warwick 1980; Springer: Berlin/Heidelberg, Germany, 1981; pp. 366–381. [Google Scholar]
- Nottale, L. Scale relativity and fractal space-time: Applications to quantum physics, cosmology and chaotic systems. Chaos Solitons Fractals 1996, 7, 877–938. [Google Scholar] [CrossRef]
- Nottale, L.; Auffray, C. Scale relativity theory and integrative systems biology: 2 Macroscopic quantum-type mechanics. Prog. Biophys. Mol. Biol. 2008, 97, 115–157. [Google Scholar] [CrossRef] [PubMed]
- Chavanis, P.-H. Derivation of a generalized Schrödinger equation from the theory of scale relativity. Eur. Phys. J. Plus 2017, 132, 286. [Google Scholar] [CrossRef]
- Roșu, I.-A.; Nica, D.-C.; Cazacu, M.M.; Agop, M. Cellular Self-Structuring and Turbulent Behaviors in Atmospheric Laminar Channels. Front. Earth Sci. 2022, 9, 801020. [Google Scholar] [CrossRef]
- Baker, G.L.; Gollub, J.P. Chaotic Dynamics: An Introduction; Cambridge University Press: New York, NY, USA, 1996. [Google Scholar]
- Ott, E. Chaos in Dynamical Systems; Cambridge University Press, University of Maryland: College Park, MD, USA, 2002; pp. 160–182. [Google Scholar] [CrossRef]
- Van den Berg, J.C. Wavelets in Physics; Cambridge University Press: Cambridge, UK, 2004; pp. 143–147. [Google Scholar]
- Cristescu, C.P. Nonlinear Dynamics and Chaos Theoretical Fundaments and Applications; Romanian Academy Publishing House: Bucharest, Romania, 2008. [Google Scholar]
- Agop, M.; Ochiuz, L.; Tesloianu, D.; Buzea, C.; Irimiciuc, S. Non-Differentiable Dynamics in Complex Systems; Nova Science Publishers: New York, NY, USA, 2018. [Google Scholar]
- Mandelbrot, B. The Fractal Geometry of Nature; W.H. Freeman Publishers: New York, NY, USA, 1982. [Google Scholar]
- Barnsley, M.F. Fractals Everywhere; Morgan Kaufmann Publisher: San Francisco, CA, USA, 1993. [Google Scholar]
- Bujoreanu, C.; Irimiciuc, Ş.; Benchea, M.; Nedeff, F.; Agop, M. A fractal approach of the sound absorption behaviour of materials. Theoretical and experimental aspects. Int. J. Non-Linear Mech. 2018, 103, 128–137. [Google Scholar] [CrossRef]
- Flamant, C.; Pelon, J.; Flamant, P.H.; Durand, P. Lidar determination of the entrainment zone thickness at the top of the unstable marine atmospheric boundary layer. Bound. Layer Meteorol. 1997, 83, 247–284. [Google Scholar] [CrossRef]
- Haeffelin, M.; Angelini, F.; Morille, Y.; Martucci, G.; Frey, S.; Gobbi, G.P.; Lolli, S.; O’Dowd, C.D.; Sauvage, L.; Xueref-Rémy, I.; et al. Evaluation of Mixing-Height Retrievals from Automatic Profiling Lidars and Ceilometers in View of Future Integrated Networks in Europe. Bound. Layer Meteorol. 2011, 143, 49–75. [Google Scholar] [CrossRef]
- Rosu, I.-A.; Cazacu, M.-M.; Prelipceanu, O.S.; Agop, M. A Turbulence-Oriented Approach to Retrieve Various Atmospheric Parameters Using Advanced Lidar Data Processing Techniques. Atmosphere 2019, 10, 38. [Google Scholar] [CrossRef]
- Orlanski, I.; Ross, B.B.; Polinsky, L.J. Diurnal Variation of the Planetary Boundary Layer in a Mesoscale Model. J. Atmospheric Sci. 1974, 31, 965–989. [Google Scholar] [CrossRef]
- Hu, X.-M.; Nielsen-Gammon, J.; Zhang, F. Evaluation of Three Planetary Boundary Layer Schemes in the WRF Model. J. Appl. Meteorol. Clim. 2010, 49, 1831–1844. [Google Scholar] [CrossRef]
- Seidel, D.J.; Ao, C.; Li, K. Estimating climatological planetary boundary layer heights from radiosonde observations: Comparison of methods and uncertainty analysis. J. Geophys. Res. Atmos. 2010, 115, 1–15. [Google Scholar] [CrossRef]
- Wyngaard, J.C. Structure of the PBL. In Lectures on Air Pollution Modeling; American Meteorological Society: Boston, MA, USA, 1988; pp. 9–61. [Google Scholar]


Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Cazacu, M.M.; Roșu, I.-A.; Bibire, L.; Vasincu, D.; Rotundu, A.M.; Agop, M. Theoretical and Experimental Designs of the Planetary Boundary Layer Dynamics through a Multifractal Theory of Motion. Fractal Fract. 2022, 6, 747. https://doi.org/10.3390/fractalfract6120747
Cazacu MM, Roșu I-A, Bibire L, Vasincu D, Rotundu AM, Agop M. Theoretical and Experimental Designs of the Planetary Boundary Layer Dynamics through a Multifractal Theory of Motion. Fractal and Fractional. 2022; 6(12):747. https://doi.org/10.3390/fractalfract6120747
Chicago/Turabian StyleCazacu, Marius Mihai, Iulian-Alin Roșu, Luminița Bibire, Decebal Vasincu, Ana Maria Rotundu, and Maricel Agop. 2022. "Theoretical and Experimental Designs of the Planetary Boundary Layer Dynamics through a Multifractal Theory of Motion" Fractal and Fractional 6, no. 12: 747. https://doi.org/10.3390/fractalfract6120747
APA StyleCazacu, M. M., Roșu, I.-A., Bibire, L., Vasincu, D., Rotundu, A. M., & Agop, M. (2022). Theoretical and Experimental Designs of the Planetary Boundary Layer Dynamics through a Multifractal Theory of Motion. Fractal and Fractional, 6(12), 747. https://doi.org/10.3390/fractalfract6120747








